맨위로가기

감마 분포

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

감마 분포는 확률 밀도 함수를 사용하여 정의되는 연속 확률 분포로, 형상 모수 k와 척도 모수 θ를 사용하거나, 형상 모수 α와 역척도 모수 λ를 사용하여 나타낼 수 있다. 감마 분포는 지수 분포, 얼랑 분포, 카이제곱 분포 등을 포함하며, 확률변수의 합, 스케일링, 지수족, 정보 엔트로피, 쿨백-라이블러 발산 등 다양한 성질을 갖는다. 통계적 추론, 최대 가능도 추정, 베이즈 추론 등 다양한 통계적 방법으로 분석되며, 대기 시간, 보험 청구 규모, 강우량, 암 발생률 모델링 등 다양한 분야에 응용된다. 또한, 난수 생성에도 사용된다.

더 읽어볼만한 페이지

  • 생존분석 - 로그순위법
    로그순위법은 생존 분석에서 두 그룹 간 생존 곡선을 비교하는 통계적 방법으로, 임상 시험과 역학 연구 등에서 치료법이나 요인이 생존 기간에 미치는 영향을 평가하는 데 활용된다.
  • 생존분석 - 베이불 분포
    베이불 분포는 고장률이 시간의 거듭제곱에 비례하는 확률 분포로, 모양 모수와 척도 모수를 사용하여 정의되며, 재료 과학, 신뢰성 공학 등 다양한 분야에서 활용된다.
  • 감마 함수 및 관련 함수 - 불완전 감마 함수
    불완전 감마 함수는 감마 함수의 적분 구간을 나누어 정의되며 상부 불완전 감마 함수와 하부 불완전 감마 함수로 나뉘고, 확률론, 통계학, 물리학 등 다양한 분야에서 응용되는 함수이다.
  • 감마 함수 및 관련 함수 - 베타 함수
    베타 함수는 실수부가 0보다 큰 복소수 x, y에 대해 정의되는 특수 함수로, 감마 함수와 함께 오일러 적분으로도 불리며 이항 계수의 일반화로 여겨지고, 대칭성을 가지며 감마 함수와 밀접한 관계를 갖고, 다양한 분야에서 응용되고 불완전 베타 함수 등으로 일반화된다.
  • 연속분포 - 로그 정규 분포
    로그 정규 분포는 확률 변수 X의 로그가 정규 분포를 따르며, 양의 실수 값을 갖고 평균 μ와 표준 편차 σ를 매개변수로 갖는 확률 분포이다.
  • 연속분포 - 연속균등분포
    특정 구간 내 모든 값이 동일한 확률을 갖는 연속 균등 분포는 통계학, 금융, 물리 등에서 활용되며 난수 생성과 표본 추출에 유용하다.
감마 분포
분포 정보
종류밀도 분포
매개변수
모양 모수k > 0
척도 모수θ > 0
비율 모수λ = 1/θ > 0
지지 구간
범위x ∈ [0, ∞)
함수
확률 밀도 함수x^(k-1) * (exp(-x/θ) / (Γ(k) * θ^k)) = (λ^k / Γ(k)) * x^(k-1) * exp(-λx)
누적 분포 함수γ(k, x/θ) / Γ(k) = γ(k, λx) / Γ(k)
통계적 속성
평균kθ = k/λ
중앙값간단한 닫힌 형태 없음
최빈값(k-1)θ = (k-1)/λ, k ≥ 1일 때
분산kθ² = k/λ²
왜도2/√k

2. 정의

감마 분포는 감마 함수를 사용하여 정의되는 확률 분포이다. 감마 분포의 확률 밀도 함수는 다음과 같이 표현된다.

: f(x;k,\theta) = x^{k-1} \frac{e^{-x/\theta}}{\theta^k \, \Gamma(k)}

\ \mathrm{for}\ x > 0 \,\!

여기서 k (> 0)는 형상모수이고, \theta (> 0)는 척도모수이다.

베이즈 통계학에서는 모양 모수 \alpha와 역 스케일 모수 \lambda = 1/\theta (비율 모수)를 사용한 매개변수화를 사용하기도 한다. 이 경우 감마 분포는 지수 분포 또는 푸아송 분포의 \lambda와 같은 역 스케일(비율) 매개변수에 대한 켤레 사전 분포로 사용된다.[7]

:

f(x;\alpha,\lambda) = \frac{ x^{\alpha-1} e^{-\lambda x} \lambda^\alpha}{\Gamma(\alpha)} \quad \text{ for } x > 0 \quad \alpha, \lambda > 0,



만약 k가 양의 정수이면, 이 분포는 얼랑 분포를 나타낸다. 즉, 각 \theta의 평균을 갖는 k개의 독립적인 지수 분포 확률 변수의 합이다.

감마 분포의 누적 분포 함수는 다음과 같이 나타낼 수 있다.

:F(x)=\int_0^x f(u)\,du=\frac{\gamma(k, x/\theta )}{\Gamma (k)} =\frac{\gamma (k, \lambda x)}{\Gamma (k)}

여기서 \gamma는 불완전 감마 함수이다.

2. 1. 확률 밀도 함수

감마 분포의 확률 밀도 함수는 형상모수 k와 척도모수 θ를 사용하여 다음과 같이 표현된다.

: f(x;k,\theta) = x^{k-1} \frac{e^{-x/\theta}}{\theta^k \, \Gamma(k)}

\ \mathrm{for}\ x > 0 \,\!

여기서 k (> 0)는 형상모수이고, θ (> 0)는 척도모수이다.

또는, 모양 모수 α와 역 스케일 모수 λ = 1/θ (비율 모수라고 한다)를 사용하여 다음과 같이 표현할 수도 있다.

:

f(x;\alpha,\lambda) = \frac{ x^{\alpha-1} e^{-\lambda x} \lambda^\alpha}{\Gamma(\alpha)} \quad \text{ for } x > 0 \quad \alpha, \lambda > 0,



여기서 \Gamma(\alpha)는 감마 함수이다. 모든 양의 정수에 대해 \Gamma(\alpha)=(\alpha-1)!이다.

2. 2. 누적 분포 함수

누적 분포 함수는 정규화된 감마 함수로 다음과 같이 표현된다.[8]

: F(x;\alpha,\theta) = \int_0^x f(u;\alpha,\theta)\,du = \frac{\gamma\left(\alpha, \frac{x}{\theta}\right)}{\Gamma(\alpha)},

여기서 \gamma\left(\alpha, \frac{x}{\theta}\right)는 하한 불완전 감마 함수이다.

\alpha가 양의 정수인 경우(즉, 분포가 얼랑 분포인 경우) 누적 분포 함수는 다음과 같은 급수 전개를 갖는다.[8]

:F(x;\alpha,\theta) = 1-\sum_{i=0}^{\alpha-1} \frac{1}{i!} \left(\frac{x}{\theta} \right)^i e^{-x/\theta} = e^{-x/\theta} \sum_{i=\alpha}^\infty \frac{1}{i!} \left( \frac{x}{\theta} \right)^i.

3. 성질

감마 분포는 다음과 같은 성질을 갖는다.


  • 확률변수 X_1, \cdots, X_n가 독립이고 각각 X_i \sim \mathrm{Gamma}(k_i, \theta)의 분포를 가질 때, 확률변수들의 합은 \sum_i X_i \sim \mathrm{Gamma}(\sum_i k_i, \theta) 분포를 따른다.[1] 감마 분포는 무한 분할성을 갖는다.

  • X \sim \mathrm{Gamma}(k, \theta)인 확률변수 X에 상수를 곱하면 척도모수에 영향을 준다.[1]


::cX \sim \mathrm{Gamma}(k, c\theta)

이는 모든 c > 0에 대해 cX \sim \mathrm{Gamma}(\alpha, c\,\theta)가 성립함을 의미한다. (적률생성함수에 의해) 또는, X \sim \mathrm{Gamma}\left( \alpha,\lambda \right) (모수-비율 모수화) 이라면, cX \sim \mathrm{Gamma}\left( \alpha, \frac \lambda c \right)이다.

X가 비율 \lambda를 갖는 지수 분포 확률 변수이면, cX는 비율 \lambda/c를 갖는 지수 확률 변수이다. 감마 변수에서도 마찬가지로, 양의 상수 c를 곱하면 비율을 나누거나 척도를 곱한다.

  • 감마 분포는 두 개의 매개변수를 갖는 지수족이며, 자연 매개변수는 ''α'' − 1과 -1/''θ'' (또는 ''α'' − 1과 -''λ'')이고, 자연 통계량은 ''X''와 ln ''X''이다. 모양 매개변수 ''α''를 고정하면, 한 개의 매개변수를 갖는 분포족은 자연 지수족이 된다.

  • 로그 기댓값과 분산은 다음과 같다.


:\operatorname{E}[\ln X] = \psi(\alpha) - \ln \lambda

또는

:\operatorname{E}[\ln X] = \psi(\alpha) + \ln \theta

여기서 \psi는 디감마 함수이다.

:\operatorname{var}[\ln X] = \psi^{(1)}(\alpha) = \psi^{(1)}(\alpha)

여기서 \psi^{(1)}은 트리감마 함수이다. 이는 감마 분포의 충분 통계량 중 하나가 \ln x이기 때문에, 지수족의 충분 통계량의 적률 생성 함수에 대한 지수족 공식을 사용하여 유도할 수 있다.

:

\begin{align}

\operatorname{H}(X) & = \operatorname{E}[-\ln p(X)] \\[4pt]

& = \operatorname{E}[-\alpha \ln \lambda + \ln \Gamma(\alpha) - (\alpha-1)\ln X + \lambda X] \\[4pt]

& = \alpha - \ln \lambda + \ln \Gamma(\alpha) + (1-\alpha)\psi(\alpha).

\end{align}



\alpha, \theta 파라미터화에서 정보 엔트로피는 다음과 같다.

:\operatorname{H}(X) =\alpha + \ln \theta + \ln \Gamma(\alpha) + (1-\alpha)\psi(\alpha).

  • 쿨백-라이블러 발산(KL 발산)은 Gamma(\alpha_p, \lambda_p)("참" 분포)에서 Gamma(\alpha_q, \lambda_q)("근사" 분포)까지 다음과 같이 주어진다.[18]


:D_{\mathrm{KL}}(\alpha_p,\lambda_p; \alpha_q, \lambda_q) = (\alpha_p-\alpha_q) \psi(\alpha_p) - \log\Gamma(\alpha_p) + \log\Gamma(\alpha_q) + \alpha_q(\log \lambda_p - \log \lambda_q) + \alpha_p\frac{\lambda_q-\lambda_p}{\lambda_p}.

\alpha, \theta 매개변수를 사용하여 작성하면, Gamma(\alpha_p, \theta_p)에서 Gamma(\alpha_q, \theta_q)까지의 KL 발산은 다음과 같이 주어진다.

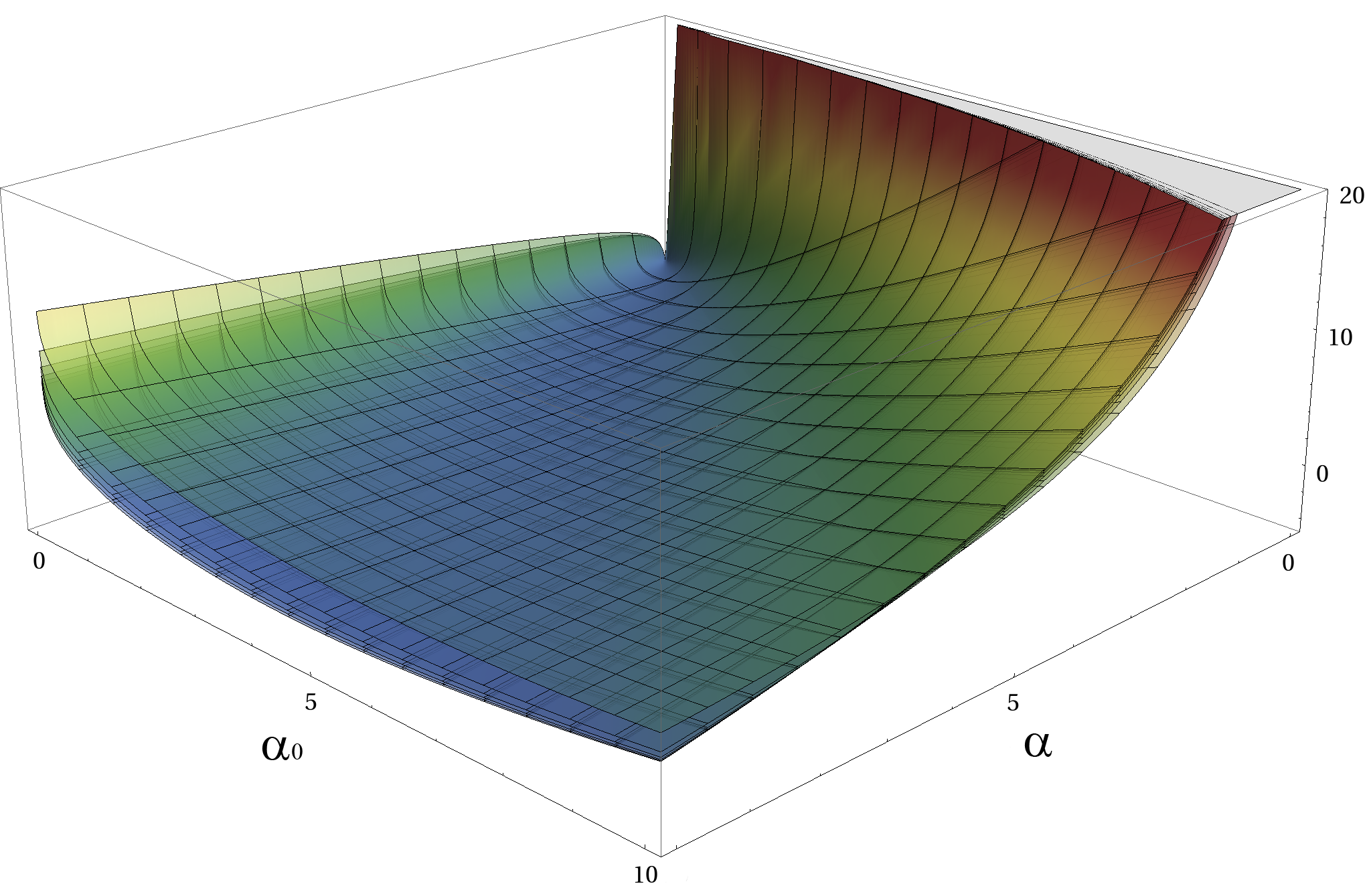
:D_{\mathrm{KL}}(\alpha_p,\theta_p; \alpha_q, \theta_q) = (\alpha_p-\alpha_q)\psi(\alpha_p) - \log\Gamma(\alpha_p) + \log\Gamma(\alpha_q) + \alpha_q(\log \theta_q - \log \theta_p) + \alpha_p \frac{\theta_p - \theta_q}{\theta_q}.


  • 감마 확률 밀도 함수의 라플라스 변환은 감마 분포의 적률생성함수로, 다음과 같다.[1]


:F(s) = \operatorname E\left( e^{sX} \right) = \frac1 {(1 + \theta s)^\alpha} = \left( \frac\lambda{s + \lambda} \right)^\alpha

(여기서 X는 해당 분포를 따르는 확률 변수이다).

3. 1. 평균과 분산

감마 분포의 평균은 모양 모수와 척도 모수의 곱으로 주어진다.

:\mu = \alpha\theta = \alpha/\lambda

분산은 다음과 같다.

:\sigma^2 = \alpha \theta^2 = \alpha/\lambda^2

역 모양 모수의 제곱근은 변동 계수를 제공한다.

:\sigma/\mu = \alpha^{-0.5} = 1/\sqrt{\alpha}

감마 분포의 확률 변수를 X라고 할 때, 평균 E(X) 및 분산 V(X)는 다음과 같이 나타낸다.

:E(X) = k\theta = \frac{k}{\lambda}

:V(X) = k\theta^2 = \frac{k}{\lambda^2}

3. 2. 왜도

감마 분포의 왜도는 모양 모수 \alpha에만 의존하며, 2/\sqrt{\alpha}와 같다.

3. 3. 고차 적률

n영어번째 원시 적률은 다음과 같이 주어진다.

:\mathrm{E}[X^n] = \theta^n \frac{\Gamma(\alpha+n)}{\Gamma(\alpha)} = \theta^n \prod_{i=1}^n(\alpha+i-1) \; \text{ for } n=1, 2, \ldots.

3. 4. 중앙값

감마 분포의 모드와 평균과는 다르게, 중앙값은 쉽게 계산할 수 있는 공식이 없다. 감마 분포의 중앙값(\nu)은 다음 방정식을 만족하는 값이다.[9]

:\frac{1}{\Gamma(\alpha) \theta^\alpha} \int_0^{\nu} x^{\alpha - 1} e^{-x/\theta} dx = \frac{1}{2}.

감마 분포의 중앙값에 대한 점근 전개와 경계를 구하는 문제는 Chen과 Rubin이 처음으로 엄밀하게 다루었다. 이들은 (\theta = 1일 때) 다음 부등식을 증명했다.[9]

:\alpha - \frac{1}{3} < \nu(\alpha) < \alpha,

여기서 \mu(\alpha) = \alpha는 평균이고, \nu(\alpha)는 \text{Gamma}(\alpha,1) 분포의 중앙값이다. 스케일 매개변수 \theta가 1이 아닐 경우, 평균은 \mu = \alpha\theta로 스케일되며, 중앙값의 경계 및 근삿값도 \theta를 곱하여 스케일된다.

K. P. Choi는 중앙값을 라마누잔 세타 함수와 비교하여 중앙값의 로랑 급수 점근 전개의 처음 5개 항을 구했다.[10] Berg와 Pedersen은 더 많은 항을 발견했다.[11]

:\nu(\alpha) = \alpha - \frac{1}{3} + \frac{8}{405\alpha} + \frac{184}{25515 \alpha^2} + \frac{2248}{3444525 \alpha^3} - \frac{19006408}{15345358875 \alpha^4} - O\left(\frac{1}{\alpha^5}\right) + \cdots

이 급수의 부분합은 충분히 큰 \alpha에 대해 좋은 근삿값을 제공한다. 그러나 낮은 \alpha 영역에서는 근사 정확도가 떨어진다.

Berg와 Pedersen은 중앙값의 여러 가지 성질을 증명했는데, 그중에는 \alpha에 대한 볼록 함수라는 것,[12] \alpha = 0 근처에서 점근적 거동이 \nu(\alpha) \approx e^{-\gamma}2^{-1/\alpha} (여기서 \gamma는 오일러-마스케로니 상수)라는 것, 그리고 모든 \alpha > 0에 대해 \alpha 2^{-1/\alpha} < \nu(\alpha) < k e^{-1/3k}로 경계가 정해진다는 것이 포함된다.[11]

2021년에 Gaunt와 Merkle은 \alpha \ge 1에 대해 더 엄밀한 선형 상한을 제시했다.[13] 이들은 Berg와 Pedersen의 결과(중앙값의 기울기가 모든 곳에서 1보다 작다)를 바탕으로 다음 부등식을 유도했다.

:\nu(\alpha) \le \alpha - 1 + \log2 (\alpha = 1에서 등호 성립)

중앙값이 볼록 함수임이 증명되었으므로, 이 상한은 모든 \alpha > 0에 대한 경계로 확장될 수 있다.[12]

높은 \alpha에서 점근적으로 정확하고, \alpha = 0.5 이하에서도 비교적 정확한 중앙값 근사는 윌슨-힐퍼티 변환으로부터 얻을 수 있다.

:\nu(\alpha) = \alpha \left( 1 - \frac{1}{9\alpha} \right)^3

이 근삿값은 \alpha < 1/9일 때 음수가 된다.

2021년에 Lyon은 \nu(\alpha) \approx 2^{-1/\alpha}(A + B\alpha) 형태의 여러 근삿값을 제안했다. 그는 이 근삿값이 모든 \alpha > 0에 대해 점근적으로 조밀한 상한 또는 하한이 되는 A와 B 값을 추측했으며,[14] 2023년에 다음과 같은 닫힌 형태의 경계를 증명했다.[15]

:\nu_{L\infty}(\alpha) = 2^{-1/\alpha}(\log 2 - \frac{1}{3} + \alpha) (하한, \alpha \to \infty에서 점근적으로 조밀)

:\nu_U(\alpha) = 2^{-1/\alpha}(e^{-\gamma} + \alpha) (상한, \alpha \to 0에서 점근적으로 조밀)

Lyon은 또한 2021년에 비공식적으로, 2023년에 엄밀하게, 닫힌 형식 표현식이 아닌 두 개의 하한을 제시했다.[14][15]

:\nu(\alpha) > \left( \frac{2}{\Gamma(\alpha+1)} \right)^{-1/\alpha} (k \to 0으로 갈 때 등호에 접근)

:\nu(\alpha) \ge \log 2 + (\alpha-1) (\gamma - 2 \operatorname{Ei}(-\log 2) - \log \log 2) ( k = 1에서 등호 성립, Ei는 지수 적분)

또한, Lyon은 경계 간의 보간을 통해 중앙값에 대한 더 나은 근사 또는 더 좁은 경계를 얻을 수 있음을 보였다. 그는 \alpha = 1 (\nu(1) = \log 2)에서 정확하고 최대 상대 오차가 0.6% 미만인 근삿값을 제시했다. 보간된 근삿값과 경계는 모두 다음과 같은 형태를 갖는다.

:\nu(\alpha) \approx \tilde{g}(\alpha)\nu_{L\infty}(\alpha) + (1 - \tilde{g}(\alpha)) \nu_U(\alpha)

여기서 \tilde{g}는 낮은 \alpha에서 0으로 시작하여 높은 \alpha에서 1로 단조롭게 증가하는 보간 함수로, 이상적인 보간 함수 g(\alpha)를 근사한다.

:g(\alpha) = \frac{\nu_U(\alpha) - \nu(\alpha)}{\nu_U(\alpha) - \nu_{L\infty}(\alpha)}

가장 간단한 보간 함수인 1차 유리 함수

:\tilde{g}_1(\alpha) = \frac{\alpha}{b_0 + \alpha}

를 사용하면, 가장 좁은 하한은

:b_0 = \frac{\frac{8}{405} + e^{-\gamma} \log 2 - \frac{\log^2 2}{2}}{e^{-\gamma} - \log 2 + \frac{1}{3}} - \log 2 \approx 0.143472

이고, 가장 좁은 상한은

:b_0 = \frac{e^{-\gamma} - \log 2 + \frac{1}{3}}{1 - \frac{e^{-\gamma} \pi^2}{12}} \approx 0.374654

이다.

감마 분포의 중앙값에 대한 경계와 점근 근사. 시안색 영역은 2021년 이전 출판된 하한과 상한 사이의 큰 간격을 나타냅니다.




감마 분포 중앙값의 상한(실선) 및 하한(점선)과 그 사이의 간격을 나타내는 로그-로그 플롯. 녹색, 노란색 및 시안 영역은 Lyon 2021 논문 이전의 간격을 나타냅니다. 녹색과 노란색은 Lyon이 증명한 하한으로 해당 간격을 좁힙니다. 2023년에 Lyon이 증명한 경계는 노란색을 더 좁게 만듭니다. 주로 노란색 내에 닫힌 형태의 유리 함수로 보간된 추정 경계가 수치적으로 계산된 중앙값(점선) 값과 함께 표시됩니다. 더 좁은 보간된 경계가 있지만 이 규모에서는 확인되지 않으므로 표시되지 않습니다.

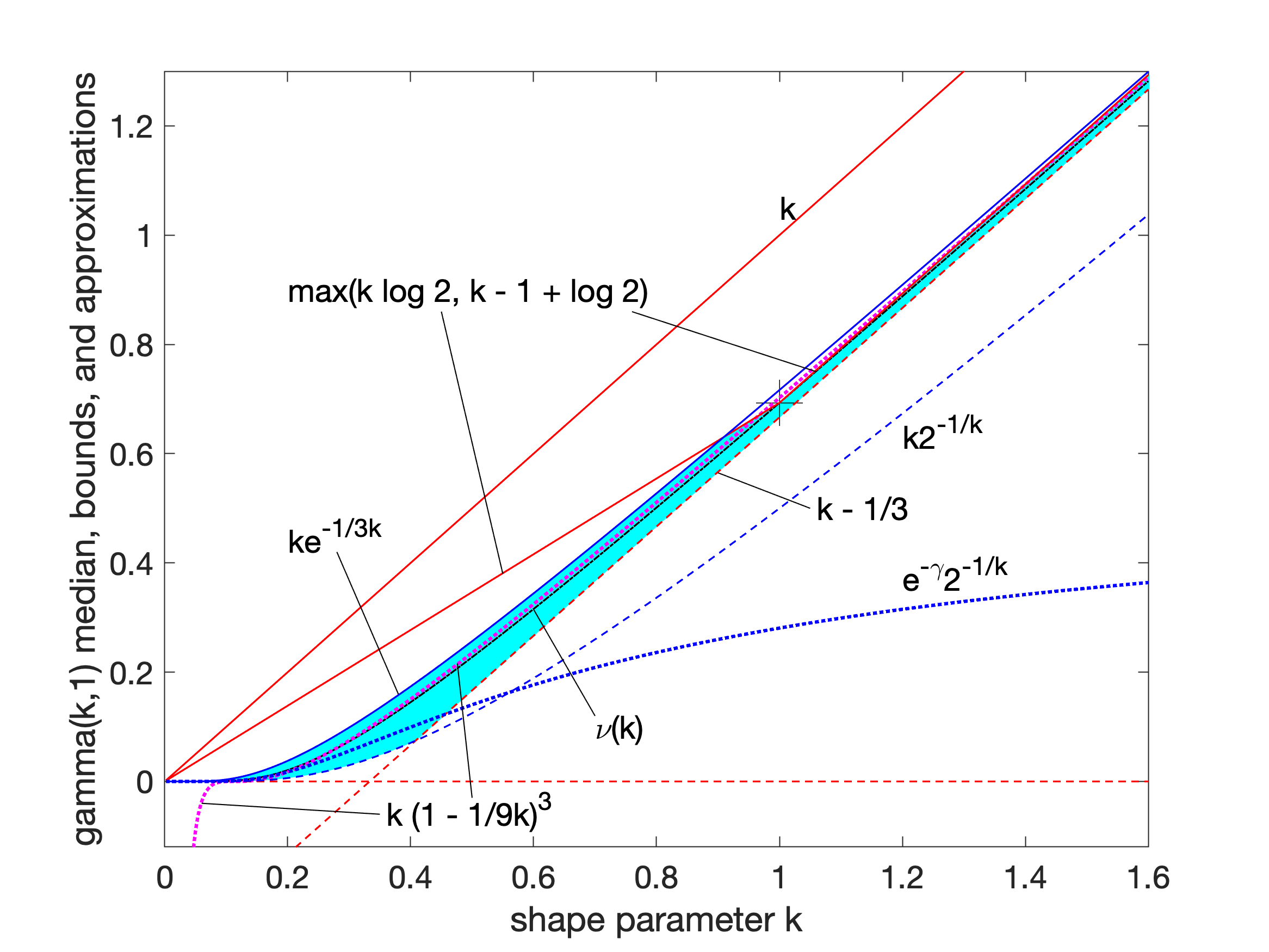
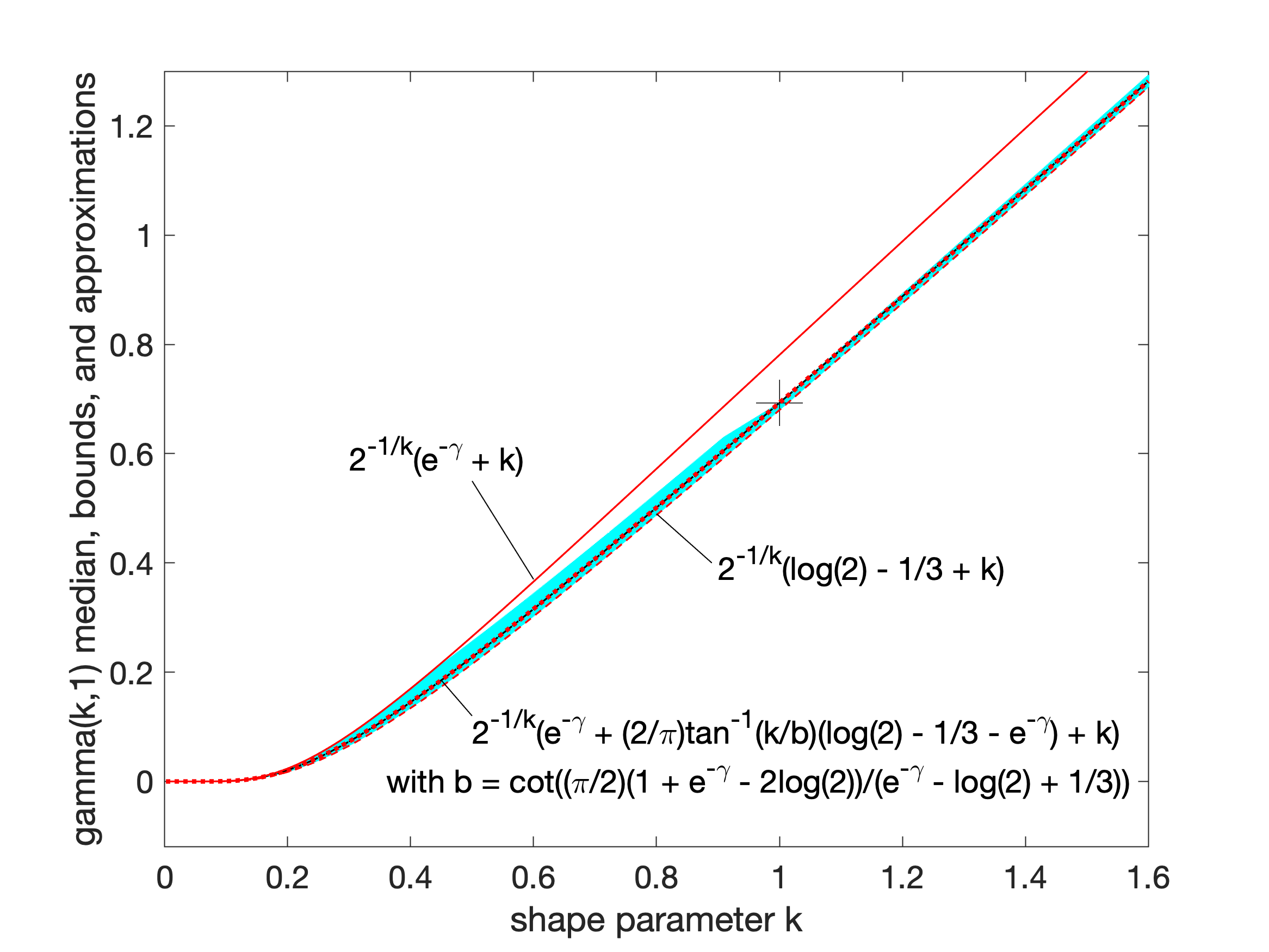
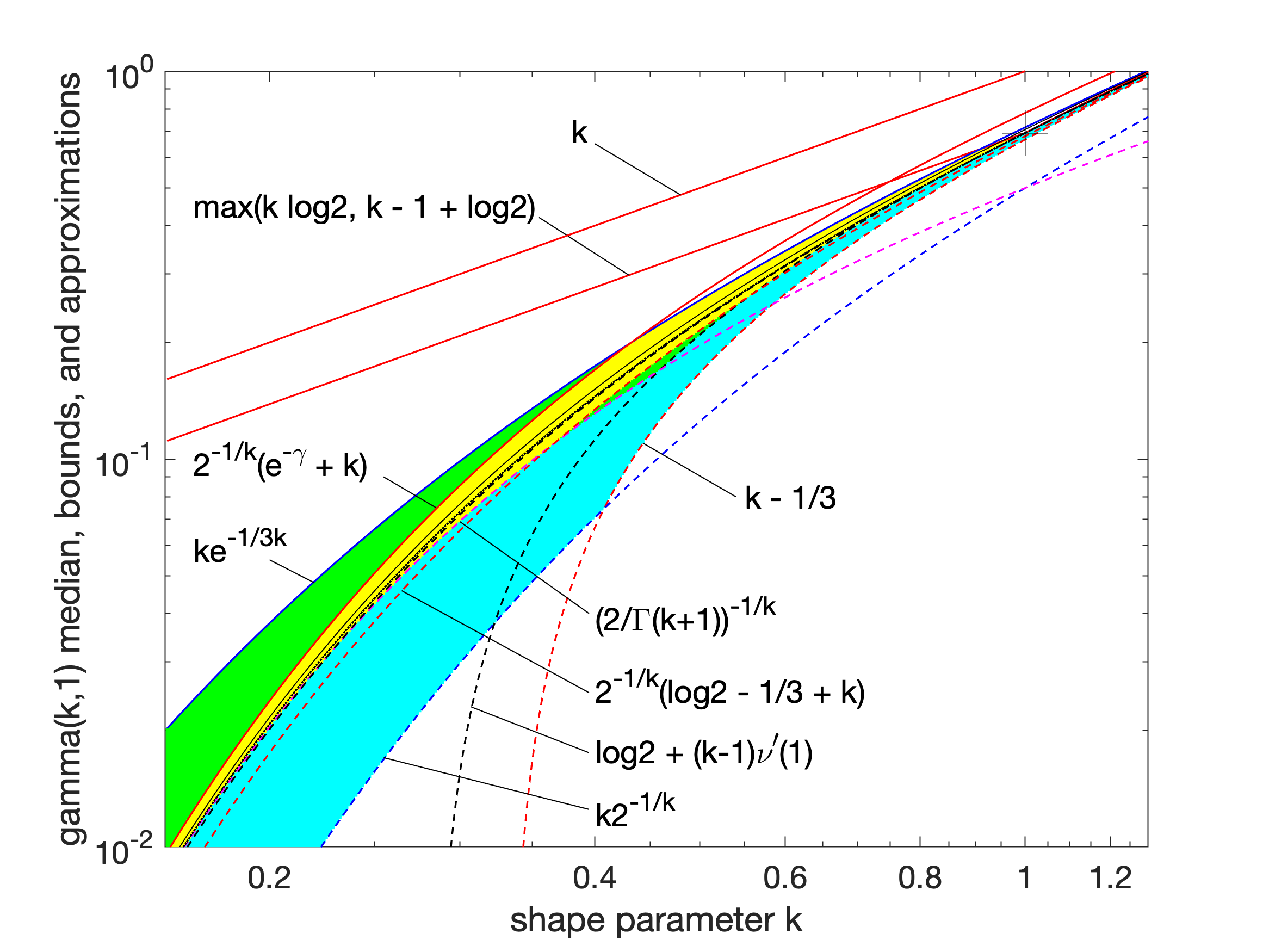
3. 5. 합

확률변수 X_1, \cdots, X_n가 독립이고 각각 X_i \sim \mathrm{Gamma}(k_i, \theta)의 분포를 가지면, 확률변수들의 합은 다음과 같은 분포를 따른다.

:\sum_i X_i \sim \mathrm{Gamma}(\sum_i k_i, \theta)

감마 분포는 무한 분할성을 갖는다.

3. 6. 스케일링

X \sim \mathrm{Gamma}(k, \theta)인 확률변수 X에 상수를 곱하면 척도모수에 영향을 준다.

:cX \sim \mathrm{Gamma}(k, c\theta)

만약

X \sim \mathrm{Gamma}(\alpha, \theta)

라면, 모든 c > 0에 대해

cX \sim \mathrm{Gamma}(\alpha, c\,\theta) 이다. (적률생성함수에 의해)

또는 동등하게, 만약

X \sim \mathrm{Gamma}\left( \alpha,\lambda \right) (모수-비율 모수화) 이라면,

cX \sim \mathrm{Gamma}\left( \alpha, \frac \lambda c \right)

이다.

X가 비율 \lambda를 갖는 지수 분포인 확률 변수이면, cX는 비율 \lambda/c를 갖는 지수 확률 변수이다. 감마 변수에서도 마찬가지이며 (적률생성함수를 사용하여 확인할 수 있다.): 양의 상수 c를 곱하면 비율을 나눈다 (또는 동등하게 척도를 곱한다).

3. 7. 지수족

감마 분포는 두 개의 매개변수를 갖는 지수족이며, 자연 매개변수는 ''α'' − 1과 -1/''θ'' (또는 ''α'' − 1과 -''λ'')이고, 자연 통계량은 ''X''와 ln ''X''이다.

모양 매개변수 ''α''를 고정하면, 결과적으로 한 개의 매개변수를 갖는 분포족은 자연 지수족이 된다.

3. 8. 로그 기댓값과 분산

다음이 성립함을 보일 수 있다.

:\operatorname{E}[\ln X] = \psi(\alpha) - \ln \lambda

또는 동등하게,

:\operatorname{E}[\ln X] = \psi(\alpha) + \ln \theta

여기서 \psi는 디감마 함수이다. 마찬가지로,

:\operatorname{var}[\ln X] = \psi^{(1)}(\alpha) = \psi^{(1)}(\alpha)

여기서 \psi^{(1)}은 트리감마 함수이다.

이는 감마 분포의 충분 통계량 중 하나가 \ln x이기 때문에, 지수족의 충분 통계량의 적률 생성 함수에 대한 지수족 공식을 사용하여 유도할 수 있다.

3. 9. 정보 엔트로피

정보 엔트로피는 다음과 같이 주어진다.

:

\begin{align}

\operatorname{H}(X) & = \operatorname{E}[-\ln p(X)] \\[4pt]

& = \operatorname{E}[-\alpha \ln \lambda + \ln \Gamma(\alpha) - (\alpha-1)\ln X + \lambda X] \\[4pt]

& = \alpha - \ln \lambda + \ln \Gamma(\alpha) + (1-\alpha)\psi(\alpha).

\end{align}



\alpha, \theta 파라미터화에서 정보 엔트로피는 다음과 같다.

:\operatorname{H}(X) =\alpha + \ln \theta + \ln \Gamma(\alpha) + (1-\alpha)\psi(\alpha).

3. 10. 쿨백-라이블러 발산



쿨백-라이블러 발산(KL 발산)은 Gamma(\alpha_p, \lambda_p)("참" 분포)에서 Gamma(\alpha_q, \lambda_q)("근사" 분포)까지 다음과 같이 주어진다.[18]

:D_{\mathrm{KL}}(\alpha_p,\lambda_p; \alpha_q, \lambda_q) = (\alpha_p-\alpha_q) \psi(\alpha_p) - \log\Gamma(\alpha_p) + \log\Gamma(\alpha_q) + \alpha_q(\log \lambda_p - \log \lambda_q) + \alpha_p\frac{\lambda_q-\lambda_p}{\lambda_p}.

\alpha, \theta 매개변수를 사용하여 작성하면, Gamma(\alpha_p, \theta_p)에서 Gamma(\alpha_q, \theta_q)까지의 KL 발산은 다음과 같이 주어진다.

:D_{\mathrm{KL}}(\alpha_p,\theta_p; \alpha_q, \theta_q) = (\alpha_p-\alpha_q)\psi(\alpha_p) - \log\Gamma(\alpha_p) + \log\Gamma(\alpha_q) + \alpha_q(\log \theta_q - \log \theta_p) + \alpha_p \frac{\theta_p - \theta_q}{\theta_q}.

3. 11. 라플라스 변환

감마 확률 밀도 함수의 라플라스 변환은 감마 분포의 적률생성함수로, 다음과 같다.[1]

:F(s) = \operatorname E\left( e^{sX} \right) = \frac1 {(1 + \theta s)^\alpha} = \left( \frac\lambda{s + \lambda} \right)^\alpha

(여기서 X는 해당 분포를 따르는 확률 변수이다).

4. 다른 분포와의 관계


  • 모양 매개변수 \(k\)가 정수이면 얼랑 분포에 포함된다.
  • \(k = 1, \theta = 1/\lambda\)이면 지수 분포가 된다.
  • \(k = \nu/2, \theta = 2\)이면 카이제곱 분포가 되며, 이 때 자유도는 \(\nu\)이다.
  • \(\alpha\)와 \(\theta\)를 사용한 매개변수화는 계량경제학 및 감마 분포가 대기 시간을 모델링하는 데 자주 사용되는 다른 응용 분야에서 더 흔하게 사용된다. 예를 들어, 가속 수명 시험에서 사망까지의 대기 시간은 감마 분포로 자주 모델링되는 확률 변수이다.[6]
  • \(\alpha\)와 \(\lambda\)를 사용한 매개변수화는 베이즈 통계학에서 더 흔하게 사용되며, 감마 분포는 지수 분포 또는 푸아송 분포의 \(\lambda\)[7]와 같은 다양한 유형의 역 스케일(비율) 매개변수에 대한 켤레 사전 분포로 사용된다.
  • \(k\)가 정수이면 얼랑 분포가 된다. 즉, 각 \(\theta\)의 평균을 갖는 \(k\)개의 독립적인 지수 분포 확률 변수의 합이다.


다음은 감마 분포의 특수한 경우이다.

4. 1. 일반적인 관계


  • 모양 매개변수 k가 정수이면 얼랑 분포에 포함된다.[19]
  • k = 1, \theta = 1/\lambda이면 지수 분포가 된다.[19]
  • k = \nu/2, \theta = 2이면 카이제곱 분포가 되며, 이 때 자유도는 \nu이다.[19]
  • 1=\theta = 1/\alpha이면 슐츠-짐 분포를 얻는다.[19]
  • \alpha가 정수이면 감마 분포는 얼랑 분포이다.[19]
  • X와 Y가 독립적으로 분포되어 있으면, X/(X+Y)는 매개변수 \alpha와 \lambda를 갖는 베타 분포를 따른다.[19]
  • 감마 분포는 일반화된 감마 분포, 일반화된 정수 감마 분포, 일반화된 역 가우스 분포의 특수한 경우이다.[19]
  • 이산 분포 중 음이항 분포는 감마 분포의 이산 유사체로 간주되기도 한다.[19]
  • 감마 분포는 트위디 분포의 지수 분산 모델 계열에 속한다.[19]
  • 감마 분포는 수정된 반정규 분포 계열에 속한다.[21]
  • 형태-척도 매개변수화 x|\theta \sim \Gamma(\alpha,\theta)에서 척도 매개변수 \theta \sim IG(b,1)이면(IG는 역 감마 분포), 주변 분포는 x \sim \lambda'(\alpha,b)이다.(\lambda'는 베타 소수 분포)[19]

4. 2. 복합 감마

모양 모수가 알려져 있지만, 역스케일 모수가 알려져 있지 않은 경우, 역스케일에 대한 감마 분포는 켤레 사전 분포를 형성한다. 역스케일을 적분하여 얻는 복합 분포는 복합 감마 분포로 알려진 폐쇄형 해를 갖는다.[22]

4. 3. 와이블 분포 및 안정 카운트 분포와의 관계

감마 분포 (\(\alpha > 1\))는 와이블 분포와 변형된 형태의 안정 카운트 분포의 곱으로 표현될 수 있다.[1] 형상 모수 \(\alpha\)는 안정 카운트 분포에서 레비의 안정성 모수의 역수로 간주될 수 있다.[1]

:\(f(x;\alpha) = \int_0^\infty \frac{1}{u} \, W_k\left(\frac{x}{u}\right) \left[ k u^{\alpha-1} \, \mathfrak{N}_{\frac{1}{\alpha}}\left(u^\alpha\right) \right] \, du ,\)

여기서 \(\mathfrak{N}_\alpha(\nu)\)는 형상 \(\alpha\)의 표준 안정 카운트 분포이고, \(W_\alpha(x)\)는 형상 \(\alpha\)의 표준 와이블 분포이다.[1]

5. 통계적 추론

감마 분포의 모수를 추정하는 방법에는 최대 가능도 추정, 폐쇄형 추정량, 베이즈 추론 등 여러 가지가 있다.

5. 1. 최대 가능도 추정

N개의 독립 동일 분포 관측치 (x_1, ..., x_N)에 대한 가능도 함수는 다음과 같습니다.

L(\alpha, \theta) = \prod_{i=1}^N f(x_i;\alpha,\theta)

이를 통해 로그 가능도 함수를 계산하면 다음과 같습니다.

\ell(\alpha, \theta) = (\alpha - 1) \sum_{i=1}^N \ln x_i - \sum_{i=1}^N \frac{x_i} \theta - Nk\ln \theta - N\ln \Gamma(\alpha)

\theta에 대해 미분하여 0으로 설정하면, \theta 매개변수의 최대 가능도 추정량을 얻을 수 있으며, 이는 표본 평균 \bar{x}를 형상 매개변수 \alpha로 나눈 값과 같습니다.

\hat{\theta} = \frac{1}{\alpha N}\sum_{i=1}^N x_i = \frac{\bar{x}}{\alpha}

이 값을 로그 가능도 함수에 대입하면 다음과 같습니다.

\ell(\alpha) = (\alpha-1)\sum_{i=1}^N \ln x_i -N\alpha - N\alpha\ln \left(\frac{\sum x_i}{\alpha N} \right) - N\ln \Gamma(\alpha)

샘플이 최소 2개 이상 필요합니다 (N\ge2). N=1인 경우, 함수 \ell(\alpha)는 \alpha\to\infty로 갈수록 무한대로 증가하기 때문입니다. \alpha>0인 경우, 폴리감마 함수의 부등식 속성을 사용하여 \ell(\alpha)가 엄격하게 오목 함수임을 확인할 수 있습니다. \alpha에 대해 미분하여 0으로 설정하면 다음과 같습니다.

\ln \alpha - \psi(\alpha) = \ln\left(\frac{1}{N}\sum_{i=1}^N x_i\right) - \frac 1 N \sum_{i=1}^N \ln x_i = \ln \bar{x} - \overline{\ln x}

여기서 \psi는 다이감마 함수이고 \overline{\ln x}는 \ln x의 표본 평균입니다. \alpha에 대한 닫힌 형식의 해는 없습니다. 이 함수는 수치적으로 매우 잘 동작하므로, 뉴턴 방법 등을 사용하여 수치적 해를 찾을 수 있습니다. k의 초기 값은 적률법을 사용하거나 다음 근사를 사용하여 찾을 수 있습니다.

\ln \alpha - \psi(\alpha) \approx \frac{1}{2\alpha}\left(1 + \frac{1}{6\alpha + 1} \right)

만약

s = \ln \left(\frac 1 N \sum_{i=1}^N x_i\right) - \frac 1 N \sum_{i=1}^N \ln x_i = \ln \bar{x} - \overline{\ln x}

라고 한다면, \alpha는 다음과 같이 근사됩니다.

k \approx \frac{3 - s + \sqrt{(s - 3)^2 + 24s}}{12s}

이 값은 정확한 값의 1.5% 이내입니다.[23] 이 초기 추측값에 대한 뉴턴-랩슨 업데이트의 명시적 형식은 다음과 같습니다.[24]

\alpha \leftarrow \alpha - \frac{ \ln \alpha - \psi(k) - s }{ \frac 1 \alpha - \psi\prime(\alpha) }.

최대 가능도 추정 (\hat \alpha,\hat\theta)에서 x와 \ln x에 대한 기대값은 경험적 평균과 일치합니다.



\begin{align}

\hat \alpha\hat\theta &= \bar x &&\text{and} &

\psi(\hat \alpha)+\ln \hat\theta &= \overline{\ln x}.

\end{align}


5. 2. 폐쇄형 추정량

독립 동일 분포 관측치 N개가 주어졌을 때, 최대 가능도 추정량은 아니지만 일관성을 가지는 폐쇄형 추정량이 존재한다.[25]

형상 매개변수 \alpha의 추정량은 다음과 같다.

\hat{\alpha} = \frac{N \sum_{i=1}^N x_i}{N \sum_{i=1}^N x_i \ln x_i - \sum_{i=1}^N x_i \sum_{i=1}^N \ln x_i}

척도 매개변수 \theta의 추정량은 다음과 같다.

\hat{\theta} = \frac{1}{N^2} \left(N \sum_{i=1}^N x_i \ln x_i - \sum_{i=1}^N x_i \sum_{i=1}^N \ln x_i\right)

위 식은 다음을 이용하여 단순화할 수 있다.

  • x의 표본 평균: \bar{x}
  • \ln x의 표본 평균: \overline{\ln x}
  • x \ln x의 표본 평균: \overline{x\ln x}


단순화된 추정량은 다음과 같다.

\hat{\alpha} = \bar{x} / \hat{\theta}

\hat{\theta} = \overline{x\ln x} - \bar{x} \overline{\ln x}.

만약 비율 매개변수화가 사용되는 경우, \hat{\lambda} = 1/\hat{\theta}를 추정값으로 사용한다.

이러한 추정량은 엄밀한 의미의 최우도 추정량은 아니지만, 혼합형 로그 모멘트 추정기라고 불린다. 그러나 최우도 추정기와 유사한 효율성을 가진다.

이러한 추정량은 일관성을 가지지만, 작은 편향이 있다. 척도 매개변수 \theta에 대한 편향 보정된 추정량은 다음과 같다.

\tilde{\theta} = \frac{N}{N - 1} \hat{\theta}

형상 매개변수 \alpha에 대한 편향 보정은 다음과 같다.[26]

\tilde{\alpha} = \hat{\alpha} - \frac{1}{N} \left(3 \hat{\alpha} - \frac{2}{3} \left(\frac{\hat{\alpha}}{1 + \hat{\alpha}}\right) - \frac{4}{5} \frac{\hat{\alpha}}{(1 + \hat{\alpha})^2} \right)

5. 3. 베이즈 최소 평균 제곱 오차

알려진 α와 알려지지 않은 θ에 대해, θ의 사후 확률 밀도 함수는 다음과 같이 나타낼 수 있다. (θ에 대한 표준 척도 불변 사전 확률을 사용한다.)

:P(\theta \mid \alpha, x_1, \dots, x_N) \propto \frac 1 \theta \prod_{i=1}^N f(x_i; \alpha, \theta)

이를 정리하면 다음과 같다.

: y \equiv \sum_{i=1}^Nx_i , \qquad P(\theta \mid \alpha, x_1, \dots, x_N) = C(x_i) \theta^{-N \alpha-1} e^{-y/\theta}

θ에 대한 적분은 변수 변환을 통해 수행할 수 있으며, 이를 통해 \frac{1}{\theta}가 매개변수 \alpha = N\alpha, \lambda = y를 갖는 감마 분포를 따른다는 것을 알 수 있다.

:\int_0^\infty \theta^{-N\alpha - 1 + m} e^{-y/\theta}\, d\theta = \int_0^\infty x^{N\alpha - 1 - m} e^{-xy} \, dx = y^{-(N\alpha - m)} \Gamma(N\alpha - m) \!

적률은 비율을 구함으로써 계산할 수 있다. (m by m = 0)

:\operatorname{E} [x^m] = \frac {\Gamma (N\alpha - m)} {\Gamma(N\alpha)} y^m

이는 θ에 대한 사후 분포의 평균 ± 표준 편차 추정치가 다음과 같음을 보여준다.

: \frac y {N\alpha - 1} \pm \sqrt{\frac {y^2} {(N\alpha - 1)^2 (N\alpha - 2)}}.

5. 4. 베이즈 추론

감마 분포는 베이즈 추론에서 푸아송 분포, 지수 분포, 평균을 알고 있는 정규 분포, 파레토 분포, 모양 σ영어가 알려진 감마 분포, 모양 모수가 알려진 역 감마 분포, 척도 모수가 알려진 곰페르츠 분포 등 여러 우도 분포에 대한 켤레 사전 분포로 사용된다.[27]

감마 분포의 켤레 사전 분포는 다음과 같다.[27]

:p(\alpha,\theta \mid p, q, r, s) = \frac{1}{Z} \frac{p^{\alpha-1} e^{-\theta^{-1} q}}{\Gamma(\alpha)^r \theta^{\alpha s}},

여기서 Z는 닫힌 형식의 해가 없는 정규화 상수이다. 사후 분포는 다음 매개변수 업데이트를 통해 계산할 수 있다.

:\begin{align}

p' &= p\prod\nolimits_i x_i,\\

q' &= q + \sum\nolimits_i x_i,\\

r' &= r + n,\\

s' &= s + n,

\end{align}

여기서 n은 관측 횟수이고, xi는 i번째 관측값이다.

6. 응용

감마 분포는 다양한 분야에서 활용된다.

일련의 사건들에서 각 사건의 대기 시간이 율 λ인 지수 분포를 따를 때, n번째 사건이 발생할 때까지의 대기 시간은 정수 형태 \alpha = n을 갖는 감마 분포를 따른다. 이러한 감마 분포의 구성은 여러 하위 사건들이 주요 사건 발생을 위해 순차적으로 발생해야 하는 다양한 현상을 모델링할 수 있게 해준다.[28]

감마 분포는 보험 청구 규모[33]와 강우량[34]을 모델링하는 데 사용되어 왔다. 또한 다단계 푸아송 회귀 모델의 오차를 모델링하는 데 사용되는데, 이는 감마 분포를 따르는 율을 가진 혼합 분포의 푸아송 분포가 음이항 분포라고 불리는 알려진 폐쇄형 분포를 갖기 때문이다. 무선 통신에서 감마 분포는 신호 전력의 다중 경로 페이딩을 모델링하는 데 사용된다.

종양학에서 암의 질병 발생률에 대한 연령 분포는 종종 감마 분포를 따르며, 신경과학에서 감마 분포는 종종 시간 부호화의 스파이크 간 간격의 분포를 설명하는 데 사용된다.[37][38]

세균 유전학의 유전자 발현에서, 구성적 발현 단백질의 사본 수 분석은 종종 감마 분포를 따른다.[39] 유전체학에서 감마 분포는 ChIP-chip[40] 및 ChIP-seq[41] 데이터 분석에서 피크 콜링 단계(신호 인식)에 적용되었다.

베이즈 통계에서 감마 분포는 켤레 사전 분포로 널리 사용된다. 계통 발생학에서 감마 분포는 사이트 간 비율 변동을 모델링하는 데 가장 일반적으로 사용되는 접근 방식이다.[42]

6. 1. 일반적인 응용

일련의 사건들에서 각 사건의 대기 시간이 율 λ인 지수 분포를 따른다고 할 때, n번째 사건이 발생할 때까지의 대기 시간은 정수 형태 \alpha = n을 갖는 감마 분포를 따른다. 이러한 감마 분포의 구성은 여러 하위 사건들이 주요 사건 발생을 위해 순차적으로 발생해야 하는 다양한 현상을 모델링할 수 있게 해준다.[28]
감마 분포가 응용되는 현상 (예시):

  • 세포 분열 사건의 대기 시간[29]
  • 주어진 돌연변이에 대한 보상 돌연변이의 수[30]
  • 유압 시스템에 수리가 필요한 시점까지의 대기 시간[31]


생물 물리학에서 ATP 합성 효소와 같은 분자 모터의 단계 간 체류 시간은 ATP 농도가 일정할 때 거의 지수적으로 나타나는데, 이는 모터의 각 단계가 단일 ATP 가수분해를 거친다는 것을 보여준다. 만약 n개의 ATP 가수분해 사건이 있다면, 이는 차수가 n인 감마 분포를 따를 것이다.[32]

감마 분포는 보험 청구 규모[33]와 강우량[34]을 모델링하는 데 사용되어 왔다. 이는 총 보험 청구액과 저수지에 축적된 강우량이 감마 과정으로 모델링된다는 것을 의미하며, 이는 지수 분포가 푸아송 과정을 생성하는 것과 유사하다.

감마 분포는 또한 다단계 푸아송 회귀 모델의 오차를 모델링하는 데 사용되는데, 이는 감마 분포를 따르는 율을 가진 혼합 분포의 푸아송 분포가 음이항 분포라고 불리는 알려진 폐쇄형 분포를 갖기 때문이다.

무선 통신에서 감마 분포는 신호 전력의 다중 경로 페이딩을 모델링하는 데 사용된다. 레일리 분포와 라이스 분포도 참조하라.

종양학에서 암의 질병 발생률에 대한 연령 분포는 종종 감마 분포를 따르며, 여기서 형상 및 척도 매개변수는 각각 발암의 원동력 사건의 수와 그 사이의 시간 간격을 예측한다.[35][36]

신경과학에서 감마 분포는 종종 시간 부호화의 스파이크 간 간격의 분포를 설명하는 데 사용된다.[37][38]

세균 유전학의 유전자 발현에서, 구성적 발현 단백질의 사본 수 분석은 종종 감마 분포를 따르며, 여기서 척도 및 형상 매개변수는 각각 세포 주기의 평균 폭발 횟수와 수명 동안 단일 mRNA에 의해 생성되는 평균 단백질 분자 수를 나타낸다.[39]

유전체학에서 감마 분포는 ChIP-chip[40] 및 ChIP-seq[41] 데이터 분석에서 피크 콜링 단계(즉, 신호 인식)에 적용되었다.

베이즈 통계에서 감마 분포는 켤레 사전 분포로 널리 사용된다. 이는 정규 분포의 정밀도 (즉, 분산의 역수)에 대한 켤레 사전 분포이다. 또한 지수 분포에 대한 켤레 사전 분포이기도 하다.

계통 발생학에서 감마 분포는 최대 우도법, 베이즈법, 또는 거리 행렬 방법이 계통수를 추정하는 데 사용될 때, 사이트 간 비율 변동을 모델링하는 데 가장 일반적으로 사용되는 접근 방식이다.[42] 비율 변동을 모델링하기 위해 감마 분포를 사용하는 계통 발생 분석은 데이터에서 단일 매개변수를 추정하는데, 이는 α = λ인 분포로 고려 사항을 제한하기 때문이다. 이 매개변수화는 이 분포의 평균이 1이고 분산이 1/α임을 의미한다. 최대 우도법과 베이즈법은 일반적으로 연속 감마 분포에 대한 이산 근사를 사용한다.[43][44]

7. 난수 생성

Ahrens-Dieter영어의 수용-거부 방법, Marsaglia영어의 변환-거부 방법 등을 사용하여 감마 분포를 따르는 난수를 생성할 수 있다.[46][49]

\theta = 1 인 감마 변수를 생성하고, 간단한 나눗셈으로 \lambda 값으로 변환할 수 있다.

Gamma(n + \delta, 1)에서 무작위 변수를 생성할 때, n은 음이 아닌 정수이고 0 < \delta < 1이다. Gamma(1, 1) 분포가 Exp(1) 분포와 동일하다는 사실과 지수 변수 생성 방법을 참고한다. U가 (0, 1]에서 균등하게 분포되어 있다면, -\ln U가 Gamma(1, 1) (즉, 역변환 표본 추출)로 분포된다. 감마 분포의 "\alpha-더하기" 속성을 사용하여 확장하면 다음과 같다.

-\sum_{k=1}^n \ln U_k \sim \Gamma(n, 1)

여기서 U_k는 모두 (0, 1]에서 균등하게 분포되어 있고 독립적이다. 0 < \delta < 1에 대해 Gamma(\delta, 1)로 분포된 변수를 생성하고 "\alpha-더하기" 속성을 다시 적용한다.

모양 매개변수의 값이 작을 경우, 알고리즘이 유효하지 않은 경우가 많다.[45] 모양 매개변수의 임의의 값에 대해 Ahrens와 Dieter[46]의 수정된 수용-거부 방법인 알고리즘 GD (모양 \alpha \ge 1) 또는 변환 방법[47]을 0 < \alpha < 1일 때 적용할 수 있다. Cheng과 Feast의 알고리즘 GKM 3[48] 또는 Marsaglia의 압착 방법도 참조할 수 있다.[49]

다음은 Ahrens-Dieter의 수용-거부 방법의 한 버전이다:[46]

# U, V, W를 iid 균등 (0, 1] 변수로 생성한다.

# 만약 U\le\frac e {e+\delta}이면 \xi=V^{1/\delta}이고 \eta=W\xi^{\delta-1}이다. 그렇지 않으면 \xi=1-\ln V이고 \eta=We^{-\xi}이다.

# 만약 \eta>\xi^{\delta-1}e^{-\xi}이면 1단계로 돌아간다.

# \xi는 \Gamma(\delta, 1)로 분포된다.

요약하면 다음과 같다.

\theta \left( \xi - \sum_{i=1}^{\lfloor \alpha \rfloor} \ln U_i \right) \sim \Gamma (\alpha, \theta)

여기서 \scriptstyle \lfloor \alpha \rfloor는 \alpha의 정수 부분이고, \xi는 1 = \delta = \{\alpha\} (\alpha의 소수 부분)를 사용하여 위의 알고리즘을 통해 생성되며, U_k는 모두 독립적이다.

Devroye영어는 이 접근 방식이 \alpha의 값에 대해 선형이며, 상황에 따라 거부 기반 또는 테이블 기반 방법을 사용할 것을 권장한다.[45]

Marsaglia영어의 간단한 변환-거부 방법은 다음과 같다:[50]

# d = a - \frac13와 c = \frac1{\sqrt{9d}}로 설정한다.

# v=(1+cX)^3로 설정한다.

# 만약 v > 0이고 \ln U < \frac{X^2}2 + d - dv + d\ln v이면 dv를 반환하고, 그렇지 않으면 2단계로 돌아간다.

1 \le a = \alpha 를 사용하면 \alpha와 거의 일정한 시간 내에 감마 분포 무작위 숫자를 생성한다. 수용률은 \alpha에 따라 다르며, \alpha = 1, 2, 4에 대해 0.95, 0.98, 0.99의 수용률을 갖는다. \alpha < 1의 경우, \gamma_\alpha = \gamma_{1+\alpha} U^{1/\alpha}를 사용하여 이 방법을 사용할 수 있도록 k를 늘릴 수 있다.

Matlab에서는 함수 gamrnd()을 사용하여 숫자를 생성할 수 있으며, 이 함수는 \alpha, \theta 표현을 사용한다.

참조

[1] 웹사이트 Gamma distribution {{!}} Probability, Statistics, Distribution {{!}} Britannica https://www.britanni[...] 2024-10-09
[2] 웹사이트 Gamma Distribution https://mathworld.wo[...] 2024-10-09
[3] 웹사이트 Gamma Distribution {{!}} Gamma Function {{!}} Properties {{!}} PDF https://www.probabil[...] 2024-10-09
[4] 웹사이트 4.5: Exponential and Gamma Distributions https://stats.libret[...] 2024-10-10
[5] 논문 Maximum entropy autoregressive conditional heteroskedasticity model https://web.archive.[...] 2011-06-02
[6] 서적 Introduction to Mathematical Statistics Macmillan
[7] arXiv Scalable Recommendation with Poisson Factorization
[8] 서적 Probability, Random Variables, and Stochastic Processes
[9] 논문 Bounds for the difference between median and mean of gamma and Poisson distributions https://dx.doi.org/1[...] 1986-10
[10] 논문 On the Medians of the Gamma Distributions and an Equation of Ramanujan https://www.ams.org/[...] 1994-05
[11] 논문 The Chen–Rubin conjecture in a continuous setting https://www.intlpres[...] 2020-04-01
[12] arXiv Convexity of the median in the gamma distribution https://arxiv.org/ab[...]
[13] 논문 On bounds for the mode and median of the generalized hyperbolic and related distributions 2021
[14] 논문 On closed-form tight bounds and approximations for the median of a gamma distribution 2021-05-13
[15] 논문 Tight bounds for the median of a gamma distribution 2021-05-13
[16] 논문 Storage capacity of a dam with gamma type inputs
[17] 논문 The distribution of the sum of independent gamma random variables
[18] 웹사이트 KL-Divergences of Normal, Gamma, Dirichlet, and Wishart densities https://www.fil.ion.[...]
[19] 웹사이트 ExpGammaDistribution—Wolfram Language Documentation https://reference.wo[...]
[20] 웹사이트 scipy.stats.loggamma — SciPy v1.8.0 Manual https://docs.scipy.o[...]
[21] 논문 The Modified-Half-Normal distribution: Properties and an efficient sampling scheme https://figshare.com[...] 2022-09-02
[22] 논문 Compound gamma, beta and F distributions 1970-12
[23] 웹사이트 Estimating a Gamma distribution https://tminka.githu[...]
[24] 논문 Maximum Likelihood Estimation of the Parameters of the Gamma Distribution and Their Bias
[25] 논문 Closed-Form Estimators for the Gamma Distribution Derived from Likelihood Equations https://amstat.tandf[...] 2019-07-27
[26] 논문 A Note on Bias of Closed-Form Estimators for the Gamma Distribution Derived from Likelihood Equations https://www.tandfonl[...] 2019-07-27
[27] 간행물 A Compendium of Conjugate Priors http://citeseerx.ist[...]
[28] 서적 Design and analysis of ecological experiments http://worldcat.org/[...] Oxford University Press 2022-05-26
[29] 논문 Applications and implications of the exponentially modified gamma distribution as a model for time variabilities related to cell proliferation and gene expression 2022-05-26
[30] 논문 The Coupon Collector and the Suppressor Mutation 2022-05-26
[31] 논문 Failure rate distributions for flexible manufacturing systems: An empirical study 2022-05-26
[32] 논문 Myosin-V stepping kinetics: A molecular model for processivity 2000-08-15
[33] 서적 Statistical and Probabilistic Methods in Actuarial Science Chapman & Hall CRC
[34] 논문 Maximum Likelihood Estimation for the Gamma Distribution Using Data Containing Zeros 1990
[35] 논문 The number of key carcinogenic events can be predicted from cancer incidence 2017-09-22
[36] 논문 The Erlang distribution approximates the age distribution of incidence of childhood and young adulthood cancers 2021-08-06
[37] 논문 Nature of the maintained discharge of Q, X, and Y retinal ganglion cells of the cat
[38] 논문 Response to best-frequency tone bursts in the ventral cochlear nucleus is governed by ordered inter-spike interval statistics
[39] 논문 Linking stochastic dynamics to population distribution: An analytical framework of gene expression
[40] 웹사이트 Model-based deconvolution of genome-wide DNA binding https://web.archive.[...]
[41] 웹사이트 Characterising ChIP-seq binding patterns by model-based peak shape deconvolution http://www.biomedcen[...]
[42] 논문 Among-site rate variation and its impact on phylogenetic analyses https://linkinghub.e[...] 2023-09-06
[43] 논문 Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: Approximate methods http://link.springer[...] 2023-09-06
[44] 논문 Taking Variation of Evolutionary Rates Between Sites into Account in Inferring Phylogenies http://link.springer[...] 2023-09-06
[45] 서적 Non-Uniform Random Variate Generation http://luc.devroye.o[...] Springer-Verlag 2012-02-26
[46] 논문 Generating gamma variates by a modified rejection technique 1982-01
[47] 논문 Computer methods for sampling from gamma, beta, Poisson and binomial distributions
[48] 논문 Some Simple Gamma Variate Generators https://www.jstor.or[...]
[49] 논문 The squeeze method for generating gamma variates
[50] 논문 A simple method for generating gamma variables


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com