솔레노이드

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

솔레노이드는 전류가 흐를 때 자기장을 생성하는 코일로, 다양한 분야에서 활용되는 전자기 부품이다. 17세기 윌리엄 길버트의 연구를 시작으로, 외르스테드와 앙페르의 실험을 거쳐 패러데이에 의해 전자기 유도 법칙이 발견되면서 솔레노이드의 원리가 정립되었다. 솔레노이드에 전류를 흘리면 전자석으로 작동하며, 앙페르의 오른나사 법칙에 따라 자기장이 형성된다. 솔레노이드의 자기장 세기는 전류의 세기와 단위 길이당 감긴 횟수에 비례하며, 유도 용량(인덕턴스)을 갖는다. 솔레노이드는 밸브, 전자석, 변압기, 액추에이터 등 다양한 형태로 활용되며, 일상생활, 자동차, 가전제품, 산업 자동화, 의료 기기 등 여러 산업 분야에서 널리 사용된다.

더 읽어볼만한 페이지

전자기 코일 - 점화 코일
점화 코일은 유도 코일 원리를 활용한 변압기로, 구리 선으로 만들어진 1차 및 2차 코일과 철심으로 구성되어 점화 플러그에 필요한 고전압을 발생시키는 장치이다.

솔레노이드
개요
솔레노이드 작동 방식 애니메이션
유형	전자기석
작동 원리	전자기 유도
용도	스위치 밸브 자동차 스타터 모터 자동판매기 도어록 기타 다양한 기계 장치
상세 정보
정의	코일 형태의 전선에 전류를 흘려 자기장을 발생시켜 기계적 에너지를 생성하는 장치
작동 방식	코일에 전류가 흐르면 자기장이 발생하고, 이 자기장이 코일 내부의 플런저 또는 아머처를 당기거나 밀어내는 방식으로 작동함
종류	선형 솔레노이드 회전 솔레노이드
특징	빠른 응답 속도 비교적 간단한 구조 제어가 용이함
장점	높은 신뢰성 긴 수명 다양한 환경에서 사용 가능
단점	비교적 낮은 힘 작동 거리가 짧음 소음 발생 가능성
응용 분야	자동차: 연료 분사 장치, 변속기, ABS 등 산업 자동화: 로봇, 컨베이어 벨트, 밸브 제어 등 의료 기기: MRI, CT 스캔, 인공호흡기 등 가전 제품: 세탁기, 냉장고, 에어컨 등
관련 용어	전자기장 전류 코일 플런저 아머처
추가 정보
참고 자료	솔레노이드 (Wikipedia 영문) 솔레노이드 작동 원리 (YouTube 영상)

2. 역사

2. 1. 길버트의 전기와 자기 연구 (17세기)

영국의 윌리엄 길버트는 자석에 대한 연구를 통해 전기와 자기 현상을 체계적으로 정리하고, 이 둘이 서로 다른 현상임을 주장했다. 길버트가 1600년에 출판한 《자석에 대하여》는 근대 전기 자기학의 출발점이 되었는데, 그는 이 책에서 처음으로 기존에 진행되었던 자석에 대한 실험 결과들을 집대성하여 전기와 자석의 성질을 종합적으로 정리했다. 이는 후에 외르스테드가 전류의 자기작용을 발견하고, 패러데이가 전자기 유도 법칙을 발견하여 전기와 자기가 통합되기 전까지 전기학과 자기학이라는 독립된 연구 분야가 만들어지는 결과를 가져왔다.

2. 2. 외르스테드의 실험과 앙페르의 법칙 (19세기 초)

1820년 4월 21일, 덴마크의 과학자 한스 크리스티안 외르스테드는 강의 시범용 장치를 설치하다가 놀라운 발견을 했다. 그는 대학원생들에게 전류가 백금전선에서 열을 어떻게 발생시키는지를 보여주고 있었다. 그때 그는 우연히 실험을 보여주던 책상 위에 나침반을 올려두었다. 나침반의 바늘은 처음에는 지구의 자기장을 따라 남-북으로 정렬되어 있었다. 그런데 외르스테드가 전선에 전류를 흐르게 하자마자 나침반의 바늘이 갑자기 백금전선과 수직인 방향으로 돌아갔다. 그리고 전류를 끊자 곧바로 바늘은 원래 위치로 돌아갔다. 당시 외르스테드는 이 현상에 몹시 당황했고 몇 달 동안 이 실험을 하지 않았다.

3개월 후 외르스테드는 전류가 나침반의 자석에 힘을 가하는지에 대하여 알아보기 위해 실험을 다시 시작했다. 또한 그는 전선과 전류에 변화를 줄 때마다 나침반의 바늘에 어떠한 일이 일어나는지 관찰했다.

몇 달 동안 연구한 뒤 외르스테드는 전류가 흐르는 전선이 자기적 성질을 보이고, 그 자기력은 기존에 아이작 뉴턴이 제시했던 힘과는 전혀 다른 종류라는 결론을 내렸다. 그리고 그는 과학계에 자신의 전자기 발견을 담은 소책자를 출판했다. 이 책은 전기와 자기는 개별적이라고 생각하던 당시의 많은 사람들에게 신선한 충격을 주었다. 또한 전자기라는 개념을 통해 앙드레 마리 앙페르와 마이클 패러데이와 같은 사람들이 이에 대한 위대한 업적을 세울 수 있었다.

1820년 9월 프랑스 과학 아카데미 주최로 파리에서 열린 논문 발표에서 앙드레 마리 앙페르는 외르스테드가 전기와 자기에 대한 논문을 발표하는 것을 듣고 흥미를 느꼈다. 앙페르는 곧 외르스테드의 실험을 직접 해보았고, 정확히 1주일 뒤에 독창적인 이론과 실험을 통해 전기와 자기와의 관계를 정확히 규명한 논문을 발표하였다. 그는 이 논문에서 오늘날 앙페르의 오른손 법칙이라고 불리는 전류의 방향과 나침반 바늘의 방향과의 관계를 밝혀냈고, 전류의 세기와 전선으로부터의 거리에 따른 전자기장의 세기에 관한 방정식을 고안하기도 하였다.

2. 3. 전동기와 원통 코일의 발명 (19세기)

영국의 화학자이자 물리학자인 마이클 패러데이는 외르스테드의 발견 후 1년이 채 안되어 전자기력을 이용하여 전선을 계속 회전시킬 수 있는 방법을 찾아내었고, 그 과정에서 간단한 형태의 전동기를 발명하였다. 또한 앙드레마리 앙페르는 자기가 자석이나 쇠막대기 없이 단지 전기의 힘만으로도 발생한다는 사실을 발견하여, 전선을 원통 형태로 감고 전류를 흘려주면 주변에 자기장이 형성되어 원통 코일이 자석과 같은 역할을 할 수 있다는 것을 알아내었다. 이 원통 코일이 바로 솔레노이드이다.

2. 4. 패러데이의 전자기 유도 법칙 (19세기)

1819년, 외르스테드의 발견을 통하여 패러데이는 전류에 의해서 자기장이 만들어진다면, 반대로 자기장으로 전류를 만들 수 있을 것이라고 생각했다. 12년이 지난 1831년 8월 29일, 패러데이는 오늘날의 변압기와 유사한 장치를 고안해내었다. 그리고 이 장치를 활용해 10월 17일 전자기 유도 현상을 발견해내었다. 그의 발표로 전자기의 상호 작용은 완벽하게 증명되었다.

자석을 원통 코일 근처에서 움직이게 되면 코일 주위에 자기장의 변화가 생기게 되는데 이것이 기전력을 발생시킴으로써 코일에 전류가 흐르게 된다. 자석의 이동이 빠를수록 전류가 더 강하고, 이동이 없을 때 전류가 흐르지 않음을 발견하였다. 또한 전선이 코일로 감겨 있어 전선이 자기장에 더 많이 노출될수록 효과는 더 컸다.

패러데이의 전자기 유도법칙은 전기를 만들어내는 새로운 방법을 제시하였다. 그때까지는 마찰 전기와 전지를 이용하여 전기를 생산해내었는데, 이 발견으로 전류를 자석을 이용하여 효과적이고 지속적으로 만들어낼 수 있게 되었다.

3. 원리

솔레노이드라는 단어는 그리스어 '관(σωλήνας,솔리나스/solínas^grc)'에서 유래한 말이다. 솔레노이드에 흐르는 전류의 양을 조절함으로써 전자석으로 사용할 수 있다. 솔레노이드는 전기에너지를 자기에너지로 변환하므로 에너지변환장치라고도 할 수 있다. 내부자기장의 크기는 전류의 크기에 비례하고 단위 길이당 감은 수에 비례한다. 도선에 전류가 흐르면 그 주변에 시계반대방향으로 자기장이 형성되는데(앙페르의 오른나사 법칙) 이 때 이 도선을 감아 솔레노이드를 만들 경우 도선이 일직선일 때 생성되었던 자기장들이 같은방향으로 정렬되면서 솔레노이드의 자기장이 벡터합으로 구해진다.

3. 1. 앙페르의 오른나사 법칙

3. 2. 자기장 생성

4. 물리학적 특성

4. 1. 자기장의 세기

솔레노이드에 전류를 흘리면 그 주변에 자기장이 유도된다. 이는 솔레노이드를 이루고 있는 도선들에 의해 유도된 자기장 벡터들의 벡터합으로 생각할 수 있다. 솔레노이드 내부의 자기장 방향은 전류가 흐르는 방향으로 오른손의 엄지손가락을 제외한 나머지 손가락으로 감았을 때 엄지손가락이 향하는 방향이다.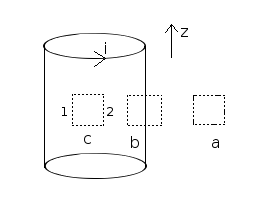

그림 1: 임의의 세 개의 암페어 루프 ''a'', ''b'', 그리고 ''c''로 표시된 무한 솔레노이드. 경로 ''c''에 대한 적분을 통해 솔레노이드 내부의 자기장이 방사상으로 균일해야 함을 알 수 있다.

== 솔레노이드 내부 자기장 ==

솔레노이드에서 앙페르 법칙을 쓰면 한 단면적에서 어느 점에서나 자기장이 일정하다는 것을 보일 수 있다. 무한한 도선에선 솔레노이드 어느 부분의 중심을 잡아도 자기장이 일정하므로 솔레노이드 모든 점에서 자기장이 균일하다.

옆의 그림에서 b의 앙페르 고리에서 앙페르의 법칙을 사용하면 직사각형의 윗변과 아랫변에서는 자기장의 방향과 적분 방향이 수직하므로 적분값이 0이고, 오른쪽 변에서는 자기장이 0이므로 적분값도 0이다. 결과적으로 직사각형의 왼쪽 변의 길이를 l이라고 하면 앙페르의 법칙에 의해

:

\int B \,dl = \mu_0 i n l

이다. 여기서 n은 단위 길이당 감겨 있는 도선의 수이다.

솔레노이드 내부에서 자기장의 세기는 일정하므로

:

\int B \,dl = B l = \mu_0 i n l

이고, 따라서

:

B = \mu_0 i n

이다.

무한히 긴 솔레노이드 내부의 자기장은 균일하며, 그 세기는 축으로부터의 거리나 솔레노이드의 단면적에 의존하지 않는다.

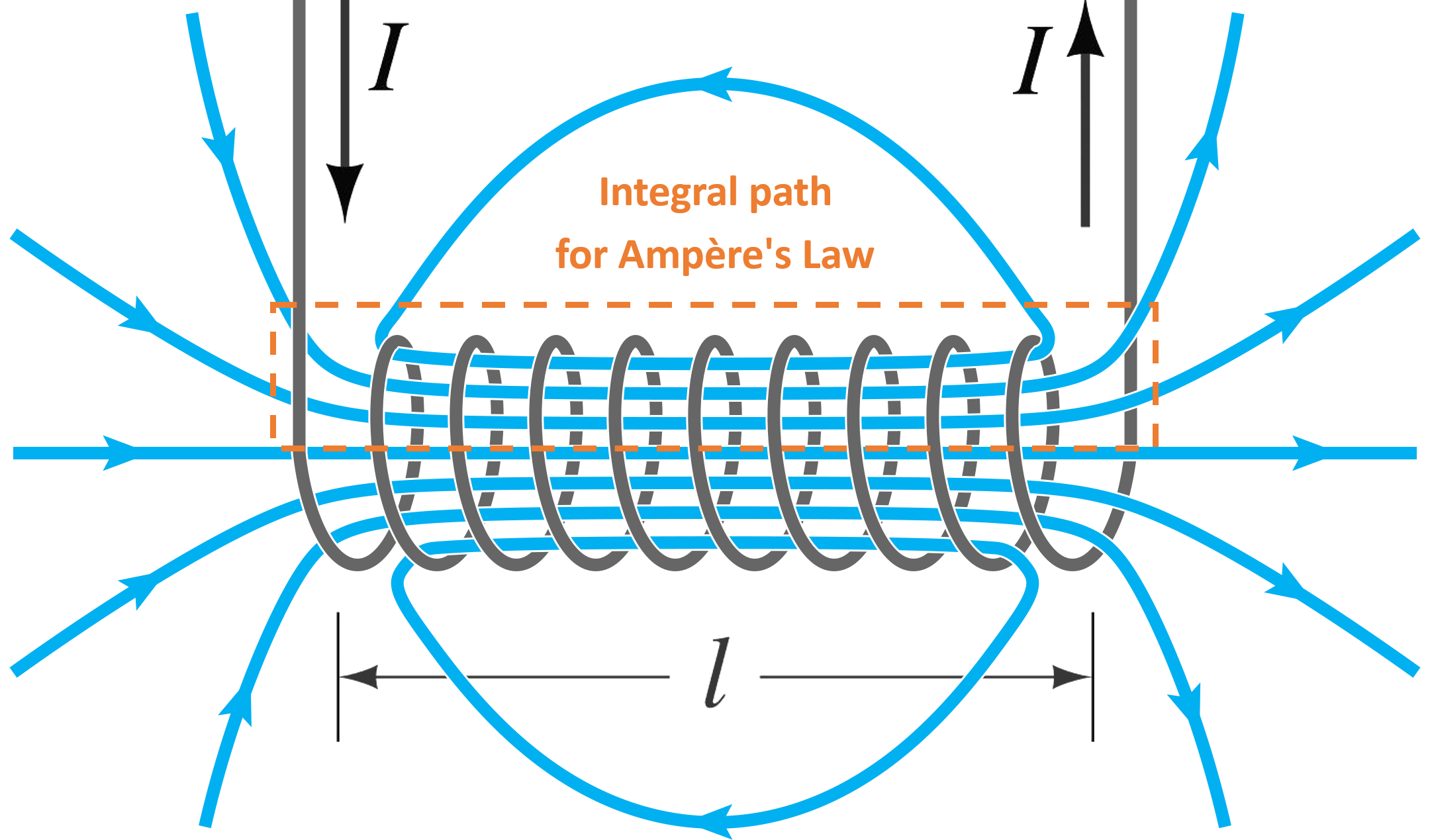
솔레노이드에 암페어의 회로 법칙을 적용하면 (오른쪽 그림 참조) 다음과 같은 결과를 얻을 수 있다.

:

B l= \mu_0 N I,

여기서

B

는 자기 선속 밀도,

l

은 솔레노이드의 길이,

\mu_0

는 자기 상수,

N

은 턴 수,

I

는 전류이다. 이로부터 다음을 얻는다.

:

B = \mu_0 \frac{N I}{l}.

이 방정식은 자유 공간에서의 솔레노이드에 유효하며, 이는 자기 경로의 투자율이 자유 공간의 투자율 μ₀와 동일함을 의미한다.

솔레노이드가 상대 투자율 μ_r인 물질에 잠겨 있는 경우, 자기장은 그만큼 증가한다.

:

B = \mu_0 \mu_{\mathrm{r}} \frac{N I}{l}.

강자성 코어, 예를 들어 철의 포함은 솔레노이드의 자기 선속 밀도의 크기를 증가시키고 자기 경로의 유효 투자율을 높인다. 이것은 다음 공식으로 표현된다.

:

B = \mu_0 \mu_{\mathrm{eff}} \frac{N I}{l} = \mu \frac{N I}{l},

여기서 ''μ''_eff는 코어의 유효 또는 외관상 투자율이다.

== 솔레노이드 외부 자기장 ==

자기력선은 전기력선과 달리 고리 형태를 이루어야 한다. 점전하는 서로 갈라지는 전기장선을 만들지만, 하나의 자기쌍극자는 고리 형태의 자기장선을 만든다. 무한히 긴 솔레노이드의 경우, 바깥 공간에 자기장을 형성할 수 없다. 실험적으로 긴 솔레노이드 밖의 자기장은 솔레노이드의 길이가 길어질수록 0에 수렴한다.^[4]

유사한 논리를 루프 ''a''에 적용하여 솔레노이드 외부의 자기장이 방사상으로 균일하거나 일정하다는 결론을 내릴 수 있다. 자기력선은 루프로만 존재하며, 전기력선처럼 한 점에서 발산하거나 수렴할 수 없다(자기장에 대한 가우스 법칙 참조). 자기력선은 솔레노이드 내부의 종방향 경로를 따르므로, 루프를 형성하기 위해 솔레노이드 외부에서 반대 방향으로 가야 한다. 그러나 솔레노이드 외부의 부피는 내부 부피보다 훨씬 크므로, 외부의 자기력선 밀도가 크게 감소한다. 외부의 자기장이 일정하다고 가정하면, 총 자기력선 수를 보존하기 위해서는 솔레노이드가 길어짐에 따라 외부의 자기장이 0으로 가야 한다. 솔레노이드가 전선 나선형으로 구성된 경우, 솔레노이드의 전체 길이를 따라 전류가 흐르기 때문에 단일 전선과 마찬가지로 외부 자기장을 방출한다.

4. 1. 1. 솔레노이드 내부 자기장

솔레노이드에서 앙페르 법칙을 쓰면 한 단면적에서 어느 점에서나 자기장이 일정하다는 것을 보일 수 있다. 무한한 도선에선 솔레노이드 어느 부분의 중심을 잡아도 자기장이 일정하므로 솔레노이드 모든 점에서 자기장이 균일하다.

옆의 그림에서 b의 앙페르 고리에서 앙페르의 법칙을 사용하면 직사각형의 윗변과 아랫변에서는 자기장의 방향과 적분 방향이 수직하므로 적분값이 0이고, 오른쪽 변에서는 자기장이 0이므로 적분값도 0이다. 결과적으로 직사각형의 왼쪽 변의 길이를 l이라고 하면 앙페르의 법칙에 의해

:

\int B \,dl = \mu_0 i n l

이다. 여기서 n은 단위 길이당 감겨 있는 도선의 수이다.

솔레노이드 내부에서 자기장의 세기는 일정하므로

:

\int B \,dl = B l = \mu_0 i n l

이고, 따라서

:

B = \mu_0 i n

이다.

무한히 긴 솔레노이드 내부의 자기장은 균일하며, 그 세기는 축으로부터의 거리나 솔레노이드의 단면적에 의존하지 않는다.

솔레노이드에 암페어의 회로 법칙을 적용하면 (오른쪽 그림 참조) 다음과 같은 결과를 얻을 수 있다.

:

B l= \mu_0 N I,

여기서

B

는 자기 선속 밀도,

l

은 솔레노이드의 길이,

\mu_0

는 자기 상수,

N

은 턴 수,

I

는 전류이다. 이로부터 다음을 얻는다.

:

B = \mu_0 \frac{N I}{l}.

이 방정식은 자유 공간에서의 솔레노이드에 유효하며, 이는 자기 경로의 투자율이 자유 공간의 투자율 μ₀와 동일함을 의미한다.

솔레노이드가 상대 투자율 μ_r인 물질에 잠겨 있는 경우, 자기장은 그만큼 증가한다.

:

B = \mu_0 \mu_{\mathrm{r}} \frac{N I}{l}.

강자성 코어, 예를 들어 철의 포함은 솔레노이드의 자기 선속 밀도의 크기를 증가시키고 자기 경로의 유효 투자율을 높인다. 이것은 다음 공식으로 표현된다.

:

B = \mu_0 \mu_{\mathrm{eff}} \frac{N I}{l} = \mu \frac{N I}{l},

여기서 ''μ''_eff는 코어의 유효 또는 외관상 투자율이다.

4. 1. 2. 솔레노이드 외부 자기장

자기력선은 전기력선과 달리 고리 형태를 이루어야 한다. 점전하는 서로 갈라지는 전기장선을 만들지만, 하나의 자기쌍극자는 고리 형태의 자기장선을 만든다. 무한히 긴 솔레노이드의 경우, 바깥 공간에 자기장을 형성할 수 없다. 실험적으로 긴 솔레노이드 밖의 자기장은 솔레노이드의 길이가 길어질수록 0에 수렴한다.^[4]

유사한 논리를 루프 ''a''에 적용하여 솔레노이드 외부의 자기장이 방사상으로 균일하거나 일정하다는 결론을 내릴 수 있다. 자기력선은 루프로만 존재하며, 전기력선처럼 한 점에서 발산하거나 수렴할 수 없다(자기장에 대한 가우스 법칙 참조). 자기력선은 솔레노이드 내부의 종방향 경로를 따르므로, 루프를 형성하기 위해 솔레노이드 외부에서 반대 방향으로 가야 한다. 그러나 솔레노이드 외부의 부피는 내부 부피보다 훨씬 크므로, 외부의 자기력선 밀도가 크게 감소한다. 외부의 자기장이 일정하다고 가정하면, 총 자기력선 수를 보존하기 위해서는 솔레노이드가 길어짐에 따라 외부의 자기장이 0으로 가야 한다. 솔레노이드가 전선 나선형으로 구성된 경우, 솔레노이드의 전체 길이를 따라 전류가 흐르기 때문에 단일 전선과 마찬가지로 외부 자기장을 방출한다.

4. 2. 유도 용량 (인덕턴스)

솔레노이드는 유도자의 종류 중 하나로 유도용량(인덕턴스)을 가지며 그 값은 다음과 같다.^[18]

: L = μ₀n²lA

단, μ₀은 진공에서의 투자율, n은 단위 길이당 감긴 도선의 수, l은 솔레노이드의 길이, A는 솔레노이드의 단면적이다.

유도용량, L은 유도자에 전류 i를 흘렸을 때 생기는 자기 플럭스, Φ_B 에 따라 코일이 N번 감겼을 때 L = NΦ_B / i 로 정의된다.

위에 나타낸 바와 같이, 코일 내부의 자기 선속 밀도 B는 실질적으로 일정하며 다음과 같다.

: B = μ₀(NI/l)

여기서 μ₀는 자기 상수, N은 감은 횟수, I는 전류, l은 코일의 길이이다. 단부 효과를 무시하면, 코일을 통과하는 총 자기 선속은 자기 선속 밀도 B에 단면적 A를 곱하여 얻는다.

: Φ = μ₀(NIA/l)

이것을 인덕턴스의 정의와 결합하면,

: L = NΦ / I

솔레노이드의 인덕턴스는 다음과 같다.

: L = μ₀(N²A/l)

다양한 지름 대 길이 비율을 가진 짧은 솔레노이드의 인덕턴스 표는 Dellinger, Whittmore 및 Ould에 의해 계산되었다.

이것과 더 복잡한 형상의 인덕턴스는 맥스웰 방정식에서 유도될 수 있다. 강체 공심 코일의 경우, 인덕턴스는 코일의 형상과 감은 횟수의 함수이며 전류와 무관하다.

유사한 분석은 자기 코어가 있는 솔레노이드에도 적용되지만, 이는 코일의 길이가 자기 코어의 상대 투자율과 지름의 곱보다 훨씬 큰 경우에만 해당한다. 이는 간단한 분석을 낮은 투자율 코어 또는 극도로 길고 얇은 솔레노이드로 제한한다. 코어의 존재는 위의 방정식에서 자기 상수 ''μ₀''를 ''μ'' 또는 ''μ₀μ_r''로 대체하여 고려할 수 있으며, 여기서 ''μ''는 투자율을 나타내고 ''μ_r''는 상대 투자율을 나타낸다. 강자성체 재료의 투자율은 가해지는 자기 선속에 따라 변하기 때문에, 강자성 코어가 있는 코일의 인덕턴스는 일반적으로 전류에 따라 달라진다는 점에 유의해야 한다.

4. 2. 1. 교류 회로에서의 역할

솔레노이드의 가장 큰 특성은 변하는 전류를 억제하려는 역기전력을 생산한다는 것이다. 이러한 특성은 곧 일정한 직류전원에 연결된 솔레노이드는 별다른 특성을 가지지 않는다는 것이다. 사인파 형태로 진동하는 기전력을 가진 교류전원에 연결되었을 때에는 마치 저항처럼 솔레노이드에서 전압강하가 일어난다. 즉, 솔레노이드를 포함한 유도자는 전류의 변화를 방해하도록 작용한다.

솔레노이드를 포함한 유도자는 변하는 전류에 대해 다음과 같은 역기전력을 만들어낸다.

::

\epsilon = -L\frac{di}{dt}\

여기서 -부호는 발생된 역기전력이 기존의 전류변화와 반대방향으로 작용됨을 의미한다. 예를 들어 전류가 감소하고 있는 경우,

di

는 음수가 되고 역기전력은 양수가 되어 전류가 흐르던 방향으로 기전력을 만든다.

솔레노이드가 포함된 간단한 회로로써 교류전원에 연결되어있는 솔레노이드를 생각해 볼 수 있다.

:

\epsilon=\epsilon_m \sin(\omega t)

로 진동하는 교류전원에 L의 유도용량을 가진 솔레노이드가 연결되었을 경우, 솔레노이드 양 끝단의 전압차는

v_L = V_L \sin(\omega t)

로 나타내어지며, 솔레노이드가 유도자이므로

v_L=L\frac{di}{dt}

가 성립한다. 따라서,

::

\frac{di}{dt} = \frac{V_L}{L} \sin(\omega t)

이다.

i

를 구하기 위해 적분하면

i = \int \,di=\frac{V_L}{L}\int \sin(\omega t)\,dt  = -\left(\frac{V_L}{\omega L}\right) \cos(\omega t)

이고

리액턴스를

X_L = \omega L

로 정의하면 옴의 법칙에서 나타난

V=IR

관계와 같이 리액턴스를 유도자의 저항으로 생각할 수 있다.

4. 2. 2. 에너지 밀도

솔레노이드 안의 자기장은 에너지를 갖고 있다. 솔레노이드에 전류가 흐름으로써 발생된 모든 에너지는 솔레노이드 외부의 자기장이 0이기 때문에 솔레노이드 안에 존재하게 된다. 내부에 자기장이 균일하기 때문에 공간의 에너지 분포도 균일하다. 따라서 솔레노이드 안의 모든 공간은 동일한 에너지 밀도를 갖게 된다.

단면적 A인 무한한 길이의 솔레노이드 중 길이 l인 부분을 살펴보면, 자기장의 에너지 밀도 u_B는 다음과 같다.

: u_B = B² / (2μ₀)

여기서 B는 솔레노이드 내부의 자기장, μ₀는 자기 상수를 나타낸다.

코일 내부의 자기 선속 밀도 B는 실질적으로 일정하며 다음과 같다.

:B = μ₀(NI/l)

여기서 μ₀는 자기 상수, N은 감은 횟수, I는 전류, l은 코일의 길이이다.

4. 3. 유한 솔레노이드

유한 솔레노이드는 유한한 길이를 가진 솔레노이드이다. 연속적이라는 것은 솔레노이드가 개별 코일이 아닌 전도성 물질의 시트에 의해 형성된다는 것을 의미한다. 표면에서 전류가 균일하게 분포되어 있으며, 표면 전류 밀도는 ''K''이고, 원통 좌표계에서는 다음과 같다.

:

\vec{K} = \frac{I}{l} \hat{\phi} .

자기장은 벡터 포텐셜을 사용하여 구할 수 있으며, 반경 ''R''과 길이 ''l''을 갖는 유한 솔레노이드의 경우 원통 좌표

(\rho, \phi, z)

에서 다음을 만족한다.^[5]^[6]

:

A_\phi = \frac{\mu_0 I}{\pi } \frac{R}{l} \left[ \frac{\zeta}{\sqrt{(R+\rho)^2+\zeta^2}} \left( \frac{m+n-mn}{mn}K(m)-\frac{1}{m}E(m) +\frac{n-1}{n} \Pi(n, m) \right) \right]_{\zeta_-}^{\zeta_+},

여기서:

$\zeta_{\pm}=z\pm \frac{l}{2}$ ,
$n = \frac{4R\rho}{(R+\rho)^2}$ ,
$m = \frac{4R\rho}{(R+\rho)^2+\zeta^2}$ ,
$K(m)=\int_0^{\frac\pi 2}\frac{d\theta}{\sqrt{1-m \sin^2 \theta }}$ ,
$E(m)=\int_0^{\frac\pi 2}{\sqrt{1-m \sin^2 \theta} } \,d\theta$ ,
$\Pi(n,m)=\int_0^{\frac\pi 2}\frac{d\theta}{(1-n \sin^2 \theta)\sqrt{1-m \sin^2 \theta }}$ .

여기서,

K(m)

,

E(m)

, 그리고

\Pi(n,m)

는 제 1, 제 2, 제 3종 완전 타원 적분이다.

다음을 사용하여:

:

\vec{B} = \nabla \times \vec{A},

자기 선속 밀도는 다음과 같이 얻어진다.^[7]^[8]^[9]

:

B_\rho = \frac{\mu_0 I}{4\pi} \frac{1}{l\,\rho} \left[\sqrt{(R+\rho)^2+\zeta^2} \biggl( (m-2)K(m) + 2 E(m)\biggr) \right]_{\zeta_-}^{\zeta_+},

:

B_z = \frac{\mu_0 I}{2\pi} \frac{1}{l} \left[ \frac{\zeta}{\sqrt{(R+\rho)^2+\zeta^2}} \left(K(m) + \frac{R-\rho}{R+\rho} \Pi(n, m)\right)\right]_{\zeta_-}^{\zeta_+}.

대칭 축에서, 방사형 성분은 사라지고 축 방향 장 성분은 다음과 같다.

:

B_z = \frac{\mu_0 NI}{2}\left( \frac{z+l/2}{l \sqrt{R^2+(z+l/2)^2}} - \frac{z-l/2}{l \sqrt{R^2+(z-l/2)^2}}\right).

솔레노이드 내부에서, 끝에서 멀리 떨어진 곳(

l/2 - |z| \gg R

)에서, 이는 상수 값

B = \mu_0 N I/l

로 접근한다.

솔레노이드의 반지름이 솔레노이드의 길이보다 훨씬 큰 경우(

R \gg l

), 솔레노이드 중심을 통과하는 자기 선속 밀도(솔레노이드 길이에 평행한 ''z'' 방향, 코일이 ''z''=0에 중심을 둠)는 단일 원형 도체 루프의 선속 밀도로 추정할 수 있다.

:

B_z \approx \frac{\mu_0 INR^2}{2\sqrt{R^2+z^2}^3}

== 불규칙 솔레노이드 ==

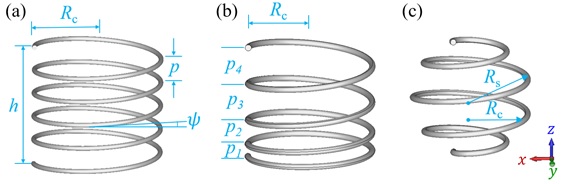
유한 솔레노이드 범주 내에는 단일 피치로 성기게 감긴 것, 다양한 피치로 성기게 감긴 것(가변 피치 솔레노이드) 및 각 루프의 반경이 다른 것(비원통형 솔레노이드)이 있다. 이를 "불규칙 솔레노이드"라고 한다. 이들은 무선 전력 전송을 위한 성긴 솔레노이드,^[10]^[11] 자기 공명 영상(MRI)을 위한 가변 피치 솔레노이드,^[12] 및 기타 의료 기기를 위한 비원통형 솔레노이드와 같은 다양한 분야에서 응용 분야를 찾았다.^[13]

내부 인덕턴스 및 커패시턴스의 계산은 기존 솔레노이드, 즉 촘촘하게 감긴 솔레노이드에 사용되는 공식을 사용하여 수행할 수 없다. 내부 인덕턴스^[14] 및 커패시턴스^[16]를 계산하기 위한 새로운 계산 방법이 제안되었다.

4. 3. 1. 불규칙 솔레노이드

유한 솔레노이드 범주 내에는 단일 피치로 성기게 감긴 것, 다양한 피치로 성기게 감긴 것(가변 피치 솔레노이드) 및 각 루프의 반경이 다른 것(비원통형 솔레노이드)이 있다. 이를 "불규칙 솔레노이드"라고 한다. 이들은 무선 전력 전송을 위한 성긴 솔레노이드,^[10]^[11] 자기 공명 영상(MRI)을 위한 가변 피치 솔레노이드,^[12] 및 기타 의료 기기를 위한 비원통형 솔레노이드와 같은 다양한 분야에서 응용 분야를 찾았다.^[13]

내부 인덕턴스 및 커패시턴스의 계산은 기존 솔레노이드, 즉 촘촘하게 감긴 솔레노이드에 사용되는 공식을 사용하여 수행할 수 없다. 내부 인덕턴스^[14] 및 커패시턴스^[16]를 계산하기 위한 새로운 계산 방법이 제안되었다.

5. 이용

솔레노이드는 제조과정이 간단하고 경제성이 있어 일상 생활용품, 사무용품, 자동차부품 등 다양한 분야에 쓰인다.

솔레노이드에 전류가 흘러 자기장이 형성되면 근처의 철제 물체에 인력을 작용하는 성질을 이용하여 관의 개폐를 전기적 신호로 제어할 수 있는 밸브를 만들 수 있다. 압축공기의 유압을 제어하여 자동으로 문을 열고 닫는 버스의 개폐문이나 정수기에서 쓰이는 자동 냉, 온수 잠금장치 등이 이러한 솔레노이드 밸브를 사용하고 있다. 또한 버튼을 눌렀다 놓을 때 흐르는 전류를 이용해 철제 종을 쳐서 소리를 내는 현관문의 알림벨도 이러한 솔레노이드의 특성을 이용한다.

왼쪽 그림에서 둥그렇게 보이는 것은 도선의 단면이고 화살표가 표기된 선들은 자기력선을 나타낸 것이다.

공학 분야 등에서는 '''솔레노이드'''라는 말로 액추에이터 등 전자기석 응용 작동 기구를 줄여서 부르는 경우가 많으며, 전자 밸브 (솔레노이드 밸브)를 줄여서 부르기도 한다. 솔레노이드 액추에이터로 스위치를 움직이는 전자 계전기를 솔레노이드 스위치라고도 한다.

솔레노이드 내에 가동 철심을 설치하고 전류를 흘려 전자기력을 얻을 수 있다. 전자기력에 의해 운동할 수 있는 범위가 좁지만 (스트로크가 짧지만), 철심 내장 솔레노이드 또는 철심 내장 복권 코일은 소형이고 전자기력이 강하며 고속 응답을 얻을 수 있으므로, 유압실린더, 공기압 실린더의 제어, 자동차용 연료 분사 장치의 인젝터 개폐 제어 등 전자기력에 의한 제어기에 사용된다.

가동 철심의 오버런을 방지하기 위해 대부분의 경우 코일의 한쪽 끝은 스토퍼로 막혀 있으며, 또한 스토퍼를 고정 철심으로 하여 자력을 추가하여 흡인력을 강화하는 경우가 많다.

솔레노이드 액추에이터와 전자석의 차이점은 전자가 가동 철심을 갖는 데 반해, 후자의 철심은 고정되어 가동부가 없다는 점이다.

솔레노이드에는 다음과 같은 분류가 있다.

; 리니어와 로터리

: 전자기력이 가동 자성체에 작용했을 경우의 작동 방향을 직선 (linear) 또는 회전 (rotary)인지 구분하기 위해 붙여진다.

; AC (교류)와 DC (직류)

: AC 솔레노이드는 가동 철심을 흡인하는 힘이 일정하며, 동작 속도가 비교적 빠르다 (약 10m/s). 가동 철심이 록되어 소정의 스트로크를 하지 않는 경우, 끌어당기는 위치에서 멀수록 고전류가 흐르므로, 보호 장치가 작동하는 경우가 있다. DC 솔레노이드는 AC 솔레노이드보다 작고 소리도 작지만, 가동 철심의 위치에 따라 흡인하는 힘이 변화하여 동작 속도는 느리고, 전기적 부하는 일정하다는 특징을 갖는다.

; 풀형, 푸시형

: 가동 철심의 어느 쪽을 작용시키는가에 따른다. 풀 (pull) 형은 가동 철심에 직접 대상을 연결하여 당기는 동작을 한다. 푸시 (push) 형은 스토퍼를 관통하여 반대쪽에 푸시 로드를 뻗어 미는 동작을 한다. 어느 쪽에서도 작용 가능한 푸시 풀 (push-pull) 형도 있다.

5. 1. 솔레노이드 밸브

솔레노이드에 전류가 흘러 자기장이 형성되면 근처의 철제 물체에 인력을 작용하는 성질을 이용하여 관의 개폐를 전기적 신호로 제어할 수 있는 밸브를 만들 수 있다. 압축공기의 유압을 제어하여 자동으로 문을 열고 닫는 버스의 개폐문이나 정수기에서 쓰이는 자동 냉, 온수 잠금장치 등이 이러한 솔레노이드 밸브를 사용하고 있다. 또한 버튼을 눌렀다 놓을 때 흐르는 전류를 이용해 철제 종을 쳐서 소리를 내는 현관문의 알림벨도 이러한 솔레노이드의 특성을 이용한다.

5. 2. 전자석

전자석은 전류가 흐르면 자기화되고, 전류를 끊으면 자기화되지 않은 원래의 상태로 되돌아가는 자석을 말한다. 전류의 공급과 상관없이 항상 자기를 유지하는 영구자석과 구분된다. 도선에 전류가 흐르면 도선 주위에 동심원 모양의 자기장이 형성된다. 이러한 원리를 이용하여 영구자석으로는 얻을 수 없는 매우 강력한 자기장을 얻을 수 있다. 원통 모양의 철심에 코일을 감아서 만든 솔레노이드가 가장 간단한 형태의 전자석이다. 전자석의 철심은 어느 정도 자기화가 진행되면 전류를 더 높여도 더 이상 자기화가 진행되지 않는다. 이를 자기포화상태라고 한다.

전자석은 전류를 인위적으로 조정하여 비교적 쉽게 자기장의 세기를 바꿀 수 있다. 그래서 통신기의 계전기부터 1t 이상의 무거운 재료를 끌어올리는 전자기식 기중기까지 널리 이용된다.

왼쪽 그림에서 둥그렇게 보이는 것은 도선의 단면이고 화살표가 표기된 선들은 자기력선을 나타낸 것이다.

5. 3. 변압기

변압기는 유도성 전기 전도체를 통해 전기 에너지를 한 회로에서 다른 회로로 전달하는 장치이다. 1차 회로의 전류 변화는 자기장 변화를 일으키고, 이는 다시 2차 회로에서 전압 변화를 유도한다. 2차 회로에 부하를 연결하면 변압기에서 전류가 생성되어 한 회로에서 다른 회로로 에너지가 전달된다. 이러한 변압기는 전류 변화가 있을 때만 작동하므로 주로 교류 전원의 전압을 변경하는 데 사용된다.

이상적인 변압기에서 2차 회로에서 유도되는 전압(

V_s

)은 1차 회로에서의 전압(

V_p

)에 비례하며, 그 비율은 2차 회로에서 도선을 감은 횟수(

N_s

)와 1차 회로에서 도선을 감은 횟수(

N_p

)의 비율과 같다.

:

\frac{V_s}{V_p} = \frac{N_s}{N_p}

5. 4. 솔레노이드 액추에이터

공학 분야 등에서는 '''솔레노이드'''라는 말로 액추에이터 등 전자기석 응용 작동 기구를 줄여서 부르는 경우가 많으며, 전자 밸브 (솔레노이드 밸브)를 줄여서 부르기도 한다. 솔레노이드 액추에이터로 스위치를 움직이는 전자 계전기를 솔레노이드 스위치라고도 한다.

솔레노이드 내에 가동 철심을 설치하고 전류를 흘려 전자기력을 얻을 수 있다. 전자기력에 의해 운동할 수 있는 범위가 좁지만 (스트로크가 짧지만), 철심 내장 솔레노이드 또는 철심 내장 복권 코일은 소형이고 전자기력이 강하며 고속 응답을 얻을 수 있으므로, 유압실린더, 공기압 실린더의 제어, 자동차용 연료 분사 장치의 인젝터 개폐 제어 등 전자기력에 의한 제어기에 사용된다.

가동 철심의 오버런을 방지하기 위해 대부분의 경우 코일의 한쪽 끝은 스토퍼로 막혀 있으며, 또한 스토퍼를 고정 철심으로 하여 자력을 추가하여 흡인력을 강화하는 경우가 많다.

솔레노이드 액추에이터와 전자석의 차이점은 전자가 가동 철심을 갖는 데 반해, 후자의 철심은 고정되어 가동부가 없다는 점이다.

솔레노이드에는 다음과 같은 분류가 있다.

'''리니어와 로터리:''' 전자기력이 가동 자성체에 작용했을 경우의 작동 방향을 직선 (linear) 또는 회전 (rotary)인지 구분하기 위해 붙여진다.
'''AC (교류)와 DC (직류):''' AC 솔레노이드는 가동 철심을 흡인하는 힘이 일정하며, 동작 속도가 비교적 빠르다 (약 10m/s). 가동 철심이 록되어 소정의 스트로크를 하지 않는 경우, 끌어당기는 위치에서 멀수록 고전류가 흐르므로, 보호 장치가 작동하는 경우가 있다. DC 솔레노이드는 AC 솔레노이드보다 작고 소리도 작지만, 가동 철심의 위치에 따라 흡인하는 힘이 변화하여 동작 속도는 느리고, 전기적 부하는 일정하다는 특징을 갖는다.
'''풀형, 푸시형:''' 가동 철심의 어느 쪽을 작용시키는가에 따른다. 풀 (pull) 형은 가동 철심에 직접 대상을 연결하여 당기는 동작을 한다. 푸시 (push) 형은 스토퍼를 관통하여 반대쪽에 푸시 로드를 뻗어 미는 동작을 한다. 어느 쪽에서도 작용 가능한 푸시 풀 (push-pull) 형도 있다.

5. 4. 1. 분류

솔레노이드에는 다음과 같은 분류가 있다.

; 리니어와 로터리

: 전자기력이 가동 자성체에 작용했을 경우의 작동 방향을 직선 (linear) 또는 회전 (rotary)인지 구분하기 위해 붙여진다.

; AC (교류)와 DC (직류)

: AC 솔레노이드는 가동 철심을 흡인하는 힘이 일정하며, 동작 속도가 비교적 빠르다 (약 10[m/s]). 가동 철심이 록되어 소정의 스트로크를 하지 않는 경우, 끌어당기는 위치에서 멀수록 고전류가 흐르므로, 보호 장치가 작동하는 경우가 있다. DC 솔레노이드는 AC 솔레노이드보다 작고 소리도 작지만, 가동 철심의 위치에 따라 흡인하는 힘이 변화하여 동작 속도는 느리고, 전기적 부하는 일정하다는 특징을 갖는다.

; 풀형, 푸시형

: 가동 철심의 어느 쪽을 작용시키는가에 따른다. 풀 (pull) 형은 가동 철심에 직접 대상을 연결하여 당기는 동작을 한다. 푸시 (push) 형은 스토퍼를 관통하여 반대쪽에 푸시 로드를 뻗어 미는 동작을 한다. 어느 쪽에서도 작용 가능한 푸시 풀 (push-pull) 형도 있다.

6. 한국의 솔레노이드 기술

6. 1. 자동차 산업

6. 2. 가전제품

6. 3. 산업 자동화

6. 4. 의료 기기

7. 전망

참조

_[1] 뉴스 solenoid: Meaning in the Cambridge English Dictionary https://dictionary.c[...] 2017-01-16
_[2] 문서 or equivalently, the diameter of the coil is assumed to be infinitesimally small (Ampère 1823, p. 267: "des courants électriques formants de très-petits circuits autour de cette ligne, dans des plans infiniment rapprochés qui lui soient perpendiculaires").
_[3] 문서 Session of the Académie des sciences of 22 December 1823, published in print in: Ampère, "Mémoire sur la théorie mathématique des phénomènes électro-dynamiques", Mémoires de l'Académie royale des sciences de l'Institut de France 6 (1827), Paris, F. Didot, pp. 267ff. (and figs. 29–33). "l'assemblage de tous les circuits qui l'entourent [viz. l'arc], assemblage auquel j'ai donné le nom de solenoid électro-dynamique, du mot grec σωληνοειδὴς, dont la signification exprime précisement ce qui a la forme d'un canal, c'est-à-dire la surface de cette forme sur laquelle se trouvent tous les circuits." (p. 267). English translation: "the assembly of all the circuits that surround it [viz. the arc], assembly to which I gave the name electro-dynamic solenoid, from the Greek word σωληνοειδὴς, whose meaning precisely expresses what has the shape of a channel, that is to say the surface of this shape on which all the circuits are located". https://www.e-rara.c[...]
_[4] 서적 Introduction to magnetism and magnetic materials CRC press
_[5] 웹사이트 Archived copy http://nukephysik101[...] 2013-03-28
_[6] 웹사이트 Archived copy http://nukephysik101[...] 2021-07-10
_[7] 논문 Berechnung der Induktivität von Spulen 1926-05-01
_[8] 논문 The magnetic field of a finite solenoid https://ntrs.nasa.go[...] 1960-10-01
_[9] 논문 Exact expression for the magnetic field of a finite cylinder with arbitrary uniform magnetization
_[10] 논문 Wireless Power Transfer via Strongly Coupled Magnetic Resonances 2007-07-06
_[11] 논문 Novel coil design for wideband wireless power transfer https://ieeexplore.i[...] 2017-09-28
_[12] 논문 The design of a short solenoid with homogeneous B1 for a low-field portable MRI scanner using genetic algorithm https://cds.ismrm.or[...] 2018-08
_[13] 논문 A Novel Targeted Magnetic Fluid Hyperthermia System Using HTS Coil Array for Tumor Treatment 2013-06
_[14] 논문 An Accurate Model for Fast Calculating the Resonant Frequency of an Irregular Solenoid 2019-07
_[15] 논문 the code for accurate model for fast calculating the resonant frequency of an irregular solenoid https://github.com/w[...] 2021-04-12
_[16] 논문 Modeling the Self-Capacitance of an Irregular Solenoid 2020-10
_[17] 논문 the code for accurate model for self-capacitance of irregular solenoids https://github.com/w[...] 2021-04-12
_[18] 서적 Radio Instruments and Measurements https://books.google[...] 2009-09-07
_[19] 웹사이트 etymonline.com - solenoid http://www.etymonlin[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com