전자기장

1. 개요

전자기장은 전기장과 자기장의 상호작용을 나타내는 물리적 장으로, 역사적으로는 고대 그리스 시대부터 연구가 시작되었다. 19세기에는 맥스웰이 전자기 현상을 통합하여 전자기파의 존재를 예측했으며, 이후 로렌츠, 톰슨 등의 연구를 통해 전자기학의 원자 모델과 전자의 발견이 이루어졌다. 전자기장은 전기장과 자기장으로 표현되며, 특수 상대성 이론에 따라 관측자에 따라 전기장과 자기장이 서로 변환된다. 전자기장은 에너지와 운동량을 가지며, 맥스웰 방정식과 양자전기역학으로 설명된다. 이러한 전자기장은 발전기, 전동기, 통신 기술 등 다양한 분야에 응용되며, 인체 건강에 미치는 영향에 대한 연구도 진행되고 있다.

2. 역사

전자기 현상에 대한 연구는 기원전 600년경 고대 그리스의 철학자 탈레스가 호박에 동물의 털을 문질러 정전기를 발생시키는 실험을 설명하면서 시작되었다. 18세기에는 같은 종류의 전하를 띤 물체는 서로 밀어내고, 다른 종류의 전하를 띤 물체는 서로 끌어당기며, 이 힘의 세기는 거리의 제곱에 반비례한다는 것이 알려졌다. 마이클 패러데이는 전하 사이에 작용하는 힘을 전기장이라는 개념으로 설명했다. 전기장은 전하가 정지해 있을 때 생성되고, 전하가 움직여 전류를 생성할 때 자기장과 전기장이 함께 생성된다. 시간이 지나면서 전기장과 자기장은 더 큰 전체인 전자기장의 두 부분으로 보는 것이 더 낫다는 것을 깨닫게 되었다.

1820년 한스 크리스티안 외르스테드는 전류가 흐르는 도선 주위에 자기장이 발생한다는 것을 발견했고, 1831년 마이클 패러데이는 시간에 따라 변하는 자기장이 전류를 유도할 수 있다는 것을 알아냈다. 1861년 제임스 클러크 맥스웰은 그 당시까지의 모든 전기 및 자기 현상에 대한 연구를 하나의 수학적 이론으로 종합하여 빛이 전자기파임을 추론했다.

맥스웰의 이론은 물질의 원자 모델을 뒷받침하는 증거가 나타날 때까지 매우 성공적이었다. 1877년 헨드릭 로런츠는 전자기 현상의 원자 모델을 제시했고, 1897년 J. J. 톰슨은 전자를 발견했다. 로런츠 이론은 전자기장 내의 자유 전하에 대해서는 작동하지만, 원자와 분자 내의 속박 전하에 대한 에너지 스펙트럼을 예측하지 못한다. 그 문제는 양자 역학이 필요하며, 궁극적으로 양자 전기 역학 이론으로 이어진다.

전자기장에 대한 새로운 이해를 바탕으로 1800년대 후반에는 발전기와 모터와 같은 실용적인 응용이 등장하기 시작했다.

2.1. 한국에서의 전자기학 발전

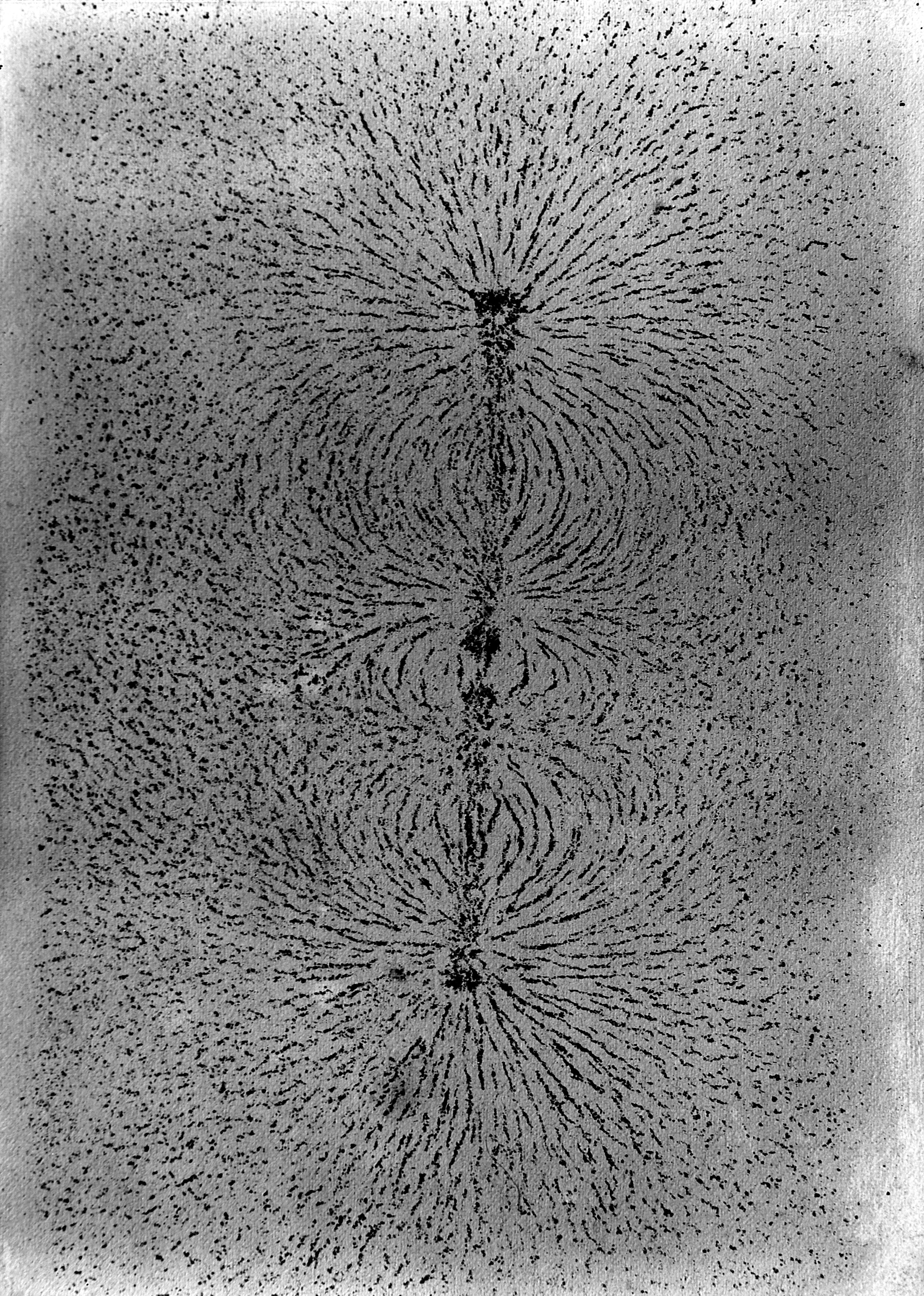
한국에서의 전자기학 발전은 고대부터 축적된 전자기 현상에 대한 이해를 바탕으로 이루어졌다. 기원전 600년경 탈레스는 호박과 동물의 털을 이용한 정전기 실험을 통해 전자기 현상을 처음으로 관찰했다. 18세기에는 같은 종류의 전하는 서로 밀어내고, 다른 종류의 전하는 서로 끌어당긴다는 사실과 이 힘의 세기가 거리의 제곱에 반비례한다는 사실이 밝혀졌다. 마이클 패러데이는 전하 사이에 작용하는 힘을 전기장이라는 개념으로 설명했다.

1820년 한스 크리스티안 외르스테드는 전류가 흐르는 도선 주위에 자기장이 발생한다는 것을 발견했고, 1831년 마이클 패러데이는 시간에 따라 변하는 자기장이 전류를 유도할 수 있다는 것을 알아냈다. 1861년 제임스 클러크 맥스웰은 전기와 자기 현상을 통합한 전자기 이론을 발표하고 빛이 전자기파의 일종임을 밝혔다.

1877년 헨드릭 로런츠는 전자기 현상의 원자 모델을 제시했고, 1897년 J. J. 톰슨은 전자를 발견했다. 이후 양자 역학과 양자 전기 역학 이론이 발전하면서 전자기장에 대한 이해가 더욱 깊어졌다. 이러한 전자기장에 대한 이해를 바탕으로 1800년대 후반에는 발전기와 모터와 같은 실용적인 응용이 등장하기 시작했다.

3. 수학적 기술

전자기장은 3차원 벡터장인 전기장(E)과 자기장(B)으로 표현된다. 이들은 공간과 시간의 함수로 나타낼 수 있으며, , 와 같이 표기한다.

만약 전기장만 존재하고 시간에 따라 변하지 않으면 정전기장, 자기장만 존재하고 시간에 따라 변하지 않으면 정자기장이라고 한다. 그러나 둘 중 하나라도 시간에 따라 변하면 맥스웰 방정식을 사용하여 두 장을 모두 결합된 전자기장으로 고려해야 한다.

특수 상대성 이론의 등장으로 물리 법칙은 텐서의 형식으로 표현되기 시작했다. 맥스웰 방정식도 텐서 형태로 쓸 수 있으며, 이는 물리학자들이 물리 법칙을 표현하는 더 우아한 방법으로 간주한다.

전기장과 자기장의 거동은 맥스웰 방정식으로 기술된다. 벡터장 형식에서 맥스웰 방정식은 다음과 같다.

; 가우스 법칙 : $\backslash nabla\; \backslash cdot\; \backslash mathbf\{E\}\; =\; \backslash frac\{\backslash rho\}\{\backslash varepsilon\_0\}$
; 자기장에 대한 가우스 법칙 : $\backslash nabla\; \backslash cdot\; \backslash mathbf\{B\}\; =\; 0$
; 패러데이 법칙 : $\backslash nabla\; \backslash times\; \backslash mathbf\{E\}\; =\; -\backslash frac\; \{\backslash partial\; \backslash mathbf\{B\}\}\{\backslash partial\; t\}$
; 앙페르-맥스웰 법칙 : $\backslash nabla\; \backslash times\; \backslash mathbf\{B\}\; =\; \backslash mu\_0\; \backslash mathbf\{J\}\; +\; \backslash mu\_0\backslash varepsilon\_0\; \backslash frac\{\backslash partial\; \backslash mathbf\{E\}\}\{\backslash partial\; t\}$

여기서 $\backslash rho$는 전하 밀도, $\backslash varepsilon\_0$는 진공 유전율, $\backslash mu\_0$는 진공 투자율, 는 전류 밀도 벡터이다. 선형 물질 내부에서는 맥스웰 방정식이 변하며, 전자기장에 대해 더 복잡한 반응을 보이는 물질에서는 복소수 또는 텐서로 표현되기도 한다.

로렌츠 힘 법칙은 전자기장과 대전된 물질의 상호 작용을 기술한다.

정전기학과 정자기학은 전하가 움직이지 않는 상황에서의 전자기 현상을 다룬다. 이 경우 맥스웰 방정식은 다음과 같이 단순화된다.

* 정전기학:
$$\backslash nabla\; \backslash cdot\; \backslash mathbf\{E\}\; =\; \backslash frac\{\backslash rho\}\{\backslash epsilon\_0\}$$
$$\backslash nabla\backslash times\backslash mathbf\{E\}\; =\; 0,$$

* 정자기학:
$$\backslash nabla\; \backslash cdot\; \backslash mathbf\{B\}\; =\; 0$$
$$\backslash nabla\; \backslash times\; \backslash mathbf\{B\}\; =\; \backslash mu\_0\; \backslash mathbf\{J\}.$$

특수 상대성 이론에 따르면, 전기장과 자기장은 관측자의 운동 상태에 따라 서로 변환된다. 즉, 한 관측자가 전기장만으로 설명하는 현상을 다른 관성 기준틀의 관측자는 전기장과 자기장의 조합으로 설명할 수 있다. 이를 장의 로렌츠 변환이라고 한다.

좌표계 O에서 전기장 $\backslash mathbf\{E\}$, 자기장(자속밀도) $\backslash mathbf\{B\}$가 존재할 때, x축 방향으로 속도 v로 운동하는 좌표계 O'에서는 다음과 같은 전자기장 $\backslash mathbf\{E\}\text{'}$, $\backslash mathbf\{B\}\text{'}$로 관측된다.

:$E\text{'}\_x\; =\; E\_x,\; \backslash \; \backslash \; E\text{'}\_y\; =\; \backslash frac\{\; E\_y\; -\; v\; B\_z\; \}\{\; \backslash sqrt\{\; 1\; -\; v^2/c^2\; \}\; \}\; ,\; \backslash \; \backslash \; E\text{'}\_z\; =\; \backslash frac\{\; E\_z\; +\; v\; B\_y\; \}\{\; \backslash sqrt\{\; 1\; -\; v^2/c^2\; \}\; \}$
:$B\text{'}\_x\; =\; B\_x,\; \backslash \; \backslash \; B\text{'}\_y\; =\; \backslash frac\{\; B\_y\; +\; v\; c^\{-2\}\; E\_z\; \}\{\; \backslash sqrt\{\; 1\; -\; v^2/c^2\; \}\; \}\; ,\; \backslash \; \backslash \; B\text{'}\_z\; =\; \backslash frac\{\; B\_z\; -\; v\; c^\{-2\}\; E\_y\; \}\{\; \backslash sqrt\{\; 1\; -\; v^2/c^2\; \}\; \}$

특히 $v\; /\; c\; \backslash ll\; 1$일 때, 다음과 같이 근사할 수 있다.

:$\backslash mathbf\{E\}\text{'}\; =\; \backslash mathbf\{E\}\; -\; \backslash mathbf\{B\}\; \backslash times\; \backslash mathbf\{v\}\; ,\; \backslash \; \backslash mathbf\{B\}\text{'}\; =\; \backslash mathbf\{B\}\; +\; \backslash frac\{\; 1\; \}\{\; c^2\; \}\; \backslash mathbf\{E\}\; \backslash times\; \backslash mathbf\{v\}$

$\backslash mathbf\{E\}^2\; -\; c^2\; \backslash mathbf\{B\}^2$와 $\backslash mathbf\{E\}\; \backslash cdot\; \backslash mathbf\{B\}$는 로렌츠 불변량이다. 전기장과 자기장은 전자기 텐서라는 단일 반대칭 텐서로 통합적으로 다룰 수 있다.

4. 전자기장의 성질

전자기장은 자체로 에너지와 운동량을 가진다. 에너지 밀도($u$)와 운동량 밀도($\backslash mathbf\{p\}$)는 다음과 같이 주어진다.

:$u\; =\; \backslash frac\{\; \backslash varepsilon\_0\; \}\{\; 2\; \}\; \backslash mathbf\{E\}^2\; +\; \backslash frac\{\; 1\; \}\{\; 2\; \backslash mu\_0\; \}\; \backslash mathbf\{B\}^2$
:$\backslash mathbf\{p\}\; =\; c^2\; \backslash mathbf\{S\}\; ,\; \backslash \; \backslash \; \backslash mathbf\{S\}\; =\; \backslash frac\{\; 1\; \}\{\; \backslash mu\_0\; \}\; \backslash mathbf\{E\}\; \backslash times\; \backslash mathbf\{B\}$

여기서 $\backslash mathbf\{S\}$는 포인팅 벡터이다.

에너지 보존 법칙은 다음 연속 방정식으로 표현된다.

:$\backslash frac\{\; \backslash partial\; u\; \}\{\; \backslash partial\; t\; \}\; +\; \backslash nabla\; \backslash cdot\; \backslash mathbf\{S\}\; =\; 0\; ,\; \backslash \; \backslash \; \backslash frac\{\; \backslash partial\; \backslash mathbf\{p\}\; \}\{\; \backslash partial\; t\; \}\; +\; \backslash nabla\; \backslash cdot\; \backslash sigma\; =\; 0$

여기서 포인팅 벡터는 전자기장의 운동량 밀도와 에너지 유속 밀도를 나타내며, $\backslash sigma$는 맥스웰의 응력 텐서이다.

:$\backslash sigma\_\{i\; j\}\; =\; \backslash varepsilon\_0\; \backslash left(\; -\; E\_i\; E\_j\; +\; \backslash frac\{\; 1\; \}\{\; 2\; \}\; \backslash delta\_\{i\; j\}\; \backslash mathbf\{E\}^2\; \backslash right)\; +\; \backslash frac\{\; 1\; \}\{\; \backslash mu\_0\; \}\; \backslash left(\; -\; B\_i\; B\_j\; +\; \backslash frac\{\; 1\; \}\{\; 2\; \}\; \backslash delta\_\{i\; j\}\; \backslash mathbf\{B\}^2\; \backslash right)$

전하가 전하 밀도 ρ로 분포하는 경우와 전류가 전류 밀도 j로 분포하는 경우, 다음과 같은 에너지를 저장할 수 있다.

* 전하 분포의 경우

:$U\_e\; =\; \backslash frac\{1\}\{2\}\; \backslash int\; \backslash rho(\backslash mathbf\{r\})\; \backslash phi(\backslash mathbf\{r\})d^3\; r$ 또는 $U\_e\; =\; \backslash frac\{1\}\{8\; \backslash pi\; \backslash varepsilon\_0\}\; \backslash int\; \backslash frac\{\backslash rho(\backslash mathbf\{r\})\; \backslash rho(\backslash mathbf\{r\}\text{'})\}$

↑ 맨 위로