맨위로가기

수소 분자 이온

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

수소 분자 이온은 수소 분자가 우주선에 의해 전자를 잃어 생성되는 분자 이온이다. 자연계에서는 우주선과 수소 분자의 상호 작용으로 형성되며, 성간 물질의 화학에서 중요한 역할을 한다. 수소 분자 이온은 수소 분자와 반응하여 삼수소 양이온을 생성하고, 실험실에서는 전자총이나 플라스마 방전을 통해 생성할 수 있다. 이온의 결합은 1/2의 결합 차수를 가지는 일전자 결합으로 설명되며, 동위체는 6가지가 존재한다. 양자역학적 분석을 통해 전자 상태와 에너지, 물리적 성질을 연구하며, 정밀 분광학을 통해 이론적 계산과 실험 결과를 비교하여 분자의 구조를 파악한다.

더 읽어볼만한 페이지

  • 양자 모형 - 상자 속 입자
    상자 속 입자는 양자역학에서 입자가 특정 영역에 갇혀 움직이는 이상적인 시스템으로, 슈뢰딩거 방정식을 통해 파동 함수와 양자화된 에너지 준위를 구할 수 있으며, 다양한 물리적 시스템을 이해하는 데 기초가 된다.
  • 양자 모형 - 유한 퍼텐셜 우물
    유한 퍼텐셜 우물은 1차원 공간에서 특정 영역 내 유한한 음의 퍼텐셜 에너지를 갖고, 그 외 영역에서는 0의 값을 가지며, 입자의 양자역학적 거동은 슈뢰딩거 방정식으로 기술되고 다양한 형태와 해를 가진다.
  • 양이온 - 양성자
    양성자는 양(+) 전하를 띠는 기본 입자이자 원자핵을 구성하는 핵자이며, 수소 원자핵으로 화학에서 수소 이온을 의미하며, 브뢴스테드-로우리 산-염기 이론에서 양성자 주개로 정의된다.
  • 양이온 - 하이드로늄 이온
    하이드로늄 이온(H₃O⁺)은 수용액에서 자체 이온화되거나 강산 첨가 시 생성되는 이온으로, 삼각뿔 형태의 분자 구조를 가지며 수용액의 산성도 pH 결정 및 성간 매질 분자 구름 내 화학 반응에 중요한 역할을 한다.
  • 수소물리학 - 보어 모형
    보어 모형은 닐스 보어가 러더퍼드 모형의 한계를 극복하기 위해 양자 개념을 도입하여 전자의 궤도와 각운동량이 양자화된다는 가정으로 수소 원자의 스펙트럼을 설명했지만, 다전자 원자와 불확정성 원리의 모순으로 양자역학에 의해 대체된 원자 모형이다.
  • 수소물리학 - 수소 이온
    수소 이온(H⁺)은 양성자와 같지만 수용액에서 물 분자와 결합하여 다양한 수화 이온을 형성하고, pH 농도 측정과 산-염기 반응, 전기 전도도, 생명체의 에너지 생산 등 다양한 현상과 관련이 있다.
수소 분자 이온 - [화학 물질]에 관한 문서
개요
수소 분자 이온의 루이스 구조
식별
화학식H₂⁺
CAS 등록번호12184-90-6
ChEBI29293
29297
29295
29296
표준 InChI1S/H2/h1H/q+1
표준 InChIKeyZZIJOQHRUPVPQC-UHFFFAOYSA-N
SMILES[HH+]
InChI (아이소토프)1S/H2/h1H/q+1/i1+0H
InChIKey (아이소토프)ZZIJOQHRUPVPQC-HXFQMGJMSA-N
SMILES (아이소토프 1)[1H][1H+]
InChI (아이소토프 2)1S/H2/h1H/q+1/i1+1D
InChIKey (아이소토프 2)ZZIJOQHRUPVPQC-VVKOMZTBSA-N
SMILES (아이소토프 2)[2H][2H+]
InChI (아이소토프 3)1S/H2/h1H/q+1/i1+2T
InChIKey (아이소토프 3)ZZIJOQHRUPVPQC-JMRXTUGHSA-N
SMILES (아이소토프 3)[3H][3H+]
속성
포뮬러 전하+

2. 형성과정

수소 분자 이온(H₂⁺)은 수소 분자(H₂)가 우주선에 의해 전자를 잃고 생성된다.[24]

:H₂ + 우주선 → H₂⁺ + e⁻ + 우주선

이후 수소 분자 이온은 주변의 수소 분자와 반응하여 삼수소 양이온(H₃⁺)을 생성한다.[24]

:H₂⁺ + H₂ → H₃⁺ + H

수소 분자의 이온화 에너지는 15.603 eV이다. 고속 전자는 약 50 eV에서 최대 단면적을 가지며 수소 분자를 이온화시킨다. 고속 양성자의 이온화에 대한 최대 단면적은 이며 단면적은 이다. 낮은 에너지의 우주선 양성자는 중성 수소 분자에서 전자를 떼어내어 중성 수소 원자와 수소 분자 양이온을 형성할 수 있으며, (\\p^+ + H2 -> H + H2^+) 약 에서 최대 단면적이 이다.[25]

2. 1. 우주 공간에서의 생성

우주선은 높은 에너지를 가지고 있어서, 수소 분자(H₂)와 충돌하면 전자를 떼어내면서 수소 분자 이온(H₂⁺)을 생성한다.[24][36]

:H₂ + 우주선 → H₂⁺ + e⁻ + 우주선

우주선 입자는 멈추기 전에 많은 분자를 이온화할 만큼 충분한 에너지를 가지고 있다.

수소 분자의 이온화 에너지는 15.603 eV이다. 고속 전자는 약 50 eV에서 최대 단면적을 가지며 수소 분자를 이온화시킨다. 고속 양성자의 이온화에 대한 최대 단면적은 이며 단면적은 이다. 낮은 에너지의 우주선 양성자는 중성 수소 분자에서 전자를 떼어내어 중성 수소 원자와 수소 분자 양이온을 형성할 수 있으며, (p⁺ + H₂ → H + H₂⁺) 약 에서 최대 단면적이 이다.[25]

이렇게 생성된 H₂⁺는 주변의 수소 분자(H₂)와 반응하여 삼수소 양이온(H₃⁺)을 생성한다.[24]

:H₂⁺ + H₂ → H₃⁺ + H

2. 2. 실험실에서의 생성

실험실에서는 전자총에서 방출된 전자를 수소 분자와 충돌시켜 수소 분자 이온을 생성할 수 있다. 인공적인 플라스마 방전 셀에서도 수소 분자 이온이 생성될 수 있다.

3. 물리적 성질

수소 분자 이온(H2^+)의 결합은 결합 차수가 1/2인 일전자 결합(또는 공유 결합)으로 설명될 수 있다.[2][27] 이온의 바닥 상태 에너지는 -0.597 하트리이다.[3][28] 결합 길이는 2.00 보어 반지름이다.

3. 1. 동위체

수소 분자 이온은 6개의 동위소체를 가지고 있다. 각 핵은 양성자(p), 중수소(d), 삼중수소 핵종(t) 중 하나가 될 수 있다.[4][5]

  • H (이수소 양이온, 흔한 것)[4][5]
  • [HD] ([H영어H영어] 수소 중수소 양이온)[4]
  • D (이중수소 양이온)[4][5]
  • [HT] ([H영어H영어] 수소 삼중수소 양이온)
  • [DT] ([H영어H영어] 중수소 삼중수소 양이온)
  • T (이삼중수소 양이온)[5]

4. 양자역학적 분석

수소 분자 이온에 대한 최초의 양자역학적 접근은 덴마크 물리학자 외빈 부라우(Øyvind Burrau)가 에르빈 슈뢰딩거의 파동 방정식 발표 1년 후인 1927년에 이루어졌다.[29] 초기 양자론을 이용한 초기 연구는 1922년 카렐 니센(Karel Niessen)한국어[30]과 볼프강 파울리[31], 1925년 해럴드 유레이[32]에 의해 발표되었다. 1928년 라이너스 폴링은 부라우의 연구와 발터 하이틀러, 프리츠 런던의 수소 분자 연구를 종합한 논문을 발표했다.[33]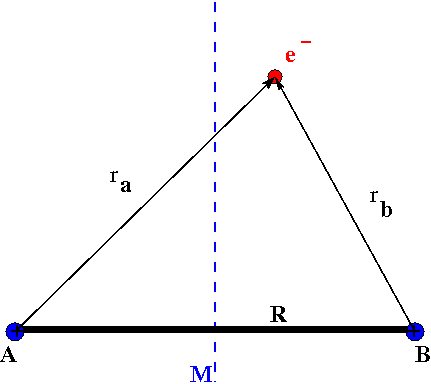

수소 분자 이온: 전자 하나와 두 개의 수소 원자핵(A, B)


수소 분자 이온은 두 개의 수소 원자핵(A, B)과 하나의 전자로 구성된다. 이 이온의 해밀토니안은 \hat{H}=-{\hbar \over 2m}\nabla^2 +V로 표현 가능하다. 여기서 V는 전자에 작용하는 쿨롱 퍼텐셜로, 다음과 같다.

V=-\frac{e^2} {4\pi \varepsilon_0}\left ( \frac{1}{r_A}+\frac{1}{r_B}-\frac{1}{R} \right )

수소 분자 이온의 전자에 대한 슈뢰딩거 방정식은 다음과 같이 쓸 수 있다.

\left (- \frac{\hbar^2}{2m} \nabla^2 +V\right )\psi=E\psi

핵의 운동은 전자에 비해 무시할 정도로 작다고 가정하면, 핵간 거리 R은 고정된 것으로 간주한다(보른-오펜하이머 근사). 이 방정식은 정확하게 풀 수 있다. 직교 좌표계 대신 타원체 좌표계를 사용하면, 파동 방정식(편미분 방정식)은 두 개의 연립 상미분 방정식으로 분리된다.[6] 이 방정식의 해, 즉 파동 함수는 두 개의 무한 멱급수 곱에 비례한다.[6] 급수의 수치적 계산은 컴퓨터로 쉽게 수행할 수 있다. 전자 에너지 고윳값에 대한 해석해는 실험 수학적 접근 방식에서 컴퓨터 대수 시스템을 통해 얻을 수 있는 램버트 W 함수의 일반화로도 표현된다.[7]

4. 1. 고정 핵 근사 (Clamped-nuclei approximation)

이수소 양이온에 대한 근사적인 설명은 원자핵의 움직임을 무시하는 것, 즉 소위 고정된 핵 근사에서 시작한다. 이 근사는 핵(양성자, 중수소 또는 삼중수소)이 전자의 1000배 이상 무겁기 때문에 좋은 근사이다.[6] 따라서 주어진(임의의) 핵-핵 거리 ''R''에 대해 전자의 움직임을 먼저 처리한다. 분자의 전자 에너지 ''E''를 계산하고, ''R''의 다른 값에 대해 계산을 반복한다. 핵-핵 반발 에너지 ''e''2/(4를 전자 에너지에 더하여 총 분자 에너지 ''E''tot(''R'')를 얻는다.

에너지 ''E''는 단일 전자에 대한 슈뢰딩거 방정식의 고유값이다. 이 방정식은 전자-전자 반발력의 부재(전자 상관 관계)로 인해 비교적 간단한 방법으로 풀 수 있다. 직교 좌표계 대신 타원체 좌표계를 사용하면 파동 방정식(편미분 방정식)이 두 개의 결합된 상미분 방정식으로 분리된다.[6] 방정식의 해석해, 즉 파동 함수는 두 개의 무한 멱급수의 곱에 비례한다.[6] 급수의 수치적 평가는 컴퓨터에서 쉽게 수행할 수 있다. 전자 에너지 고유값에 대한 해석해는 또한 실험 수학적 접근 방식 내에서 컴퓨터 대수 시스템을 사용하여 얻을 수 있는 램버트 W 함수의 ''일반화''이다.[7]

수소 분자 이온은 두 개의 수소 원자핵 A, B와 하나의 전자를 갖는다.

해밀토니안은 \hat{H}=-{\hbar \over 2m}\nabla^2 +V로 쓸 수 있다. 여기서 V는 전자에 작용하는 쿨롱 퍼텐셜이며, 다음과 같다.

V=-\frac{e^2} {4\pi \varepsilon_0}\left ( \frac{1}{r_A}+\frac{1}{r_B}-\frac{1}{R} \right )

수소 분자 이온의 전자에 대한 슈뢰딩거 방정식은 다음과 같이 기술할 수 있다.

\left (- \frac{\hbar^2}{2m} \nabla^2 +V\right )\psi=E\psi

여기서 핵의 운동은 전자의 운동에 비해 무시할 수 있을 정도로 작다는 가정에서 핵간 거리 R은 고정되어 있다고 한다(보른-오펜하이머 근사)면, 이 방정식은 엄밀하게 풀 수 있다.

4. 2. 보른-오펜하이머 근사 (Born-Oppenheimer approximation)



수소 분자 이온은 두 개의 수소 원자핵 A, B와 하나의 전자를 갖는다.

해밀토니안은 \hat{H}=-{\hbar \over 2m}\nabla^2 +V로 쓸 수 있다. 여기서 V는 전자에 작용하는 쿨롱 퍼텐셜이며, 다음과 같다.

V=-\frac{e^2} {4\pi \varepsilon_0}\left ( \frac{1}{r_A}+\frac{1}{r_B}-\frac{1}{R} \right )

수소 분자 이온의 전자에 대한 슈뢰딩거 방정식은 다음과 같이 기술할 수 있다.

\left (- \frac{\hbar^2}{2m} \nabla^2 +V\right )\psi=E\psi

핵의 운동은 전자의 운동에 비해 무시할 수 있을 정도로 작다는 가정에서 핵간 거리 R은 고정되어 있다고 한다(보른-오펜하이머 근사). 이 방정식은 엄밀하게 풀 수 있다.

전체 에너지 함수 ''E''tot(''R'')이 얻어지면, 핵의 회전 및 진동 운동의 양자 상태, 따라서 전체 분자의 양자 상태를 계산할 수 있다. 해당 '핵' 슈뢰딩거 방정식은 핵-핵 거리 ''R''이 독립 좌표인 1차원 상미분 방정식이다. 이 방정식은 두 핵의 환산 질량과 같은 질량을 가진 가상 입자가 포텐셜 ''E''tot(''R'') + ''V''''L''(''R'') 내에서 움직이는 것을 설명하며, 여기서 두 번째 항은 양자수 ''L''로 설명되는 각운동량으로 인한 원심 포텐셜이다. 이 슈뢰딩거 방정식의 고유 에너지는 전자 에너지와 핵 에너지를 합한 전체 분자의 에너지이다.

4. 3. LCAO-MO (Linear Combination of Atomic Orbitals - Molecular Orbital) 방법

분자 궤도법에 따르면, 수소 분자 이온의 분자 궤도 함수는 두 개의 수소 원자의 1s 원자 궤도 함수(\chi)의 선형 결합(LCAO)으로 나타낼 수 있다. 이를 LCAO-MO (Linear Combination of Atomic Orbitals - Molecular Orbital) 방법이라고 한다.

:\psi^{MO}=c_A \chi_A+c_B \chi_B

여기서 c_A와 c_B는 각 원자 궤도 함수의 계수이다. 변분 원리를 사용하여 에너지 기대값이 최소가 되는 \psi^{MO}를 결정한다. 에너지 기대값은 다음과 같이 계산된다.

:E=\frac{\int \psi^{MO^*}\hat{H} \psi^{MO} d\tau}{\int \psi^{MO^*}\psi^{MO} d\tau}

위 식을 전개하면 다음과 같다.

:E = \frac

여기서 H_{AA}=\langle \chi_A |\hat{H}|\chi_A \rangle, H_{AB}=\langle \chi_A |\hat{H}|\chi_B \rangle이며, S_{AB}는 중첩 적분으로 S_{AB}=\langle \chi_A |\chi_B \rangle = \langle \chi_B |\chi_A \rangle이다.

에너지 기대값이 정류값을 갖는 조건은 각 계수에 대한 편미분이 0인 것이다. 이 조건으로부터 다음의 식을 얻는다.

:\begin{cases} \bigl( H_{AA}-E \bigr)c_A+ \bigl( H_{AB}-S_{AB}E \bigr)c_B

=0 \\ \bigl( H_{AB}-S_{AB}E \bigr)c_A+\bigl( H_{BB}-E\bigr)c_B=0 \end{cases}

c_A=c_B=0인 경우는 분자 궤도 함수가 0이 되어 전자가 존재하지 않게 되므로, 물리적으로 의미가 없다. 따라서 다음 영년 방정식을 얻는다.

:\begin{vmatrix} H_{AA}-E & H_{AB} - S_{AB}E \\ H_{AB}-S_{AB}E & H_{BB}-E \end{vmatrix}=0

이 방정식을 풀면, 다음과 같은 두 개의 고유 에너지를 얻는다.

:\begin{cases} E_0=\frac{H_{AA}+H_{AB}}{1+S_{AB}} \\ E_1=\frac{H_{AA}-H_{AB}}{1-S_{AB}} \end{cases}

H_{AA}와 H_{AB}는 다음과 같이 표현된다.

:H_{AA}=E_{H(1s)}+\frac{e^2}{4\pi \varepsilon_0}\left(\frac{1}{R}-J\right)

:H_{AB}=E_{H(1s)}+\frac{e^2}{4\pi \varepsilon_0}\left(\frac{1}{R}-K\right)

따라서, 고유 에너지는 다음과 같이 정리된다.

:\begin{cases} E_0=E_{H(1s)}-\frac{e^2}{4\pi \varepsilon_0}\frac{J+K}{1+S_{AB}}+\frac{e^2}{4\pi \varepsilon_0}\frac{1}{R}

\\ E_1=E_{H(1s)}-\frac{e^2}{4\pi \varepsilon_0}\frac{J-K}{1-S_{AB}}+\frac{e^2}{4\pi \varepsilon_0}\frac{1}{R} \end{cases}

각 식의 두 번째 항은 전자가 안정화되는 정도를, 세 번째 항은 핵 간 반발로 인해 불안정해지는 정도를 나타낸다.

최종적으로, 수소 분자 이온의 분자 궤도 함수는 다음과 같이 구해진다.[34]

:\begin{cases}\psi_0=\frac{1}{\sqrt{2(1+S_{AB})}} (\chi_A+\chi_B) \\ \psi_1=\frac{1}{\sqrt{2(1-S_{AB})}} (\chi_A-\chi_B) \end{cases}

4. 4. 전자 상태와 에너지

수소 분자 이온의 에너지 E를 핵간 거리 R의 함수로 나타낸 그림.


원자핵 간의 중점을 좌표의 원점으로 선택한다. 일반적인 대칭 원리에 따라 분자 궤도 함수는 반전 조작 \boldsymbol{r}\rightarrow-\boldsymbol{r}에 대해 대칭인 파동 함수 \psi_g (\boldsymbol{r})과 비대칭인 파동 함수 \psi_u (\boldsymbol{r})이 존재한다. 즉,

:\psi_{g/u}(-\boldsymbol{r})=\pm \psi_{g/u}(\boldsymbol{r})

여기서, 아래 첨자 g와 u는 독일어로 각각 짝수와 홀수를 나타내는 gerade와 ungerade에서 유래하며, ''g'' 및 ''u'' 첨자로 나타낸다. 이 용어는 이원자 분자의 전자 상태를 지정하는 데 표준적으로 사용되는 반면, 원자 상태의 경우 ''even''과 ''odd''라는 용어가 사용된다.[13] 수소 분자 이온의 바닥 상태(가장 낮은 상태)는 X2Σ 또는 1sσg로 표시되며 gerade이다. 첫 번째 여기 상태는 A2Σ (2pσ''u'')인데, 이것은 ungerade이다.

두 에너지의 차이는 교환 에너지 분할이라고 하며, 핵간 거리 R이 커짐에 따라 지수 함수적으로 감소하며, 다음 식으로 나타낸다.[16][35]

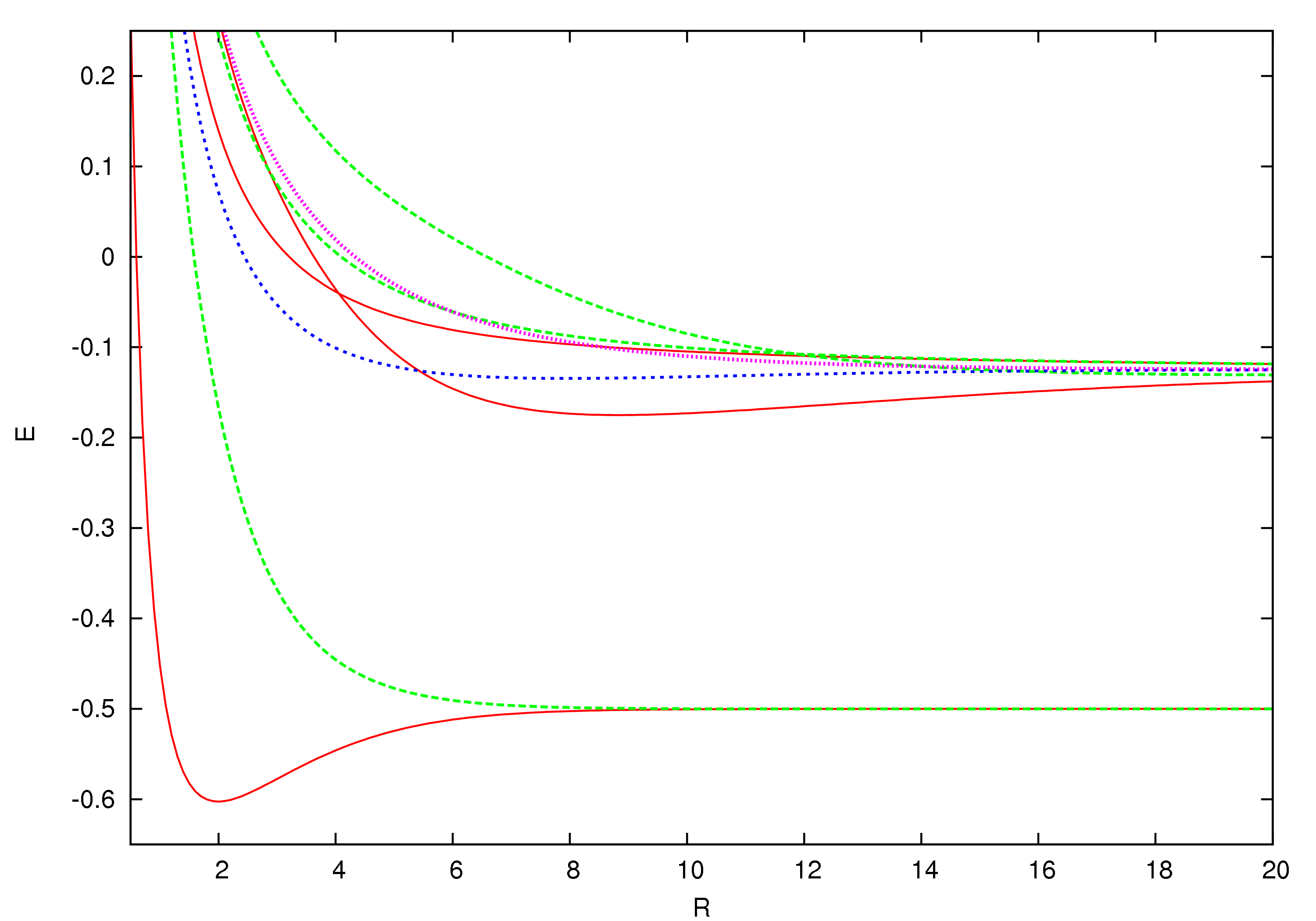
:\Delta E=E_u -E_g=\frac{4}{e}Re^{-R} \left[1+\frac{1}{2R}+O\left(R^{-2}\right)\right]

각 전자 상태에서의 핵간 거리에 대한 에너지를 그래프로 나타낸다. 이것들은 일반화된 램버트 W 함수를 통해 임의의 정밀도 내에서 구할 수 있다.[7]

그래프 내의 빨간 실선은 2Σ 상태, 녹색 파선은 2Σ 상태, 파란 파선은 2Πu 상태, 분홍색 점선은 2Πg 상태를 나타낸다.

5. 실험적 연구

수소 분자 이온은 분광학적 연구를 통해 그 성질이 정밀하게 분석되고 있다.

5. 1. 정밀 분광학 (Precision spectroscopy)

수소 분자 이온은 상대적으로 단순하여, 에너지 준위에 대한 이론적 계산이 실험 결과와 매우 높은 수준으로 일치하는, 가장 정확하게 이해되는 분자이다.

구체적으로, 분광학적으로 결정된 특정 동위체 HD|에이치디영어⁺의 순수 회전 및 회전-진동 전이 주파수는 이론적으로 계산된 전이 주파수와 일치한다. 4개의 고정밀 실험에서 총 불확실성이 에서 사이인 비교 결과가 도출되었다.[22] 이러한 일치 수준은 이론이나 실험 자체의 한계가 아니라, 계산에 사용되는 입자 질량 값의 불확실성 때문에 제한된다.

수소 분자 이온의 전이 주파수를 높은 정확도로 측정하려면 특별한 조건이 필요하다. HD|에이치디영어⁺ 이온 집단은 사중극자 이온 트랩 내 초고진공 상태에 가두고, 레이저 냉각된 베릴륨 이온으로 공명 냉각시킨 후, 특정 분광 기술을 사용하여 분석해야 한다.

동핵 동위체 H2|에이치투영어⁺의 초미세 구조는 1969년 Jefferts에 의해 광범위하고 정확하게 측정되었다. 2021년에는 ab initio 이론 계산을 통해 실험 데이터의 불확실성()보다 작은 불확실성으로 구조의 정량적 세부 사항을 제공할 수 있었다. 측정된 초미세 구조에 대한 일부 기여는 약 수준에서 이론적으로 확인되었다.[23]

이러한 일치는 전자 질량과 감소된 양성자-중수소 질량 비 (''m''e/''m''p+''m''e/''m''d)의 분광학적 값을 추론할 수 있게 한다. 이 비는 이론적 예측과 실험 결과가 일치하도록 조정된다. 얻어진 비의 불확실성은 페닝 트랩 내 사이클로트론 공명을 이용한 양성자, 중수소, 전자, HD⁺의 직접 질량 측정에서 얻은 불확실성과 유사하다.

6. 우주 공간에서의 존재

수소 분자 이온(H₂⁺)은 우주선과 수소 분자의 상호 작용으로 자연적으로 형성되기 때문에 성간 물질의 화학에서 중요한 역할을 한다.[24]

우주선은 수소 분자에서 전자를 떼어내어 수소 분자 이온을 생성한다.

:H₂ + 우주선 → H₂⁺ + e⁻ + 우주선

우주선 입자는 멈추기 전에 많은 분자를 이온화할 만큼 충분한 에너지를 가지고 있다. 수소 분자의 이온화 에너지는 15.603 eV이다. 고속 전자도 약 50 eV에서 최대 단면적을 가지며 수소 분자를 이온화시킨다. 고속 양성자의 이온화에 대한 최대 단면적은 70000 eV이며 단면적은 2.5×10⁻¹⁶ cm²이다. 낮은 에너지의 우주선 양성자는 중성 수소 분자에서 전자를 떼어내어 중성 수소 원자와 수소 분자 양이온을 형성할 수 있으며(p⁺ + H₂ → H + H₂⁺), 약 8000 eV에서 최대 단면적이 8×10⁻¹⁶ cm²이다.[25]

6. 1. 파괴 과정

자연에서 수소 분자 이온은 다른 수소 분자와 반응하여 삼수소 양이온(H₃⁺)을 형성하며 파괴된다.[36]

참조

[1] 논문 Precision spectroscopy of the molecular hydrogen ions: an introduction. https://www.tandfonl[...]
[2] 서적 Valency and bonding: a natural bond orbital donor-acceptor perspective Cambridge University Press
[3] 논문 Nonadiabatic wavefunctions as linear expansions of correlated exponentials. A quantum Monte Carlo application to H2+ and Ps2
[4] 논문 Adiabatic Jacobi corrections on the vibrational energy levels of H2(+) isotopologues
[5] 논문 Kinetic-energy release of fragments from electron-impact dissociation of the molecular hydrogen ion and its isotopologues
[6] 논문 Correction for nuclear motion in H2+
[7] 논문 New Approach for the Electronic Energies of the Hydrogen Molecular Ion
[8] 문서 Zur Quantentheorie des Wasserstoffmolekülions
[9] 논문 Über das Modell des Wasserstoffmolekülions
[10] 논문 The Structure of the Hydrogen Molecule Ion 1925-10
[11] 논문 Berechnung des Energiewertes des Wasserstoffmolekel-Ions ({{chem|H|2|+}}) im Normalzustand. http://gymarkiv.sdu.[...]
[12] 논문 The Application of the Quantum Mechanics to the Structure of the Hydrogen Molecule and Hydrogen Molecule-Ion and to Related Problems
[13] 서적 Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules Van Nostrand Reinhold
[14] 논문 1/''R'' expansion for {{chem|H|2|+}}: Calculation of exponentially small terms and asymptotics
[15] 논문 Behavior of molecular potential energy curves for large nuclear separations https://doi.org/10.1[...] 1980
[16] 논문 Exchange Energy of {{chem|H|2|+}} Calculated from Polarization Perturbation Theory and the Holstein-Herring Method
[17] 논문 The Killingbeck method for the one-electron two-centre problem
[18] 논문 Hyperfine-Induced Ungerade-Gerade Symmetry Breaking in a Homonuclear Diatomic Molecule near a Dissociation Limit: 127I2 at the 2P3/2 − 2P1/2 Limit
[19] 논문 Direct Measurement of a Pure Rotation Transition in {{chem|H|2|+}}
[20] 논문 Variational Methods in the Quantum Mechanical Three-Body Problem with a Coulomb Interaction
[21] 논문 Rovibrational spin-averaged transitions in the hydrogen molecular ions
[22] 논문 Test of charged baryon interaction with high-resolution vibrational spectroscopy of molecular hydrogen ions
[23] 논문 Higher-order corrections to spin–orbit and spin–spin tensor interactions in hydrogen molecular ions: theory and application to H2+
[24] 논문 The Astrochemistry of {{chem|H|3|+}}
[25] 논문 Cosmic-ray ionization of molecular clouds
[26] 논문 New Approach for the Electronic Energies of the Hydrogen Molecular Ion
[27] 서적 Valency and bonding: a natural bond orbital donor-acceptor perspective Cambridge University Press
[28] 논문 Nonadiabatic wavefunctions as linear expansions of correlated exponentials. A quantum Monte Carlo application to H2+ and Ps2 https://linkinghub.e[...] 1997-07
[29] 논문 Berechnung des Energiewertes des Wasserstoffmolekel-Ions (H2+) im Normalzustand. http://www.royalacad[...]
[30] 문서 Zur Quantentheorie des Wasserstoffmolekülions
[31] 논문 Über das Modell des Wasserstoffmolekülions
[32] 논문 The Structure of the Hydrogen Molecule Ion
[33] 논문 The Application of the Quantum Mechanics to the Structure of the Hydrogen Molecule and Hydrogen Molecule-Ion and to Related Problems
[34] 서적 マッカリーサイモン物理化学(上)分子論的アプローチ 第7版 東京化学同人 2007-03-01
[35] 논문 Exchange Energy of {{chem|H|2|+}} Calculated from Polarization Perturbation Theory and the Holstein-Herring Method
[36] 간행물 The astrochemistry of H 3 + https://royalsociety[...] 2000-09-15


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com