순방향 신경망
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
순방향 신경망은 인공 신경망의 한 종류로, 정보를 입력층에서 출력층으로 단방향으로 전달하는 구조를 가진다. 활성화 함수는 뉴런의 출력을 결정하며, 학습은 오류를 기반으로 가중치를 조정하는 역전파 알고리즘을 통해 이루어진다. 주요 모델로는 단층 퍼셉트론, 다층 퍼셉트론(MLP) 등이 있으며, 컨볼루션 신경망과 방사 기저 함수 네트워크도 순방향 신경망의 일종이다. 19세기 말부터 연구가 시작되어 1980년대 이후 오차 역전파 알고리즘의 발전과 함께 딥 러닝 분야에서 중요한 역할을 하고 있다.
더 읽어볼만한 페이지
| 순방향 신경망 | |
|---|---|
| 인공신경망 | |
 | |
| 유형 | 인공신경망 |
| 구조 | 계층형 |
| 연결 방향 | 단방향 |
| 학습 방법 | 지도 학습, 비지도 학습, 강화 학습 |
| 활성화 함수 | 다양한 함수 사용 가능 (예: 시그모이드 함수, ReLU) |
| 특징 | |
| 설명 | 입력층에서 출력층으로 정보가 단방향으로 전달되는 신경망 구조 |
| 응용 분야 | 패턴 인식 함수 근사 분류 제어 |
| 관련 개념 | |
| 관련 개념 | 심층 신경망 역전파 경사 하강법 손실 함수 |
| 종류 | |
| 종류 | 단층 퍼셉트론 다층 퍼셉트론 방사 기저 함수 신경망 |
2. 수학적 기초
순방향 신경망은 입력값에 가중치를 곱하고 활성화 함수를 적용하여 출력을 계산하는 방식으로 작동한다.
번째 뉴런의 출력 는 입력값들의 가중치 합 에 활성화 함수를 적용하여 얻어진다. 시그모이드 함수인 쌍곡 탄젠트(-1에서 1 사이의 값)나 로지스틱 함수(0에서 1 사이의 값)가 전통적으로 사용되었다.
최근 딥 러닝에서는 기울기 소실 문제를 해결하기 위해 정류 선형 유닛(ReLU)이 주로 사용된다. 이 외에도 정류 함수, 소프트플러스 함수, 방사 기저 함수 등이 활성화 함수로 쓰인다.
2. 1. 활성화 함수
역사적으로 흔히 사용된 두 가지 활성화 함수는 모두 시그모이드 함수이며, 다음과 같다.- 쌍곡 탄젠트: -1에서 1까지의 범위를 가진다.
- 로지스틱 함수: 모양은 쌍곡 탄젠트와 비슷하지만 0에서 1까지의 범위를 갖는다.
여기서 는 번째 노드(뉴런)의 출력이고, 는 입력 연결의 가중치 합이다. 정류 함수 및 소프트플러스 함수를 포함한 대안적인 활성 함수가 제안되었다. 더 특수한 활성 함수로는 방사 기저 함수 네트워크에서 사용되는 방사 기저 함수가 있다.
최근 딥 러닝 개발에서 정류 선형 유닛(ReLU)은 시그모이드와 관련된 수치적 기울기 소실 문제를 극복하는 가능한 방법 중 하나로 더 자주 사용된다.
2. 2. 학습
학습은 예상 결과와 비교하여 출력의 오류 양에 따라 각 데이터 조각을 처리한 후 연결 가중치를 변경하여 발생한다. 이는 지도 학습의 예이며, 역전파를 통해 수행된다.출력 노드 에서 번째 데이터 포인트(훈련 예시)의 오류 정도는 로 나타낼 수 있다. 여기서 은 노드 에서 번째 데이터 포인트에 대한 원하는 목표 값이고, 은 번째 데이터 포인트가 입력으로 주어졌을 때 노드 에서 생성된 값이다.
그런 다음 노드 가중치는 번째 데이터 포인트에 대한 전체 출력의 오류를 최소화하는 수정 사항을 기반으로 조정할 수 있다.
:.
경사 하강법을 사용하면 각 가중치 의 변화는 다음과 같다.
:
여기서 은 이전 뉴런 의 출력이고, 는 진동 없이 가중치가 응답으로 빠르게 수렴되도록 선택된 학습률이다. 이전 표현식에서 은 뉴런 의 입력 연결의 가중 합 에 따른 오류 의 편미분을 나타낸다.
계산할 미분은 유도된 국소장 에 따라 달라지며, 이는 그 자체로 변한다. 출력 노드의 경우 이 미분을 다음과 같이 단순화할 수 있다.
:
여기서 는 활성화 함수의 미분이며, 그 자체는 변하지 않는다. 가중치가 숨겨진 노드로 변경되는 것에 대한 분석은 더 어렵지만, 관련 미분은 다음과 같다.
:.
이는 출력 계층을 나타내는 번째 노드의 가중치 변화에 따라 달라진다. 따라서 숨겨진 계층 가중치를 변경하려면 활성화 함수의 미분에 따라 출력 계층 가중치가 변경되므로 이 알고리즘은 활성화 함수의 역전파를 나타낸다.[10]
3. 역사
인공신경망 연구는 다음과 같은 역사를 거쳤다.
- 1800년경, 르장드르와 가우스는 최소제곱법으로 훈련되는 가장 단순한 형태의 순방향 네트워크를 만들었다. 이는 선형 회귀라고도 불리며, 행성 움직임을 예측하는 데 사용되었다.[11][12][21][13][14]
- 1943년, 워렌 맥컬록과 월터 피츠는 생물학적 신경망의 논리적 모델로 이진 인공 뉴런을 제안했다.[15]
- 1958년, 프랭크 로젠블랫은 다층 퍼셉트론 모델을 제안했다.[16] R. D. Joseph는 이보다 이른 시기에 퍼셉트론과 유사한 장치를 언급했다.[17][21]
- 1960년, Joseph는 적응형 은닉 계층을 가진 다층 퍼셉트론에 대해 논의했다.[17]
- 1970년, 세포 린나이마는 석사 논문에서 오차 역전파의 현대적 형태를 발표했다.[23][24][21]
- 1982년, 폴 워보스는 신경망에 오차 역전파를 적용했다.[26][27]
- 1986년, 데이비드 E. 루멜하트 등은 오차 역전파를 대중화했다.[30][8]
- 2003년, 요슈아 벤지오 연구팀은 딥 러닝을 언어 모델링에 적용하여 큰 성공을 거두었다.[31]
3. 1. 초기 모델 (19세기 말 ~ 20세기 중반)
- 1800년경, 르장드르(1805)와 가우스(1795)는 선형 활성화 함수를 가진 단일 가중치 레이어로 구성된 가장 단순한 순방향 네트워크를 만들었다. 이는 최소 제곱법으로 훈련되었으며, 평균 제곱 오차를 최소화하여 선형 회귀라고도 불린다. 르장드르와 가우스는 훈련 데이터를 기반으로 행성 움직임을 예측하는 데 사용했다.[11][12][21][13][14]
- 1943년, 워렌 맥컬록과 월터 피츠는 생물학적 신경망의 논리적 모델로 이진 인공 뉴런을 제안했다.[15]
- 1958년, 프랭크 로젠블랫은 입력 계층, 학습하지 않는 무작위 가중치를 가진 은닉 계층, 학습 가능한 연결을 가진 출력 계층으로 구성된 다층 퍼셉트론 모델을 제안했다.[16] R. D. Joseph (1960)[17]는 이보다 훨씬 더 이른 퍼셉트론과 유사한 장치를 언급했다.[21] "MIT 링컨 연구소의 팔리(Farley)와 클락(Clark)은 실제로 로젠블랫보다 먼저 퍼셉트론과 유사한 장치를 개발했다." 그러나 "그들은 이 주제를 중단했다."
- 1960년, Joseph[17]는 적응형 은닉 계층을 가진 다층 퍼셉트론에 대해서도 논의했다. 로젠블랫 (1962)[18]은 이러한 아이디어를 인용하고 채택했으며, H. D. 블록(Block)과 B. W. 나이트(Knight)의 작업도 언급했다.
3. 2. 퍼셉트론 (1950년대 ~ 1960년대)
가장 단순한 형태의 신경망은 출력 노드들의 단층으로 구성되는 단층 퍼셉트론이다. 입력은 일련의 가중치를 통해 출력에 직접 전달된다.- 1800년경, 르장드르(1805)와 가우스(1795)는 선형 활성화 함수를 가진 단일 가중치 레이어로 구성된 가장 단순한 순방향 네트워크를 만들었다. 이는 최소 제곱법으로 훈련되었으며, 평균 제곱 오차를 최소화하여 선형 회귀라고도 불린다. 르장드르와 가우스는 훈련 데이터를 기반으로 행성 움직임을 예측하는 데 사용했다.[11][12][21][13][14]
- 1943년, 워렌 맥컬록과 월터 피츠는 생물학적 신경망의 논리적 모델로 이진 인공 뉴런을 제안했다.[15]
- 1958년, 프랭크 로젠블랫은 입력 계층, 학습하지 않는 무작위 가중치를 가진 은닉 계층, 학습 가능한 연결을 가진 출력 계층으로 구성된 다층 퍼셉트론 모델을 제안했다.[16] R. D. Joseph (1960)[17]는 이보다 훨씬 더 이른 퍼셉트론과 유사한 장치를 언급했다:[21] "MIT 링컨 연구소의 팔리(Farley)와 클락(Clark)은 실제로 로젠블랫보다 먼저 퍼셉트론과 유사한 장치를 개발했다." 그러나 "그들은 이 주제를 중단했다."
- 1960년, Joseph[17]는 적응형 은닉 계층을 가진 다층 퍼셉트론에 대해서도 논의했다. 로젠블랫 (1962)[18]은 이러한 아이디어를 인용하고 채택했으며, H. D. 블록(Block)과 B. W. 나이트(Knight)의 작업도 언급했다. 불행히도 이러한 초기 노력은 은닉 유닛, 즉 딥 러닝을 위한 작동하는 학습 알고리즘으로 이어지지 못했다.
3. 3. 침체기 (1970년대)
1970년, 세포 린나이마는 석사 논문에서 오차 역전파의 현대적 형태를 발표했다.[23][24][21] G.M. 오스트로브스키 등은 1971년에 이를 재발행했다.[25][29] 1982년, 폴 워보스는 신경망에 오차 역전파를 적용했다.[26][27] 1986년, 데이비드 E. 루멜하트 등은 오차 역전파를 대중화했지만 원래의 연구는 인용하지 않았다.[30][8]3. 4. 부활과 발전 (1980년대 ~ 현재)
오차 역전파 알고리즘은 1970년 세포 린나이마의 석사 논문에서 현대적인 형태로 발표되었고,[23][24][21] 1982년 폴 워보스에 의해 신경망에 적용되었다.[26][27] 1986년 데이비드 E. 루멜하트 등이 오차 역전파를 대중화하면서[30][8] 딥 러닝 연구가 다시 활기를 띠기 시작했다.2003년에는 요슈아 벤지오 연구팀이 딥 러닝을 언어 모델링에 적용하여 큰 성공을 거두면서 오차 역전파 네트워크에 대한 관심이 다시 높아졌다.[31]
4. 주요 모델
인공신경망의 대표적인 모델은 다음과 같다.
- 단층 퍼셉트론: 가장 단순한 형태의 신경망으로, 출력 노드들의 단층으로 구성된다. 입력은 가중치를 통해 출력에 직접 전달된다.[32]
- 다층 퍼셉트론: 여러 층의 연산 유닛으로 구성되며, 일반적으로 피드포워드(feedforward) 방식으로 서로 연결되어 있다. 한 층의 각 뉴런은 다음 층의 뉴런으로 방향이 있는 연결을 가진다.
- 기타 피드포워드 네트워크: 컨볼루션 신경망, 방사 기저 함수 네트워크 등이 있으며, 이들은 서로 다른 활성화 함수를 사용한다.
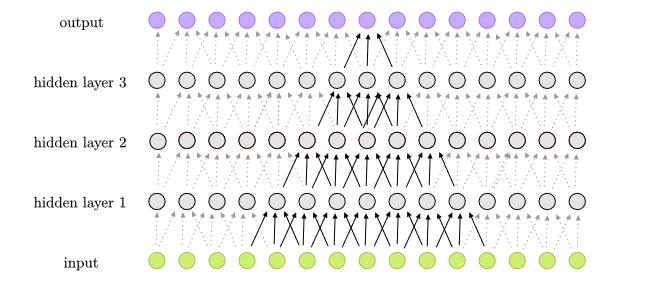
왼쪽
4. 1. 단층 퍼셉트론
가장 단순한 종류의 신경망은 출력 노드들의 단층으로 구성되는 단층 퍼셉트론이다. 입력은 일련의 가중치를 통해 출력에 직접 피드(feed)된다.[32]선형 활성 함수를 사용하는 경우, 결과적인 ''선형 임계치 유닛''을 ''퍼셉트론''이라고 한다. 여러 개의 병렬 비선형 유닛은 선형 임계 함수를 가진 단일 유닛의 제한된 계산 능력에도 불구하고, 실수 집합의 콤팩트 구간에서 구간 [-1,1]로의 모든 연속 함수를 근사할 수 있다.[32]
퍼셉트론은 일반적으로 ''델타 규칙''이라고 하는 간단한 학습 알고리즘으로 훈련될 수 있다. 이 알고리즘은 계산된 출력과 샘플 출력 데이터 간의 오류를 계산하고 이를 사용하여 가중치를 조정하여 경사 하강법의 한 형태를 구현한다.[32]
4. 2. 다층 퍼셉트론 (MLP)
다층 퍼셉트론(MLP)은 여러 층의 연산 유닛으로 구성되어 있으며, 일반적으로 피드포워드(feedforward) 방식으로 서로 연결되어 있다. 한 층의 각 뉴런은 다음 층의 뉴런으로 방향이 있는 연결을 가진다.다층 퍼셉트론은 완전 연결된 뉴런으로 구성되며, 주로 비선형 활성화 함수를 사용하고, 최소 세 개의 층을 가지는 현대적인 피드포워드 인공 신경망을 의미한다. 이러한 구조 덕분에 다층 퍼셉트론은 선형 분리 불가능한 데이터를 구별할 수 있다.[33]
4. 3. 기타 피드포워드 네트워크
다른 순방향 네트워크의 예시로는 컨볼루션 신경망과 방사 기저 함수 네트워크가 있으며, 이들은 서로 다른 활성화 함수를 사용한다.
참조
[1]
서적
Neural Networks for Babies
Sourcebooks
[2]
서적
Simulation Neuronaler Netze
Addison-Wesley
[3]
저널
Deep learning in neural networks: An overview
2015-01-01
[4]
학위논문
The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors
University of Helsinki
[5]
저널
Gradient theory of optimal flight paths
[6]
서적
Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms
Spartan Books, Washington DC
[7]
서적
System modeling and optimization
Springer
2017-07-02
[8]
문서
Learning Internal Representations by Error Propagation
https://apps.dtic.mi[...]
MIT Press
[9]
서적
The Elements of Statistical Learning: Data Mining, Inference, and Prediction
Springer, New York, NY
[10]
서적
Neural Networks: A Comprehensive Foundation
Prentice Hall
[11]
간행물
A List of Writings Relating to the Method of Least Squares: With Historical and Critical Notes
Academy
[12]
저널
Gauss and the Invention of Least Squares
[13]
서적
Linear Algebra With Applications
Prentice Hall
[14]
서적
The History of Statistics: The Measurement of Uncertainty before 1900
https://archive.org/[...]
Harvard
[15]
저널
A logical calculus of the ideas immanent in nervous activity
https://doi.org/10.1[...]
1943-12-01
[16]
저널
The Perceptron: A Probabilistic Model For Information Storage And Organization in the Brain
[17]
서적
Contributions to Perceptron Theory, Cornell Aeronautical Laboratory Report No. VG-11 96--G-7, Buffalo
[18]
서적
Principles of Neurodynamics
Spartan, New York
[19]
서적
Cybernetic Predicting Devices
CCM Information Corporation
[20]
서적
Cybernetics and forecasting techniques
American Elsevier Pub. Co.
[21]
논문
Annotated History of Modern AI and Deep Learning
2022
[22]
저널
A theory of adaptive pattern classifier
1967
[23]
학위논문
The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors
University of Helsinki
[24]
저널
Taylor expansion of the accumulated rounding error
[25]
간행물
On the computation of derivatives
[26]
서적
System modeling and optimization
Springer
2017-07-02
[27]
웹사이트
Talking Nets: An Oral History of Neural Networks
https://direct.mit.e[...]
The MIT Press
2000
[28]
서적
The Roots of Backpropagation : From Ordered Derivatives to Neural Networks and Political Forecasting
John Wiley & Sons
[29]
웹사이트
Who Invented Backpropagation?
https://people.idsia[...]
IDSIA, Switzerland
2014-10-25
[30]
저널
Learning representations by back-propagating errors
https://www.nature.c[...]
1986-10
[31]
저널
A neural probabilistic language model
https://dl.acm.org/d[...]
2003-03
[32]
저널
A learning rule for very simple universal approximators consisting of a single layer of perceptrons
http://www.igi.tugra[...]
2009-09-08
[33]
간행물
Approximation by superpositions of a sigmoidal function
[34]
서적
Simulation Neuronaler Netze
Addison-Wesley
[35]
저널
Deep learning in neural networks: An overview
2015-01-01
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com