슈뢰더 방정식

3. 수학적 성질

슈뢰더 방정식은 자기유사성을 나타내기에 적합하여 비선형계(혼돈 이론) 연구에 널리 쓰인다. 특히 난류 연구와 재규격화군에도 사용된다.^[4][5]

슈뢰더 방정식은 여러 형태로 변환될 수 있다. 슈뢰더 켤레 함수의 역 \(\Phi=\Psi^{-1} \)에 대한 슈뢰더 방정식의 등가 전치 형식은 \(h(\Phi(y))=\Phi(sy) \)이다. 변수 \(\alpha(x)=\log(\Psi(x))/\log(s) \)(아벨 함수)를 사용하면, 슈뢰더 방정식은 아벨 방정식 \(\alpha(h(x))=\alpha(x)+1 \)으로 변환된다. 마찬가지로, 변수 변환 \(\Psi(x)=\log(\varphi(x))\)은 슈뢰더 방정식을 뵈처 방정식 \(\varphi(h(x))=(\varphi(x))^s \)로 변환한다.^[4][5]

또한, 속도 \(\beta(x)=\Psi/\Psi' \)에 대해^[5], 줄리아 방정식 \(\beta(f(x))= f'(x)\beta(x)\)이 성립한다.

슈뢰더 방정식 해의 \(n\) 제곱은 고유값 \(s^n\)을 갖는 슈뢰더 방정식의 해를 제공한다. 같은 맥락에서 슈뢰더 방정식의 가역적 해 \(\Psi(x)\)에 대해 (비가역) 함수 \(\Psi(x)k\log(\Psi(x))\)도 주기가 \(\log(s) \)인 주기 함수 \(k(x)\)에 대한 해이다. 슈뢰더 방정식의 모든 해는 이러한 방식으로 관련되어 있다.

가브리엘 쾨니히스는 1884년에 \(0<|h'(0)|<1\)일 때, 즉 h(x)가 끌개 고정점(초끌개 고정점은 아님)인 경우 슈뢰더 방정식의 해석적 해가 존재함을 증명하였다.^[6][7] \(|h'(0)|=0\)인 초끌개 고정점의 경우, 슈뢰더 방정식은 다루기 힘들어서 뵈처 방정식으로 변환하는 것이 가장 좋다.^[8]

에른스트 슈뢰더의 1870년 원본 논문으로 거슬러 올라가는 특정 해가 많이 있다.^[1] 고정점 주변의 급수 전개와 결과 궤도에 대한 해의 관련 수렴 성질 및 해당 해석적 성질은 세케레시에 의해 설득력 있게 요약되었다.^[9] 몇몇 해는 점근적 급수로 제공된다.

3. 1. 기본 형태

3. 2. 변환

3. 3. 해의 존재성과 유일성

3. 4. 해의 특성

4. 응용

슈뢰더 방정식은 자기유사성을 나타내는 데 적합하여 비선형계(혼돈 이론) 연구에 널리 사용된다. 특히 난류 연구와 재규격화군에 응용된다.^[4][5]

슈뢰더 방정식은 이산 동역학계를 분석하는 데 사용된다. 즉, 새로운 좌표계를 찾아 이산 단위 시간 단계 ($x\backslash rightarrow\; h(x)$)에 해당하는 계가 매끄러운 궤도를 가지도록 한다.

일반적으로 '모든 함수적 반복'은 궤도에 의해 제공되는데, 실수 ($t$, 반드시 양수이거나 정수일 필요는 없다)에 대해 다음과 같다.

:$h\_t(x)\; =\; \backslash Psi^\{-1\}\backslash big(s^t\; \backslash Psi(x)\backslash big),$

초기 이산 재귀 $x\backslash rightarrow\; h(x)$의 홀로그램 연속 보간이 구성되었으며,^[10] 이는 사실상 전체 궤도이다.

예를 들어, 범함수 제곱근은 $h\_\{1/2\}(x)=\backslash Psi^\{-1\}(s^\{1/2\}\backslash Psi(x))$이므로 $h\_\{1/2\}(h\_\{1/2\}(x))=h(x)$이다.

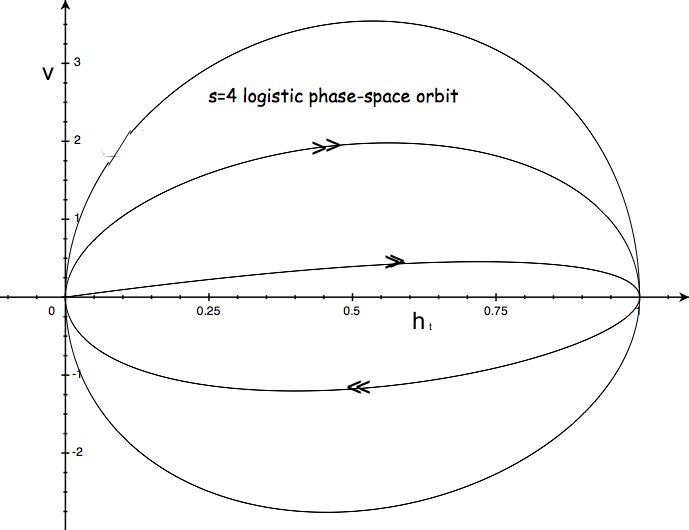
혼돈의 경우, 로지스틱 사상 ($h(x)=4x(1-x)$)의 특수 사례는 슈뢰더가 그의 원본 논문^[1]에서 다음과 같이 제시하였다.

: $\backslash Psi(x)\; =\; (\backslash arcsin\; \backslash sqrt\; x)^2$, $s\; =\; 4$, $h\_t(x)\; =\; \backslash sin^2\; (2^t\; \backslash arcsin\; \backslash sqrt\; x)$.

이 해는 일련의 스위치백 전위^[12] $V(x)\backslash propto\; x(x-1)(n\backslash pi+\backslash arcsin\backslash sqrt\; x)^2$에 의해 결정되는 동작으로 나타나는 것으로 보인다. 이는 슈뢰더 방정식의 영향을 받는 연속 반복의 일반적인 특징이다.

그는 또한 자신의 방법 $h(x)=2x(1-x)$로 설명했던 혼돈이 아닌 경우를 다음과 같이 나타낸다.

: $\backslash Psi(x)\; =\; -\backslash frac\{1\}\{2\}\backslash ln(1\; -\; 2x)$, $h\_t(x)\; =\; -\backslash frac\{1\}\{2\}((1\; -\; 2x)^\{2^t\}\; -\; 1)$.

마찬가지로 베버튼-홀트 모델 $h(x)=x/\; (2-x)$의 경우^[10] $\backslash Psi(x)=x/\; (1-x)$를 쉽게 찾을 수 있으므로,^[13]

:$h\_t(x)=\; \backslash Psi^\{-1\}\backslash big(2^\{-t\}\; \backslash Psi(x)\backslash big)\; =\; \backslash frac\{x\}\{2^t\; +\; x(1\; -\; 2^t)\}.$

4. 1. 동역학계 분석

4. 2. 혼돈 이론

4. 3. 재규격화군

4. 4. 기타 응용

참조

_[1] 논문 Ueber iterirte Functionen 1870
_[2] 서적 Complex Dynamics https://archive.org/[...] Springer-Verlag 1993
_[3] 서적 Functional equations in a single variable https://archive.org/[...] PWN – Polish Scientific Publishers 1968
_[4] 논문 Quantum Electrodynamics at Small Distances https://authors.libr[...] 1954
_[5] 논문 Renormalization Group Functional Equations 2011-03
_[6] 논문 Recherches sur les intégrales de certaines équations fonctionelles http://www.numdam.or[...] 1884
_[7] 논문 On Analytic Iteration 1960
_[8] 논문 The principal laws of convergence of iterates and their application to analysis 1904
_[9] 논문 Regular iteration of real and complex functions 1958
_[10] 논문 Evolution Profiles and Functional Equations 2009
_[11] 웹사이트 Evolution surfaces and Schröder functional methods http://www.physics.m[...] 2014-10-30
_[12] 논문 Chaotic Maps, Hamiltonian Flows, and Holographic Methods 2010
_[13] 논문 Random dispersal in theoretical populations 1951