유체동역학

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

유체동역학은 유체의 움직임을 연구하는 학문으로, 고전역학의 보존 법칙(질량, 운동량, 에너지 보존)을 기반으로 한다. 유체의 압력, 유동의 분류(압축성/비압축성, 점성/비점성, 정상/비정상, 층류/난류, 뉴턴/비뉴턴 유체), 주요 방정식(연속, 운동량, 에너지 방정식, 베르누이, 오일러, 나비에-스토크스 방정식 등)을 다룬다. 항공우주, 조선해양, 기계, 토목, 생명/의공학 등 다양한 분야에 응용되며, 전산 유체 역학, 자기유체역학, 상대론적 유체역학, 반응 유동, 요동 유체역학과 같은 다학제적 연구도 수행된다.

더 읽어볼만한 페이지

유체동역학 - 항력
항력은 유체 내에서 움직이는 물체에 작용하여 물체의 운동을 방해하는 유체 저항력이며, 유체의 밀도, 물체의 속도, 기준 면적, 항력 계수 등에 의해 결정된다.
유체동역학 - 비점성 흐름
비점성 흐름은 유체 역학에서 점성을 무시할 수 있는 유체의 흐름을 의미하며, 레이놀즈 수가 무한대에 가까울 때 나타나 오일러 방정식으로 설명되고, 프란틀의 경계층 가설을 통해 실제 유체 흐름 모델링에 활용하며, 초유체는 점성이 없는 물질의 상태로 헬륨-4가 2.2K 이하로 냉각될 때 나타난다.
연속체역학 - 온도
온도는 물체의 뜨겁고 차가운 정도를 나타내는 물리량으로, 열역학적으로는 에너지 이동 방향으로 정의되며, 미시적으로는 분자 운동 에너지의 평균값으로 정의되고, 화학 반응 속도와 생명체에 큰 영향을 미친다.
연속체역학 - 밀도
밀도는 단위 부피당 질량을 나타내는 물리량으로 질량을 부피로 나눈 값으로 계산되며, 온도와 압력에 따라 변하고, 진밀도, 겉보기밀도, 부피밀도, 탭밀도 등 여러 종류가 있고, 고대 그리스 시대부터 발전해왔다.

유체동역학
개요
학문 분야	역학, 유체, 연속체 역학
분야	응용물리학
세부 분야	공기역학 수력학 지하수 해양학 기상학 생체 유체 역학 열역학
설명
유체 동역학	유체의 움직임을 다루는 유체역학의 한 분야이다.
연구 대상	액체 (물) 과 기체 (공기)
관련 개념
관련 개념	베르누이 원리 항력 점성 난류 유선 유속 연속 방정식 나비에-스토크스 방정식 레이놀즈 수 마하 수 점성

2. 주요 개념

유체 동역학은 보존 법칙을 기본으로 하며, 질량 보존의 법칙, 운동량 보존의 법칙(뉴턴의 제2법칙), 에너지 보존의 법칙(열역학 제1법칙)을 포함한다. 이러한 법칙들은 고전 역학에 기반하며, 레이놀즈 수송 정리를 통해 표현된다.^[2]

유체역학 문제를 해결하기 위해 사용되는 세 가지 보존 법칙은 적분 또는 미분 형태로 나타낼 수 있다.

법칙	설명
질량 연속성 (질량 보존)	제어 체적 내 유체 질량 변화율은 체적으로 유입되는 유체 흐름의 순율과 같다. 즉, 제어 체적 내에서 질량이 생성되거나 파괴되지 않는다.^[2]
운동량 보존	뉴턴의 운동 제2법칙에 따라, 제어 체적 내 유체 운동량 변화는 체적 내로 유입되는 운동량의 순 흐름과 체적 내 유체에 작용하는 외부 힘에 의해 발생한다.
에너지 보존	에너지는 한 형태에서 다른 형태로 변환될 수 있지만, 닫힌 계 내의 총 에너지는 일정하게 유지된다.

유체는 분자로 구성되어 서로 충돌하지만, 연속체 가정에서는 유체를 연속적인 것으로 간주한다. 따라서 밀도, 압력, 온도, 속도 등은 매우 작은 점에서도 정의 가능하며, 연속적으로 변한다고 가정한다.

움직이는 유체에서 압력은 필수적인 개념이다. 정지한 유체가 가하는 압력을 '''정압력'''이라 한다. 움직이는 유체가 정지하는 지점에서는 운동 에너지가 압력 에너지로 전환되어 정압력보다 높은 압력이 측정되는데, 이를 '''동압력'''이라 한다. 정압력과 동압력의 합은 '''전압력'''(또는 정체 압력)이다. 베르누이 방정식은 전압력, 정압력, 동압력 간의 관계를 보여준다.

유체 유동(fluid flow)은 여러 기준으로 분류할 수 있다.

압축성 유동과 비압축성 유동: 마하 수가 약 0.3 미만인 기체 유동이나 액체 유동은 밀도 변화를 무시하고 '''비압축성''' 유동으로 간주한다. 음파와 같이 압축성을 고려해야 하는 경우도 있다.^[5]
점성 유동과 비점성 유동: 유체 마찰력 효과를 무시할 수 없는 유동은 점성 유동이며, 레이놀즈 수로 판단한다. 점성 효과가 작으면 '''비점성''' 유동으로 가정하고, 오일러 방정식으로 묘사한다. 유선을 따라 적분하면 베르누이 방정식이 된다. 비회전이면서 비점성 유동인 경우 퍼텐셜 유동이라 한다. 경계층과 같이 점성을 무시할 수 없는 경우도 있다.^[6]
정상 유동과 비정상 유동: 시간에 따라 유동장이 변하지 않으면 정상 유동, 변하면 비정상 유동이다. 관측계에 따라 달라질 수 있으며, 주기적인 유동은 비정상 유동이지만 정상 유동처럼 풀 수 있다.^[7]
층류 유동과 난류 유동: 재순환 유동, 에디, 임의성에 의해 지배되는 유동은 난류이고, 그렇지 않으면 층류이다. 난류 유동은 나비에-스토크스 방정식으로 설명되며, 직접 수치 모사법(DNS)으로 모사할 수 있다. 높은 레이놀즈 수에서는 난류 모델이 필요하다.^[9]
뉴턴 유체와 비뉴턴 유체: 아이작 뉴턴은 변형률과 전단 응력이 선형적인 관계를 가지는 유체를 밝혔으며, 이를 뉴턴 유체라고 한다. 점성은 이 관계의 계수이다. 응력과 변형률 관계가 복잡한 비뉴턴 유체도 존재한다.^[10]

2. 1. 보존 법칙

유체 동역학의 기본 공리는 보존 법칙이며, 구체적으로 질량 보존의 법칙, 운동량 보존의 법칙(뉴턴의 제2법칙), 에너지 보존의 법칙(열역학 제1법칙)이다. 이들은 고전 역학에 기반하며, 레이놀즈 수송 정리를 사용하여 표현된다.^[2]

유체역학 문제를 풀기 위해 세 가지 보존 법칙이 사용되며, 이는 적분 또는 미분 형태로 작성될 수 있다.

법칙	설명
질량 연속성 (질량 보존)	제어 체적 내의 유체 질량 변화율은 체적으로 유입되는 유체 흐름의 순율과 같아야 한다. 물리적으로, 이 진술은 제어 체적 내에서 질량이 생성되거나 파괴되지 않음을 요구한다.^[2]
운동량 보존	뉴턴의 운동 제2법칙에 따르면, 해당 제어 체적 내의 유체의 운동량 변화는 체적 내로 유입되는 운동량의 순 흐름과 체적 내의 유체에 작용하는 외부 힘의 작용에 의해 발생한다.
에너지 보존	에너지는 한 형태에서 다른 형태로 변환될 수 있지만, 닫힌 계 내의 총 에너지는 일정하게 유지된다.

2. 2. 연속체 가정

유체는 분자로 이루어져 있어서 분자끼리 서로 충돌하거나 고체인 물체와 충돌한다. 그러나 연속체 가정에서는 유체가 불연속적인 분자가 아닌 연속적인 것이라고 가정한다. 결과적으로 밀도, 압력, 온도, 속도 등의 성질들을 아무리 작은 점에서라도 정의할 수 있으며, 이러한 성질들은 한 지점에서 다른 지점으로 갈 때 연속적으로 변화한다고 가정한다. 유체가 불연속적인 분자로 되어 있다는 사실은 무시한다.

2. 3. 압력

이 개념은 움직이는 유체를 다루는 유체 동역학에서 반드시 필요한 개념이다. 압력의 개념은 유체 정역학 및 유체 역학 연구의 핵심이며, 유체가 움직이는지 여부에 관계없이 유체 내의 모든 지점에 대해 압력을 식별할 수 있다. 유체 역학 연구에 필요한 몇 가지 용어는 다른 유사한 연구 분야에서는 찾아볼 수 없으며, 특히 유체 역학에 사용되는 일부 용어는 유체 정역학에서는 사용되지 않는다.

2. 3. 1. 정압력, 동압력 및 전압력

일반적으로 '''압력(pressure)'''이라 하면 '''정압력(static pressure)'''을 가리킨다. 정압력이란, 정지해 있는 유체가 가하는 압력을 말한다.

그러나 유체가 움직이는 경우, 그 움직이는 유체가 정지하는 지점에서는 유체의 운동 에너지가 모두 압력 에너지로 전환되어, 그 지점에서의 압력은 정압력보다 더 높게 측정된다. 운동에너지가 압력에너지로 전환되는 만큼을 '''동압력(dynamic pressure)'''이라 하고, 정압력과 동압력의 합을 '''전압력(total pressure)''' 혹은 '''정체 압력(stagnation pressure)'''이라 한다.

전압력, 정압력 및 동압력 사이의 관계는 베르누이 방정식에서 확인할 수 있다. 압력은 압력계, 부르동관, 수은 기둥 또는 기타 다양한 방법을 사용하여 측정할 수 있다.

베르누이 방정식에서 파생된 전압과 동압의 개념은 모든 유체 흐름 연구에서 중요하다. (이 두 압력은 통상적인 의미의 압력이 아니며, 아네로이드, 부르동관 또는 수은주를 사용하여 측정할 수 없다.) 유체 역학에서 압력을 언급할 때 잠재적인 모호성을 피하기 위해 많은 저자들은 정압이라는 용어를 사용하여 전압과 동압을 구분한다. 정압은 압력과 동일하며 유체 흐름장의 모든 지점에서 식별할 수 있다.

유체 흐름에서 흐름이 정지된 지점(즉, 유체 흐름에 잠긴 고체 근처에서 속도가 0과 같음)은 특별한 의미를 지닌다. 이는 매우 중요하기 때문에 특별한 이름인 정체점이 주어집니다. 정체점에서의 정압은 특별한 의미를 가지며 고유한 이름인 정체압이 주어집니다. 비압축성 흐름에서 정체점의 정체압은 흐름장 전체의 전압과 같다.

2. 4. 유동의 분류

유체동역학에서 유동(fluid flow)은 여러 기준으로 분류할 수 있다.

압축성 유동과 비압축성 유동: 모든 유체는 압력이나 온도 변화에 따라 밀도가 변하는 압축성을 가진다. 하지만 밀도 변화가 매우 작아 무시할 수 있는 경우 '''비압축성''' 유동으로 간주한다. 마하 수가 약 0.3 미만인 기체 유동이나, 액체 유동의 경우 비압축성 가정이 가능하다. 음파와 같이 압축성 고려가 필수적인 경우도 있다.^[5]
점성 유동과 비점성 유동: 유체의 마찰력 효과를 무시할 수 없는 유동을 점성 유동이라고 하며, 레이놀즈 수를 기준으로 판단한다. 점성 효과가 매우 작아 무시 가능한 경우 '''비점성''' 유동으로 가정하며, 오일러 방정식으로 묘사할 수 있다. 유선을 따라 적분하면 베르누이 방정식이 도출된다. 비회전이면서 비점성 유동인 경우 퍼텐셜 유동이라고 한다. 하지만, 경계층과 같이 점성을 무시할 수 없는 경우도 있다.^[6]
정상 유동과 비정상 유동: 시간에 따라 유동장이 변하지 않는 경우를 정상 유동, 변하는 경우를 비정상 유동이라고 한다. 이는 관측계에 따라 달라질 수 있다. 주기적인 성질을 가진 유동은 비정상 유동이지만, 정상 유동처럼 풀 수 있다.^[7]
층류 유동과 난류 유동: 재순환 유동, 에디, 임의성에 의해 지배되는 유동은 난류이고, 그렇지 않은 유동은 층류이다. 난류 유동은 나비에-스토크스 방정식으로 설명될 수 있으며, 직접 수치 모사법(DNS)으로 모사할 수 있다. 하지만, 높은 레이놀즈 수에서는 난류 모델이 필요하다.^[9]
뉴턴 유체와 비뉴턴 유체: 아이작 뉴턴은 변형률과 전단 응력이 선형적인 관계를 가지는 유체를 밝혔으며, 이를 뉴턴 유체라고 한다. 점성은 이 관계의 계수이다. 하지만, 응력과 변형률 관계가 복잡한 비뉴턴 유체도 존재한다.^[10]

2. 4. 1. 압축성 유동과 비압축성 유동

모든 유체는 어느 정도 '''압축성'''을 가진다. 즉, 압력이나 온도가 변하면 밀도가 변한다. 그러나 많은 경우 압력이나 온도가 변할 때 밀도 변화가 너무 작아 무시할 수 있다. 이런 경우 유동을 '''비압축성''' 유동 방정식으로 묘사할 수 있다. 그렇지 않다면 더 일반적인 압축성 유동 방정식을 사용해야 한다.

비압축성은 수학적으로 유체 다발이 유동장 내에서 움직일 때 그 밀도

\rho

가 변하지 않음을 의미하며, 다음과 같은 식으로 표현된다.

:

{d \rho \over d t} = 0

이 식을 사용하면 지배 방정식을 단순화할 수 있다.

기체 유동에서 압축성 식을 쓸지 비압축성 식을 쓸지는 유동의 마하 수로 결정한다. 엄밀한 기준은 아니지만, 마하 수가 약 0.3 미만일 때에는 압축성 효과를 무시할 수 있다. 액체의 경우 비압축성 가정이 유효한지는 유체의 성질(특히 유체의 임계 압력 및 임계 온도) 및 유동 조건(실제 유동 압력이 얼마나 임계 압력에 가까운가)에 따라 좌우된다.

음향학적인 문제에는 항상 압축성이 고려되어야 한다. 왜냐하면 음파란 매질 내에서 전파할 때 압력과 밀도가 변화하는 압축파이기 때문이다.

2. 4. 2. 점성 유동과 비점성 유동

유동에서 유체의 마찰력이 가지는 효과를 무시할 수 없다면 이는 '''점성(viscous) 유동'''이 된다. 어떤 유동이 점성 유동인지 아닌지는 레이놀즈 수를 사용하여 판단할 수 있다.

관성력에 비하여 점성 효과가 매우 작아서 무시할 수 있는 경우, 이 유동은 '''비점성(invisid) 유동'''으로 가정할 수 있다. 비점성 유동을 묘사하는 방정식이 오일러 방정식이다. 유선을 따라 오일러 방정식을 적분하면 베르누이 방정식이 나온다. 유동이 비회전(irrotational), 비점성이면 유동장 전체에 대해 베르누이 방정식을 쓸 수 있다. 이러한 유동을 퍼텐셜 유동이라고 한다.

레이놀즈 수는 무차원 수로, 점성 효과의 크기에 비해 관성 효과의 크기를 특징짓는다. 낮은 레이놀즈 수(Re << 1)는 관성력에 비해 점성력이 매우 강함을 나타낸다. 이러한 경우, 관성력은 때때로 무시되며, 이 유동 체제를 스토크스 유동 또는 크리핑 유동이라고 한다.

반대로, 높은 레이놀즈 수(Re >> 1)는 관성 효과가 점성(마찰) 효과보다 속도장에 더 큰 영향을 미친다는 것을 나타낸다. 높은 레이놀즈 수 유동에서, 유동은 종종 점성이 완전히 무시되는 근사인 비점성 유동으로 모델링된다. 점성을 제거하면 나비에-스토크스 방정식을 오일러 방정식으로 단순화할 수 있다. 비점성 유동에서 유선에 따라 오일러 방정식을 적분하면 베르누이 방정식이 도출된다. 비점성인 것 외에도, 유동이 모든 곳에서 비회전일 때, 베르누이 방정식은 모든 곳에서 유동을 완전히 설명할 수 있다. 이러한 유동을 포텐셜 유동이라고 하는데, 이는 속도장을 포텐셜 에너지 표현의 기울기로 표현할 수 있기 때문이다.

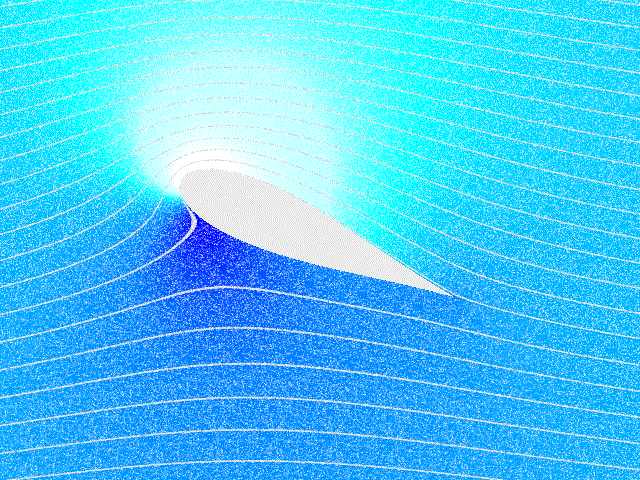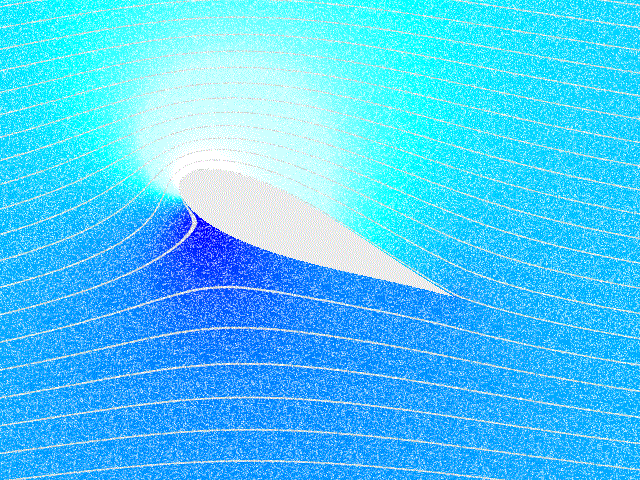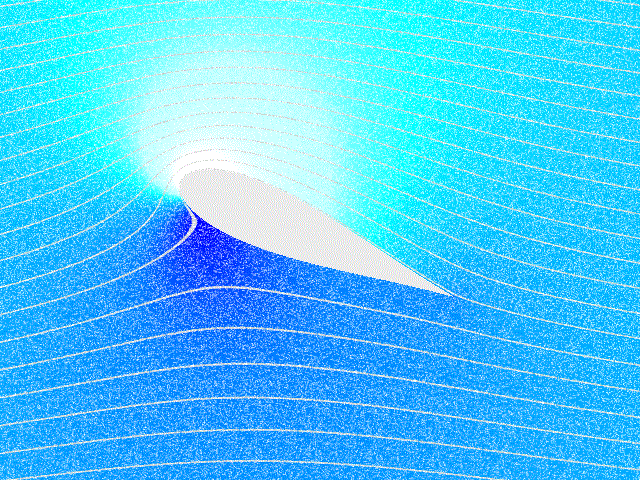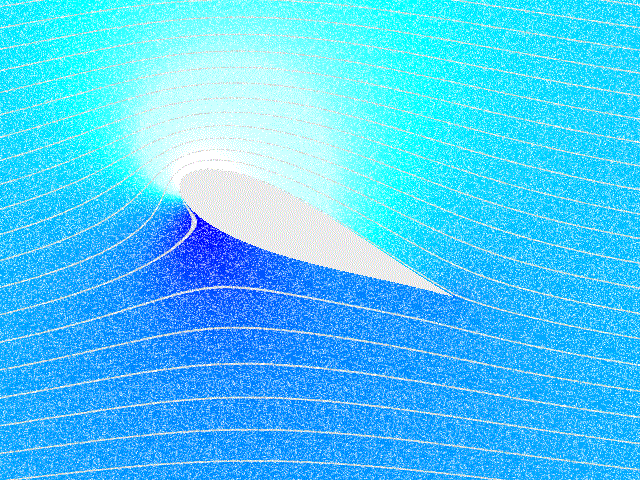
이 아이디어는 레이놀즈 수가 높을 때 상당히 잘 작동할 수 있다. 그러나 고체 경계를 포함하는 문제와 같은 경우에는 점성을 포함해야 할 수 있다. 미끄럼 없음 조건이 큰 변형률을 갖는 얇은 영역인 경계층을 생성하고, 여기서 점성 효과가 지배적이며, 따라서 와도를 생성하기 때문에, 고체 경계 근처에서는 점성을 무시할 수 없다. 따라서 날개와 같은 물체에 작용하는 순 힘을 계산하려면 점성 유동 방정식을 사용해야 한다. 비점성 유동 이론은 항력을 예측하지 못하는 데 실패하며, 이는 달랑베르의 역설로 알려진 한계이다.^[6]

2. 4. 3. 정상 유동과 비정상 유동

주어진 유동장(fluid field)이 시간에 따라 변하지 않으면 '''정상(steady) 유동'''이라고 하며, 시간에 따라 변하는 경우를 '''비정상(unsteady) 유동'''이라고 한다. 주어진 유동이 정상이냐 비정상이냐 하는 것은 관측계(frame of reference)에 따라 달라질 수 있다.^[7]

시간에 따라 주기적인 성질을 가진 유동은 엄밀하게는 비정상 유동이지만, 정상 유동 문제를 푸는 것과 같은 기법으로 풀 수 있다. 예를 들어, 구 주위의 층류는 구에 대해 정지해 있는 좌표계에서 정상 유동이다. 배경 유동에 대해 정지해 있는 좌표계에서는 유동이 비정상 유동이다.^[8]

난류는 정의상 비정상 유동이다. 그러나 난류는 정상 과정일 수 있다. 난류 속도장이 모든 통계량이 시간에 대한 이동에 불변일 경우 통계적으로 정상적이다.^[9] 이는 대략적으로 모든 통계적 특성이 시간에 따라 일정하다는 것을 의미한다.

정상 유동은 그렇지 않은 유사한 비정상 유동보다 종종 더 다루기 쉽다. 정상 문제의 지배 방정식은 유동장의 정상성을 이용하지 않은 동일한 문제의 지배 방정식보다 차원이 하나 적다(시간).

2. 4. 4. 층류 유동과 난류 유동

재순환 유동, 에디, 임의성에 의해 지배되는 유동을 '''난류(turbulent) 유동'''이라고 한다. 난류성을 보이지 않는 유동은 '''층류(laminar) 유동'''이라고 한다. 그러나 에디나 재순환이 있다고 해서 반드시 난류 유동인 것은 아니며, 이러한 현상은 층류 유동에서도 나타날 수 있다.^[10]

난류 유동은 나비에-스토크스 방정식을 따르는 것으로 여겨지고 있다. 이 방정식을 이용한 직접 수치 모사법(Direct Numerical Simulation; DNS)을 사용하면 중간 정도의 레이놀즈 수에 해당하는 난류 유동을 모사하는 것이 가능하다. 그 모사 결과는 시험 데이터와 일치한다.

그러나 관심의 대상이 되는 대부분의 유동은 레이놀즈 수가 너무 높아 DNS를 사용할 수가 없다. 예를 들어 에어버스 A300이나 보잉 747의 날개 유동은 4천만 정도이다. 이러한 실질적인 문제를 풀기 위해서는 난류 모델의 도입이 필수적이다. 레이놀즈 평균 나비에-스토크스 방정식(RANS)는 난류 모델링과 결합되어 난류 유동의 효과에 대한 모델을 제공한다. 이러한 모델링은 주로 레이놀즈 응력에 의한 추가적인 운동량 전달을 제공하지만, 난류는 또한 열 전달 및 물질 전달을 향상시킨다. 또 다른 유망한 방법론은 특히 분리 와동 시뮬레이션(DES)의 형태인 대와동 시뮬레이션(LES)이며, LES와 RANS 난류 모델링의 조합이다.

2. 4. 5. 뉴턴 유체와 비뉴턴 유체

뉴턴은 물이나 공기 등 많은 유체에 대하여 변형률과 전단 응력이 선형적인 관계가 있음을 밝혔다. 이러한 유체를 뉴턴 유체라 하며, 변형률과 전단 응력 사이의 계수가 바로 '''점성'''이다. 이 점성은 유체에 따라 다르다.

그러나 어떤 유체는 응력과 변형률의 관계가 선형적이지 않고 더 복잡하며, 이러한 유체를 비뉴턴 유체라 한다.^[5] 유동학은 유제와 슬러리, 혈액과 일부 고분자와 같은 점탄성 물질, 그리고 라텍스, 꿀, 윤활유와 같은 "끈적한 액체"를 포함하는 이러한 유체의 응력-변형 거동을 설명하는 하위 분야이다.^[5]

3. 주요 방정식

유체동역학의 주요 방정식은 다음과 같다.

유체 역학의 기본 공리는 질량 보존의 법칙, 운동량 보존의 법칙, 에너지 보존의 법칙(열역학 제1법칙)과 같은 보존 법칙이다. 이 법칙들은 고전 역학에 기반하며, 양자 역학과 일반 상대성 이론에서 수정된다. 또한 레이놀즈 수송 정리를 사용하여 표현된다.

유체는 연속체 가설을 따른다고 가정한다. 연속체 가설은 작은 규모에서 분자로 구성되어 서로 및 고체 물체와 충돌하는 유체가 연속적이라고 가정한다. 결과적으로 밀도, 압력, 온도, 유속과 같은 속성은 공간의 아주 작은 점에서도 잘 정의되며 한 점에서 다른 점으로 연속적으로 변한다고 가정한다.

유체가 연속체가 되기에 충분히 조밀하고, 이온화된 종을 포함하지 않으며, 유체의 속도가 빛의 속도에 비해 작은 경우, 뉴턴 유체에 대한 운동량 방정식은 나비에-스토크스 방정식이다. 이는 응력이 유속 기울기 및 압력에 선형적으로 의존하는 유체의 흐름을 설명하는 비선형 미분 방정식 집합이다. 이 방정식은 여러 가지 방법으로 단순화할 수 있으며, 이를 통해 일부 간단한 유체 역학 문제는 풀 수 있다.

질량, 운동량, 에너지 보존 방정식 외에도, 압력을 다른 열역학 변수의 함수로 나타내는 열역학 상태 방정식이 문제를 완전히 설명하는 데 필요하다. 이에 대한 예로 이상 기체 상태 방정식이 있다.

:

p= \frac{\rho R_u T}{M}

여기서 p는 압력, ρ는 밀도, T는 절대 온도이며, R_u는 기체 상수이고 M은 특정 기체의 몰 질량이다.

3. 1. 연속 방정식

적분 또는 미분 형태로 표현 가능한 세 가지 보존 법칙 중 하나로, 제어 체적 내 유체 질량 변화율은 체적으로 유입되는 유체 흐름의 순율과 같다는 법칙이다.^[2] 이는 제어 체적 내에서 질량이 생성되거나 파괴되지 않음을 의미한다.

연속 방정식의 적분 형태는 다음과 같다.

:

\frac{\partial}{\partial t} \iiint_V \rho \, dV = - \, {}

여기서 는 유체 밀도, 는 유속 벡터, 는 시간이다. 위 식에서 좌변은 체적 내 질량 증가율을 나타내며 제어 체적에 대한 삼중 적분을 포함하고, 우변은 체계로 유입되는 질량의 체적 표면에 대한 적분을 포함한다. 체계로의 질량 흐름은 양수로 간주되며, 표면에 대한 법선 벡터는 체계로 유입되는 흐름의 반대이므로 항은 부정이 된다.

발산 정리를 이용하면 연속 방정식의 미분 형태를 다음과 같이 얻을 수 있다.

:

\ \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0

3. 2. 운동량 방정식 (나비에-스토크스 방정식)

뉴턴의 운동 제2법칙을 제어 체적에 적용하면, 해당 제어 체적 내 유체의 운동량 변화는 체적 내로 유입되는 운동량의 순 흐름과 체적 내 유체에 작용하는 외부 힘의 작용에 의해 발생한다는 것을 알 수 있다. 이를 운동량 보존 법칙이라고 한다.

운동량 보존 법칙의 적분 형태는 다음과 같다.

:

\frac{\partial}{\partial t} \iiint_{\scriptstyle V} \rho\mathbf{u} \, dV = -\, {}

(\rho\mathbf{u}\cdot d\mathbf{S}) \mathbf{u} -{}

\displaystyle{}+ \iiint_{\scriptstyle V} \rho \mathbf{f}_\text{body} \, dV + \mathbf{F}_\text{surf}

위 식에서 좌변의 항은 체적 내 운동량의 순 변화를 나타낸다. 우변의 첫 번째 항은 운동량이 체적으로 유입되는 순율을, 두 번째 항은 체적의 표면에 가해지는 압력에 의한 힘을 나타낸다. 우변의 처음 두 항은 체계로 유입되는 운동량이 양수로 간주되고, 법선은 속도 및 압력 힘의 반대 방향이므로 음(-)의 부호를 가진다. 우변의 세 번째 항은 체적력 (여기서는

\mathbf{f}_\text{body}

로 표시)에 의한 체적 내 질량의 순 가속도이다. 표면력 (예: 점성력)은

\mathbf{F}_\text{surf}

로 표시되며, 체적 표면에 작용하는 전단력에 의한 순 힘이다.

운동량 보존 법칙의 미분 형태는 다음과 같다. 여기서 체적은 무한히 작은 점으로 축소되고, 표면력과 체적력 모두 하나의 총 힘

\mathbf{F}

로 간주된다.

:

\ \frac{D \mathbf{u}}{D t} = \mathbf{F} - \frac{\nabla p}{\rho}

항공역학에서 공기는 뉴턴 유체로 간주되는데, 이는 전단 응력(내부 마찰력)과 유체의 변형률 사이의 선형 관계를 가정한다. 위의 방정식은 3차원 흐름에서의 벡터 방정식이지만, 세 좌표 방향에서 세 개의 스칼라 방정식으로 표현될 수 있다. 압축성, 점성 흐름에 대한 운동량 보존 방정식은 나비에-스토크스 방정식이라고 한다.^[2]

3. 3. 에너지 방정식

에너지는 한 형태에서 다른 형태로 변환될 수 있지만, 닫힌 계 내의 총 에너지는 일정하게 유지된다.^[4]

:

\ \rho \frac{Dh}{Dt} = \frac{D p}{D t} + \nabla \cdot \left( k \nabla T\right) + \Phi

위 식에서 h^영어는 비 엔탈피, k^영어는 유체의 열전도율, T^영어는 온도, Φ는 점성 소산 함수이다. 점성 소산 함수는 흐름의 기계적 에너지가 열로 변환되는 속도를 제어한다. 열역학 제2법칙에 따르면 소산 항은 항상 양수여야 한다. 즉, 점성은 제어 체적 내에서 에너지를 생성할 수 없다.^[4] 좌변의 식은 물질 미분이다.

3. 4. 이상 기체 상태 방정식

질량, 운동량, 에너지 보존 방정식 외에도, 압력을 다른 열역학 변수의 함수로 제공하는 열역학 상태 방정식이 문제를 완전히 설명하는 데 필요하다. 이에 대한 예로는 이상 기체 법칙이 있다.

:

p= \frac{\rho R_u T}{M}

여기서 는 압력, 는 밀도, 는 절대 온도이며, 는 기체 상수이고 는 특정 기체의 몰 질량이다. 구성 방정식도 유용할 수 있다.

4. 유체역학의 응용

유체역학은 다양한 분야에 응용된다.

5. 다학제적 접근

(주어진 원본 소스가 없으므로 내용을 생성할 수 없습니다.)

5. 1. 자기유체역학 (MHD)

자기유체역학은 전기 전도 유체의 흐름을 전자기학적 장에서 연구하는 다학제적 연구 분야이다. 이러한 유체의 예로는 플라스마, 액체 금속, 염수 등이 있다. 유체 흐름 방정식은 전자기학의 맥스웰 방정식과 동시에 풀린다.

5. 2. 상대론적 유체역학

상대론적 유체역학은 광속에 필적하는 큰 속도에서의 거시적 및 미시적 유체 운동을 연구한다.^[11] 이 분야는 특수 상대성 이론과 일반 상대성 이론 모두에서 상대론적 효과를 고려한다. 지배 방정식은 민코프스키 시공간에 대해 리만 기하학에서 유도된다.

5. 3. 반응 유동

반응 유동은 화학적으로 반응하는 유동으로, 연소(내연 기관), 추진 장치(로켓, 제트 엔진 등), 폭발, 화재 및 안전 위험, 천체 물리학 등 많은 분야에서 응용된다. 질량, 운동량 및 에너지 보존 외에도 개별 종의 보존(예: 메탄 연소 시 메탄의 질량 분율)을 유도해야 하며, 여기서 임의 종의 생성/고갈 속도는 화학 반응 속도론 방정식을 동시에 풀어서 얻는다.

5. 4. 요동 유체역학

열적 변동을 모델링하는 확률적 플럭스를 사용하여 표준 유체역학 방정식을 보강한다.^[12] 란다우와 리프시츠가 공식화한 바와 같이,^[13] 통계 역학의 요동-소산 정리에서 얻은 백색 잡음 기여가 점성 응력 텐서와 열 플럭스에 추가된다.

6. 한국의 유체역학 연구

(이전 출력이 비어있으므로, 수정할 내용이 없습니다. 원본 소스와 요약 정보가 제공되면 해당 내용을 기반으로 위키텍스트를 작성할 수 있습니다.)

참조

_[1] 서적 The Dawn of Fluid Dynamics: A Discipline Between Science and Technology Wiley
_[2] 서적 Fundamentals of Aerodynamics McGraw–Hill
_[3] 논문 A moving control volume approach to computing hydrodynamic forces and torques on immersed bodies
_[4] 서적 Viscous Fluid Flow McGraw–Hill
_[5] 논문 What is Rheology? 2018-02
_[6] 논문 Book Review: Cebeci, T. and Cousteix, J., Modeling and Computation of Boundary-Layer Flows http://dx.doi.org/10[...] 2006-12-01
_[7] 웹사이트 Parallel AMR Code for Compressible MHD or HD Equations http://math.lanl.gov[...] Los Alamos National Laboratory
_[8] 웹사이트 Transient state or unsteady state? -- CFD Online Discussion Forums https://www.cfd-onli[...]
_[9] 서적 Turbulent Flows Cambridge University Press
_[10] 논문 Schlatter et al, Phys. Fluids 21, 051702 (2009)
_[11] 서적 Fluid Mechanics Pergamon
_[12] 서적 Hydrodynamic Fluctuations in Fluids and Fluid Mixtures Elsevier
_[13] 서적 Fluid Mechanics Pergamon

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com