전기적 위치 에너지

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 단일 점전하의 정전기적 위치 에너지
  - 2.1.1. 다른 점전하 ''Q''가 존재할 때
  - 2.1.2. 여러 점전하 ''Q_i''가 존재할 때
- 2.2. 전하계에 저장된 정전기적 위치 에너지
3. 전위 표시
4. 전기 에너지 밀도
- 4.1. 자유 공간에서의 전기 에너지 밀도
- 4.2. 유전체 내에서의 전기 에너지 밀도
5. 전자 소자에 저장된 에너지
- 5.1. 축전기(Capacitor)
참조

1. 개요

전기적 위치 에너지는 무한대 거리에서부터 전하들을 가까이 가져와 조립하는 데 필요한 일 또는 외부 요인이 무한대에서 현재 구성까지 전하를 가져오는 데 수행하는 총 일로 정의된다. 단일 점전하의 경우, 다른 점전하가 만드는 전기장 내에서 위치에 따라 에너지가 결정되며, 여러 점전하가 존재할 때는 각 전하쌍 사이의 에너지 합으로 나타낼 수 있다. 또한, 전기적 위치 에너지는 전위, 전기장, 전하 밀도 등을 이용하여 표현할 수 있으며, 전자 소자인 축전기에 저장되는 에너지와 전기 에너지 밀도에 대한 내용도 포함한다.

더 읽어볼만한 페이지

전압 - 전위
전위는 전기장 내 단위 전하의 위치 에너지로, 정전기학에서는 기준점에 따라 정의되며 전위차만이 의미를 갖고, 전기장의 음의 기울기로 표현되고, 전기 공학에서는 회로 해석에 활용된다.
전압 - 고전압
고전압은 국제전기기술위원회(IEC) 등에서 교류 1,000V 이상, 직류 1,500V 이상으로 정의하며, 전력 송배전, 산업, 과학 등 다양한 분야에서 활용되지만 감전 등의 위험이 따르므로 안전에 유의해야 한다.
전자기학 - 전력
전력은 전압과 전류의 곱으로 계산되며, 발전소에서 생산되어 송전 및 배전을 통해 소비자에게 공급되고, 에너지 저장 기술을 통해 안정적으로 공급될 수 있으며, 산업, 상업, 가정 등 다양한 분야에서 소비된다.
전자기학 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.

전기적 위치 에너지

2. 정의

점전하 ''Q''가 만들어 내는 전기장 ''E''에 또 다른 점전하 ''q''가 놓여 있을 경우, 두 점전하는 정전기력에 의해 위치가 변화한다. ''Q''의 상대적 위치를 원점으로 하여 ''q''의 위치 변화만을 계산할 때, 최초 위치를 '''r'''_ref, 변화된 위치를 '''r'''이라 하면 ''q''의 전위 에너지 변화는 다음의 선적분에 의해 계산할 수 있다.^[8] 이때, 전기장은 점전하에서 모든 방향으로 균등하게 방사되며 변화가 없다고 가정한다.

: $U_E(r) - U_E(r_{\rm ref}) = -W_{r_{\rm ref} \rightarrow r } = -\int_^r \mathbf{F} \cdot \mathrm{d} \mathbf{r} = -q \int_^r \mathbf{E} \cdot \mathrm{d} \mathbf{r}$

'''r''': 3차원 공간에서 '''r'''은 '''r''' = (''x'', ''y'', ''z'')의 위치에서 ''r'' = |'''r'''| 의 크기를 갖는 위치 벡터이다.
$\scriptstyle W_{r_{\rm ref} \rightarrow r }$ : 점전하 ''q''가 '''r'''_ref에서 '''r'''로 이동하였음을 의미한다.
'''F''': ''Q''에 의해 ''q''에 가해진 힘이다.
'''E''': ''Q''에 의한 전기장이다.

일반적으로 ''U_E''를 0으로, '''r'''_ref을 무한대로 놓아 다음과 같이 표기한다.

:

U_E (r_{\rm ref}=\infty) = 0

따라서,

:

U_E(r) = -\int_\infty^r \mathbf{F} \cdot \mathrm{d} \mathbf{r} = -q \int_\infty^r \mathbf{E} \cdot \mathrm{d} \mathbf{r}

가 되고, 이 때 '''E''', '''F''', '''r'''은 모두 ''Q''에 의해 방사상으로 이끌리고, '''F'''와 d'''r'''은 역평행이어야 하므로,

:

\mathbf{F} \cdot \mathrm{d} \mathbf{r} = |\mathbf{F}| \cdot |\mathrm{d}\mathbf{r}|\cos(\pi) = - F \mathrm{d}r

이다.

쿨롱의 법칙에 따라

:

F = \frac{1}{4\pi\varepsilon_0}\frac{qQ}{r^2}

이므로, 적분을 간단히 하면:

:

U_E(r) = -\int_\infty^r \mathbf{F} \mathrm{d} \mathbf{r} = -\int_\infty^r \frac{1}{4\pi\varepsilon_0}\frac{qQ}{r^2}{\rm d}r = \frac{1}{4\pi\varepsilon_0}\frac{qQ}{r}

이 된다.

국제단위계에서 쿨롱 상수는

:

k_e = \frac{1}{4 \pi \varepsilon_0}

(이때,

\varepsilon_0

는 진공의 유전율)

이므로 다음과 같이 표시하기도 한다.

:

U_E(r) = k_e \frac{qQ}{r}

즉, 점전하 ''Q''가 만들어 내는 전기장 ''E''에 놓인 점전하 ''q''가 '''r''' 만큼 위치가 변화하였을 때의 에너지는 두 점전하 사이의 거리에 반비례하고 전하량의 곱에 비례한다.

정전기적 위치 에너지는 무한대 거리에서부터 전하들을 가져와 현재의 전하 배치를 구성하는 데 필요한 일, 또는 외부 요인이 전하를 무한대에서 현재 위치까지 가속 없이 이동시키는 데 필요한 총 일로 정의된다.

2. 1. 단일 점전하의 정전기적 위치 에너지

전기장 '''E''' 내에서 위치 '''r'''에 있는 점전하 ''q''의 정전기적 위치 에너지 ''U_E''는 기준 위치 '''r'''_ref에서 해당 위치 '''r'''로 가져오는 데 정전기력이 수행한 일 ''W''의 음수로 정의된다.^[1]^[2]^[3]

:

U_\mathrm{E}(\mathbf r) = -W_{r_{\rm ref} \rightarrow r } = -\int__{\rm ref}}^\mathbf{r} q\mathbf{E}(\mathbf{r'}) \cdot \mathrm{d} \mathbf{r'}

여기서 '''E'''는 정전기장이고 d'''r''''은 기준 위치 '''r'''_ref에서 최종 위치 '''r'''까지의 곡선에서 변위 벡터이다.

정전기적 위치 에너지는 전위

V

가 있는 위치 '''r'''에 있는 하나의 점전하 ''q''의 정전기적 위치 에너지 ''U_E''는 전하와 전위의 곱으로도 정의될 수 있다.

:

U_\mathrm{E}(\mathbf r) = qV(\mathbf r)

여기서

V

는 위치 '''r'''의 함수인 전하에 의해 생성된 전위이다.

점전하계의 전기적 위치 에너지는 무한대 거리에서부터 이 시스템의 전하들을 가까이 가져와 조립하는 데 필요한 일로 정의된다. 또는 주어진 전하 또는 전하계의 전기적 위치 에너지는 가속 없이 외부 요인이 무한대에서 현재 구성까지 전하 또는 전하계를 가져오는 데 수행하는 총 일로 정의된다.

2. 1. 1. 다른 점전하 ''Q''가 존재할 때

점전하 ''Q''가 만들어 내는 전기장 ''E''에 또 다른 점전하 ''q''가 놓여 있을 경우, 두 점전하는 정전기력에 의해 위치가 변화하게 된다. 일반적으로

U_E

를 0으로,

\mathbf{r}_{ref}

을 무한대로 놓아 식을 표현한다.^[8]

:

U_E (r_{\rm ref}=\infty) = 0

따라서,

:

U_E(r) = -\int_\infty^r \mathbf{F} \cdot \mathrm{d} \mathbf{r} = -q \int_\infty^r \mathbf{E} \cdot \mathrm{d} \mathbf{r}

가 되고, 이 때 '''E''', '''F''', '''r'''은 모두 ''Q''에 의해 방사상으로 이끌리고, '''F'''와

\mathrm{d}\mathbf{r}

은 역평행이어야 하므로,

:

\mathbf{F} \cdot \mathrm{d} \mathbf{r} = |\mathbf{F}| \cdot |\mathrm{d}\mathbf{r}|\cos(\pi) = - F \mathrm{d}r

이다.

쿨롱의 법칙에 따라

:

F = \frac{1}{4\pi\varepsilon_0}\frac{qQ}{r^2}

이므로, 적분을 간단히 하면:

:

U_E(r) = -\int_\infty^r \mathbf{F} \mathrm{d} \mathbf{r} = -\int_\infty^r \frac{1}{4\pi\varepsilon_0}\frac{qQ}{r^2}{\rm d}r = \frac{1}{4\pi\varepsilon_0}\frac{qQ}{r}

이 된다.

국제단위계에서 쿨롱 상수는

:

k_e = \frac{1}{4 \pi \varepsilon_0}

(이때,

\varepsilon_0

는 진공의 유전율)

이므로 다음과 같이 표시하기도 한다.

:

U_E(r) = k_e \frac{qQ}{r}

즉, 점전하 ''Q''가 만들어 내는 전기장 ''E''에 놓인 점전하 ''q''가

\mathbf{r}

만큼 위치가 변화하였을 때의 에너지는 두 점전하 사이의 거리에 반비례하고 전하량의 곱에 비례한다.

2. 1. 2. 여러 점전하 ''Q_i''가 존재할 때

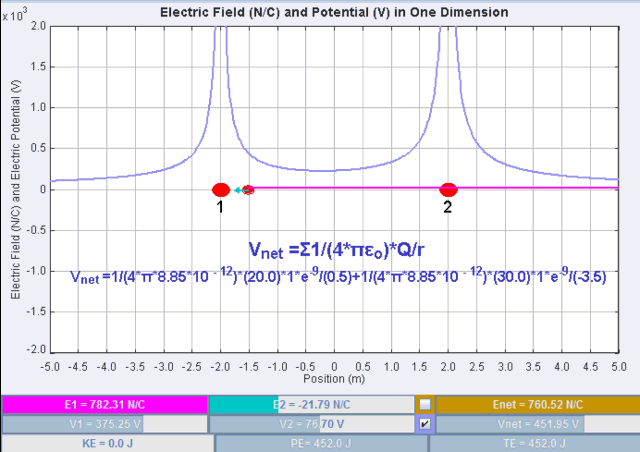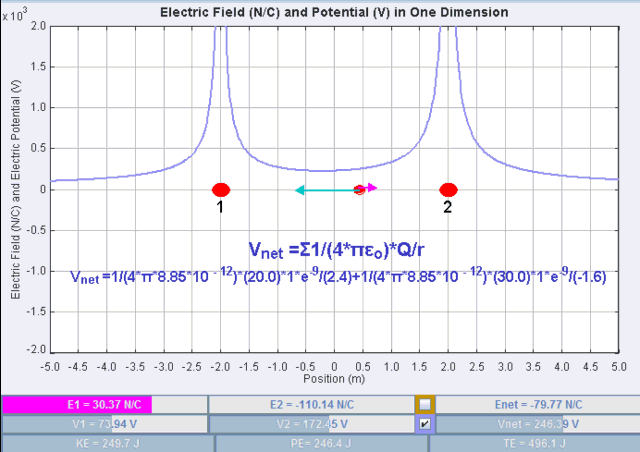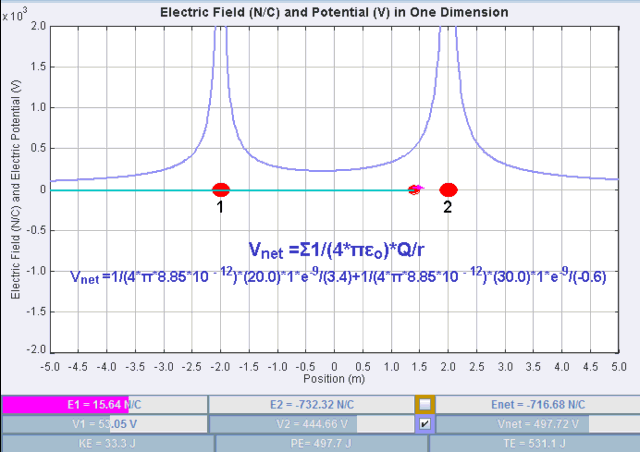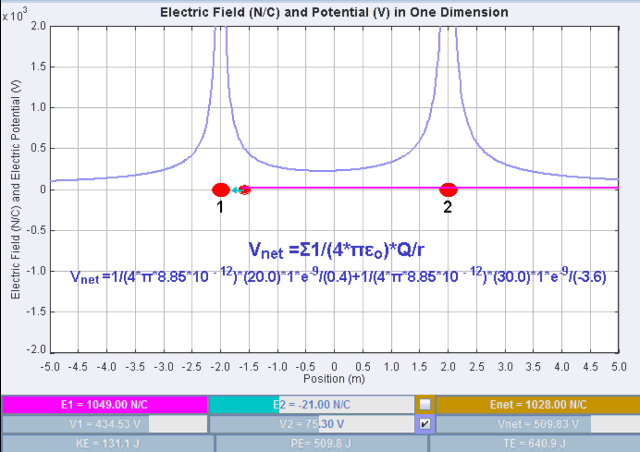
전하 간의 무한 분리를 기준 위치로 삼았을 때, ''n''개의 점전하 ''Q_i''가 있는 상태에서 하나의 점전하 ''q''의 정전기적 위치 에너지 ''U_E''는 다음과 같다.

:

U_E(r) =  \frac{q}{4\pi\varepsilon_0} \sum_{i=1}^n \frac{Q_i}{r_i},

여기서 ''r_i''는 점전하 ''q''와 ''Q_i'' 사이의 거리이며, ''q''와 ''Q_i''는 전하의 할당된 값이다.

2. 2. 전하계에 저장된 정전기적 위치 에너지

여러 점전하로 구성된 계에 저장된 정전기적 위치 에너지는 각 전하쌍 사이의 정전기적 위치 에너지의 합으로 나타낼 수 있다. ''N''개의 점전하

q_i

(

i=1, 2, ..., N

)가 위치

\mathbf{r}_i

에 있을 때, 전하계에 저장된 정전기적 위치 에너지는 다음과 같다.^[1] 여기서

V(\mathbf{r}_i)

는

q_i

를 제외한 다른 모든 전하에 의한

\mathbf{r}_i

에서의 전위이고,

r_{ij}

는

q_i

와

q_j

사이의 거리이다.

:

U_\mathrm{E} = \frac{1}{2} \sum_{i=1}^N q_i V(\mathbf{r}_i) = \frac{1}{2} k_e\sum_{i=1}^N q_i \sum_\stackrel{j=1}{j \ne i}^N \frac{q_j}{r_{ij}}

^[1]

여기서 각 ''i'' 값에 대해

V(\mathbf{r}_i)

는

\mathbf{r}_i

에 있는 전하를 제외한 모든 점전하로 인한 정전기적 위치 에너지이며, 다음과 같다.

:

V(\mathbf{r}_i) = k_e\sum_\stackrel{j=1}{j \ne i}^N \frac{q_j}{r_{ij}}

전기적 위치 에너지는 한 점전하만을 포함하는 시스템의 경우 0이다. 왜냐하면 외부 작용자가 무한대에서 최종 위치로 점전하를 이동시키는 데 대해 일을 해야 하는 다른 정전기력의 원천이 없기 때문이다. 점전하가 자신의 정전기적 위치와 상호작용하는 것은 시스템의 저장된 에너지에 기여하지 않는다.

점전하 ''q''를 점전하 ''Q''₁ 근처의 최종 위치로 가져올 때, ''Q''₁에 의한 전위 V('''r''')는 다음과 같다.

:

V(\mathbf r) = k_e \frac{Q_1}{r}

따라서 ''Q''₁의 전위에서 ''q''의 정전기적 위치 에너지는 다음과 같다.

:

U_E = \frac{1}{4\pi\varepsilon_0} \frac{q Q_1}{r_1}

여기서 ''r''₁는 두 점전하 사이의 거리이다.

세 전하 시스템의 정전기적 위치 에너지는 두 전하 ''Q''₂와 ''Q''₃에 의한 ''Q''₁의 정전기적 위치 에너지와 혼동해서는 안 된다. 후자는 두 전하 ''Q''₂와 ''Q''₃의 시스템의 정전기적 위치 에너지를 포함하지 않기 때문이다. 세 전하 시스템에 저장된 정전기적 위치 에너지는 다음과 같다.

:

U_\mathrm{E} = \frac{1}{4\pi\varepsilon_0} \left[ \frac{Q_1 Q_2}{r_{12}} + \frac{Q_1 Q_3}{r_{13}} + \frac{Q_2 Q_3}{r_{23}} \right]

3. 전위 표시

시간에 따라 변하지 않는 정전기장의 경우, 정전 포텐셜을 사용하여 다음 식으로 나타낼 수 있다.

: $\begin{align}U &=-\frac{\epsilon_0}{2} \int_V \boldsymbol{E}\cdot \operatorname{grad}\phi\, d^3x \\&=\frac{\epsilon_0}{2} \int_V \phi\, \operatorname{div}\boldsymbol{E}\, d^3x$

\frac{\epsilon_0}{2} \int_V \operatorname{div} (\phi \boldsymbol{E})\, d^3x \\

&=\frac{1}{2} \int_V \rho\, \phi\, d^3x

\frac{\epsilon_0}{2} \oint_{\partial V} (\phi \boldsymbol{E})\cdot d\boldsymbol{S} \\

\end{align}

경계에서 포텐셜이 0이 된다는 조건을 적용하여 두 번째 항을 없애면

:

U =\frac{1}{2} \int \rho\, \phi\, d^3x

가 된다.^[6] 여기서 ρ는 전하 밀도이고, 적분은 전체 공간에 대해 수행된다.

전위 인 도체에 전하 가 충전되었을 때,

:

U =\frac{1}{2} \sum_i q_i \phi_i

이다. 정전 용량을 사용하면

:

U =\frac{1}{2} \sum_{i,j} C_{ij} \phi_i \phi_j

가 된다.^[6]

4. 전기 에너지 밀도

연속적인 전하 분포 $\rho( \mathbf r )$ 에 의한 에너지는 다음과 같이 쓸 수 있다.

: $U = \frac{1}{2} \int \rho V d\tau = \frac{\epsilon_0 }{2} \left[\int_{\mathcal V} E^2 d\tau + \oint_{\mathcal S} V \mathbf E \cdot d\mathbf a \right]$

여기서 $\mathcal S$ 는 $\mathcal V$ 의 경계면이다. 그런데 $\mathcal V$ 를 무한대로 보내면 $\mathcal S$ 에서 $\mathbf E$ 와 $V$ 모두 $0$ 에 수렴하므로 위 적분은 다음과 같이 나타내어진다.

: $U = \frac{\epsilon_0 }{2} \int_{\mathcal V} E^2 d\tau$

따라서 전기 에너지 밀도를 다음과 같이 나타낼 수 있다.

: $u_E = \frac{1}{2} \epsilon_0 E^2$

4. 1. 자유 공간에서의 전기 에너지 밀도

연속적인 전하 분포의 정전기장의 에너지 밀도, 즉 단위 부피당 에너지

\frac{dU}{dV}

는 다음과 같다.^[6]

:

u_e = \frac{dU}{dV} = \frac{1}{2} \varepsilon_0 \left|{\mathbf{E}}\right|^2.

자유 공간에서 전기장 '''E'''가 있을 때, 전기 에너지 밀도 ''u''는 다음과 같다.^[6]

:

u =\frac{\epsilon_0}{2} \boldsymbol{E}^2

여기서

\epsilon_0

는 진공 유전율이다.

특정 영역 내의 총 정전기 에너지는 다음 적분으로 계산된다.^[6]

:

U =\frac{\epsilon_0}{2} \int_V \boldsymbol{E}^2\, d^3x

4. 2. 유전체 내에서의 전기 에너지 밀도

매질이 있는 경우에는, 전기 변위 '''D'''에 의해 다음과 같이 주어진다.^[7]

:u|^영어 = ∫'''E'''•d'''D'''

구성 방정식을 사용하면, 유전 분극 '''P'''에 의해 다음과 같이 나타낼 수 있다.

:u|^영어 = ε₀/2 '''E'''² + ∫'''E'''•d'''P'''

특히 선형 매질의 경우에는 다음과 같다.

:u|^영어 = ε/2 '''E'''²

5. 전자 소자에 저장된 에너지

전자 회로의 소자들은 전기 에너지를 다른 형태로 변환하거나 저장할 수 있다. 저항기는 전기 에너지를 줄 효과를 통해 열로 변환한다. 축전기는 전하를 전기장에 저장한다.

5. 1. 축전기(Capacitor)

축전기는 전기에너지(전하)를 전기장 안에 저장한다. 축전기에 저장된 총 정전기적 위치 에너지는 다음과 같다.^[5]

:

U_E = \frac{1}{2}QV = \frac{1}{2} CV^2 = \frac{Q^2}{2C}

여기서 ''C''는 전기 용량, ''V''는 전위차, ''Q''는 축전기에 저장된 전하이다.

총 정전기적 위치 에너지는 전기장 형태로 다음과 같이 표현될 수 있다.

:

U_E = \frac{1}{2} \int_V \mathrm{E} \cdot \mathrm{D} \, dV

여기서

\mathrm{D}

는 유전체 내의 전기 변위장이며, 적분은 유전체의 전체 부피에 대해 수행된다.

인가 전압

V

로 전하

Q

가 충전된 축전기가 갖는 정전 에너지는 두 전극판에서 전하가

q_1=Q

,

q_2=-Q

이고, 전위가

\phi_1-\phi_2 =V

이므로

:

U =\frac{1}{2}(q_1\phi_1 +q_2\phi_2) =\frac{1}{2} Q(\phi_1 -\phi_2) =\frac{1}{2} QV

로 유도된다. 정전 용량을 사용하면

:

U =\frac{1}{2} CV^2 =\frac{Q^2}{2C}

가 된다.

참조

_[1] 문서
_[2] 서적 Electromagnetism
_[3] 서적 Fundamentals of Physics https://archive.org/[...] John Wiley & Sons
_[4] 문서
_[5] 간행물 A new constituent of electrostatic energy in semiconductors 2016-06-01
_[6] 서적 ジャクソン『電磁気学』
_[7] 서적 ジャクソン『電磁気学』
_[8] 서적 Electromagnetism

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com