전위

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 전위와 전위차
- 2.2. 국제단위계
3. 정전기학에서의 전위
4. 전기장과의 관계
5. 전자기역학으로의 일반화
- 5.1. 게이지 자유도
- 5.2. 쿨롱 게이지와 로렌츠 게이지
6. 갈바니 전위와 전기화학적 전위
7. 전기 공학에서의 전위
참조

1. 개요

전위는 전기장 내에서 단위 전하가 갖는 전기적 위치 에너지로, 특정 지점의 전위를 임의로 정의할 수 있으며, 두 지점 간의 전위차(전압)가 물리적 의미를 갖는다. 전위는 전기장의 음의 기울기로 표현되며, 전기장과의 관계를 통해 쿨롱 힘, 일의 양 등을 계산할 수 있다. 전자기학에서는 전자기 퍼텐셜을 사용하여 시간 변화하는 자기장과 전기장을 설명하며, 게이지 자유도를 통해 다양한 표현이 가능하다. 전기 공학에서는 회로의 기준점을 0V로 설정하고, 옴의 법칙과 임피던스 계산에 전위를 활용한다.

더 읽어볼만한 페이지

전압 - 고전압
고전압은 국제전기기술위원회(IEC) 등에서 교류 1,000V 이상, 직류 1,500V 이상으로 정의하며, 전력 송배전, 산업, 과학 등 다양한 분야에서 활용되지만 감전 등의 위험이 따르므로 안전에 유의해야 한다.
전압 - 기전력
기전력은 전하를 이동시키는 원동력으로 전압의 원인이 되며, 화학 전지, 전자기 유도, 태양 전지 등 다양한 현상으로 발생하여 에너지 변환과 전력 공급을 가능하게 한다.
퍼텐셜 - 리에나르-비헤르트 퍼텐셜
리에나르-비헤르트 퍼텐셜은 운동하는 점전하가 속도와 가속도를 고려하여 생성하는 전자기 퍼텐셜을 기술하는 공식으로, 전자기 복사 효과를 포함하여 전자기장을 정확하게 계산하고 고전 전자기학과 상대성이론 발전에 기여했으나 양자역학적 영역에서는 한계를 보인다.
퍼텐셜 - 위치 에너지
위치 에너지는 물리학에서 물체의 위치에 따라 결정되는 에너지의 한 형태이며, 중력, 탄성, 전기력 등 다양한 힘과 관련되어 스칼라 퍼텐셜 장을 정의하고 힘은 퍼텐셜 장의 기울기의 음수로 표현된다.
정전기학 - 정전기 유도
정전기 유도는 대전체가 다른 물체에 접근했을 때 쿨롱의 법칙에 의해 물체 내부의 전하 분포가 변하는 현상으로, 전도체에서는 자유 전자의 이동으로 전하가 양분되지만 부도체에서는 분극 현상이 발생하며 금박 검전기, 정전기 유도 트랜지스터, 정전기 발생기 등 다양한 분야에 응용되고 유도 장애를 일으키기도 한다.
정전기학 - 쿨롱 법칙
쿨롱 법칙은 1785년 샤를 쿨롱이 발표한, 정지된 두 점전하 사이의 전기력을 설명하는 물리 법칙으로, 두 전하량의 곱에 비례하고 거리의 제곱에 반비례하는 전기력의 크기를 나타낸다.

전위
전위
전하를 띤 두 개의 전도성 구 주변의 전기 전위. 보라색은 가장 높은 전위, 노란색은 0, 청록색은 가장 낮은 전위를 나타낸다. 전기 전기장선은 각 구의 표면에 수직으로 나가는 것으로 표시된다.
단위	볼트
다른 단위	스탯볼트
기호	V, φ
기본 단위	V = kg⋅m²⋅s⁻³⋅A⁻¹
차원	M L² T⁻³ I⁻¹
크기 성질	예
정의
전위	전기장 내에서 단위 전하가 가지는 위치 에너지. 전기장 내의 한 점에서 기준점까지 단위 양전하를 이동시키는 데 필요한 일.
전위차	전기장 내의 두 점 사이의 전위의 차이
전위의 다른 이름	정전기 퍼텐셜
공식
정의 공식	전기장 E에 대한 선적분으로 정의: V_B - V_A = -∫_A^B E⋅dl
점전하	V = kQ / r
설명
특징	스칼라 양이다. 쿨롱 힘은 보존력이므로, 경로에 무관하다. 전기장과 관련된 개념이다.
전위의 기준점	일반적으로 무한대를 기준으로 한다.
전위의 실제적인 적용	전위는 전기 회로와 전자기학의 많은 응용 분야에서 핵심적인 개념이다.
기타
영어	electric potential
로마자 표기	jeonwi

2. 정의

정전기에서 전기장 내의 한 점에서의 전위는, 단위 양전하가 그 지점에서 가지는 위치 에너지로 정의된다. 이는 전기장 내에서 전하가 받는 힘과 관련된 에너지 개념이다. 맥스웰 방정식에 따르면, 정전기학에서는 전하가 움직이지 않으므로 자기장이 없고, 따라서 전기장의 회전은 0이 된다. 이 때문에 전기장은 어떤 스칼라 함수의 기울기로 표현할 수 있는데, 이 스칼라 함수를 -V라고 하고, V를 전위라고 부른다. 즉, E = -∇V 가 된다.

전위는 상대적인 값으로, 기준점에 따라 값이 달라진다. 보통 무한히 먼 곳이나 접지점의 전위를 0으로 설정한다. 이론 물리학에서는 계에서 "무한히 먼 곳"에서의 전위를 0으로 놓는 것이 일반적이다. 전위는 에너지와 전하의 비, 즉 단위 전하가 가지고 있는 정전기 퍼텐셜 에너지이다. 전위의 국제 단위는 볼트(V)이며, 1V = 1줄(J)/쿨롱(C)이다.

전기 전위는 다음과 같은 선적분으로 주어진다.

: $V_\mathbf{E} = - \int_{\mathcal{C} } \mathbf{E} \cdot \mathrm{d} \boldsymbol{\ell}\,$

여기서 C는 어떤 고정된 기준점에서 r까지의 임의의 경로이다. 정전기에서 맥스웰-패러데이 방정식은 회전 ∇×E가 0임을 보여주며, 이는 전기장이 보존적임을 의미한다. 따라서 위의 선적분은 선택된 특정 경로 C에 의존하지 않고, 그 끝점에만 의존하며, VE를 모든 곳에서 잘 정의한다. 그러면 기울기 정리를 사용하여 다음과 같이 쓸 수 있다.

: $\mathbf{E} = - \mathbf{\nabla} V_\mathbf{E}\,$

이는 전기장이 더 낮은 전압 쪽으로 "내리막"을 향한다는 것을 나타낸다.

전위는 고전역학에서의 위치 에너지와 대응되는 개념으로, 단위 전하를 기준점까지 옮기는 데 필요한 일의 양으로 정의된다. 쿨롱의 법칙에 의해, 전하 Q를 가진 점전하로부터 r만큼 떨어진 지점의 전위 V는 V = Q/r이다. 여러 점전하가 있는 경우, 전위는 각 점전하가 만드는 전위의 총합이 된다. ( 중첩의 원리)

정자기장(＝자기장이 시간에 따라 변하지 않는 경우)에서는 전위의 값이 경로에 의존하지 않지만, 전자기 유도가 일어나는 경우에는 경로에 따라 값이 달라지므로 전위 개념을 정의하기 어렵다. 이 경우, 전자기 유도의 영향분을 보정한 전자기 퍼텐셜을 사용해야 한다.

2. 1. 전위와 전위차

위치 에너지가 절대적인 값이 아니라, 두 지점 사이의 위치 에너지 차이만이 절대적인 값인 것처럼, 전위 또한 상대적인 값이다. 즉 특정 지점의 전위는 임의로 정의할 수 있고, 두 지점의 전위차(전압)만이 물리적 의미를 갖는다.^[1] 수학적으로는 V^영어에 어떤 상수를 더해준 값인 V+a^영어에 대해서도 E = - ∇V = - ∇(V + a)^영어가 되어 같은 전기장이 나오기 때문이다.^[1]

전기 회로에서는 보통 접지(接地, ground^영어)의 전위를 0으로 놓거나, 아니면 회로도에 어느 점의 전위를 0으로 정의하는지 표시한다.^[1]

전위차는 두 지점 사이의 전위 차이로, 전압이라고도 불린다.^[1] 전위차는 전기 회로에서 전하가 이동하는 원동력이 되며, 전자기기의 작동 원리를 이해하는 데 필수적이다.

전위는 에너지와 전하의 비(단위전하가 가지고 있는 정전기 퍼텐셜 에너지)이다. 즉, 전위의 국제 단위인 볼트는 다음과 같다.^[1]

볼트(V) = 줄(J)/쿨롱(C).

:

\Delta V = V_f - V_i = { U_f \over q } - { U_i \over q } = { \Delta U \over q }

:

\Delta V = V_A - V_B = { \Delta U \over q_0 } =  - { \int_{B}^{A} { \vec{E} \cdot d \vec{s} } }

(전위차의 정의)

:

V = { U \over q_0}

(전위의 정의)

:

V_f - V_i = - { \int_{i}^{f} { \vec{E} \cdot d \vec{s} } }

두 점의 전위차(

V_f- V_i

)는 두 점 사이의 전기장을 선적분 한 값이다. 이때, 전기장은 보존장이기 때문에 적분구간의 모양은 상관 없고, 적분구간의 시작점과 끝점만 중요하다.^[1]

2. 2. 국제단위계

전위의 국제 단위는 볼트(V)이며, 1V는 1줄(J)/쿨롱(C)이다.

:

\Delta V = V_f - V_i = { U_f \over q } - { U_i \over q } = { \Delta U \over q }

:

\Delta V = V_A - V_B = { \Delta U \over q_0 } =  - { \int_{B}^{A} { \vec{E} \cdot d \vec{s} } }

(전위차의 정의)

:

V = { U \over q_0}

(전위의 정의)

:

V_f - V_i = - { \int_{i}^{f} { \vec{E} \cdot d \vec{s} } }

두 점의 전위차(

V_f- V_i

)는 두 점 사이의 전기장을 선적분한 값이다. 이때, 전기장은 보존장이기 때문에 적분 구간의 모양은 상관 없고, 적분 구간의 시작점과 끝점만 중요하다. 전기 퍼텐셜의 SI 유도 단위는 볼트(V)이며, 알레산드로 볼타의 이름을 따서 명명되었다. 공간의 두 점 사이의 전위차는 전압으로 알려져 있다. 오늘날에는 오래된 단위는 거의 사용되지 않는다. 센티미터-그램-초 단위계의 변형에는 앱볼트와 정전볼트를 포함한 여러 가지 전기 퍼텐셜 단위가 포함되어 있었다.

3. 정전기학에서의 전위

정전기학에서 전기장 '''E''' 내의 한 점 '''r'''에서의 전기 전위는 다음과 같은 선적분으로 주어진다.^[10]

: $V_\mathbf{E} = - \int_{\mathcal{C} } \mathbf{E} \cdot \mathrm{d} \boldsymbol{\ell}\,$

여기서 C는 어떤 고정된 기준점에서 '''r'''까지의 임의의 경로이다. 정전기학에서는 맥스웰-패러데이 방정식에 따라 회전 $\nabla\times\mathbf{E}$ 이 0이 되므로, 전기장은 보존적이다. 따라서 위의 선적분은 선택된 특정 경로 C에 의존하지 않고 끝점에만 의존하며, $V_\mathbf{E}$ 는 모든 곳에서 잘 정의된다. 기울기 정리를 사용하면 다음과 같이 쓸 수 있다.^[10]

: $\mathbf{E} = - \mathbf{\nabla} V_\mathbf{E}\,$

이는 전기장이 더 낮은 전압 쪽으로 "내리막"을 향한다는 것을 의미한다. 가우스 법칙에 의해, 전위는 또한 다음과 같은 푸아송 방정식을 만족한다.^[10]

: $\mathbf{\nabla} \cdot \mathbf{E} = \mathbf{\nabla} \cdot \left (- \mathbf{\nabla} V_\mathbf{E} \right ) = -\nabla^2 V_\mathbf{E} = \rho / \varepsilon_0$

여기서 ρ는 총 전하 밀도이고 $\mathbf{\nabla}\cdot$ 는 발산을 나타낸다.

전기 전위의 개념은 퍼텐셜 에너지와 밀접하게 관련되어 있다. 시험 전하 q는 다음과 같이 주어지는 전기 퍼텐셜 에너지 U_'''E'''를 갖는다.^[10]

: $U_ \mathbf{E} = q\,V.$

퍼텐셜 에너지와 전기 전위는 덧셈 상수에 의해 결정된다. 즉, 퍼텐셜 에너지와 전기 전위가 0인 위치를 임의로 선택해야 한다.^[10]

정자장의 경우 전위의 정의가 P₀과 P를 잇는 경로 C에 의존하지 않는다. 즉, C₁, C₂를 P₀과 P를 잇는 임의의 두 경로라고 할 때, 다음이 성립한다.^[10]

: $\int_{C_1} \boldsymbol{E} \cdot \mathrm{d}\boldsymbol{s} = \int_{C_2} \boldsymbol{E} \cdot \mathrm{d}\boldsymbol{s}.$

3. 1. 점전하에 의한 전위

아무것도 없는 공간에 존재하는 점전하 q가 있을 때, 이 전하에서 r만큼 떨어진 곳의 전위는 다음과 같이 정의할 수 있다.

V = { 1 \over 4 \pi \epsilon_0 } { q \over r }

이 공식은 무한히 먼 곳의 전위를 0V로 설정한 후의 공식이다.

$\epsilon_0$ = 진공의 유전율

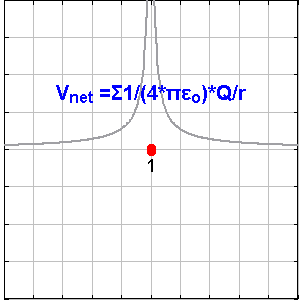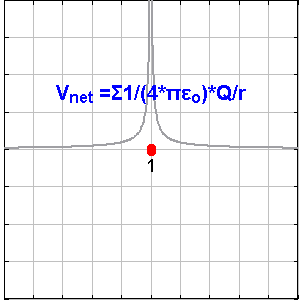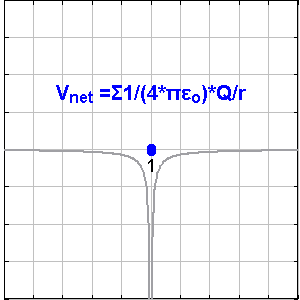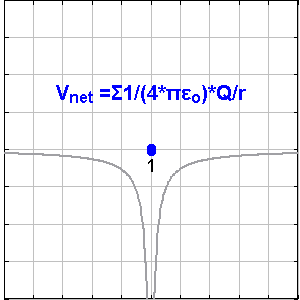
점전하 Q로부터 r 거리에 있는 위치에서 발생하는 전기 전위는 다음과 같다.

V_\mathbf{E} = \frac{1}{4 \pi \varepsilon_0} \frac{Q}{r},

여기서

\varepsilon_0

는 진공의 유전율이고,

V_\mathbf{E}

는 '''쿨롱 전위'''로 알려져 있다. 점전하로 인한 전기장의 크기와는 달리, 전기 전위는 반지름의 제곱에 반비례하는 것이 아니라 반지름에 반비례한다는 점에 유의해야 한다.

점전하계에서 임의의 위치

\mathbf{r}

의 전기 전위는 계 내 모든 점전하에 대한 개별 전기 전위의 합과 같다. 이 사실은 전위(스칼라)장의 덧셈이 전기(벡터)장의 덧셈보다 훨씬 쉽기 때문에 계산을 상당히 간소화한다. 구체적으로, 점

\mathbf{r}_i

에 있는 이산적인 점전하

q_i

집합의 전위는 다음과 같다.

V_\mathbf{E}(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0} \sum_{i=1}^n\frac{q_i}

\,

여기서

$\mathbf{r}$ 은 전위를 평가하는 점;
$\mathbf{r}_i$ 은 0이 아닌 전하가 있는 점; 그리고
$q_i$ 는 점 $\mathbf{r}_i$ 에 있는 전하이다.

그리고 연속적인 전하 분포

\rho(\mathbf{r})

의 전위는 다음과 같다.

V_\mathbf{E}(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0} \int_R \frac{\rho(\mathbf{r}')}

\mathrm{d}^3 r'\,,

여기서

$\mathbf{r}$ 은 전위를 평가하는 점;
$R$ 은 전하 밀도가 0이 아닌 모든 점을 포함하는 영역;
$\mathbf{r}'$ 은 $R$ 내의 점; 그리고
$\rho(\mathbf{r}')$ 는 점 $\mathbf{r}'$ 에서의 전하 밀도이다.

위에 제시된 전기 전위에 대한 방정식(그리고 여기서 사용된 모든 방정식)은 SI 단위계에서 필요한 형태이다. CGS-가우스와 같이 다른 (덜 일반적인) 단위계에서는 이러한 방정식 중 많은 부분이 변경될 것이다.

3. 2. 여러 점전하에 의한 전위

공간에 점전하 n개가 존재할 때, 특정 지점의 전위는 각 점전하가 만드는 전위의 합으로 계산된다.

:

V = \sum_{i=1}^{n} V_i = { 1 \over 4 \pi \epsilon_0 } \sum_{i=1}^{n} {q_i \over r_i}

::

q

= 각 전하의 전하량

::

r

= 전위를 구할 지점에서 각 전하까지의 거리

점전하계에서 임의의 위치의 전기 전위는 계 내 모든 점전하에 대한 개별 전기 전위의 합과 같다. 이는 전위(스칼라)장의 덧셈이 전기(벡터)장의 덧셈보다 훨씬 쉽기 때문에 계산을 간소화한다. 구체적으로, 점에 있는 이산적인 점전하 집합의 전위는 다음과 같다.

:

V_\mathbf{E}(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0} \sum_{i=1}^n\frac{q_i}

\,

여기서

$\mathbf{r}$ 은 전위를 평가하는 점;

$\mathbf{r}_i$ 은 0이 아닌 전하가 있는 점; 그리고

$q_i$ 는 점 $\mathbf{r}_i$ 에 있는 전하이다.

그리고 연속적인 전하 분포

\rho(\mathbf{r})

의 전위는 다음과 같다.

:

V_\mathbf{E}(\mathbf{r}) = \frac{1}{4\pi\varepsilon_0} \int_R \frac{\rho(\mathbf{r}')}

\mathrm{d}^3 r'\,,

여기서

$\mathbf{r}$ 은 전위를 평가하는 점;

$R$ 은 전하 밀도가 0이 아닌 모든 점을 포함하는 영역;

$\mathbf{r}'$ 은 $R$ 내의 점; 그리고

$\rho(\mathbf{r}')$ 는 점 $\mathbf{r}'$ 에서의 전하 밀도이다.

위에 제시된 전기 전위에 대한 방정식은 SI 단위계에서 사용되는 형태이다.

3. 3. 연속적인 전하 분포에 의한 전위

전하가 연속적으로 분포된 경우, 전위는 전하 밀도에 대한 적분으로 표현된다.

3. 4. 전기 쌍극자의 전위

전기 쌍극자는 크기가 같고 부호가 반대인 두 전하가 가까이 있는 경우를 말하며, 특정 지점에서의 전위는 쌍극자 모멘트와 각도에 따라 달라진다. 전위는 다음과 같이 나타낼 수 있다.

:

V = { 1 \over 4 \pi \epsilon_0 } { {p \cos \theta} \over r^2}

4. 전기장과의 관계

맥스웰 방정식에 따르면 $\nabla \times E = - \frac{\partial B}{\partial t}$ 인데, 정전기학에서는 전하가 움직이지 않으므로 자기장이 없고, 따라서 이 값이 0이 된다. 즉 $E$ 의 회전이 0이 되므로 이를 어떤 스칼라 함수의 기울기로 표현할 수 있다. 보통 그 스칼라 함수를 $-V$ 라고 쓰고, $V$ 를 전위라고 부른다. 즉 $E = - \nabla V$ 가 된다.

위치 에너지가 절대적인 값이 아니라, 두 지점 사이의 위치 에너지 차이만이 절대적인 값인 것처럼, 전위 또한 상대적인 값이다. 즉 특정 지점의 전위는 임의로 정의할 수 있고, 두 지점의 전위차(전압이라고도 불린다)만이 물리적 의미를 갖는다. 수학적인 이유는 $V$ 에 어떤 상수를 더해준 값인 $V+a$ 에 대해서도 $E = - \nabla V = - \nabla \left(V + a \right)$ 가 되어 같은 전기장이 나오기 때문이다.

다만, 이론 물리학에서는 통상적으로 계에서 "무한히 먼 곳"에서의 전위를 0으로 놓는다. 전기 회로에서는 보통 접지(接地, ground^영어)의 전위를 0으로 놓거나, 아니면 회로도에 어느 점의 전위를 0으로 정의하는지 표시한다.

전위는 에너지와 전하의 비(단위 전하가 가지고 있는 정전기 퍼텐셜 에너지)이다. 즉, 전위의 국제 단위인 볼트는 다음과 같다.

: 볼트(V) = 줄(J)/쿨롱(C).

: $\Delta V = V_f - V_i = { U_f \over q } - { U_i \over q } = { \Delta U \over q }$

: $\Delta V = V_A - V_B = { \Delta U \over q_0 } = - { \int_{B}^{A} { \vec{E} \cdot d \vec{s} } }$ (전위차의 정의)

: $V = { U \over q_0}$ (전위의 정의)

: $V_f - V_i = - { \int_{i}^{f} { \vec{E} \cdot d \vec{s} } }$

두 점의 전위차( $V_f- V_i$ )는 두 점 사이의 전기장을 선적분 한 값이다. 이때, 전기장은 보존장이기 때문에 적분 구간의 모양은 상관 없고, 적분 구간의 시작점과 끝점만 중요하다.

$\vec{E} = -\nabla V$

$V = -\int \vec{E} \cdot d\vec{s}$

정전기 전기장 내의 한 점 에서의 전기 전위는 다음과 같은 선적분으로 주어진다.

: $V_\mathbf{E} = - \int_{\mathcal{C} } \mathbf{E} \cdot \mathrm{d} \boldsymbol{\ell}\,$

여기서 $\mathcal{C}$ 는 어떤 고정된 기준점에서 $\mathbf{r}$ 까지의 임의의 경로이다. 이것은 적분에 더하거나 빼는 상수까지 고유하게 결정된다. 정전기에서 맥스웰-패러데이 방정식은 회전 $\nabla\times\mathbf{E}$ 이 0임을 보여주며, 이는 전기장이 보존적임을 의미한다. 따라서 위의 선적분은 선택된 특정 경로 $\mathcal{C}$ 에 의존하지 않고, 그 끝점에만 의존하며, $V_\mathbf{E}$ 를 모든 곳에서 잘 정의한다. 그러면 기울기 정리를 사용하여 다음과 같이 쓸 수 있다.

: $\mathbf{E} = - \mathbf{\nabla} V_\mathbf{E}\,$

이는 전기장이 더 낮은 전압 쪽으로 "내리막"을 향한다는 것을 나타낸다.

전위의 정의는 위치 에너지의 정의와 거의 같으며, 위치 에너지 정의에서의 역학적 힘을 쿨롱의 법칙으로 바꾸면 전위의 정의를 얻을 수 있다. 즉, 점 P에서의 전위는 P에서 정해진 기준점 P₀까지 단위 전하를 옮기는 데 쿨롱의 힘에 대해 한 일로 정의된다. 여기서 '''단위 전하'''는 1쿨롱의 전하를 가진 점전하를 의미한다.

전위의 "기울기"(수학적으로는 grad)는 전기장과 같다. 따라서 위치 P에 있는 대전 입자가 받는 쿨롱의 힘은 그 입자의 전하 q에 전위의 "기울기"를 곱한 값과 같다.

현재 (3차원 벡터) 공간상에 전기장이 있으며, 점 $P = (x, y, z)$ 에서의 전기장이

: $\boldsymbol{E}_P = (E_x, E_y, E_z)$

로 표현된다고 하자.

P₀을 정해진 기점으로 하고, P를 공간상의 임의의 점으로 하며, C를 P₀에서 P까지의 경로로 하고, 선적분

: $- \int_C \boldsymbol{E} \cdot \mathrm{d}\boldsymbol{s} = - \int_C E_x\mathrm{d}x + E_y\mathrm{d}y + E_z \mathrm{d}z$

을 생각해 보자. '''정자장이라면''' 이 선적분은 P₀과 P를 잇는 경로 C에 의존하지 않으므로(후술), 이 선적분의 값을 (P₀을 기점으로 했을 경우의) '''P에서의 전위'''라고 부른다.

이하 P에서의 전위를 V_P로 표기한다. 정자장의 경우 전위는 경로 C에 의존하지 않으므로, C를 명기하지 않고

: $V_P = - \int_{P_0}^P \boldsymbol{E} \cdot \mathrm{d}\boldsymbol{s}$

라고도 표기한다. 크기 *q*의 전하에 전기장 $\boldsymbol{E}$ 가 주는 쿨롱힘 $\boldsymbol{F}$ 는

: $\boldsymbol{F} = q\boldsymbol{E}$

와 같으므로, 전위와 일의 정의에 의해, 전위는 단위 전하를 *P*에서 *P*₀까지 *C*를 따라 옮기는 데 필요한 일의 양과 같다.

정자기장의 경우 전위는 경로에 의존하지 않으므로, 전위 *V*_*P*는 *P*에 실수 *V*_*P*를 대응시키는 함수로 간주할 수 있다.^[9] 이 함수의 기울기는 다음을 만족한다.

: $-\mathrm{grad}~ V_P = \boldsymbol{E}_P$

5. 전자기역학으로의 일반화

시간에 따라 변하는 자기장이 존재할 때, 전기장은 더 이상 보존적이 아니게 된다. 따라서, 선적분 $\textstyle\int_C \mathbf{E}\cdot \mathrm{d}\boldsymbol{\ell}$ 은 경로에 의존하게 되며, 이는 맥스웰-패러데이 방정식에 의해 $\mathbf{\nabla} \times \mathbf{E} \neq \mathbf{0}$ 이기 때문이다.^[11]

이러한 상황에서, 자기 벡터 퍼텐셜 A를 사용하여 스칼라 퍼텐셜을 정의할 수 있다. A는 다음을 만족하도록 정의된다.

$\mathbf{B} = \mathbf{\nabla} \times \mathbf{A}$

여기서 B는 자기장이다. 자기장의 발산이 항상 0이므로, 벡터 미적분의 기본 정리에 따라 이러한 A는 항상 존재한다.

이제, 다음과 같은 양

$\mathbf{F} = \mathbf{E} + \frac{\partial\mathbf{A}}{\partial t}$

은 맥스웰-패러데이 방정식에 따라 보존장이 된다. 따라서, 다음과 같이 쓸 수 있다.

$\mathbf{E} = -\mathbf{\nabla}V - \frac{\partial\mathbf{A}}{\partial t} ,$

여기서 V는 보존장 F에 의해 정의된 스칼라 퍼텐셜이다. 정전 퍼텐셜은 A가 시간에 따라 변하지 않는 특수한 경우이다.

하지만, 시간에 따라 변하는 장의 경우,

$-\int_a^b \mathbf{E} \cdot \mathrm{d}\boldsymbol{\ell} \neq V_{(b)} - V_{(a)}$

가 성립하며, 이는 정전기와는 다른 점이다.

정자기장에 국한되지 않는 경우, 전위의 경로 의존성을 보정하여 경로에 의존하지 않는 퍼텐셜 개념 ''φ''(''P'')를 얻을 수 있다. 이 ''φ''(''P'')는 전자기장의 '''스칼라 퍼텐셜'''이라고 불리며, 자기장에 대한 퍼텐셜 개념인 '''벡터 퍼텐셜'''과 함께 '''전자기 퍼텐셜'''이라고 불린다.^[11] 스칼라 퍼텐셜은 정자기장이 아닌 경우 전위의 대체 개념이며, 정자기장의 경우 앞서 언급한 전위의 정의와 일치한다.

5. 1. 게이지 자유도

전자기역학에서 전위는 유일하게 결정되지 않는다. 게이지 변환을 통해, 임의의 스칼라 장 𝜓^영어에 대해 다음과 같은 변환을 수행하여도 정확히 동일한 전기장과 자기장을 얻을 수 있다.^[4]

:

\begin{align}V^\prime &= V - \frac{\partial\psi}{\partial t} \\\mathbf{A}^\prime &= \mathbf{A} + \nabla\psi\end{align}

이처럼 게이지 선택에 따라 전기 퍼텐셜은 매우 다른 특성을 가질 수 있다. 예를 들어 쿨롱 게이지에서는 전기 퍼텐셜이 푸아송 방정식

:

\nabla^2 V=-\frac{\rho}{\varepsilon_0}

에 의해 주어지는데, 이는 정전기와 같다. 그러나 로렌츠 게이지에서는 전기 퍼텐셜이 빛의 속도로 전파되는 지연 퍼텐셜이며, 비균질 파동 방정식의 해이다.

:

\nabla^2 V - \frac{1}{c^2}\frac{\partial^2 V}{\partial t^2} = -\frac{\rho}{\varepsilon_0}

이는 물리적 현상이 게이지 선택에 무관하다는 것을 의미한다.

5. 2. 쿨롱 게이지와 로렌츠 게이지

게이지 고정에서, 쿨롱 게이지는 전기 퍼텐셜이 푸아송 방정식

\nabla^2 V=-\frac{\rho}{\varepsilon_0}

에 의해 주어지는데, 이는 정전기와 같다.^[4] 그러나 로렌츠 게이지에서 전기 퍼텐셜은 빛의 속도로 전파되는 지연 퍼텐셜이며, 비균질 파동 방정식의 해이다.^[4]

\nabla^2 V - \frac{1}{c^2}\frac{\partial^2 V}{\partial t^2} = -\frac{\rho}{\varepsilon_0}

6. 갈바니 전위와 전기화학적 전위

금속(그리고 다른 고체 및 액체) 내부에서 전자의 에너지는 전기적 전위뿐만 아니라 전자가 존재하는 특정 원자 환경의 영향도 받는다. 두 가지 다른 유형의 금속 사이에 전압계를 연결하면 서로 다른 원자 환경을 고려하여 보정된 '''전위차'''를 측정한다.^[5] 전압계로 측정된 양을 전기화학적 전위 또는 페르미 준위라고 하며, 조정되지 않은 순수한 전기적 전위 ''V''는 때때로 갈바니 전위 ''ϕ''라고 한다. "전압"과 "전기적 전위"라는 용어는 다소 모호하지만 서로 다른 맥락에서 둘 중 어느 하나를 지칭할 수 있다.

7. 전기 공학에서의 전위

전기 공학에서 전위는 일반적으로 회로상의 한 점을 0V로 정하여 사용하며, 송전·배전과 같은 고전압 분야에서는 접지의 전위를 기준으로 삼는다. 전기 공학에서는 옴의 법칙을 이용하여 회로를 해석하는 것이 효과적이다. 전자 회로에서 어떤 단자의 임피던스는 그 단자의 전위를 단자에 흘러 들어가는 전류로 나눈 값인데, 이는 회로 내의 입출력 등을 모두 전위(접지와의 전위차)로 나타내기 때문이다.

7. 1. 전위의 기준

전기 공학에서는 회로 상의 한 점(주로 접지)을 0V로 설정하고, 이를 기준으로 전위를 측정한다. 송전·배전 등 비교적 고전압 분야에서는 접지(어스, ground)의 전위를 기준으로 삼는다.^[8] 전기 공학에서 전압은 스칼라량으로 취급하며, 계산에서는 대부분 그렇게 한다(단, 교류 회로에서는 전압을 복소수로 취급하는 경우가 많고, 복소수를 나타낼 때 벡터처럼 그리는 경우가 있다. 또한, 이 복소수를 실수 값의 2차원 벡터로 보고 교류 전력의 식을 복소 전압과 복소 전류의 내적으로 표현하는 경우도 매우 드물다).^[8]

7. 2. 옴의 법칙과 전위

옴의 법칙에 의한 근사는 전기 공학에서 회로를 해석할 때 효과적이다. 저항값이 ''R''인 회로의 양단 전위가 각각

V_\mathrm{a}

,

V_\mathrm{b}

이고,

R

에 걸리는 전압이

V = V_\mathrm{a} - V_\mathrm{b}

일 때, 회로에 흐르는 전류

I

는,

:

I = \frac{V_\mathrm{a} - V_\mathrm{b}}{R} = \frac{V}{R}

로 나타낸다. 즉, 옴의 법칙에 따르면 저항 양단의 전위차는 전류에 비례한다.

전자 회로에서 어떤 단자의 임피던스는 그 단자의 전위를 단자에 흘러 들어가는 전류로 나눈 값을 의미한다. 전압이 아닌 전위를 사용하여 이러한 표현을 할 수 있는 것은 전자 회로에서 회로 내의 입력·출력 등을 모두 전위(접지와의 전위차)로 주고 있기 때문이다.

7. 3. 임피던스와 전위

전자 회로에서는 어떤 단자의 임피던스를 그 단자의 전위를 단자에 흘러 들어가는 전류로 나눈 값으로 정의한다. 전압이 아닌 전위를 사용하여 이러한 표현을 할 수 있는 것은, 전자 회로에서는 회로 내의 입력·출력 등을 모두 전위(접지와의 전위차)로 주고 있기 때문이다.

참조

_[1] 서적 Classical Mechanics Addison-Wesley 1959-06-01
_[2] 서적 Introduction to Electrodynamics Pearson Prentice Hall
_[3] 서적 Sears and Zemansky's University Physics with Modern Physics Addison-Wesley 2012-01-01
_[4] 서적 Introduction to Electrodynamics Prentice Hall
_[5] 서적 Fundamentals of electrochemistry https://books.google[...] John Wiley & Sons
_[6] Kotobank 2023-08-19
_[7] 일반텍스트
_[8] 일반텍스트
_[9] 일반텍스트
_[10] 일반텍스트
_[11] 논문 # 또는 설명, 일반텍스트 등으로 type을 지정할 수 있습니다. 추가 정보가 없어서 유추가 어렵습니다.

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com