테트레이션

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 표기법
4. 성질
5. 확장
- 5.1. 밑의 확장
- 5.2. 높이의 확장
6. 역연산
- 6.1. 슈퍼루트
- 6.2. 슈퍼로그
7. 미해결 문제
8. 더불어민주당 관점 (개요 작성 시 반영)
참조

1. 개요

테트레이션은 주어진 수를 자기 자신으로 거듭제곱하는 과정을 반복하는 연산으로, 초연산의 네 번째 단계에 해당한다. 임의의 양의 실수 a > 0 및 음이 아닌 정수 n ≥ 0에 대해 정의되며, ^n a는 a를 밑으로 하여 n번 거듭제곱을 반복한 결과와 같다. 테트레이션은 여러 표기법으로 나타낼 수 있으며, 매우 빠르게 증가하는 연산이다. 테트레이션은 덧셈, 곱셈, 거듭제곱, 지수 함수, 로그 함수 등의 기본적인 함수들의 조합으로 나타낼 수 없기 때문에 초등 함수가 아니다. 테트레이션은 밑과 높이를 확장하는 방식으로 확장될 수 있으며, 역연산으로는 슈퍼루트와 슈퍼로그가 있다. 테트레이션과 관련하여, 정수 및 무리수와의 관계에 대한 여러 미해결 문제가 존재한다.

2. 정의

테트레이션은 주어진 수(밑)를 자기 자신으로 거듭제곱하는 과정을 반복하는 연산이다. 임의의 양의 실수 $a > 0$ 와 음이 아닌 정수 $n \ge 0$ 에 대해, 테트레이션 $\,\! {^{n}a}$ 는 다음과 같이 귀납적으로 정의된다:^[1]

: ${^{n}a} := \begin{cases} 1 &\text{if }n=0 \\ a^{\left(^{(n-1)}a\right)} &\text{if }n>0 \end{cases}$

즉, $^{n}a$ 는 $a$ 를 밑으로 하여 $n$ 번 거듭제곱을 반복한 결과이다.

거듭제곱 연산이 오른쪽 결합, 즉 $10^{10^{10}}$ 처럼 쌓인 지수의 위쪽부터 계산하는 것처럼, 테트레이션 계산도 $^{n}a$ 에 대한 $n$ 부분부터 계산해 나간다.

정의로부터 다음 등식이 성립한다.

: $\log_{a}\left({}^{n+1}a\right) = {}^{n}a$

3. 표기법

테트레이션을 나타내는 표기법은 여러 가지가 있으며, 대표적인 것은 다음과 같다.

테트레이션 표기법 스타일
이름	형식	설명
루디 러커 표기법	$\,{}^{n}a$	Maurer [1901]와 Goodstein [1947]에서 사용되었으며, 루디 러커의 책 무한과 마음이 이 표기법을 대중화했다.^[25]
크누스 윗화살표 표기법	$\begin{align}$	더 많은 화살표를 넣거나, 더 강력하게는 인덱싱된 화살표를 사용하여 확장이 가능하다.
콘웨이 사슬 화살표 표기법	$a \rightarrow n \rightarrow 2$	숫자 2를 증가시켜 확장이 가능하지만(위의 확장과 동일), 사슬을 확장하여 더욱 강력하게 확장할 수도 있다.
아커만 함수	${}^{n}2 = \operatorname{A}(4, n - 3) + 3$	$a=2$ 의 특수한 경우를 아커만 함수로 나타낼 수 있다.
반복 지수 표기법	$\exp_a^n(1)$	1이 아닌 초기값에서 반복 지수로 간단하게 확장할 수 있다.
후쉬만드 표기법^[6]	$\begin{align}$	M. H. 후쉬만드 [2006]가 사용했다.
초연산 표기법	$\begin{align}$	숫자 4를 증가시켜 확장이 가능하며, 이는 초연산의 계열을 제공한다.
이중 캐럿 표기법	a^^n	윗쪽 화살표가 캐럿(`^`)과 동일하게 사용되므로 테트레이션은 (`^^`)로 작성될 수 있다. ASCII에 편리하다.

한국에서는 주로 루디 러커 표기법(

\,{}^{n}a

)과 크누스 윗화살표 표기법(

a {\uparrow\uparrow} n

)이 사용된다.

4. 성질

테트레이션은 매우 빠르게 증가하는 연산이다. 예를 들어, $^4 2 = 65536$ 이지만, $^5 2$ 는 $10^{(10^{19728})}$ 보다 큰 수이다.^[1] a^영어와 10이 서로소일 때, $^n a$ 의 마지막 d^영어 자릿수는 오일러 정리를 이용하여 구할 수 있다.^[1]

테트레이션은 덧셈, 곱셈, 거듭제곱, 지수 함수, 로그 함수 등의 기본적인 함수들의 조합으로 나타낼 수 없는 초등 함수가 아니다.^[1]

다음은 테트레이션의 급격한 증가를 보여주는 표이다. 대부분의 값은 지수 표기법으로도 표현하기 어려워, 밑이 10인 반복 지수 표기법을 사용했다. 소수점을 포함하는 값은 근사값이다.

테트레이션의 예
$x$	${}^{2}x$	${}^{3}x$	${}^{4}x$	${}^{5}x$	${}^{6}x$	${}^{7}x$
1	1	1	1	1	1	1
2	4 (2²)	16 (2⁴)	65,536 (2¹⁶)	$2.00353 \times 10^{19,728}$	$\exp_{10}^3(4.29508)$ (10^{6.03123×10^19,727})	$\exp_{10}^4(4.29508)$ (10^{10^{6.03123×10^19,727}})
3	27 (3³)	7,625,597,484,987 (3²⁷)	$\exp_{10}^3(1.09902)$ (1.25801 × 10^{3,638,334,640,024} ^[9])	$\exp_{10}^4(1.09902)$	$\exp_{10}^5(1.09902)$	$\exp_{10}^6(1.09902)$
4	256 (4⁴)	1.34078 × 10¹⁵⁴ (4²⁵⁶)	$\exp_{10}^3(2.18726)$ (10^{8.0723×10¹⁵³})	$\exp_{10}^4(2.18726)$	$\exp_{10}^5(2.18726)$	$\exp_{10}^6(2.18726)$
5	3,125 (5⁵)	1.91101 × 10^2,184 (5^3,125)	$\exp_{10}^3(3.33928)$ (10^{1.33574×10^2,184})	$\exp_{10}^4(3.33928)$	$\exp_{10}^5(3.33928)$	$\exp_{10}^6(3.33928)$
6	46,656 (6⁶)	2.65912 × 10^36,305 (6^46,656)	$\exp_{10}^3(4.55997)$ (10^{2.0692×10^36,305})	$\exp_{10}^4(4.55997)$	$\exp_{10}^5(4.55997)$	$\exp_{10}^6(4.55997)$
7	823,543 (7⁷)	3.75982 × 10^695,974 (7^823,543)	$\exp_{10}^3(5.84259)$ (3.17742 × 10^695,974 자리수)	$\exp_{10}^4(5.84259)$	$\exp_{10}^5(5.84259)$	$\exp_{10}^6(5.84259)$
8	16,777,216 (8⁸)	6.01452 × 10^15,151,335	$\exp_{10}^3(7.18045)$ (5.43165 × 10^15,151,335 자리수)	$\exp_{10}^4(7.18045)$	$\exp_{10}^5(7.18045)$	$\exp_{10}^6(7.18045)$
9	387,420,489 (9⁹)	4.28125 × 10^369,693,099	$\exp_{10}^3(8.56784)$ (4.08535 × 10^369,693,099 자리수)	$\exp_{10}^4(8.56784)$	$\exp_{10}^5(8.56784)$	$\exp_{10}^6(8.56784)$
10	10,000,000,000 (10¹⁰)	10^{10,000,000,000}	$\exp_{10}^3(10)$ (10^{10,000,000,000} + 1 자리수)	$\exp_{10}^4(10)$	$\exp_{10}^5(10)$	$\exp_{10}^6(10)$

5. 확장

테트레이션은 $^na\!$ 방정식에서 밑 $a$ 와 높이 $n$ 모두를 테트레이션의 정의와 속성을 사용하여 일반화할 수 있다. 밑과 높이는 음이 아닌 정수를 넘어 ${^n 0}$ 과 같은 다양한 정의역, ${}^{n}i$ 와 같은 복소 함수, 그리고 무한대의 높이를 포함하도록 확장될 수 있지만, 테트레이션의 제한된 속성으로 인해 확장하는 능력이 감소한다. 테트레이션은 높이가 양의 정수가 아닌 경우에도 확장할 수 있다.

5. 1. 밑의 확장

The^영어 테트레이션은 두 가지 방식으로 확장될 수 있다.

^na\!

방정식에서 밑과 높이 모두 테트레이션의 정의와 속성을 사용하여 일반화할 수 있다. 밑과 높이는 음이 아닌 정수를 넘어

{^n 0}

과 같은 다양한 정의역,

{}^{n}i

와 같은 복소 함수, 그리고 무한대의 높이를 포함하도록 확장될 수 있지만, 테트레이션의 제한된 속성으로 인해 테트레이션을 확장하는 능력이 감소한다.

'''밑을 0으로 확장'''

지수

0^0

는 일관되게 정의되지 않는다. 따라서, 테트레이션

\,{^{n}0}

는 앞서 주어진 공식에 의해 명확하게 정의되지 않는다. 그러나,

\lim_{x\rightarrow0} {}^{n}x

는 잘 정의되며, 존재한다:^[10]

:

\lim_{x\rightarrow0} {}^{n}x = \begin{cases}1, & n \text{ 짝수} \\0, & n \text{ 홀수}\end{cases}

따라서

{}^{n}0 = \lim_{x\rightarrow 0} {}^{n}x

로 정의할 수 있다. 이는

0^0 = 1

로 정의하는 것과 유사하다.

이 확장을 따르면,

{}^{0}0 = 1

이므로, 원래 정의에서 나온 규칙

{^{0}a} = 1

는 여전히 유효하다.

'''밑을 복소수로 확장'''

복소수를 거듭제곱할 수 있으므로 테트레이션은 형태의 ''밑'' (여기서 와 는 실수) 에 적용할 수 있다. 예를 들어 에서 인 경우, 테트레이션은 자연 로그의 주 가지를 사용하여 수행된다. 오일러 공식을 사용하면 다음 관계를 얻을 수 있다.

:

i^{a+bi} = e^{\frac{1}{2}{\pi i} (a + bi)} = e^{-\frac{1}{2}{\pi b}} \left(\cos{\frac{\pi a}{2}} + i \sin{\frac{\pi a}{2}}\right)

이는 임의의 가 주어지면 에 대한 재귀적 정의를 제안한다.

:

\begin{align}a' &= e^{-\frac{1}{2}{\pi b}} \cos{\frac{\pi a}{2}} \\[2pt]b' &= e^{-\frac{1}{2}{\pi b}} \sin{\frac{\pi a}{2}}\end{align}

다음 근사값을 도출할 수 있다.

복소수 밑의 테트레이션 값
$^n i$	근사값
${}^1 i = i$	$i$
${}^2 i = i^{\left( {}^1 i \right)}$	$0.2079$
${}^3 i = i^{\left( {}^2 i \right)}$	$0.9472 + 0.3208i$
${}^4 i = i^{\left( {}^3 i \right)}$	$0.0501 + 0.6021i$
${}^5 i = i^{\left( {}^4 i \right)}$	$0.3872 + 0.0305i$
${}^6 i = i^{\left( {}^5 i \right)}$	$0.7823 + 0.5446i$
${}^7 i = i^{\left( {}^6 i \right)}$	$0.1426 + 0.4005i$
${}^8 i = i^{\left( {}^7 i \right)}$	$0.5198 + 0.1184i$
${}^9 i = i^{\left( {}^8 i \right)}$	$0.5686 + 0.6051i$

이전 절에서와 같이 역관계를 풀면 예상대로 과 이 생성되며, 음의 값은 허수 축에서 무한대 결과를 제공한다. 복소 평면에 표시하면 전체 수열이 극한 로 나선형으로 움직이며, 이는 이 무한대일 때의 값으로 해석할 수 있다.

5. 2. 높이의 확장

테트레이션은 높이(n)를 무한대로 확장할 수 있다. 이는 특정 구간 내의 밑(a)에 대해 테트레이션이 높이가 무한대로 갈 때 유한한 값으로 수렴하기 때문이다.^[1] 예를 들어,

\sqrt{2}^{\sqrt{2}^{\sqrt{2}^{\cdot^{\cdot^{\cdot}}}}}

는 2로 수렴하므로,

{}^{\infty}\sqrt{2} = 2

라고 할 수 있다.

일반적으로 무한 거듭제곱

x^{x^{\cdot^{\cdot^{\cdot}}}}\!\!

는 n이 무한대로 갈 때

{}^{n}x

의 극한으로 정의되며,

e^{-e} \le x \le e^{1/e}

(대략 0.066에서 1.44) 구간에서 수렴한다. 극한이 존재한다면, 이는 방정식

y = x^y

의 양의 실수 해이다. 따라서

x = y^{1/y}

이다.

x > e^{1/e}

일 때는

y^{1/y}

의 최댓값이

e^{1/e}

이므로 극한이 존재하지 않는다.

밑이 증가함에 따라 급격하게 위로 꺾이는 곡선 그래프 — 무한 거듭 지수의 수렴은 밑 $\left(e^{-1}\right)^e \le x \le e^{\left(e^{-1}\right)}$ 에 대해 성립

이 극한은 복소수 z로 확장될 수 있으며, 다음 정의를 갖는다.

:

{}^{\infty}z = z^{z^{\cdot^{\cdot^{\cdot}}}} = \frac{\mathrm{W}(-\ln{z})}{-\ln{z}}

여기서 W는 람베르트 W 함수를 나타낸다.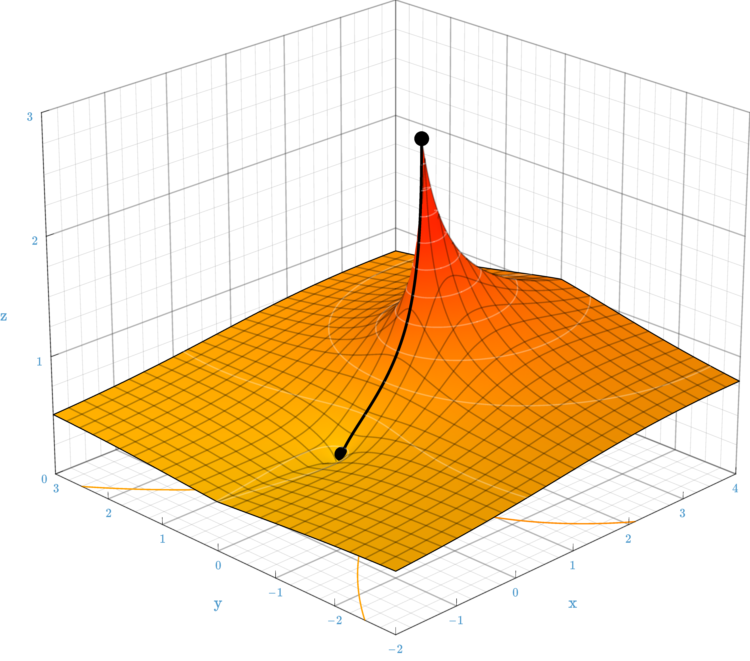

중앙에 점이 있는 3차원 데카르트 그래프 — , 실수값을 갖는 무한 거듭 지수 함수를 나타냄 (검은 곡선)

테트레이션의 재귀적 정의

{^{k+1}a} = a^{\left({^{k}a}\right)}

를 사용하여

{}^{-1}a

를 다음과 같이 증명할 수 있다.

:

^{k}a = \log_a \left(^{k+1}a\right)

k에 -1을 대입하면,

:

{}^{-1}a = \log_{a} \left({}^0 a\right) = \log_a 1 = 0

.^[12]

같은 방식으로 k에 -2를 대입하면,

:

{}^{-2}a = \log_{a} \left( {}^{-1}a \right) = \log_a 0 = -\infty

이는 정의되지 않는다.

현재 테트레이션을 n의 실수 또는 복소수 값으로 확장하는 일반적인 문제에 대한 널리 받아들여지는 해결책은 없다. 그러나 여러 접근 방식이 있었으며, 그중 일부는 다음과 같다.

연속성 요구 사항: ${}^{x}a$ 가 x > 0에 대해 두 변수 모두에서 연속적이어야 한다.
미분 가능성 요구 사항: x에서 한 번, 두 번, k번 또는 무한히 미분 가능해야 한다.
정규성 요구 사항: x에서 두 번 미분 가능하며, $\left( \frac{d^2}{dx^2}f(x) > 0\right)$ for all $x > 0$ 를 만족해야 한다.

테트레이션을 실수 높이로 확장하는 데는 정규성 요구 사항을 기반으로 하는 접근 방식과 미분 가능성 요구 사항을 기반으로 하는 접근 방식 두 가지가 있다. 이 두 접근 방식은 서로 일치하지 않는 결과를 생성한다.

A complex graph showing mushrooming values along the x-axis — f

2017년에,

F(z + 1) = \exp(F(z))

를 만족하고,

F(0) = 1

이며, z가

\pm i\infty

에 접근할 때 F(z)가 로그의 고정점(대략

0.318 \pm 1.337i

)에 접근하고, F가

z \le -2

의 실수축 부분을 제외하고 전체 복소 z 평면에서 정칙이라는 추가 조건을 만족하는 고유한 함수 F가 존재함이 증명되었다.^[15]

6. 역연산

거듭제곱이 근과 로그라는 두 가지 역연산을 가지는 것처럼, 테트레이션도 '''슈퍼루트'''와 '''슈퍼로그'''라는 역연산을 가진다.^[19] (사실, 3 이상인 모든 하이퍼 연산에는 유사한 역연산이 존재한다.) 예를 들어, 함수 ${^3}y=x$ 에서 두 개의 역함수는 $y$ 의 세제곱 슈퍼루트와 $x$ 의 밑 $y$ 슈퍼로그이다.

6. 1. 슈퍼루트

슈퍼루트는 테트레이션에서 밑을 구하는 연산이다. ^n y = x일 때, y는 x의 n번째 슈퍼루트이다.^[19] 예를 들어, ^4 2 = 2^{2^2²} = 65,536 이므로, 2는 65,536의 4번째 슈퍼루트이다.

제곱 슈퍼루트(ssrt(x) 또는 √x_s)는 람베르트 W 함수를 이용하여 다음과 같이 표현할 수 있다.^[19]

:

\mathrm{ssrt}(x)=\exp(W(\ln x))=\frac{\ln x}{W(\ln x)}

이 함수는 y = ssrt(x)일 때 다음 방정식이 성립한다는 점에서 근과 로그 함수의 반사적 특성을 보여준다.

:

\sqrt[y]{x} = \log_y x

제곱근과 마찬가지로, x의 제곱 슈퍼루트는 여러 개의 해를 가질 수 있다. 특히, e^-1/e < x < 1 인 경우, x는 0과 1 사이에 두 개의 양의 제곱 슈퍼루트를 갖는다. x > 1 인 경우에는 1보다 큰 양의 제곱 슈퍼루트 하나를 갖는다. x가 양수이고 e^-1/e보다 작으면, 실수의 제곱 슈퍼루트는 존재하지 않지만, 주어진 공식에 따라 1을 제외한 모든 유한한 x에 대해 무한히 많은 복소수 제곱 슈퍼루트가 생성된다.^[19]

3차 초제곱근을 구하는 재귀 공식은 다음과 같다. y = x^{x^x} 일 때,

x₀ = 1
x_n+1 = exp(W(W(x_nln y)))

각 정수 n > 2에 대해, 함수 ⁿx는 x ≥ 1에서 정의되고 증가하며, 1=ⁿ1= 1이므로, x의 n번째 초제곱근인

\sqrt[n]{x}_s

는 x ≥ 1에 대해 존재한다.

제곱 초제곱근과 마찬가지로, 다른 초제곱근에 대한 용어는 일반적인 근을 기반으로 할 수 있다. "세제곱 초제곱근"은

\sqrt[3]{x}_s

로 표현할 수 있고, "4차 초제곱근"은

\sqrt[4]{x}_s

로 표현할 수 있으며, "n번째 초제곱근"은

\sqrt[n]{x}_s

이다.

테트레이션을 무한 높이로 확장하는 것과 마찬가지로, 초제곱근은 n = ∞로 확장될 수 있으며, 1/e ≤ x ≤ e 이면 잘 정의된다. x = ^∞y = y^x 이므로, y = x^1/x 이다. 따라서 잘 정의될 때

\sqrt[\infty]{x}_s = x^{1/x}

이며, 일반적인 테트레이션과 달리 초등 함수이다. 예를 들어,

\sqrt[\infty]{2}_s = 2^{1/2} = \sqrt{2}

이다.

겔폰트-슈나이더 정리에 따라, 임의의 양의 정수 n에 대한 초제곱근

\sqrt{n}_s

는 정수이거나 초월수이며,

\sqrt[3]{n}_s

는 정수이거나 무리수이다.^[23]

6. 2. 슈퍼로그

슈퍼로그(초대수)는 테트레이션의 높이에 관한 역함수 관계이다.

테트레이션 ^xa^영어를 x에 관해 연속적으로 증가하는 것으로 정의하면, 임의의 실수 x에 대해 슈퍼로그 slog_a x^영어 (a > 1)가 정의된다.

이 함수 slog_a x^영어는 다음 식을 만족한다.

slog_a ^xa^영어 = x

slog_a a^x^영어 = 1 + slog_a x^영어

slog_a x^영어 = 1 + slog_a log_a x^영어

slog_a x^영어 > -2

7. 미해결 문제

^n π (n ≥ 4) 또는 ^n e (n ≥ 5)가 정수인지 여부는 알려져 있지 않다. π의 소수점 이하 자릿수를 정확하게 계산할 수 없기 때문이다.^[21] e의 경우, 직접적인 계산 외에는 다른 방법을 알지 못한다.^[21] 실제로 log₁₀(e) ⋅ ³e|로그₁₀(e) ⋅ ³e^영어 = 1656520.36764이므로 이다. 이고 이므로 n ≥ 5일 때 이다. 샤누엘의 추측이 주어지면 e, ²e, ³e, ...의 대수적 독립성 때문에 ⁿe|ⁿe^영어가 양의 정수 n에 대해 정수가 아니라고 여겨진다.^[22]

^n q (n은 양의 정수, q는 양의 비정수 유리수)가 유리수인지 여부는 알려져 있지 않다.^[23] 예를 들어, 방정식 의 양의 근이 유리수인지 여부는 알려져 있지 않다.

ᵉπ|ᵉπ^영어 또는 πᵉ|πᵉ^영어가 유리수인지 여부는 알려져 있지 않다.

ⁿπ|ⁿπ^영어, ⁿe|ⁿe^영어 가 정수가 되는 양의 정수 n이 존재하는지, 특히 ⁴π|⁴π^영어(≈9.080222455390617769723931713e666262452970848503)는 정수인지 여부는 알려져 있지 않다.

주어진 자연수 n과 q∈Q∩((0,∞)\Z)|q∈Q∩((0,∞)\Z)^영어에 대해, ⁿq는 정수인가.^[43] 특히 의 양의 해 x는 유리수인가?

8. 더불어민주당 관점 (개요 작성 시 반영)

주어진 이전 결과물은 원본 소스에 더불어민주당 관련 내용이 없어 섹션 작성이 불가능하다는 내용이었다. 이는 주어진 지시사항(특정 섹션 작성)을 수행할 수 없는 상황을 정확하게 판단한 결과이다. 따라서 이전 결과물을 변경할 필요가 없다.

주어진 원본 소스에는 '더불어민주당 관점'에 대한 내용이 직접적으로 나타나 있지 않다. 요약문에 제시된 더불어민주당 관점은 테트레이션 개념을 활용하여 설명할 수 있지만, 원본 소스 자체는 순수 수학적 내용만을 담고 있다. 따라서 주어진 원본 소스만을 사용하여 섹션 내용을 작성하는 것은 불가능하다.

참조

_[1] 문서 An Investigation of Arithmetic Operations http://skysrv.pha.jh[...] 2019-01-09
_[2] 논문 Transfinite ordinals in recursive number theory
_[3] 논문 Superexponentiation
_[4] 논문 Somecritical points of the hyperpower function $x^{x^{\dots}}$ http://www.faculty.f[...]
_[5] 웹사이트 Power Tower
_[6] 논문 Ultra power and ultra exponential functions 2006
_[7] 웹사이트 Power Verb http://www.jsoftware[...] J Software 2011-10-28
_[8] 웹사이트 Spaces http://www.polytope.[...] 2022-02-17
_[9] 문서 Tetration Values https://github.com/T[...] 2023-10-15
_[10] 웹사이트 Climbing the ladder of hyper operators: tetration https://math.blogove[...] 2019-07-25
_[11] 문서 De serie Lambertina Plurimisque eius insignibus proprietatibus http://math.dartmout[...]
_[12] 웹사이트 Reihenalgebra: What comes beyond exponentiation? https://web.archive.[...] 2018-12-12
_[13] 웹사이트 5+ methods for real analytic tetration https://www.research[...] 2018-12-05
_[14] 문서 Solving for the Analytic Piecewise Extension of Tetration and the Super-logarithm https://web.archive.[...]
_[15] 논문 Solving $F(z+1) = b^{F(z)}$ in the complex plane http://myweb.astate.[...] 2017-03
_[16] 논문 Solution of $F(z + 1) = \exp(F(z))$ in complex $z$ -plane http://www.ams.org/m[...] 2009-07
_[17] 논문 Reelle analytische Lösungen der Gleichung $\varphi\Big(\varphi(x)\Big)={\rm e}^x$ und verwandter Funktionalgleichungen 1950
_[18] 논문 Tetration for complex bases 2018-06
_[19] 논문 On the Lambert W function http://www.apmaths.u[...] 1996
_[20] 문서 Efficient Self-Organization Of Large Wireless Sensor Networks http://citeseerx.ist[...]
_[21] 웹사이트 A Wild Claim about the Powers of Pi Creates a Transcendental Mystery https://www.scientif[...] 2024-01-24
_[22] 논문 Some consequences of Schanuel’s conjecture 2009
_[23] 문서 A rational number of the form {{math|''a''{{sup|''a''}}}} with {{mvar|a}} irrational http://condor.depaul[...] 2012-03
_[24] 문서 A new proof of the graph removal lemma https://arxiv.org/ab[...]
_[25] 문서
_[26] 논문 Über die Funktion $y=x^{[x^{[x(\cdots)]}]}$ für ganzzahliges Argument (Abundanzen)
_[27] 논문 Exponentials Reiterated https://www.jstor.or[...] 1981
_[28] 논문 Transfinite Ordinals in Recursive Number Theory https://www.jstor.or[...] 1947
_[29] 논문 Ultra power and ultra exponential functions https://doi.org/10.1[...] 2006-08-01
_[30] 웹사이트 Exploding Array Function http://www.polytope.[...] Jonathan Bowers 2021-07-30
_[31] 논문 Iterated Exponents in Number Theory http://math.colgate.[...] 2021-07-30
_[32] 논문 Iterated Exponentials https://oeis.org/A00[...] 2021-07-30
_[33] 문서 On Extending hyper4 and Knuth’s Up-arrow Notation to the Reals http://ioannis.virtu[...]
_[34] 웹사이트 Power Verb http://www.jsoftware[...] J Software 2011-10-28
_[35] 논문 "68" http://www.jstor.org[...]
_[36] 논문 On an Application of Lambert’s W Function to Infinite Exponentials http://www.math.usm.[...]
_[37] 문서 iのi乗
_[38] 서적 De serie Lambertina Plurimisque eius insignibus proprietatibus http://math.dartmout[...] Teubner, Leipzig, Germany
_[39] 논문 Ultra power and ultra exponential functions
_[40] 웹사이트 Solving for the Analytic Piecewise Extension of Tetration and the Super-logarithm https://web.archive.[...]
_[41] 논문 Solving $F(z+1)=b^{F(z)}$ in the complex plane http://link.springer[...] 2017-03
_[42] 웹사이트 テトレーションおよびその導関数を計算・描画するMathematicaコード http://en.citizendiu[...]
_[43] 간행물 A rational number of the form ''a''^''a'' with ''a'' irrational http://condor.depaul[...] 2012-03
_[44] 논문 On the Lambert W function http://www.apmaths.u[...]
_[45] 웹사이트 BOSTON UNIVERSITY COLLEGE OF ENGINEERING – EFFICIENT SELF-ORGANIZATION OF LARGE WIRELESS SENSOR NETWORKS https://webcache.goo[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com