푸앵카레-벤딕손 정리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 1차원 푸앵카레-벤딕손 정리
3. 이론
4. 논의
5. 응용
6. 일반화 및 확장
7. 역사
참조

1. 개요

푸앵카레-벤딕손 정리는 평면에서 정의된 연속 시간 동역학계의 궤도 거동에 대한 정리이다. 이 정리는 궤도의 ω-극한 집합이 고정점, 주기 궤도 또는 이들을 연결하는 궤도로 구성된다는 것을 보장한다. 1901년 이바르 벤딕손이 엄밀한 증명을 제시했으며, 2차원 연속 동역학계에서 스트레인지 어트랙터가 발생할 수 없음을 보여주는 데 응용된다. 푸앵카레-벤딕손 정리는 평면, 구면, 원통과 같은 위상 공간에서 성립하지만, 토러스나 3차원 이상의 공간에서는 성립하지 않는다.

더 읽어볼만한 페이지

동역학계 - 가상일
가상일은 역학계에서 외력이 가상 변위에 대해 하는 일의 합으로, 정역학에서는 계의 정적 평형 조건으로 활용되며, 달랑베르 원리를 통해 동역학에도 적용되어 구조 해석 및 계산에 널리 쓰이는 물리량이다.
동역학계 - 위상 공간 (물리학)
위상 공간은 역학계의 모든 가능한 상태를 모아 시스템의 상태 변수를 좌표로 나타낸 공간으로, 시간의 흐름에 따라 궤적을 그리며 시스템의 동역학적 거동을 분석하는 데 사용된다.

푸앵카레-벤딕손 정리
푸앵카레-벤딕손 정리
개요
분야	동역학계
이름의 유래	앙리 푸앵카레, 이바르 오토 벤딕손
관련 개념	극한 집합 안정 다양체 불변 집합 동역학계
내용
설명	평면에서 유계된 궤도가 극한 집합을 가지면, 그 극한 집합은 평형점이거나 주기 궤도이다.
조건	2차원 평면 또는 다양체, 연속적인 동역학계
중요성	2차원 동역학계의 장기적인 거동 분석에 유용하다. 혼돈 현상이 3차원 이상에서만 발생할 수 있음을 보여준다.
활용 분야	미분 방정식 수학 물리학 공학
같이 보기
관련 항목	동역학계 혼돈 이론 미분 방정식

2. 정의

$U \subseteq \mathbb R^2$ 가 평면 속의 열린집합이라고 하자. $U$ 위의 2차원 연속 시간 동역학계

: $\Phi \colon \mathbb R \times U \to U$

: $\Phi(t, \Phi(t', x)) = \Phi(t+t', x) \qquad \forall t, t' \in \mathbb R, \; x \in U$

가 $\mathcal C^1$ 함수라고 하자.

$x \in U$ 의 '''궤도'''(orbit^영어) $\gamma(x)$ 는 다음과 같다.

: $\gamma(x) := \{\Phi(t, x) \colon t \in \mathbb R\}$

$x \in U$ 의 '''ω₊-극한 집합'''(ω₊-limit set^영어) $\omega_+(x)$ 은 다음과 같다.

: $\omega_+(x) := \left\{y \in U \colon \exists (t_i)_{i \in \mathbb N} \colon \lim_{i \to \infty} t_i = \infty, \; \lim \Phi(t_i, x) = y \right\}$

$x \in U$ 의 '''ω_--극한 집합'''(ω_--limit set^영어) $\omega_-(x)$ 은 다음과 같다.

: $\omega_-(x) := \left\{y \in U \colon \exists (t_i)_{i \in \mathbb N} \colon \lim_{i \to \infty} t_i = -\infty, \; \lim \Phi(t_i, x) = y \right\}$

$\omega_+(x)$ 가 다음 네 조건들을 만족시킨다고 하자.

$\omega_+(x) \ne \varnothing$
$\omega_+(x)$ 는 콤팩트 집합이다.
$\omega_+(x)$ 는 연결 공간이다.
$\omega_+(x)$ 에 속하는 고정점은 유한 개이다.

그렇다면, '''푸앵카레-벤딕손 정리'''에 따르면 다음 세 조건 가운데 하나가 성립한다.^[18]

$\omega_+(x) = \{x_1\}$ 는 고정점이다.
$\omega_+(x) = \gamma(y)$ 는 (양의 주기를 갖는) 주기적 궤도이다. 즉, $\Phi(t, y) = y$ 인 $t > 0$ 가 존재한다.
$\omega_+(x) = \{x_1, \dots, x_k\} \cup \gamma(y_1) \cup \cdots \cup \gamma(y_n)$ 는 유한 개의 고정점 $x_1, \dots, x_k$ 과 비주기 궤도 $\gamma(y_1), \dots, \gamma(y_n)$ 들로 구성되며, 모든 $i = 1, \dots, n$ 및 $\sigma \in \{+, -\}$ 에 대하여, $\omega_\sigma(y_i) = \{x_{j(\sigma, i)}\}$ 가 되는 $j \colon \{+, -\} \times \{1, \dots, n\} \to \{1, \dots, k\}$ 가 존재한다. 즉, 각 $\gamma(y_i)$ 는 $x_{j(-, i)}$ 에서 $x_{j(+, i)}$ 로 가는 궤도이다.

\omega_-

에 대해서도 마찬가지 정리가 성립한다.

평면의 열린 집합에서 정의된 미분 가능한 실수 역학계가 주어졌을 때, 유한 개의 고정점을 포함하는 궤도의 모든 비어 있지 않은 콤팩트 ω-극한 집합은 다음 중 하나이다.^[2]

고정점
주기 궤도
이러한 점들을 연결하는 유한 개의 고정점과 호모클리닉 및 헤테로클리닉 궤도로 구성된 연결 집합.

동일한 방향에서 서로 다른 고정점을 연결하는 궤도는 최대 하나 존재한다. 그러나 하나의 고정점을 연결하는 가산 개의 호모클리닉 궤도가 존재할 수 있다.

2. 1. 1차원 푸앵카레-벤딕손 정리

푸앵카레-벤딕손 정리는 1차원에서도 (자명하게) 성립한다.^[18] 즉, 실수 (

\mathbb R

)의 열린집합 위에서의 연속 시간

\mathcal C^1

동역학계에서, 공집합이 아닌, 유한 개의 고정점을 포함하는 콤팩트 연결

\omega_+

-극한 집합은 다음 두 가지 가운데 하나이다.

$\omega_+(x)=\{x_1\}$ 은 고정점이다.
$\omega_+(x)=[x_0,x_1]$ 에서, $x_0$ 과 $x_1$ 은 고정점이며, $\gamma(y)=(x_0,x_1)$ 인 $y\in(x_0,x_1)$ 가 존재한다.

이는 "1차원 벡터장"(=실수 함수)의 중간값 정리의 보조 정리이다.

3. 이론

$U\subseteq\mathbb R^2$ 가 평면 속의 열린집합이라고 하자. $U$ 위의 2차원 연속 시간 동역학계

: $\Phi\colon\mathbb R\times U\to U$

: $\Phi(t,\Phi(t',x))=\Phi(t+t',x)\qquad\forall t,t'\in\mathbb R,\;x\in U$

가 $\mathcal C^1$ 함수라고 하자.

$x\in U$ 의 '''궤도'''(orbit^영어) $\gamma(x)$ 는 다음과 같다.

: $\gamma(x):=\{\Phi(t,x)\colon t\in\mathbb R\}$

$x\in U$ 의 '''ω₊-극한 집합'''(ω₊-limit set^영어) $\omega_+(x)$ 은 다음과 같다.

: $\omega_+(x):=\left\{y\in U\colon\exists(t_i)_{i\in\mathbb N}\colon \lim_{i\to\infty}t_i=\infty,\;\lim\Phi(t_i,x)=y\right\}$

$x\in U$ 의 '''ω₋-극한 집합'''(ω₋-limit set^영어) $\omega_-(x)$ 은 다음과 같다.

: $\omega_-(x):=\left\{y\in U\colon\exists(t_i)_{i\in\mathbb N}\colon \lim_{i\to\infty}t_i=-\infty,\;\lim\Phi(t_i,x)=y\right\}$

$\omega_+(x)$ 가 다음 네 조건들을 만족시킨다고 하자.

$\omega_+(x)\ne\varnothing$
$\omega_+(x)$ 는 콤팩트 집합이다.
$\omega_+(x)$ 는 연결 공간이다.
$\omega_+(x)$ 에 속하는 고정점은 유한 개이다.

그렇다면, '''푸앵카레-벤딕손 정리'''에 따르면 다음 세 조건 가운데 하나가 성립한다.^[18]

$\omega_+(x)=\{x_1\}$ 는 고정점이다.
$\omega_+(x)=\gamma(y)$ 는 (양의 주기를 갖는) 주기적 궤도이다. 즉, $\Phi(t,y)=y$ 인 $t>0$ 가 존재한다.
$\omega_+(x)=\{x_1,\dots,x_k\}\cup\gamma(y_1)\cup\cdots\cup\gamma(y_n)$ 는 유한 개의 고정점 $x_1,\dots,x_k$ 과 비주기 궤도 $\gamma(y_1),\dots,\gamma(y_n)$ 들로 구성되며, 모든 $i=1,\dots,n$ 및 $\sigma\in\{+,-\}$ 에 대하여, $\omega_\sigma(y_i)=\{x_{j(\sigma,i)}\}$ 가 되는 $j\colon\{+,-\}\times\{1,\dots,n\}\to\{1,\dots,k\}$ 가 존재한다. 즉, 각 $\gamma(y_i)$ 는 $x_{j(-,i)}$ 에서 $x_{j(+,i)}$ 로 가는 궤도이다.

\omega_-

에 대해서도 마찬가지 정리가 성립한다.

평면의 열린 집합에서 정의된 미분 가능한 실수 역학계가 주어졌을 때, 유한 개의 고정점을 포함하는 궤도의 모든 비어 있지 않은 콤팩트 ''ω''-극한 집합은 다음 중 하나이다.^[2]

고정점
주기 궤도
이러한 점들을 연결하는 유한 개의 고정점과 호모클리닉 및 헤테로클리닉 궤도로 구성된 연결 집합.

게다가, 동일한 방향에서 서로 다른 고정점을 연결하는 궤도는 최대 하나 존재한다. 그러나 하나의 고정점을 연결하는 가산 개의 호모클리닉 궤도가 존재할 수 있다.

독립 변수를 로 하고, 종속 변수를 로 한다. 미지 함수 에 대해 다음과 같은 일반적인 자려적 2원 연립 1계 상미분 방정식계를 고려한다.

:

\boldsymbol{\dot{x}} = \boldsymbol{f}(\boldsymbol{x}(t))

또는

:

\dot{x} = f(x(t),\ y(t))

:

\dot{y} = g(x(t),\ y(t))

여기서 는 실수를, 위첨자 ˙ 는 미분 을, 오른쪽 어깨 는 전치를 나타낸다. 독립 변수 는 시간으로 간주하며, 시간의 경과에 따라 의 값도 변한다는 식으로 미분 방정식의 의미를 파악한다. 종속 변수의 정의역 은 의 부분열린 집합이며, 을 상 공간이라고도 한다. 전체로도 정리는 성립한다. 는 급 함수 로 한다. 는 위에 벡터장을 정한다.

에 대해 주어지는 의 값 를 초깃값이라고 한다. 이하, 편의상 로 고정한다. 초깃값 를 만족하고, 시간 일 때의 의 값을 반환하는 사상 를 미분 방정식이 정하는 '''흐름''' 또는 연속 역학계라고 한다. 가 급이므로, 위의 미분 방정식계는 해의 존재성과 유일성을 만족하고, 흐름 는

#

# 임의의 에 대해

을 만족한다.

초깃값 를 정하고, 를 에서 까지 움직이면서 가 반환하는 값을 상 공간 위에 그리면, 그것은 위의 하나의 곡선이 된다. 이 곡선을 를 지나는 '''궤도'''라고 한다. 를 지나는 궤도를 로 나타낸다. 미분 방정식의 해의 유일성에 의해, 어떤 를 지나는 는 단 하나로 제한된다. 특히 가 비음의 궤도

:

O_{+}(\boldsymbol{x}_{0})= \left \{ \phi (t,\ \boldsymbol{x}_{0}) \mid 0 \le t < \infty \right \}

를 '''양의 반궤도'''라고 하며, 로 나타낸다. 가 급이므로 궤도는 (이하의 평형점인 경우를 제외하고) 매끄러운 곡선이며, 곡선상의 각 점의 접벡터가 미분 방정식의 에 대응한다.

초깃값 에 대해 가 되는 경우, 미분 방정식의 해는 상수가 된다. 이 때의 궤도는 가 되고, 상 공간상의 1점이다. 이러한 을 만족하는 를 '''평형점'''이라고 한다.

또한, 에 대해, 이고 를 만족하는 가 존재할 때, 이를 만족할 때의 의 궤도를 '''주기 궤도'''라고 한다. 상 공간상의 주기 궤도는, 원과 같이 자기 자신과 교차하지 않는 닫힌 곡선이 된다.

주기 궤도(리미트 사이클)와 이를 극한 집합으로 하는 점 의 예. 시각의 열 에서 극한 집합 위의 극한점 에 수렴한다.

시간이 무한대로 발산할 때의 궤도 의 점근적인 거동을 조사하기 위해, 의 극한 집합이 중요하게 된다. 어떤 점 에 대해 시각 의 열 를 하나 적당히 선택하면

:

\lim_{k \rightarrow \infty} \phi(t_{k},\ \boldsymbol{x}) = \boldsymbol{y} \isin M

가 될 때, 를 의 극한점이라고 한다. 그리고, 의 극한점 전체로 이루어진 집합을 의 ''' 극한 집합'''이라고 하며, 로 나타낸다. 시간을 역방향 으로 한 쪽은 ''' 극한 집합'''이라고 하며, 로 나타낸다. 극한 집합 또는 극한 집합을 총칭하여 극한 집합이라고 한다.

가 평형점 또는 주기 궤도라면, 와 는 그 자체와 동일하게 된다. 극한 집합 또는 가 주기 궤도이고, 그럼에도 불구하고 자체가 이들 또는 에 포함되지 않을 때, 이러한 극한 집합을 리미트 사이클이라고 한다. 리미트 사이클에 대해, 궤도는 감기는 형태로 수렴한다.

푸앵카레-벤딕손 정리란 다음과 같은 주장이다.

정리에서는 가 아니라, 가 콤팩트라고 가정해도 좋다. 또한, 가 아니라, 구면 이나 원통 위의 흐름이라고 가정해도 좋다. 정리는 의 극한 집합에 대해서도 마찬가지로 성립한다. 즉, 또는 가 콤팩트이고 평형점을 포함하지 않으면, 또는 는 주기 궤도이다.

같은 2차원 다양체라도 위상 공간이 그림과 같이 토러스이면 푸앵카레-벤딕손 정리는 성립하지 않는다.

푸앵카레-벤딕손 정리는 위상 공간이 평면, 구면, 원통인 흐름(벡터장)에서는 성립하지만, 같은 2차원 다양체라도 토러스 와 같은 종수가 양수인 곡면에서는 성립하지 않는다. 또한, 위상 공간이 3차원 이상에서도 성립하지 않는다. 2차원 벡터장이 비자율계로 주어질 때에도, 실질적으로 위상 공간은 3차원이므로 성립하지 않는다. 정리가 성립하는 근본적인 이유는 조르당 곡선 정리로 알려진, 자기 교차하지 않는 연속적인 닫힌 곡선은 평면을 2개의 영역으로 나눈다는 사실에 있으며, 토러스나 3차원의 위상 공간에서는 이것이 성립하지 않으므로, 푸앵카레-벤딕손 정리도 또한 성립하지 않는다.

푸앵카레-벤딕손 정리의 주장을 직관적으로 바꿔 말하면, 다음과 같이 설명할 수도 있다. 평면상의 제한된 영역 내에 궤도가 있고, 궤도는 거기에서 벗어나지 않는다고 가정한다. 만약 궤도가 한 점(평형점)에 정착하지 않는다면, 궤도는 그 영역 내에서 영구히 움직여야 한다. 궤도의 곡선이 자기 교차를 하지 않고, 게다가 매끄러운 조건 하에서, 평면상에서 그러한 것이 가능한 것은 궤도가 닫힌 곡선(주기 궤도)에 정착하는 경우뿐이라는 것이 푸앵카레-벤딕손 정리이다.

또 다른 푸앵카레-벤딕손 정리라고 불리는 다른 형태로, 혹은 위의 정리에서 유도할 수 있는 다른 정리로, 다음과 같은 주장이 있다.

평형점이 유한 개밖에 존재하지 않는다는 가정은 평면상의 이론을 구성하는 데 반드시 필요한 것은 아니지만, 논의를 간단하게 하기 위해 도입된다. 예를 들어 라는 계는 평형점이 의 직선상의 모든 점으로 존재한다. 그러나, 대부분의 경우에 다루어지는 미분 방정식은 평형점이 유한이라는 조건을 만족한다.

정리의 세 번째 극한 집합에는, 헤테로클리닉 궤도나 호모클리닉 궤도가 해당한다. 대략적으로 말하면, 헤테로클리닉 궤도란 어떤 두 평형점 를 잇는 곡선으로, 그 위의 점은 에서 에 수렴하고, 에서 에 수렴하는 성질을 갖는다. 호모클리닉 궤도란 하나의 평형점 에서 나와 로 돌아가는 곡선으로, 그 위의 점은 에서 에 수렴하고, 에서도 에 수렴하는 성질을 갖는다.

푸앵카레-벤딕손 정리의 증명은 평면의 특성을 활용하여 기하학적인 접근 방식으로 이루어진다. 다음에서는 주로 에 따라 대략적인 증명 개요를 기술한다.

먼저, 평면에 한정되지 않는 상의 자율계 벡터장에서 일반적으로 성립하는 극한 집합의 성질로서 다음과 같은 것들이 있으며, 이것들은 푸앵카레-벤딕손 정리의 증명에도 사용된다.

# 는 불변 집합

# 는 닫힌 집합

# 가 유계이면 는 공집합이 아니다.

# 가 유계이면 는 연결 집합

푸앵카레-벤딕손 정리의 증명상의 도구로서 푸앵카레 사상의 생각이 유용하다. 정리의 가정 하에서, 평면상의 비평형점 에 대해, 를 통과하는 직선 을 평면상에 긋는다. 의 근방 를 취하여, 과의 교집합 로 만들어지는 선분을 로 한다. 이 때, 상의 임의의 점도 비평형점이 되도록 할 수 있으며, 더욱이, 를 통과하는 임의의 궤도는 에 접하지 않고 를 통과하도록 할 수 있다. 이러한 는 횡단선 또는 절단선이라고 불린다. 는 호여도 되며, 그 경우에는 횡단호 등으로 불린다. 또한, 에 포함되는 의 근방 를 충분히 작게 잡으면, 상의 임의의 점에서 출발하는 궤도는 어떤 유한 시간 후에 를 통과하도록 할 수 있다.

다음에, 어떤 점 의 극한 집합 를 생각한다. 는 정리의 가정처럼 평형점을 포함하지 않는다고 하고, 그 위의 어떤 비평형점 에 대해 위와 같은 횡단선 를 긋는다. 또한, 에서 출발하는 궤도 가 만약 주기 궤도라면, 가 되어, 분명히 정리가 성립한다. 따라서 이하에서는 는 주기 궤도가 아니라고 한다.

선분 와 로 닫힌 곡선이 구성되며, 이 닫힌 곡선의 바깥쪽 와 안쪽 로 평면은 이분된다. 선분 를 통과하는 궤도는 에서 로 향하거나, 에서 로 향하는 둘 중 하나가 된다. 그림은 에서 로 향하는 패턴을 나타낸다.

이 는 극한점이므로, 그 정의에 의해 에 수렴하는 무한 점열을 선택할 수 있다. 따라서, 는 를 무한 번 통과하고, 를 통과한 후에는 다시 로 돌아와서 를 통과해야 한다. 가 를 통과할 때의 하나의 교점을 로 하고, 다음에 를 통과하는 교점을 로 한다. 이 때, 평면상에는 선분 와 를 따라 에서 까지 그어진 호 로 구성된 닫힌 곡선이 생긴다. 이 닫힌 곡선을 로 한다. 요르단 곡선 정리로부터 는 의 안쪽 영역 와 의 바깥쪽 영역 로 나누어진다. 상술한 바와 같이, 이 정리가 평면에서 성립한다는 점이 푸앵카레-벤딕손 정리의 성립의 본질적인 이유라고 할 수 있다.

의 성질로부터, 선분 를 통과하는 궤도는 모두 에서 로 향하거나, 모두 에서 로 향하는 둘 중 하나가 된다. 또한, 미분 방정식의 해의 유일성으로부터 를 가로지르는 궤도는 존재하지 않는다. 어느 경우든 똑같이 논의할 수 있지만, 이하에서는 선분 를 통과하는 궤도는 에서 로 향한다고 한다. 그러면, 모든 에 대해 이다. 따라서, 다음에 가 와 교차하는 교점을 이라고 하면, 은 를 경계로 의 반대쪽에 존재한다. 일반화하면, 이것은 이면, 상에서 는 항상 와 의 사이에 있다는 것을 의미하며, 이 사실을 점렬이 를 따라 단조라고 하거나, 단조 점렬로 와 교차한다고 한다. 이 단조 점렬의 결론으로서, 일반적으로 와 의 교점은 뿐이라는 것이 보조정리로 증명된다. 주장의 역을 취하여 이고 라는 2점의 존재를 가정하면, 단조 점렬과의 모순이 유도되어, 귀류법에 의해 주장이 옳다는 것이 확인된다.

다음에, 상의 임의의 점 의 극한 집합 가 와 일치한다는 것을 증명한다. 이것도 귀류법으로 생각한다. 주장의 역이 성립하면, 차집합 가 존재하게 된다. 이 전제와, 극한 집합은 닫혀 있고 유계인 궤도의 극한 집합은 연결되어 있다는 성질을 이용하여 논의하면, 상의 어떤 점에서 횡단선과 복수 교차한다는, 상기 보조정리와 모순된 결론을 얻는다.

마지막으로, 에서 출발하는 궤도 가 주기 궤도임을 증명한다. 이므로, 는 어떤 무한 점렬 로 자신에 수렴한다. 의 근방 에 포함되는 점렬상의 1점 를 취하면, 어떤 시간 경과 후에 를 통과한다. 따라서, 가 와 교차하게 되는데, 극한 집합은 불변이라는 성질로부터 는 상의 점인 동시에 상의 점이기도 하다. 상기 보조정리로부터 상에서 와 교차하는 것은 1점이어야 하므로, 가 만족되므로, 는 를 주기로 하는 주기 궤도이다. 따라서 는 주기 궤도이다.

4. 논의

푸앵카레-벤딕손 정리의 더 약한 버전은 앙리 푸앵카레에 의해 처음 고안되었지만, 그는 완전한 증명을 제시하지 못했고, 이는 나중에 이바르 오토 벤딕손에 의해 제공되었다.^[3]

토러스에서는 주기적이지 않은 재발 궤도를 가질 수 있으며,^[3] 3차원 시스템은 스트레인지 어트랙터를 가질 수 있다. 그럼에도 불구하고, 아서 J. 슈워츠의 일반화를 통해 임의의 2차원 콤팩트하고 연결된 다양체에서 연속적인 역학적 시스템의 극소 집합을 분류하는 것이 가능하다.^[4]^[5]

5. 응용

푸앵카레-벤딕손 정리는 2차원 연속 동역학계에서 스트레인지 어트랙터가 발생할 수 없음을 보여준다. 만약 스트레인지 어트랙터 '''C'''가 존재한다면, 이는 위상 공간의 닫힌 유계 부분 집합에 포함될 수 있다. 이 부분 집합을 충분히 작게 만들어 근처의 모든 정지점을 제외하면, 푸앵카레-벤딕손 정리에 의해 '''C'''는 스트레인지 어트랙터가 아니라 극한 주기이거나 극한 주기로 수렴하게 된다.^[18]

이는 이산 동역학계에는 적용되지 않으며, 이산 동역학계에서는 2차원 또는 1차원 시스템에서도 혼돈적 거동이 발생할 수 있다는 점을 유의해야 한다.

푸앵카레-벤딕손 정리는 주어진 계에 주기 궤도가 존재함을 보일 수 있는 몇 안 되는 방법 중 하나이다.^[6] 이 정리를 사용하면, 평면 위의 자율계 상미분 방정식 계 또는 연속 역학계를 해석하는 데 유용하다. 해 또는 궤도가 극적으로 안정되는 곳은 본질적으로 평형점 또는 주기 궤도로 제한되기 때문이다.

정리의 활용 예시로, 다음과 같은 미분 방정식 계를 생각할 수 있다.^[6]

: $\dot{x} = 10 - x - \frac{4xy}{1+x^2}$

: $\dot{y} = x \left ( 1 - \frac{y}{1+x^2} \right )$

이 계의 평형점은 -평면 위에 에 유일하게 존재하며, 소용돌이점이다. 이 점을 덮는 충분히 작은 원 을 생각하면, 경계의 임의의 점은 바깥쪽으로 향하는 벡터를 갖는다. 또한, 범위의 사각형 의 경계는 안쪽으로 향하거나 경계에 접하는 벡터를 갖는다. 따라서 사각형에서 작은 원을 잘라낸 영역 에는 푸앵카레-벤딕손 정리에 의해 주기 궤도가 존재한다.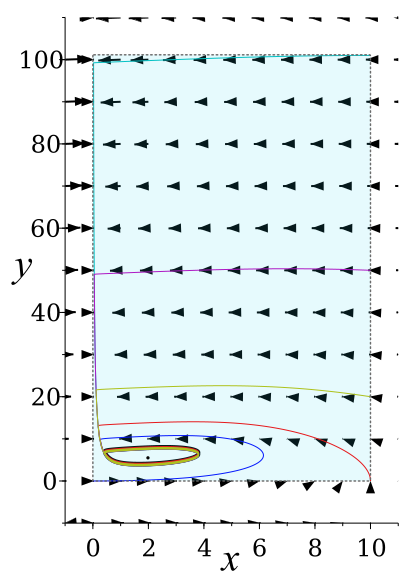

예시 미분 방정식 계의 벡터장. 파란색 범위의 경계에서는 임의의 벡터가 안쪽으로 향하거나 경계에 접한다. 색이 있는 곡선은 궤도로, 주기 궤도(검은 굵은 선)를 감고 있다.

푸앵카레-벤딕손 정리의 또 다른 중요한 결과는 평면에서는 평형점 또는 주기 궤도에 수렴하는 동작으로 제한되며, 이보다 더 복잡한 동작은 일어나지 않는다는 점이다. 따라서 평면 위의 연속 역학계에서는 스트레인지 어트랙터(카오스)는 존재할 수 없다. 연속 역학계에서 카오스는 3차원 이상의 상 공간을 갖는 계에서 일어난다.

6. 일반화 및 확장

푸앵카레-벤딕손 정리에는 다양한 일반화 및 확장 결과가 존재한다.^[5]

위상 공간이 평면이나 구면이 아닌 경우, 다음과 같은 결과들이 있다. 토러스 위의 급 자율계 미분 방정식으로 정의되는 흐름에 대해, 이 흐름의 극소 집합은 평형점, 주기 궤도, 전체 중 하나이다.^[5] 또한 을 급 콤팩트 연결 2차원 다양체라고 가정하면, 흐름의 극소 집합은 일 때는 평형점 또는 주기 궤도이고, 일 때는 평형점, 주기 궤도, 전체 중 하나로 일반화할 수 있다.^[5]

이 클라인 병 인 경우, 위의 흐름에서 어떤 점 가 자신의 극한 집합에 속하면 ( 또는 ), 는 평형점 또는 주기점이다.^[5]

이 고차원인 경우로의 확장도 연구되었으나,^[5]^[4] 의 경계 위의 모든 벡터가 안쪽을 향하는 유계 영역에 평형점 또는 주기 궤도 중 어느 것이든 반드시 존재하는지에 대한 문제는 아직 해결되지 않았다.^[4]

푸앵카레-벤딕손 정리를 과거 방향으로 풀 수 없는 비가역 과정을 기술하는 비선형 편미분 방정식에서 중요하게 다루어지는 반류(半流) 또는 반동역학계(半動力學系)로 확장할 수 있다.^[7] 횡단선(횡단 호)의 반류용 확장 및, 또는 위의 반류에 대해 이면 는 평형점 또는 주기점이라는 결과 등이 알려져 있다.^[5]

평형점을 무한히 포함하는 극한 집합에 대해 푸앵카레-벤딕손 정리를 일반화하는 연구도 진행되었다.^[5] 평형점이 의 연결 성분으로 포함되는 경우, 에 포함되는 평형점이 아닌 궤도의 수는 기껏해야 가산 무한 개이며, 임의의 비평형점 에 대해 와 는 위의 평형점의 연결 성분 중 어느 하나에 포함된다는 사실 등이 밝혀졌다.^[5]

오토마르 하예크(Otomar Hájek)는 푸앵카레-벤딕손 정리의 성립에 미분 가능성의 가정이 불필요하다는 것을 증명하였다.^[5] 해슬러 휘트니(Hassler Whitney)와 미하일 베부토프(Mikhail Valer'evich Bebutov)는 미분 가능성을 필요로 하지 않고 거리 공간 위의 임의의 비평형점에서 국소 횡단면을 구성할 수 있다는 것(휘트니-베부토프 정리)을 보였다.^[5] 그리고 하예크가 2차원 다양체 위의 국소 횡단면은 조르당 호 또는 단순 폐곡선 중 하나임을 보였고, 미분 가능성을 가정하지 않는 흐름에 기초한 푸앵카레-벤딕손 정리의 증명을 제시했다.^[5]

7. 역사

앙리 푸앵카레^[19]^[20]^[21]^[22]^[23]^[24]^[25]가 1880년대에 이 정리를 제시했지만, 엄밀한 증명을 제시하지는 않았다. 1881년부터 1886년까지 푸앵카레는 다음 네 편의 논문을 발표했다.^[8]^[9]^[10]^[11]

"미분 방정식으로 정의되는 곡선에 관하여 (1부)"
"미분 방정식으로 정의되는 곡선에 관하여 (2부)"
"미분 방정식으로 정의되는 곡선에 관하여 (3부)"
"미분 방정식으로 정의되는 곡선에 관하여"

이 논문들에서 푸앵카레는 구적법으로 풀 수 없는 상미분 방정식 계에 대한 정성적 이론이라는 새로운 연구 방법을 도입했다.^[12] 푸앵카레는 미분 방정식의 궤도를 조사하기 위해 위상적 수법을 사용했고, 푸앵카레-벤딕손 정리의 첫 번째 형태도 이 논문들에서 발표되었다. 이 논문은 역학계 이론의 출발점으로 자주 언급된다. 횡단 호, 푸앵카레 사상, 리미트 사이클 같은 개념도 이 논문에서 도입되었다.

이후 1901년에 Ivar Otto Bendixson|이바르 오토 벤딕손^sv^[26]이 이 정리에 대한 엄밀한 증명을 제시하였다.^[13] 벤딕손은 푸앵카레의 연구를 확장하여, 더 일반적인 평면상의 자율적 미분 방정식 계에 대해 연구했다. 푸앵카레는 다항식으로 한정했지만, 벤딕손은 더 약한 가정을 전제로 엄밀한 증명을 제시했다.^[15] 벤딕손의 논문에서는 위상적, 기하학적 측면이 더 강조되었다.

푸앵카레 사후에는 미국의 수학자 조지 데이비드 버코프가 푸앵카레의 정성적 이론을 발전시켰다. 버코프는 1927년에 "Dynamical Systems"(역학계)라는 모노그래프를 간행했고, 극한 집합 개념을 명확히 정의하여 역학계 이론에 도입했다.

푸앵카레-벤딕손 정리는 현재까지도 수학에 영향을 주고 있으며, 해의 거동을 더 정확하게 기술하거나, 새로운 현상을 포착하거나, 더 넓은 범위로 일반화하는 등 다양한 방향으로 연구가 진행되고 있다.

참조

_[1] 서적 Theory of Ordinary Differential Equations https://archive.org/[...] McGraw-Hill
_[2] 서적 Ordinary Differential Equations and Dynamical Systems https://www.mat.univ[...] American Mathematical Society
_[3] 저널 A third order autonomous differential equation with almost periodic solutions Elsevier 1961
_[4] 저널 A Generalization of a Poincare-Bendixson Theorem to Closed Two-Dimensional Manifolds https://www.jstor.or[...] 1963
_[5] 서적 Introduction to the Modern Theory of Dynamical Systems https://www.cambridg[...] Cambridge University Press 1995-04-28
_[6] 서적 力学と微分方程式 https://www.iwanami.[...] 岩波書店
_[7] 저널 非線形偏微分方程式と無限次元力学系日本数学会
_[8] 웹사이트 Mémoire sur les courbes définies par une équation différentielle (1ère partie) http://henripoincare[...] 2023-05-09
_[9] 웹사이트 Mémoire sur les courbes définies par une équation différentielle (2nde partie) http://henripoincare[...] 2023-05-09
_[10] 웹사이트 Sur les courbes définies par les équations différentielles (3ème partie) http://henripoincare[...] 2023-05-09
_[11] 웹사이트 Sur les courbes définies par les équations différentielles http://henripoincare[...] 2023-05-09
_[12] 저널 力学系の発展について日本数学会
_[13] 저널 Sur les courbes définies par des équations différentielles
_[14] 저널 力学系の大域的理論日本物理学会
_[15] 웹사이트 Ivar Otto Bendixson https://mathshistory[...] 2023-05-14
_[16] 웹사이트 Poincaré-Bendixson theory https://encyclopedia[...] EMS Press 2023-05-13
_[17] 웹사이트 ポアンカレ=ベンディクソンの理論 2023-05-13
_[18] 서적 Ordinary differential equations and dynamical systems http://www.mat.univi[...] American Mathematical Society
_[19] 저널 http://gallica.bnf.f[...]
_[20] 저널 http://sites.mathdoc[...]
_[21] 저널 http://gallica.bnf.f[...]
_[22] 저널 http://sites.mathdoc[...]
_[23] 저널
_[24] 저널 http://sites.mathdoc[...]
_[25] 저널 http://sites.mathdoc[...]
_[26] 저널 Sur les courbes définies par des équations différentielles

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com