기하학사
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
기하학사는 고대 문명부터 현대에 이르기까지 기하학의 발전 과정을 다루는 학문이다. 초기 기하학은 농경과 건축을 위해 사용되었으며, 바빌로니아와 이집트에서 실용적인 형태로 발전했다. 고대 그리스에서는 연역적 증명 방법을 통해 고전 기하학을 정립했으며, 유클리드의 '원론'은 기하학의 체계적인 기초를 마련했다. 이후 구장산술, 브라마굽타의 업적, 이슬람 수학 등을 거쳐 르네상스 시대에 원근법이 발전하고, 해석기하학이 등장하면서 기하학은 새로운 전기를 맞이했다. 19세기에는 비유클리드 기하학이 등장하여 기하학의 지평을 넓혔으며, 위상수학, 유한체 기하학, 프랙탈 이론, 끈 이론 등 다양한 분야로 확장되었다.
더 읽어볼만한 페이지
- 수학사 - 베르누이가
16세기부터 스위스를 중심으로 활동한 베르누이가는 니콜라우스 베르누이를 시조로 야코프, 요한, 다니엘 베르누이 등 수많은 학자를 배출하며 수학, 물리학 분야에서 베르누이 수, 베르누이의 원리 등 다양한 개념과 법칙을 정립하여 과학 발전에 크게 기여한 가문이다. - 수학사 - 분석
분석은 대상의 내용을 구성 요소로 나누어 속성, 관계 등을 밝히는 방법으로, 다양한 분야에서 활용되며 사회과학에서는 사실 해명적 분석과 규범적 분석으로 나뉜다. - 기하학 - 밀러 지수
밀러 지수는 결정학에서 결정 면과 방향을 나타내기 위해 사용되는 지수이며, 역격자 벡터 또는 격자 벡터 절편의 역수를 통해 정의되며, 물질의 물리적, 화학적 성질 및 기술적 응용에 중요한 역할을 한다. - 기하학 - 반지름
반지름은 원의 중심에서 원 위의 점까지의 거리로, 원의 지름과 둘레, 넓이 계산에 사용될 뿐 아니라 정다각형 외접원, 그래프 이론, 극좌표계 등 다양한 분야에서 활용되며, 여러 도형의 반지름을 구하는 공식이 존재하고 한국의 교육, 건축, 디자인 분야에서도 널리 쓰인다. - 빈 문단이 포함된 문서 - 광주고등법원
광주고등법원은 1952년에 설치되어 광주광역시, 전라남도, 전북특별자치도, 제주특별자치도를 관할하며, 제주와 전주에 원외재판부를 두고 있다. - 빈 문단이 포함된 문서 - 1502년
1502년은 율리우스력으로 수요일에 시작하는 평년으로, 이사벨 1세의 이슬람교 금지 칙령 발표, 콜럼버스의 중앙아메리카 해안 탐험, 바스쿠 다 가마의 인도 상관 설립, 크리미아 칸국의 킵차크 칸국 멸망, 비텐베르크 대학교 설립, 최초의 아프리카 노예들의 신대륙 도착 등의 주요 사건이 있었다.
| 기하학사 | |
|---|---|
| 개요 | |
| 고대 기하학 | |
| 중세 기하학 | |
| 근대 기하학 | |
| 현대 기하학 | |
| 기하학의 응용 | |
2. 초기 기하학

세계의 여러 고대 문명에서 농경과 건축을 위해 기하학을 사용하였다.[43] 메소포타미아 시기의 신화인 길가메시 서사시는 우루크의 성벽이 구운 벽돌로 지어진 것임을 자랑한다.[44] 고대 수학은 크게 보아 산술과 기하로 나눌 수 있으며, 대략 기원전 5000년부터 기원전 3000년 사이에 고대 동양 일부 지역에서 공학과 농업 및 상업적인 업무와 종교 의식을 보조하기 위한 실용적인 학문으로 등장하였다.[45] 오늘날 남아있는 고대 수학 연구 기록은 주로 바빌로니아의 설형문자 점토판과 고대 이집트의 파피루스 문서에서 확인된다. 반면에 고대 인도에서 사용한 나무껍질이나 고대 중국에서 사용한 죽편은 쉽게 썩기 때문에 기하학에 대해 남겨진 기록이 거의 없다. 고대 문명기의 수학은 경험에 근거한 일종의 레시피로서 시행 착오에 의해 유래되었다.[46]
기하학의 가장 초창기 기록은 기원전 3000년경의 고대 인더스 문명(하라파 수학)과 바빌로니아(바빌로니아 수학)에서 찾아볼 수 있다. 초기 기하학은 측량, 건축, 천문학 등 여러 분야의 실용적인 요구를 충족시키기 위해 개발된 길이, 각도, 면적, 부피에 관한 경험적으로 발견된 원리들의 집합이었다. 이 중에는 놀랍도록 정교한 원리들도 있었으며, 현대 수학자도 미적분과 대수를 사용하지 않고는 이들 중 일부를 유도하기 어려울 정도였다. 예를 들어, 이집트와 바빌론은 피타고라스보다 약 1500년 전에 피타고라스의 정리를 알고 있었고, 기원전 800년경 인도의 술바 수트라에는 이 정리에 대한 최초의 설명이 있었다. 또한, 이집트인들은 사각뿔대의 부피에 대한 정확한 공식을 가지고 있었다.
고대 이집트에서는 린드 수학 파피루스를 통해 원의 넓이와 원주율의 근사값, 사각뿔 절두체의 부피를 구하는 방법 등을 제시하고 있다. 바빌로니아 수학은 60진법에 기초를 둔 수학으로, 피타고라스의 정리를 알고 있었고, 원주율의 근사값을 계산하였다. 베다 시대 인도 수학은 술바 수트라를 통해 피타고라스의 수를 언급하고 있다.
2. 1. 고대 이집트의 기하학
고대 이집트의 수학자였던 아메스가 집필한 린드 수학 파피루스의 제30번 문제는 원의 넓이를 구하는 방법으로 다음과 같은 식을 제시하고 있다.[47]
::::원의 넓이 ≈ [ (지름) x 8/9 ]2.
이는 원주율의 근사값을 3.160493… 로 계산한 것이다. 한편 제48번 문제에서는 원주율의 근사값으로 3.111…을 채택하고 있어 당시 사용한 원주율의 근사값이 여러 종류가 있었음을 알게 한다.
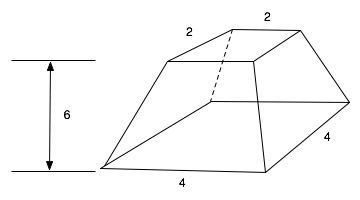
모스크바 수학 파피루스의 제14번 문제는 별다른 증명없이 사각뿔 절두체의 부피를 구하는 방법으로 다음과 같은 방식을 제시하고 있다.[48]
: (h: 높이, a: 밑면 한 변의 길이, b: 윗면 한 변의 길이)
위 계산은 오늘날 사용되는 사각뿔 절두체의 부피를 구하는 식과 정확히 일치한다.[49]
아메스 파피루스 50번 문제는 이 방법들을 사용하여 원의 면적을 계산하는데, 그 규칙에 따르면 면적은 원 지름의 8/9의 제곱과 같다. 이는 원주율이 4×(8/9)2 (또는 3.160493...)이며, 오차는 0.63%를 약간 넘는다고 가정한다.
아메스는 원주율의 근사치로 현대적인 22/7을 알고 있었고, 이를 사용하여 헤카트를 분할했다. 그러나 아메스는 원통에서 발견된 헤카트 부피를 계산하기 위해 원주율의 전통적인 256/81 값을 계속 사용했다.
48번 문제는 변의 길이가 9단위인 정사각형을 사용했다. 이 정사각형은 3x3 그리드로 잘렸다. 구석 정사각형의 대각선을 사용하여 면적이 63단위인 불규칙한 팔각형을 만들었다. 이는 원주율에 대한 두 번째 값 3.111...을 제공했다.
두 문제는 함께 원주율에 대한 3.11과 3.16 사이의 값 범위를 나타낸다.
2. 2. 바빌로니아 수학
세계의 여러 고대 문명에서 농경과 건축을 위해 기하학을 사용하였다.[43] 메소포타미아 시기의 신화인 길가메시 서사시는 우루크의 성벽이 구운 벽돌로 지어진 것임을 자랑한다.[44] 고대 수학은 산술과 기하로 나눌 수 있으며, 메소포타미아 지역에서 발달한 바빌로니아 수학은 60진법에 기초를 둔 것이었다.



바빌로니아의 수학자들은 피타고라스의 정리를 알고 있었고, 이를 통하여 의 근사값을 계산하였다. 원주율은 3과 1/8, 즉 3.125로 계산하였다.[51] 바빌로니아인들은 면적과 부피를 측정하는 일반적인 규칙을 알고 있었다. 그들은 원의 둘레를 지름의 3배로, 면적을 둘레 제곱의 12분의 1로 측정했는데, 이는 ''π''를 3으로 추정할 경우 정확한 값이다. 원기둥의 부피는 밑면과 높이의 곱으로 간주되었지만, 원뿔 또는 정사각뿔의 절두체의 부피는 높이와 밑면의 합의 절반을 곱한 값으로 잘못 계산되었다. 피타고라스 정리 역시 바빌로니아인들에게 알려져 있었다. 또한, 최근 발견된 석판에는 ''π''를 3과 1/8로 사용한 흔적이 있다. 바빌로니아인들은 오늘날 약 7마일에 해당하는 거리 측정 단위인 바빌로니아 마일로도 유명하다. 이러한 거리 측정은 결국 태양의 이동을 측정하는 데 사용되는 시간 마일로 전환되었고, 이는 시간을 나타냈다.[3] 최근 발견에 따르면 고대 바빌로니아인들이 유럽인보다 거의 1400년 전에 천문 기하학을 발견했을 수 있다고 한다.[4]
2. 3. 베다 시대 인도 수학
베다 시대인 기원전 700년 무렵 쓰인 샤타파타 브라마나(शतपथ ब्राह्मण, 일백 장의 제의서sa)에는 번제 의식을 위해 모양이 달라도 넓이가 같은 제단을 마련하는 방법이 적혀있다.[52] 술바 수트라에서는 제단 마련을 위해 (3,4,5), (5,12,13)과 같이 당시 알려져 있던 피타고라스의 수를 언급하고 있다.[53]인도의 베다 시대는 정교한 제단을 만드는 데 주로 사용된 기하학 전통을 가지고 있었다. 이 주제에 관한 초기 인도 텍스트(기원전 1천 년)로는 ''사타파타 브라흐마나''와 ''Śulba Sūtras''가 있다.[5][6][7] ''Śulba Sūtras''는 피타고라스의 정리에 대한 세계 최초의 현존하는 언어적 표현"으로 묘사되었지만, 이미 고대 바빌로니아인들에게 알려져 있었다. 이들은 피타고라스 수, 즉 디오판토스 방정식의 특별한 경우를 사용한다.[8][9]
수학자 S. G. Dani에 따르면, 기원전 1850년경에 쓰여진 바빌로니아 쐐기 문자 점토판 플림턴 322에는[10] "꽤 큰 항목을 포함한 15개의 피타고라스 수가 있으며, (13500, 12709, 18541)은 원시적인 수이다.[11] 이는 특히 기원전 1850년 메소포타미아에서 이 주제에 대한 정교한 이해가 있었음을 나타낸다." "이러한 점토판은 슐바수트라 시대보다 수 세기 앞서므로, 일부 삼중항의 맥락적 출현을 고려할 때, 인도에서도 유사한 이해가 있었을 것으로 예상하는 것이 합리적이다."라고 Dani는 말한다.
Dani는 또한 다음과 같이 말한다.
>''슐바수트라''의 주요 목적은 제단의 건설과 관련된 기하학적 원리를 설명하는 것이었기 때문에, 피타고라스 수의 주제는 잘 이해되었다 하더라도 ''슐바수트라''에 포함되지 않았을 수도 있다. 슐바수트라에서 삼중항의 발생은 건축 또는 기타 유사한 응용 분야의 입문서에서 접할 수 있는 수학과 유사하며, 당시 해당 주제에 대한 전반적인 지식과 직접적으로 일치하지 않는다. 불행히도 다른 동시대 자료가 발견되지 않았기 때문에 이 문제를 만족스럽게 해결하는 것은 불가능할 수 있다.
3. 고전 기하학
고대 그리스는 메소포타미아, 이집트와 같은 지역에서 발달한 기하학을 수용하여 고전 기하학을 정립하였다. 고대 그리스의 기하학은 자명하다고 인정되는 것에서부터 출발하여 기존에 알고 있는 것들 만으로 새로운 사실을 증명하는 연역적 방법을 정립하였다. 고대 그리스 이전의 수학 지식이 문제 해결을 위한 일종의 처방전 모음이었던데 비해 고대 그리스의 수학은 단계적으로 전개하여 필연적인 결론을 이끌어내는 추상적 논리학이 되었다.[54]
기원전 600년부터 400년 사이 고대 그리스의 수학자들은 기존의 경험적 방법에 의한 문제 해결을 버리고 모든 수학적 결론은 반드시 연역적으로 증명되어야 한다고 결정하였다. 프로클로스가 《원론》 주석서 머리에 소개한 〈에우데무스 요약〉에서 탈레스가 처음으로 수학적 지식의 증명을 시도하였으며, 원이 임의의 지름으로 이등분 된다는 것과 이등변삼각형의 두 밑각이 서로 같다는 점 등을 증명하였다고 소개하고 있다. 〈요약〉은 이어서 피타고라스 학파의 업적을 소개하고 있다. 치오스의 히포크라테스는 자명한 사실에서 연쇄적으로 유도되는 정리의 사실을 연결하여, 모든 기하학을 하나의 긴 사슬 형태로 논리적인 전개를 시도하였다.[56]
헬레니즘 시기인 프톨레마이오스 왕조의 알렉산드리아에 살았던 에우클레이데스는 《원론》을 집필하여 주어진 정의와 공리만으로 수학 정리를 증명하는 방법을 완성하였다.[57]
《원론》은 다음과 같은 공리를 채택하고 있다.[58]
# 임의의 서로 다른 두 점 P, Q에 대해 두 점을 지나는 직선은 유일하다.
# 임의의 두 선분 AB, CD에 대해 B가 A와 E 사이에 위치하고 선분 BE의 길이가 선분 CD의 길이와 같게 되는 점 E는 유일하다.
# 점 O를 정점으로 하고 반지름이 OP인 원을 그릴 수 있다.
# 모든 직각은 합동이다.
# 하나의 직선 위에 있지 않은 점 P를 지나는 평행선은 유일하다.
《원론》은 위의 공리를 바탕으로 피타고라스의 정리와 같은 수학적 사실을 증명한다. 이렇게 증명된 수학적 사실을 정리(定理)라고 한다.[58] 정의, 공리, 증명, 정리와 같은 논리적 단계는 오늘날에도 여전히 사용된다. 하나의 공리계에서 참으로 증명된 정리는 공리계가 바뀌지 않는 한 계속하여 참이 된다.[54]
아르키메데스는 도형의 넓이와 부피의 계산에 탁월한 업적을 남겼다. 아르키메데스는 원의 넓이가 반지름의 거듭 제곱에 원주율을 곱한 것과 같다는 것을 증명하였고, 원주율의 근사값을 약 3.1416으로 계산하였다.[60] 또한, 구의 부피는 같은 높이의 원기둥의 부피에 대해 3분의 2이라는 것을 증명하였으며, 포물선과 직선으로 둘러싸인 도형의 넓이를 구하는 방법을 발견하였다.[61]
탈레스 (기원전 635–543년)는 현재 터키 남서부에 위치한 밀레투스 출신으로, 수학적 연역법을 최초로 사용한 인물로 여겨진다. 피타고라스 (기원전 582–496년)는 이오니아 출신으로, 이후 그리스인들이 식민지화한 이탈리아로 이주했으며, 탈레스의 제자였을 가능성이 있고, 바빌론과 이집트를 여행했다. 그는 수학, 음악, 철학을 연구하기 위해 학생들을 모았고, 그들은 함께 오늘날 고등학생들이 기하학 수업에서 배우는 대부분의 내용을 발견했다. 또한, 그들은 무공약 길이와 무리수를 발견하는 심오한 발견을 했다.
플라톤(기원전 427년~기원전 347년)은 그리스인들이 매우 존경했던 철학자였다. 그의 유명한 학교 입구에 "기하학을 모르는 자는 여기 들어오지 못한다."라고 새겨놓았다는 이야기가 전해지지만, 이 이야기는 사실이 아닌 것으로 여겨진다.[12] 그는 수학자는 아니었지만, 수학에 대한 그의 견해는 큰 영향을 미쳤다. 그리하여 수학자들은 기하학은 컴퍼스와 눈금 없는 자만 사용해야 하며, 눈금이 있는 자나 각도기와 같은 측정 도구는 사용해서는 안 된다는 그의 믿음을 받아들였다.
《구장산술》은 기원후 179년 처음 발간된 중국의 수학서로, 최초 저자는 알려져 있지 않다. 삼국시대 위나라의 유휘가 263년에 주석을 달아 정본(定本)이 되었는데, 그의 서문에 따르면 전한의 학자가 진나라 때의 유문을 모아 편집한 것이라고 한다. 당나라 때에는 이순풍의 주석이 더해져 관리 교과서로 쓰인 산경십서 중 하나로 채택되었다.[62]
구장산술은 모두 아홉 개의 장으로 나뉘어 있는데, 도형의 넓이를 재는 방전(方田), 곡물 교역에서 환율을 계산하는 속미(粟米), 봉록이나 조세의 비율 배분을 계산하는 쇠분(衰分), 제곱근 계산과 원의 넓이를 다루는 소광(少廣), 토목공사의 공정과 부피를 계산하는 상공(商功), 운반 거리의 멀고 가까움을 고려하여 비용을 동등하게 계산하는 복잡한 비율을 다루는 균수(均輸), 일차방정식의 해를 이용하여 남거나 모자람을 계산하는 영부족(盈不足), 양수와 음수가 섞여있는 연립일차방정식 계산을 위한 방정(方程), 피타고라스 정리를 다루는 구고(勾股)로 이루어져 있다.[62]
초기 구장산술은 원주율의 근사값으로 3을 사용하는 등 부정확한 점이 있었으나, 유휘는 극한 개념을 도입한 할원술(割圓術)을 도입하여 보다 정확한 원주율을 제시하였다.[63] 가우스 소거법과 동일한 방식의 행렬 계산을 다루는 등 복잡한 계산도 다루고 있다.[64] 특히 피타고라스 정리를 다루는 구고(勾股)는 고대 중국의 기하학 지식 수준이 매우 높았다는 것을 보여준다.
한나라(기원전 202년 – 서기 220년) 시대에 조위 왕국의 수학자 유휘는 ''구장산술''을 편집하고 주석을 달았다. 이 책에는 정사각형과 원의 표면적, 다양한 3차원 도형의 부피를 구하는 등 기하학이 적용된 많은 문제들이 포함되어 있으며, 피타고라스 정리의 사용도 포함되어 있다. 유휘는 192각형 정다각형을 사용하여 파이를 3.141014로, 3072각형 정다각형을 사용하여 파이를 3.14159로 계산했다. 이는 유휘의 동시대인이자 동오의 수학자이자 천문학자인 왕번이 142⁄45을 사용하여 파이를 3.1555로 계산한 것보다 더 정확했다.[29] 유휘는 또한 깊이, 높이, 너비 및 표면적의 거리 측정을 계산하기 위해 수학적 측량에 대해 썼다. 입체 기하학에서 그는 직사각형 밑면과 양쪽이 경사진 쐐기가 피라미드와 사면체 쐐기로 분해될 수 있다는 것을 알아냈다.[30] 그는 또한 사다리꼴 밑면과 양쪽이 경사진 쐐기가 피라미드에 의해 분리된 두 개의 사면체 쐐기를 만들 수 있다는 것을 알아냈다.[30] 또한 유휘는 부피에 대한 카발리에리의 원리와 가우스 소거법을 설명했다. ''구장산술''에서 제시된 기하학적 공식들은 다음과 같다.
'''면적'''[31]
| 도형 | |||
|---|---|---|---|
| 두 개의 정사각형 면을 가진 평행육면체 | |||
| 정사각형 면이 없는 평행육면체 | 피라미드 | ||
| 정사각형 밑면을 가진 각뿔대 | 변의 길이가 다른 직사각형 밑면을 가진 각뿔대 | ||
| 정육면체 | 각기둥 | ||
| 직사각형 밑면과 양쪽이 경사진 쐐기 | 사다리꼴 밑면과 양쪽이 경사진 쐐기 | ||
| 사면체 쐐기 | 두 번째 유형의 쐐기 잘린 꼴 (공학적 응용 분야에 사용됨) | ||
| 원기둥 | 원형 밑면을 가진 원뿔 | 원뿔대 | 구 |
브라마굽타는 7세기 무렵 인도의 천문학자 겸 수학자로, 당시 인도의 수학을 정리한 《브라마스푸타시단타》(ब्राह्मस्फुटसिद्धान्त|브라마 원리 선집hi)를 저술하였다.[65] 그의 책에는 0의 도입과 같은 인도 수학의 중요 업적이 소개되어 있으며, 제12장에서는 원에 내접하는 사각형의 넓이를 계산하는 브라마굽타의 공식을 서술하였다.[65]
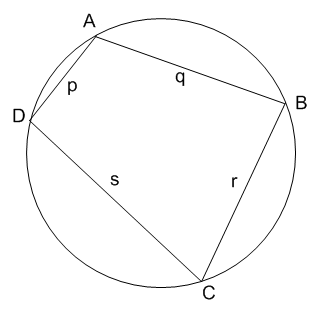 | |
| 원에 내접하는 사각형의 각 선분의 길이가 a, b, c, d일 때, 사각형의 넓이 S는 |
브라마굽타는 이 외에도 브라마굽타 정리도 함께 서술하고 있다.
그는 628년에 천문학 작품인 《브라마스푸타시단타》를 저술했는데, 66개의 산스크리트어 구절이 포함된 12장은 "기본 연산"(세제곱근, 분수, 비율 및 비례, 물물교환 포함)과 "실용 수학"(혼합물, 수학적 수열, 평면 도형, 벽돌 쌓기, 목재 켜기, 곡물 쌓기 포함)의 두 부분으로 나뉘었다.[16] 후자 부분에서 그는 원주 사각형의 대각선에 대한 유명한 정리를 다음과 같이 진술했다.[16]
'''브라마굽타의 정리:''' 원주 사각형의 대각선이 서로 수직이면, 대각선의 교차점에서 사각형의 임의의 변에 그은 수직선은 항상 반대쪽 변을 이등분한다.
9세기 바그다드에서 활동한 박학가 타비트 이븐 꾸라(ثابت بن قرة|사비트 이븐 쿠라ar)는 수학에서도 여러 가지 업적을 남겼다. 그는 양의 실수를 도입하여 수의 영역을 확장하였고, 적분법의 개념을 발전시켰으며, 구면삼각법을 연구하였다. 특히 기하학과 관련하여 에우클레이데스의 평행선 공리에 대해 의문을 나타내고 비유클리드 기하학의 기초를 놓았다. 타비트의 저술은 라틴어로 번역되어 유럽 수학 발전에 큰 영향을 주었다.[66]
사비트 이븐 쿠라는 축소와 구성의 방법을 사용하여 모든 삼각형에 대한 피타고라스 정리의 두 가지 일반적인 수학적 증명을 제공했다.[32]
3. 1. 고대 그리스의 기하학
고대 그리스는 메소포타미아, 이집트와 같은 지역에서 발달한 기하학을 수용하여 고전 기하학을 정립하였다. 고대 그리스의 기하학은 자명하다고 인정되는 것에서부터 출발하여 기존에 알고 있는 것들 만으로 새로운 사실을 증명하는 연역적 방법을 정립하였다. 고대 그리스 이전의 수학 지식이 문제 해결을 위한 일종의 처방전 모음이었던데 비해 고대 그리스의 수학은 단계적으로 전개하여 필연적인 결론을 이끌어내는 추상적 논리학이 되었다.[54]기원전 600년부터 400년 사이 고대 그리스의 수학자들은 기존의 경험적 방법에 의한 문제 해결을 버리고 모든 수학적 결론은 반드시 연역적으로 증명되어야 한다고 결정하였다. 이러한 결정이 어떤 이유로 이루어진 것인지는 명확하지 않으나 경험적 주장이 진위를 가리기 힘들다는 점과 그리스인의 질서와 아름다움에 대한 집착이 영향을 주었을 것이다.[55] 고대 그리스 시기의 수학에 대해 알 수 있는 자료는 프로클로스가 《원론》 주석서 머리에 소개한 〈에우데무스 요약〉이 거의 유일하다. 에우데무스는 아리스토텔레스의 제자로 〈요약〉에서 탈레스가 처음으로 수학적 지식의 증명을 시도하였으며, 원이 임의의 지름으로 이등분 된다는 것과 이등변삼각형의 두 밑각이 서로 같다는 점 등을 증명하였다고 소개하고 있다. 〈요약〉은 이어서 피타고라스 학파의 업적을 소개하고 있다. 피타고라스 학파의 일원이었던 치오스의 히포크라테스는 자명한 사실에서 연쇄적으로 유도되는 정리의 사실을 연결하여, 모든 기하학을 하나의 긴 사슬 형태로 논리적인 전개를 시도하였다.[56]
자명한 사실에서 연역적 논리 전개에 따라 모든 기하학의 정리를 증명하는 시도는 에우클레이데스에 의해 집대성되었다. 헬레니즘 시기인 프톨레마이오스 왕조의 알렉산드리아에 살았던 에우클레이데스는 《원론》을 집필하여 주어진 정의와 공리만으로 수학 정리를 증명하는 방법을 완성하였다.[57] 에우클레이데스는 먼저 기하학이 다루는 대상을 정의하고, 이러한 대상들이 갖는 자명하다고 인정되는 공리를 설정하였다. 《원론》은 다음과 같은 공리를 채택하고 있다.[58]
# 임의의 서로 다른 두 점 P, Q에 대해 두 점을 지나는 직선은 유일하다.
# 임의의 두 선분 AB, CD에 대해 B가 A와 E 사이에 위치하고 선분 BE의 길이가 선분 CD의 길이와 같게 되는 점 E는 유일하다.
# 점 O를 정점으로 하고 반지름이 OP인 원을 그릴 수 있다.
# 모든 직각은 합동이다.
# 하나의 직선 위에 있지 않은 점 P를 지나는 평행선은 유일하다.
《원론》은 위의 공리를 바탕으로 피타고라스의 정리와 같은 수학적 사실을 증명한다. 이렇게 증명된 수학적 사실을 정리(定理)라고 한다.[58] 정의, 공리, 증명, 정리와 같은 논리적 단계는 오늘날에도 여전히 사용된다. 하나의 공리계에서 참으로 증명된 정리는 공리계가 바뀌지 않는 한 계속하여 참이 된다.[54]
아르키메데스는 에우클레이데스보다 후대의 사람으로[59] 도형의 넓이와 부피의 계산에 탁월한 업적을 남겼다. 아르키메데스는 원의 넓이가 반지름의 거듭 제곱에 원주율을 곱한 것과 같다는 것을 증명하였고, 원주율의 근사값을 약 3.1416으로 계산하였다.[60] 또한, 구의 부피는 같은 높이의 원기둥의 부피에 대해 3분의 2이라는 것을 증명하였으며, 포물선과 직선으로 둘러싸인 도형의 넓이를 구하는 방법을 발견하였다.[61]

탈레스 (기원전 635–543년)는 현재 터키 남서부에 위치한 밀레투스 출신으로, 수학적 연역법을 최초로 사용한 인물로 여겨진다. 탈레스는 5개의 기하학적 명제에 대한 연역적 증명을 기록했지만, 그의 증거는 전해지지 않는다. 피타고라스 (기원전 582–496년)는 이오니아 출신으로, 이후 그리스인들이 식민지화한 이탈리아로 이주했으며, 탈레스의 제자였을 가능성이 있고, 바빌론과 이집트를 여행했다. 그의 이름을 딴 정리는 그가 발견한 것이 아닐 수도 있지만, 그는 아마도 이 정리에 대한 연역적 증명을 최초로 제시한 사람 중 한 명일 것이다. 그는 수학, 음악, 철학을 연구하기 위해 학생들을 모았고, 그들은 함께 오늘날 고등학생들이 기하학 수업에서 배우는 대부분의 내용을 발견했다. 또한, 그들은 무공약 길이와 무리수를 발견하는 심오한 발견을 했다.
플라톤(기원전 427년~기원전 347년)은 그리스인들이 매우 존경했던 철학자였다. 그의 유명한 학교 입구에 "기하학을 모르는 자는 여기 들어오지 못한다."라고 새겨놓았다는 이야기가 전해지지만, 이 이야기는 사실이 아닌 것으로 여겨진다.[12] 그는 수학자는 아니었지만, 수학에 대한 그의 견해는 큰 영향을 미쳤다. 그리하여 수학자들은 기하학은 컴퍼스와 눈금 없는 자만 사용해야 하며, 눈금이 있는 자나 각도기와 같은 측정 도구는 사용해서는 안 된다는 그의 믿음을 받아들였다. 왜냐하면 이러한 도구들은 학자가 아닌, 일꾼의 도구였기 때문이다. 이 칙령은 가능한 컴퍼스와 눈금 없는 자 작도에 대한 심도 있는 연구를 이끌었고, 세 가지 고전적인 작도 문제로 이어졌다: 이러한 도구를 사용하여 각의 3등분, 주어진 정육면체의 두 배 부피를 갖는 정육면체 작도, 그리고 주어진 원과 면적이 같은 정사각형 작도. 19세기에 이르러 마침내 이 작도들의 불가능성이 증명되면서, 실수 체계의 심오한 구조에 대한 중요한 원리들이 밝혀졌다. 플라톤의 가장 위대한 제자인 아리스토텔레스(기원전 384년~기원전 322년)는 연역적 증명에 사용되는 추론 방법에 관한 논문을 썼는데(논리학 참조), 이 논문은 19세기에 이르러서야 실질적으로 개선되었다.
3. 2. 구장산술
《구장산술》은 기원후 179년 처음 발간된 중국의 수학서로, 최초 저자는 알려져 있지 않다. 삼국시대 위나라의 유휘가 263년에 주석을 달아 정본(定本)이 되었는데, 그의 서문에 따르면 전한의 학자가 진나라 때의 유문을 모아 편집한 것이라고 한다. 당나라 때에는 이순풍의 주석이 더해져 관리 교과서로 쓰인 산경십서 중 하나로 채택되었다.[62]구장산술은 모두 아홉 개의 장으로 나뉘어 있는데, 도형의 넓이를 재는 방전(方田), 곡물 교역에서 환율을 계산하는 속미(粟米), 봉록이나 조세의 비율 배분을 계산하는 쇠분(衰分), 제곱근 계산과 원의 넓이를 다루는 소광(少廣), 토목공사의 공정과 부피를 계산하는 상공(商功), 운반 거리의 멀고 가까움을 고려하여 비용을 동등하게 계산하는 복잡한 비율을 다루는 균수(均輸), 일차방정식의 해를 이용하여 남거나 모자람을 계산하는 영부족(盈不足), 양수와 음수가 섞여있는 연립일차방정식 계산을 위한 방정(方程), 피타고라스 정리를 다루는 구고(勾股)로 이루어져 있다.[62]
초기 구장산술은 원주율의 근사값으로 3을 사용하는 등 부정확한 점이 있었으나, 유휘는 극한 개념을 도입한 할원술(割圓術)을 도입하여 보다 정확한 원주율을 제시하였다.[63] 가우스 소거법과 동일한 방식의 행렬 계산을 다루는 등 복잡한 계산도 다루고 있다.[64] 특히 피타고라스 정리를 다루는 구고(勾股)는 고대 중국의 기하학 지식 수준이 매우 높았다는 것을 보여준다.
한나라(기원전 202년 – 서기 220년) 시대에 조위 왕국의 수학자 유휘는 ''구장산술''을 편집하고 주석을 달았다. 이 책에는 정사각형과 원의 표면적, 다양한 3차원 도형의 부피를 구하는 등 기하학이 적용된 많은 문제들이 포함되어 있으며, 피타고라스 정리의 사용도 포함되어 있다. 이 책은 피타고라스 정리에 대한 그림 증명을 제공했고,[27] 초기 주공과 상고가 직각 삼각형과 피타고라스 정리의 속성에 대해 나눈 대화가 기록되어 있으며, 천문학적인 규형, 원과 사각형, 높이와 거리의 측정에 대해서도 언급하고 있다.[28] 유휘는 192각형 정다각형을 사용하여 파이를 3.141014로, 3072각형 정다각형을 사용하여 파이를 3.14159로 계산했다. 이는 유휘의 동시대인이자 동오의 수학자이자 천문학자인 왕번이 142⁄45을 사용하여 파이를 3.1555로 계산한 것보다 더 정확했다.[29] 유휘는 또한 깊이, 높이, 너비 및 표면적의 거리 측정을 계산하기 위해 수학적 측량에 대해 썼다. 입체 기하학에서 그는 직사각형 밑면과 양쪽이 경사진 쐐기가 피라미드와 사면체 쐐기로 분해될 수 있다는 것을 알아냈다.[30] 그는 또한 사다리꼴 밑면과 양쪽이 경사진 쐐기가 피라미드에 의해 분리된 두 개의 사면체 쐐기를 만들 수 있다는 것을 알아냈다.[30] 또한 유휘는 부피에 대한 카발리에리의 원리와 가우스 소거법을 설명했다. ''구장산술''에서 전한(기원전 202년 ~ 서기 9년) 시대에 알려진 기하학적 공식들은 다음과 같다.
'''면적'''[31]
| 도형 |
|---|
| 두 개의 정사각형 면을 가진 평행육면체 |
| 정사각형 면이 없는 평행육면체 |
| 피라미드 |
| 정사각형 밑면을 가진 각뿔대 |
| 변의 길이가 다른 직사각형 밑면을 가진 각뿔대 |
| 정육면체 |
| 각기둥 |
| 직사각형 밑면과 양쪽이 경사진 쐐기 |
| 사다리꼴 밑면과 양쪽이 경사진 쐐기 |
| 사면체 쐐기 |
| 두 번째 유형의 쐐기 잘린 꼴 (공학적 응용 분야에 사용됨) |
| 원기둥 |
| 원형 밑면을 가진 원뿔 |
| 원뿔대 |
| 구 |
3. 3. 브라마굽타
브라마굽타는 7세기 무렵 인도의 천문학자 겸 수학자로, 당시 인도의 수학을 정리한 《브라마스푸타시단타》(ब्राह्मस्फुटसिद्धान्त|브라마 원리 선집hi)를 저술하였다.[65] 그의 책에는 0의 도입과 같은 인도 수학의 중요 업적이 소개되어 있으며, 제12장에서는 원에 내접하는 사각형의 넓이를 계산하는 브라마굽타의 공식을 서술하였다.[65]| 원에 내접하는 사각형의 각 선분의 길이가 a, b, c, d일 때, 사각형의 넓이 S는 |
브라마굽타는 이 외에도 브라마굽타 정리도 함께 서술하고 있다.
그는 628년에 천문학 작품인 《브라마스푸타시단타》를 저술했는데, 66개의 산스크리트어 구절이 포함된 12장은 "기본 연산"(세제곱근, 분수, 비율 및 비례, 물물교환 포함)과 "실용 수학"(혼합물, 수학적 수열, 평면 도형, 벽돌 쌓기, 목재 켜기, 곡물 쌓기 포함)의 두 부분으로 나뉘었다.[16] 후자 부분에서 그는 원주 사각형의 대각선에 대한 유명한 정리를 다음과 같이 진술했다.[16]
'''브라마굽타의 정리:''' 원주 사각형의 대각선이 서로 수직이면, 대각선의 교차점에서 사각형의 임의의 변에 그은 수직선은 항상 반대쪽 변을 이등분한다.
12장에는 또한 원주 사각형의 면적에 대한 공식(헤론의 공식의 일반화)과 유리수 삼각형(즉, 유리수 변과 유리수 면적을 갖는 삼각형)에 대한 완전한 설명이 포함되어 있다.
'''브라마굽타의 공식:''' 변의 길이가 각각 ''a'', ''b'', ''c'', ''d''인 원주 사각형의 면적 ''A''는 다음과 같다.
:
여기서 ''s''는 반둘레이며, 다음으로 주어진다:
'''유리수 삼각형에 대한 브라마굽타의 정리:''' 유리수 변 와 유리수 면적을 갖는 삼각형은 다음 형태이다.
:
어떤 유리수 및 에 대해.[17]
3. 4. 이슬람 수학
9세기 바그다드에서 활동한 박학가 타비트 이븐 꾸라(ثابت بن قرة|사비트 이븐 쿠라ar)는 수학에서도 여러 가지 업적을 남겼다. 그는 양의 실수를 도입하여 수의 영역을 확장하였고, 적분법의 개념을 발전시켰으며, 구면삼각법을 연구하였다. 특히 기하학과 관련하여 에우클레이데스의 평행선 공리에 대해 의문을 나타내고 비유클리드 기하학의 기초를 놓았다. 타비트의 저술은 라틴어로 번역되어 유럽 수학 발전에 큰 영향을 주었다.[66] 구면삼각법에서는 유클리드의 공준과 달리 한 점을 지나는 평행선은 없게 되고 삼각형 내각의 합은 언제나 180°보다 크다.사비트 이븐 쿠라는 축소와 구성의 방법을 사용하여 모든 삼각형에 대한 피타고라스 정리의 두 가지 일반적인 수학적 증명을 제공했으며, 이전에는 특별한 경우의 특수 직각 삼각형에 대해서만 정리에 대한 증명이 존재했다.[32]
2007년 학술지 ''사이언스''의 한 논문은 지리 타일이 자기 유사 프랙탈 준결정 타일링, 예를 들어 펜로즈 타일링과 일치하는 속성을 가지고 있음을 시사했다.[33][34]
4. 근대 기하학
해석기하학은 피에르 드 페르마와 르네 데카르트에 의해 수립되었다. 1629년 페르마는 해석기하학을 발명하였으며, 그의 아이디어는 원고 상태로 1637년 초부터 돌아다녔지만 생전에 출간하지는 않았다. 데카르트는 페르마의 원고를 가지고 있었으며 《방법서설》의 부록으로 출판한 〈기하학〉에서 대수학을 사용하여 기하학 문제를 다루는 개념을 설명하였다. 페르마는 직교 좌표계를 고안하고 이를 이용하여 직선, 원, 포물선, 타원, 쌍곡선의 방정식을 구하였다. 데카르트는 이러한 직교 좌표계를 널리 알리는 데 공헌하였고, 이 때문에 데카르트 좌표계라고도 불리게 되었다.[67]
페르마는 함수의 극한을 이용하여 그래프의 접선을 구하는 문제 역시 고찰하여 일반적인 풀이법을 발견하였다.[67] 그러나 미적분학을 정립하고 완성시킨 것은 아이작 뉴턴과 고트프리트 빌헬름 라이프니츠였다. 뉴턴은 기하학을 바탕으로 순간적인 변화량을 구하는 방법을 발견하고 이를 유율법(fluxion영어)이라고 불렀다. 뉴턴은 1687년 《자연 철학의 수학적 원리》에 유율법을 발표하였다. 한편, 라이프니츠는 함수 f(x)에서 x가 무한히 작은 증분인 미분(differential영어)의 변화량을 가질 때 f(x)의 변화량을 구하는 방법으로서 미분을 발견하였다. 라이프니츠는 1677년 무렵에는 미분의 계산방법과 표기법을 완성하였다. 오늘날에는 보다 수학적으로 효율적인 라이프니츠의 방법이 주로 쓰인다.[68]
17세기 초 기하학에서 두 가지 중요한 발전이 있었는데, 첫 번째는 르네 데카르트와 피에르 드 페르마에 의한 해석 기하학 즉, 좌표계와 방정식을 사용하는 기하학의 창조였다. 이는 미적분학의 발전과 정확한 정량적 물리학 과학의 발전에 필요한 전조였다. 두번째는 아이작 뉴턴과 고트프리트 빌헬름 라이프니츠에 의해 미적분학이 독립적으로 거의 동시에 개발된것이다.
지오바니 지롤라모 사케리는 《모든 오류로부터 해방된 유클리드》(Euclides ab omninaevo vindicatusla)를 출판하면서 평행선 공리를 받아들이지 않을 경우 이등변양직각사각형의 자명하지 않은 두 각은 서로 크기가 같지만 그것이 반드시 직각이라고 말할 수 없다는 점을 발견하였다.[72]
19세기에 들어 카를 프리드리히 가우스, 보여이 야노시, 니콜라이 로바쳅스키는 각자 독립적으로 평행선 공준이 거짓인 자기 일관적인 기하학을 개발하기 시작했다. 그 결과 최초의 비유클리드 기하학을 창조했다.[73] 1854년, 가우스의 제자였던 베른하르트 리만은 모든 매끄러운 표면의 고유(자체 포함) 기하학에 대한 획기적인 연구에 미적분학적 방법을 적용하여, 다른 비유클리드 기하학을 발견했다. 리만의 이 연구는 나중에 알베르트 아인슈타인의 상대성 이론의 기초가 되었다. 오늘날 사케리, 가우스, 보여이, 리만은 비유클리드 기하학의 창시자로 인정받고 있다.[74]
18세기에 오일러가 위상수학의 아이디어를 구체화했다. 위상수학은 기하학에서 다루는 길이, 부피 등 측정할 수 있는 양이 아닌 공간이나 도형의 근원적인 성질을 다루는 수학이다. 다면체에 대한 오일러의 공식 $V-E+F=2$는 면, 변, 꼭짓점의 개수가 수학의 대상이 되었음을 보였고, 이는 위상수학 탄생의 계기가 되었다.
4. 1. 해석기하학의 발전
해석기하학은 피에르 드 페르마와 르네 데카르트에 의해 수립되었다. 1629년 페르마는 해석기하학을 발명하였으며 아이디어를 짤막한 글로 설명하여 놓았는데, 그의 아이디어는 원고 상태로 1637년 초부터 돌아다녔지만 생전에 출간하지는 않았다. 데카르트는 페르마의 원고를 가지고 있었으며 《방법서설》의 부록으로 출판한 〈기하학〉에서 대수학을 사용하여 기하학 문제를 다루는 개념을 설명하였다. 페르마는 직교 좌표계를 고안하고 이를 이용하여 직선과 원의 일반적인 방정식과 포물선, 타원, 쌍곡선의 간단한 방정식을 구하였다. 뿐만 아니라 모든 일차 또는 이차방정식이 이러한 형태 중의 하나가 됨을 체계적이고 완전한 방법으로 보였다. 데카르트는 이러한 직교 좌표계를 널리 알리는 데 공헌하였고, 이 때문에 직교 좌표계는 데카르트의 이름을 따 데카르트 좌표계라고도 불리게 되었다.[67]페르마는 함수의 극한을 이용하여 그래프의 접선을 구하는 문제 역시 고찰하여 일반적인 풀이법을 발견하였다.[67] 그러나 미적분학을 정립하고 완성시킨 것은 아이작 뉴턴과 고트프리트 빌헬름 라이프니츠였다. 둘은 각자 독립적인 방법으로 미적분학을 완성하였다. 뉴턴은 기하학을 바탕으로 순간적인 변화량을 구하는 방법을 발견하고 이를 유율법(fluxion영어)이라고 불렀다. 뉴턴은 유율법을 곡선에 대한 접선과 곡률의 견지에서 파악하였다. 뉴턴은 1687년 《자연 철학의 수학적 원리》에 유율법을 발표하였다. 한편, 라이프니츠는 함수 f(x)에서 x가 무한히 작은 증분인 미분(differential영어)의 변화량을 가질 때 f(x)의 변화량을 구하는 방법으로서 미분을 발견하였다. 라이프니츠는 1677년 무렵에는 미분의 계산방법과 표기법을 완성하였다. 오늘날에는 보다 수학적으로 효율적인 라이프니츠의 방법이 주로 쓰인다. 뉴턴과 라이프니츠는 미분의 발견 공로를 놓고 오랫동안 다투었으며 이로 인해 유럽의 수학계는 둘 중 누구를 지지하는 가를 놓고 심한 대립을 보이기도 하였다. 뉴턴과 라이프니츠는 서로 상대방이 자신의 아이디어를 훔쳤다고 비난하였다. 이러한 대립은 라이프니츠가 사망한 이후에도 계속되었다. 오늘날에는 뉴턴과 라이프니츠가 각자 독자적인 방법으로 미분을 발견했다고 본다.[68]
17세기 초 기하학에서 두 가지 중요한 발전이 있었다. 첫 번째이자 가장 중요한 것은 르네 데카르트(1596–1650)와 피에르 드 페르마(1601–1665)에 의한 해석 기하학 즉, 좌표계와 방정식을 사용하는 기하학의 창조였다. 이는 미적분학의 발전과 정확한 정량적 물리학 과학의 발전에 필요한 전조였다.
17세기 후반에 아이작 뉴턴 (1642–1727)과 고트프리트 빌헬름 라이프니츠 (1646–1716)에 의해 미적분학이 독립적으로 거의 동시에 개발되었다. 이것은 현재 해석학이라고 불리는 새로운 수학 분야의 시작이었다. 기하학의 한 분야는 아니지만, 기하학에 적용할 수 있으며, 오랫동안 거의 해결할 수 없었던 두 가지 부류의 문제를 해결했다. 즉, 기묘한 곡선에 접선을 찾고, 해당 곡선으로 둘러싸인 면적을 찾는 것이었다. 미적분학의 방법은 이러한 문제들을 대부분 단순한 계산 문제로 축소했다.
4. 2. 비유클리드 기하학의 출현
에우클레이데스의 공리계 가운데 평행선 공리는 오랫동안 논란의 대상이었다. 이 공리는 다른 공리들에 대해 독립적이며 유도되지도 않는다. 다른 공리로부터 평행선 공리를 유도하려는 수많은 시도가 있었으나 모두 실패하였고, 근대에 이르기까지 미해결 문제로 남아있었다.[71] 1733년 지오바니 지롤라모 사케리는 《모든 오류로부터 해방된 유클리드》(Euclides ab omninaevo vindicatusla)를 출판하면서 평행선 공리를 받아들이지 않을 경우 이등변양직각사각형의 자명하지 않은 두 각은 서로 크기가 같지만 그것이 반드시 직각이라고 말할 수 없다는 점을 발견하였다. 사케리는 에우클레이데스의 평행선 공리를 지지하기 위해 예각이거나 둔각인 경우 모순이 생긴다는 점을 발견하고자 하였으나, 평행선 공리와 논리적으로 동치인 가정을 하지 않고는 이를 해결할 수 없었다.[72]19세기에 들어 카를 프리드리히 가우스, 보여이 야노시, 니콜라이 로바쳅스키는 각자 독립적으로 평행선 공준을 증명하는 것이 불가능하다는 것을 의심하기 시작했고, 평행선 공준이 거짓인 자기 일관적인 기하학을 개발하기 시작했다. 이들은 성공했고, 그 결과 최초의 비유클리드 기하학을 창조했다.[73] 가우스는 삼각형의 내각의 합이 180°보다 작을 경우에도 기하학의 다른 공리들이 여전히 유효하다는 것을 증명하였다. 1832년 보여이 야노시가 가우스와 동일한 발견을 하고 가우스에게 이를 알리자 가우스는 자신이 이미 30년 전에 동일한 결과를 발견했었다고 답신을 보냈다. 얼마 지나지 않아 보여이는 1829년 러시아의 수학자 니콜라이 로바쳅스키 역시 비유클리드 기하학의 해설서를 발표하였다는 것을 알게 된다. 한편 베른하르트 리만은 직선의 길이가 무한하다는 에우클레이데스의 두 번째 공리에 의문을 제기하고 유한한 길이를 가지면서 한계는 없는 직선을 도입하여 삼각형 내각의 합이 180°보다 큰 기하학 역시 가능하다는 것을 보였다.[74]
1854년, 가우스의 제자였던 베른하르트 리만은 모든 매끄러운 표면의 고유(자체 포함) 기하학에 대한 획기적인 연구에 미적분학적 방법을 적용하여, 다른 비유클리드 기하학을 발견했다. 리만의 이 연구는 나중에 알베르트 아인슈타인의 상대성 이론의 기초가 되었다.
오늘날 사케리, 가우스, 보여이, 리만은 비유클리드 기하학의 창시자로 인정받고 있다.[74] 비유클리드 기하학이 유클리드 기하학과 마찬가지로 자기 일관적이라는 것을 수학적으로 증명해야 했으며, 이는 1868년 에우제니오 벨트라미에 의해 처음으로 이루어졌다. 이를 통해 비유클리드 기하학은 유클리드 기하학과 동등한 수학적 지위를 얻게 되었다.
4. 3. 위상수학
18세기에 오일러가 위상수학의 아이디어를 구체화했다. 위상수학은 기하학에서 다루는 길이, 부피 등 측정할 수 있는 양이 아닌 공간이나 도형의 근원적인 성질을 다루는 수학이다. 다면체에 대한 오일러의 공식 $V-E+F=2$는 면, 변, 꼭짓점의 개수가 수학의 대상이 되었음을 보였고, 이는 위상수학 탄생의 계기가 되었다.18세기 중반, 수직선, 2차원, 3차원에서 유사한 아이디어를 연구할 때 특정 수학적 추론이 반복되는 현상이 나타났다. 따라서 일반적인 거리 공간 개념이 만들어져 추론을 일반적인 방식으로 수행하고 특수한 경우에 적용할 수 있게 되었다. 미적분학 및 해석학 관련 개념을 연구하는 이러한 방법은 분석 사이투스(analysis situs)로 불렸으며, 이후 위상수학으로 알려지게 되었다. 위상수학의 중요한 주제는 연결성 및 경계와 같이 유클리드 기하학 및 비유클리드 기하학의 초점이었던 직선, 길이, 각도 측정의 정확한 등가와는 다른, 더 일반적인 도형의 속성이었다. 위상수학은 곧 기하학 또는 해석학의 하위 분야가 아닌, 독자적인 주요 분야로 발전하였다.
5. 현대 기하학
현대 기하학은 유한체 기하학, 프랙탈 이론, 끈 이론 등 다양한 분야로 발전해왔다.
5. 1. 유한체 기하학
대수기하학의 발전은 앙드레 베유, 알렉산더 그로텐디크, 장피에르 세르 등의 연구를 통해 입증된 것처럼 유한체 위의 곡선과 표면 연구를 포함했으며, 실수 또는 복소수 위에서도 연구가 이루어졌다. 유한 기하학 자체, 즉 유한 개의 점만 있는 공간에 대한 연구는 부호 이론과 암호학에 응용되었다. 컴퓨터의 출현과 함께 계산 기하학 또는 디지털 기하학과 같은 새로운 분야가 기하학적 알고리즘, 기하학적 데이터의 이산 표현 등을 다루게 되었다.5. 2. 프랙탈 이론
5. 3. 끈 이론
(원문 소스에 내용이 없으므로, 이전 출력과 동일하게 빈 섹션으로 유지)참조
[1]
서적
An Introduction to the History of Mathematics
Saunders
[2]
서적
Modern School Mathematics: Geometry
Houghton Mifflin Company
[3]
문서
Chapter 2
[4]
뉴스
Clay tablets reveal Babylonians discovered astronomical geometry 1,400 years before Europeans - The Washington Post
https://www.washingt[...]
[5]
논문
The origin of mathematics
[6]
인용
[7]
문서
[8]
문서
Pythagorean triples
[9]
문서
[10]
웹사이트
The Babylonian tabled Plimpton 322
http://www.math.ubc.[...]
[11]
문서
Plimpton 322
[12]
웹사이트
What precisely was written over the door of Plato's Academy?
http://www.math.ucde[...]
2015-04-08
[13]
웹사이트
Archimedes
https://www.britanni[...]
Encyclopedia Britannica
[14]
서적
The Vanished Library
https://books.google[...]
University of California Press
[15]
인용
[16]
인용
[17]
인용
[18]
논문
Parameshvara's rule for the circumradius of a cyclic quadrilateral
[19]
문서
[20]
문서
[21]
문서
[22]
문서
[23]
문서
[24]
문서
[25]
문서
[26]
문서
[27]
문서
[28]
문서
[29]
문서
[30]
문서
[31]
문서
[32]
논문
Thabit ibn Qurra's Generalization of the Pythagorean Theorem
[33]
논문
Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture
http://www.physics.h[...]
[34]
웹사이트
Supplemental figures
http://www.physics.h[...]
[35]
서적
Translations and Translators
Harvard Univ. Pr.
[36]
논문
Translations and Translators
[37]
서적
Filippo Brunelleschi: The Buildings
Zwemmer
[38]
서적
Lives of the Artists
[39]
서적
Lives of the Artists
[40]
서적
The Secret Language of the Renaissance
[41]
서적
과학의 역사 1
한울
[42]
서적
An Introduction to the History of Mathematics
Saunders
[43]
서적
과학의 역사 1
한울
[44]
서적
길가메시 서사시
범우사
[45]
서적
수학의 기초와 기본 개념
경문사
[46]
서적
수학의 기초와 기본 개념
경문사
[47]
서적
Modern School Mathematics: Geometry
Houghton Mifflin Company
[48]
웹인용
The Moscow Papyrus
http://www.math.tamu[...]
2015-04-20
[49]
간행물
사각뿔대 부피를 구하는 다양한 방법에 대한 탐구
http://ocean.kisti.r[...]
2010-08
[50]
웹인용
Babylonian numerals
http://www-gap.dcs.s[...]
2015-04-26
[51]
서적
An Introduction to the History of Mathematics
Saunders
[52]
서적
Indian Mathematics
The Johns Hopkins University Press
[53]
서적
The Crest of the Peacock: The Non-European Roots of Mathematics
Princeton University Press
[54]
서적
페르마의 마지막 정리
영림카디널
[55]
서적
수학의 기초와 기본 개념
경문사
[56]
서적
수학의 기초와 기본 개념
경문사
[57]
서적
위대한 수학자들 유레카! 수학으로 새로운 세계를 열다
맑은소리
[58]
서적
수학자를 알면 공식이 보인다
성우
[59]
웹사이트
PROCLUS, Summary
http://www.loebclass[...]
[60]
서적
친절한 도형 교과서
부키
[61]
서적
아르키메데스
경문사
[62]
서적
구장산술
서해문집
[63]
서적
지도로 보는 세계 과학사
시그마북스
[64]
서적
수학자를 알면 공식이 보인다
성우
[65]
서적
Indian Mathematics
Basil Blackwell
[66]
웹사이트
Thābit ibn Qurra
http://islamsci.mcgi[...]
Springer
[67]
서적
미적분학과 해석기하
경문사
[68]
서적
오일러가 사랑한 수 e
경문사
[69]
문서
즉 정의역과 치역이 같은 집합이 되는
[70]
서적
수학의 기초와 기본 개념
경문사
[71]
서적
수학의 천재들
경문사
[72]
서적
수학의 기초와 기본 개념
경문사
[73]
서적
수학의 천재들
경문사
[74]
서적
수학의 천재들
경문사
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com



