비유클리드 기하학
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
비유클리드 기하학은 유클리드의 평행선 공준을 부정하거나 수정한 기하학 체계를 통칭한다. 유클리드 기하학의 대안으로, 평행선의 존재 여부와 삼각형 내각의 합 등에서 차이를 보인다. 역사적으로는 유클리드 기하학의 한계를 극복하려는 시도에서 시작되었으며, 로바체프스키, 볼라이, 리만 등에 의해 쌍곡 기하학, 타원 기하학 등이 발전했다. 비유클리드 기하학은 과학적 패러다임의 전환을 가져왔으며, 아인슈타인의 일반 상대성 이론 등 현대 과학에도 중요한 영향을 미쳤다. 비유클리드 기하학은 절대 기하학, 쌍곡 기하학, 타원 기하학, 택시 기하학 등 다양한 종류가 있으며, 각각 다른 특징과 모델을 가진다.
카를 프리드리히 가우스는 "비유클리드 기하학"이라는 용어를 처음 사용했다.[13] 그는 오늘날 쌍곡 기하학 또는 로바체프스키 기하학이라고 불리는 자신의 연구를 이 용어로 지칭했다. 일부 현대 저자들은 여전히 ''비유클리드 기하학''을 ''쌍곡 기하학''과 같은 의미로 사용한다.[14]
2. 역사
아서 케일리는 원뿔 내부의 두 점 사이의 거리가 로그와 사영 교차비 함수로 정의될 수 있음을 언급했다. 이 방법은 케일리-클라인 계량이라고 불리게 되었는데, 이는 펠릭스 클라인이 1871년과 1873년에 발표한 논문[15]과 이후 책에서 비유클리드 기하학을 설명하기 위해 활용했기 때문이다. 케일리-클라인 계량은 유클리드 기하학뿐만 아니라 쌍곡선 및 타원 계량 기하학의 작동 모델을 제공했다.
클라인은 "쌍곡선" 및 "타원"이라는 용어를 사용하게 된 장본인이다 (그의 체계에서 그는 유클리드 기하학을 ''포물선''이라고 불렀다.[16]). 그의 영향으로 현재 "비유클리드 기하학"이라는 용어는 "쌍곡선" 또는 "타원" 기하학을 의미하는 데 사용되고 있다.
일부 수학자들은 "비유클리드"라고 불려야 하는 기하학의 목록을 확장하려고 한다.[17] 리만 기하학과 같이 유클리드 기하학과 매우 다르지만 "비유클리드 기하학"의 일반적인 의미에 반드시 포함되지 않는 기하학도 많이 있다.
비유클리드 기하학의 역사는 유클리드 기하학의 평행선 공준에 대한 의문에서 시작되었다. 유클리드의 《원론》에 제시된 평행선 공준은 다른 공준에 비해 자명성이 떨어지고 내용이 길었기 때문에, 이를 증명하거나 더 간결한 명제로 대체하려는 시도가 이어졌다.
조반니 지롤라모 사케리는 1733년 저서 "모든 오점에서 정화된 유클리드"에서 평행선 공준을 부정하여 모순을 찾으려고 시도했다. 그는 예각, 직각, 둔각 가설을 설정하고 연구를 진행했으나, 평행선 공준에 의존하는 명제를 사용하여 증명에 실패했다. 요한 하인리히 람베르트는 1766년에 집필하고 1786년에 발견된 논문 "평행선의 이론"에서 비슷한 연구를 진행했지만, 모순을 발견하지 못했다. 카를 프리드리히 가우스는 1824년 편지에서 예각 가설 하에 정합적인 기하학이 성립할 가능성을 언급했지만, 연구 결과를 공표하지는 않았다.
2. 1. 유클리드 기하학

유클리드 기하학(Euclidean geometry)은 BC330?~BC275?경 그리스 수학의 유클리드가 구축한 수학 체계로, 그의 《원론》은 기하학에 관한 최초의 체계적인 논의로 알려져 있다. 유클리드의 방법은 직관적으로 인지되는 공리를 참으로 간주하고, 그것들로부터 연역적으로 명제(정리)를 이끌어내는 것이다. 이러한 공리론적 구성에서는 직선 · 평면 등의 기본적인 개념이 무정의(無定意) 요소이다. 2천년 동안 유클리드의 공리는 어떤 정리도 유도해 낼 수 있을 만큼 직관적으로 매우 명백한 것으로 보였고, 절대적인 의미에서 참으로 간주되었다.
유클리드가 저술한 『원론』(''Elements''영어) 1~4권에서는 오늘날의 유클리드 기하학에 관한 고대 그리스 수학의 성과가 정리되어 있다. "원론"에 언급된 공리·공준 가운데 제5공준은 평행선 공준이라 불리는데, 그 내용은 다음과 같다.
두 직선에 다른 한 직선이 교차하여 생기는 같은 쪽의 내각의 합이 2직각보다 작으면, 이 두 직선을 연장하면 2직각보다 작은 쪽에서 교차한다.
이 공준은 다른 공리에 비해 자명성이 낮고, 내용이 길었기 때문에, 다음 두 가지 의문이 제기되었다.
이에 따라 평행선 공준을 증명하거나, 다른 표현으로 바꾸려는 시도가 시작되었다.
유클리드 기하학은 여러 방식으로 공리적으로 설명될 수 있다. 유클리드의 다섯 가지 공준(공리)으로 이루어진 원래 시스템은 그의 증명이 공리로 간주되어야 할 여러 명시되지 않은 가정을 사용했기 때문에 이러한 설명 중 하나가 아니다. 20개의 공리로 구성된 힐베르트의 시스템[18]은 유클리드의 접근 방식을 가장 가깝게 따르고 유클리드의 모든 증명에 대한 정당성을 제공한다. 다른 시스템들은 서로 다른 정의되지 않은 용어 집합을 사용하여 다른 경로로 동일한 기하학을 얻는다. 그러나 모든 접근 방식은 유클리드의 다섯 번째 공준인 평행선 공준과 논리적으로 동일한 공리를 가지고 있다. 힐베르트는 플레이페어 공리 형태를 사용하고, 비르크호프는 "합동하지 않지만 닮은 삼각형 쌍이 존재한다"는 공리를 사용한다. 이러한 시스템에서 평행선 공준과 동등한 하나의 공리(어떤 형태이든)를 제거하고 다른 모든 공리를 그대로 두면 절대 기하학이 생성된다. 유클리드의 ''원론''의 처음 28개의 명제는 평행선 공준 또는 그와 동등한 것을 사용할 필요가 없으므로, 절대 기하학에서 모두 참된 명제이다.[19]
비유클리드 기하학을 얻으려면 평행선 공준(또는 그와 동등한 것)을 반드시 부정으로 대체해야 한다. 플레이페어의 공준 형태를 부정하는 것은 ( ... 단 하나만 존재한다 ... ) 복합 문장이므로 두 가지 방식으로 수행할 수 있다.2. 1. 1. 유클리드 공준
유클리드가 제시한 다섯 가지 공준은 다음과 같다.[1]
# 임의의 점에서 다른 한 점을 연결하는 직선은 단 하나뿐이다.
# 임의의 선분은 양끝으로 얼마든지 연장할 수 있다.
# 임의의 점을 중심으로 하고 임의의 길이를 반지름으로 하는 원을 그릴 수 있다.
# 직각은 모두 서로 같다.
# 두 직선이 한 직선과 만날 때, 같은 쪽에 있는 내각의 합이 2직각(180˚)보다 작으면 이 두 직선을 연장할 때 2직각(180˚)보다 작은 내각을 이루는 쪽에서 반드시 만난다.
이 중 다섯 번째 공준은 '평행선 공준'이라고 불리며, 다른 공준들에 비해 복잡하여 다른 공준들로부터 유도될 수 있는 정리가 아닌지에 대한 의문이 제기되었다.[1] 이븐 알하이삼(11세기),[1] 오마르 하이얌(12세기), 나시르 알딘 알투시(13세기), 조반니 지롤라모 사케리(18세기) 등 많은 수학자들이 평행선 공준을 증명하려 시도했다.
2. 2. 비유클리드 기하학의 탄생
유클리드의 《원론》 1~4권에는 고대 그리스 수학의 평면 기하학에 대한 성과가 정리되어 있다. 《원론》에 제시된 공리와 공준 중 제5공준, 즉 평행선 공준은 다음과 같다.
: 두 직선에 다른 한 직선이 교차하여 생기는 같은 쪽의 내각의 합이 2직각보다 작으면, 이 두 직선을 연장하면 2직각보다 작은 쪽에서 교차한다.
이 공준은 다른 공준에 비해 자명성이 떨어지고 장황하여 다음과 같은 의문이 제기되었다.
이러한 의문에서 평행선 공준을 증명하거나 다른 명제로 대체하려는 시도가 시작되었다. 고대 그리스 이후 많은 "평행선 공준의 증명"이 제시되었으나, 대부분 프톨레마이오스와 같은 오류를 범했다. 그러나 이 과정에서 평행선 공준과 동치인 명제들이 발견되었다.
조반니 지롤라모 사케리는 1733년 저서 "모든 오점에서 정화된 유클리드"에서 예각·직각·둔각 가설을 설정하고, 직각 가설에서 평행선 공준을 유도할 수 있음을 보였다. 각 가설은 다음과 같이 요약할 수 있다.
사케리는 둔각 가설과 예각 가설이 모순된다고 주장했지만, 실제로는 평행선 공준에 의존하는 명제를 사용하여 증명에 실패했다. 그러나 이 세 가지 가설은 이후 비유클리드 기하학 발전에 큰 영향을 미쳤다.
요한 하인리히 람베르트는 1766년에 집필하고 1786년에 발견된 논문 "평행선의 이론"에서 유사한 주장을 펼쳤다.
카를 프리드리히 가우스는 1824년 11월 8일 편지에서 예각 가설 하에 정합적인 기하학이 성립할 가능성을 언급하며, 어떤 정수(현대 용어로 공간의 곡률 ''k''에 대해 -(1/''k''))가 존재하여 이 값이 클수록 통상적인 기하학에 가까워진다고 말했다. 가우스는 비유클리드 기하학의 존재를 확신했지만, 연구 결과를 공표하지는 않았다.
니콜라이 이바노비치 로바체프스키는 1829년 논문 「기하학의 새로운 원리 및 평행선의 완전한 이론」에서 "허(虛)기하학"으로 명명된 쌍곡 기하학(예각 가정을 포함하는 기하학) 모델을 제시했다.
보야이 야노시는 아버지 보야이 파르카스의 연구를 이어받아 1832년 「공간론」을 출판했다. 「공간론」에서는 평행선 공준을 가정한 기하학(Σ)과 평행선 공준의 부정을 가정한 기하학(S)을 다루었다. 1835년에는 Σ와 S 중 어느 것이 현실에 부합하는지는 논리적으로 결정될 수 없음을 증명했다.
베른하르트 리만은 리만 구로 불리는 타원 기하학 모델을 구성했다.
세 종류의 비유클리드 기하학은 다음 표와 같이 정리할 수 있다. 여기서 굽은 면이나 공간 내의 "직선"은 두 점 사이의 최단 거리(측지선)를 의미하며, 평행선은 절대로 교차하지 않는 두 직선을 의미한다.
| 결론 | 타원 기하학 | 유클리드 기하학(포물 기하학) | 쌍곡 기하학 |
|---|---|---|---|
| 평행선의 수 | 0개 | 1개 | 2개 이상 |
| 대표적인 모델 | 리만 구 | 유클리드 평면 | 유사 구면 |
2. 2. 1. 고대와 중세의 연구
프로클로스는 《원론》 주석에서 평행선 공준이 정리가 아닌지 의문을 제기했다.[37] 클라우디오스 프톨레마이오스는 평행선 공준을 증명했다고 주장했지만, 그 증명은 《원론》 제1권 명제 29에 의존했고, 명제 29는 평행선 공준으로 증명되므로 옳지 않았다.[37]11세기 페르시아의 오마르 하이얌은 《유클리드의 난점에 관한 논의》(Risâla fî sharh mâ ashkala min musâdarât Kitâb 'Uglîdis)를 저술했다.[37] 이 저작은 조반니 지롤라모 사케리에게 많은 영향을 주었다. 13세기 이슬람 세계를 대표하는 학자인 나시르 알딘 알투시의 유고를 엮은 《유클리드 원론 편술》은 1294년에 발표되었다.[37] 여기서 그는 제5공준을 "모든 삼각형의 내각의 합은 2직각과 같다"라고 바꾸었는데, 이는 사케리에게 영향을 주어 "직각 가정"이라고 불렀다.[37]
《유클리드 원론 편술》은 바스의 아델라드에 의해 라틴어로 번역되었고,[37] 노바라의 캄파누스가 주석을 단 판본을 기반으로 에르하르트 라트돌트에 의해 1482년 베네치아에서 처음 출판되었다.[37][38]
2. 2. 2. 근대 유럽의 연구
조반니 지롤라모 사케리는 1733년에 출판한 "모든 오점에서 정화된 유클리드" (''Euclides ab Omni Naevo Vindicatus'')라는 논문에서 평행선 공준을 부정하여 모순을 찾으려고 시도했다. 그는 예각 가설, 직각 가설, 둔각 가설이라는 세 가지 가설을 설정하고, 직각 가설에서 평행선 공준을 유도할 수 있음을 보였다. 사케리는 둔각 가설과 예각 가설이 모순을 일으킨다고 주장했지만, 실제로는 평행선 공준에 의존하는 명제를 사용하여 증명에 실패했다. 그러나 이 세 가지 분류는 이후 비유클리드 기하학 발전에 큰 영향을 주었다.[2]요한 하인리히 람베르트도 1766년에 집필한 "평행선의 이론"이라는 논문에서 비슷한 연구를 진행했다. 이 논문은 1786년에 발견되었다. 그는 사케리와 마찬가지로 네 번째 각이 둔각일 가능성을 제거하고, 예각을 가정하여 여러 정리를 증명했다. 사케리와 달리 람베르트는 이 가정에서 모순을 발견하지 못했고, 삼각형의 면적이 감소함에 따라 각의 합이 증가한다는 비유클리드적 결과를 증명했다. 그는 허구 반지름을 가진 구에서 예각의 모델 가능성을 추측했지만, 더 발전시키지는 않았다.[7]
카를 프리드리히 가우스는 1824년 11월 8일의 편지에서 예각 가설 하에 정합적인 기하학이 성립할 가능성을 언급하며, 어떤 정수가 존재하여 이 값이 클수록 통상적인 기하학에 가까워진다고 말했다. 가우스가 말하는 정수는 현대 용어로 공간의 곡률 ''k''에 대해 -(1/''k'')를 의미한다. 가우스는 비유클리드 기하학의 존재를 확신했지만, 연구 결과를 발표하지는 않았다.
3. 비유클리드 기하학의 분류
아서 케일리는 원뿔 내부의 두 점 사이의 거리가 로그와 사영 교차비 함수로 정의될 수 있음을 언급했다. 이 방법은 케일리-클라인 계량이라고 불리게 되었는데, 이는 펠릭스 클라인이 비유클리드 기하학을 설명하기 위해 활용했기 때문이다.[15] 케일리-클라인 계량은 유클리드 기하학뿐만 아니라 쌍곡 및 타원 계량 기하학의 작동 모델을 제공했다.
클라인은 "쌍곡" 및 "타원"이라는 용어를 사용하게 된 장본인이다 (그의 체계에서 그는 유클리드 기하학을 일반적으로 사용되지 않는 용어인 ''포물선''이라고 불렀다.[16]).
3. 1. 쌍곡 기하학
쌍곡 기하학은 비유클리드 기하학의 시초로, 가우스, 로바쳅스키, 보야이가 만들었다. 곡률이 음수인 공간에서 성립하며, 의구(또는 위구)와 같은 공간에서 나타난다.이 공간은 양쪽 끝으로 갈수록 점점 작아져 간격이 0에 가까워지고, 가운데로 갈수록 점점 커져 간격이 무한대로 커지는, 안으로 휘어진 공간이다. 나팔 두 개를 서로 맞대어 붙여 놓은 것과 비슷한 모양이다. 이 공간에서는 유클리드 기하학의 평행선 공준이 성립하지 않는다. 즉, 한 직선 ''l''과 그 위에 있지 않은 점 P가 주어졌을 때, 점 P를 지나면서 ''l''과 평행한 직선은 무수히 많이 존재한다.
쌍곡 공간에서 두 평행선 사이의 거리는 양쪽 끝 방향으로 가면 0에 점점 가까워지지만 만나지는 않고, 가운데 방향으로 가면 그 거리가 무한히 멀어진다. 또한, 삼각형의 세 내각의 크기 합은 180°보다 작다. 이는 쌍곡면 위에서는 평행선에서 동위각과 엇각의 크기가 같다는 성질이 성립하지 않기 때문이다. 삼각형을 그려보면 공간 자체가 안으로 굽어 있어 삼각형도 안으로 굽은 오목한 모양이 된다.
3. 1. 1. 쌍곡 기하학의 특징
쌍곡 기하학은 유클리드 기하학의 평행선 공준이 성립하지 않는 기하학으로, 가우스, 로바쳅스키, 보야이가 만들었다. 이 기하학은 곡률이 음수인 공간, 예를 들어 의구(pseudosphere)와 같은 곳에서 성립한다.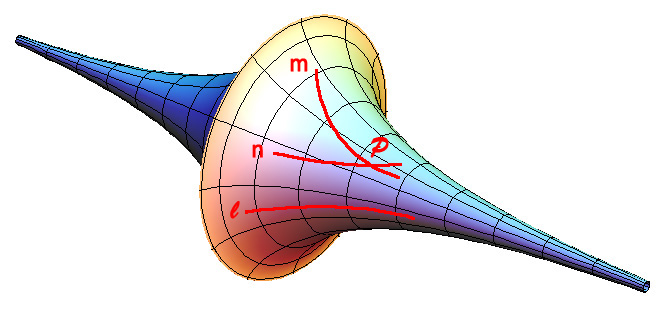
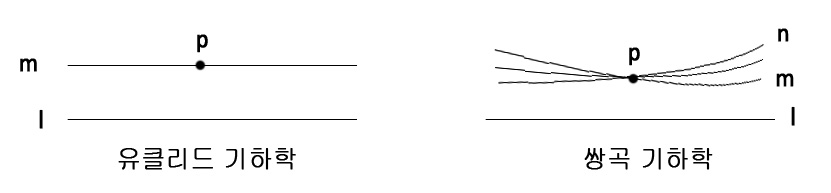

쌍곡 기하학에서는 한 직선 위에 있지 않은 점을 지나는 평행선이 무수히 많다. 유클리드의 평행선 공준에 따르면, 한 직선과 그 위에 있지 않은 한 점이 주어졌을 때, 그 점을 지나면서 주어진 직선과 만나지 않는 직선은 단 하나만 존재한다. 그러나 쌍곡 기하학에서는 이 공준이 성립하지 않아, 주어진 점을 지나면서 주어진 직선과 만나지 않는 직선이 무한히 많이 존재한다.
이 공간에서 삼각형을 그려보면, 공간 자체가 안으로 굽어 있어 삼각형도 안으로 굽은 오목한 모양이 된다. 따라서 삼각형의 세 내각의 크기는 모두 작아져 그 합이 180°보다 작다. 또한, 삼각형의 크기가 커질수록 변이 더 많이 휘어져 세 내각의 크기 합은 더욱 작아진다.


쌍곡 기하학과 유클리드 기하학의 차이점은 다음과 같이 비교할 수 있다.
- 평행선:
- 유클리드 기하학: 한 직선과 그 위에 있지 않은 한 점을 지나는 평행선은 유일하다.
- 쌍곡 기하학: 한 직선과 그 위에 있지 않은 한 점을 지나는 평행선은 무수히 많다.
- 삼각형 내각의 합:
- 유클리드 기하학: 삼각형 내각의 합은 180°이다.
- 쌍곡 기하학: 삼각형 내각의 합은 180°보다 작다. 삼각형이 커질수록 내각의 합은 더 작아진다.
- 람베르트 사각형: 세 개의 직각을 가진 사각형의 네 번째 각은 쌍곡 기하학에서 예각이다.
- 사케리 사각형: 길이가 같은 두 변이 밑변에 수직인 사각형에서, 나머지 두 각(정점 각)은 쌍곡 기하학에서 예각이다.
3. 2. 타원 기하학
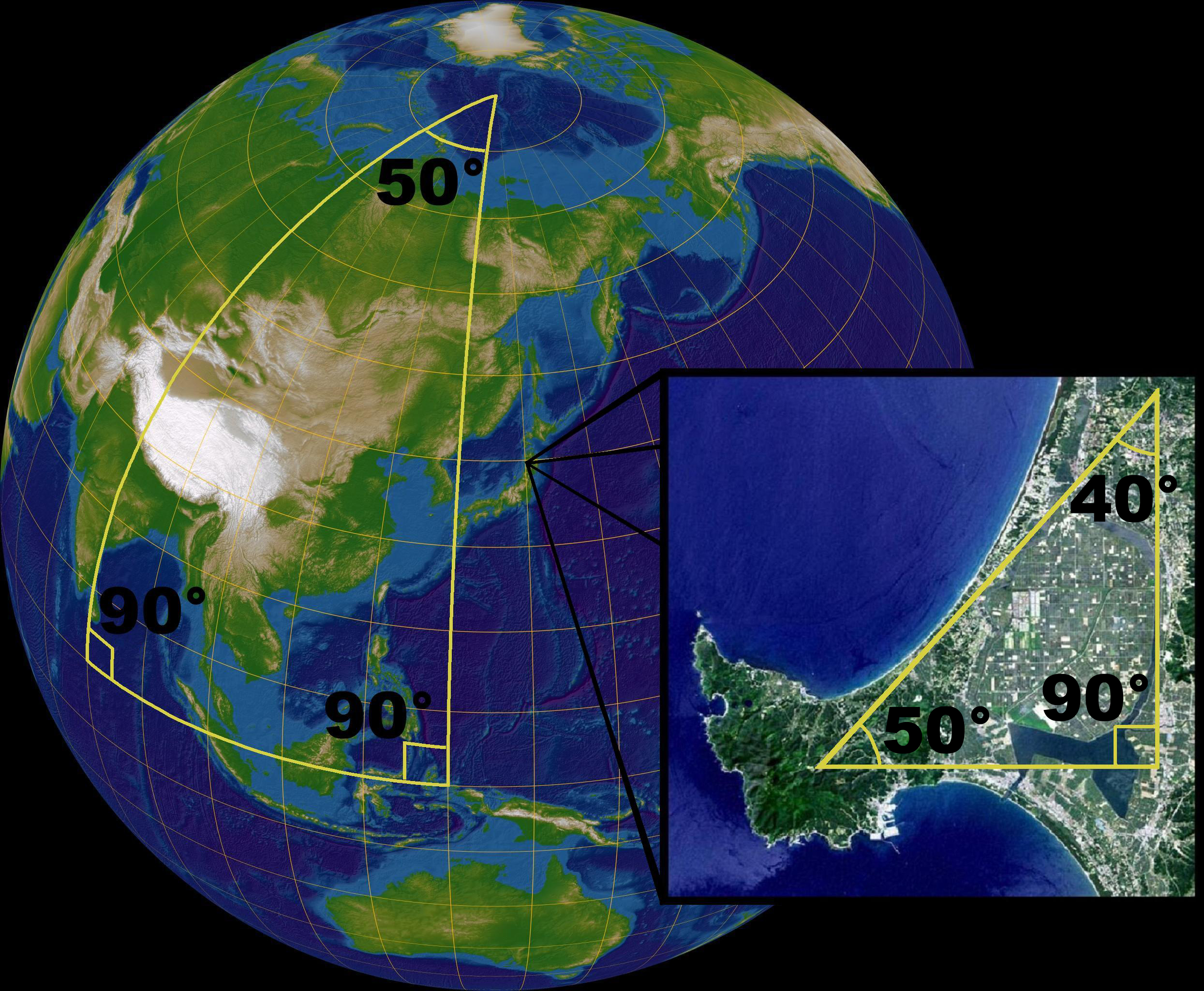
타원 기하학은 비유클리드 기하학 중 하나로, 평행선 공준을 부정하고 "한 직선과 그 위에 있지 않은 한 점을 지나면서, 그 직선과 평행한 직선은 존재하지 않는다"는 공리를 채택한다. 이는 베른하르트 리만에 의해 연구되었다.타원 기하학의 가장 간단한 모델은 구이며, 이 구에서 대원을 직선으로 간주한다. 이때 구의 중심을 지나는 평면과 구의 교선이 직선이 되며, 평행 공리가 성립하지 않음을 알 수 있다. 구면 위의 삼각형 내각의 합은 180°보다 크다.
플레이페어 공리에 따르면, 2차원 평면에서 주어진 직선 과 그 위에 있지 않은 점 ''A''에 대해, ''A''를 지나고 과 교차하지 않는 직선은 정확히 하나 존재한다. 그러나 타원 기하학에서는 ''A''를 지나는 모든 직선이 과 교차한다.[3]
2차원 평면에서 세 번째 직선에 모두 수직인 두 개의 직선을 무한히 연장했을 때, 타원 기하학에서는 이 직선들이 서로 수렴하여 교차한다.[3]
3. 2. 1. 타원 기하학의 특징
타원 기하학은 비유클리드 기하학의 한 종류로, 구면 위에서 성립하는 법칙들을 다룬다. 이 기하학은 리만 기하학이라고도 불린다.타원 기하학에서는 유클리드의 평행선 공리가 성립하지 않는다. 즉, 한 직선과 그 위에 있지 않은 점이 주어졌을 때, 그 점을 지나면서 주어진 직선과 만나지 않는 직선은 존재하지 않는다. 대신, 그 점을 지나는 모든 직선은 주어진 직선과 교차한다.[3]
타원 기하학의 간단한 모델은 구(球)이다. 구에서 대원(예: 적도 또는 자오선)을 직선으로 생각하면, 서로 반대편에 있는 점(대척점)은 같은 점으로 간주한다. 이 모델에서 주어진 직선과 그 위에 있지 않은 점을 지나는 모든 직선은 반드시 주어진 직선과 만나게 된다.[3]
타원 기하학의 주요 특징은 다음과 같다.
- 서로 다른 두 직선은 두 점에서 만난다.
- 삼각형 내각의 합은 항상 180°보다 크고 540°보다 작다.
- 같은 구면 위에 있는 삼각형의 면적비는 내각의 합에서 180°를 뺀 값의 비와 같다.
- 같은 구면 위에는 합동을 제외한 닮음은 존재하지 않는다.
- 곡률이 양수인 공간에서 성립하는 기하학이다.
람베르트 사각형은 세 개의 직각을 가진 사각형인데, 타원 기하학에서 람베르트 사각형의 네 번째 각은 둔각이다.[4] 사케리 사각형은 길이가 같은 두 변이 밑변에 수직인 사각형인데, 타원 기하학에서 사케리 사각형의 나머지 두 각(정점 각)은 둔각이다.[4]
타원 기하학에서 삼각형의 각의 크기 합은 180°보다 크다.[4] 삼각형의 ''결함''은 (180° - 삼각형 각의 크기의 합)으로 정의되는데, 타원 기하학에서 삼각형의 결함은 음수이다.[4]
3. 3. 택시 기하학
헤르만 민코프스키가 19세기에 고안한 택시 기하학은 맨해튼 거리를 അടിസ്ഥാന으로 하는 비유클리드 기하학의 한 종류이다. 택시 기하학은 유클리드 기하학과 거리 함수가 다르다.유클리드 기하학에서 두 점 사이의 거리는 피타고라스 정리를 이용하여 와 같이 계산한다. 반면 택시 기하학에서는 바둑판 모양의 도로망을 가진 도시에서 택시가 이동하는 거리를 생각하여 와 같이 계산한다.
3. 3. 1. 택시 기하학의 특징
헤르만 민코프스키가 19세기에 고안한 택시 기하학은 유클리드 기하학과 거의 유사하지만 거리함수가 다르다. 택시 기하학에서 두 점 사이의 거리는 바둑판 모양의 블록 도로망을 가진 도시에서 택시를 타고 이동하는 경우를 생각하여 측정한다. 두 점 A, B 사이에 건물이 있어 A에서 B로 곧바로 가지 못하고 다른 지점(C)을 거쳐서 이동하는 거리로 계산한다.[28]택시 기하학에서 두 점 '''''A(a,b)'''''와 '''''B(c,d)''''' 사이의 거리()는 다음과 같이 나타낸다.
:
실생활에서 두 지점 사이의 거리는 택시 거리로 측정하는 것이 더 현실적이며, 택시 평면 위에서 유클리드 기하학의 내용이 적용되지 않기 때문에 택시 기하학은 비유클리드 기하학에 분류된다. 택시 기하학에서는 삼각형의 합동 공리가 성립하지 않고, 원의 모양이 정사각형으로 나타나는 등 유클리드 기하학과 다른 특징을 보인다.
3. 4. 절대 기하학
유클리드 기하학의 처음 네 공준만을 기반으로 하는 기하학 체계이다. 평행선 공준을 포함하지 않으므로, 유클리드 기하학과 비유클리드 기하학 모두에 적용될 수 있다. 보여이 야노시에 의해 연구되었다.[19] 유클리드의 ''원론''의 처음 28개의 명제는 평행선 공준 또는 그와 동등한 것을 사용할 필요가 없으므로, 절대 기하학에서 모두 참된 명제이다.4. 비유클리드 기하학과 유클리드 기하학의 비교
유클리드 기하학은 평평한 공간(곡률이 0)을 다루는 반면, 비유클리드 기하학은 굽은 공간(곡률이 0이 아닌)을 다룬다. 유클리드의 다섯 번째 공준인 평행선 공준은 플레이페어의 공리와 동치이며, 2차원 평면에서 주어진 직선과 그 위에 있지 않은 점 ''A''에 대해, ''A''를 지나고 주어진 직선과 교차하지 않는 직선은 정확히 하나 존재한다고 말한다. 그러나 쌍곡 기하학에서는 ''A''를 지나고 주어진 직선과 교차하지 않는 직선이 무한히 많고, 타원 기하학에서는 ''A''를 지나는 모든 직선이 주어진 직선과 교차한다.[2]
이러한 기하학적 차이점을 설명하는 또 다른 방법은 2차원 평면에서 세 번째 직선에 모두 수직인 두 개의 직선을 무한히 연장하는 것이다.
- 유클리드 기하학에서, 이 직선들은 서로 일정한 거리를 유지하며 평행선으로 알려져 있다.
- 쌍곡 기하학에서, 이 직선들은 서로 멀어져 공통 수직선과의 교차점으로부터 멀어질수록 거리가 증가하며, 이러한 직선들은 종종 초평행선이라고 불린다.
- 타원 기하학에서, 이 직선들은 서로 수렴하여 교차한다.[2]
조반니 지롤라모 사케리는 1733년에 발표한 자신의 저서에서 예각 가설·직각 가설·둔각 가설이라는 서로 배반되며 어느 하나는 성립하는 듯한 가설을 설정하고, 직각 가설에서 평행선 공준을 이끌어낼 수 있음을 보였다.
| 유클리드 기하학 | 쌍곡 기하학 | 구면 기하학 | |
|---|---|---|---|
| 평행선 | 단 한 개 존재한다. | 수없이 많이 존재한다. | 존재하지 않는다. |
| 삼각형의 세 내각의 합 | 180° 삼각형의 넓이에 관계없이 세 내각의 크기의 합은 일정하다. | 180°보다 작다. 삼각형의 넓이가 넓어질수록 세 내각의 크기의 합은 작아진다. | 180°보다 크다. 삼각형의 넓이가 넓어질수록 세 내각의 크기의 합은 커진다. |
| 측지선 | 직선 길이는 무한대이다. 두 점을 지나는 직선은 단 한 개이다. | 곡선 길이는 무한대이다. 두 점을 지나는 직선은 한 개이다. | 대원 길이가 유한하고 일정하다. 두 점을 지나는 직선은 단 한 개로 한정하지 않는다.(2개 이상) |
니콜라이 이바노비치 로바체프스키는 1829년에 "허(虛)기하학"으로 명명된 쌍곡 기하학의 모델을 제시했고, 보야이 야노시는 1832년에 자신의 저서에서 평행선 공준을 가정한 기하학과 평행선 공준의 부정을 가정한 기하학을 논했다. 베른하르트 리만은 리만 구라고 불리는 타원 기하학의 모델을 구성했다.[4]
5. 비유클리드 기하학의 중요성
비유클리드 기하학은 과학사에서 중요한 패러다임 전환을 가져왔다.[24] 2천 년간 공간을 설명하는 유일한 방법으로 여겨졌던 유클리드 기하학과 달리, 비유클리드 기하학은 인간의 사고를 유클리드 공간 너머로 확장시켰다.
칸트는 산술과 유클리드 기하학이 경험이 아닌 이성에서 비롯되는 선험적이고 보편타당하며 필연적인 관념이라고 주장했다. 그러나 비유클리드 기하학의 등장으로 유클리드 기하학의 관점은 크게 흔들렸고, 칸트의 인식론에 대한 비판이 제기되었다. 로바쳅스키는 인식이 지각을 통해 획득되며, 선천적인 것이 아니라고 주장했다.[13]
아인슈타인은 일반상대성이론에서 우주가 평평하지 않고 중력에 의해 휘어져 있다는 것을 보이며, 비유클리드 기하학을 공간에 대한 기초 이론으로 삼았다. 아인슈타인은 "만일 내가 그 기하학(비유클리드 기하학)을 몰랐다면 나는 결코 상대성 이론을 만들어 낼 수 없었을 것이다."라고 말했다.
비유클리드 기하학의 발견은 수학과 과학뿐만 아니라 철학, 신학, 교육 등 다양한 분야에 영향을 미쳤다.[23][27] 특히 빅토리아 시대 잉글랜드에서는 유클리드 기하학 기반의 교육에 대한 재검토를 촉발하는 주요 요인이 되었다. 루이스 캐럴로 더 잘 알려진 찰스 루트위지 도지슨은 자신의 저서 ''유클리드와 그의 현대 경쟁자들''에서 이 문제를 다루기도 했다.
6. 현대 과학과의 연관성
아인슈타인(Albert Einstein, 1879~1955)은 우주가 평평하지 않고 중력에 의해 휘어 있음을 보였고, 일반 상대성 이론의 공간에 대한 기초 이론을 비유클리드 기하학에서 찾았다.[22] 이처럼 유클리드의 다섯 번째 공리에 관한 의심에서 출발한 비유클리드 기하학은 미시공간과 극대 공간을 해석하는 이론으로 폭넓게 사용되고 있다. 아인슈타인은 "만일 내가 그 기하학(비유클리드 기하학)을 몰랐다면 나는 결코 상대성 이론을 만들어 낼 수 없었을 것이다."라고 언급하며 비유클리드 기하학의 중요성을 강조했다.
쌍곡 기하학은 1908년 헤르만 민코프스키가 도입한 물리 우주론을 통해 운동학에 적용되었다. 민코프스키는 세계선 및 고유 시간과 같은 용어를 수리물리학에 도입했다. 그는 미래의 한 순간 고유 시간을 갖는 부분다양체가 3차원 쌍곡 공간으로 간주될 수 있음을 깨달았다.[30][31]
비유클리드 평면 대수는 평면에서 운동학적 기하학을 지원한다. 예를 들어, 분할 복소수 ''z'' = e''a''j는 속도 ''a''의 기준 틀의 미래의 한 순간의 시공간 사건을 나타낼 수 있다. 또한, ''z''를 곱하는 것은 속도가 0인 틀을 속도가 ''a''인 틀로 매핑하는 로렌츠 부스트에 해당한다.
이중수를 사용하면 고전적인 운동 묘사를 나타낼 수 있는데, 방정식과 선형대수를 통해 표현이 가능하다.[32]
1912년 E. B. 윌슨과 길버트 루이스는 특수 상대성 이론을 비유클리드 기하학으로 보는 또 다른 관점을 제안했다.[33][34]
7. 비유클리드 기하학의 모델
'''비유클리드 기하학의 모델'''은 주어진 선 ''l'' 위에 있지 않은 점을 지날 때 ''l''에 평행선을 그릴 수 없다는 점에서 비유클리드 기하학의 수학적 모형이다. 쌍곡 기하학 모델에서는 ''A''를 지나 ''l''에 평행한 선이 무한히 많으며, 타원 기하학 모델에서는 평행선이 존재하지 않는다.
유클리드 기하학은 "평평한 평면"의 개념으로 모델링된다.
타원 기하학의 가장 간단한 모델은 구이며, 선은 "대원" (예: 적도 또는 자오선)이고 서로 반대편에 있는 점은 동일하게 식별된다. 의사구는 쌍곡 기하학을 모델링하기에 적절한 곡률을 가지고 있다.
쌍곡 모형에서 2차원 평면 내에서 주어진 직선과 그 위에 있지 않은 점 ''A''에 대해, ''A''를 지나고 주어진 직선과 만나지 않는 직선이 무한히 많다.
이러한 모형에서 비유클리드 기하학의 개념은 유클리드 환경에서 유클리드 객체로 표현된다. 이는 비유클리드 기하학의 직선이 시각적으로 굽어 보이는 유클리드 곡선으로 표현되는 지각적 왜곡을 초래한다. 이러한 "굽힘"은 비유클리드 직선의 속성이 아니라, 그것들이 표현되는 방식의 인위적인 결과일 뿐이다.
참조
[1]
간행물
Views of Euclid's Parallel Postulate in Ancient Greece and in Medieval Islam
http://www.math.rutg[...]
Rutgers University
2008-01-23
[2]
인용
"Three scientists, Ibn al-Haytham, Khayyam, and al-Tusi, had made the most considerable contribution to this branch of geometry, whose importance was completely recognized only in the nineteenth century. In essence, their propositions concerning the properties of quadrangle—which they considered assuming that some of the angles of these figures were acute of obtuse—embodied the first few theorems of the hyperbolic and the elliptic geometries. Their other proposals showed that various geometric statements were equivalent to the Euclidean postulate V. It is extremely important that these scholars established the mutual connection between this postulate and the sum of the angles of a triangle and a quadrangle. By their works on the theory of parallel lines Arab mathematicians directly influenced the relevant investigations of their European counterparts. The first European attempt to prove the postulate on parallel lines – made by [[Witelo]], the Polish scientists of the thirteenth century, while revising [[Ibn al-Haytham]]'s ''[[Book of Optics]]'' (''Kitab al-Manazir'') – was undoubtedly prompted by Arabic sources. The proofs put forward in the fourteenth century by the Jewish scholar [[Levi ben Gerson]], who lived in southern France, and by the above-mentioned Alfonso from Spain directly border on Ibn al-Haytham's demonstration. Above, we have demonstrated that ''Pseudo-Tusi's Exposition of Euclid'' had stimulated both J. Wallis's and G. [[Saccheri]]'s studies of the theory of parallel lines."
Routledge
[3]
서적
Geometry
Routledge
[4]
인용
"In ''Pseudo-Tusi's Exposition of Euclid'', [...] another statement is used instead of a postulate. It was independent of the Euclidean postulate V and easy to prove. [...] He essentially revised both the Euclidean system of axioms and postulates and the proofs of many propositions from the ''Elements''."
Routledge
[5]
인용
"But in a manuscript probably written by his son Sadr al-Din in 1298, based on Nasir al-Din's later thoughts on the subject, there is a new argument based on another hypothesis, also equivalent to Euclid's, [...] The importance of this latter work is that it was published in Rome in 1594 and was studied by European geometers. In particular, it became the starting point for the work of Saccheri and ultimately for the discovery of non-Euclidean geometry."
Addison–Wesley
[6]
웹사이트
MacTutor's Giovanni Girolamo Saccheri
http://www-history.m[...]
[7]
웹사이트
Johann Heinrich Lambert
http://www-history.m[...]
2011-09-16
[8]
문서
A Treatise of Human Nature
Oxford University Press
[9]
간행물
Werke
http://gdz.sub.uni-g[...]
B. G. Teubner
[10]
서적
Non-Euclidean geometry: A critical and historical study of its development
https://archive.org/[...]
Open Court
[11]
문서
In the letter to Wolfgang (Farkas) Bolyai of March 6, 1832 Gauss claims to have worked on the problem for thirty or thirty-five years
[12]
문서
However, other axioms besides the parallel postulate must be changed to make this a feasible geometry.
[13]
서적
Elementary Mathematics from an Advanced Standpoint: Geometry
Dover
[14]
서적
Non-Euclidean Geometry
https://archive.org/[...]
Pergamon
[15]
간행물
Über die sogenannte nichteuklidische Geometrie
[16]
문서
The Euclidean plane is still referred to as parabolic in the context of conformal geometry
[17]
문서
for instance
[18]
문서
a 21st axiom appeared in the French translation of Hilbert's Grundlagen der Geometrie
[19]
문서
Harvard citation
[20]
문서
while only two lines are postulated, it is easily shown that there must be an infinite number of such lines.
[21]
문서
Book I Proposition 27 of Euclid's Elements
[22]
서적
Three-dimensional geometry and topology. Vol. 1
Princeton University Press
[23]
간행물
Gott und Geometrie: Eine viktorianische Kontroverse
[24]
문서
see
[25]
서적
Men of Mathematics
Touchstone Books
[26]
인용
"What [[Vesalius]] was to [[Galen]], what [[Copernicus]] was to [[Ptolemy]] that was Lobachevsky to [[Euclid]]."
[27]
문서
Harvard citation
[28]
서적
Complex Numbers in Geometry
Academic Press
[29]
서적
Theory of Relativity of Motion
[30]
문서
Space and Time
[31]
문서
Non-Euclidean Style of Special Relativity
http://www.univ-nanc[...]
[32]
서적
A simple non-Euclidean geometry and its physical basis : an elementary account of Galilean geometry and the Galilean principle of relativity
Springer
[33]
간행물
"The Space-time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics"
[34]
웹사이트
Synthetic Spacetime
https://web.archive.[...]
[35]
웹사이트
The Call of Cthulhu
http://www.hplovecra[...]
[36]
웹사이트
HyperRogue website
http://www.roguetemp[...]
[37]
웹사이트
慶應義塾大学メディアセンターデジタルコレクション
https://dcollections[...]
2021-09-30
[38]
논문
<論考> アラビア語とサンスクリット版ユークリッド『原論』にみる三平方の定理 (経済学部特集号: 本多三郎教授退職記念号)
https://www.i-reposi[...]
2010-07
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com