드루드 모형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 가정
4. 설명
5. 드루드 모형의 응용 및 한계
- 5.1. 응용
- 5.2. 한계
6. 현대적 관점
참조

1. 개요

드루드 모형은 1900년 파울 드루드가 제안한 금속 내 전도 현상을 설명하는 모형이다. 이 모형은 금속을 양이온과 자유 전자로 구성된 것으로 가정하고, 전자의 운동과 충돌을 통해 전기 전도도와 열전도도를 설명한다. 드루드 모형은 옴의 법칙과 비데만-프란츠 법칙을 설명하지만, 전자의 비열 용량을 과대평가하는 등 한계가 있다. 이후 양자역학을 도입한 드루드-조머펠트 모형으로 발전했으며, 현대 고체물리학의 기초가 되었다. 드루드 모형은 금속의 직류 및 교류 전도, 홀 효과, 열전도 현상을 설명하지만, 전자의 띠 구조나 2THz 이상의 주파수에서의 전기 전도도 산란 경향 등은 설명하지 못한다.

더 읽어볼만한 페이지

전류 - 직류
직류(DC)는 전압이나 전류의 크기와 방향이 시간에 따라 변하지 않고 일정한 전력 시스템으로, 전지나 정전기에 의해 발생하며, 초기에는 발전 사업에 사용되었으나 교류에 밀려났다가 고압 직류 송전 기술 개발로 장거리 송전 분야에서 다시 활용된다.
전류 - 누전
누설은 전기 회로 또는 전자 소자에서 의도치 않은 경로로 전류가 흐르거나 에너지가 전달되는 현상으로, 다양한 원인으로 발생하며 전력 소비 증가 및 회로 오작동을 유발할 수 있어 억제 기술 및 안전 기준이 적용된다.
응집물질물리학 - 띠구조
띠구조는 결정 내 전자의 에너지 범위를 나타내는 개념으로, 에너지 띠와 띠틈으로 구성되며, 도체, 절연체, 반도체의 전기적 특성을 결정하는 데 중요한 역할을 한다.
응집물질물리학 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.

드루드 모형
지도
일반 정보
이름	드루드 모형
분야	고체물리학
로마자 표기	Deurude mohyeong
개요
설명	금속의 전기 전도를 설명하는 고전적인 모형이다. 1900년경에 파울 드루데가 제안했다.
기본 가정	금속 내의 전자는 자유롭게 움직인다. 전자들은 원자와의 충돌을 제외하고는 서로 상호작용하지 않는다. 충돌은 순간적으로 일어나고, 충돌 후 전자는 새로운 속도를 갖는다.
주요 개념
전도 전자	금속 내부에서 자유롭게 움직이는 전자
평균 자유 시간	전자가 다음 충돌까지 이동하는 평균 시간 ()
완화 시간	전자의 평균 자유 시간 ()
이동도	전자의 드리프트 속도와 전기장 세기의 비례 상수
수식
장점
설명력	옴의 법칙을 설명한다.
이해 용이성	비교적 단순하여 이해하기 쉽다.
한계
실험 결과 불일치	금속의 비열을 정확하게 예측하지 못한다. 홀 효과의 부호를 정확하게 예측하지 못한다. 온도에 따른 저항의 변화를 정확하게 예측하지 못한다.
양자역학적 효과 무시	전자의 파동성을 고려하지 않는다.
발전 및 수정
발전된 모형	조머펠트 모형, 페르미 액체 이론
관련 인물
제안자	파울 드루데

2. 역사

파울 드루드는 1900년에 드루드 모형을 처음 제안했다.^[14] 1905년 헨드릭 로런츠는 드루드 모형을 보다 정확하게 발전시킨 '''드루드-로렌츠 모형'''을 제안했다. 알베르트 아인슈타인은 1905년에 브라운 운동 이론을 통해 원자의 존재를 증명하였고, 이는 드루드 모형을 포함한 초기 원자 모형 발전에 큰 영향을 미쳤다. J.J. 톰슨은 1897년에 전자를 발견하였고, 드루드는 이를 바탕으로 자신의 모형을 만들었다.^[16] 1933년 한스 베테와 아르놀트 조머펠트는 양자역학을 도입하여 드루드 모형을 확장한 드루드-조머펠트 모형을 제시하였다.^[17]

3. 가정

드루드 모형은 다음과 같은 가정을 기반으로 한다.

드루드 모형은 높은 밀도에도 불구하고 희박 기체의 운동론을 적용했으므로, 충돌을 제외한 전자-전자 및 전자-이온 상호 작용을 무시했다.^[21]
금속이 일정 수의 "자유 전자"가 분리된 양으로 대전된 이온들의 집합으로 형성된다고 간주한다. 이러한 전자들은 다른 원자들의 전기장 때문에 비편재화된 원자들의 원자가 전자라고 생각할 수 있다.^[22]
전자와 이온 사이 또는 전자들 사이의 장거리 상호 작용을 무시한다. 이를 독립 전자 근사라고 한다.^[20]
전자는 한 충돌에서 다른 충돌 사이에 직선으로 움직인다. 이를 자유 전자 근사라고 한다.^[20]
자유 전자와 환경의 유일한 상호 작용은 투과 불가능한 이온 코어와의 충돌로 취급되었다.^[20]
이러한 전자의 후속 충돌 사이의 평균 시간은 τ이며, 무기억 푸아송 분포를 따른다. 전자의 충돌 파트너의 성질은 드루드 모형의 계산과 결론에 중요하지 않다.^[20]
충돌 사건 후, 전자의 속도와 방향의 분포는 국소 온도에 의해서만 결정되며, 충돌 전 전자의 속도와는 무관하다.^[20] 전자는 충돌 후 즉시 국소 온도와 평형 상태에 있는 것으로 간주된다.

4. 설명

드루드 모형은 금속을 양으로 대전된 이온과 거기서 방출된 수많은 "자유 전자"로 구성되어 있다고 가정한다. 이는 원자핵 주변의 전자가 다른 원자들의 영향을 받아 특정 위치에 얽매이지 않고 자유롭게 움직일 수 있게 되는 현상으로 설명할 수 있다.^[2]

드루드 모형에서는 전자와 이온 간의, 또는 전자들 사이의 장거리 상호작용은 무시한다. 자유 전자는 오직 충돌하는 순간에만 주변 환경과 상호작용하며, 다음 충돌까지의 평균 시간은 τ로 표시한다. 이 충돌의 상대가 누구인지는 드루드 모형의 계산 결과에 영향을 주지 않는다.^[2]

전기장 E가 균일하게 가해진 상황에서, 전자는 열운동을 통해 충분한 속도를 가지며, τ 시간마다 충돌하며 운동량 p를 축적한다고 가정한다.^[6]

시간 t에서 전자는 마지막 충돌 이후 평균적으로 τ 시간 동안 운동량을 축적했으므로, 축적된 운동량은 다음과 같다.

: $\Delta\langle\boldsymbol{p}\rangle=q\boldsymbol{E}\tau$

마지막 충돌에서 전자가 튕겨 나가는 방향은 무작위적이므로, 이전 운동량은 무시할 수 있다. 따라서 전자의 평균 운동량은 다음과 같이 표현된다.

: $\langle\boldsymbol{p}\rangle=q\boldsymbol{E}\tau$

이 식과 다음 두 식을 통해 옴의 법칙을 유도할 수 있다.

: $\langle\boldsymbol{p}\rangle=m\langle\boldsymbol{v}\rangle$

: $\boldsymbol{J}=nq\langle\boldsymbol{v}\rangle$

: $\boldsymbol{J}=\left(\frac{nq^2\tau}{m}\right)\boldsymbol{E}$

시간 t_0 + dt 에서 전자의 평균 운동량은 다음과 같이 나타낼 수 있다.

: $\langle\boldsymbol{p}(t_0+\mathrm dt)\rangle=\left(1-\frac{\mathrm dt}{\tau}\right)\left(\langle\boldsymbol{p}(t_0)\rangle+q\boldsymbol{E} \mathrm dt\right)$

이는 평균적으로 1 - dt/τ 만큼의 전자는 아직 충돌하지 않았을 것이고, 이미 충돌한 전자는 총 운동량에 무시할 수 있는 정도의 기여만 하기 때문이다.^[11]

대수적 처리를 거쳐 dt² 차수의 항을 무시하면 다음과 같은 미분 방정식을 얻는다.

: $\frac{\mathrm d}{\mathrm dt}\langle\boldsymbol{p}(t)\rangle=q\boldsymbol{E}-\frac{\langle\boldsymbol{p}(t)\rangle}{\tau}$

여기서 ⟨p⟩는 평균 운동량을 나타낸다. 이 방정식의 일반해는 다음과 같다.

: $\langle\boldsymbol{p}(t)\rangle=q\tau\boldsymbol{E}(1-e^{-t/\tau})+\langle\boldsymbol{p(0)}\rangle e^{-t/\tau}$

따라서, 정상 상태에서(d⟨p⟩/dt = 0)는

: $\langle\boldsymbol{p}\rangle=q\tau\boldsymbol{E}$

평균 운동량은 평균 속도와 관련되며, 이는 다시 전류 밀도와 연결된다.

: $\langle\boldsymbol{p}\rangle=m\langle\boldsymbol{v}\rangle$

: $\boldsymbol{J}=nq\langle\boldsymbol{v}\rangle$

이를 통해, 직류 전기 전도도 σ₀를 만족하는 물질은 다음을 만족함을 알 수 있다.

: $\boldsymbol{J}=\left(\frac{nq^2\tau}{m}\right)\boldsymbol{E}$

드루드 모형은 각진동수 ω로 시간에 따라 변하는 전기장에 대한 반응도 예측할 수 있다.

:

\sigma(\omega)=\frac{\sigma_0}{1+i\omega\tau}=\frac{\sigma_0}{1+\omega^2\tau^2}+i\omega\tau\frac{\sigma_0}{1+\omega^2\tau^2}

여기서 다음 두 가지를 가정한다.

:

E(t)=\Re(E_0e^{i\omega t});

:

J(t)=\Re(\sigma(\omega)E_0e^{i\omega t})

i를 모두 -i로 대체한 식을 사용하는 경우도 있다. 허수부는 전자가 변동하는 전기장에 따라 가속될 때까지 약 τ의 시간이 걸린다는 것에 기인하는 전류의 전기장에 대한 지연을 나타낸다. 드루드 모델은 전자와 정공(반도체 내의 양으로 대전된 전하 운반자) 모두에 적용할 수 있다.

4. 1. 직류 전도

드루드 모형을 가장 간단하게 분석하려면, 우선 전기장

\mathbf{E}

가 균일하고 일정하다고 가정해야 한다. 또한, 전자의 열적 속도는 전자가 이온과의 충돌 사이의 평균 시간인

\tau

(타우) 동안 미소 운동량

d\mathbf{p}

를 축적하기에 충분히 빠르다고 가정한다.^[9]

이때 전자는

\tau

시간 동안 마지막 충돌 이후 운동량을 축적하게 되고, 미소 운동량의 변화량은 다음과 같다.

:

d\langle\mathbf{p}\rangle = q \mathbf{E} \tau.

마지막 충돌에서 이 전자는 앞으로 튕겨 나간 것만큼 뒤로도 튕겨 나갔을 것이므로, 이전의 전자 운동량 기여는 상쇄된다. 따라서 전자의 평균 운동량은 다음과 같이 표현된다.

:

\langle\mathbf{p}\rangle = q \mathbf{E} \tau.

이를 다음 식에 대입하면,

:

\langle\mathbf{p}\rangle = m \langle\mathbf{v}\rangle,

:

\mathbf{J} = n q \langle\mathbf{v}\rangle,

옴의 법칙을 유도할 수 있다.

:

\mathbf{J} = \left( \frac{n q^2 \tau}{m} \right) \mathbf{E}.

여기서,

$\mathbf{J}$ 는 전류 밀도
$n$ 은 전자 밀도
$q$ 는 전자의 전하량
$\tau$ 는 이온과의 충돌 사이의 평균 시간
$m$ 은 전자의 질량
$\mathbf{E}$ 는 전기장
$\langle\mathbf{p}\rangle$ 는 전자의 평균 운동량
$\langle\mathbf{v}\rangle$ 는 전자의 평균 속도

4. 2. 교류 전도

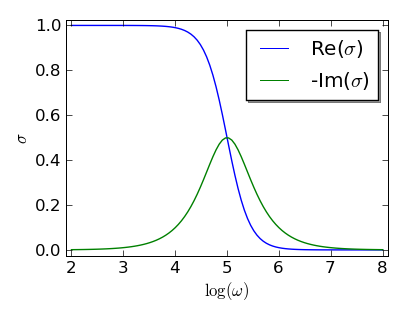
드루드 모형은 시간에 따라 변하는 전기장에 대한 전자의 응답을 예측할 수 있다. 각 주파수 ω를 갖는 시간 의존 전기장에 대한 복소 전도도는 다음과 같이 표현된다.^[26]

:

\sigma(\omega) = \frac{\sigma_0}{1 - i\omega\tau}= \frac{\sigma_0}{1 + \omega^2\tau^2}+ i\omega\tau\frac{\sigma_0}{1 + \omega^2\tau^2}.

여기서 σ₀는 직류 전도도, τ는 충돌 시간, ω는 각주파수이다.

위 식에서 허수 부분은 전류가 전기장보다 위상이 뒤처짐을 나타낸다. 이는 전자가 전기장의 변화에 따라 가속되는 데 약 τ 시간이 걸리기 때문이다. 드루드 모형은 전자뿐만 아니라 반도체 내의 양전하 운반자인 정공에도 적용될 수 있다.^[29]

4. 3. 분산

절연체 내에서 전자는 분자에 속박되어 용수철처럼 진동하는 것으로 가정한다. 외부 전기장에 의한 전자의 변위와 쌍극자 모멘트를 계산하고, 이를 통해 유전율 ε과 굴절률 n을 진동수 ω의 함수로 유도한다.

전자가 받는 전기장을

:

\vec{E} = E_{0}\hat{y}e^{i(kx-\omega t)}

라고 할 때, 전자의 위치에 대한 방정식은 다음과 같다.

:

\ddot{y} = -\sigma \dot{y} - \omega_0 ^2 y +

여기서

\omega_0 ^2 = k/m

는 고유진동수이다.

이 방정식을 풀면 y의 값은 다음과 같다.

:

y_0 = E_0

이에 따라 쌍극자 모멘트는 다음과 같이 주어진다.

:

P = qy_0 = E

일반적인 원자 내 전자에 대해 공식을 적용하면 다음과 같다.

:

P = \Sigma g_j{1\over{(\omega_j^2 - \omega^2)-ir_j\omega)}}E_0, \Sigma g_j = Z

여기서 N은 단위 부피당 분자의 개수, Z는 분자당 전자의 개수,

g_j

는 진동수

\omega_j

를 가지는 분자당 전자의 개수,

\sigma_j

는 '''감쇠 인자'''(damping factor^영어)이다.

전기장

\vec{D} = \varepsilon_0\vec{E}+\vec{P} = \varepsilon\vec{E}

이므로, 유전율

\varepsilon

은 다음과 같다.

:

\varepsilon=\varepsilon_{0}[1+\frac{Nq^{2}}{m\varepsilon_{0}}\sum\frac{f_{j}}{(\omega_{j}^{2}-\omega^{2})-i\gamma_{j}\omega}]

일반적으로 ε의 두 번째 항이 작으므로 다음과 같이 근사할 수 있다.

:

k\cong\frac{\omega}{c}[1+\frac{Nq^{2}}{2m\varepsilon_{0}}\sum\frac{f_{j}}{(\omega_{j}^{2}-\omega^{2})-i\gamma_{j}\omega}]

따라서 굴절률은 다음과 같다.

:

n\cong[1+\frac{Nq^{2}}{2m\varepsilon_{0}}\sum\frac{f_{j}(\omega_{j}^{2}-\omega^{2})}{(\omega_{j}^{2}-\omega^{2})^{2}+\gamma_{j}\omega}]

위 식에서 진동수가 공명 진동수 근처가 되면 굴절률이 증가하였다 감소하는데, 일반적으로 잘 일어나지 않는다. 진동수가 공명 진동수와 유사할 때를 제외하면, 진동수가 커질 때 굴절률이 감소한다. 진동수가 무한으로 커진다면 굴절률은 1에 수렴한다.

시간 에서 평균 전자의 운동량은 다음과 같다.

:

\langle\mathbf{p}(t_0+dt)\rangle=\left( 1 - \frac{dt}{\tau} \right) \left(\langle\mathbf{p}(t_0)\rangle + q\mathbf{E} \, dt\right),

:

\frac{d}{dt}\langle\mathbf{p}(t)\rangle = q\mathbf{E} - \frac{\langle\mathbf{p}(t)\rangle}{\tau},

정상 상태 해는 다음과 같다.

:

\langle\mathbf{p}\rangle = q \tau \mathbf{E}.

평균 운동량, 평균 속도, 전류 밀도의 관계는 다음과 같다.

:

\begin{align}\langle\mathbf{p}\rangle &= m \langle\mathbf{v}\rangle, \\\mathbf{J} &= n q \langle\mathbf{v}\rangle,\end{align}

DC 전도도를 갖는 옴의 법칙은 다음과 같다.

:

\sigma_0 = \frac{n q^2 \tau}{m}

복소 전도도는 다음과 같다.

:

\sigma(\omega) = \frac{\sigma_0}{1 - i\omega\tau}= \frac{\sigma_0}{1 + \omega^2\tau^2}+ i\omega\tau\frac{\sigma_0}{1 + \omega^2\tau^2}.

전류가 전기장보다 뒤쳐지는 이유는 전자가 전기장의 변화에 대한 응답으로 가속되는 데 약 τ 시간이 필요하기 때문이다.

주파수 ω를 갖는 정현파적으로 변하는 전기장이 가해지면, 시료가 분극되고 반대 표면에 과잉 전하가 생긴다. 시료의 유전율은 다음과 같다.

:

\varepsilon = \frac {D}{\varepsilon_0 E} = 1 + \frac {P}{\varepsilon_0 E}

여기서 D는 전기 변위이고 P는 분극 밀도이다. 분극 밀도는 다음과 같이 쓸 수 있다.

:

P(t) = \Re{\left(P_0e^{i\omega t}\right)}

:

P = - n e x

분극 밀도와 전기장 사이의 관계는 다음과 같다.

:

P = - \frac{ne^2}{m\omega^2} E

고체의 주파수 의존 유전 함수는 다음과 같다.

:

\varepsilon(\omega) = 1 - \frac {n e^2}{\varepsilon_0m \omega^2}

'''플라스마 주파수'''라고 하는 공명 주파수 ω_p에서 유전 함수는 음수에서 양수로 부호가 바뀌고 유전 함수의 실수 부분은 0으로 떨어진다.

:

\omega_{\rm p} = \sqrt{\frac{n e^2}{\varepsilon_0 m}}

플라스마 주파수는 플라스마 진동 공명 또는 플라스몬을 나타내며, 고체 내 원자가 전자 밀도의 제곱근을 직접 측정하는 데 사용될 수 있다.^[28] 플라스마 주파수 이하에서는 장이 시료에 침투할 수 없고, 빛은 완전히 반사된다. 플라스마 주파수 이상에서는 빛파가 시료에 침투할 수 있다.^[29]

5. 드루드 모형의 응용 및 한계

고전적인 드루드 모형은 금속의 직류 및 교류 전도, 홀 효과, 실온에서 전자에 의한 열전도를 설명하는 데 유용하다.^[30]

5. 1. 응용

드루드 모형은 금속의 직류 및 교류 전도, 홀 효과, 그리고 실온에서 전자에 의한 열전도를 잘 설명한다.^[30] 특히, 드루드 모형은 비데만-프란츠 법칙을 설명하는 데 성공했는데, 이는 드루드의 원래 계산에서 우연히 오류가 상쇄된 결과였다.^[30] 드루드는 로렌츠 수(

\frac{\kappa}{\sigma T}

)를 다음과 같이 예측했다.

\frac {\kappa}{\sigma T} = \frac{3}{2}\left(\frac{k_{\rm B}}{e}\right)^2 = 1.11 \times 10^{-8} \, \mathrm{W{\cdot}\Omega/K^2}

실험값은 0~100℃ 사이의 금속에서

2-3 \times 10^{-8} ~ \mathrm{W{\cdot}\Omega/K^2}

범위로, 예측값과 유사하다.^[30]

드루드는 전도 전자의 비열 용량(

c_v = \tfrac{3}{2}nk_{\rm B}

)을 실제보다 100배 크게, 전자의 평균 제곱 속도(

\tfrac{1}{2}mv^2 = \tfrac{3}{2}k_{\rm B}T

)를 100배 작게 가정하는 오류를 범했다. 이 두 오류가 상쇄되어 로렌츠 수 예측값이 실험값과 비슷하게 나오는 결과를 낳았다.^[31]

드루드 모형은 열전력(thermo power)도 예측할 수 있다. 열전력(

Q

)은 열전장(

\mathbf{E} = Q \nabla T

)을 발생시키는 원인으로, 드루드 모형의 예측치는 다음과 같다.

Q = - \frac{c_v}{3ne} = - \frac{k_{\rm B}}{2e} = 0.43 \times 10^{-4} \mathrm{~V/K}

하지만 실제 금속의 열전력은 상온에서 마이크로볼트(μV/K) 정도로, 드루드 모형의 예측치보다 100배 정도 작다.^[33] 이는 드루드 모형에서 비열을 과대평가했기 때문이다.^[33]

5. 2. 한계

드루드 모형은 고전적인 모형으로, 전자의 양자역학적 성질을 고려하지 않기 때문에 다음과 같은 한계를 갖는다.

전자의 비열을 실제보다 훨씬 크게 예측한다.
실제 금속의 띠 구조에 의한 효과를 설명하지 못한다.^[36]^[37]
대략 2 THz 이상의 주파수에 대한 전기 전도도의 산란 경향을 설명하지 못한다.^[36]^[37]

6. 현대적 관점

드루드 모형은 금속의 직류 및 교류 전도, 홀 효과, 그리고 실온에서 전자에 의한 열전도 등을 잘 설명한다.^[14] 그러나 금속 내 전자의 열용량은 크게 과대평가하는데, 실제로 금속과 부도체는 상온에서 거의 같은 열용량을 갖는다.^[15]

오늘날 드루드 모형과 조머펠트 모형은 고체의 정성적 거동을 이해하고 특정 실험 설정에 대한 첫 번째 정성적 이해를 얻는 데 여전히 중요하다.^[18] 고체 물리학에서는 더 정확한 예측을 위해 모델의 복잡성을 점진적으로 높이는 방법을 일반적으로 사용한다. 수많은 입자와 상호 작용으로 인한 복잡성 때문에 처음부터 완전한 양자장 이론을 사용하는 것은 덜 일반적이다.^[19]

일반적인 단순 금속(예: 상온의 나트륨, 은, 금)에서는 띠 구조 등 드루드 모형에서 고려되지 않은 다른 특징들이 중요하여, 실험에서 드루드 모형의 예측과 일치하는 거동을 관찰하기 어렵다.^[36] 그러나 도핑된 반도체 단결정,^[38] 고이동도 이차원 전자 기체,^[39] 강상관 전자계 금속^[40]의 경우에는 드루드 모형이 잘 들어맞는다.^[36]

역사적으로 드루드 모형은 전하 운반체를 이상 기체로 간주하는 잘못된 가정에서 유도되었다. 현재는 전하 운반체가 페르미 분포를 따르며 무시할 수 없는 상호 작용을 갖는다는 것이 알려져 있지만, 1957년 란다우의 연구를 통해 금속 내 전도 전자에 드루드 모형이 유효하다는 것이 밝혀졌다.

참조

_[1] 논문 Zur Elektronentheorie der Metalle 2019-02-00 #dead link date
_[2] 논문 Zur Elektronentheorie der Metalle; II. Teil. Galvanomagnetische und thermomagnetische Effecte http://www3.intersci[...] 2019-02-00 #dead link date
_[3] 서적 Free electrons in solid springer
_[4] 서적
_[5] 서적
_[6] 서적
_[7] 서적
_[8] 서적
_[9] 서적
_[10] 서적 Electricity and Magnetism https://archive.org/[...] McGraw-Hill
_[11] 서적 Introduction to Electrodynamics https://archive.org/[...] Prentice-Hall
_[12] 논문
_[13] 논문
_[14] 웹사이트 Niels bohr Nobel Lecture https://www.nobelpri[...]
_[15] 논문
_[16] 논문
_[17] 학술지 The motion of electrons in metallic bodies I https://dwc.knaw.nl/[...] 1905
_[18] 논문
_[19] Youtube Solid State Physics, Lec ture 3: Drude Theory and Sommerfeld Free Electron https://www.youtube.[...]
_[20] 논문
_[21] 논문
_[22] 논문
_[23] 논문 Quantum Theory of the Monatomic Ideal Gas
_[24] 웹사이트 Solid State Physics, Lecture17: Dynamics of Electrons in Bands https://www.youtube.[...]
_[25] 논문
_[26] 논문
_[27] 논문
_[28] 서적 Introduction to Solid State Physics Wiley & Sons
_[29] 논문
_[30] 논문
_[31] 서적
_[32] 서적
_[33] 서적
_[34] 서적
_[35] 서적
_[36] 논문 Verifying the Drude response
_[37] 논문 Electrical characterization of conducting polypyrrole by THz time-domain spectroscopy http://dx.doi.org/10[...] 2000-10-16
_[38] 논문 Carrier dynamics of electrons and holes in moderately doped silicon https://shareok.org/[...]
_[39] 논문 High frequency conductivity of the high-mobility two-dimensional electron gas https://authors.libr[...]
_[40] 논문 Extremely slow Drude relaxation of correlated electrons
_[41] 설명
_[42] 설명

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com