분수계 미적분학

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사적 배경
3. 분수 계 적분
4. 분수 계 도함수
5. 분수 미적분학의 성질
6. 응용 분야
참조

1. 개요

분수 미적분학은 미분과 적분 연산자를 정수 차수가 아닌 실수 또는 복소수 차수로 일반화한 수학 분야이다. 1695년 라이프니츠의 편지에서 처음 개념이 제시되었으며, 리우빌, 아벨, 헤비사이드 등의 연구를 거쳐 발전했다. 분수 계 적분과 도함수를 정의하며, 리만-리우빌, 카푸토, 아타나나-발레아누 등 다양한 분수 계 도함수 정의가 존재한다. 분수 미적분학은 반군 성질을 가지며, 비국소적 성질을 나타낸다. 응용 분야는 질량 보존, 전기화학 분석, 지하수 흐름, 분수 이류 분산 방정식, 구조 감쇠 모델, PID 제어기, 음향파 방정식, 분수 슈뢰딩거 방정식 등 매우 다양하다.

더 읽어볼만한 페이지

일반화 - 해석적 연속
해석적 연속은 복소해석학에서 정칙함수 $f$의 정의역을 확장하여 더 큰 영역에서 $f$와 일치하는 정칙함수 $F$를 찾는 방법으로, 항등정리에 의해 유일성이 보장되지만 모든 함수가 가능한 것은 아니며, 유리형 함수는 로랑 급수로 정의될 수 있다.
일반화 - 약도함수
약도함수는 리만 다양체 위에서 정의되며, 함수와 벡터장의 적분 형태로 표현되고 일반적인 도함수를 확장한 개념으로, 편미분 방정식 및 함수 해석학에 활용된다.
미적분학 - 미분방정식
미분방정식은 미지 함수와 도함수 사이의 관계를 나타내는 방정식으로, 상미분방정식과 편미분방정식으로 나뉘며, 물리학, 공학 등 다양한 분야에서 자연 현상과 시스템을 모델링하는 데 사용되고 해석적, 수치적 해법으로 해를 구하며, 소프트웨어를 활용해 분석한다.
미적분학 - 회전 (벡터)
회전(벡터)은 벡터장의 국소적인 회전 정도를 나타내는 벡터량으로, 벡터장을 선적분한 값과 폐곡선이 둘러싸는 면적의 비의 극한으로 정의되며, 물리적 현상 기술에 중요한 역할을 한다.

분수계 미적분학

2. 역사적 배경

분수 미적분학의 개념은 1695년 고트프리트 빌헬름 라이프니츠가 기욤 드 로피탈에게 보낸 편지에서 처음 등장했다.^[3] 라이프니츠는 베르누이 형제 중 한 명에게 이항 정리가 두 함수의 곱의 분수 계 도함수에 대한 라이프니츠 규칙과 유사하다는 점을 설명하는 편지를 쓰기도 했다.

닐스 헨리크 아벨은 분수 차수 적분 및 미분 개념, 이들 간의 상호 역관계, 분수 차수 미분 및 적분을 동일한 일반화된 연산으로 간주할 수 있다는 이해, 임의의 실수 차수의 미분 및 적분을 위한 통일된 표기법을 제시하여 분수 미적분학의 초기 연구를 수행했다.^[4]^[5] 1832년 리우빌은 분수 미적분학의 기초를 마련하는 논문을 발표했다.^[6]^[7]^[8] 1890년경 올리버 헤비사이드는 전기 전송선 분석에 분수 미분 연산자를 실용적으로 사용했다.^[9] 19세기와 20세기에 걸쳐 분수 미적분학의 이론과 응용이 크게 확장되었으며, 다양한 분수 계 도함수와 적분에 대한 정의가 제시되었다.^[10]

3. 분수 계 적분

분수 계 적분은 정적분을 정수가 아닌 차수로 일반화한 것이다.

자크 아다마르가 도입한 분수 계 적분은 다음 공식으로 주어진다.^[77]

: $_a\mathbf{D}_t^{-\alpha} f(t) = \frac{1}{\Gamma(\alpha)}\int_a^t \left(\log\frac{t}{\tau}\right)^{\alpha -1} f(\tau)\frac{d\tau}{\tau}, \qquad t > a.$

Atangana–Baleanu fractional integral^영어 (AB 분수 계 적분)은 연속 함수에 대해 다음과 같이 정의된다.^[1]

: $\sideset{_{\hphantom{A}a}^\operatorname{AB}}{_t^\alpha}I f(t)=\frac{1-\alpha}{\operatorname{AB}(\alpha)}f(t)+\frac{\alpha}{\operatorname{AB}(\alpha)\Gamma(\alpha)}\int_a^t \left(t-\tau\right)^{\alpha-1} f(\tau) \, d\tau$

3. 1. 반복 적분을 위한 코시 공식

함수 f(x)가 x > 0에 대해 정의되어 있다고 가정할 때, 0에서 x까지의 정적분을 반복하면 다음과 같이 나타낼 수 있다.

\begin{align}\left( J^2 f \right) (x) &= \int_0^x (Jf)(t) \,dt \\&= \int_0^x \left(\int_0^t f(s) \,ds \right) dt \,,\end{align}

이는 임의로 확장 가능하다.

반복 적분을 위한 코시 공식은 다음과 같다.

\left(J^n f\right) ( x ) = \frac{1}{ (n-1) ! } \int_0^x \left(x-t\right)^{n-1} f(t) \, dt \,,

이는 실수 n에 대한 일반화로 이어진다. 감마 함수를 사용하여 팩토리얼 함수의 이산성을 제거하면 분수 적분 연산자를 다음과 같이 적용할 수 있다.

\left(J^\alpha f\right) ( x ) = \frac{1}{ \Gamma ( \alpha ) } \int_0^x \left(x-t\right)^{\alpha-1} f(t) \, dt \,.

J 연산자는 다음을 만족한다.

\begin{align}\left(J^\alpha\right) \left(J^\beta f\right)(x) &= \left(J^\beta\right) \left(J^\alpha f\right)(x) \\&= \left(J^{\alpha+\beta} f\right)(x) \\&= \frac{1}{ \Gamma ( \alpha + \beta) } \int_0^x \left(x-t\right)^{\alpha+\beta-1} f(t) \, dt \,.\end{align}

3. 2. 리만-리우빌 분수 계 적분

함수 f(x)가 x > 0 에 대해 정의되어 있다고 가정한다. 0에서 x까지의 정적분을 구성하면 다음과 같다.

( J f ) ( x ) = \int_0^x f(t) \, dt \,.

이 과정을 반복하면 다음과 같다.

\begin{align}\left( J^2 f \right) (x) &= \int_0^x (Jf)(t) \,dt \\&= \int_0^x \left(\int_0^t f(s) \,ds \right) dt \,,\end{align}

이는 임의로 확장될 수 있다.

반복 적분을 위한 코시 공식은 다음과 같다.

\left(J^n f\right) ( x ) = \frac{1}{ (n-1) ! } \int_0^x \left(x-t\right)^{n-1} f(t) \, dt \,,

이것은 실수 α에 대한 일반화로 직접 이어진다. 감마 함수를 사용하여 팩토리얼 함수의 이산성을 제거하면 분수 적분 연산자를 다음과 같이 적용할 수 있다.

\left(J^\alpha f\right) ( x ) = \frac{1}{ \Gamma ( \alpha ) } \int_0^x \left(x-t\right)^{\alpha-1} f(t) \, dt \,.

이는 잘 정의된 연산자이다.

J 연산자가 다음을 만족한다는 것을 보일 수 있다.

\begin{align}\left(J^\alpha\right) \left(J^\beta f\right)(x) &= \left(J^\beta\right) \left(J^\alpha f\right)(x) \\&= \left(J^{\alpha+\beta} f\right)(x) \\&= \frac{1}{ \Gamma ( \alpha + \beta) } \int_0^x \left(x-t\right)^{\alpha+\beta-1} f(t) \, dt \,.\end{align}

이 관계는 분수 미분적분학 연산자의 반군 속성이라고 한다. 분수 미적분학의 고전적인 형태는 리만-리우빌 적분으로, 위에서 설명한 내용과 같다. 구간 [a, b]를 고려하면, 적분은 다음과 같이 정의된다.

\begin{align}\sideset{_a}{_t^{-\alpha}}D f(t) &= \sideset{_a}{_t^\alpha}I f(t) \\&=\frac{1}{\Gamma(\alpha)}\int_a^t \left(t-\tau\right)^{\alpha-1} f(\tau) \, d\tau \\\sideset{_t}{_b^{-\alpha}}D f(t) &= \sideset{_t}{_b^\alpha}I f(t) \\&=\frac{1}{\Gamma(\alpha)}\int_t^b \left(\tau-t\right)^{\alpha-1} f(\tau) \, d\tau\end{align}

여기서 전자는 t > a에 유효하고 후자는 t < b에 유효하다.^[11]

양의 실수 축에서의 적분(즉, a = 0)은 아벨-리만 적분, 전체 실수선에서의 적분은 리우빌-바일 적분으로 부른다.^[61]

3. 3. 아다마르 분수 계 적분

자크 아다마르가 도입한 분수 계 적분은 다음 공식으로 주어진다.^[77]

:

_a\mathbf{D}_t^{-\alpha} f(t) = \frac{1}{\Gamma(\alpha)}\int_a^t \left(\log\frac{t}{\tau}\right)^{\alpha -1} f(\tau)\frac{d\tau}{\tau}, \qquad t > a.

3. 4. 아탕가나-발레아누 분수 계 적분 (AB 분수 계 적분)

Atangana–Baleanu fractional integral^영어 (AB 분수 계 적분)은 연속 함수에 대해 다음과 같이 정의된다.^[1]

:

\sideset{_{\hphantom{A}a}^\operatorname{AB}}{_t^\alpha}I f(t)=\frac{1-\alpha}{\operatorname{AB}(\alpha)}f(t)+\frac{\alpha}{\operatorname{AB}(\alpha)\Gamma(\alpha)}\int_a^t \left(t-\tau\right)^{\alpha-1} f(\tau) \, d\tau

4. 분수 계 도함수

분수 계 도함수는 미분 연산자를 정수가 아닌 차수로 일반화한 것이다.

고전적인 뉴턴 미분과 달리 분수 미분은 부드러운 함수조차도 항상 동일한 결과를 얻지 못하는 다양한 방식으로 정의될 수 있다. 이 중 일부는 분수 적분을 통해 정의된다. 정의가 서로 호환되지 않기 때문에 어떤 정의가 사용되는지 명시적으로 언급해야 하는 경우가 많다.^[13]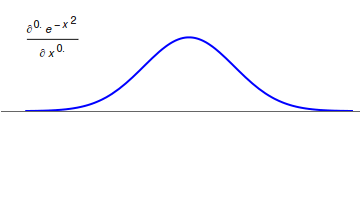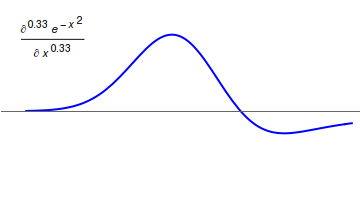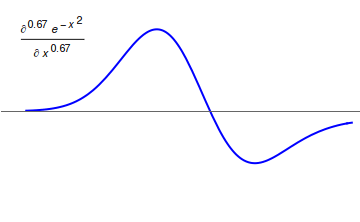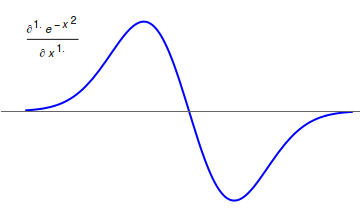

가우스 함수의 분수 미분, 함수와 첫 번째 도함수 사이를 연속적으로 보간한다.

이러한 이론은 1832년부터 리우빌의 논문에서 그 기초를 찾아볼 수 있다.^[74]^[75] 함수의 차수의 분수 계 미분은 오늘날에는 종종 푸리에 변환 또는 멜린 변환과 같은 적분 변환을 통해 정의된다.

'''반미분''' (half-derivative^영어)은 다음을 만족하는 연산자 로 정의할 수 있다.

:

H^2 f(x) = Df(x) = \frac{d}{dx} f(x) = f'(x)

이러한 연산자는 실제로 존재한다. 임의의 실수값 > 0에 대해 다음을 만족하는 연산자 가 존재한다.

:

(P^{a}f)(x) = Df(x) = \frac{d}{dx} f(x) = f'(x)

즉, -계 미분 의 을 임의의 실수값으로 확장할 수 있다.

좀 더 자세히 설명하면, 계승을 비정수값으로 확장한 감마 함수 Γ에서 시작한다. 감마 함수는 다음을 만족한다.

:

n! = \Gamma(n+1)

> 0에서 함수 ()가 모순 없이 정의되고, 0부터 까지의 정적분은 다음과 같다.

:

(Jf)(x) = {d ^{-1} \over dx^{-1}}f(x) = \int_0^x f(t) \; dt

.

이를 반복하면 다음과 같다.

:

(J^2 f)(x) = {d ^{-2} \over dx^{-2}}f(x) = \int_0^x (Jf)(t)\;dt = \int_0^x \left(\int_0^t f(s)\; ds\right)dt

반복 적분에 관한 코시 공식에 따라 임의의 자연수 거듭제곱 로 확장할 수 있다.

:

(J^n f)(x) = {d ^{-n} \over dx^{-n}}f(x) = {1 \over (n-1)!} \int_0^x (x-t)^{n-1} f(t) \; dt

계승 함수 대신 감마 함수로 대체하면 (Γ( + 1) = ! 또는 Γ() = ( − 1)!) 다음과 같다.

:

(J^n f)(x) = {d ^{-n} \over dx^{-n}}f(x) = {1 \over \Gamma(n)} \int_0^x (x-t)^{n-1} f(t) \; dt

이를 통해 이 실수뿐만 아니라 복소수인 경우까지 일반화할 수 있다. 즉, 감마 함수를 복소수 범위까지 확장하여 적분 연산자를 "분수(음의 정수를 제외한 복소수) 차수를 적용하는" 연산자로 정의할 수 있다.

:

(J^\alpha f)(x) = {d ^{-\alpha} \over dx^{-\alpha}}f(x) = {1 \over \Gamma(\alpha)} \int_0^x (x-t)^{\alpha-1}f(t) \; dt

이는 실제로 연산자로서 모순 없이 정의된다.

연산자 는 가환적이고 가법적이다.

:

(J^\alpha) (J^\beta) f = (J^\beta) (J^\alpha) f = (J^{\alpha+\beta} ) f = { 1 \over \Gamma ( \alpha + \beta) } \int_0^x (x-t)^{\alpha+\beta-1} f(t) \; dt

함수 ()가 다음과 같은 단항식일 때,

:

f(x) = x^k

1계 도함수는 다음과 같다.

:

f'(x) = \frac{d}{dx} f(x) = k x^{k-1}

2계 도함수는 다음과 같다.

:

f''(x) = \frac{d^2}{dx^2} f(x) = k(k-1) x^{k-2}

미분을 반복하면 일반적으로 다음을 얻는다.

:

f^{(a)}(x) = \frac{d^a}{dx^a} x^k = { _kP_a } x^{k-a} = \frac{k!}{(k - a)!} x^{k-a}

계승을 감마 함수로 대체하면 다음과 같다.

:

\frac{d^a}{dx^a} x^k = \frac{k!}{(k - a)!} x^{k-a} = \frac{\Gamma(k+1)}{\Gamma(k-a+1)} x^{k-a}

예를 들어 의 반미분 (이분 일계 도함수)은 다음과 같다.

:

\frac{d^{1/2}}{dx^{1/2}}x = \frac{\Gamma(1 + 1)}{\Gamma (1-1/2+1)}x^{1-1/2} = \frac{\Gamma(2)}{\Gamma(3/2)} x^{1/2} = \frac{2}{\pi^{1/2}}x^{-1/2} = 2 \pi^{-1/2} x^{1/2} = 2 \sqrt{\frac{x}{\pi}}

이것을 한 번 더 수행하면 다음을 얻는다.

:

\frac{d^{1/2}}{dx^{1/2}} \frac{2 }{ \pi^{1/2} }x^{1/2} = \frac{2 }{ \pi^{1/2} } \frac{\Gamma(1/2+1)}{\Gamma(1/2 - 1/2 + 1)} x^{1/2 - 1/2} = \frac{2 }{ \pi^{1/2} } \frac{\Gamma(3/2)}{\Gamma(1)} x^0 = \frac{2 }{ \pi^{1/2} } \frac{\frac{\pi^{1/2}}2}1  = 1

이는 다음 성질이 만족됨을 의미한다.

:

\left( \frac{d^{1/2}}{dx^{1/2}} \frac{d^{1/2}}{dx^{1/2}} \right) x = { d \over dx } x = 1

4. 1. 리만-리우빌 분수 계 도함수

해당 도함수는 미분 연산자에 대한 라그랑주 규칙을 사용하여 계산된다.^[14]^[15] α 차 도함수를 구하기 위해, n이 α 보다 큰 가장 작은 정수(즉, n = ⌈α⌉)일 때, (n - α) 차 적분의 n차 도함수가 계산된다. 리만-리우빌 분수 도함수와 적분은 토카막 시스템과 같은 다중 시스템, 가변 차수 분수 매개변수와 같은 경우의 방정식 해와 같은 여러 응용 분야를 가지고 있다.^[14]^[15] 리만-리우빌 적분 정의와 유사하게, 도함수에는 상한 및 하한 변형이 있다.^[16]

:

\begin{align}\sideset{_a}{_t^\alpha}D f(t) &= \frac{d^n}{dt^n} \sideset{_a}{_t^{-(n-\alpha)}}Df(t) \\&= \frac{d^n}{dt^n} \sideset{_a}{_t^{n-\alpha}}I f(t) \\\sideset{_t}{_b^\alpha}D f(t) &= \frac{d^n}{dt^n} \sideset{_t}{_b^{-(n-\alpha)}}Df(t) \\&= \frac{d^n}{dt^n} \sideset{_t}{_b^{n-\alpha}}I f(t)\end{align}

4. 2. 카푸토 분수 계 도함수

미켈레 카푸토가 1967년 자신의 논문에서 소개한 분수 계 도함수이다.^[17] 카푸토 분수 미분은 다음과 같이 정의된다. 여기서 이다.

:

\sideset{^C}{_t^\alpha}D f(t)=\frac{1}{\Gamma(n-\alpha)} \int_0^t \frac{f^{(n)}(\tau)}{\left(t-\tau\right)^{\alpha+1-n}}\, d\tau.

가 상수일 때 0이 되고, 라플라스 변환이 함수와 그 도함수의 초기값을 통해 표현된다는 장점이 있다.

분포 차수의 카푸토 분수 미분은 다음과 같이 정의된다.

:

\begin{align}\sideset{_a^b}{^nu}Df(t) &= \int_a^b \phi(\nu)\left[D^{(\nu)}f(t)\right]\,d\nu \\&= \int_a^b\left[\frac{\phi(\nu)}{\Gamma(1-\nu)}\int_0^t \left(t-u\right)^{-\nu}f'(u)\,du \right]\,d\nu\end{align}

여기서 는 가중 함수이며, 다중 메모리 형식의 존재를 수학적으로 나타내는 데 사용된다.

리우빌-분수 미분과 달리, 카푸토의 정의를 사용하여 미분 방정식을 풀 때는 분수 차수의 초기 조건을 정의할 필요가 없다.

4. 3. 카푸토-파브리치오 분수 계 도함수

2015년 논문에서 M. 카푸토(M. Caputo)와 M. 파브리치오(M. Fabrizio)는 derivative 함수

f(t)

에 대해 특이점이 없는 커널을 갖는 분수 도함수를 다음과 같이 정의했다.^[18]

:

\sideset{_{\hphantom{C}a}^\text{CF}}{_t^\alpha}Df(t)=\frac{1}{1-\alpha} \int_a^t f'(\tau) \ e^\left(-\alpha\frac{t-\tau}{1-\alpha}\right) \ d\tau,

여기서

a < 0, \alpha \in (0,1]

이다.

4. 4. 아탕가나-발레아누 분수 계 도함수

2016년, 아타나나와 발레아누는 일반화된 미타그-레플러 함수

E_{\alpha}

를 기반으로 한 미분 연산자를 제안했다. 이는 비특이 비국소 커널을 가진 분수 미분 연산자를 도입하기 위한 것이었다.^[29]^[19]

C^1

의 함수

f(t)

에 대해, 리만-리우빌 의미와 카푸토 의미에서의 아타나나-발레아누 분수 미분 연산자는 각각 다음과 같이 주어진다.

\sideset{_{\hphantom{AB}a}^{\text{ABC}}}{_t^\alpha}D f(t)=\frac{\operatorname{AB}(\alpha)}{1-\alpha} \int_a^t f'(\tau)E_{\alpha}\left(-\alpha\frac{(t-\tau)^{\alpha}}{1-\alpha}\right)d\tau,

함수가 연속적일 경우, 리만-리우빌 의미에서의 아타나나-발레아누 도함수는 다음과 같다.

\sideset{_{\hphantom{AB}a}^{\text{ABC}}}{_t^\alpha}D f(t)=\frac{\operatorname{AB}(\alpha)}{1-\alpha} \frac{d}{dt}\int_a^t f(\tau)E_{\alpha}\left(-\alpha\frac{(t-\tau)^{\alpha}}{1-\alpha}\right)d\tau,

아타나나-발레아누 분수 도함수에서 사용되는 커널은 누적 분포 함수의 몇 가지 속성을 가지고 있다. 예를 들어, 모든

\alpha \in (0, 1]

에 대해, 함수

E_\alpha

는 실수선에서 증가하고,

- \infty

에서 0으로 수렴하며,

E_\alpha (0) = 1

이다. 따라서 함수

x \mapsto 1-E_\alpha (-x^\alpha)

는 양의 실수에 대한 확률 측도의 누적 분포 함수이다. 따라서 분포가 정의되고, 이의 모든 배수는 차수

\alpha

의 미타그-레플러 분포라고 한다. 또한, 이러한 모든 확률 분포는 절대 연속이라는 것이 잘 알려져 있다. 특히, 함수 미타그-레플러는 지수 함수인

E_1

을 갖는 특정 경우이므로, 차수

1

의 미타그-레플러 분포는 지수 분포이다. 그러나

\alpha \in (0, 1)

에 대해, 미타그-레플러 분포는 헤비테일이다. 그들의 라플라스 변환은 다음과 같이 주어진다.

\mathbb{E} (e^{- \lambda X_\alpha}) = \frac{1}{1+\lambda^\alpha},

이는

\alpha \in (0, 1)

에 대해, 기댓값이 무한대임을 직접적으로 의미한다. 또한, 이러한 분포는 기하학적 안정 분포이다.

4. 5. 리에스 도함수

푸리에 변환을 사용하여 다음과 같이 정의된다.

:

\mathcal{F} \left\{ \frac{\partial^\alpha u}{\partial \left|x\right|^\alpha} \right\}(k) = -\left|k\right|^{\alpha} \mathcal{F} \{u \}(k),

여기서

\mathcal{F}

는 푸리에 변환을 나타낸다.^[20]^[21]

4. 6. 기타 분수 계 도함수

그륀발트-레트니코프 미분^[22]^[23], 소닌-레트니코프 미분^[23], 마르쇼 미분^[22], 밀러-로스 미분^[22], 바일 적분^[25]^[26]^[22], 에르델리-코버 미분^[22], 코임브라 미분^[22], 카투감폴라 미분^[28], 힐퍼 미분^[22], 데이비슨 미분^[22], 첸 미분^[22] 등이 있다.

코임브라 미분은 물리 모델링에 사용된다.^[31] 역학 및 광학 분야에서 코임브라와 공동 연구자의 연구에서 많은 응용 분야를 찾을 수 있으며,^[32]^[33]^[34]^[35]^[36]^[37]^[38] 다른 저자들의 여러 연구에서 연구된 물리적 문제 및 수치적 구현에 대한 추가적인 응용 분야도 찾을 수 있다.^[39]^[40]^[41]^[42]

5. 분수 미적분학의 성질

분수 미적분 연산자는 국소적 성질을 갖지 않는다. 즉, 점 $x=c$ 에서의 함수 $f$ 의 분수 계 도함수는 $f$ 의 모든 값, 심지어 $c$ 에서 멀리 떨어진 값에도 의존한다.^[45] 이는 정수 계 도함수가 해당 점 주변의 정보에만 의존하는 것과 대조적이다.

분수 계 도함수는 종종 푸리에 변환 또는 멜린 변환과 같은 적분 변환을 사용하여 정의된다.^[74]^[75] 이러한 정의는 조제프 리우빌의 연구에 기초한다.

분수 미적분학에서 중요한 질문 중 하나는 반미분 연산자 $H$ 의 존재 여부이다. 반미분은 제곱했을 때 원래 함수의 도함수를 반환하는 연산자이다. 즉, $H^2 f(x) = \frac{d}{dx} f(x)$ 를 만족한다. 이러한 연산자는 실제로 존재하며, 임의의 양의 실수 $a$ 에 대해 $(P^{a}f(x) = \frac{d}{dx} f(x)$ 를 만족하는 연산자 $P$ 가 존재한다. 이는 미분 연산의 차수 $n$ 을 임의의 실수값으로 확장할 수 있음을 의미한다.

반복 적분에 관한 코시 공식을 통해 적분 연산자 $J$ 를 다음과 같이 정의할 수 있다.

: $(J^n f)(x) = {d ^{-n} \over dx^{-n}}f(x) = {1 \over (n-1)!} \int_0^x (x-t)^{n-1} f(t) \; dt$

감마 함수를 이용하여 이를 일반화하면 다음과 같다.

: $(J^\alpha f)(x) = {d ^{-\alpha} \over dx^{-\alpha}}f(x) = {1 \over \Gamma(\alpha)} \int_0^x (x-t)^{\alpha-1}f(t) \; dt$

이 연산자는 잘 정의되어 있으며, 다음과 같은 가환성과 가법성을 만족한다.

: $(J^\alpha) (J^\beta) f = (J^\beta) (J^\alpha) f = (J^{\alpha+\beta} ) f = { 1 \over \Gamma ( \alpha + \beta) } \int_0^x (x-t)^{\alpha+\beta-1} f(t) \; dt$

이러한 성질을 분수 계 미분 적분 연산자의 반군성이라고 한다. 하지만 미분 연산자 $D$ 는 일반적으로 가환적이지도 가법적이지도 않다.

6. 응용 분야

분수 미적분학은 여러 분야에 걸쳐 널리 응용되고 있다.

질량 보존: 제어 체적이 이질성 규모에 비해 충분히 크지 않고, 제어 체적 내 유속이 비선형적일 때, 유체 흐름을 모델링하기 위해 분수 질량 보존 방정식이 필요하다.^[48]
전기화학 분석: 전극 표면의 기질 농도를 전류와 연결하여 전기화학적 운동론에서 메커니즘 거동을 설명하고, 전기화학적 환원에 따른 기질의 이량체화 속도를 연구하는 데 사용된다.^[49]^[50]
지하수 흐름 문제: 다르시 법칙을 일반화하여 지하수 흐름에 대한 새로운 방정식을 도출하는 데 사용된다.^[51]^[52]
분수 이류 분산 방정식: 이질적인 다공성 매질에서 오염 물질의 흐름을 모델링하는 데 유용하다.^[53]^[54]^[55]
시간-공간 분수 확산 방정식 모델: 복잡한 매질에서의 이상 확산 과정을 특성화하는 데 사용된다.^[57]^[58]
구조 감쇠 모델: 고분자를 비롯한 특정 유형의 재료에서 나타나는 점탄성 감쇠 현상을 모델링하는 데 사용된다.^[61]
PID 제어기: 분수 계수 PID 제어기를 일반화하여 자유도를 높일 수 있다.
복잡한 매질에서의 음향파 방정식: 생체 조직과 같은 복잡한 매질 내 음향파 전파를 설명하는 데 사용된다.^[63]
분수 슈뢰딩거 방정식: 분수 양자역학의 기본 방정식으로 사용된다.^[70]^[71]
기타 응용 분야: 분수 차수 시스템, 분수 푸리에 변환, Prabhakar 함수 등에 응용된다.

라플라스 변환은 분수계 미분 방정식을 푸는 데 유용하게 사용된다.

6. 1. 질량 보존

Wheatcraft와 Meerschaert (2008)의 연구에 따르면,^[48] 제어 체적이 이질성 규모에 비해 충분히 크지 않고, 제어 체적 내 유속이 비선형적일 때, 유체 흐름을 모델링하기 위해 분수 질량 보존 방정식이 필요하다고 한다.

6. 2. 전기화학 분석

용액 내 기질의 산화 환원 반응을 연구할 때, 전극 표면에 전압을 가하여 전극과 기질 간의 전자 이동을 유도한다. 이때 발생하는 전자 이동은 전류로 측정되며, 이 전류는 전극 표면의 기질 농도에 따라 달라진다. 기질이 소모됨에 따라 새로운 기질이 피크의 확산 법칙에 의해 전극으로 확산된다. 이 관계는 전극 표면의 기질 농도를 전류와 연결한다.^[49] 전기화학적 운동론에서 메커니즘 거동을 설명하는 데 사용되며, 전기화학적 환원에 따른 기질의 이량체화 속도를 연구하는 데 사용되었다.^[50]

6. 3. 지하수 흐름 문제

2013-2014년에 아탕가나(Atangana) 등은 분수 차수의 도함수 개념을 사용하여 일부 지하수 흐름 문제를 설명했다.^[51]^[52] 이 연구에서 고전적인 다르시 법칙은 피에조미터 수두의 비정수 차수 도함수의 함수로 물의 흐름을 간주하여 일반화되었다. 이 일반화된 법칙과 질량 보존 법칙을 사용하여 지하수 흐름에 대한 새로운 방정식을 도출했다.

6. 4. 분수 이류 분산 방정식

이 방정식은 이질적인 다공성 매질에서 오염 물질의 흐름을 모델링하는 데 유용한 것으로 나타났다.^[53]^[54]^[55]

Atangana와 Kilicman은 분수 아대류 분산 방정식을 가변 차수 방정식으로 확장했다. 그들의 연구에서 수리학적 분산 방정식은 변동 차수 미분의 개념을 사용하여 일반화되었다. 수정된 방정식은 크랭크-니콜슨 방법을 통해 수치적으로 풀었다. 수치 시뮬레이션에서 안정성과 수렴성은 수정된 방정식이 상수 분수 및 정수 미분 방정식을 사용하는 방정식보다 변형 가능한 대수층에서 오염의 움직임을 예측하는 데 더 신뢰할 수 있음을 보여주었다.^[56]

6. 5. 시간-공간 분수 확산 방정식 모델

복잡한 매질에서의 이상 확산 과정은 분수 차수 확산 방정식 모델을 사용하여 잘 특성화될 수 있다.^[57]^[58] 시간 미분 항은 장시간 헤비 테일 감쇠에 해당하며 공간 미분 항은 확산 비국소성에 해당한다. 시간-공간 분수 확산 지배 방정식은 다음과 같이 쓸 수 있다.

분수 미분의 간단한 확장은 변수 차수 분수 미분이며, α(알파)와 β(베타)는 α(x, t)(알파(x, t))와 β(x, t)(베타(x, t))로 변경된다. 이상 확산 모델링에서의 적용 사례는 다음 참고 문헌에서 찾을 수 있다.^[56]^[59]^[60]

6. 6. 구조 감쇠 모델

분수 미분은 고분자를 비롯한 특정 유형의 재료에서 나타나는 점탄성 감쇠 현상을 모델링하는 데 사용된다.^[61]

6. 7. PID 제어기

분수 계수 PID 제어기를 일반화하여 사용하면 자유도를 높일 수 있다. 측정된 '오차 값' ''e''(''t'')을 기준으로 '제어 변수' ''u''(''t'')를 연관시키는 새로운 방정식은 다음과 같다.

:

u(t) = K_\mathrm{p} e(t) + K_\mathrm{i} D_t^{-\alpha} e(t) + K_\mathrm{d} D_t^{\beta} e(t)

여기서 α와 β는 양의 분수 차수이며, ''K''_p, ''K''_i, ''K''_d는 모두 음수가 아닌 값으로 각각 비례 제어, 적분, 미분 항의 계수를 나타낸다(때로는 P, I, D로 표시됨).^[62]

6. 8. 복잡한 매질에서의 음향파 방정식

생체 조직과 같은 복잡한 매질 내 음향파의 전파는 일반적으로 주파수 거듭제곱 법칙을 따르는 감쇠를 수반한다. 이러한 현상은 분수 시간 미분을 통합하는 인과 관계 파동 방정식을 사용하여 설명할 수 있다.^[63]

:

\nabla^2 u -\dfrac 1{c_0^2} \frac{\partial^2 u}{\partial t^2} + \tau_\sigma^\alpha \dfrac{\partial^\alpha}{\partial t^\alpha}\nabla^2 u - \dfrac {\tau_\epsilon^\beta}{c_0^2} \dfrac{\partial^{\beta+2} u}{\partial t^{\beta+2}} = 0\,.

이러한 모델은 복잡한 매질에서 측정된 감쇠를 유발하는 다중 완화 현상에 대한 일반적으로 인식되는 가설과 관련이 있다. 이와 관련된 내용은 Näsholm & Holm (2011b)^[64], 조사 논문^[65] 및 음향 감쇠 문서에서 추가로 설명하고 있다. 거듭제곱 법칙 감쇠를 모델링하는 분수 파동 방정식을 비교하는 논문으로는 Holm & Nasholm (2013)^[66]이 있으며, 거듭제곱 법칙 감쇠에 관한 책^[67]에서도 이 주제를 더 자세히 다룬다.

Pandey와 Holm은 물리적 원리에서 분수 미분 방정식을 유도하고, 유체 포화 입상 비고결 해양 퇴적물 등 음향 매질의 매개변수와 관련하여 분수 차수를 해석함으로써 분수 미분 방정식에 물리적 의미를 부여했다.^[68] 흥미롭게도 Pandey와 Holm은 분수 미적분학 프레임워크를 사용하여 지진학에서 롬니츠의 법칙과 비뉴턴 유체 비뉴턴 유변학에서 Nutting의 법칙을 유도했다.^[69] Nutting의 법칙은 분수 미분을 사용하여 해양 퇴적물에서 파동 전파를 모델링하는 데 사용되었다.^[68]

6. 9. 분수 슈뢰딩거 방정식

분수 양자역학의 기본 방정식으로 다음과 같은 형태를 갖는다.^[70]^[71]

:

i\hbar \frac{\partial \psi (\mathbf{r},t)}{\partial t}=D_{\alpha } \left(-\hbar^2\Delta \right)^{\frac{\alpha}{2}}\psi (\mathbf{r},t)+V(\mathbf{r},t)\psi (\mathbf{r},t)\,.

여기서 방정식의 해는 파동 함수 ψ(r, t)^영어이며, 주어진 시간에서 입자가 주어진 위치 벡터 r^영어를 가질 확률 진폭을 나타내고, ħ^영어는 환원 플랑크 상수이다. 퍼텐셜 에너지 함수 V(r, t)^영어는 시스템에 따라 다르다.

또한,

\Delta = \frac{\partial^2}{\partial\mathbf{r}^2}

는 라플라스 연산자이고, D_α^영어는 물리적 차원 1=[D_α] = J^{1 − α}·m^α·s^−α = kg^{1 − α}·m^{2 − α}·s^{α − 2}^영어를 갖는 스케일 상수이다 (α = 2^영어일 때 질량 m^영어인 입자에 대해

D_2 = \frac{1}{2m}

). 연산자 (−ħ²Δ)^α/2^영어는 다음과 같이 정의되는 3차원 분수 양자 리에스 도함수이다.

:

(-\hbar^2\Delta)^\frac{\alpha}{2}\psi (\mathbf{r},t) = \frac 1 {(2\pi \hbar)^3} \int d^3 p e^{\frac{i}{\hbar} \mathbf{p}\cdot\mathbf{r}}|\mathbf{p}|^\alpha \varphi (\mathbf{p},t) \,.

분수 슈뢰딩거 방정식에서 지수 α^영어는 레비 지수이며, 1 < α ≤ 2^영어이다.

분수 슈뢰딩거 방정식의 자연스러운 일반화로서, 가변 차수 분수 슈뢰딩거 방정식은 다음과 같은 분수 양자 현상을 연구하는 데 활용되어 왔다:^[72]

:

i\hbar \frac{\partial \psi^{\alpha(\mathbf{r})} (\mathbf{r},t)}{\partial t^{\alpha(\mathbf{r})} } = \left(-\hbar^2\Delta \right)^{\frac{\beta(t)}{2}}\psi (\mathbf{r},t)+V(\mathbf{r},t)\psi (\mathbf{r},t),

여기서

\Delta = \frac{\partial^2}{\partial\mathbf{r}^2}

는 라플라스 연산자이고, 연산자 (−ħ²Δ)^β(t)/2^영어는 가변 차수 분수 양자 리에즈 미분이다.

6. 10. 기타 응용 분야

분수 차수 시스템
분수 푸리에 변환
Prabhakar 함수

라플라스 변환을 이용하여 분수계 미적분학 문제를 고려할 수 있다. 함수 ''f''의 라플라스 변환을

\mathcal L\{f\}

라고 할 때, 다음이 성립한다.

:

\mathcal L \left\{\int_0^t f(\tau)\,d\tau\right\}(s)=\frac{1}{s}(\mathcal L\left\{f\right\})(s)

이를 이용하여 ''J''^α''f''를 다음과 같이 정의할 수 있다.

:

J^\alpha f=\mathcal L^{-1}\left\{s^{-\alpha}(\mathcal L\{f\})(s)\right\}

예를 들어, 다음과 같다.

:

J^\alpha\left(t^k\right)=\mathcal L^{-1}\left\\right\}={\Gamma(k+1)\over\Gamma(\alpha+k+1)}t^{\alpha+k}

합성곱 공식

\mathcal L\{f*g\}=(\mathcal L\{f\})(\mathcal L\{g\})

을 이용하면, 다음을 얻을 수 있다.

:

(J^\alpha f)(t)=\frac{1}{\Gamma(\alpha)}\int_0^t(t-\tau)^{\alpha-1}f(\tau)\,d\tau

이는 코시의 공식과 같다.

라플라스 변환은 계산 가능한 함수가 제한적이지만, 분수계 미분 방정식을 푸는 데 유용하게 사용된다.

참조

_[1] 문서
_[2] 서적 Handbook of Differential Equations https://books.google[...] Elsevier Science 2014-05-12
_[3] 논문 A New Approach To Generalized Fractional Derivatives https://www.emis.de/[...] 2014-10-15
_[4] 논문 Oplösning af et Par Opgaver ved Hjelp af bestemte Integraler (Solution de quelques problèmes à l'aide d'intégrales définies, Solution of a couple of problems by means of definite integrals) https://abelprize.no[...]
_[5] 논문 Niels Henrik Abel and the birth of fractional calculus
_[6] 논문 Mémoire sur quelques questions de géométrie et de mécanique, et sur un nouveau genre de calcul pour résoudre ces questions https://gallica.bnf.[...]
_[7] 논문 Mémoire sur le calcul des différentielles à indices quelconques https://gallica.bnf.[...]
_[8] 문서
_[9] 논문 The development of fractional calculus 1695–1900
_[10] 논문 Some pioneers of the applications of fractional calculus 2014-01-01
_[11] 서적 Fractional Calculus: An Introduction for Physicists World Scientific Publishing 2014
_[12] 논문 Essai sur l'étude des fonctions données par leur développement de Taylor http://sites.mathdoc[...] 1892
_[13] 서적 Theory And Applications of Fractional Differential Equations https://books.google[...] Elsevier 2006
_[14] 논문 Fractional paradigms in quantum chemistry
_[15] 논문 Applying fractional quantum mechanics to systems with electrical screening effects https://www.scienced[...]
_[16] 서적 Fractional Calculus World Scientific Publishing Co. 2014
_[17] 논문 Linear model of dissipation whose ''Q'' is almost frequency independent. II
_[18] 논문 A new Definition of Fractional Derivative without Singular Kernel https://www.naturals[...] 2020-08-07
_[19] 논문 New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model http://www.doiserbia[...] 2016
_[20] 논문 High-Order Algorithms for Riesz Derivative and Their Applications 2014-05-22
_[21] 논문 Definition of the Riesz derivative and its application to space fractional quantum mechanics 2016-12-05
_[22] 논문 A Review of Definitions for Fractional Derivatives and Integral 2014-06-10
_[23] 논문 An analytic approach to a class of fractional differential-difference equations of rational type via symbolic computation 2015-01-15
_[24] 논문 On hadamard fractional calculus 2017-05-11
_[25] 서적 Fractional Calculus and Its Applications Springer 1975
_[26] 논문 Weyl and Marchaud Derivatives: A Forgotten History 2018-01
_[27] 서적 Fractal Calculus and its Applications https://worldscienti[...] World Scientific Pub Co Inc 2022
_[28] 논문 Properties of the Katugampola fractional derivative with potential application in quantum mechanics 2015-06-01
_[29] 논문 Comparing the Atangana–Baleanu and Caputo–Fabrizio derivative with fractional order: Allen Cahn model https://www.scienced[...] 2016-08-01
_[30] 논문 Applications of New Time and Spatial Fractional Derivatives with Exponential Kernels 2016-01-01
_[31] 문서
_[32] 문서
_[33] 문서
_[34] 문서
_[35] 문서
_[36] 논문 On the Variable Order Dynamics of the Nonlinear Wake Caused by a Sedimenting Particle 2011
_[37] 논문 Fractional Dynamics of Tethered Particles in Oscillatory Stokes Flows 2014
_[38] 논문 On the Control and Stability of Variable Order Mechanical Systems 2016
_[39] 논문 A Review of Definitions for Fractional Derivatives and Integral 2014
_[40] 논문 Numerical techniques for the variable order time fractional diffusion equation 2012
_[41] 논문 The Numerical Simulation of Space-Time Variable Fractional Order Diffusion Equation
_[42] 논문 A novel numerical method for the time variable fractional order mobile-immobile advection-dispersion model 2013
_[43] 간행물 Methods of using generalized order differentiation and integration of input variables to forecast trends U.S. Patent Application 13,641,083 2013
_[44] 논문 Variable-order Modeling of Nonlocal Emergence in Many-body Systems: Application to Radiative Dispersion 2018
_[45] 웹사이트 Fractional Calculus home/kmath616/kmath6[...]
_[46] 논문 On some functional transformations
_[47] 논문 On fractional integrals and derivatives
_[48] 논문 Fractional conservation of mass https://www.stt.msu.[...] 2008-10
_[49] 논문
_[50] 논문
_[51] 논문 The Use of Fractional Order Derivative to Predict the Groundwater Flow
_[52] 논문 Analytical Solutions of a Space-Time Fractional Derivative of Groundwater Flow Equation
_[53] 논문 Application of a fractional advection-dispersion equation
_[54] 논문 The fractional-order governing equation of Lévy motion
_[55] 논문 Fractional Dispersion, Lévy Motion, and the MADE Tracer Tests 2001-01-01
_[56] 논문 On the Generalized Mass Transport Equation to the Concept of Variable Fractional Derivative
_[57] 논문 The random walk's guide to anomalous diffusion: a fractional dynamics approach
_[58] 논문 The fundamental solution of the space-time fractional diffusion equation
_[59] 서적 Processes with Long-Range Correlations 2007
_[60] 논문 Scaling laws of passive-scalar diffusion in the interstellar medium
_[61] 서적 Fractional Calculus and Waves in Linear Viscoelasticity Imperial College Press 2010-05
_[62] 논문 Some Applications of Fractional Calculus in Engineering 2010
_[63] 논문 A causal and fractional all-frequency wave equation for lossy media
_[64] 논문 Linking multiple relaxation, power-law attenuation, and fractional wave equations
_[65] 논문 On a Fractional Zener Elastic Wave Equation
_[66] 논문 Comparison of fractional wave equations for power law attenuation in ultrasound and elastography
_[67] 서적 Waves with Power-Law Attenuation https://link.springe[...] Springer and Acoustical Society of America Press
_[68] 논문 Connecting the grain-shearing mechanism of wave propagation in marine sediments to fractional order wave equations 2016-12-01
_[69] 논문 Linking the fractional derivative and the Lomnitz creep law to non-Newtonian time-varying viscosity 2016-09-23
_[70] 논문 Fractional Schrodinger equation
_[71] 서적 Fractional Quantum Mechanics
_[72] 논문 An improved collocation method for multi-dimensional space–time variable-order fractional Schrödinger equations
_[73] 문서 ここで積分作用素の {{mvar|J}} は integration の頭文字 {{mvar|I}} を用いるところ、{{mvar|I}} は恒等写像など他の意味に使われたり、{{mvar|I}} に似た字形の記号・文字がいろいろと使われたりすることによる混同を避けるためにしばしば使われる。
_[74] 간행물 Mémoire sur quelques questions de géométrie et de mécanique, et sur un nouveau genre de calcul pour résoudre ces questions https://gallica.bnf.[...]
_[75] 간행물 Mémoire sur le calcul des différentielles à indices quelconques https://gallica.bnf.[...]
_[76] 문서 この主題の歴史については、以下の修士論文（フランス語）Stéphane Dugowson, [http://s.dugowson.free.fr/recherche/dones/index.html Les différentielles métaphysiques] (histoire et philosophie de la généralisation de l'ordre de dérivation), Thèse, Université Paris Nord (1994) を参照。
_[77] 간행물 Essai sur l'étude des fonctions données par leur développement de Taylor https://eudml.org/do[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com