브라운 운동

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 발견의 역사
3. 이론
- 3.1. 정성적 설명
- 3.2. 정량적 이론 (아인슈타인의 이론)
4. 활용
5. 수리 모델
- 5.1. 위너 과정의 정의
- 5.2. 위너 과정의 성질
참조

1. 개요

브라운 운동은 액체나 기체 속의 미세 입자가 불규칙하게 움직이는 현상으로, 1827년 로버트 브라운에 의해 처음 관찰되었다. 아인슈타인과 스몰루호프스키는 이 현상을 분자들의 무작위 운동으로 설명하며 원자 존재를 증명하는 데 기여했고, 장 바티스트 페랭의 실험으로 아인슈타인의 이론이 검증되었다. 브라운 운동은 원자론 확립, 통계역학 발전, 금융 시장 모델 등 다양한 분야에 응용되며, 수학적으로는 위너 과정으로 모델링된다.

더 읽어볼만한 페이지

계면화학 - 흡착
흡착은 엔트로피 감소를 동반하는 발열 반응으로, 흡착질이 흡착제 표면에 달라붙는 현상이며, 랭뮤어 및 BET 등온식 등으로 모델링하여 실리카겔, 제올라이트, 활성탄 등 다양한 흡착제를 활용, 기체 및 액체 분리, 정제, 저장 등에 사용되며 미래에는 수소 저장, 탄소 포집 등 다양한 분야에서 중요성이 커질 것으로 예상된다.
계면화학 - 전기영동
전기영동은 전기장을 사용하여 하전된 입자를 분리하는 기술로, 무담체와 담체 방식으로 나뉘며 겔, 모세관, 등전점, 이차원, 펄스 필드 등 다양한 방법으로 응용되고 있다.
프랙탈 - 프랙탈 우주론
프랙탈 우주론은 우주의 구조가 프랙탈 기하학적 특성을 갖는다는 이론이며, 관측 결과는 우주가 균질하다는 것을 보여주지만, 이론적 연구에서는 큰 규모나 미시적 규모에서 프랙탈 구조를 제안하기도 한다.
프랙탈 - 프랙탈 압축
프랙탈 압축은 반복 함수 시스템을 사용하여 이미지의 자기 유사성을 찾아 압축하는 방식으로, 인코딩은 계산 비용이 많이 들지만 디코딩은 빠르며, 해상도 독립성을 갖지만 블록 노이즈가 발생하고 비가역 압축이라는 특징을 가진다.
확률 과정 - 마르코프 연쇄
마르코프 연쇄는 현재 상태가 주어졌을 때 과거와 미래 상태가 독립적인 확률 변수 순서열로, 시간 동질성, 상태 공간 유형, 시간 매개변수 유형에 따라 다양한 유형으로 분류되며 여러 분야에서 활용되는 확률적 모델링 방법이다.
확률 과정 - 대기행렬이론
대기행렬 이론은 1909년 에를랑에 의해 연구된 수학 이론으로, 서버, 대기실, 고객으로 구성된 시스템을 분석하며, 켄달의 표기법을 사용하여 대기열 모델의 특징을 나타내고, 컴퓨터 과학 등 다양한 분야에 응용되어 시스템 성능 분석 및 최적화에 활용된다.

브라운 운동
브라운 운동
현미경으로 본 브라운 운동.
짧은 설명	유체에 부유된 입자의 무작위 운동
다른 이름	브라운 운동
설명	브라운 운동은 액체나 기체와 같은 유체에 부유된 입자가 불규칙하게 움직이는 현상이다. 이러한 운동은 유체 분자의 무작위적인 충돌에 의해 발생한다. 이러한 운동은 유체 분자의 무작위적인 충돌에 의해 발생하며, 입자 크기가 작을수록 운동이 더욱 활발하게 나타난다. 이 운동은 눈으로 직접 관찰할 수 있으며, 미시적인 세계의 역동성을 보여주는 중요한 현상이다. 알베르트 아인슈타인은 1905년 논문에서 브라운 운동을 설명했으며, 이를 통해 원자의 존재를 증명하는 데 기여했다.
발견자	로버트 브라운 (1827년 발견\|isbn=978-4-7536-5637-0\|ncid=BB00508924\|oclc=491332824\|asin=4753656373\|pages=17-21}}。}}).
이론적 배경
관련 이론	통계역학 확률론 랜덤 워크 위너 과정
최초의 이론적 설명	알베르트 아인슈타인 (1905년) 위리엄 서덜랜드 (1905년) 마리안 스몰루초프스키 (1906년)
수학적 모델링
수학적 모델	확률 과정 마르코프 과정 레비 과정 위너 과정 (브라운 운동의 수학적 모델) 확산 방정식 랑주뱅 방정식
수학적 분석	이론 물리학 확률론
중요성
중요성	원자의 존재 증명 통계역학의 발전 물리 화학, 생물학, 금융 공학 등 다양한 분야에 응용 열역학과 비평형 통계역학의 중요한 개념 수학적 모델링의 기반
추가 정보
추가 정보	루이 바슐리에는 1900년 박사 논문에서 브라운 운동을 사용하여 주식 시장 가격 변동을 모델링했다. 장 바티스트 페랭은 브라운 운동에 대한 실험적 연구로 1926년 노벨 물리학상을 수상했다. 브라운 운동은 에르고딕성을 보여주는 예시이다. 분자 운동 이론의 직접적인 증거이다. 브라운 운동은 확산의 원인이 된다. 브라운 운동은 입자들의 무작위 운동을 설명한다. 돈스커 불변성 원리는 브라운 운동과 관련된 중요한 수학적 개념이다.
참고 문헌	리처드 파인만의 파인만 물리학 강의 1권 41장 "브라운 운동" 얀 필립 메이부르크와 데틀레프 디징의 논문 "컴퓨터 실험에서 나노구조의 성장, 숙성 및 응집 교육" 루멘 체코프의 논문 "분자의 브라운 운동: 고전 이론" 프랭크 B. 나이트의 논문 "랜덤 워크와 브라운 운동에 관하여"

2. 발견의 역사

로버트 브라운이 클라키아 풀켈라(Clarkia pulchella)의 수정 과정을 연구하던 중, 물에 띄운 꽃가루 입자들이 불규칙적으로 운동하는 현상을 발견한 것이 브라운 운동 연구의 시초이다. 브라운 이전에도 이러한 현상을 관찰한 사람들은 있었지만, 이 현상을 본격적으로 연구한 것은 브라운이 처음이었다.^[8] 이전에는 이러한 운동을 하는 입자들을 스스로 움직이는 생명체인 '극미동물(animalcules)'로 생각했으나, 브라운은 무기물 등을 이용한 실험을 통해 생명체가 아닌 물리적 요인에 의한 현상임을 밝혀냈다.

로마 시대의 철학자 루크레티우스(Lucretius)는 그의 과학 서사시 "사물의 본성에 관하여"에서 먼지 입자의 움직임을 통해 원자의 존재를 설명했다. 그는 햇빛 속에서 먼지 입자들이 끊임없이 움직이는 것은 보이지 않는 원자들의 충돌 때문이라고 주장했다. 그러나 먼지 입자의 운동은 주로 공기의 흐름에 의한 것이며, 작은 먼지 입자의 미세한 움직임만이 브라운 운동에 해당한다.

얀 잉겐하우스(Jan Ingenhousz)는 1785년에 에탄올 표면에서 석탄 먼지 입자의 불규칙한 운동을 관찰했지만, 브라운 운동의 발견은 1827년 로버트 브라운의 연구로 인정받고 있다.

이후 브라운 운동은 토르발드 N. 티엘레(Thorvald N. Thiele) (1880년), 루이 바슐리에(Louis Bachelier) (1900년) 등에 의해 수학적으로 연구되었으며, 알베르트 아인슈타인과 마리안 스몰루호프스키(Marian Smoluchowski)는 이 현상을 원자와 분자의 존재를 증명하는 간접적인 증거로 제시했다. 장 바티스트 페랭(Jean Baptiste Perrin)은 1908년 실험을 통해 아인슈타인과 스몰루호프스키의 이론을 검증하였다.

2. 1. 로버트 브라운의 관찰

로버트 브라운은 스코틀랜드의 식물학자로, 클라키아 풀켈라(Clarkia pulchella)라는 식물의 수정 과정을 연구하기 위해 물에 띄운 꽃가루 입자를 현미경으로 관찰했다. 그러던 중 꽃가루 입자들이 물 위에서 끊임없이 불규칙하게 움직이는 현상을 발견하였다. 이러한 현상은 브라운 이전에도 다른 사람들에 의해 관찰되었지만, 실제로 연구를 한 사람은 브라운이 처음이었다. 이전에는 이러한 운동을 하는 입자들을 스스로 액체 속에서 움직이는 살아있는 생명체인 ‘극미동물(anialcules)'로 생각했었다. 하지만 브라운은 곱게 갈아낸 무기물, 유리, 금속, 바위 등을 액체에 뿌려 관찰한 결과 꽃가루와 똑같은 불규칙 운동을 한다는 것을 알아내었고, 이것이 살아있는 생물 때문이 아님을 밝혀냈다.^[8] 이처럼 운동의 원인이 생물이 아닌 물리적인 것에 있다는 사실이 알려진 후, 브라운 운동은 물리학자들의 연구 대상이 되었다.

장 바티스트 페랭(Jean Baptiste Perrin)의 저서 ''Les Atomes''에서 재현한 그림. 현미경으로 관찰한 반지름 0.53 μm의 콜로이드 입자의 운동 궤적 세 가지가 표시되어 있다. 30초마다의 연속적인 위치를 직선으로 연결하였다(격자 크기는 3.2 μm).

2. 2. 아인슈타인의 이론

1905년 알베르트 아인슈타인은 브라운 운동을 통계역학적으로 설명하는 논문을 발표했다.^[45] 아인슈타인은 액체 분자들의 불규칙한 운동이 미세 입자에 충돌하여 브라운 운동을 일으킨다고 설명했다. 그의 이론은 당시 논쟁의 대상이었던 원자의 실재를 뒷받침하는 강력한 증거가 되었다.

아인슈타인의 이론은 두 부분으로 구성된다.^[11] 첫 번째 부분은 브라운 운동 입자에 대한 확산 방정식을 수립하고, 확산 계수를 브라운 운동 입자의 평균 제곱 변위와 연관시키는 것이다. 두 번째 부분은 확산 계수를 측정 가능한 물리량과 연결하여, 원자의 크기와 아보가드로 수를 결정할 수 있게 한다.^[12]

아인슈타인은 주어진 시간 간격 동안 브라운 운동 입자가 얼마나 이동하는지 결정하기 위해, 1차원 공간에서 입자 위치 증분을 확률 변수로 간주했다.^[3] 그는 확률 밀도 함수와 테일러 급수를 이용하여 수 밀도 변화를 나타내고, 이를 통해 확산 방정식을 유도했다.

:

\frac{\partial\rho}{\partial t} = D\cdot \frac{\partial^2\rho}{\partial x^2}

여기서 D는 질량 확산계수이다. 초기 조건에서 확산 방정식의 해는 다음과 같다.

:

\rho(x,t) = \frac{N}{\sqrt{4\pi Dt}} \exp{\left(-\frac{x^2}{4Dt}\right)}

이 식을 통해 아인슈타인은 평균 제곱 변위를 다음과 같이 계산했다.

:

\mathbb{E}{\left[x^2\right]} = 2 D t

이 식은 평균 제곱 변위가 시간과 확산 계수에 비례함을 보여준다. 아인슈타인은 이 관계를 통해 브라운 운동 입자의 변위가 시간이 아닌 시간의 제곱근에 비례한다고 주장했다.^[11]

아인슈타인 이론의 두 번째 부분은 확산 상수를 물리적으로 측정 가능한 양과 연결한다. 그는 삼투압과 중력장에서의 입자 분포 등 다양한 방법을 통해 결론에 도달할 수 있음을 보였다. 동적 평형 상태에서 입자의 분포는 기압 공식을 따르며, 픽의 확산 법칙을 통해 확산 계수와 관련된 아인슈타인 관계를 유도할 수 있다.

:

\frac{\mathbb{E}{\left[x^2\right]}}{2t} = D = \mu k_\text{B} T = \frac{\mu R T}{N_\text{A}} = \frac{RT}{6\pi\eta r N_\text{A}}

이 식을 통해 평균 제곱 변위, 기체 상수, 온도, 점성, 입자 반지름을 측정하여 아보가드로 수를 결정할 수 있다.

1906년 폴란드의 마리안 스몰루호프스키는 아인슈타인과 다른 방법으로 분자운동론을 고려하여 유사한 공식을 유도했다. 아인슈타인의 공식은 이후 장 바티스트 페랭 등에 의해 실험적으로 증명되었다.

2. 3. 스몰루호프스키의 연구

1906년, 폴란드의 마리안 스몰루호프스키는 알베르트 아인슈타인과 독립적으로 브라운 운동에 대한 이론을 발표했다.^[20] 그는 분자 운동론을 바탕으로 아인슈타인과 유사한 결론을 도출했다. 스몰루호프스키는 브라운 입자의 평균 제곱 변위에 대한 식을 유도했는데, 이는 아인슈타인이 구한 값과 차이가 있었다.^[21]

스몰루호프스키는 브라운 입자가 더 작은 입자들의 충격으로 인해 변위되는 이유를 설명하고자 했다. 그는 전방과 후방에서 입자를 타격할 확률이 동일하더라도, 투표 정리(ballot theorem)에 따라 브라운 입자를 계속 운동 상태로 유지하는 순 경향이 있음을 보였다.^[22]

그는 1차원 모델을 제시하여 브라운 운동을 정성적으로 설명했다.^[23] 이 모델은 입자 충돌이 1차원으로 제한되고, 시험 입자가 왼쪽이나 오른쪽에서 동일한 확률로 맞을 수 있으며, 모든 충돌은 항상 동일한 크기의 속도 변화를 전달한다고 가정했다. 하지만 실제 브라운 운동에서는 이러한 가정이 항상 성립하지는 않는다.

2. 4. 장 바티스트 페랭의 실험

1908년, 프랑스의 물리화학자 장 바티스트 페랭은 브라운 운동에 대한 실험을 수행했다. 알베르트 아인슈타인은 지름이 0.001mm인 부유 입자들을 17°C의 물속에 넣고 현미경으로 1분 동안 입자들이 이동한 수평 거리를 기록하면 0.006mm가 될 것이라고 예상했다. 페랭은 반지름이 알려진 입자를 사용하여 실험을 진행했는데, 처음에는 크기가 다른 자황 입자들(0.45µm와 0.212µm)을 사용하고, 두 번째에는 반지름이 0.0052mm인 유향 입자들을 이용했다. 측정치를 분석하여 아인슈타인의 공식이 예측한 수평 거리를 실험적으로 증명했다.^[44] 이 연구로 페랭은 1926년 노벨 물리학상을 수상했다.

브라운 운동에 대해 다음 식이 성립한다.

:

\left\langle(x-x_0)^2\right\rangle=\frac{2 R T}{N_\mathrm A f}t

여기서, 식의 좌변은 브라운 운동하는 물체의 평형 위치 $x_0$로부터의 변위 제곱의 평균이다(계는 1차원으로 한다). $R$은 기체 상수, $T$는 절대 온도, $f$는 이동도^[43], $t$는 충분히 경과한 시간(극한으로는 $t \to \infty$)이다. 그리고 $N_A$는 아보가드로 수이다. 아보가드로 수를 제외하고는 브라운 운동과는 관계없이 구할 수 있는 양이며, 장 바티스트 페랭은 1908년 브라운 운동 관측을 바탕으로 $N_A = 7.05 \times 10^{23}$ (자료에 따라 값이 다름)이라는 값을 얻었다.^[44]

참고로, 볼츠만 상수 $k_B = R / N_A$를 사용하여 표기하면 다음 식이 된다.

:

\left\langle(x-x_0)^2\right\rangle=\frac{2 k_\mathrm B T}{f}t

3. 이론

1905년 알베르트 아인슈타인은 원자의 실제 존재와 통계적 요동을 바탕으로 브라운 운동을 설명했다. 아인슈타인은 브라운 운동을 확산 현상으로 간주하고, 확산 방정식을 이용하여 입자의 평균 이동 거리를 계산했다.^[11]

아인슈타인이 제시한 평균 제곱 변위 공식은 다음과 같다.

: $\sqrt {\bar{\Delta {x} ^{2}}} = \sqrt {kT} {\sqrt {t} \over {\sqrt {3 \pi \mu r}}}$

위 식에서 $\mu$ 는 액체의 점성 계수, $r$ 은 입자의 반지름을 나타낸다. 이 식을 통해 질량은 브라운 운동과 관련이 없음을 알 수 있다. 여기서 상수 $k$ 는 현재 볼츠만 상수로 알려져 있으며, 원자의 존재와 직접적인 관련이 있어 중요한 의미를 갖는다.^[11]

아인슈타인의 이론은 브라운 운동 입자에 대한 확산 방정식을 세우고, 확산 계수를 측정 가능한 물리량과 연결하여 아보가드로 수를 구하는 두 부분으로 구성된다.^[11] 아보가드로의 법칙에 따르면, 표준 온도 및 압력에서 22.414리터의 부피에 포함된 원자의 수를 아보가드로 수라고 하며, 이 수를 구하는 것은 원자 질량을 아는 것과 같다.

아인슈타인은 주어진 시간 간격 동안 브라운 운동 입자가 얼마나 이동하는지를 결정하고자 했다.^[3] 그러나 고전 역학으로는 브라운 운동 입자가 초당 약 10¹⁴번의 충돌을 받기 때문에 이 거리를 결정할 수 없었다.^[2]

아인슈타인은 1차원 공간(''x'')에서 시간 τ 동안의 입자 위치 증분을 확률 변수로 간주하고, 확률 밀도 함수 φ(q)를 도입했다. 또한 입자 수 보존을 가정하고, 시간 t + τ에서 x 주변의 수 밀도 ρ(x,t+τ)를 테일러 급수로 전개하여 다음과 같은 관계를 얻었다.

:

\frac{\partial\rho}{\partial t}= \frac{\partial^2 \rho}{\partial x^2} \cdot \int_{-\infty}^{\infty} \frac{q^2}{2 \tau} \varphi(q) \, dq + \text{고차 짝수 모멘트.}

여기서 변위 q의 확률의 두 번째 모멘트는 질량 확산계수 ''D''로 해석된다.

:

D = \int_{-\infty}^{\infty} \frac{q^2}{2 \tau} \varphi(q) \, dq.

이를 통해 시간 t에서 점 x에서 브라운 운동 입자의 밀도 ρ는 확산 방정식을 만족한다는 것을 보였다.

:

\frac{\partial\rho}{\partial t} = D\cdot \frac{\partial^2\rho}{\partial x^2},

초기 시간 t = 0에서 원점에서 N개의 입자가 시작한다고 가정하면, 확산 방정식의 해는 다음과 같다.

:

\rho(x,t) = \frac{N}{\sqrt{4\pi Dt}} \exp{\left(-\frac{x^2}{4Dt}\right)}.

이 식은 정규 분포이며, 아인슈타인은 이 식을 사용하여 모멘트를 계산했다. 첫 번째 모멘트는 0으로, 브라운 운동 입자가 왼쪽으로 이동할 확률과 오른쪽으로 이동할 확률이 같음을 의미한다. 두 번째 모멘트는 다음과 같이 주어진다.

:

\mathbb{E}{\left[x^2\right]} = 2 D t.

이 방정식은 평균 제곱 변위가 경과 시간과 확산 계수에 의해 결정됨을 나타낸다. 아인슈타인은 이 식을 통해 브라운 운동 입자의 변위가 경과 시간에 비례하는 것이 아니라 제곱근에 비례한다고 주장했다.^[11]

아인슈타인 이론의 두 번째 부분은 확산 상수를 물리적으로 측정 가능한 양과 관련짓는 것이다. 그는 서로 반대되는 힘 사이에 동적 평형이 확립되는 상황을 분석하여, 아보가드로 수와 분자 크기를 실험적으로 결정할 수 있는 방법을 제시했다.

삼투압 실험 외에도, 중력장에서 점성 유체에 현탁된 입자를 예로 들어 설명할 수 있다. 중력은 입자를 침전시키지만, 확산은 입자를 균질화하여 농도가 낮은 영역으로 이동시킨다. 동적 평형 상태에서 입자는 기압 분포에 따라 분포한다.

:

\rho = \rho_o \, \exp{\left({-\frac{m g h}{k_\text{B} T}}\right),

플럭스는 픽의 법칙에 의해 주어진다.

:

J = -D \frac{d\rho}{dh},

이 두 식을 결합하면, 확산 계수에 대한 아인슈타인 관계를 얻을 수 있다.

:

\frac{\mathbb{E}{\left[x^2\right]}}{2t} = D = \mu k_\text{B} T= \frac{\mu R T}{N_\text{A}} = \frac{RT}{6\pi\eta r N_\text{A}}.

이 식을 통해 시간 간격에 따른 평균 제곱 변위, 기체 상수 R, 온도 T, 점성 η, 입자 반지름 r을 측정하여 아보가드로 수 N_A를 결정할 수 있다.

3. 1. 정성적 설명

아인슈타인은 부유입자들의 무작위 운동으로 인해 확산이 일어난다는 점에 주목했다. 이는 액체 분자들의 무작위 운동 때문에 일어나는 것으로, 각각의 움직임은 결국 서로 영향을 주게 되고 모든 입자들의 지그재그 움직임을 만들어낸다.

통계적으로 많은 수는 평균을 이룰수록 안정된 것으로 여겨진다. 기체나 액체의 표본에서 분자 수는 매우 크기 때문에, 평균에서 벗어나는 행동을 기대하기 어렵다. 볼츠만과 깁스는 기체와 액체에서 평균에서 벗어나는 행동은 관찰될 수 없을 거라고 주장했다. 즉, 통계적 요동이 존재하지 않는다고 생각한 것이다. 하지만 아인슈타인은 이러한 기존의 틀을 깨고 통계적 요동을 가정했다.

물 분자들은 꽃가루 입자에 비해서 질량이 매우 작기 때문에, 물 분자가 꽃가루 입자를 미는 힘은 입자의 모든 표면에서 미세하게 작용한다. 이를 평균적인 것으로만 생각하면 가해지는 알짜힘은 결국 0이 되어 정지해 있게 된다는 것이 요동이 없는 상황에서의 예측이다. 하지만 꽃가루 입자 주위의 액체 분자들은 불규칙적으로 운동하며 꽃가루를 밀게 되고, 모든 표면에 동일한 힘이 가해지지 않게 되어 약한 힘으로 부딪치는 방향으로 입자는 운동한다. 결국 요동이 꽃가루를 운동시키게 된다. 요동이 무작위이기 때문에 입자의 운동도 불규칙적이다.

3. 2. 정량적 이론 (아인슈타인의 이론)

1905년 알베르트 아인슈타인은 당시 학계에서 파격적이었던 원자의 실제 존재와 통계적 요동을 바탕으로 브라운 운동을 설명했다. 아인슈타인은 브라운 운동을 확산 현상으로 간주하고, 확산 방정식을 이용하여 입자의 평균 이동 거리를 계산했다.^[11]

아인슈타인이 제시한 평균 제곱 변위 공식은 다음과 같다.

:

\sqrt {\bar{\Delta {x}  ^{2}}} = \sqrt {kT} {\sqrt {t} \over {\sqrt {3 \pi  \mu r}}}

위 식에서

\mu

는 액체의 점성 계수,

r

은 입자의 반지름을 나타낸다. 이 식을 통해 질량은 브라운 운동과 관련이 없음을 알 수 있다. 여기서 상수

k

는 현재 볼츠만 상수로 알려져 있으며, 원자의 존재와 직접적인 관련이 있어 중요한 의미를 갖는다.^[11]

아인슈타인의 이론은 두 부분으로 구성된다.^[11] 첫 번째는 브라운 운동 입자에 대한 확산 방정식을 세우는 것이다. 이 방정식에서 확산 계수는 브라운 운동 입자의 평균 제곱 변위와 관련된다. 두 번째 부분은 확산 계수를 측정 가능한 물리량과 연결하는 것이다. 이를 통해 아인슈타인은 원자의 크기와 몰(mole) 당 원자의 개수, 즉 기체의 분자량(g)을 결정할 수 있었다.^[12] 아보가드로의 법칙에 따르면, 이 부피는 모든 이상 기체에서 동일하며, 표준 온도 및 압력에서 22.414리터이다. 이 부피에 포함된 원자의 수를 아보가드로 수라고 하며, 이 수를 구하는 것은 원자 질량을 아는 것과 같다.

아인슈타인은 주어진 시간 간격 동안 브라운 운동 입자가 얼마나 이동하는지를 결정하고자 했다.^[3] 그러나 고전 역학으로는 브라운 운동 입자가 초당 약 10¹⁴번의 충돌을 받기 때문에 이 거리를 결정할 수 없었다.^[2]

아인슈타인은 1차원 공간(''x'')에서 시간 τ 동안의 입자 위치 증분을 확률 변수로 간주하고, 확률 밀도 함수 φ(q)를 도입했다. 또한 입자 수 보존을 가정하고, 시간 t + τ에서 x 주변의 수 밀도 ρ(x,t+τ)를 테일러 급수로 전개하여 다음과 같은 관계를 얻었다.

:

\frac{\partial\rho}{\partial t}= \frac{\partial^2 \rho}{\partial x^2} \cdot \int_{-\infty}^{\infty} \frac{q^2}{2 \tau} \varphi(q) \, dq + \text{고차 짝수 모멘트.}

여기서 변위 q의 확률의 두 번째 모멘트는 질량 확산계수 ''D''로 해석된다.

:

D = \int_{-\infty}^{\infty} \frac{q^2}{2 \tau} \varphi(q) \, dq.

이를 통해 시간 t에서 점 x에서 브라운 운동 입자의 밀도 ρ는 확산 방정식을 만족한다는 것을 보였다.

:

\frac{\partial\rho}{\partial t} = D\cdot \frac{\partial^2\rho}{\partial x^2},

초기 시간 t = 0에서 원점에서 N개의 입자가 시작한다고 가정하면, 확산 방정식의 해는 다음과 같다.

:

\rho(x,t) = \frac{N}{\sqrt{4\pi Dt}} \exp{\left(-\frac{x^2}{4Dt}\right)}.

이 식은 정규 분포이며, 아인슈타인은 이 식을 사용하여 모멘트를 계산했다. 첫 번째 모멘트는 0으로, 브라운 운동 입자가 왼쪽으로 이동할 확률과 오른쪽으로 이동할 확률이 같음을 의미한다. 두 번째 모멘트는 다음과 같이 주어진다.

:

\mathbb{E}{\left[x^2\right]} = 2 D t.

이 방정식은 평균 제곱 변위가 경과 시간과 확산 계수에 의해 결정됨을 나타낸다. 아인슈타인은 이 식을 통해 브라운 운동 입자의 변위가 경과 시간에 비례하는 것이 아니라 제곱근에 비례한다고 주장했다.^[11]

아인슈타인 이론의 두 번째 부분은 확산 상수를 물리적으로 측정 가능한 양과 관련짓는 것이다. 그는 서로 반대되는 힘 사이에 동적 평형이 확립되는 상황을 분석하여, 아보가드로 수와 분자 크기를 실험적으로 결정할 수 있는 방법을 제시했다.

삼투압 실험 외에도, 중력장에서 점성 유체에 현탁된 입자를 예로 들어 설명할 수 있다. 중력은 입자를 침전시키지만, 확산은 입자를 균질화하여 농도가 낮은 영역으로 이동시킨다. 동적 평형 상태에서 입자는 기압 분포에 따라 분포한다.

:

\rho = \rho_o \, \exp{\left({-\frac{m g h}{k_\text{B} T}}\right),

플럭스는 픽의 법칙에 의해 주어진다.

:

J = -D \frac{d\rho}{dh},

이 두 식을 결합하면, 확산 계수에 대한 아인슈타인 관계를 얻을 수 있다.

:

\frac{\mathbb{E}{\left[x^2\right]}}{2t} = D = \mu k_\text{B} T= \frac{\mu R T}{N_\text{A}} = \frac{RT}{6\pi\eta r N_\text{A}}.

이 식을 통해 시간 간격에 따른 평균 제곱 변위, 기체 상수 R, 온도 T, 점성 η, 입자 반지름 r을 측정하여 아보가드로 수 N_A를 결정할 수 있다.

4. 활용

브라운 운동은 여러 분야에서 다양하게 활용되고 있다.

1905년 알베르트 아인슈타인은 브라운 운동을 원자의 실재와 통계적 요동을 바탕으로 설명하는 논문을 발표했고,^[45] 이후 장 바티스트 페랭 등에 의해 실험적으로 증명되면서 원자론 확립에 기여하였다. 또한, 통계역학적 관점에서 미시적 세계를 이해하는 데 중요한 발판을 마련하여 통계역학 발전에 기여하였다.

루이 바슐리에는 1900년 박사 학위 논문 《투기이론》에서 금융시장의 가격변동을 브라운 운동으로 모형화하였고, 이후 1950년대 중반 미국의 경제학자 폴 새뮤얼슨이 바슐리에의 이론을 수정해 기하 브라운 운동(Geometric Brownian motion)을 만들어내는 등 다양한 분야에서 활용되고 있다.

4. 1. 원자론 확립

1905년 알베르트 아인슈타인(Albert Einstein)은 브라운 운동을 원자의 실재와 통계적 요동을 바탕으로 설명하는 논문을 발표했다.^[45] 이 이론은 이후 장 바티스트 페랭(Jean Baptiste Perrin) 등에 의해 실험적으로 증명되었다.

1808년 영국의 돌턴(John Dalton)이 주장한 원자론은 아보가드로(Amedeo Avogadro)와 볼츠만(Ludwig Eduard Boltzmann)으로 이어졌으나, 원자의 존재를 직접 증명하지 못해 에른스트 마흐(Ernst Mach)와 같은 물리학자들의 반대에 부딪혔다.

아인슈타인과 페랭은 브라운 운동에 대한 설명을 통해 주어진 시간 동안 입자가 움직인 거리를 측정하여, 일정 부피의 기체와 액체 속에 있는 분자의 수를 계산할 수 있게 되었다. 즉, 아보가드로 수를 얻어낸 것이다. 아인슈타인이 구한 값은 2.1 × 10²³으로 지금의 값과 오차가 있지만, 원자와 분자의 존재를 증명했다는 점에서 큰 의미를 갖는다.

브라운 운동에 대해 다음 식이 성립한다.

\left\langle(x-x_0)^2\right\rangle=\frac{2 R T}{N_\mathrm A f}t

여기서 x₀는 브라운 운동하는 물체의 평형 위치, R은 기체 상수, T는 절대온도, f는 이동도^[43], t는 충분히 경과한 시간(극한으로는 t → ∞)이다. 그리고 N_A는 아보가드로수이다. 아보가드로수를 제외하고는 브라운 운동과 관계없이 구할 수 있는 양이며, 프랑스의 물리화학자 장 페랭은 1908년 브라운 운동 관측을 바탕으로 N_A = 7.05 × 10²³ (자료에 따라 값이 다름)이라는 값을 얻었다.^[44]

볼츠만 상수 k_B = R / N_A를 사용하여 표기하면 다음 식이 된다.

\left\langle(x-x_0)^2\right\rangle=\frac{2 k_\mathrm B T}{f}t

1905년 아인슈타인의 논문에 의해, 브라운 운동은 원자의 존재를 명백하게 증명하는 사실이 되었다.

4. 2. 통계역학의 발전

브라운 운동은 통계역학적 관점에서 미시적 세계를 이해하는 데 중요한 발판을 마련했다. 고전 열역학에서는 거시적 성질만을 설명할 수 있었지만, 통계역학은 확률이론을 사용하여 분자의 자발적 움직임을 미시적 수준에서 이해할 수 있게 한다. 아인슈타인은 기존의 틀을 깨고 통계적 요동을 가정하여, 물 분자들의 불규칙적인 운동이 꽃가루 입자를 움직이게 한다는 것을 보였다. 이러한 불규칙적인 운동을 이산적 걸음으로 나타내는 것이 무작위 행보이며, 이는 분자의 확산 등 여러 현상을 설명하는 데 사용된다.^[45]

아인슈타인의 브라운 운동 이론은 열역학 법칙들이 통계적이라는 사실을 보여주었고, 볼츠만이 주장한 엔트로피에 대한 확률적, 통계적 해석을 뒷받침했다. 또한, 무작위 행보 개념은 통계역학의 여러 분야에 응용되고 있다.

4. 3. 다양한 분야로의 응용

루이 바슐리에는 1900년에 박사 학위 논문 《투기이론》에서 금융시장의 가격변동을 브라운 운동으로 모형화했다. 이는 주식 가격이 무작위적인 양만큼 상승하거나 하락하는 것을 담고 있다. 이후 1950년대 중반 미국의 경제학자 폴 새뮤얼슨이 바슐리에의 이론을 수정해서 기하 브라운 운동(Geometric Brownian motion)을 만들어냈다. 이처럼 시장을 움직이는 규칙을 찾기 위해 브라운 운동이 설명 도구로 쓰이고 있다.

노버트 위너는 브라운 운동을 수학적 확률 과정으로 만들었는데, 개념적으로는 무작위 행보와 유사하지만 불연속이 아닌 연속적인 변동을 다루는 위너 과정이라는 공식을 만들어냈다. 브라운 운동은 확률 보행으로 모델링될 수 있다.^[29]

일반적인 경우, 브라운 운동은 마르코프 과정이며 확률적 적분 방정식으로 설명된다.^[30]

5. 수리 모델

수학에서 브라운 운동은 노버트 위너의 이름을 딴 연속 시간 확률 과정인 '''위너 과정'''으로 설명된다. 위너 과정은 가장 잘 알려진 레비 과정(정상적인 독립 증분을 갖는 카들락 확률 과정) 중 하나이며, 순수 및 응용 수학, 경제학, 물리학에서 자주 발생한다.^[27]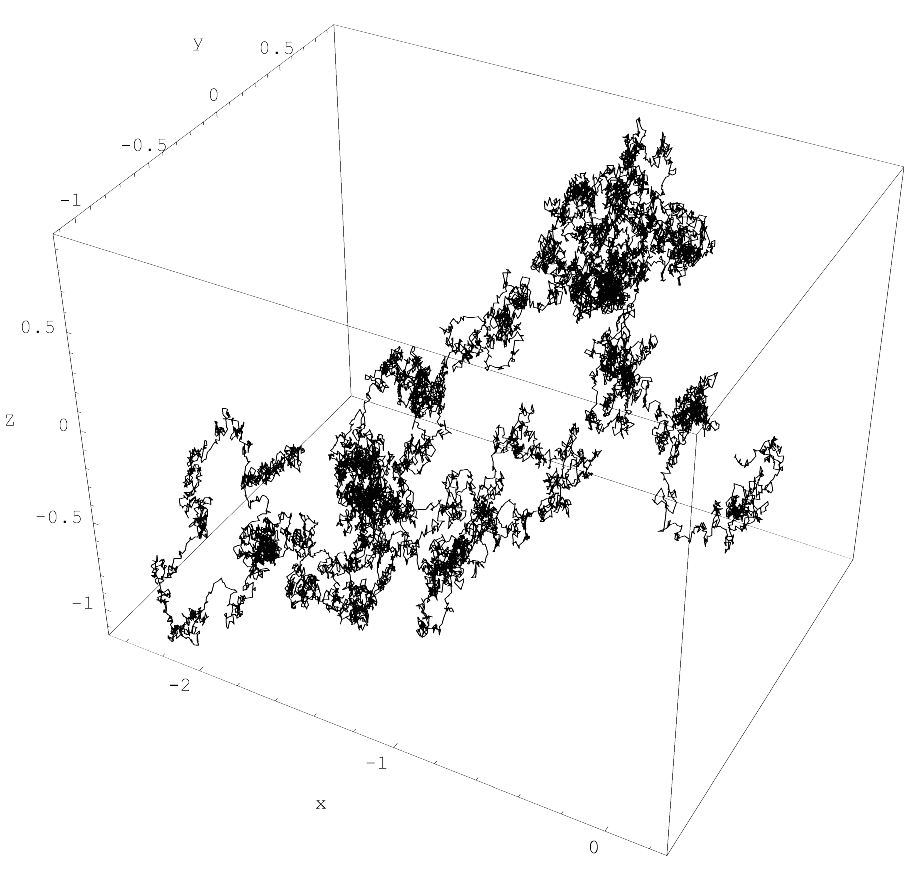

토러스에서 브라운 운동과 유사한 확률 보행의 애니메이션 예시. 스케일링 극한에서 확률 보행은 돈스커 정리에 따라 위너 과정에 접근한다.

위너 과정 는 다음 네 가지 사실로 특징지어진다.^[27]

는 거의 확실히 연속적이다.
는 독립 증분을 갖는다.
$W_t-W_s\sim \mathcal{N}(0,t-s)$ ()

\mathcal{N}(\mu, \sigma^2)

는 기댓값 과 분산 을 갖는 정규 분포를 나타낸다. 독립 증분을 갖는다는 조건은

0 \leq s_1 < t_1 \leq s_2 < t_2

이면

W_{t_1}-W_{s_1}

과

W_{t_2}-W_{s_2}

가 독립적인 확률 변수임을 의미한다.

위너 과정의 대안적인 특징은 소위 ''레비 특징화''인데, 이는 위너 과정이 이고 이차 변분 인 거의 확실히 연속적인 마팅게일이라는 것이다.

위너 과정은 확률 보행 또는 정상적인 독립 증분을 갖는 다른 이산 시간 확률 과정의 스케일링 극한으로 구성될 수 있다. 이는 돈스커 정리로 알려져 있다. 확률 보행과 마찬가지로 위너 과정은 1차원 또는 2차원에서 순환적이다(즉, 원점의 임의의 고정된 근방으로 거의 확실히 무한히 자주 돌아온다는 것을 의미한다). 그러나 3차원 이상에서는 순환적이지 않다. 확률 보행과 달리, 그것은 스케일 불변이다.

브라운 입자 자체의 위치의 시간적 진화는 랑주뱅 방정식으로 근사적으로 설명될 수 있는데, 이 방정식은 브라운 입자에 대한 용매의 열적 요동의 효과를 나타내는 무작위 힘장을 포함한다.

상의 브라운 운동의 무한소 생성자는 로 쉽게 계산할 수 있다. 여기서 는 라플라스 연산자를 나타낸다. 이 관찰은 차원 리만 다양체 상의 브라운 운동을 정의하는 데 유용하다. 상의 '''브라운 운동'''은 국소 좌표 , 에서 특성 작용소

\mathcal{A}

가 로 주어지는 상의 확산으로 정의된다. 여기서 는 국소 좌표에서 다음과 같이 주어지는 라플라스-벨트라미 연산자이다.

\Delta_{\mathrm{LB}}

위너 과정은 이산형인 랜덤 워크의 극한이 되는 확률 과정으로서 확률론, 확률 해석에서 매우 중요한 개념이다. 그리고 이것이 미분(특히 2차 미분)에 의해 어떤 종류의 무한소 잉여항을 생성한다는 규약을 설정한^[46] 특별한 미분(확률 미분)을 생각함으로써, 확률 적분 등의 개념이 정식화되고, 확률 해석이라는 한 분야가 전개된다. 매우 많은 입자의 영향이 브라운 운동의 불규칙성을 만든다는 생각은, 역시 수많은 원인에 의해 복잡한 변동을 보이는 주식 거래 등의 경제 활동에도 응용할 수 있기 때문에, 위너 과정이나 확률 미분을 응용한 확률 해석은 금융 공학 등의 분야에서도 활발하게 사용되고 있다.

5. 1. 위너 과정의 정의

확률 공간 $(\Omega,\mathcal{F},P)$ 상에서 정의된 연속 확률 과정 $W(t)$는 다음 성질을 만족하면 위너 과정이라고 한다.^[46]

임의의 $t_1 < t_2 < \dots < t_n$에 대해, $W(t_1) - W(0), W(t_2) - W(t_1), \dots, W(t_n) - W(t_{n-1})$는 독립이다.
임의의 $t \ge s$에 대해, $W(t) - W(s)$는 정규 분포 $N(0, t-s)$를 따른다.

(주의) 이러한 확률 과정이 수학적으로 존재한다는 것은 증명이 필요하다.^[46]

5. 2. 위너 과정의 성질

위너 과정은 다음과 같은 성질을 갖는다.

샘플 패스(sample path)는 확률 1로 미분 불가능하다. 즉, 브라운 운동은 매우 울퉁불퉁한 곡선이 된다.^[46]
는 마팅게일(martingale)이 된다. 이것은 브라운 운동에 관한 확률 적분을 생각할 때 매우 중요한 성질이다.

참조

_[1] 논문 Teaching the Growth, Ripening, and Agglomeration of Nanostructures in Computer Experiments
_[2] 서적 The Feynman Lectures of Physics, Volume I
_[3] 논문 Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen http://www.physik.un[...] 1905-01-01
_[4] 웹사이트 The Nobel Prize in Physics 1926 https://www.nobelpri[...] 2019-05-29
_[5] 논문 Brownian motion of molecules: the classical theory 1995-01-01
_[6] 논문 On the random walk and Brownian motion https://www.ams.org/[...] 1962-02-01
_[7] 웹사이트 Donsker invariance principle - Encyclopedia of Mathematics https://encyclopedia[...] 2020-06-28
_[8] 서적 Atoms https://archive.org/[...] London : Constable
_[9] 서적 Gases, Liquids and Solids: And Other States of Matter https://books.google[...] Cambridge University Press
_[10] 서적 The (Mis)behavior of Markets: A Fractal View of Risk, Ruin, and Reward https://archive.org/[...] Basic Books
_[11] 서적 Investigations on the Theory of the Brownian Movement http://users.physik.[...] Dover Publications 2013-12-25
_[12] 서적 The Collected Papers of Albert Einstein, Volume 2 Princeton University Press
_[13] 서적 Nonequilibrium Statistical Thermodynamics https://archive.org/[...] John Wiley & Sons
_[14] 서적 Electricity and Matter https://archive.org/[...] Yale University Press
_[15] 논문 Zur Kinetik der in Lösung befindlichen Körper
_[16] 서적 La Relativité, Poincaré et Einstein, Planck, Hilbert Harmattan
_[17] 서적 Electricity in Gases https://archive.org/[...] Clarendon Press
_[18] 문서 See P. Clark 1976, p. 97
_[19] 문서 See P. Clark 1976 for this whole paragraph
_[20] 논문 Sur le chemin moyen parcouru par les molécules d'un gaz et sur son rapport avec la théorie de la diffusion https://archive.org/[...]
_[21] 논문 Zum Andenken an Marian von Smoluchowski
_[22] 논문 Essai d'une théorie cinétique du mouvement Brownien et des milieux troubles https://archive.org/[...]
_[23] 논문 Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen https://zenodo.org/r[...]
_[24] 논문 Measurement of the instantaneous velocity of a Brownian particle http://chaos.utexas.[...]
_[25] 서적 Dynamics and Evolution of Galactic Nuclei Princeton University Press
_[26] 논문 The Proper Motion of Sagittarius A*. II. The Mass of Sagittarius A*
_[27] 서적 Stochastic Processes https://www.cambridg[...] Cambridge University Press 2011-01-01
_[28] 논문 Gaussian free fields for mathematicians https://link.springe[...] 2007-05-09
_[29] 서적 Aspects and applications of the random walk North Holland
_[30] 논문 Spherical particle Brownian motion in viscous medium as non-Markovian random process
_[31] 서적 Fundamentals of Noise and Vibration Analysis for Engineers by M. P. Norton 2003-01-01
_[32] 논문 Power spectral density of a single Brownian trajectory: what one can and cannot learn from it https://iopscience.i[...] 2018-01-01
_[33] 서적 材料における拡散：格子上のランダム・ウォーク http://www.rokakuho.[...] 内田老鶴圃 2009-12-01
_[34] 웹사이트 ウィーナー過程とブラウン運動 http://www.findai.co[...] 金融大学 2015-12-27
_[35] 문서 Brown 1828
_[36] 웹사이트 ブラウン運動と非平衡統計力学 http://www.gakushuin[...] 学校法人学習院 2015-12-27
_[37] Harvtxt 1905
_[38] 웹사이트 Stokes-Einstein-Sutherland equation http://www.physik.un[...] 2017-01-11
_[39] Harvtxt 1906
_[40] Harvtxt 1900
_[41] 웹사이트 ブラウン運動 http://tsukubabiryuu[...] NPO法人筑波微粒子・界面・環境研究会 2015-12-27
_[42] 문서 ブラウン運動抵抗の熱雑音 https://granite.phys[...]
_[43] 문서 媒질의 점성에 관계, 브라운 운동하는 물체의 속도를 v라 하면, fv는 그 속도에 비례하는 저항력이 된다.
_[44] 웹사이트 Brownian Motion and Molecular Reality http://web.lemoyne.e[...]
_[45] Harvtxt 1905
_[46] 문서 이토 규약과 스트라토노비치 규약

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com