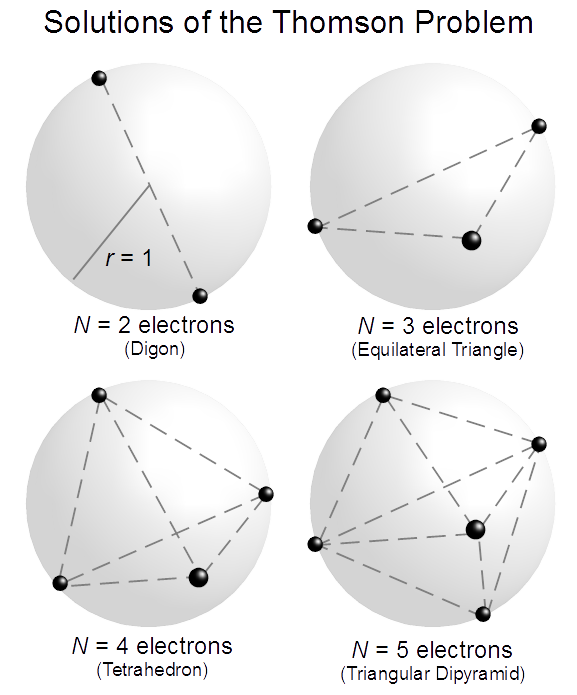
삼각쌍뿔

1. 개요

삼각쌍뿔은 두 개의 정사면체를 면과 면을 맞대어 붙여 만든 다면체로, 5개의 꼭짓점, 9개의 모서리, 6개의 면으로 구성된다. 정삼각형 면을 갖는 삼각쌍뿔은 존슨 다면체 중 하나이며, 겉넓이는 $\{3\backslash sqrt\{3\}\backslash over2\}a^2$, 부피는 $\{\backslash sqrt\{2\}\backslash over6\}a^3$이다. 삼각쌍뿔은 삼각 프리즘의 쌍대 다면체이며, 톰슨 문제의 해와 분자 기하학, 색채 이론 등 다양한 분야에서 활용된다.

2. 특수한 경우

삼각쌍뿔은 두 개의 정사면체를 면과 면을 맞대어 붙여서 만들 수 있으며, 이를 정이각뿔이라고 한다. 이 다면체는 여섯 개의 정삼각형, 다섯 개의 꼭짓점, 아홉 개의 모서리를 갖는다. 두 정사면체가 대칭적으로 규칙적이고 두 꼭짓점이 밑면의 중심을 지나는 직선 위에 있으면 '정'삼각쌍뿔이라고 한다.

모든 면이 정삼각형인 삼각쌍뿔은 델타다면체이자 존슨 다면체(J12)가 된다.

2. 1. 정이각뿔

다른 이면체와 마찬가지로, 삼각쌍뿔은 두 개의 정사면체를 면과 면을 맞대어 붙여서 만들 수 있다. 이때 만들어지는 다면체는 여섯 개의 정삼각형, 다섯 개의 꼭짓점, 아홉 개의 모서리를 갖는다. 삼각쌍뿔에서 두 정사면체가 대칭적으로 규칙적이고 두 꼭짓점이 밑면의 중심을 지나는 직선 위에 있으면 '정'삼각쌍뿔이라고 한다. 그렇지 않으면 '사'삼각쌍뿔이다.

2. 2. 존슨 다면체

삼각쌍뿔의 모든 면이 정삼각형이면 델타다면체이자 존슨 다면체(J12)가 된다. 존슨 다면체는 모든 면이 정다각형인 볼록 다면체를 말한다.

3. 성질

삼각쌍뿔은 5개의 꼭짓점, 9개의 모서리, 6개의 정삼각형 면으로 구성된 다면체이다. 슈타이니츠 정리에 따르면, 삼각쌍뿔은 9개의 모서리를 가진 그래프로 나타낼 수 있으며, 정사면체를 나타내는 바퀴 그래프의 꼭짓점에 하나의 꼭짓점을 추가하여 구성된다.

삼각쌍뿔은 3차원 점군 대칭성, 즉 12차의 이면체군 $D\_\{3\; \backslash mathrm\{h\}\}$을 갖는다. 이는 회전 대칭축(두 꼭짓점과 밑면의 중심을 수직으로 지나는 직선)을 중심으로 1/3, 2/3, 1배 각도만큼 회전해도 모양이 변하지 않는 회전 대칭과, 밑면의 각 이등분선에 대한 거울 대칭, 그리고 수평면에 대한 반사 대칭을 포함한다. 또한, 삼각쌍뿔은 면 전이적이다.

모든 면이 정삼각형인 삼각쌍뿔은 델타다면체이자 존슨 다면체 $J\_\{12\}$에 속한다. 두 개의 정사면체를 붙여 만든 합성 다면체의 예이기도 하다.

모서리 길이가 $a$인 정삼각쌍뿔의 표면적 $A$와 부피 $V$는 다음과 같다.

$$\backslash begin\{align\}$$

A &= \frac{3\sqrt{3}}{2}a^2 &\approx 2.598a^2, \\

V &= \frac{\sqrt{2}}{6}a^3 &\approx 0.238a^3.

\end{align}

삼각쌍뿔의 이면각은 두 개의 정사면체 이면각을 더하여 구할 수 있다. 인접한 삼각형 면 사이의 삼각쌍뿔 이면각은 정사면체의 이면각과 같은 70.5도이고, 두 정사면체가 붙어 있는 모서리에서 인접한 삼각형의 이면각은 이의 두 배인 141.1도이다.

4. 그래프

슈타이니츠 정리에 따르면, 어떤 그래프가 다면체의 골격으로 나타낼 수 있으려면 평면 그래프(그래프의 모서리가 교차하지 않고 한 점에서 만남)이자 3-연결 그래프(두 꼭짓점 중 어느 하나를 제거해도 연결된 부분 그래프가 남음)여야 한다. 삼각쌍뿔은 아홉 개의 모서리를 가진 그래프로 나타낼 수 있으며, 정사면체를 나타내는 바퀴 그래프의 꼭짓점에 하나의 꼭짓점을 추가하여 구성된다.

5. 쌍대다면체

삼각쌍뿔은 삼각기둥의 쌍대 다면체이다. 삼각쌍뿔의 꼭짓점은 삼각기둥의 면에 대응하고, 삼각쌍뿔의 모서리는 삼각기둥의 모서리에 대응한다. 삼각기둥은 삼각쌍뿔과 같은 대칭성을 가진 다섯 개의 면, 아홉 개의 모서리, 여섯 개의 꼭짓점을 가지고 있다.

'''정삼각기둥의 쌍대'''는 아르키메데스의 정삼각기둥(밑면과 옆면이 모두 정다각형인 정삼각기둥)의 쌍대가 되는 다면체이다. 카탈란의 다면체와 마찬가지로 이면각이 같다는 성질을 가진다.

성질
구성면: 이등변삼각형(꼭지각 97.18°, 밑각 41.41°, 변의 비율 1:1:1.5) 6개
모서리: 9
꼭짓점: 5
쌍대: 아르키메데스의 정삼각기둥

6. 관련 다면체

（반으로 나누기）--
（중간에 정삼각기둥 추가）

（각뿔의 꼭짓점 수 증가）--
（확장）--
（특정한 두 개의 정삼각형을 정사각형으로 대체）