삼차 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 성질
4. 응용
- 4.1. 보간법
5. 기타
- 5.1. 공선점
- 5.2. 삼차 포물선
참조

1. 개요

삼차 함수는 최고차항의 차수가 3인 다항식 함수를 의미하며, 대수학, 기하학 등 다양한 분야에서 연구되어 왔다. 삼차 방정식의 해법은 고대부터 연구되었으며, 16세기에는 이탈리아 수학자들에 의해 대수적 해법이 발견되었다.

삼차 함수의 그래프는 변곡점에 대해 점대칭이며, 최대 세 개의 실근을 가질 수 있다. 그래프는 임계점, 변곡점 등의 특이점을 가지며, 판별식을 통해 근의 개수를 파악할 수 있다. 삼차 함수는 스플라인 보간법과 같은 응용 분야에서 활용되며, 삼차 포물선이라고도 불린다.

더 읽어볼만한 페이지

함수 방정식 - 이차 함수
이차 함수는 $f(x)=ax^2+bx+c$ ( $a\ne0$ ) 꼴의 차수가 2인 다항함수로서 포물선 형태의 그래프를 가지며 다양한 수학적 성질과 응용 분야를 가진다.
함수 방정식 - 일차 함수
일차 함수는 실수 집합을 정의역과 공역으로 하는 함수로, f(x) = ax + b 꼴로 표현되며, 기울기와 y절편을 가지는 직선의 그래프를 나타낸다.
초등대수학 - 이차 방정식
이차 방정식은 최고차항이 2차인 대수 방정식으로, $ax^2 + bx + c = 0$ 형태로 표현되며 근의 공식으로 해를 구하고 판별식에 따라 실근 또는 허근을 가지며 여러 분야에 응용된다.
초등대수학 - 방정식
방정식은 수학에서 두 식이 등호로 연결된 형태로, 미지수의 값을 구하는 것을 목표로 하며, 다양한 종류로 분류되어 여러 수학 및 과학 분야에서 활용된다.
방정식 - 피타고라스 정리
피타고라스 정리는 직각삼각형에서 직각변의 제곱의 합이 빗변의 제곱과 같다는 정리로, a² + b² = c²으로 표현되며, 한 변의 길이를 계산하는 데 사용되고, 여러 지역에서 알려졌으나 피타고라스 학파에 의해 체계화되었다고 전해진다.
방정식 - 케플러 방정식
케플러 방정식은 천체의 궤도를 기술하는 초월 방정식으로, 행성의 위치를 결정하는 데 사용되며 평균 이상, 편심 이상, 이심률 간의 관계를 나타낸다.

삼차 함수
개요
함수 종류	다항 함수
차수	3
변수 종류	실변수
정의역	R (실수 전체 집합)
일반적인 형태
함수식	f(x) = ax³ + bx² + cx + d (단, a ≠ 0)
변수	a b c d
특징
근	삼차 방정식의 해는 1개 또는 3개의 실근을 가짐

2. 역사

삼차 방정식의 해법은 고대 바빌로니아, 그리스, 이집트, 인도, 중국 등에서 기하학적 문제를 풀기 위한 방법으로 연구되었다.^[1] 바빌로니아 사람들은 정육면체의 부피를 2배로 하는 문제나 세 변의 길이의 비가 주어진 직육면체의 부피를 구하는 문제 등을 다루면서 삼차 방정식의 해법을 연구하였다.^[1]

기원전 4세기경 플라톤은 정육면체의 부피를 2배로 늘리는 문제에 대한 해법을 제시하였고, 메나이크모스는 원뿔 곡선을 이용하여 정육면체의 한 변의 길이를 작도하는 방법을 발견하였다.^[2]

이후 16세기 이탈리아의 수학자 시피오네 델 페로가 최초로 일반적인 삼차 방정식의 해법을 발견하였으나, 델 페로는 자신의 해법을 공개하지 않았다.^[3] 델 페로의 제자였던 안토니오 마리아 피오르는 델 페로의 해법을 전수받았고, 니콜로 폰타나 탈리아와의 수학 시합에서 삼차 방정식 문제들을 모두 풀어내면서 유명해졌다.^[3] 탈리아는 독자적으로 삼차 방정식의 해법을 발견하였고, 지롤라모 카르다노에게 자신의 해법을 전수하였다.^[3] 카르다노는 탈리아의 해법을 바탕으로 연구를 계속하여 1545년 자신의 저서 《위대한 술법》에서 삼차 방정식과 사차 방정식의 일반적인 해법을 발표하였다.^[3]

3. 성질

삼차 함수는 연속 함수이므로 중간값 정리에 의해 적어도 하나의 실근을 갖는다. 또한, 대수학의 기본 정리에 의해 최대 3개의 실근을 가질 수 있다.

삼차 함수의 근의 판별식은 다음과 같다.

: $D = b^2c^2 - 4ac^3 - 4b^3d -27a^2d^2 + 18abcd$

판별식의 값에 따라 근을 다음과 같이 분류할 수 있다.

$D > 0$ 이면 서로 다른 세 개의 실근을 갖는다.
$D < 0$ 이면 하나의 실근을 갖는다.
$D = 0$ 이면 하나의 단순근과 다른 하나의 중근을 갖거나 하나의 삼중근을 갖는다.

뉴턴 방법 등을 통해 근을 수치적으로 구할 수도 있다.

최고차항 계수에 따라 무한대에서의 극한값은 다음과 같다.

최고차항 계수가 양수일 때:

:

\lim\limits_{x \to +\infty} f(x) = +\infty

,

\lim\limits_{x \to -\infty} f(x) = -\infty

최고차항 계수가 음수일 때:

:

\lim\limits_{x \to +\infty} f(x) = -\infty

,

\lim\limits_{x \to -\infty} f(x) = +\infty

삼차 함수의 그래프는 삼차 곡선이지만, 모든 삼차 곡선이 함수의 그래프는 아니다. 삼차 함수는 y|y^영어=x|x^영어³+px|px^영어 형태의 함수의 그래프와 닮음이다. 평행 이동, 동일 비율 확대/축소, y|y^영어축에 대한 반사 등을 통해 그래프를 변환할 수 있다.

아핀 변환을 기준으로 삼차 함수의 그래프는 다음 세 가지 중 하나로 나타낼 수 있다.

y|y^영어=x|x^영어³+x|x^영어
y|y^영어=x|x^영어³
y|y^영어=x|x^영어³-x|x^영어

일반적인 삼차 함수 y|y^영어=ax|ax^영어³+bx|bx^영어²+cx|cx^영어+d|d^영어는 다음과 같은 변환을 통해 정규형으로 바꿀 수 있다.

1. a|a^영어 < 0이면 x|x^영어 → –x|x^영어로 변환하여 a|a^영어 > 0으로 만든다.

2. x|x^영어 = x|x^영어₁ – b|b^영어/3a|a^영어로 변환하여 y|y^영어=ax|ax^영어₁³+px|px^영어₁+q|q^영어 형태로 만든다.

3. y|y^영어 = y|y^영어₁ + q|q^영어로 변환하여 y|y^영어₁=ax|ax^영어₁³+px|px^영어₁ 형태로 만든다.

4. x|x^영어₁=x|x^영어₂/a|a^영어, y|y^영어₁=y|y^영어₂/a|a^영어로 변환하여 y|y^영어₂=x|x^영어₂³+px|px^영어₂ 형태로 만든다.

5. p|p^영어 ≠ 0이면 x|x^영어₂=x|x^영어₃p|p^영어, y|y^영어₂=y|y^영어₃p|p^영어³로 변환하여 y|y^영어₃ =x|x^영어₃³ + x|x^영어₃sgn(p)|sgn(p)^영어 형태로 만든다.

최종적으로 g(u)|g(u)^영어=u|u^영어³ + k u|k u^영어 (k|k^영어 ∈ −1, 0, 1|−1, 0, 1^영어}) 형태의 정규형을 얻을 수 있으며, k|k^영어 값에 따라 극값의 유무가 결정된다.

3. 1. 임계점과 변곡점

삼차 함수의 임계점은 함수의 기울기가 0이 되는 점, 즉 정지점이다.^[2] 삼차 함수 f|f^영어가 다음과 같이 정의될 때:

:f(x)|f(x)^영어 = ''ax''³ + ''bx''² + ''cx'' + ''d''

임계점은 함수의 도함수가 0이 되는 x|x^영어 값에서 발생한다.

:

3ax^2 + 2bx + c = 0

이 방정식의 해는 근의 공식을 사용하여 다음과 같이 나타낼 수 있다.

:

x_\text{critical}=\frac{-b \pm \sqrt {b^2-3ac}}{3a}.

제곱근 내부의 표현식 (b^2 – 3ac|b^2 – 3ac^영어)의 부호는 임계점의 수를 결정한다. 이 값이 양수이면 두 개의 임계점(극댓값, 극솟값)을 갖는다. 0이면 하나의 임계점(변곡점)을 갖는다. 음수이면 (실수) 임계점은 존재하지 않는다.

함수의 변곡점은 오목성이 바뀌는 지점이다.^[3] 변곡점은 이계도함수

f''(x) = 6ax + 2b

가 0이고 삼계도함수가 0이 아닌 경우에 발생한다. 따라서 삼차 함수는 항상 하나의 변곡점을 가지며, 이는 다음과 같다.

:

x_\text{inflection} = -\frac{b}{3a}.

즉, 삼차 함수 f|f^영어는 단 하나의 변곡점을 가지며, 이 변곡점은 이계도함수의 유일한 영점이다.

:

x_W = -\frac{b}{3a}

삼차 함수 f|f^영어의 그래프는 변곡점에 대해 점대칭이다.^[5]

3. 2. 대칭성

기함수인

y=x^3+px

형태의 삼차 함수는 변곡점이 원점이다. 그래프는 변곡점에 대해 대칭이며 변곡점을 중심으로 반 바퀴 회전해도 변하지 않는다. 이러한 성질은 닮음에 의해 변하지 않으므로 모든 삼차 함수에 대해 다음이 성립한다.^[5]

삼차 함수의 그래프는 변곡점에 대해 대칭이며 변곡점을 중심으로 반 바퀴 회전해도 변하지 않는다.

각 삼차 함수는 단 하나의 변곡점을 가지며, 이 변곡점은 이계도함수의 유일한 영점이다. 삼차 함수의 그래프는 변곡점에 관해 점대칭이다.^[5]

3. 3. 근

(임의의 다항식 함수가 그러하듯이) 삼차 함수는 연속 함수이므로 중간값 정리가 적용되어, 삼차 함수가 적어도 하나의 실근을 가짐을 알 수 있다. 한편, 대수학의 기본 정리에 의해, 임의의 n차 다항식 함수의 근의 개수는 최대 n개이므로, 삼차 함수의 실근의 개수는 하나 이상 셋 이하이다.

삼차 함수의 근의 배치에 대해서는 삼차 방정식 항목에서 다룬다. 일반적인 삼차 함수에 대한 판별식은 다음과 같다.

:

D = b^2c^2 - 4ac^3 - 4b^3d -27a^2d^2 + 18abcd

이 판별식을 사용하여 근을 분류할 수 있다.

$D > 0$ 이면 서로 다른 세 개의 실근을 갖는다.
$D < 0$ 이면 하나의 실근을 갖는다.
$D = 0$ 이면 하나의 단순근과 다른 하나의 중근을 갖거나 하나의 삼중근을 갖는다.

뉴턴 방법 등의 수치적인 근 탐색도 수행할 수 있다.

3. 4. 무한대에서의 거동

최고차항 계수가 양수일 때,

:

\lim\limits_{x \to +\infty} f(x) = +\infty

,

\lim\limits_{x \to -\infty} f(x) = -\infty

최고차항 계수가 음수일 때,

:

\lim\limits_{x \to +\infty} f(x) = -\infty

,

\lim\limits_{x \to -\infty} f(x) = +\infty

가 성립한다.

3. 5. 분류

삼차 함수의 그래프는 삼차 곡선이지만, 모든 삼차 곡선이 함수의 그래프는 아니다.

삼차 함수는 네 개의 매개변수에 의존하지만, 그래프는 몇 가지 모양만 가질 수 있다. 실제로, 삼차 함수의 그래프는 항상 y|y^영어=x|x^영어³+px|px^영어 형태의 함수의 그래프와 닮음이다. 이러한 유사성은 좌표축에 평행한 평행 이동, 동일 비율 확대/축소 및 필요에 따라 y|y^영어축에 대한 반사(거울상)의 조합으로 만들 수 있다. 추가적인 비균일 스케일링은 그래프를 다음 세 가지 삼차 함수 중 하나의 그래프로 변환할 수 있다.

y|y^영어=x|x^영어³+x|x^영어
y|y^영어=x|x^영어³
y|y^영어=x|x^영어³-x|x^영어

이는 아핀 변환을 기준으로 삼차 함수의 그래프가 세 개뿐임을 의미한다.

일반적인 삼차 함수 y|y^영어=ax|ax^영어³+bx|bx^영어²+cx|cx^영어+d|d^영어에서 시작할 때, 위의 기하학적 변환은 다음과 같은 방식으로 만들 수 있다.

1. a|a^영어 < 0이면 변수 변경 x|x^영어 → –x|x^영어를 통해 a|a^영어 > 0이라고 가정할 수 있다. 이 변수 변경 후, 새 그래프는 y|y^영어축에 대한 이전 그래프의 거울상이다.

2. 변수 변경 x|x^영어 = x|x^영어₁ – b|b^영어/3a|a^영어는 y|y^영어=ax|ax^영어₁³+px|px^영어₁+q|q^영어 형태의 함수를 제공한다. 이는 x|x^영어축에 평행한 평행 이동에 해당한다.

3. 변수 변경 y|y^영어 = y|y^영어₁ + q|q^영어는 y|y^영어축에 대한 평행 이동에 해당하며 y|y^영어₁=ax|ax^영어₁³+px|px^영어₁ 형태의 함수를 제공한다.

4. 변수 변경 x|x^영어₁=x|x^영어₂/a|a^영어, y|y^영어₁=y|y^영어₂/a|a^영어는 균일한 스케일링에 해당하며 a|a^영어로 곱한 후 y|y^영어₂=x|x^영어₂³+px|px^영어₂, 유사성을 통해 얻을 수 있는 가장 간단한 형태의 함수를 제공한다.

5. p|p^영어 ≠ 0이면 비균일 스케일링 x|x^영어₂=x|x^영어₃p|p^영어, y|y^영어₂=y|y^영어₃p|p^영어³는 p|p^영어³으로 나눈 후 y|y^영어₃ =x|x^영어₃³ + x|x^영어₃sgn(p)|sgn(p)^영어를 제공하며, 여기서 sgn(p)|sgn(p)^영어는 p|p^영어의 부호에 따라 1 또는 –1의 값을 갖는다. 만약 sgn(0)|sgn(0)^영어=0을 정의하면, 함수의 마지막 형태는 모든 경우에 적용된다(x|x^영어₂ = x|x^영어₃ 및 y|y^영어₂ = y|y^영어₃).

적절한 평행 이동 및 원점에 대한 확대 축소를 수행하여 임의의 삼차 함수 f|f^영어를 g(u)|g(u)^영어=u|u^영어³ + k u|k u^영어 형태의 삼차 함수 g|g^영어로 바꿀 수 있다. 여기서 1차항의 계수는 k|k^영어 ∈ −1, 0, 1|−1, 0, 1^영어}로 취할 수 있다. 이러한 정규형(normal form)은 다음과 같이 특징을 설명할 수 있다.

k|k^영어 = −1: g|g^영어는 두 개의 극값을 가진다.
k|k^영어 = 0: 극값은 일치하여 하나의 안장점이 된다.
k|k^영어 = 1: g|g^영어는 극값도 안장점도 가지지 않는다(실제로 이 때 도함수는 항상 양수이다).

이 정규형을 얻기 위해 수행한 변환은 극값의 존재성을 바꾸지 않으므로, 이러한 특징은 원래 함수 f|f^영어에도 적용할 수 있다. 사실 계수 k|k^영어는 f|f^영어의 1계 도함수의 판별식의 부호를 바꾼 것이 된다.

4. 응용

삼차 함수는 보간법에 응용된다.

4. 1. 보간법

스플라인 보간법

함수 값과 두 점에서의 미분 값을 알면, 동일한 네 개의 값을 갖는 단 하나의 삼차 함수가 존재하며, 이를 삼차 에르미트 스플라인이라고 한다.

이 사실을 사용하는 표준적인 방법은 두 가지가 있다. 첫째, 물리적 측정 등으로 어떤 샘플링 지점에서 함수 값과 그 미분 값을 알고 있다면, 연속적 미분 가능 함수인 구간별 삼차 함수로 함수를 ''보간''할 수 있다.

둘째, 함수 값이 여러 지점에서 알려져 있는 경우, 삼차 보간법은 연속적 미분 가능 함수이며 구간별 삼차 함수로 함수를 근사하는 것이다. 고유하게 정의된 보간을 위해서는 끝점에서의 미분 값 또는 끝점에서의 영 곡률과 같은 두 가지 제약 조건을 추가해야 한다.

5. 기타

(이전 결과물에서 '기타' 섹션 내용이 없어 수정할 내용이 없습니다.)

5. 1. 공선점

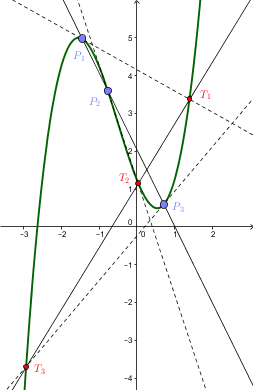
점 , , (파란색)는 공선점이며 의 그래프에 속한다. 점 , , (빨간색)는 이 점들에서 그래프에 대한 (점선) 접선과 그래프 자체의 교차점이다. 이 점들 또한 공선점이다.

삼차 함수 그래프 위의 세 공선점에서 그은 접선은 다른 공선점에서 다시 삼차 함수와 교차한다.^[4] 이는 다음과 같이 확인할 수 있다.

이 성질은 강체 변환에 불변하므로, 함수를 다음 형식으로 가정할 수 있다.

:

f(x)=x^3+px.

만약 가 실수라면, 점 에서 의 그래프에 대한 접선은 다음과 같다.

:}.

이 직선과 의 그래프 사이의 교차점은 방정식 를 풀어서 얻을 수 있다.

:

x^3+px=\alpha^3+p\alpha+ (x-\alpha)(3\alpha^2+p)

위 식은 다음과 같이 다시 쓸 수 있다.

:

x^3 - 3\alpha^2 x +2\alpha^3=0,

이는 다음과 같이 인수분해된다.

:

(x-\alpha)^2(x+2\alpha)=0.

따라서 접선은 다음 점에서 삼차 함수와 교차한다.

:

(-2\alpha, -8\alpha^3-2p\alpha)=(-2\alpha, -8f(\alpha)+6p\alpha).

그러므로 그래프의 점 를 접선이 그래프와 교차하는 다른 점에 대응시키는 함수는 다음과 같다.

:

(x,y)\mapsto (-2x, -8y+6px).

이것은 공선점을 공선점으로 변환하는 아핀 변환이다. 따라서 이 결과는 성립한다.

5. 2. 삼차 포물선

'''삼차 포물선''' 또는 '''입방 포물선'''^[6]은 삼차 함수의 그래프가 그리는 평면 삼차 곡선으로 정의된다. 곡선의 성질은 평행 이동 불변이므로 이 곡선의 특징을 조사하려면 인 삼차 다항식만 보면 충분하다.

참조

_[1] 서적 Pure Mathematics 2 https://books.google[...] Nelson Thornes 1979
_[2] 웹사이트 Stationary Point https://mathworld.wo[...] 2020-07-27
_[3] 서적 Applied Calculus https://books.google[...] John Wiley & Sons 2017-12-11
_[4] 간행물 Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions https://archive.org/[...] Deighton, Bell, and Co. 2016-06-17
_[5] 웹사이트 All cubic polynomials are point symmetric http://educadores.di[...] 2015-12-14
_[6] 서적 グラフ教授 https://books.google[...] 大阪修文館

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com