판별식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

판별식은 대수학에서 다항식의 근의 성질을 나타내는 중요한 개념이다.

판별식은 대수적으로 닫힌 체 K 계수의 다항식 f(x) = a₀ + a₁x + a₂x² + ... + aₙxⁿ = aₙ(x - x₁)(x - x₂) ... (x - xₙ) ∈ K[x] (aₙ ≠ 0)에 대해 정의되며, aₙ²ⁿ⁻²∏ᵢ<ⱼ(xᵢ - xⱼ)² 또는 다른 등가 표현으로 나타낼 수 있다. 판별식은 다항식이 중근을 갖는지 여부를 판별하는 데 사용되며, 2차 다항식의 경우 b² - 4ac로 계산된다. 3차 다항식의 경우 b²c² - 4ac³ - 4b³d - 27a²d² + 18abcd로 계산되며, 4차 다항식의 판별식은 더욱 복잡한 형태로 나타난다.

판별식은 중근의 존재, 갈루아 군과의 관계, 변수의 사영 변환에 대한 불변성, 다항식 곱과의 관계, 동차성 등 다양한 성질을 갖는다. 판별식은 대수적 수체의 정수환의 크기를 측정하는 데 사용되며, 이차 형식, 원뿔 곡선, 이차 곡면 등 다양한 대수적 구조로 일반화된다. 대수기하학에서는 평면 대수 곡선이나 초곡면을 연구하는 데 활용된다.

더 읽어볼만한 페이지

행렬식 - 부피 형식
부피 형식은 다양체의 방향 결정, 측도 정의, 벡터장 발산 계산에 사용되는 미분 형식의 일종으로, 유향 다양체에서는 밀도와 관련되며, 리 군, 심플렉틱 다양체, 준-리만 다양체 등에서 자연스럽게 정의된다.
행렬식 - 야코비 행렬
야코비 행렬은 열린 집합 U에서 정의된 함수 f의 각 성분 편도함수를 요소로 가지는 행렬이며, 함수가 미분 가능할 때 전미분을 나타내고, n=m일 경우 행렬식은 함수의 동작에 대한 정보를 제공하며 다양한 분야에 응용된다.
원뿔 곡선 - 이심률
이심률은 원뿔곡선의 형태를 결정하는 값으로, 초점과 준선으로부터의 거리 비율로 정의되며, 값에 따라 원, 타원, 포물선, 쌍곡선으로 구분되고, 타원과 쌍곡선의 경우 중심과 초점 사이의 거리와 반장축의 비율로 나타낼 수 있으며, 이심률이 같은 원뿔곡선은 서로 닮음이다.
원뿔 곡선 - 포물선
포물선은 원뿔 곡선의 일종으로, 메나이크모스에 의해 처음 연구되었으며, 아르키메데스와 아폴로니오스에 의해 성질이 연구되었고, 고전역학, 광학 등 다양한 분야에 응용되며, 초점과 준선, 이차 함수의 그래프 등의 기하학적 성질을 가진다.
이차 형식 - 밀너 환
밀너 환은 체 위의 가역원군으로 정의되는 등급환으로, 각 등급 성분인 밀너 K군은 대수적 K-이론, 고차 류체론, 갈루아 코호몰로지, 에탈 코호몰로지, 이차 형식 등 여러 수학 분야와 연결되는 심오한 추측들과 연관된다.
이차 형식 - 클리퍼드 대수
클리퍼드 대수는 가환환 위의 가군과 이차 형식으로부터 정의되는 단위 결합 대수로서, 보편 성질이나 텐서 대수의 몫대수를 통해 정의 및 구성되며, 물리학, 컴퓨터 비전, K이론 등 다양한 분야에서 응용되는 대수적 구조이다.

판별식
개요
정의	다항식 계수의 함수로, 다항식의 근에 대한 정보를 제공함
관련 항목	판별식
이차 방정식
방정식	ax²+bx+c=0
판별식	D = b² - 4ac
근의 개수	D > 0: 서로 다른 두 실근 D = 0: 중근 (실근) D < 0: 서로 다른 두 허근
삼차 방정식
방정식	ax³+bx²+cx+d=0
판별식	D = b²c² - 4ac³ - 4b³d - 27a²d² + 18abcd
근의 개수	판별식의 부호에 따라 실근의 개수 판별 가능
일반적인 정의
대상	임의의 다항식
내용	주어진 다항식의 근이 중근을 가지는지 여부를 판별하는 데 사용됨.
계산	주어진 다항식과 그 도함수의 결과식으로부터 계산 가능
역할
정보	다항식의 근에 대한 정보 제공 (중근 여부, 실근/허근 개수 등)

2. 정의

주어진 다항식의 계수들로 이루어진 특정 식으로, 다항식의 근의 성질, 특히 중근의 존재 여부에 대한 정보를 제공한다. 일반적으로 대문자 $D$ 또는 그리스 문자 Δ로 표기한다.

판별식은 다항식의 근들의 차이의 제곱과 관련하여 정의될 수도 있고(반데르몬드 행렬식 관련), 다항식과 그 도함수의 종결식을 이용하여 계수만으로 계산할 수도 있다. 이 두 가지 접근 방식은 동등한 결과를 제공한다.

판별식의 가장 중요한 성질 중 하나는 그 값이 0이 되는 것이 다항식이 중근을 가지는 것과 필요충분조건이라는 점이다. 즉, 판별식 $D=0$ 은 다항식이 적어도 하나의 중복된 근을 가진다는 것을 의미한다.

실수 계수를 가지는 다항식의 경우, 판별식의 부호는 실수 근의 개수에 대한 정보를 제공하기도 한다. 예를 들어, 이차 방정식의 판별식이 양수이면 서로 다른 두 실근을, 0이면 중근(실근 1개)을, 음수이면 서로 다른 두 허근(실근 0개)을 가진다. 그러나 삼차 이상의 방정식에서는 판별식의 부호만으로 실수 근의 개수를 완전히 판별할 수는 없으며, 추가적인 정보가 필요할 수 있다.

"판별식"이라는 용어는 1851년 영국의 수학자 제임스 조셉 실베스터가 처음 사용하였다.^[14] 판별식의 구체적인 계산 방법, 다양한 차수 방정식의 판별식 공식, 그리고 판별식의 여러 성질에 대한 자세한 내용은 하위 섹션에서 다룬다.

2. 1. 일반적인 정의

대수적으로 닫힌 체

K

를 계수로 가지는 0이 아닌 다항식

f(x)

가 다음과 같이 주어졌다고 하자.

:

f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n=a_n(x-x_1)(x-x_2)\cdots(x-x_n)\in K[x]

여기서

a_0,a_1,a_2,\dots,a_n\in K

이고

a_n\ne 0

이며,

x_1,x_2,\dots,x_n\in K

는 다항식

f(x)

의 근들이다. 이때

f(x)

의 '''판별식'''(

\operatorname{disc}(f)

또는

D(f)

,

\Delta(f)

)은 근들의 차이의 제곱의 곱으로 정의되며, 최고차항 계수

a_n

을 포함하여 다음과 같이 나타낼 수 있다.^[21]

:

\operatorname{disc}(f) = a_n^{2n-2}\prod_{1 \le i < j \le n}(x_i-x_j)^2

이는 다음과 같이 표현할 수도 있다.

:

\operatorname{disc}(f) = (-1)^{n(n-1)/2}a_n^{2n-2}\prod_{i\ne j}(x_i-x_j)

판별식은 다항식의 계수

a_0, \ldots, a_n

만으로 계산할 수 있다. 다항식

f(x)

와 그 도함수

f'(x)

의 종결식

\operatorname{res}(f, f')

을 이용하여 다음과 같이 정의하기도 한다. 여기서 종결식

\operatorname{res}(f, f')

은

f(x)

와

f'(x)

의 실베스터 행렬의 행렬식으로 계산된다.

:

\operatorname{disc}(f) = (-1)^{n(n-1)/2}a_n^{-1}\operatorname{res}(f,f')

종결식

\operatorname{res}(f,f')

은 다음과 같다.

:

\operatorname{res}(f,f') =\begin{vmatrix}a_n & a_{n-1} & \cdots & a_1 & a_0 \\& \ddots & \ddots & \ddots & \ddots & \ddots \\&& a_n & a_{n-1} & \cdots & a_1 & a_0 \\na_n & (n-1)a_{n-1} & \cdots & a_1 \\& \ddots & \ddots & \ddots & \ddots \\&& na_n & (n-1)a_{n-1} & \cdots & a_1 \\&&& na_n & (n-1)a_{n-1} & \cdots & a_1\end{vmatrix}

(행렬식의 크기는

(2n-1)\times(2n-1)

이다. 위쪽

n-1

행은

f(x)

의 계수를, 아래쪽

n

행은

f'(x)

의 계수를 이용하여 구성된다.)

따라서 판별식은 다음과 같은 행렬식으로도 표현된다.

:

D = \frac{(-1)^{n(n-1)/2}}{a_n} \operatorname{res}(f,f') = \frac{(-1)^{n(n-1)/2}}{a_n}\begin{vmatrix}a_n & a_{n-1} & \cdots & a_1 & a_0 \\& \ddots & \ddots & \ddots & \ddots & \ddots \\&& a_n & a_{n-1} & \cdots & a_1 & a_0 \\na_n & (n-1)a_{n-1} & \cdots & a_1 \\& \ddots & \ddots & \ddots & \ddots \\&& na_n & (n-1)a_{n-1} & \cdots & a_1 \\&&& na_n & (n-1)a_{n-1} & \cdots & a_1\end{vmatrix}

판별식의 값은 다항식의 계수

a_0, \dots, a_n

에 대한 정수 계수를 가지는 다항식이다. 역사적으로 부호

(-1)^{n(n-1)/2}

는 실수 계수 다항식의 모든 근이 실수일 때 판별식이 양수가 되도록 선택되었다. "판별식"이라는 용어는 1851년 영국의 수학자 제임스 조셉 실베스터가 만들었다.^[14]

판별식의 정의로부터, 판별식의 값이 0인 것은 다항식

f(x)

가 중근(즉, 중복도가 2 이상인 근)을 가지는 것과 동치이다.

실수 계수를 가지는 대수 방정식의 경우, 판별식의 부호는 실수해의 개수에 대한 정보를 제공한다.

이차 방정식 $ax^2+bx+c=0$ 의 판별식은 $\Delta = b^2-4ac$ 이다. $\Delta > 0$ 이면 서로 다른 두 실근, $\Delta = 0$ 이면 중근(실근 1개), $\Delta < 0$ 이면 서로 다른 두 허근(실근 0개)을 가진다.
삼차 방정식 $ax^3+bx^2+cx+d=0$ 의 판별식은 $\Delta = b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd$ 이다. $\Delta > 0$ 이면 서로 다른 세 실근, $\Delta = 0$ 이면 중근을 가지며 (실근 2개 또는 1개), $\Delta < 0$ 이면 하나의 실근과 켤레 복소수 허근 쌍을 가진다 (실근 1개). 삼차 방정식의 경우 판별식만으로는 실근의 개수를 완전히 판별할 수 없으며 추가적인 정보가 필요하다.
사차 방정식 $ax^4+bx^3+cx^2+dx+e=0$ 의 판별식은 다음과 같다.

:

\begin{align}\Delta = &\; 256a^3e^3-192a^2bde^2-128a^2c^2e^2+144a^2cd^2e-27a^2d^4\\&\ +144ab^2ce^2-6ab^2d^2e-80abc^2de+18abcd^3+16ac^4e\\&\ -4ac^3d^2-27b^4e^2+18b^3cde-4b^3d^3-4b^2c^3e+b^2c^2d^2\end{align}

더 고차의 방정식에 대해서도 판별식은 정의되지만, 계수에 대한 다항식 표현은 매우 길어진다. 오차 방정식의 판별식은 59개의 항을 가지며^[15], 육차 방정식의 판별식은 246개의 항을 가진다.^[16] 항의 개수는 차수에 따라 지수적으로 증가한다. 사차까지의 대수 방정식에서는 판별식이 근의 공식에 나타나지만, 아벨-루피니 정리에 의해 오차 이상의 일반적인 대수 방정식은 근의 공식이 존재하지 않음에도 판별식은 항상 정의된다.

판별식의 개념은 계수가 체가 아닌 일반적인 가환환

R

에 속하는 다항식에 대해서도 확장될 수 있다. 만약

R

이 정역이라면 위의 정의를 그대로 사용할 수 있고, 판별식은

R

의 원소가 된다. 특히 정수 계수 다항식의 판별식은 항상 정수이며, 이는 수론에서 중요하게 사용된다. 만약 환

R

이 영인자를 가지는 경우,

a_n

으로 나누는 것이 정의되지 않을 수 있으므로, 종결식을 이용한 정의에서

a_n

으로 나누는 대신 실베스터 행렬의 첫 번째 열에서

a_n

을 1로 대체하여 계산하기도 한다.

이 일반화된 판별식은 대수 기하학에서도 중요한 역할을 한다. 예를 들어,

f(X, Y)

를 실수 계수를 가지는 2변수 다항식이라 하고

f(X, Y)=0

이 평면 대수 곡선의 방정식을 나타낸다고 하자.

f

를

Y

에 대한 다항식으로 보고 판별식을 계산하면, 그 판별식은

X

에 대한 다항식이 된다. 이

X

-다항식의 근은 원래 곡선의 특이점,

Y

축에 평행한 접선을 가지는 점, 또는

Y

축에 평행한 점근선과 관련된 점들의

X

좌표에 해당한다. 즉,

Y

에 대한 판별식과

X

에 대한 판별식의 근을 계산함으로써 곡선의 중요한 점들(변곡점 제외)을 찾는 데 활용될 수 있다.

2. 2. 동차 이변수 다항식의 판별식

다음과 같은 두 개의 미지수를 가진 차수

n

의 동차 다항식이 있다고 하자.

:

A(x,y) = a_0x^n+ a_1 x^{n-1}y + \cdots + a_n y^n=\sum_{i=0}^n a_i x^{n-i}y^i

잠시

a_0

과

a_n

이 모두 0이 아니라고 가정하면, 다음과 같은 관계가 성립한다.

:

\operatorname{Disc}_x(A(x,1))=\operatorname{Disc}_y(A(1,y)).

이 값을

\operatorname{Disc}^h (A)

로 나타내면, 다음을 얻는다.

:

\operatorname{Disc}_x (A) =y^{n(n-1)} \operatorname{Disc}^h (A),

\operatorname{Disc}_y (A) =x^{n(n-1)} \operatorname{Disc}^h (A).

이러한 성질 때문에,

\operatorname{Disc}^h (A)

는 ''A''의 판별식 또는 동차 판별식이라고 불린다.

만약

a_0

과

a_n

이 0이 되는 경우, 다항식 ''A''(''x'', 1)와 ''A''(1, ''y'')는 ''n''보다 작은 차수를 가질 수 있다. 이 경우, 위의 공식과 정의는 모든 다항식이 차수 ''n''을 갖는 것처럼 판별식을 계산하면 유효하다. 즉,

a_0

과

a_n

을 미지수로 하여 판별식을 계산해야 하며, 실제 값으로의 대입은 이 계산을 ''이후''에 수행해야 한다. 이는 환 준동형 사상에 대한 불변성의 공식을 사용해야 함을 의미한다.

3. 성질

판별식은 다항식의 근과 관련된 여러 중요한 성질을 가지며, 일반적으로 대문자 $D$ 또는 그리스 문자 대문자 델타( $\Delta$ )로 표기한다. "판별식"이라는 용어는 1851년 영국의 수학자 제임스 조셉 실베스터가 처음 사용했다.^[14]

판별식의 중요한 성질 중 하나는 다항식이 중근을 갖는지 여부를 판별하는 것이다. 대수적으로 닫힌 체 위에서 정의된 다항식의 판별식 값이 0인 것은 그 다항식이 중근을 갖는 것과 동치이다. 실수 계수를 갖는 대수 방정식의 경우, 판별식의 부호는 실수해의 개수에 대한 정보를 제공하지만, 삼차 방정식 이상에서는 판별식만으로 개수를 완전히 결정하기는 어렵다.

또한 판별식은 다항식의 갈루아 군과도 밀접한 관련이 있다. 특정 조건 하에서 판별식의 제곱근이 원래 계수 체에 속하는지 여부는 갈루아 군의 구조에 대한 정보를 제공한다.

판별식의 개념은 계수가 일반적인 정역 $R$ 에 속하는 경우에도 정의될 수 있다. 특히, 정수 계수를 갖는 다항식의 판별식은 항상 정수가 되는데, 이 성질은 수론에서 중요하게 활용된다.

이 외에도 판별식은 변수 변환에 대한 불변성, 다항식의 곱셈과의 관계, 계수 및 근에 대한 동차성 등 다양한 대수적 성질을 지닌다.

3. 1. 중근의 존재

대수적으로 닫힌 체

K

에 속하는 계수를 가진 0이 아닌 다항식

f \in K[x]

에 대해, 다음 두 조건은 서로 동치이다.

$f$ 는 중근을 갖는다.
판별식 $\operatorname{disc}(f) = 0$ 이다.

이는 판별식의 정의 중 하나인 근

r_1, r_2, \dots, r_n

을 이용한 표현식에서도 명확히 드러난다. 다항식

f(x) = a_n x^n + \dots + a_1 x + a_0

의 판별식은 다음과 같이 정의될 수 있다.

:

\operatorname{Disc}_x(f) = a_n^{2n-2}\prod_{i < j} (r_i-r_j)^2

이 식에서 만약 다항식

f

가 중근을 가진다면, 즉 어떤 서로 다른

i, j

에 대해

r_i = r_j

라면,

(r_i - r_j)^2 = 0

이 되어 전체 곱셈 결과인 판별식의 값은 0이 된다. 역으로 판별식이 0이라면, 적어도 하나의

(r_i - r_j)^2

항이 0이어야 하므로,

r_i = r_j

인

i \neq j

가 존재하여 중근을 갖게 된다.

일반적인 체 위에서 정의된 다항식의 경우, 판별식이 0이라는 것은 그 다항식이 어떤 체 확대에서 중근을 갖는다는 것과 동치이다.

계수가 정역에 속하는 다항식의 경우, 판별식이 0인 것은 다항식과 그 도함수가 상수항이 아닌 공통 약수를 갖는다는 것과 동치이다.

표수가 0인 체 위에서는, 판별식이 0인 것은 다항식이 제곱 인수가 없는 다항식이 아니라는 것, 즉 상수항이 아닌 다항식의 제곱으로 나누어떨어진다는 것을 의미한다. 이는 중근 또는 그 이상의 중복도를 가진 근이 존재함을 뜻한다.

표수가

p > 0

인 체 위에서는 상황이 조금 더 복잡하다. 판별식이 0인 것은 다항식이 제곱 인수가 없는 다항식이 아니거나, 또는 기약 인수 중 분리 불가능한 것(즉,

x^p

의 다항식 형태인 기약 인수)이 존재한다는 것을 의미한다.

가장 간단한 예로 이차 방정식

ax^2 + bx + c = 0

(

a \neq 0

)을 들 수 있다. 이 방정식의 판별식

\Delta = b^2 - 4ac

가 0일 때, 방정식의 해는

x = -b/(2a)

로 유일하며, 이는 중근에 해당한다.

삼차 이상의 방정식에서는 판별식이 0일 때 중근(중복도 2)뿐만 아니라, 중복도가 3 이상인 근을 가질 수도 있다. 예를 들어, 삼차 방정식의 판별식이 0이면 중복도 2인 근과 다른 하나의 단일근을 갖거나, 중복도 3인 근 하나만을 가질 수 있다.

3. 2. 갈루아 군과의 관계

체

K

및

n

차 분해 가능 기약 다항식

f\in K[x]

에 대하여, 갈루아 군

\operatorname{Gal}(f)

는 근의 집합 위에서 충실하게 작용하며, 이는 단사 군 준동형

:

\operatorname{Gal}(f)\hookrightarrow\operatorname{Sym}(n)

을 정의한다. 여기서

\operatorname{Sym}(n)

은

n

개의 원소에 대한 대칭군을 나타낸다.

만약

\operatorname{char}K\ne2

(즉, 체

K

의 표수가 2가 아니라면), 다음 두 조건은 서로 동치이다.^[17]

$\operatorname{Gal}(f)$ 의 상(image)은 교대군 $\operatorname{Alt}(n)$ 의 부분군이다. 즉, 갈루아 군의 모든 원소는 근들의 짝치환으로 작용한다.
판별식의 제곱근 $\sqrt{\operatorname{disc}(f)}$ 이 체 $K$ 에 속한다.

판별식

\operatorname{disc}(f)

는 다항식

f

의 근

\alpha_1, \dots, \alpha_n

들에 대한 대칭식이다. 즉, 근들의 순서를 어떻게 바꾸어도 판별식의 값은 변하지 않는다. 반면, 판별식의 제곱근인 반데르몬드 다항식

\textstyle \prod_{1 \le i < j \le n} (\alpha_i - \alpha_j)

은 교대식이다. 즉, 근들의 순서를 바꾸는 홀치환에 대해서는 부호가 반전되고, 짝치환에 대해서는 불변이다.

n

개의 변수에 대한 대칭 다항식 환

\Lambda_n

에 판별식의 제곱근을 첨가하면 교대식의 환을 얻게 되며, 이는

\Lambda_n

의 이차 확대이다. 이는 갈루아 군의 상이 교대군

\operatorname{Alt}(n)

에 포함되는지 여부가 판별식의 제곱근이 원래 체에 포함되는지 여부와 관련된 이유를 설명해 준다.

3. 3. 불변성

다항식의 판별식은 변수에 대한 사영 변환을 적용했을 때, 스케일링(크기 조절) 요소를 제외하고는 그 값이 변하지 않는 중요한 성질을 가진다. 사영 변환은 평행이동, 닮음 변환, 반전과 같은 기본적인 변환들의 조합으로 이해할 수 있다. 최고차항의 계수가

a_n

이고 차수가

n

인 다항식

P(x)

에 대해, 각 변환에 따른 판별식의 변화는 다음과 같다.

'''평행이동에 대한 불변성''': 다항식을 $x$ 축 방향으로 $\alpha$ 만큼 평행이동해도 판별식은 변하지 않는다.

:

\operatorname{Disc}_x(P(x+\alpha)) = \operatorname{Disc}_x(P(x))

:이 성질은 판별식을 다항식의 근들 사이의 차이의 제곱 곱으로 정의하는 식으로부터 쉽게 유도될 수 있다. 근들이 동일한 값만큼 이동해도 그 차이는 변하지 않기 때문이다.

'''닮음 변환에 대한 불변성''': 변수 $x$ 를 $\alpha$ 배하여 닮음 변환을 적용하면 판별식은 $\alpha^{n(n-1)}$ 배가 된다.

:

\operatorname{Disc}_x(P(\alpha x)) = \alpha^{n(n-1)}\operatorname{Disc}_x(P(x))

:이것 역시 근을 이용한 정의나 판별식의 준동차성(quasi-homogeneity)으로부터 유도된다.

'''반전에 대한 불변성''': 다항식의 계수를 역순으로 배열하여 얻는 역수 다항식 $P^{\mathrm{r}}\!\!\;(x)$ 의 판별식은 원래 다항식의 판별식과 같다. 단, 상수항 $P(0)$ 이 0이 아니어야 한다.

:

\operatorname{Disc}_x(P^{\mathrm{r}}\!\!\;(x)) = \operatorname{Disc}_x(P(x))

:여기서

P(x) = a_nx^n + \cdots + a_1x + a_0

(

a_0 \neq 0

)일 때, 역수 다항식은

P^{\mathrm{r}}\!\!\;(x) = x^nP(1/x) = a_0x^n + a_1x^{n-1} + \cdots + a_n

으로 정의된다.

판별식은 또한 환 준동형 사상

\varphi\colon R \to S

에 대해서도 일정한 불변성을 보인다. 환

R

의 원소를 계수로 가지는 다항식

A = a_nx^n+a_{n-1}x^{n-1}+\cdots+a_0

가 주어졌을 때, 준동형 사상

\varphi

를 각 계수에 적용하여 환

S

의 원소를 계수로 가지는 새로운 다항식

A^\varphi = \varphi(a_n)x^n+\varphi(a_{n-1})x^{n-1}+ \cdots+\varphi(a_0)

를 만들 수 있다.

이때 판별식의 불변성은 다음과 같이 나타난다.

만약 변환된 다항식

A^\varphi

의 최고차항 계수

\varphi(a_n)

이 0이 아니라면, 변환된 다항식의 판별식은 원래 다항식의 판별식에 준동형 사상을 적용한 값과 같다.

:

\operatorname{Disc}_x(A^\varphi) = \varphi(\operatorname{Disc}_x(A)).

판별식은 계수들로 구성된 행렬의 행렬식으로 정의될 수 있으므로, 이 성질은 행렬식에 대한 유사한 성질로부터 직접적으로 유도된다.

만약 준동형 사상에 의해 최고차항 계수가 0이 되는 경우, 즉

\varphi(a_n)= 0

이라면, 관계는 조금 더 복잡해진다.

:

\varphi(\operatorname{Disc}_x(A)) = \varphi(a_{n-1})^2\operatorname{Disc}_x(A^\varphi).

이 경우, 원래 판별식에 사상을 적용한 값

\varphi(\operatorname{Disc}_x(A))

는 0이 될 수도 있고 아닐 수도 있다.

특히 대수 기하학 등에서 판별식이 0인지 아닌지에 주로 관심을 가질 때, 이러한 불변성은 다음과 같이 요약될 수 있다:

\varphi(\operatorname{Disc}_x(A)) = 0

이라는 조건은, 변환된 다항식

A^\varphi

의 판별식이 0이거나 (

\operatorname{Disc}_x(A^\varphi)=0

), 또는 변환 과정에서 다항식의 차수가 최소 2 이상 감소하는 경우(

\deg(A)-\deg(A^\varphi)\ge 2

)와 동치이다.

이는 종종

\varphi(\operatorname{Disc}_x(A)) = 0

이라는 조건이 변환된 다항식

A^\varphi

가 중근을 가지는 것과 필요충분조건이라고 해석된다. 여기서 중근은 무한대에서의 중근까지 포함하는 개념으로 확장될 수 있다.

3. 4. 다항식 곱과의 관계

만약

R = PQ

가

x

에 대한 다항식의 곱이라면, 다음과 같은 관계가 성립한다.

:

\begin{align}\operatorname{disc}_x(R) &= \operatorname{disc}_x(P)\operatorname{Res}_x(P,Q)^2\operatorname{disc}_x(Q)\\[5pt]{}&=(-1)^{pq}\operatorname{disc}_x(P)\operatorname{Res}_x(P,Q)\operatorname{Res}_x(Q,P)\operatorname{disc}_x(Q),\end{align}

여기서

\operatorname{Res}_x

는 변수

x

에 대한 종결식을 나타내며,

p

와

q

는 각각

P

와

Q

의 차수이다.

이 속성은 종결식과 판별식의 표현식을 해당 다항식의 근을 사용하여 대입하면 바로 얻을 수 있다. 여기서는 문헌^[17]에 게재된 방법에 의해 증명한다.

(증명)

:

\textstyle \prod\limits_{i,j (i

:

= (-1)^{n(n-1)/2} \textstyle \prod\limits_{i,j (i \neq j)} ( \alpha_i - \alpha_j )

:

= (-1)^{n(n-1)/2} \textstyle \prod\limits_{i=1}^n \prod\limits_{j (j \neq i)} ( \alpha_i - \alpha_j ) \quad \cdots \ (1)

:

f(x)= a_n \textstyle \prod\limits_{j=1}^n ( x- \alpha_j )

:

f'(x)= a_n \textstyle \sum\limits_{k=1}^n \prod\limits_{j (j \neq k)} ( x- \alpha_j )

:

f'( \alpha_i )= a_n \textstyle \prod\limits_{j (j \neq i)} ( \alpha_i - \alpha_j ) \quad \cdots \ (2)

:여기서,

f'(x) = 0

의 근을

\beta_1, \dots, \beta_{n-1}

로 한다.

:

f'(x)=n a_n \textstyle \prod\limits_{j=1}^{n-1} ( x- \beta_j )

:

f'( \alpha_i )=n a_n \textstyle \prod\limits_{j=1}^{n-1} ( \alpha_i - \beta_j ) \quad \cdots \ (3)

:(2) = (3) 에서,

a_n \neq 0

에 주의하여

:

\textstyle \prod\limits_{j (j \neq i)} ( \alpha_i - \alpha_j ) = n \prod\limits_{j=1}^{n-1} ( \alpha_i - \beta_j ) \quad \cdots \ (4)

:(4)를 (1)에 대입하면,

:

\textstyle \prod\limits_{i,j (i

:여기서, '''종결식'''에서 잘 알려진 다음 등식을 사용한다.

::

f(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0 \ (a_n \neq 0)

의 근을

\alpha_1, \dots, \alpha_n

,

::

g(x) = b_m x^m + b_{m-1} x^{m-1} + \dots + b_1 x + b_0 \ (b_m \neq 0)

의 근을

\beta_1, \dots, \beta_m

::라고 하면, 다음이 성립한다.

:::

{a_n}^m {b_m}^n \textstyle \prod\limits_{i,j} ( \alpha_i - \beta_j ) = \begin{vmatrix}a_n &a_{n-1} &\cdots &\cdots  &a_0     &       &    \\&\ddots  &\ddots &        &        &\ddots &    \\&        &a_n    &a_{n-1} &\cdots  &\cdots &a_0 \\b_m &b_{m-1} &\cdots &b_0     &        &       &    \\&\ddots  &\ddots &        &\ddots  &       &    \\&        &\ddots &\ddots  &        &\ddots &    \\&        &       &b_m     &b_{m-1} &\cdots &b_0\end{vmatrix}

:(대각 성분에

a_n

가

m

개,

b_0

가

n

개)

:이 등식을

f, f'

에 적용하면,

:

{a_n}^{n-1} (n a_n )^n \textstyle \prod\limits_{i,j} ( \alpha_i - \beta_j )

:

= \begin{vmatrix}a_n  &a_{n-1}      &\cdots &\cdots  &a_0          &       &    \\&\ddots       &\ddots &        &             &\ddots &    \\&             &a_n    &a_{n-1} &\cdots       &\cdots &a_0 \\na_n &(n-1)a_{n-1} &\cdots &1a_1    &             &       &    \\&\ddots       &\ddots &        &\ddots       &       &    \\&             &\ddots &\ddots  &             &\ddots &    \\&             &       &na_n    &(n-1)a_{n-1} &\cdots &1a_1\end{vmatrix} \quad \cdots \ (6)

:(5), (6) 에서,

:

{a_n}^{2n-2} \textstyle \prod\limits_{i,j (i

:

= \frac{(-1)^{n(n-1)/2}}{a_n} \begin{vmatrix}a_n  &a_{n-1}      &\cdots &\cdots  &a_0          &       &    \\&\ddots       &\ddots &        &             &\ddots &    \\&             &a_n    &a_{n-1} &\cdots       &\cdots &a_0 \\na_n &(n-1)a_{n-1} &\cdots &1a_1    &             &       &    \\&\ddots       &\ddots &        &\ddots       &       &    \\&             &\ddots &\ddots  &             &\ddots &    \\&             &       &na_n    &(n-1)a_{n-1} &\cdots &1a_1\end{vmatrix} \ \blacksquare

3. 5. 동차성

판별식은 계수에 대한 동차 다항식이며, 근에 대한 동차 다항식이기도 하다. 따라서 계수에 대해 준동차 다항식이기도 하다.

'''계수에 대한 동차성'''

n

차 다항식

A(x) = a_n x^n + \dots + a_0

의 판별식은 계수

a_0, \dots, a_n

에 대해

2n-2

차 동차 다항식이다. 이는 두 가지 방식으로 이해할 수 있다.

1. 근과 최고차항 계수를 이용한 판별식 공식

\operatorname{Disc}_x(A) = a_n^{2n-2}\prod_{i < j} (r_i-r_j)^2

을 생각해보자. 모든 계수

a_i

에

\lambda

를 곱하면, 근

r_i

는 변하지 않지만 최고차항 계수는

\lambda a_n

이 된다. 따라서 판별식은

(\lambda a_n)^{2n-2}\prod_{i < j} (r_i-r_j)^2 = \lambda^{2n-2} (a_n^{2n-2}\prod_{i < j} (r_i-r_j)^2)

가 되어

\lambda^{2n-2}

배가 된다. 즉, 계수에 대해

2n-2

차 동차이다.

2. 판별식을

(2n-1) \times (2n-1)

크기의 실베스터 행렬의 행렬식을

a_n

으로 나눈 것으로 정의할 수도 있다. 행렬식 자체는 행렬의 성분(계수)에 대해

2n-1

차 동차이다. 이를

a_n

(1차 동차)으로 나누면 판별식은

(2n-1) - 1 = 2n-2

차 동차가 된다.

'''근에 대한 동차성'''

n

차 다항식의 판별식은 근

r_1, \dots, r_n

에 대해

n(n-1)

차 동차이다. 이는 판별식 공식

\operatorname{Disc}_x(A) = a_n^{2n-2}\prod_{i < j} (r_i-r_j)^2

에서 확인할 수 있다. 근의 차이

(r_i-r_j)

항은 총

\binom{n}{2} = \frac{n(n-1)}{2}

개가 있고, 각각 제곱되어 있으므로 근에 대한 총 차수는

2 \times \frac{n(n-1)}{2} = n(n-1)

이다.

'''준동차성'''

판별식은 계수에 대해 준동차 다항식이기도 하다.

각 계수 $a_i$ ( $x^i$ 의 계수)에 가중치 $n-i$ 를 부여하면, 판별식은 총 가중치 $n(n-1)$ 을 갖는 준동차 다항식이 된다.
각 계수 $a_i$ 에 가중치 $i$ 를 부여해도, 판별식은 총 가중치 $n(n-1)$ 을 갖는 준동차 다항식이 된다.

이는 근에 대한 동차이고 대칭 다항식인 모든 다항식은 근의 기본 대칭 함수(즉, 비에타의 공식에 의해 계수와 관련된 값들)에 대한 준동차 다항식으로 표현될 수 있다는 일반적인 성질 때문이다.

다항식

P=a_nx^n+a_{n-1}x^{n-1}+ \cdots +a_0

의 판별식에 나타나는 모든 단항식

a_0^{i_0} a_1^{i_1} \dots a_n^{i_n}

의 지수

i_0, i_1, \dots, i_n

은 다음 두 식을 만족해야 한다.

$\sum_{k=0}^n i_k = i_0+i_1+\cdots+i_n = 2n-2$ (계수에 대한 동차성)
$\sum_{k=1}^n k i_k = i_1+2i_2 + \cdots+n i_n = n(n-1)$ (가중치 $i$ 부여 시 준동차성)

또한, 이 두 식으로부터 다음 식도 유도된다.

$\sum_{k=0}^{n-1} (n-k) i_k = ni_0 +(n-1)i_1+ \cdots+ i_{n-1} = n(n-1)$ (가중치 $n-i$ 부여 시 준동차성)

이러한 동차성 및 준동차성 조건은 판별식을 구성하는 항들을 제한한다.

예를 들어, 일반적인 이차 다항식 $ax^2+bx+c$ ( $n=2$ )의 판별식 $b^2-4ac$ ( $a_2=a, a_1=b, a_0=c$ )는 계수에 대해 $2n-2=2$ 차 동차이다. 항은 $b^2 = a_1^2$ 과 $ac = a_2^1 a_0^1$ 두 개뿐이다. ( $a_1^2$ 의 지수 합: 2, 가중합( $i$ ): $1 \times 2 = 2 = n(n-1)$ . $a_2^1 a_0^1$ 의 지수 합: $1+1=2$ , 가중합( $i$ ): $2 \times 1 + 0 \times 1 = 2 = n(n-1)$ ). 반면, 3개의 변수( $a, b, c$ )로 만들 수 있는 일반적인 2차 동차 다항식은 $a^2, b^2, c^2, ab, bc, ca$ 의 6개 항을 가질 수 있다.
일반적인 삼차 다항식( $n=3$ )의 판별식은 계수에 대해 $2n-2=4$ 차 동차이며, 위 규칙을 만족하는 5개의 항으로 구성된다. 반면, 4개의 변수로 만들 수 있는 일반적인 4차 동차 다항식은 35개의 항을 가질 수 있다.

고차 다항식의 경우, 위의 동차성 및 준동차성 규칙을 만족하더라도 판별식에 실제로는 나타나지 않는 단항식이 있을 수 있다. 예를 들어, 사차 다항식

ax^4 + bx^3 + cx^2 + dx + e

(

n=4

)의 경우, 단항식

bc^4d

(

a_3^1 a_2^4 a_1^1

)는 계수에 대한 차수(

1+4+1=6 = 2n-2

)와 가중치

i

에 대한 준동차성(

3 \times 1 + 2 \times 4 + 1 \times 1 = 12 = n(n-1)

) 조건을 모두 만족하지만, 실제 사차 판별식에는 이 항이 포함되지 않는다.

4. 예시

1차 선형 다항식의 판별식은 거의 고려되지 않는다. 필요하다면, 일반적으로 1과 같다고 정의된다. 이는 빈 곱에 대한 일반적인 규칙을 따르고 실베스터 행렬의 두 블록 중 하나가 빈 행렬임을 고려한 결과이다. 상수 다항식, 즉 차수가 0인 다항식의 판별식에 대한 일반적인 규칙은 없다.

다항식의 차수가 낮을 경우 판별식은 비교적 간단하지만, 차수가 높아지면 매우 복잡해질 수 있다. 예를 들어, 일반적인 사차 함수의 판별식은 16개의 항을 가지고,^[3] 오차 함수의 판별식은 59개의 항을 가지며,^[4] 육차 방정식의 판별식은 246개의 항을 가진다.^[5] 이는 OEIS 수열 A007878에 해당한다.

일반적으로 실수 계수를 가지는 $n$ 차 대수 방정식의 판별식을 $D$ 라고 할 때, 판별식의 부호에 따라 근의 종류를 다음과 같이 개략적으로 파악할 수 있다.

$D > 0$ : $0 \leq k \leq \frac{n}{4}$ 인 어떤 정수 $k$ 에 대해, $2k$ 쌍의 공액 허수 해와 $(n - 4k)$ 개의 실수 해가 있으며, 모든 근은 서로 다르다.
$D < 0$ : $0 \leq k \leq \frac{n-2}{4}$ 인 어떤 정수 $k$ 에 대해, $(2k + 1)$ 쌍의 공액 허수 해와 $(n - 4k - 2)$ 개의 실수 해가 있으며, 모든 근은 서로 다르다.
$D = 0$ : 적어도 하나의 중근이 존재한다. 실수 계수 방정식이라도 중근은 실수일 수도 있고 허수일 수도 있다.

4차 이하의 대수 방정식의 경우, 해를 구하는 공식에 판별식이 나타난다. 그러나 5차 이상의 대수 방정식에 대해서는 아벨-루피니의 정리에 따라 근의 공식이 일반적으로 존재하지 않는다. 판별식은 종결식을 이용하여 계산할 수 있다.

4. 1. 2차 다항식

2차 다항식

ax^2+bx+c

의 판별식

D

는 다음과 같이 정의된다.

:

D=b^2-4ac

판별식은 2차 다항식의 근을 구하는 근의 공식에 나타난다. 2차 방정식

ax^2+bx+c=0

의 두 근

x_{1,2}

는 다음과 같다.

:

x_{1,2}=\frac{-b \pm \sqrt {b^2-4ac}}{2a} = \frac{-b \pm \sqrt{D}}{2a}

판별식

D

는 두 근이 같을 때, 즉 방정식이 중근을 가질 때 0이 된다.^[6]

특히 계수

a, b, c

가 실수인 경우, 판별식

D

의 부호에 따라 2차 방정식의 근의 종류를 다음과 같이 판별할 수 있다.

$D > 0$ : 방정식은 서로 다른 두 실근을 갖는다.
$D = 0$ : 방정식은 하나의 중근인 실수해 $x = -\frac{b}{2a}$ 를 갖는다.
$D < 0$ : 방정식은 서로 복소켤레 관계인 두 허근 $x = \frac{-b \pm i \sqrt{-D}}{2a}$ 를 갖는다.

만약 계수

a, b, c

가 유리수라면, 판별식

D

가 유리수의 제곱일 경우에만 두 근이 유리수가 된다.

또한, 일차항의 계수

b

가 짝수일 때, 즉

b = 2b'

(단,

b'

은 정수 또는 실수)일 경우, 계산의 편의를 위해 다음과 같은 짝수 판별식 또는 판별식/4 (

D/4

)를 사용하기도 한다.

:

\frac{D}{4} = (b')^2 - ac

^[18]

이 경우 근의 공식은

x = \frac{-b' \pm \sqrt{(b')^2 - ac}}{a} = \frac{-b' \pm \sqrt{D/4}}{a}

로 간단히 표현할 수 있다. 짝수 판별식

\frac{D}{4}

의 부호에 따른 근의 판별은 원래 판별식

D

와 동일하다.

4. 2. 3차 다항식

복소수를 계수로 가지는 일반적인 3차 다항식 ''f''(''x'') = ''ax''³ + ''bx''² + ''cx'' + ''d''의 판별식(Δ)은 다음과 같다.^[7]^[8]

:Δ = disc(''f'') = ''b''²''c''² - 4''ac''³ - 4''b''³''d'' - 27''a''²''d''² + 18''abcd''

특히, 이차항이 없는 형태인 ''x''³ + ''px'' + ''q''의 판별식은 다음과 같이 간단해진다.

:Δ = -4''p''³ - 27''q''²

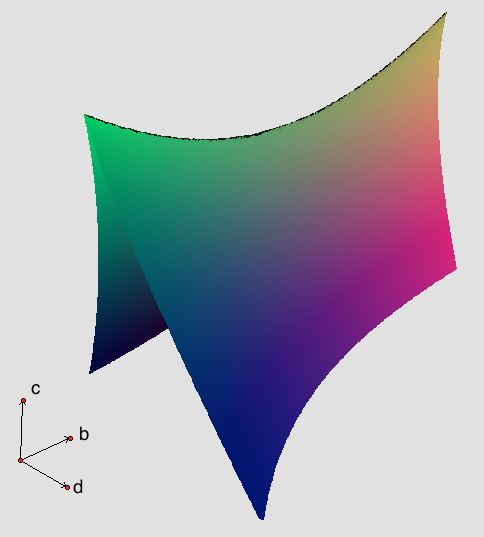
계수가 실수일 경우, 판별식 Δ의 부호에 따라 삼차 방정식의 근의 종류가 결정된다.^[22]^[9]

판별식 (Δ)	근의 종류
Δ > 0	서로 다른 세 실근
Δ = 0	중근을 포함하는 세 실근 (적어도 두 근이 같다)
Δ < 0	하나의 실근과 서로 켤레인 두 허근

판별식이 양수(Δ > 0)일 때, 세 실근은 허수의 거듭제곱근을 사용하여 나타낼 수 있으며, 계수가 유리수인 기약 다항식의 경우 실수의 거듭제곱근만으로는 나타낼 수 없다. 이를 환원 불능의 경우(casus irreducibilis|카수스 이레두키빌리스^la)라고 한다.^[22] 판별식이 0일 경우, 실근들은 항상 실수의 거듭제곱근을 사용하여 나타낼 수 있다.^[22]

계수가 유리수인 3차 기약 다항식의 경우, 판별식 Δ는 해당 방정식의 갈루아 군과 관련이 있다. 판별식의 제곱근 √Δ가 유리수이면 갈루아 군은 위수 3의 순환군(교대군 A₃와 동형)이고, 유리수가 아니면 대칭군 S₃와 동형이다.

4. 3. 4차 다항식

복소수 계수를 가지는 4차 다항식

:

p(x)=ax^4+bx^3+cx^2+dx+e

의 판별식은 다음과 같다.

:

\begin{align}\operatorname{disc}(p)& = 256a^3e^3-192a^2bde^2-128a^2c^2e^2+144a^2cd^2e \\& \qquad -27a^2d^4+144ab^2ce^2-6ab^2d^2e-80abc^2de \\& \qquad\qquad +18abcd^3+16ac^4e-4ac^3d^2-27b^4e^2 \\& \qquad\qquad\qquad +18b^3cde-4b^3d^3-4b^2c^3e+b^2c^2d^2\end{align}

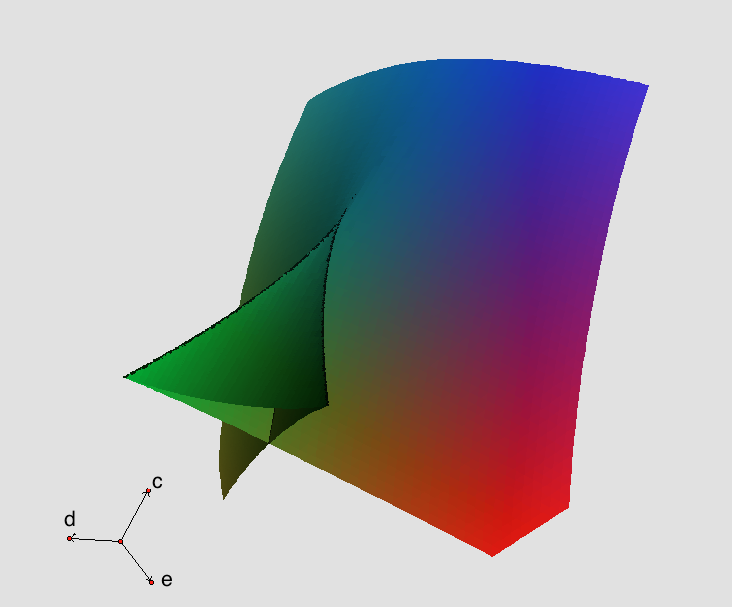
4차 다항식 ''x''⁴ + ''cx''² + ''dx'' + ''e''의 판별식. 표면은 다항식이 중근을 갖는 점(''c'', ''d'', ''e'')을 나타낸다. 첨점 모서리는 삼중근을 갖는 다항식에 해당하고, 자기 교차는 서로 다른 두 개의 중근을 갖는 다항식에 해당한다.

특히, 다음과 같은 형태의 4차 다항식

:

x^4+cx^2+dx+e\,

의 판별식은 아래와 같이 더 간단하게 표현된다.

:

\begin{align}{} & 16c^4e -4c^3d^2 -128c^2e^2+144cd^2e -27d^4 + 256e^3\,.\end{align}

판별식은 대수 방정식의 근 중 적어도 두 개가 같을 경우, 즉 중근을 가질 경우에만 0이 된다. 만약 다항식의 계수가 모두 실수일 때, 판별식의 부호에 따라 근의 종류를 판별할 수 있다.

판별식이 0보다 작으면 (음수이면), 서로 다른 실근 2개와 서로 켤레 관계인 복소수 근 2개를 가진다.
판별식이 0보다 크면 (양수이면), 모든 근이 실수이거나 (서로 다른 실근 4개 또는 중근 포함 실근), 모든 근이 허수이다 (서로 켤레 관계인 복소수 근 쌍 2개).

대수 방정식의 판별식은 종결식을 이용하여 계산할 수 있다. 판별식을 D로 표기하기도 한다.

5. 역사

1851년 영국의 수학자 제임스 조지프 실베스터가 "판별식"이라는 용어를 처음 사용하였다.^[2]^[14]

6. 일반화

판별식 개념에는 두 가지 종류가 있다. 첫 번째는 대수적 수체의 판별식으로, 이차체를 포함한 일부 경우 이 판별식은 체를 정의하는 다항식의 판별식과 같다. 이는 아래에서 더 자세히 다룬다.

두 번째 종류의 판별식은 계수에 따라 문제의 성질이 달라지는 경우, 특히 문제의 퇴화된 사례나 특이점이 계수에 대한 단일 다항식이 0이 되는 조건으로 특징지어질 때 나타난다. 이는 다항식의 두 근이 같아질 때 0이 되는 판별식의 경우와 유사하다. 이러한 일반화된 판별식이 정의되는 대표적인 예는 다음과 같다.

체 K의 표수가 0이거나, 다항식의 차수를 나누지 않는 소수라고 하자. K 위에서 정의된 $n$ 개의 변수를 갖는 동차 다항식 $A$ 는 사영 초곡면을 정의한다. 이 초곡면은 $A$ 의 $n$ 개 편미분이 자명하지 않은 공통 함수의 영점을 가질 때, 그리고 오직 그럴 때만 특이점을 가진다. 이는 이 편미분들의 다변량 종결식이 0일 때와 동치이며, 이 종결식은 $A$ 의 판별식으로 간주될 수 있다. 그러나 미분 과정에서 생기는 정수 계수 때문에, 이 다변량 종결식은 $n$ 의 거듭제곱으로 나누어질 수 있다. 따라서 판별식으로는 일반적인 계수로 계산된 종결식의 원시 부분을 사용하는 것이 더 적절하다. 표수에 대한 제한 조건이 필요한 이유는, 이 조건이 없다면 편미분의 공통 영점이 반드시 원래 다항식의 영점이라고 보장할 수 없기 때문이다(동차 다항식에 대한 오일러 항등식 참조).

차수가 $d$ 인 동차 이변량 다항식의 경우, 위에서 설명한 일반 판별식은 일반적인 판별식 정의에 $d^{d-2}$ 를 곱한 값과 같다. 일반 정의의 예시가 되는 다른 고전적인 판별식 유형으로는 이차 형식의 판별식과 원뿔 곡선의 판별식 등이 있으며, 이는 아래 섹션들에서 설명된다.

"판별식(discriminant)"이라는 용어는 1851년 영국의 수학자 제임스 조셉 실베스터가 만들었다.^[14] 일반적으로 대문자 $D$ 또는 그리스 문자 대문자 Δ로 표기한다.

구체적으로, 변수 $x$ 에 대한 $n$ 차 다항식

: $f(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0 \quad (a_n \neq 0)$

의 근을 중복도를 포함하여 $\alpha_1, \dots, \alpha_n$ 이라고 할 때, 판별식 $D$ 는 다음과 같이 정의된다.

: $D = a_n^{2n-2} \prod_{1 \le i < j \le n} (\alpha_i - \alpha_j)^2 = (-1)^{n(n-1)/2} a_n^{2n-2} \prod_{i \ne j} (\alpha_i - \alpha_j)$

이 정의식은 다음 과정을 통해 계수 $a_n, a_{n-1}, \dots, a_1, a_0$ 에 대한 식으로 표현될 수 있다 (실제로는 다항식이 된다).

# $D$ 는 근 $\alpha_1, \dots, \alpha_n$ 에 대한 대칭식이다.

# 근들의 대칭식은 근들의 기본 대칭식에 대한 다항식으로 나타낼 수 있다.

# 근들의 기본 대칭식은 근과 계수의 관계에 의해 계수 $a_n, \dots, a_0$ 에 대한 식으로 표현된다.

판별식 $D$ 를 계수 $a_n, \dots, a_0$ 로 나타내기 위해 결합식(실베스터 행렬의 행렬식)을 사용하는 것이 편리하다. 다항식 $f$ 의 판별식 $D$ 는 $f$ 와 그 도함수 $f'$ 의 결합식 $\mathrm{Res}(f, f')$ 과 다음과 같은 관계를 가진다.

: $D = \frac{(-1)^{n(n-1)/2}}{a_n} \mathrm{Res}(f, f') = \frac{(-1)^{n(n-1)/2}}{a_n} \det(S(f, f'))$

여기서 $S(f, f')$ 는 $f$ 와 $f'$ 에 대한 실베스터 행렬이다. 구체적인 행렬식 형태는 다음과 같다.

: $D = \frac{(-1)^{n(n-1)/2}}{a_n} \begin{vmatrix}a_n &a_{n-1} &\cdots &\cdots &a_0 & & \\&\ddots &\ddots & & &\ddots & \\& &a_n &a_{n-1} &\cdots &\cdots &a_0 \\na_n &(n-1)a_{n-1} &\cdots &1a_1 & & & \\&\ddots &\ddots & &\ddots & & \\& &\ddots &\ddots & &\ddots & \\& & &na_n &(n-1)a_{n-1} &\cdots &1a_1\end{vmatrix}$

(행렬의 크기는 $(2n-1) \times (2n-1)$ 이며, 첫 번째 블록은 $(n-1)$ 행, 두 번째 블록은 $n$ 행으로 구성된다.)

낮은 차수의 방정식에 대한 판별식은 다음과 같다.

이차 방정식 $ax^2 + bx + c = 0$ 의 판별식: $\Delta = b^2 - 4ac$
삼차 방정식 $ax^3 + bx^2 + cx + d = 0$ 의 판별식: $\Delta = b^2c^2 - 4ac^3 - 4b^3d - 27a^2d^2 + 18abcd$
사차 방정식 $ax^4 + bx^3 + cx^2 + dx + e = 0$ 의 판별식:

:

\begin{align}    \Delta = &\; 256a^3e^3-192a^2bde^2-128a^2c^2e^2+144a^2cd^2e-27a^2d^4\\    &\ +144ab^2ce^2-6ab^2d^2e-80abc^2de+18abcd^3+16ac^4e\\    &\ -4ac^3d^2-27b^4e^2+18b^3cde-4b^3d^3-4b^2c^3e+b^2c^2d^2    \end{align}

더 높은 차수의 방정식에 대해서도 판별식은 정의되며 계수들의 다항식으로 표현되지만, 그 식은 매우 길어진다. 오차 방정식의 판별식은 59개의 항을 가지고^[15], 육차 방정식의 판별식은 246개의 항을 가진다.^[16] 항의 개수는 차수가 증가함에 따라 지수적으로 늘어난다.

사차 이하의 대수 방정식에서는 판별식이 근의 공식에 나타나기 때문에, 판별식이 근의 공식의 일부로 오해될 수 있다. 그러나 아벨-루피니 정리에 따라 오차 이상의 대수 방정식에 대한 일반적인 근의 공식은 존재하지 않지만, 판별식은 차수에 관계없이 항상 정의된다.

정의에 따라, 판별식의 값이 0인 것은 방정식이 중근(즉, 중복도가 2 이상인 근)을 가지는 것과 동치이다.

실수 계수를 갖는 대수 방정식의 경우, 판별식의 부호는 실수해의 개수에 대한 정보를 제공한다.

이차 방정식: 판별식이 양수이면 서로 다른 두 실근, 0이면 중복된 실근(하나의 실근), 음수이면 두 개의 켤레 복소수 근(실근 없음)을 가진다.
삼차 방정식: 판별식이 양수이면 세 개의 서로 다른 실근, 0이면 중근을 포함하여 모든 근이 실수(두 개의 실근 또는 하나의 실근), 음수이면 하나의 실근과 두 개의 켤레 복소수 근을 가진다.

삼차 이상에서는 판별식만으로는 실수해의 개수를 완전히 판별할 수 없으며, 다른 지표가 필요하다.

판별식의 개념은 계수가 복소수체가 아닌 경우에도 적용될 수 있다. 계수가 정역 ''R''에 속하면 판별식도 ''R''의 원소가 된다. 특히, 정수 계수 다항식의 판별식은 항상 정수이며, 이 성질은 수론에서 중요하게 사용된다.

계수가 일반적인 가환환 ''A''에 속하는 대수 방정식에 대해서도 판별식을 정의할 수 있다. 다만, 환 ''A''가 정역이 아닐 경우 나눗셈이 항상 정의되지 않으므로, 결합식을 이용한 정의에서 최고차항 계수

a_n

으로 나누는 대신, 최고차항 계수를 1로 가정하거나 다른 방식으로 정의를 수정해야 할 수 있다. 이 일반화된 판별식은 대수 기하학에서 다음과 같은 기본적인 성질을 가진다.

''f''를 가환환 ''A''에 계수를 갖는 다항식이라 하고, ''D''를 그 판별식이라고 하자. φ를 ''A''에서 체 ''K''로 가는 환 준동형 사상이라 하고, φ(''f'')를 ''f''의 계수를 φ를 통해 ''K''의 원소로 보낸 다항식이라고 하자. 이때 φ(''D'') = 0일 필요충분조건은, ''f''와 φ(''f'')의 차수가 2 이상 차이 나거나, 또는 φ(''f'')가 ''K''의 대수적 폐포에서 중근을 갖는 것이다. 첫 번째 경우는 φ(''f'')가 무한 원점에서 중근을 갖는 것으로 해석될 수 있다.

이 성질은 ''A''가 체 ''k'' 위의 다항식 환이고 φ가 ''A''의 변수들에 ''k''의 체 확대 ''K''의 원소를 대입하는 경우에 자주 응용된다. 예를 들어, ''f''가 실수 계수를 갖는 ''X''와 ''Y''의 이변수 다항식이고 ''f'' = 0이 평면 대수 곡선의 음함수 방정식이라고 하자. ''f''를 ''Y''에 대한 일변수 다항식(계수는 ''X''에 대한 식)으로 보면, 그 판별식은 ''X''에 대한 다항식이 된다. 이 판별식의 근은 곡선의 특이점, ''Y''축에 평행한 접선을 갖는 점, 또는 ''Y''축에 평행한 점근선과 관련된 점들의 ''X''좌표에 해당한다. 즉, ''Y''에 대한 판별식과 ''X''에 대한 판별식의 근을 계산하면 변곡점을 제외한 곡선의 주요 특징점들을 찾을 수 있다.

판별식의 개념은 일변수 다항식을 넘어 원뿔 곡선, 이차 형식, 대수적 수체 등 다른 대수적 구조로 일반화된다. 대수적 정수론에서의 판별식은 분기 현상과 밀접하게 연관되어 있다. 이처럼 판별식은 다양한 수학 분야에서 핵심적인 역할을 하는 대수적 개념이다.

판별식은 근들의 대칭식이다. 판별식의 제곱근(반데르몬드 다항식)은 근들의 짝수 순열에 대해서는 불변이지만 홀수 순열에 대해서는 부호가 바뀌는 교대식이다.

n

개의 변수에 대한 대칭 다항식 환

\Lambda_n

에 이 반데르몬드 다항식을 추가하면 교대식의 환을 얻게 되며, 이는

\Lambda_n

의 이차 확대이다.

6. 1. 대수적 수체의 판별식

대수적 수체의 판별식은 해당 수체의 정수환 크기를 측정하는 중요한 불변량이다. 더 구체적으로 말하면, 정수환의 기본 영역의 제곱 부피에 비례하며, 어떤 소수가 분기되는지를 규제한다.

판별식은 수체의 가장 기본적인 불변량 중 하나이며, ''K''의 데데킨트 제타 함수의 함수 방정식과 ''K''에 대한 해석적 유수 공식과 같은 몇 가지 중요한 해석적 수론 공식에 나타난다. 에르미트의 정리에 따르면, 유한한 수의 경계된 판별식을 갖는 수체만 존재하지만, 이 양을 결정하는 것은 여전히 미해결 문제이며 현재 연구의 대상이다.^[13]

''K''를 대수적 수체라고 하고, ''O_K''를 그 정수환이라고 하자. ''b''₁, ..., ''b_n''을 ''O_K''의 정수 기저 (즉, '''Z'''-가군으로서의 기저)라고 하고, {σ₁, ..., σ_''n''}을 ''K''를 복소수 체 '''C'''로의 임베딩 집합 (즉, 단사 환 준동형 ''K'' → '''C''')이라고 하자. ''K''의 '''판별식'''은 (''i'',''j'')-항이 σ_''i''(''b_j'')인 ''n'' x ''n'' 행렬 ''B''의 행렬식의 제곱이다. 기호로 표현하면 다음과 같다.

:

\Delta_K=\det\left(\begin{array}{cccc}\sigma_1(b_1) & \sigma_1(b_2) &\cdots & \sigma_1(b_n) \\\sigma_2(b_1) & \ddots & & \vdots \\\vdots & & \ddots & \vdots \\\sigma_n(b_1) & \cdots & \cdots & \sigma_n(b_n)\end{array}\right)^2.

''K''의 판별식은 수체 ''K''/''L''의 체 확대의 판별식과 구별하기 위해 ''K''의 '''절대 판별식'''이라고 할 수 있다. 후자는 ''L''의 정수환의 아이디얼이며, 절대 판별식과 마찬가지로 어떤 소수가 ''K''/''L''에서 분기되는지 나타낸다. 이는 ''L''이 '''Q'''보다 더 클 수 있도록 허용하는 절대 판별식의 일반화이다. 사실, ''L'' = '''Q'''일 때, ''K''/'''Q'''의 상대 판별식은 ''K''의 절대 판별식 Δ_''K''에 의해 생성된 '''Z'''의 주 아이디얼이다.

"판별식"이라는 용어는 1851년 영국의 수학자 제임스 조셉 실베스터에 의해 만들어졌다.^[14]

6. 2. 이차 형식의 판별식

이차 형식은 특정 기저에 대해 2차 동차 다항식으로 표현되는 벡터 공간 위의 함수이다.

:

Q(x_1,\ldots,x_n) \ =\ \sum_{i=1}^n a_{ii} x_i^2+\sum_{1\le i

이를 행렬 형식으로 나타내면 다음과 같다.

:

Q(X) =X A X^\mathrm T

여기서

A=(a_{ij})

는

n\times n

대칭 행렬,

X=(x_1,\ldots,x_n)

는

1\times n

행 벡터,

X^{\mathrm{T}}

는

n\times 1

열 벡터이다. 표수가 2가 아닌^[10] 체 위에서 이차 형식

Q

의 '''판별식''' 또는 '''행렬식'''은 대칭 행렬

A

의 행렬식

\det A

로 정의된다.^[11]

이차 형식

Q

의 헤세 행렬식은 판별식의

2^n

배와 같다. 또한,

Q

의 편도함수들의 다변량 종결자는 헤세 행렬식과 같다. 따라서 이차 형식의 판별식은 일반적인 다항식 판별식 정의의 특수한 경우로 볼 수 있다.

이차 형식의 판별식은 변수의 선형 변환, 즉 이차 형식이 정의된 벡터 공간의 기저 변경에 대해 중요한 불변성을 가진다. 변수의 선형 변환은 비특이 행렬

S

로 정의되며, 이 변환에 의해 대칭 행렬

A

는

S^\mathrm T A\,S

로 변환된다. 변환된 행렬의 행렬식은

\det(S^\mathrm T A\,S) = (\det S)^2 \det A

가 되므로, 판별식은 원래 판별식에

S

의 행렬식의 제곱이 곱해진 값으로 바뀐다. 이는 판별식의 값이 0이 아닌 제곱 인자를 곱하는 것을 제외하면 변하지 않음을 의미한다. 즉, 체

K

위에서의 이차 형식 판별식은

K/(K^\times)^2

의 원소로 잘 정의된다. 여기서

K/(K^\times)^2

는 체

K

의 원소들을 0이 아닌 제곱수들의 곱셈에 대한 동치류로 나눈 집합이다.

복소수 체 $\mathbb{C}$ 에서는 모든 0이 아닌 수가 제곱수이므로, 판별식의 동치류는 0 또는 1 (0이 아닌 모든 수를 대표) 두 가지뿐이다.
실수 체 $\mathbb{R}$ 에서는 0이 아닌 제곱수는 양수이므로, 판별식의 동치류는 -1 (음수 대표), 0, 1 (양수 대표) 세 가지이다.
유리수 체 $\mathbb{Q}$ 에서는 판별식의 동치류는 유일한 제곱 없는 정수로 표현될 수 있다.

야코비의 정리에 따르면, 표수가 2가 아닌 체 위에서의 모든 이차 형식은 적절한 변수 변환을 통해 다음과 같은 '''대각 형식'''으로 표현될 수 있다.

:

a_1x_1^2 + \cdots + a_nx_n^2

더 정확하게는, 이차 형식은 독립적인 선형 형식

L_i

들의 제곱합으로 나타낼 수 있다 (

n

은 변수의 개수).

:

\sum_{i=1}^n a_i L_i^2

이때, 일부

a_i

는 0일 수 있다. 대각 형식에서의 판별식은 계수

a_1, \ldots, a_n

들의 곱

a_1 \cdots a_n

이며, 이 값은

K/(K^\times)^2

의 원소로서 유일하게 결정된다.

기하학적으로 이차 형식의 판별식은 다음과 같은 의미를 가진다.

변수가 3개인 이차 형식은 사영 평면에서 원뿔 곡선 또는 이차 곡선을 정의한다. 판별식이 0인 경우는 곡선이 두 개의 직선으로 분해되는 경우(체 확장 상에서 포함)와 동치이다.
변수가 4개인 이차 형식은 사영 공간에서 이차 곡면을 정의한다. 판별식이 0인 경우는 곡면이 특이점을 가지는 경우와 동치이다. 이 경우 곡면은 두 개의 평면으로 분해되거나, 하나의 특이점을 가지는 원뿔 또는 원통이 된다.
실수체 위에서, 판별식이 양수이면 곡면은 실수점을 가지지 않거나 모든 점에서 가우스 곡률이 음수이다. 판별식이 음수이면 곡면은 실수점을 가지며 가우스 곡률이 음수이다.

"판별식(discriminant)"이라는 용어는 1851년 영국의 수학자 제임스 조셉 실베스터가 처음 사용했다.^[14] 일반적으로 대문자

D

또는 그리스 문자 대문자 Δ로 표기한다.

이차 형식의 판별식 개념은 이차 다항식의 판별식과 밀접하게 연관된다. 이차 다항식

ax^2+bx+c

를 동차화하면 이차 형식

ax^2+bxy+cy^2

를 얻는다. 이 이차 형식에 대응하는 대칭 행렬은 다음과 같다.

:

\begin{bmatrix} a & b/2 \\ b/2 & c \end{bmatrix}

이 행렬의 행렬식, 즉 이차 형식의 판별식은

ac - (b/2)^2 = ac - b^2/4

이다. 이는 이차 방정식

ax^2+bx+c=0

의 판별식

\Delta = b^2-4ac

에

-1/4

를 곱한 값과 같다. 즉, 두 판별식은 상수 배의 차이만 있을 뿐 본질적으로 같은 정보를 담고 있다.

실수체 위에서 이차 형식

ax^2+bxy+cy^2

의 판별식

ac-b^2/4

의 부호(양, 0, 음)는 해당 형식이 나타내는 원뿔 곡선의 종류가 각각 타원, 포물선, 쌍곡선임을 나타낸다. 이는 일반적인 이차 방정식

Ax^2+Bxy+Cy^2+Dx+Ey+F=0

의 판별식

B^2-4AC

의 부호 판정 기준과는 부호가 반대일 수 있음에 유의해야 한다.

6. 3. 원뿔 곡선의 판별식

원뿔 곡선은 일반적으로 다음과 같은 2차 음함수 방정식으로 표현되는 평면 곡선이다.

:

Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0

여기서 ''A'', ''B'', ''C'', ''D'', ''E'', ''F''는 실수 계수이다.

이 원뿔 곡선과 관련하여 두 가지 주요 판별식이 있다.

첫 번째 판별식은 방정식 전체를 동차 형식으로 만들었을 때의 이차 형식과 관련되며, 다음과 같은 행렬식으로 표현된다.

:

\begin{vmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{vmatrix}

이 행렬식의 값이 0이면 원뿔 곡선이 두 개의 직선, 하나의 이중선, 또는 하나의 점과 같이 퇴화된 형태임을 의미한다.

두 번째 판별식은 방정식의 2차 항 부분(

Ax^2 + Bxy + Cy^2

)과 관련된 것으로, 원뿔 곡선의 기하학적 형태를 결정하는 데 주로 사용된다.^[12]^[19] 이 판별식은 다음과 같이 정의된다.

:

\Delta = B^2 - 4AC

이 판별식

\Delta

의 부호에 따라 원뿔 곡선의 종류가 결정된다.

판별식( $B^2 - 4AC$ ) 값에 따른 원뿔 곡선의 분류
판별식 ( $\Delta = B^2 - 4AC$ )	원뿔 곡선의 형태 (퇴화되지 않은 경우)	퇴화된 경우 (첫 번째 판별식 = 0)
< 0	타원 또는 원	점
= 0	포물선	두 개의 평행선 또는 이중선
> 0	쌍곡선	교차하는 두 직선

구체적으로, 판별식 $\Delta$ 가 0보다 작으면( $\Delta < 0$ ) 곡선은 타원 또는 원이다. 판별식이 0과 같으면( $\Delta = 0$ ) 곡선은 포물선이다. 판별식이 0보다 크면( $\Delta > 0$ ) 곡선은 쌍곡선이다. 이러한 분류는 원뿔 곡선이 퇴화되지 않았을 때 적용되며, 퇴화된 경우는 위의 표와 같이 다른 형태를 가진다.

6. 4. 실수 이차 곡면의 판별식

3차원 유클리드 공간에서 실수 이차 곡면은 세 변수에 대한 2차 다항식의 영점으로 정의될 수 있는 곡면이다. 원뿔 곡선처럼 자연스럽게 정의될 수 있는 두 개의 판별식이 있으며, 이들은 이차 곡면의 특성에 대한 정보를 얻는 데 유용하다.

''P''(x,y,z)를 실수 이차 곡면을 정의하는 세 변수에 대한 2차 다항식이라고 하자. 첫 번째 관련 2차 형식 ''Q''₄는 네 개의 변수에 의존하며, ''P''의 동차화를 통해 얻어진다. 즉,

:

Q_4(x,y,z,t)=t^2P(x/t,y/t, z/t).

이것의 판별식을

\Delta_4

로 표기한다.

두 번째 2차 형식 ''Q''₃는 세 개의 변수에 의존하며, ''P''의 2차 항으로 구성된다. 즉,

:

Q_3(x,y,z)=Q_4(x, y,z,0).

이것의 판별식을

\Delta_3

로 표기한다.

만약

\Delta_4 > 0

이고 곡면에 실수 점이 있다면, 이는 쌍곡 포물면 또는 일엽 쌍곡면이다. 두 경우 모두, 모든 점에서 음의 가우스 곡률을 갖는 유리 곡면이다.

만약

\Delta_4 < 0

이면, 곡면은 타원체, 이엽 쌍곡면 또는 타원 포물면이다. 모든 경우에서, 이는 모든 점에서 양의 가우스 곡률을 갖는다.

만약

\Delta_4 = 0

이면, 곡면은 특이점을 가지며, 이는 무한원점에 있을 수도 있다. 특이점이 하나만 있으면, 곡면은 원기둥 또는 원뿔이다. 특이점이 여러 개 있으면 곡면은 두 개의 평면, 이중 평면 또는 단일 선으로 구성된다.

\Delta_4 \ne 0

일 때,

\Delta_3

의 부호가 0이 아닌 경우는 유용한 정보를 제공하지 않는다. 왜냐하면 ''P''를 −''P''로 변경해도 곡면은 변하지 않지만,

\Delta_3

의 부호는 변경되기 때문이다. 그러나 만약

\Delta_4 \ne 0

이고

\Delta_3 = 0

이면, 곡면은 포물면이며,

\Delta_4

의 부호에 따라 타원형 또는 쌍곡선형이다.

7. 응용

대수기하학에서 판별식은 평면 대수 곡선이나 더 일반적인 초곡면의 성질을 연구하는 데 유용하게 사용된다. 이러한 곡선이나 초곡면 V는 여러 변수를 가진 다변수 다항식의 값이 0이 되는 점들의 집합으로 정의된다. 이 다항식을 특정 변수(예: Y)에 대한 단변수 다항식으로 간주하고, 다른 변수들(예: X)을 계수로 취급할 수 있다.

이렇게 만들어진 단변수 다항식에 대해 판별식을 계산하면, 이는 다른 변수들(X)의 공간에서 새로운 초곡면 W를 정의한다. 이 초곡면 W 위의 점들은 원래 곡선이나 초곡면 V가 가지는 특별한 점들, 즉 특이점이거나 선택된 특정 축(Y축)에 평행한 접선을 갖는 점들의 투영에 해당한다. 이는 무한대점을 포함할 수도 있다.

예를 들어, 실수 계수를 가지는 두 변수 X와 Y에 대한 이변수 다항식 ''f''(X, Y) = 0 이 있다고 하자. 이 식은 실수 평면 위에 그려지는 대수 곡선의 음함수 방정식을 나타낸다. 이 다항식 ''f''를 Y에 대한 단변수 다항식으로 보고 (X는 계수처럼 취급) 판별식을 계산하면, 그 결과는 X에 대한 다항식이 된다. 이 X에 대한 판별식의 근(해가 되는 X값)은 원래 곡선의 특이점, Y축에 평행한 접선을 가지는 점, 그리고 Y축에 평행한 일부 점근선의 X좌표가 된다. 따라서 Y에 대한 판별식과 X에 대한 판별식의 근을 계산하면, 변곡점을 제외하고 곡선의 주목할 만한 점들을 대부분 찾아낼 수 있다.

참조

_[1] 웹사이트 Discriminant {{!}} mathematics https://www.britanni[...] 2020-08-09
_[2] 간행물 On a remarkable discovery in the theory of canonical forms and of hyperdeterminants 1851
_[3] 서적 Elimination practice: software tools and applications https://books.google[...] Imperial College Press
_[4] 서적 Discriminants, resultants and multidimensional determinants http://blms.oxfordjo[...] Birkhäuser
_[5] 서적 Solving polynomial equations: foundations, algorithms, and applications https://books.google[...] Springer Science+Business Media
_[6] 서적 Integers, polynomials, and rings https://books.google[...] Springer-Verlag New York, Inc.
_[7] 웹사이트 Cubic Discriminant {{!}} Brilliant Math & Science Wiki https://brilliant.or[...] 2023-03-21
_[8] 웹사이트 Discriminant of a cubic equation https://www.johndcoo[...] 2019-07-14
_[9] 서적 Integers, polynomials, and rings https://books.google[...] Springer-Verlag New York, Inc.
_[10] 문서 In characteristic 2, the discriminant of a quadratic form is not defined, and is replaced by the [[Arf invariant]].
_[11] 서적 Rational Quadratic Forms Academic Press
_[12] 서적 Math refresher for scientists and engineers https://books.google[...] John Wiley and Sons
_[13] 간행물 Algorithmic Number Theory, Proceedings, 5th International Syposium, ANTS-V, University of Sydney, July 2002 Springer-Verlag
_[14] 간행물 On a remarkable discovery in the theory of canonical forms and of hyperdeterminants Philosophical Magazine 1851
_[15] 서적 Discriminants, resultants and multidimensional determinants https://academic.oup[...] Birkhäuser
_[16] 서적 Solving polynomial equations: foundations, algorithms, and applications https://books.google[...] Springer
_[17] 서적 線形代数問題集森北出版 1989-01-01
_[18] 문서 二次方程式の一次項が偶数の時に簡便な計算方法として利用されるほか、[[コーシー＝シュワルツの不等式#証明|コーシー＝シュワルツの不等式]]の一般解を二次式と判別式で証明する際などに利用されることがある。
_[19] 간행물 Math refresher for scientists and engineers https://books.google[...] John Wiley and Sons
_[20] 서적 Rational Quadratic Forms Academic Press
_[21] 서적
_[22] 서적

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com