세계선

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 세계선의 기본 개념
- 2.1. 민코프스키 도표와 세계선
- 2.2. 빛원뿔(Light cone)
3. 다양한 세계선과 그 의미
- 3.1. 입자의 충돌과 세계선
4. 특수 상대성 이론에서의 세계선
5. 일반 상대성 이론에서의 세계선
6. 양자장론에서의 세계선
7. 세계선의 문학적 표현
참조

1. 개요

세계선은 시공간에서 물체의 역사를 나타내는 4차원 곡선으로, 각 점은 물체의 시간과 공간 위치를 의미한다. 특수 상대성 이론에서는 빛의 속도가 상수인 관성 좌표계에서 자유 낙하하는 물체의 세계선은 직선인 측지선으로 나타나며, 일반 상대성 이론에서는 시공간의 곡률을 고려하여 측지선이 정의된다. 양자장론에서도 세계선 개념이 활용되며, 문학 작품에서도 세계선을 인간의 삶이나 시간의 흐름을 비유하는 표현으로 사용한다.

더 읽어볼만한 페이지

민코프스키 시공간 - 고유 시간
고유 시간은 시공간에서 물체가 실제로 경험하는 시간 간격으로, 세계선을 따라 적분한 값으로 계산되며 로렌츠 변환에 대해 불변하는 양으로, 상대성 이론에서 시간 간격을 정의하고 쌍둥이 역설과 같은 상대론적 효과를 설명하는 데 사용된다.
민코프스키 시공간 - 전자기장 텐서
전자기장 텐서는 전자기 퍼텐셜의 도함수로 이루어진 2계 텐서로, 전자기장을 상대론적으로 기술하고 맥스웰 방정식을 간결하게 표현하며 로런츠 힘을 기술하는 데 사용된다.
상대성이론 - 시공간
시공간은 시간과 공간을 4차원 연속체로 통합한 개념으로, 아인슈타인의 상대성이론에 따라 상대적이며, 일반 상대성이론에서는 중력을 시공간의 곡률로 설명하고, 현대 물리학과 우주론 연구에 필수적이다.
상대성이론 - 대응원리
대응 원리는 플랑크 상수가 0에 가까워지는 극한에서 양자역학이 고전역학으로 근사적으로 환원됨을 보이는 원리로서, 초기 양자역학 발전에 기여했으나 현대에는 유추적인 역할로 중요성이 감소하였지만, 고전역학과 양자역학의 수학적 대응 관계 연구를 통해 계승되고 있다.

세계선
일반 정보
정의	어떤 물체가 시공간을 지나가는 유일한 경로
다른 용어	세계선 (월드라인, worldline)
관련 개념
관련 용어	세계면 (world sheet), 세계부피 (world volume), 세계선 (worldline)

2. 세계선의 기본 개념

물체(일반적으로 입자 또는 관찰자)의 세계선은 그 물체의 역사에 해당하는 시공간 사건들의 연속이다. 세계선은 시공간에서 특수한 종류의 곡선으로, 시간적 또는 영적 곡선이다. 세계선의 각 점은 그 시간에 물체의 시간과 공간 위치를 나타내는 사건이다.^[1]

예를 들어, 지구의 우주 궤도는 공간에서 근사적으로 원이지만, 매년 같은 지점에 돌아오는 시간은 다르다. 따라서 지구의 세계선은 시공간에서 나선형이다.

시공간은 사건들의 집합이며, 각 사건은 시간 좌표와 세 개의 공간 좌표로 표시된다. 시공간은 4차원 다양체이며, 고차원 공간에도 적용될 수 있다. 4차원을 쉽게 시각화하기 위해 종종 두 개의 공간 좌표를 생략하고, 민코프스키 다이어그램을 사용한다.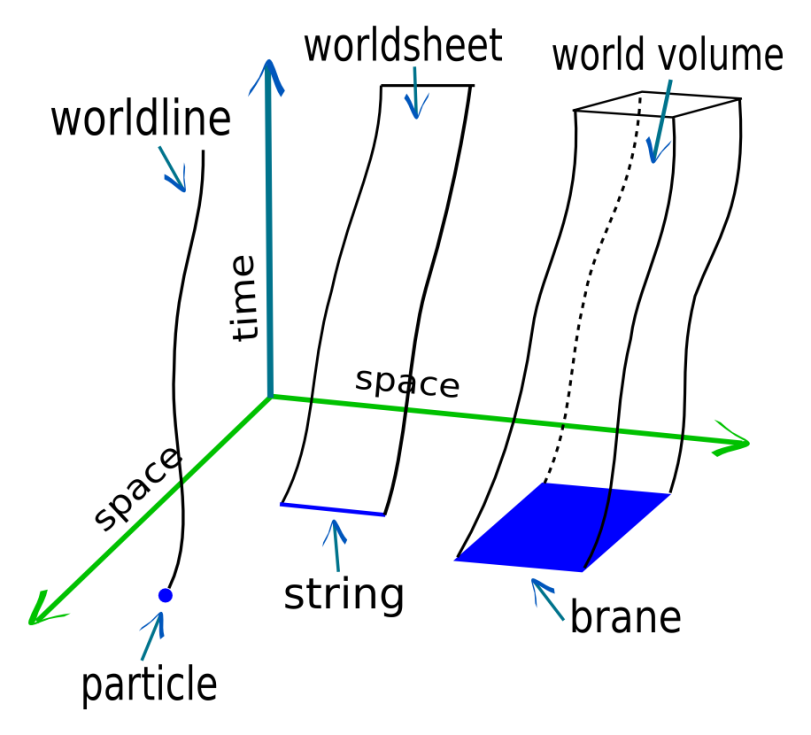

세계선은 시공간에서 단일 점의 경로를 추적하며, 부피가 있는 물체는 세계관을 그린다. 1차원 선 또는 곡선은 한 매개변수의 함수로서 좌표로 나타낼 수 있으며, 각 매개변수 값은 시공간의 한 점에 해당한다. 세계선은 입자, 관찰자 또는 작은 물체의 시간 역사를 추적하는 시공간의 곡선이며, 일반적으로 고유 시간을 곡선 매개변수로 사용한다.^[1]

세계선을 정의하는 네 개의 좌표 함수는 실수 함수이며, 미분 가능하다. 매개변수 값에서 곡선상의 점 사이의 차이를 통해 사차속도라고 하는 접선 벡터를 정의할 수 있다. 점 p에 대한 모든 접선 벡터는 선형 공간을 이루며, 이를 점 p에서의 접공간이라고 한다.

특수 상대성 이론은 가능한 세계선에 제약 조건을 부여하며, 관성 기준계에서 빛의 속도는 상수이다. 시공간의 구조는 이차 형식에 의해 결정된다. 자유 낙하하는 입자의 세계선은 측지선이라고 하며, 특수 상대성 이론에서 이들은 민코프스키 공간의 직선이다.^[1]

일반 상대성 이론에서 세계선은 특수 상대성 이론과 기본적으로 동일하지만, 시공간이 곡률을 가질 수 있다는 점이 다르다. 계량은 아인슈타인 장 방정식에 의해 결정되고 시공간의 질량-에너지 분포에 따라 달라진다.

2. 1. 민코프스키 도표와 세계선

민코프스키 도표는 공간과 시간 축으로 구성된 그림으로, 세계에서 일어나는 일에 대한 개념 지도 역할을 한다. 물체의 세계선은 그 물체의 역사에 해당하는 시공간 사건들의 연속을 나타내며, 시공간에서 특수한 종류의 곡선이다. 세계선의 각 점은 그 시간에 물체의 시간과 공간 위치를 나타내는 사건이다. 예를 들어, 지구의 세계선은 시공간에서 나선형이며, 매년 같은 공간 위치로 돌아오지만 시간은 다르다.^[1]

시공간은 사건들의 집합이며, 각 사건은 네 개의 숫자(시간 좌표와 세 개의 공간 좌표)로 표시된다. 4차원을 시각화하기 위해 종종 두 개의 공간 좌표를 생략하고, 시간 좌표(t)를 수직으로, 공간 좌표(x)를 수평으로 그리는 민코프스키 다이어그램을 사용한다. 세계선은 시공간에서 단일 점의 경로를 추적하며, 물체가 부피를 가지면 세계관을 그리게 된다.^[1]

상수 4속도로 이동하는 세 가지 다른 세계선. ''t''는 시간이고 ''x''는 거리이다.

세계선은 시공간에서 입자, 관찰자 또는 작은 물체의 시간 역사를 추적하는 곡선이다. 상수 공간 좌표의 선은 정지 상태의 입자를 나타내며, 기울어진 선은 상수 좌표 속도를 가진 입자를 나타낸다. 두 세계선이 교차하면 충돌 또는 "만남"을 의미하며, 광자의 세계선과 상호 연결될 수 있다.^[1]

특수 상대성 이론은 가능한 세계선에 제약 조건을 부여하며, 관성 기준계에서 빛의 속도는 상수이다. 시공간의 구조는 이차 형식 η에 의해 결정되며, 이는 각 사건 쌍에 대해 실수를 제공한다. 자유 낙하하는 입자의 세계선은 측지선이라고 하며, 특수 상대성 이론에서 이들은 민코프스키 공간의 직선이다.^[1]

시공간에서 유용한 곡선은 세 가지 유형으로 나뉜다.

'''광선 같은 곡선'''은 각 지점에서 빛의 속도를 가지며, 시공간에서 원뿔을 형성한다.

급가속하는 관측자(중앙)의 궤적("세계선")을 따라 순간적으로 공동 이동하는 관성 프레임. 수직 방향은 시간을, 수평 방향은 거리를 나타내며, 점선은 관측자의 시공간이다. 작은 점들은 시공간에서 특정 사건이다. 관측자가 가속할 때 순간적으로 공동 이동하는 관성 프레임이 어떻게 변하는지 주목하십시오.

'''시간 같은 곡선'''은 빛의 속도보다 느린 속도를 가지며, 빛 같은 곡선에 의해 정의된 원뿔 내에 있어야 한다.
'''공간 같은 곡선'''은 빛 원뿔 외부에 있으며, 물리적 물체의 길이를 나타낼 수 있다.^[1]

세계선의 주어진 사건에서 시공간은 미래, 과거, 빛 원뿔, 어디에도 아닌 곳으로 나뉜다. "어디에도 아닌 곳"에는 동시 초평면이 포함되며, 이는 주어진 관측자에 대해 그들의 세계선에 대해 쌍곡 직교인 공간에 의해 정의된다.

2. 2. 빛원뿔(Light cone)

민코프스키 공간에서 원점에서 나오는 빛이 만드는 곡면을 빛원뿔(광원뿔)이라고 한다. 3차원 공간에서 X축과 Y축은 공간, Z축은 시간에 해당한다. 아래쪽 원뿔은 과거, 위쪽 원뿔은 미래의 시공간을 나타내며, 두 원뿔이 만나는 점은 현재이다. 원뿔의 모선은 빛의 속도 C를 나타내며, 빛원뿔 밖의 공간은 빛보다 빠른 속도로만 도달할 수 있다.^[1]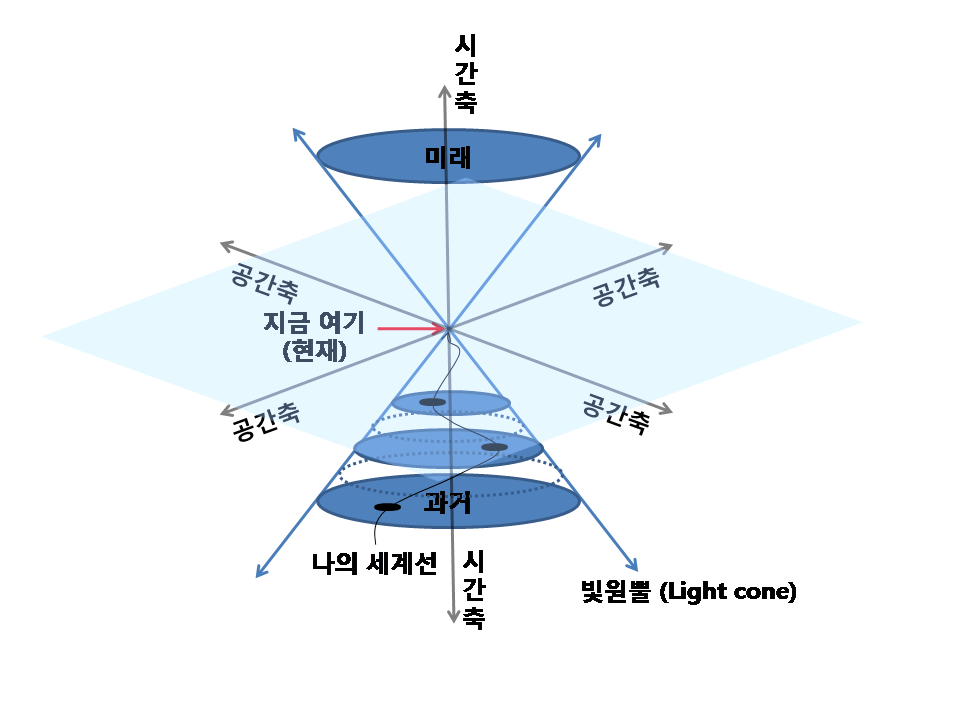

특수 상대성 이론에서 로런츠 변환에 의해 일반적인 시공간 방향은 서로 다르게 변환되지만, 빛원뿔에서 모든 빛의 방향은 변환될 수 있으므로 빛원뿔은 공간 내에서 변하지 않는다. 즉, 모든 빛은 자신의 빛원뿔 상에서 이동할 수 있다. 이는 민코프스키 공간의 고유한 성질이다.^[1]

세계선의 주어진 사건에서 시공간(민코프스키 공간)은 세 부분으로 나뉜다.

주어진 사건의 '''미래'''는 미래 빛원뿔 내에 있는 시간 같은 곡선을 통해 도달할 수 있는 모든 사건으로 구성된다.
주어진 사건의 '''과거'''는 사건에 영향을 미칠 수 있는(즉, 과거 빛 원뿔 내의 세계선을 통해 주어진 사건과 연결될 수 있는) 모든 사건으로 구성된다.
주어진 사건의 '''빛 원뿔'''은 빛의 경로를 통해 사건과 연결될 수 있는 모든 사건으로 구성된다. 우리가 밤하늘을 관찰할 때, 우리는 기본적으로 전체 시공간 내의 과거 빛 원뿔만 본다.
'''어디에도 아닌 곳'''은 두 빛 원뿔 사이의 영역이다.
"어디에도 아닌 곳"에는 '''동시 초평면'''이 포함된다.
'''현재'''는 종종 고려 중인 단일 시공간 사건을 의미한다.

일반적으로 시공간에서 유용한 곡선은 세 가지 유형이 있다.

'''빛 같은 곡선'''은 각 지점에서 빛의 속도를 갖는다. 이들은 시공간에서 원뿔을 형성하여 시공간을 두 부분으로 나눈다.
'''시간 같은 곡선'''은 빛의 속도보다 느린 속도를 갖는다. 이러한 곡선은 빛 같은 곡선에 의해 정의된 원뿔 내에 있어야 한다.
'''공간 같은 곡선'''은 빛 원뿔 외부에 있다.

물체의 속도가 일정한 세계선을 측지선이라고 하며, 세계선의 곡선은 광적, 시간적, 공간적으로 구분된다. 시공간이 휘어져 있다는 점은 특수상대성이론의 경우와 다르다. 계량과 그 안에서의 운동은 아인슈타인의 장 방정식에 의해 결정된다. 그것은 시공간상의 질량 분포에 의존한다. 또한, 계량으로부터 광적(null), 공간적(space-like), 시간적(time-like)이 결정된다. 하지만, 광원추는 일정한 각도일 필요는 없고, 좌표를 선택하는 방식에 따라 광원추의 외관 형태의 자유도가 있다.

3. 다양한 세계선과 그 의미

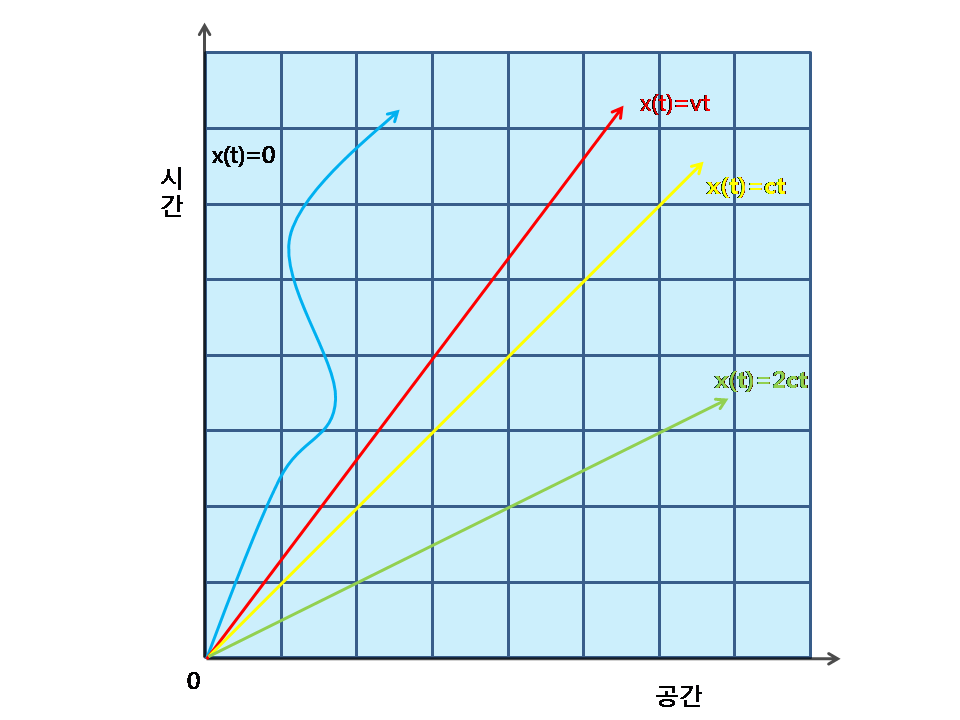
시공간을 통한 경로는 보통 세계선이라고 불린다. 오른쪽 그림에 나타난 다양한 세계선들은 모두 원점(x = 0으로 표시된 점의 시간 0)에서 시작한다. 이 점은 임의로 선택된 기준점일 뿐 특별한 의미는 없다.

검은색 화살표(시간 축과 일치)는 x = 0 지점에 정지해 있는 물체를 나타낸다. 노란색 화살표는 광자의 세계선, 즉 빛의 파동을 나타낸다. 다른 직선들은 일정한 속도로 움직이는 물체들이다. 붉은색 화살표는 빛의 속도의 3/4(V = 3/4c)로 이동하는 물체, 녹색 화살표(유령)는 광속의 두 배로 이동하는 물체를 나타낸다. 파동치는 하늘색 세계선은 가속과 감속을 반복하며 움직이는 물체를 나타낸다. 이 물체의 속도는 각 순간 곡선의 접선 기울기로 결정된다. 공간 축과 일치하는 화살표는 무한대의 속도를, 공간 축 아래로 내려가는 세계선은 시간을 거슬러 올라가는 것처럼 보이는 여행을 나타낸다.

세계선은 이처럼 여행자의 운동 역사를 정확하게 설명해준다.

민코프스키 시공간에서 세계선은 다음과 같이 세 가지 유형으로 분류할 수 있다.

유형	설명	그림 예시
시간 꼴 간격 (time-like interval)	빛보다 느린 모든 물체의 세계선. 빛원뿔 안쪽에 위치.	시간 축과 일치하는 검은 세계선, 하늘색 세계선, 붉은색 세계선
light-like interval	빛과 같은 속도로 움직이는 모든 물체의 세계선 (광자 포함).	노란 세계선
공간 꼴 간격 (space-like interval)	빛보다 빠른 모든 물체의 세계선. 빛원뿔 바깥쪽에 위치하며, 원점과 인과관계로 연결되지 않음. 그밖의 다른 장소(elsewhere)라고도 불림.	녹색 세계선, 공간 축과 일치하는 검은 세계선

특수 상대성 이론은 가능한 세계선에 몇 가지 제약 조건을 부여한다. 관성 좌표계에서 빛의 속도는 상수이며, 자유 낙하하는 물체의 세계선은 측지선(민코프스키 공간의 직선)으로 표현된다.

thumb, 시공간의 한 점에 도달하고 출발하는 모든 가능한 빛의 경로의 3차원 표면의 예. 여기서는 한 공간 차원이 생략되어 표현되어 있습니다.]]

세계선의 주어진 사건에서 시공간은 다음과 같이 세 부분으로 나뉜다.

'''미래''': 미래 빛 원뿔 내에 있는 시간 같은 곡선을 통해 도달 가능한 사건들.
'''과거''': 과거 빛 원뿔 내의 세계선을 통해 주어진 사건에 영향을 줄 수 있는 사건들.
'''빛 원뿔''': 빛의 경로를 통해 사건과 연결될 수 있는 모든 사건들. 밤하늘을 관찰할 때, 우리는 과거 빛 원뿔만 본다.
'''어디에도 아닌 곳''': 두 빛 원뿔 사이의 영역. 관측자에게 접근 불가능하며, 과거의 점만이 관측자에게 신호를 보낼 수 있다.
'''동시 초평면''': "어디에도 아닌 곳"에 포함되며, 주어진 관측자에 대해 그들의 세계선에 쌍곡 직교하는 공간으로 정의된다.

일반적으로 시공간에서 유용한 곡선은 빛 같은 곡선, 시간 같은 곡선, 공간 같은 곡선의 세 가지 유형이 있다.

3. 1. 입자의 충돌과 세계선

입자의 세계선은 입자가 겪는 모든 사건, 즉 "순간마다 입자의 위치"를 나타낸다. 시공간에서 입자는 점이 아니라 곡선으로 표현된다. A와 B라는 두 입자의 세계선이 점 P에서 만난다고 가정하면, 이는 두 입자가 물리적으로 충돌하는 것을 의미한다. 세계선의 교차는 충돌을 나타내며, 교차하지 않으면 충돌하지 않는다.^[1]

수평선분(상수 좌표 시간의 선)은 시공간에서 막대를 나타낼 수 있지만, 진정한 의미의 세계선은 아니다. 상수 공간 좌표의 선(수직선)은 정지 상태의 입자를 나타내며, 기울어진 선은 상수 좌표 속도를 가진 입자를 나타낸다. 선이 수직에서 더 많이 기울어질수록 속도가 커진다.^[1]

분리되어 시작하여 교차하는 두 세계선은 충돌 또는 "만남"을 의미한다. 시공간의 같은 사건에서 시작하여 각각 나중에 자체 경로를 따르는 두 세계선은 입자가 두 개의 다른 입자로 붕괴되거나 한 입자가 다른 입자에 의해 방출되는 것을 나타낼 수 있다.^[1]

입자와 관측자의 세계선은 광자의 세계선(빛의 경로)과 상호 연결될 수 있으며, 이는 입자에 의해 방출된 광자가 그 후 관측자에 의해 관찰되거나(또는 다른 입자에 의해 흡수됨) 그려진 다이어그램을 형성한다.^[1]

4. 특수 상대성 이론에서의 세계선

특수 상대성 이론에서 시공간의 기술은 가속되지 않는 특수 좌표계, 즉 관성 좌표계로 제한된다. 이러한 좌표계에서 빛의 속도는 상수이다. 시공간의 구조는 이차 형식 η에 의해 결정되는데, 이는 각 사건 쌍에 대해 실수를 제공한다. 이차 형식은 때때로 '시공간 메트릭'이라고도 하지만, 수학의 메트릭 공간의 메트릭과 달리 서로 다른 사건이 때때로 0의 값을 생성하므로, 이차 형식은 시공간에 대한 수학적 메트릭이 아니다.^[1]

자유 낙하하는 입자/물체의 세계선을 측지선이라고 한다. 특수 상대성 이론에서 이들은 민코프스키 공간의 직선이다.

종종 시간 단위는 빛의 속도가 특정 각도(일반적으로 45도)의 선으로 표현되도록 선택되는데, 이는 수직(시간) 축으로 원뿔을 형성한다. 일반적으로 시공간에서 유용한 곡선은 세 가지 유형이 있을 수 있다(다른 유형은 부분적으로 하나의 유형, 부분적으로 다른 유형일 것이다).

'''빛 같은 곡선'''은 각 지점에서 빛의 속도를 갖는다. 이들은 시공간에서 원뿔을 형성하여 시공간을 두 부분으로 나눈다. 원뿔은 시공간에서 3차원이며, 두 차원이 생략된 그림에서는 선으로, 한 공간 차원이 생략된 그림에서는 원뿔로 나타난다.

'''시간 같은 곡선'''은 빛의 속도보다 느린 속도를 갖는다. 이러한 곡선은 빛 같은 곡선에 의해 정의된 원뿔 내에 있어야 한다. '''세계선은 시공간에서 시간 같은 곡선이다'''.
'''공간 같은 곡선'''은 빛 원뿔 외부에 있다. 이러한 곡선은 예를 들어 물리적 물체의 길이를 나타낼 수 있다. 원통의 둘레와 막대의 길이는 공간 같은 곡선이다.

세계선의 주어진 사건에서 시공간(민코프스키 공간)은 세 부분으로 나뉜다.

주어진 사건의 '''미래'''는 미래 빛 원뿔 내에 있는 시간 같은 곡선을 통해 도달할 수 있는 모든 사건으로 구성된다.
주어진 사건의 '''과거'''는 사건에 영향을 미칠 수 있는(즉, 과거 빛 원뿔 내의 세계선을 통해 주어진 사건과 연결될 수 있는) 모든 사건으로 구성된다.
주어진 사건의 '''빛 원뿔'''은 빛의 경로를 통해 사건과 연결될 수 있는 모든 사건으로 구성된다. 우리가 밤하늘을 관찰할 때, 우리는 기본적으로 전체 시공간 내의 과거 빛 원뿔만 본다.
'''어디에도 아닌 곳'''은 두 빛 원뿔 사이의 영역이다. 관측자의 '''어디에도 아닌 곳'''에 있는 점은 관측자에게 접근할 수 없다. 과거의 점만이 관측자에게 신호를 보낼 수 있다. 일반적인 실험실 경험에서 일반적인 단위와 측정 방법을 사용하면 현재를 보는 것처럼 보일 수 있지만, 실제로는 빛이 전파되는 데 항상 지연 시간이 있다. 예를 들어, 우리는 태양을 "지금"의 모습이 아니라 약 8분 전의 모습으로 본다. 갈릴레이/뉴턴 이론의 '''현재'''와 달리 '''어디에도 아닌 곳'''은 두껍다. 3차원 부피가 아니라 4차원 시공간 영역이다.
"어디에도 아닌 곳"에는 '''동시 초평면'''이 포함되는데, 이는 주어진 관측자에 대해 그들의 세계선에 대해 쌍곡 직교인 공간에 의해 정의된다. 그림에서는 한 차원을 버렸기 때문에 2평면이지만 실제로는 3차원이다. 주어진 시공간 사건에서 모든 관측자에 대한 빛 원뿔은 동일하지만, 시공간에서 사건(점)에서 일치하지만 속도가 다른 관측자는 상대 속도에 의해 결정되는 각도로 서로 교차하는 세계선을 가지므로 동시 초평면이 다릅니다.
'''현재'''는 종종 고려 중인 단일 시공간 사건을 의미한다.

세계선

w(\tau) \isin R^4

는 시간적(time-like)인 4차원 속도 벡터

v = \frac {dw}{d\tau}

를 결정하므로, 민코프스키 형식(Minkowski form)

\eta(v,x)

는

x \mapsto \eta( v , x )

에 의해 선형 함수

R^4 \rarr R

를 결정한다. 이 선형 함수의 영공간을 ''N''이라고 하자. 그러면 ''N''을 ''v''에 대한 '''동시 초평면'''이라고 한다. 동시성의 상대성은 ''N''이 ''v''에 의존한다는 명제이다. 실제로, ''N''은 η에 대한 ''v''의 직교 여공간이다.

두 세계선 ''u''와 ''w''가

\frac {du}{d\tau} = \frac {dw}{d\tau}

의 관계를 가질 때, 이들은 동일한 동시 초평면을 공유한다. 이 초평면은 수학적으로 존재하지만, 상대성 이론에서의 물리적 관계는 빛에 의한 정보의 이동을 포함한다. 예를 들어, 쿨롱의 법칙으로 설명되는 전통적인 정전기적 힘은 동시 초평면에서 나타낼 수 있지만, 전하와 힘의 상대론적 관계는 지체 퍼텐셜을 포함한다.

5. 일반 상대성 이론에서의 세계선

일반 상대성 이론에서 세계선의 사용은 특수 상대성 이론과 기본적으로 동일하지만, 시공간이 곡률을 가질 수 있다는 점이 다르다. 계량이 존재하며, 그 동역학은 아인슈타인 장 방정식에 의해 결정되고 시공간의 질량-에너지 분포에 따라 달라진다.^[1] 마찬가지로 계량은 광구형(널), 공간형, 시간형 곡선을 정의한다.

일반 상대성 이론에서 세계선은 시공간의 시간형 곡선과 널 곡선을 포함하며, 시간형 곡선은 광원추 내에 속한다. 그러나 광원추는 시간축에 대해 반드시 45도로 기울어져 있는 것은 아니다. 에딩턴-핑켈슈타인 좌표도 참조할 수 있다. 하지만 이것은 선택된 좌표계의 인공물이며, 일반 상대성 이론의 좌표 자유도(미분 동형 불변성)를 반영한다. 모든 시간형 곡선은 "시간축"이 해당 곡선에 해당하는 동참 관측자를 허용하며, 어떤 관측자도 특권을 가지지 않으므로 광원추가 시간축에 대해 45도로 기울어진 국소 좌표계를 항상 찾을 수 있다.

자유 낙하하는 입자나 물체(예: 태양 주위의 행성 또는 우주에 있는 우주비행사)의 세계선을 측지선이라고 한다.

6. 양자장론에서의 세계선

양자장론은 현대 입자물리학을 기술하는 틀로서 일반적으로 양자화된 장의 이론으로 설명된다. 그러나 널리 알려지지는 않았지만, 파인만^[2]의 연구 이후로 많은 양자장론이 세계선의 관점에서 동등하게 기술될 수 있다는 것이 알려져 왔다. 이는 나중에 더 표준적인 공식이 된 그의 많은 연구^[3]에 앞선 것이다. 양자장론의 세계선 공식은 게이지 이론^[4]^[5]^[6]에서 다양한 계산과 전자기장의 비선형 효과^[7]^[8]를 설명하는 데 특히 유용함을 증명했다.

7. 세계선의 문학적 표현

C. H. 힌턴은 1884년에 "4차원이란 무엇인가?"라는 에세이를 과학 소설 형태로 발표하면서, 4차원 존재가 바로 우리 자신이며 우리의 연속적인 상태가 3차원 공간을 통과하는 것일 수 있다고 언급했다.^[9]

상대성 이론 초기 토론토 대학교의 J. C. 필즈는 인간의 세계선에 대한 대중적인 설명을 제시했다. 그는 사람이 태어나는 순간부터 모든 인간은 긴 필라멘트나 실과 같은 영적 기운을 가지며, 이것이 평생 뒤따라 다닌다고 가정했다. 그리고 각 개인이 다른 개인과의 관계에서 얽히는 복잡한 과정을 묘사하며, 젊은 시절의 단순한 얽힘을 나이가 들면서 생기는 복잡한 매듭에 비유했다.^[10]

쿠르트 보네거트는 소설 『슬레이터하우스 5』에서 별과 사람들의 세계선을 묘사했다. 트랄파마도어인들은 우주를 빛나는 스파게티로 보며, 인간을 "한쪽 끝에는 아기 다리가 있고 다른 쪽 끝에는 노인의 다리가 있는" 큰 지네로 본다고 묘사했다.

시간 여행을 다루는 공상 과학 소설들은 이 개념을 1차원 시간선으로 단순화하는 경향이 있다. 이러한 타임머신은 종종 내용물이 한 시간에 출발하여 다른 시간에 도착하지만, 공간적으로는 같은 지리적 지점에 도착하는 즉각적인 것으로 묘사된다.

올리버 프랭클린은 2008년에 일반인을 위한 가설의 단순화된 설명을 담은 『World Lines』라는 공상 과학 작품을 출판했다.^[11]

로버트 A. 하인라인은 단편 소설 『라이프라인』에서 한 사람의 세계선을 긴 분홍색 벌레로 비유하며, 한쪽 끝은 어머니의 자궁에, 다른 쪽 끝은 무덤에 있다고 묘사했다.^[12]

제임스 블리시의 『시간의 퀸컨스』와 하인라인의 『메투셀라의 아이들』에서도 이 용어가 사용된다.

5pb.가 제작한 비주얼 노벨인 슈타인즈;게이트는 세계선의 변화를 기반으로 하는 이야기를 들려주며, 디랙의 바다와 같은 세계선 및 기타 물리적 개념도 사용된다.

닐 스티븐슨의 소설 『아나템』에서는 플라톤적 실재론과 명목론 사이의 철학적 논쟁 중에 저녁 식사 자리에서 세계선에 대한 긴 논의가 이루어진다.

절대 선택은 다른 세계선을 부차적 줄거리와 설정 장치로 묘사한다.

찰스 스트로스의 "특이점 스카이"에서는 (거의) 닫힌 시간적 경로를 전략적 기동으로 완성하려는 우주 함대가 배경과 주요 줄거리 장치를 형성한다.

참조

_[1] 서적 Spinors and Calibrations https://books.google[...] Academic Press
_[2] 학술지 Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction https://journals.aps[...]
_[3] 학술지 An operator calculus having applications in quantum electrodynamics https://authors.libr[...]
_[4] 학술지 Efficient calculation of one-loop QCD amplitudes
_[5] 학술지 Progress in one-loop QCD computations http://www.slac.stan[...]
_[6] 학술지 Perturbative quantum field theory in the string-inspired formalism
_[7] 학술지 Pair production at strong coupling in weak external fields
_[8] 학술지 Worldline instantons and pair production in inhomogenous fields https://cds.cern.ch/[...]
_[9] 서적 Scientific Romances: First Series https://archive.org/[...] Swan Sonnenschein
_[10] 서적 The Mathematics Department in the University of Toronto, 1827–1978 University of Toronto Press
_[11] 서적 World Lines Epic Press
_[12] 웹사이트 Technovelgy: Chronovitameter http://www.technovel[...] 2010-09-08

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com