솔 크립키

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 생애
3. 주요 업적
4. 저작
- 4.1. 저서
- 4.2. 주요 논문
5. 수상 및 영예
6. 솔 크립키 센터
참조

1. 개요

솔 크립키는 1940년 뉴욕에서 태어난 미국의 철학자이자 논리학자이다. 그는 양상 논리, 언어 철학, 비트겐슈타인 연구, 진리 이론, 집합론 등 다양한 분야에 걸쳐 혁신적인 업적을 남겼다. 특히, 크립키는 양상 논리의 크립키 의미론, 고유명사의 의미와 지칭에 대한 '이름과 필연성' 이론, 비트겐슈타인의 '철학적 탐구'에 대한 해석 등을 통해 20세기 후반 철학에 큰 영향을 미쳤다. 그는 하버드 대학교, 록펠러 대학교, 프린스턴 대학교, 뉴욕 시립 대학교 등에서 교수로 재직했으며, 2001년에는 쇼크상을 수상했다. 2022년 췌장암으로 사망했으며, 그의 업적을 기리는 솔 크립키 센터가 뉴욕 시립 대학교에 설립되었다.

더 읽어볼만한 페이지

양상 - 양상 논리
양상 논리는 필연성, 가능성, 의무 등과 같은 양상을 다루는 논리 체계로, 솔 크립키의 크립키 의미론은 가능세계 개념을 도입하여 다양한 양상 논리 체계를 설명하는 데 기여했으며 철학적 분석과 컴퓨터 과학 등 다양한 분야에서 활용된다.
양상 - 가능세계론
가능세계론은 현실 세계 외에 다른 가능한 세계들이 존재한다는 철학 이론이며, 명제의 참/거짓, 가능성, 필연성을 설명하는 데 사용되고 양상 논리, 반사실 조건문 분석 등 다양한 분야에서 활용된다.
루트비히 비트겐슈타인 - 버트런드 러셀
버트런드 러셀은 20세기 분석철학의 기초를 다지고 수학의 논리적 환원을 시도한 영국의 철학자, 논리학자, 수학자, 역사가, 사회 비평가, 정치 운동가로, 평화 운동에 참여했으며 노벨 문학상을 수상하여 여러 분야에 영향을 미쳤다.
루트비히 비트겐슈타인 - 라이너 마리아 릴케
라이너 마리아 릴케는 20세기 초 오스트리아-헝가리 제국 출신의 독일어 시인이자 소설가, 서간 작가로, 그의 작품은 삶의 경험과 연관되어 종교적 신비주의, 죽음과 실존, 예술가의 고뇌 등을 다루며 20세기 문학에 큰 영향을 미쳤다.
미국의 논리학자 - 에밀 포스트
에밀 포스트는 폴란드 태생 미국 수학자이자 논리학자로, 계산 이론과 재귀 이론에 기여했으며, 포스트-튜링 기계 개발, 포스트 대응 문제, 다항 연산 그룹 이론 연구 등을 수행했다.
미국의 논리학자 - 리처드 제프리
리처드 제프리는 베이즈주의적 접근 방식을 발전시킨 미국의 철학자이며, 급진적 확률주의를 옹호하고 제프리 조건화를 제안했으며, MIT, 스탠퍼드 대학교 등에서 교직을 맡았다.

솔 크립키 - [인물]에 관한 문서
기본 정보
2005년의 크립키
이름	솔 크립키
로마자 표기	Saul Kripke
출생일	1940년 11월 13일
출생지	미국 뉴욕주 사포크 군 베이쇼어
사망일	2022년 9월 15일
사망지	플레인즈버러 (뉴저지), 미국
학문 분야
학파	분석철학
주요 관심사	논리학 (특히 양상논리학) 언어철학 형이상학 집합론 인식론 심리철학 분석철학사
주요 아이디어	크립키-플라텍 집합론 지시 이론 (지시의 인과 이론, 인과-역사적 지시 이론, 직접 지시 이론, 프레게-러셀 관점 비판) 허용 순서수 크립키 구조 고정 지시자 vs 유동적 지시자 아포스테리적인 필연성 분석적인 아포스테리 판단의 가능성 진리 의미론 (크립키의 진리 이론) 비분석적인, 아포스테리적인 필연적 진리 우연적인 선험적인 크립키 의미론 탈인용 원리 접근성 관계 규칙-따름 역설 (크립켄슈타인) 험프리 반론
영향	흄 프레게 하스켈 커리 C.I. 루이스 러셀 타르스키 비트겐슈타인 마이클 더밋 콰인 튜링
영향을 줌	존 P. 버제스 폴 보고시안 타일러 버지 데이비드 차머스 마이클 데빗 가레스 에반스 (철학자) 하틀리 필드 데이비드 카플란 힐러리 퍼트넘 네이선 새먼 시드니 슈메이커 스콧 소메즈 스티븐 야블로
학력 및 경력
학력	하버드 대학교 (BA)
소속 기관	프린스턴 대학교 CUNY 대학원 센터
수상
수상	롤프 쇼크 상 논리학 및 철학 부문 (2001년)

2. 생애

솔 크립키는 1940년 뉴욕주 베이쇼어에서 유대인 가정의 1남 2녀 중 장남으로 태어났다. 아버지는 랍비 마이어 크립키(Myer S. Kripke^영어)였으며, 어머니는 유대교 교육 서적 작가인 도로시 크립키(Dorothy K. Kripke^영어)였다. 두 여동생은 매들린(Madeline^영어)과 네타(Netta^영어)였다.^[9]

어려서부터 신동으로 불렸는데, 6세에 고대 히브리어를 읽었고, 9세에 윌리엄 셰익스피어 전집을 독파했으며, 초등학교 입학 전에 르네 데카르트의 수학 저술을 읽었다.^[10]^[11] 17세에 양상 논리의 완전성 정리를 증명하고 18세에 출판했다.

1958년 고등학교를 졸업하고 하버드 대학교에 입학하여 수학을 전공, 1962년 전교 수석(summa cum laude^la)으로 졸업하였다. 하버드 학부 2학년 때는 매사추세츠 공과대학교에서 논리학 대학원 과정을 강의하기도 했다.^[12] 졸업 후 풀브라이트 장학금을 받았고, 1963년에는 펠로우십 협회에 임명되었다.^[13]

이후 하버드 대학교에서 강의하다가 1967년 록펠러 대학교로 이전하였다. 1977년 프린스턴 대학교 정교수로 임용되었고, 1988년 인문학 분야에서 뛰어난 업적으로 베르만 상을 받았다. 2002년 뉴욕 시립 대학교에서 강의를 시작, 2003년 철학 석좌 교수(distinguished professor of philosophy^영어)가 되었다. 뉴욕 시립 대학교에는 크립키의 업적을 연구·보존하는 솔 크립키 센터(Saul Kripke Center^영어)가 창립되었다.

네브래스카 대학교 오마하(1977), 존스 홉킨스 대학교(1997), 이스라엘 하이파 대학교(1998), 펜실베이니아 대학교(2005)에서 명예 학위를 받았다. 미국 철학회 회원이자 미국 예술 과학 아카데미 회원, 1985년 영국 학사원 통신 펠로우였다.^[16] 2001년 쇼크 논리 및 철학상을 수상했다.^[17]

철학자 마가렛 길버트와 결혼했다. 2022년 9월 15일, 췌장암으로 81세의 나이로 사망했다.^[18]^[19]^[20]

2. 1. 초기 생애 및 교육

뉴욕주 베이쇼어에서 유대인 가정의 1남 2녀 가운데 장남으로 태어났다. 아버지는 랍비 마이어 크립키(Myer S. Kripke^영어)였으며, 어머니는 도로시 크립키(Dorothy K. Kripke^영어)였다. 두 여동생은 매들린(Madeline^영어)과 네타(Netta^영어)였다.^[9]

6세에 이미 고대 히브리어를 읽을 수 있었고, 9세에 윌리엄 셰익스피어 전집을 독파하였으며, 초등학교에 입학하기 이전에 이미 르네 데카르트의 수학적 저술을 읽었다.^[10]^[11] 17세에 양상 논리의 완전성 정리를 증명하였고, 18세에 출판하였다.

1958년에 고등학교를 졸업하고 하버드 대학교에 입학하여 수학을 전공하였고, 전교 수석(summa cum laude^la)으로 졸업하였다. 하버드 학부 2학년 동안에는 인근의 매사추세츠 공과대학교에서 논리학 대학원 과정을 강의하기도 하였다.^[12] 졸업 후 풀브라이트 장학금을 받았다. 크립키는 "대학을 건너뛸 수 있었으면 좋았을 텐데. 몇몇 흥미로운 사람들을 알게 되었지만, 내가 뭘 배웠다고 말할 수는 없어요. 아마도 혼자 읽으면서 어쨌든 다 배웠을 거예요."라고 말했다.^[13]

2. 2. 학문적 경력

크립키는 1958년에 고등학교를 졸업하고 하버드 대학교에 입학하여 수학을 전공하였고, 전교 수석(summa cum laude^la)으로 졸업하였다. 하버드 학부 2학년 동안에는 인근의 매사추세츠 공과대학교에서 논리학 대학원 과정을 강의하기도 하였다.^[12] 졸업 후에는 풀브라이트 장학금을 받았고, 1963년에는 펠로우십 협회에 임명되었다.^[13]

이후 하버드 대학교에서 강의하다가 1967년 록펠러 대학교로 이전하였다.^[15] 1977년에는 프린스턴 대학교 정교수로 임용되었고,^[15] 1988년에는 인문학 분야에서 뛰어난 업적으로 대학의 베르만 상을 받았다. 2002년에는 뉴욕 시립 대학교에서 강의하기 시작하였고, 2003년에 철학 석좌 교수(distinguished professor of philosophy^영어)가 되었다. 뉴욕 시립 대학교에서는 크립키의 업적을 연구·보존하는 솔 크립키 센터(Saul Kripke Center^영어)가 창립되었다.

크립키는 네브래스카 대학교 오마하(1977), 존스 홉킨스 대학교(1997), 이스라엘 하이파 대학교(1998), 펜실베이니아 대학교(2005)에서 명예 학위를 받았다. 그는 미국 철학회 회원이자 미국 예술 과학 아카데미의 회원이었고, 1985년에는 영국 학사원의 통신 펠로우였다.^[16] 그는 2001년 쇼크 논리 및 철학상을 수상했다.^[17]

2. 3. 개인적 삶과 죽음

솔 크립키는 뉴욕주 베이쇼어에서 랍비인 아버지 마이어 크립키와 유대교 교육 서적 작가인 어머니 도로시 크립키 사이에서 1남 2녀 중 장남으로 태어났다.^[9] 두 여동생은 매들린과 네타였다. 그는 6세에 고대 히브리어를 읽고, 9세에 윌리엄 셰익스피어 전집을 읽었으며, 초등학교 입학 전에 르네 데카르트의 수학 저술을 읽는 등 신동으로 불렸다.^[10]^[11] 17세에 양상 논리의 완전성 정리를 증명하고 18세에 출판했다.

1958년 고등학교를 졸업하고 하버드 대학교에 입학하여 수학을 전공, 1962년에 최우등 졸업(전교 수석)했다. 하버드 학부 2학년 때는 매사추세츠 공과대학교에서 논리학 대학원 과정을 강의하기도 했다.^[12] 졸업 후에는 풀브라이트 장학금을 받았다.

이후 하버드 대학교에서 강의하다가 1967년 록펠러 대학교로, 1977년에는 프린스턴 대학교 정교수로 임용되었다. 2002년에는 뉴욕 시립 대학교에서 강의하기 시작, 2003년에 철학 석좌 교수가 되었다. 뉴욕 시립 대학교에는 그의 업적을 연구·보존하는 솔 크립키 센터가 창립되었다.

네브래스카 대학교, 존스 홉킨스 대학교, 하이파 대학교, 펜실베이니아 대학교에서 명예 학위를 받았다. 미국 철학회 회원이자 미국 예술 과학 아카데미 회원, 영국 학사원의 통신 펠로우였다.^[16] 2001년에는 쇼크 논리 및 철학상을 수상했다.^[17]

철학자 마가렛 길버트와 결혼했다.

2022년 9월 15일, 췌장암으로 81세의 나이로 사망했다.^[18]^[19]^[20]

3. 주요 업적

솔 크립키의 주요 업적은 다음과 같다.

양상 논리 및 직관 논리 연구: 크립키 의미론을 개발하여 양상 논리와 직관 논리의 의미론을 정립했다.

언어 철학에 대한 새로운 이론 제시: 1970년 프린스턴 대학교 강연을 묶은 저서 《이름과 필연》(Naming and Necessity^영어)에서 이름 기술 이론을 비판하고 참조의 인과 이론을 제시하여 언어 철학에 큰 영향을 주었다.

비트겐슈타인 철학 해석: 《규칙과 사적 언어에 대한 비트겐슈타인》(Wittgenstein on Rules and Private Language^영어)에서 비트겐슈타인의 《철학적 탐구》를 독창적으로 해석하여 "크립켄슈타인"이라는 별칭을 얻었다.
진리 이론: 《진리 이론의 개략》(Outline of a Theory of Truth^영어)에서 알프레드 타르스키의 타르스키 증명 불가능성 정리를 우회하여 자체 진리 정의를 포함하는 형식 언어의 예를 제시했다.
집합론에 기여: 크립키-플레이텍 집합론을 도입하였다.
재귀 이론에 기여: 크립키-플레이텍 집합론 및 허용 순서수 연구.

3. 1. 크립키 의미론

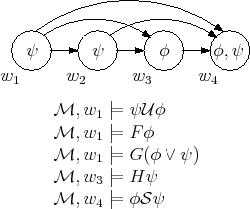
양상 논리와 직관 논리의 의미론을 정의하는 크립키 의미론이 있다. 크립키는 현재 표준이 된 크립키 의미론(관계 의미론 또는 프레임 의미론이라고도 함)을 양상 논리에 도입했다. 크립키 의미론은 비고전 논리 시스템을 위한 형식 의미론이다. 처음에는 양상 논리를 위해 만들어졌으며, 나중에는 직관 논리 및 기타 비고전 시스템에 적용되었다. 크립키 의미론의 발견은 비고전 논리의 제작에 있어 획기적인 사건이었다. 왜냐하면 크립키 이전에는 그러한 논리의 모델 이론이 부재했기 때문이다.

'''크립키 프레임''' 또는 '''양상 프레임'''은 쌍

\langle W,R\rangle

이며, 여기서 ''W''는 공집합이 아닌 집합이고, ''R''은 ''W''에 대한 이항 관계이다. ''W''의 원소는 ''노드'' 또는 ''세계''라고 불리며, ''R''은 접근 가능성 관계로 알려져 있다. 접근 가능성 관계의 속성 (추이성, 반사성 등)에 따라, 해당 프레임은 확장하여 추이적, 반사적 등으로 설명된다.

'''크립키 모델'''은 삼중항

\langle W,R,\Vdash\rangle

이며, 여기서

\langle W,R\rangle

는 크립키 프레임이고,

\Vdash

는 ''W''의 노드와 양상 논리식 사이의 관계이며, 다음과 같다.

$w\Vdash\neg A$ 는 $w\nVdash A$ 인 경우에만 성립한다.
$w\Vdash A\to B$ 는 $w\nVdash A$ 이거나 $w\Vdash B$ 인 경우에만 성립한다.
$w\Vdash\Box A$ 는 $\forall u\,(w\; R\; u$ 는 $u\Vdash A)$ 임을 의미하는 경우에만 성립한다.

w\Vdash A

는 "''w''는 ''A''를 만족한다", "''A''는 ''w''에서 만족된다", 또는 "''w''는 ''A''를 강제한다"라고 읽는다. 관계

\Vdash

는 ''만족 관계'', ''평가'' 또는 ''강제 관계''라고 불린다. 만족 관계는 명제 변수에 대한 값에 의해 고유하게 결정된다.

논리식 ''A''는 다음에 대해 '''유효'''하다.

모델 $\langle W,R,\Vdash\rangle$ 에서, 모든 ''w'' ∈ ''W''에 대해 $w\Vdash A$ 인 경우,
프레임 $\langle W,R\rangle$ 에서, 모든 가능한 $\Vdash$ 선택에 대해 $\langle W,R,\Vdash\rangle$ 에서 유효한 경우,
프레임 또는 모델의 클래스 ''C''에서, ''C''의 모든 멤버에서 유효한 경우.

Thm(''C'')는 ''C''에서 유효한 모든 논리식의 집합으로 정의한다. 반대로, ''X''가 논리식의 집합인 경우, Mod(''X'')는 ''X''에서 모든 논리식을 유효하게 하는 모든 프레임의 클래스이다.

양상 논리 (즉, 논리식의 집합) ''L''은 프레임의 클래스 ''C''에 대해 '''건전'''하다면, ''L'' ⊆ Thm(''C'')이다. ''L''은 ''C''에 대해 '''완전'''하다면, ''L'' ⊇ Thm(''C'')이다.

의미론은 논리 (즉, 유도 시스템)를 조사하는 데 유용하다면, 의미론적 함축 관계가 구문적 대응 관계인 ''consequence'' 관계 (''유도 가능성'')를 반영한다. 어떤 양상 논리가 크립키 프레임의 클래스에 대해 건전하고 완전한지, 그리고 그러한 논리에 대해 어떤 클래스인지 아는 것이 중요하다.

크립키 프레임의 모든 클래스 ''C''에 대해, Thm(''C'')는 정규 양상 논리이다 (특히, 최소 정규 양상 논리 ''K''의 정리는 모든 크립키 모델에서 유효하다). 그러나 그 반대는 일반적으로 성립하지 않는다. 크립키 불완전한 정규 양상 논리가 있는데, 이는 문제가 되지 않는다. 왜냐하면 연구된 대부분의 양상 시스템은 간단한 조건으로 설명되는 프레임의 클래스에 대해 완전하기 때문이다.

정규 양상 논리 ''L''은 프레임의 클래스 ''C''에 '''대응'''한다면, ''C'' = Mod(''L'')이다. 즉, ''C''는 ''L''이 ''C''에 대해 건전한 가장 큰 프레임의 클래스이다. 따라서 ''L''은 대응하는 클래스에 대해 완전한 경우에만 크립키 완전하다.

스키마 '''T'''를 생각해 보자:

\Box A\to A

. '''T'''는 모든 반사적 프레임

\langle W,R\rangle

에서 유효하다: 만약

w\Vdash \Box A

라면, ''w'' ''R'' ''w''이므로

w\Vdash A

이다. 반면에, '''T'''를 유효하게 하는 프레임은 반사적이어야 한다: ''w'' ∈ ''W''를 고정하고, 명제 변수 ''p''의 만족을 다음과 같이 정의한다:

u\Vdash p

는 ''w'' ''R'' ''u''인 경우에만 성립한다. 그러면

w\Vdash \Box p

이고, 따라서 '''T'''에 의해

w\Vdash p

이며, 이는

\Vdash

의 정의를 사용하여 ''w'' ''R'' ''w''임을 의미한다. '''T'''는 반사적 크립키 프레임의 클래스에 대응한다.

완전성을 증명하는 것보다 ''L''의 해당 클래스를 특징짓는 것이 훨씬 더 쉬운 경우가 많으므로, 대응은 완전성 증명의 지침으로 사용된다. 대응은 또한 양상 논리의 ''불완전성''을 보여주는 데 사용된다: 만약 ''L''₁ ⊆ ''L''₂가 동일한 프레임 클래스에 대응하는 정규 양상 논리이지만 ''L''₁이 ''L''₂의 모든 정리를 증명하지 못한다고 가정해 보자. 그러면 ''L''₁은 크립키 불완전하다. 예를 들어, 스키마

\Box(A\equiv\Box A)\to\Box A

는 '''GL'''과 동일한 프레임 클래스 (즉, 추이적이고 역 잘 정렬된 프레임)에 대응하지만, '''GL'''-항진명제

\Box A\to\Box\Box A

를 증명하지 않으므로 불완전한 논리를 생성한다.

모든 정규 양상 논리 ''L''에 대해, 최대 무모순 집합을 모델로 사용하는 표준 기술의 변형을 통해 정확히 ''L''의 정리를 검증하는 크립키 모델('''표준 모델''')을 구성할 수 있다. 표준 크립키 모델은 대수적 의미론에서 린덴바움-타르스키 대수 구성과 유사한 역할을 한다.

명제 집합은 ''L''의 공리를 사용하여 그로부터 추론 규칙인 modus ponens를 통해 모순이 파생될 수 없는 경우 ''L''-''무모순''하다. ''최대 L-무모순 집합''(줄여서 ''L''-''MCS'')은 적절한 ''L''-무모순 상위 집합을 갖지 않는 ''L''-무모순 집합이다.

''L''의 '''표준 모델'''은 크립키 모델

\langle W,R,\Vdash\rangle

이며, 여기서 ''W''는 모든 ''L''-''MCS''의 집합이고, 관계 ''R''과

\Vdash

는 다음과 같다.

:

X\;R\;Y

는 모든 명제

A

에 대해,

\Box A\in X

이면

A\in Y

일 경우에만 해당한다.

:

X\Vdash A

는

A\in X

일 경우에만 해당한다.

표준 모델은 모든 ''L''-''MCS''가 ''L''의 모든 정리를 포함하므로 ''L''의 모델이다. Zorn의 보조정리에 의해, 각 ''L''-무모순 집합은 ''L''-''MCS''에 포함되어 있으며, 특히 ''L''에서 증명 불가능한 모든 명제는 표준 모델에서 반례를 갖는다.

표준 모델의 주요 적용 분야는 완전성 증명이다. '''K'''의 표준 모델의 속성은 모든 크립키 프레임의 클래스에 대한 '''K'''의 완전성을 즉시 암시한다. 이 논증은 임의의 ''L''에 대해서는 작동하지 않는다. 왜냐하면 표준 모델의 기본 ''프레임''이 ''L''의 프레임 조건을 만족한다는 보장이 없기 때문입니다.

우리는 크립키 프레임의 속성 ''P''에 대해 명제 또는 명제 집합 ''X''가 '''표준'''이라고 말한다.

''X''는 ''P''를 만족하는 모든 프레임에서 유효하다.
''X''를 포함하는 임의의 정규 양상 논리 ''L''에 대해, ''L''의 표준 모델의 기본 프레임은 ''P''를 만족한다.

표준 명제 집합의 합집합 자체도 표준이다. 앞의 논의에서 알 수 있듯이, 표준 명제 집합으로 공리화된 모든 논리는 크립키 완전하고 콤팩트성 정리에 의해 콤팩트하다.

공리 T, 4, D, B, 5, H, G (및 이들의 조합)는 표준이다. GL과 Grz는 콤팩트하지 않기 때문에 표준이 아니다. 공리 M 자체는 표준이 아니지만(Goldblatt, 1991), 결합된 논리 '''S4.1''' (사실, 심지어 '''K4.1''')도 표준이다.

일반적으로, 주어진 공리가 표준인지 여부는 결정 문제이다. 우리는 좋은 충분 조건을 알고 있다. H. 샐퀴스트는 광범위한 명제 클래스(현재는 샐퀴스트 명제라고 함)를 식별했다.

샐퀴스트 명제는 표준이다.
샐퀴스트 명제에 해당하는 프레임 클래스는 일차 논리로 정의할 수 있다.
주어진 샐퀴스트 명제에 해당하는 프레임 조건을 계산하는 알고리즘이 있다.

이것은 강력한 기준이다. 예를 들어, 표준으로 나열된 모든 공리는 (동등하게) 샐퀴스트 명제이다. 논리는 유한 프레임의 클래스에 대해 완전하면 유한 모델 성질 (FMP)을 갖는다. 이 개념의 적용은 결정 가능성 문제입니다. 재귀적으로 공리화된 양상 논리 L이 FMP를 갖고, 주어진 유한 프레임이 L의 모델인지 여부를 결정할 수 있다면, 포스트의 정리에 의해 결정 가능합니다. 특히, FMP를 가진 모든 유한하게 공리화 가능한 논리는 결정 가능합니다.

주어진 논리에 대한 FMP를 확립하는 다양한 방법이 있다. 표준 모델 구성을 정제하고 확장하는 것은 종종 필터링 또는 언래블링과 같은 도구를 사용하여 작동합니다. 또 다른 가능성으로, 컷 없는 시퀀트 미적분을 기반으로 한 완전성 증명은 일반적으로 유한 모델을 직접 생성합니다.

실제로 사용되는 대부분의 양상 시스템(위에 나열된 모든 시스템 포함)은 FMP를 갖는다.

어떤 경우에는 FMP를 사용하여 논리의 크립키 완전성을 증명할 수 있다. 모든 정규 양상 논리는 양상 대수의 클래스에 대해 완전하며, 유한 양상 대수는 크립키 프레임으로 변환할 수 있다. 예를 들어, 로버트 불은 이 방법을 사용하여 S4.3의 모든 정규 확장이 FMP를 갖고 크립키 완전하다는 것을 증명했다.

크립키 의미론은 둘 이상의 양상을 가진 논리로의 직접적인 일반화를 갖는다.

\{\Box_i\mid\,i\in I\}

를 필요성 연산자의 집합으로 갖는 언어에 대한 크립키 프레임은 각 ''i'' ∈ ''I''에 대한 이진 관계 ''R_i''가 갖춰진 비어 있지 않은 집합 ''W''로 구성됩니다. 만족 관계의 정의는 다음과 같이 수정된다.

:

w\Vdash\Box_i A

는

\forall u\,(w\;R_i\;u\Rightarrow u\Vdash A)

일 경우에만 해당한다.

팀 칼슨(Tim Carlson)이 발견한 단순화된 의미론은 종종 다중 양상 증명 가능성 논리에 사용된다.^[22] '''칼슨 모델'''은 단일 접근 관계 ''R''과 각 양상에 대한 부분 집합 ''D_i'' ⊆ ''W''를 갖는 구조

\langle W,R,\{D_i\}_{i\in I},\Vdash\rangle

이다. 만족도는 다음과 같이 정의된다.

:

w\Vdash\Box_i A

if and only if

\forall u\in D_i\,(w\;R\;u\Rightarrow u\Vdash A).

칼슨 모델은 일반적인 다중 양상 크립키 모델보다 시각화하고 다루기 더 쉽다. 그러나 칼슨 불완전한 크립키 완전 다중 양상 논리도 있다.

직관 논리에 대한 크립키 의미론은 양상 논리의 의미론과 동일한 원칙을 따르지만, 만족도에 대한 다른 정의를 사용한다.

'''직관적 크립키 모델'''은 삼중항

\langle W,\le,\Vdash\rangle

이며, 여기서

\langle W,\le\rangle

는 부분 순서 집합인 크립키 틀이고,

\Vdash

는 다음 조건을 만족한다.

''p''가 명제 변수이고, $w\le u$ 이며, $w\Vdash p$ 이면 $u\Vdash p$ (''지속성'' 조건)
$w\Vdash A\land B$ 는 $w\Vdash A$ 이고 $w\Vdash B$ 일 경우에만 해당
$w\Vdash A\lor B$ 는 $w\Vdash A$ 이거나 $w\Vdash B$ 일 경우에만 해당
$w\Vdash A\to B$ 는 모든 $u\ge w$ 에 대해 $u\Vdash A$ 가 $u\Vdash B$ 를 함의할 경우에만 해당
$w\Vdash\bot$ 아님

직관 논리는 크립키 의미론에 대해 건전하고 완전하며, 유한 모델 속성을 갖는다.

'''직관적 일차 논리'''

''L''을 일차 논리 언어라고 하자. ''L''의 크립키 모델은 삼중항

\langle W,\le,\{M_w\}_{w\in W}\rangle

이며, 여기서

\langle W,\le\rangle

는 직관적 크립키 틀이고, 각 노드 ''w'' ∈ ''W''에 대해 ''M_w''는

(고전적) ''L''-구조이며, 다음 호환성 조건이 ''u'' ≤ ''v''일 때마다 적용된다.

''M_u''의 도메인은 ''M_v''의 도메인에 포함된다.
''M_u''와 ''M_v''의 함수 기호의 실현은 ''M_u''의 요소에 대해 일치한다.
각 ''n''항 술어 ''P''와 요소 ''a''₁,...,''a_n'' ∈ ''M_u''에 대해: 만약 ''P''(''a''₁,...,''a_n'')이 ''M_u''에서 성립한다면, ''M_v''에서도 성립한다.

변수를 ''M_w''의 요소로 평가 ''e''가 주어지면, 만족 관계

w\Vdash A[e]

를 정의한다.

$w\Vdash P(t_1,\dots,t_n)[e]$ 는 $P(t_1[e],\dots,t_n[e])$ 가 ''M_w''에서 성립하는 경우에만 해당
$w\Vdash(A\land B)[e]$ 는 $w\Vdash A[e]$ 이고 $w\Vdash B[e]$ 일 경우에만 해당
$w\Vdash(A\lor B)[e]$ 는 $w\Vdash A[e]$ 이거나 $w\Vdash B[e]$ 일 경우에만 해당
$w\Vdash(A\to B)[e]$ 는 모든 $u\ge w$ 에 대해 $u\Vdash A[e]$ 가 $u\Vdash B[e]$ 를 함의할 경우에만 해당
$w\Vdash\bot[e]$ 아님
$w\Vdash(\exists x\,A)[e]$ 는 $w\Vdash A[e(x\to a)]$ 를 만족하는 $a\in M_w$ 가 존재하는 경우에만 해당
$w\Vdash(\forall x\,A)[e]$ 는 모든 $u\ge w$ 와 모든 $a\in M_u$ 에 대해 $u\Vdash A[e(x\to a)]$ 인 경우에만 해당

여기서 ''e''(''x''→''a'')는 ''x''에게 값 ''a''를 부여하고 그렇지 않으면 ''e''와 일치하는 평가이다.

3. 2. 이름과 필연

''이름과 필연성''을 구성하는 세 개의 강의는 이름 기술 이론에 대한 비판을 담고 있다. 크립키는 프레게, 러셀, 비트겐슈타인, 설 등의 철학자들이 제시한 기술 이론의 다양한 변형들을 비판한다. 기술 이론에 따르면, 고유명사는 기술과 동의어이거나, 대상이 고유하게 만족시키는 설명이나 설명 묶음과 이름이 연관됨으로써 참조가 결정된다. 크립키는 이러한 종류의 기술주의를 모두 거부한다. 그는 기술주의가 이름이 어떻게 참조를 얻는지에 대한 이론으로서 적절하지 않다는 것을 보여주기 위해 몇 가지 예를 제시한다. 예를 들어, 아리스토텔레스가 두 살에 죽어 그의 이름과 연관된 설명 중 어느 것도 만족시키지 못했을 수 있지만, 그를 여전히 아리스토텔레스라고 부르는 것은 잘못된 것처럼 보인다.^[24]

대안으로, 크립키는 참조의 인과 이론을 제시했는데, 이에 따르면 이름은 화자 공동체를 통해 매개된 대상과의 인과적 연결을 통해 대상을 참조한다. 그는 대부분의 설명과 달리, 고유명사는 강성 지시어라는 점을 지적한다. 즉, 고유명사는 대상이 존재하는 모든 가능 세계에서 명명된 대상을 참조하는 반면, 대부분의 설명은 다른 가능 세계에서 다른 대상을 지칭할 수 있다. 예를 들어, "리처드 닉슨"은 닉슨이 존재하는 모든 가능 세계에서 같은 사람을 지칭하는 반면, "1968년 미국 대통령 선거에서 승리한 사람"은 다른 가능 세계에서 닉슨, 험프리 또는 다른 사람을 지칭할 수 있다.

크립키는 또한 ''사후적 필연성''의 가능성을 제기했다. 즉, 경험적 조사를 통해서만 알 수 있지만 필연적으로 참인 사실이다. 예로는 "헤스페루스는 포스포루스이다", "키케로는 툴리이다", "물은 H₂O이다"와 같은 두 이름이 동일한 대상을 지칭하는 기타 정체성 주장이 있다. 크립키에 따르면, 분석적/종합적, ''선험적''/''사후적'', 우연적/필연적인 칸트의 구분은 서로 일치하지 않는다. 오히려 분석적/종합적은 의미론적 구분이고, ''선험적''/''사후적''은 인식론적 구분이며, 우연적/필연적은 형이상학적 구분이다.

마지막으로, 크립키는 마음의 철학에서 정체성 유물론, 즉 모든 정신적 개별자가 어떤 물리적 개별자와 동일하다는 관점에 대한 논증을 제시했다. 크립키는 이러한 정체성을 방어하는 유일한 방법은 ''사후적'' 필연적 정체성으로 하는 것이지만, 그러한 정체성(예: 고통이 C-섬유의 발화라는 것)은 고통이 C-섬유의 발화와 분리되거나 C-섬유의 발화가 고통과 분리될 수 있다는 (명확하게 상상 가능한) 가능성을 고려할 때 필연적일 수 없다고 주장했다. (비슷한 논증이 이후 데이비드 찰머스에 의해 제기되었다.)^[24] 어쨌든, 크립키에 따르면 정신-물리적 정체성 이론가는 이러한 상황의 겉보기 논리적 가능성을 설명해야 할 변증법적 의무를 갖게 되는데, 이는 그러한 이론가에 따르면 불가능해야 하기 때문이다.

크립키는 1973년 옥스퍼드에서 철학 존 로크 강좌를 했다. ''참조와 존재''라는 제목으로, 여러 면에서 ''이름과 필연성''의 연속이었으며 허구적 이름과 지각적 오류의 주제를 다루었다. 2013년 옥스퍼드 대학교 출판부는 이 강좌를 책으로 출판했으며, 제목도 ''참조와 존재''였다.

1995년 논문에서 철학자 퀘스틴 스미스는 크립키의 새로운 참조 이론의 핵심 개념이 10년 이상 전에 루스 바르칸 마르쿠스의 연구에서 시작되었다고 주장했다.^[25] 스미스는 마르쿠스가 개발했다고 주장하는 신이론의 여섯 가지 중요한 아이디어를 식별했다. (1) 고유명사는 포함된 정의로 구성되지 않는 직접적 참조라는 것, (2) 설명을 통해 하나의 사물을 선택할 수 있지만, 이 설명은 이 사물의 고유명사와 동등하지 않다는 것, (3) 고유명사가 직접적인 지시적이며 위장된 설명이 아니라는 양상 논증, (4) 정체성의 필연성에 대한 형식적인 양상 논리 증명, (5) 크립키가 그 용어를 만들었지만, 강성 지시어의 개념, 그리고 (6) ''사후적'' 정체성. 스미스는 크립키가 당시 마르쿠스의 이론을 이해하지 못했지만 나중에 그의 신이론에서 많은 핵심 개념적 주제를 채택했다고 주장했다.

다른 학자들은 이후 표절이 발생하지 않았다고 주장하는 자세한 답변을 제시했다.^[26]^[27]

3. 3. 비트겐슈타인 해석

1982년에 처음 출판된 크립키의 ''규칙과 사적 언어에 대한 비트겐슈타인''(Wittgenstein on Rules and Private Language)은 루트비히 비트겐슈타인의 ''철학적 탐구''(Philosophical Investigations)의 핵심 주장이 언어 사용에서 우리가 규칙을 따르는 가능성을 훼손하는 파괴적인 규칙 준수 역설에 집중되어 있다고 주장한다. 크립키는 이 역설이 "철학이 지금까지 보아온 가장 급진적이고 독창적인 회의론적 문제"이며, 비트겐슈타인은 규칙 준수 역설로 이끄는 주장을 거부하지 않고 받아들여 역설의 파괴적인 영향을 완화하기 위한 "회의론적 해결책"을 제시한다고 적었다.^[29]

대부분의 해설자들은 ''철학적 탐구''가 크립키가 제시하는 규칙 준수 역설을 포함하고 있다는 데 동의하지만, 비트겐슈타인에게 회의론적 해결책을 귀속시키는 데 동의하는 사람은 거의 없다. 크립키 자신은 ''규칙과 사적 언어에 대한 비트겐슈타인''에서 비트겐슈타인이 ''철학적 탐구''에 대한 자신의 해석을 지지할지 의문을 표명한다. 그는 이 작품이 비트겐슈타인의 견해를 정확하게 진술하려는 시도로 읽혀서는 안 되며, 오히려 비트겐슈타인의 주장이 "크립키에게 어떤 식으로 다가왔는지, 그에게 어떤 문제를 제시했는지"에 대한 설명으로 읽혀야 한다고 말한다.^[29]

"크립켄슈타인"(Kripkenstein)이라는 혼성어는 ''철학적 탐구''에 대한 크립키의 해석을 위해 만들어졌다. 크립켄슈타인의 주요 의의는 "의미 회의론"이라고 불리는 새로운 종류의 회의론에 대한 명확한 진술이었다. 이는 고립된 개인의 경우 단어 사용을 통해 다른 것이 아닌 한 가지를 의미하는 사실이 없다는 생각이다. 의미 회의론에 대한 크립키의 "회의론적 해결책"은 의미를 공동체의 행동에 근거하는 것이다.^[29]

크립키의 저서는 방대한 2차 문헌을 생성했으며, 그의 회의론적 문제를 흥미롭고 통찰력 있게 생각하는 사람들과, 그의 의미 회의론이 비트겐슈타인에 대한 혼란스럽고 선택적인 해석에서 비롯된 가짜 문제라고 주장하는 고든 베이커, 피터 해커, 콜린 맥긴과 같은 사람들로 나뉜다. 크립키의 입장은 이러한 공격과 다른 공격에 맞서 마틴 쿠쉬라는 케임브리지 철학자에 의해 옹호되었으며, 비트겐슈타인 학자 데이비드 G. 스턴(David G. Stern)은 크립키의 저서를 1980년대 이후 비트겐슈타인에 관한 "가장 영향력 있고 널리 논의된" 저서로 평가한다.^[29]

3. 4. 진리 이론

알프레드 타르스키가 불가능하다고 여겼던, 언어가 자체 진리 술어를 일관되게 포함할 수 있음을 1975년 논문 "진리 이론의 개요"에서 크립키는 보였다.^[30] 이 접근 방식은 진리가 언어 내에서 문법적으로 올바른 문장의 집합에 대한 부분적으로 정의된 속성이 되도록 하는 것을 포함한다. 크립키는 언어에 진리 술어를 포함하지 않는 표현의 집합에서 시작하여, 해당 부분에 대한 진리 술어를 정의함으로써 이를 재귀적으로 수행하는 방법을 보였다. 이 작업은 언어에 새로운 문장을 추가하고, 그에 따라 진리가 모두 정의된다. 그러나 타르스키의 접근 방식과 달리, 크립키의 접근 방식은 "진리"가 이러한 모든 정의 단계의 합집합이 되도록 한다. 가산 무한 번의 단계를 거친 후, 언어는 크립키의 방법을 사용하여 진리 술어를 확장해도 언어가 더 이상 변경되지 않는 "고정점"에 도달한다. 이러한 고정점은 자체 진리 술어를 포함하는 자연 언어의 기본 형태로 간주될 수 있다. 그러나 이 술어는 진리 술어를 포함하지 않는 더 간단한 문장에 대해서는 정의되지 않는다. 즉, "'눈은 하얗다'는 참이다"는 잘 정의되고, "'눈은 하얗다'는 참이다'는 참이다" 등도 마찬가지이지만, "이 문장은 참이다" 또는 "이 문장은 참이 아니다"는 진리 조건을 받지 않는다. 크립키의 용어로는, 그것들은 "근거가 없다."

괴델의 제1 불완전성 정리는 자기 지시가 무심코 피할 수 없음을 보여준다. 왜냐하면 (정수와 같은)겉보기에는 관련이 없는 객체에 대한 명제가 비공식적인 자기 지시적 의미를 가질 수 있고, 이러한 아이디어는 — 대각선 보조정리에 의해 나타나며 — 타르스키의 정리의 기초가 되기 때문이다. 이 정리는 진리가 일관되게 정의될 수 없다고 말한다. 그러나 크립키의 진리 술어는 타르스키의 증명에서 구성된 명제와 같은 명제에 진리값(참/거짓)을 부여하지 않는다. 왜냐하면 모든 유한한

n

에 대해

n

단계에서 정의되지 않음이 귀납법에 의해 증명될 수 있기 때문이다.

크립키의 제안은 언어가 자체의 "진리" 술어(적어도 부분적으로)를 포함하지만, 거짓말쟁이 문장("이 문장은 거짓이다")과 같은 일부 문장은 정의되지 않은 진리값을 가지지만, 언어는 자체 "정의되지 않음" 술어를 포함하지 않는다는 점에서 문제가 있다. 사실, 이는 불가능한데, 그 이유는 거짓말쟁이의 역설의 새로운 버전인 ''강화된 거짓말쟁이의 역설''(이 문장은 거짓이거나 정의되지 않았다)을 생성하기 때문이다. 따라서 거짓말쟁이 문장은 언어에서 정의되지 않지만, 언어는 그것이 정의되지 않았다는 것을 표현할 수 없다.^[30]

3. 5. 기타 업적

양상 논리와 직관 논리의 의미론을 정의하는 크립키 의미론을 정의하였다.
《이름과 필연》(Naming and Necessity^영어)에서 언어철학의 새로운 이론을 제시하였다.
《비트겐슈타인: 규칙과 사적 언어》(Wittgenstein on Rules and Private Language^영어)에서 루트비히 비트겐슈타인의 《철학 탐구》의 독창적인 해석을 제시하였다. 이 해석은 통상적으로 비트겐슈타인 자신의 관점과는 다르지만, 철학적으로 매우 흥미로운 관점으로 여겨지며, 비트겐슈타인 본인과 구별하기 위해 보통 '''크립켄슈타인'''(Kripkenstein^영어)으로 불린다.
《진리 이론의 개략》(Outline of a Theory of Truth^영어)에서 타르스키 증명 불가능성 정리를 피해, 스스로의 진리의 정의를 포함하는 형식적 언어의 예를 제시하였다.
집합론에서는 크립키-플레이텍 집합론을 도입하였다.
재귀 이론에도 기여하였다. (허용 순서수, 크립키-플레이텍 집합론 참조).

4. 저작

솔 크립키의 주요 저작은 다음과 같다.

''이름과 필연성(Naming and Necessity)'' (1972, 1980)^[1]
''규칙과 사적 언어에 대한 비트겐슈타인(Wittgenstein on Rules and Private Language: an Elementary Exposition)'' (1982)^[2]
''철학적 문제: 논문집 1권''(Philosophical Troubles. Collected Papers Vol. 1) (2011)^[3]
''지칭과 존재 - 존 로크 강좌(Reference and Existence – The John Locke Lectures)'' (2013)^[4]
''대체적 수량화에 대한 문제는 있는가?''(Is There a Problem about Substitutional Quantification?) (1976)
''Marian Boykan Pour-El and Saul Kripke, Deduction-preserving "recursive isomorphisms" between theories, Fundamenta Mathematicae. 61 (1967) pp.141-163''

Philosophical Troubles. Collected Papers Vol. 1^영어과 Reference and Existence – The John Locke Lectures^영어는 하위 섹션 '저서'에 이미 언급되어 있으므로, 여기서는 중복을 피하기 위해 제목과 출판 연도만 간략하게 표기했다.

4. 1. 저서

''Naming and Necessity^영어''. Cambridge, Mass.: Harvard University Press. 1972.
* 정대현·김영주 역, ''이름과 필연''. 필로소픽, 2014.
''Wittgenstein on Rules and Private Language: an Elementary Exposition^영어''. Cambridge, Mass.: Harvard University Press, 1982.
* 남기창 역, ''비트겐슈타인: 규칙과 사적 언어''. 철학과현실사, 2008.
''Philosophical Troubles. Collected Papers Vol. 1^영어''. New York: Oxford University Press, 2011.
''Reference and Existence. The John Locke Lectures^영어''. New York: Oxford University Press, 2013.
''이름과 필연성''(Naming and Necessity^영어), 1980.
야기사와 케이・노이에 케이이치 역, ''명칭과 필연성──양상의 형이상학과 심신 문제''. 산업도서, 1985.
''규칙과 사적 언어에 대한 비트겐슈타인''(Wittgenstein on Rules and Private Language^영어), 1982.
쿠로사키 히로시 역, ''비트겐슈타인의 역설──규칙・사적 언어・타인의 마음''. 산업도서, 1983/치쿠마 학예 문고, 2022.
''대체적 수량화에 대한 문제는 있는가?''(Is There a Problem about Substitutional Quantification?^영어), 1976.
Marian Boykan Pour-El and Saul Kripke, Deduction-preserving "recursive isomorphisms" between theories, Fundamenta Mathematicae. 61 (1967) pp.141-163^영어

4. 2. 주요 논문

연도	제목	저널/출판사
1959	"A Completeness Theorem in Modal Logic"	Journal of Symbolic Logic 24(1):1–14.
1959	"Distinguished Constituents" (abstract)	The Journal of Symbolic Logic, 24(4):323.
1959	"Semantical Analysis of Modal Logic" (abstract)	The Journal of Symbolic Logic, 24(4):323-324.
1959	"The Problem of Entailment" (abstract)	The Journal of Symbolic Logic, 24(4):324.
1962	"Flexible Predicates of Formal Number Theory"	Proceedings of the American Mathematical Society, 13(4):647-650.
1962	"The Undecidability of Monadic Modal Quantification Theory"	Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 8:113–116
1963	"Semantical Considerations on Modal Logic"	Acta Philosophica Fennica 16:83–94
1963	"Semantical Analysis of Modal Logic I: Normal Modal Propositional Calculi"	Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 9:67–96
1964	"Transfinite Recursions on Admissible Ordinals, I" (abstract)	The Journal of Symbolic Logic, Vol. 29, No. 3, p. 162.
1964	"Transfinite Recursions on Admissible Ordinals, II" (abstract)	The Journal of Symbolic Logic, Vol. 29, No. 3, p. 162.
1964	"Admissible Ordinals and the Analytic Hierarchy" (abstract)	The Journal of Symbolic Logic, Vol. 29, No. 3, p. 162.
1965	"Semantical Analysis of Intuitionistic Logic I"	Formal Systems and Recursive Functions, edited by M. Dummett and J. N. Crossley. Amsterdam: North-Holland Publishing Co.
1965	"Semantical Analysis of Modal Logic II: Non-Normal Modal Propositional Calculi"	The Theory of Models, edited by J. W. Addison, L. Henkin and A. Tarski. Amsterdam: North-Holland Publishing Co.
1967	"Deduction-preserving Recursive Isomorphisms between Theories" (with Marian Boykan Pour-El)	Bulletin of the American Mathematical Society, 73:145-148.
1967	"An Extension of a Theorem of Gaifman-Hales-Solovay"	Fundamenta Mathematicae, Vol. 61, pp. 29–32.
1967	"Transfinite Recursion, Constructible Sets, and Analogues of Cardinals"	Summaries of Talks Prepared in Connection with the Summer Institute on Axiomatic Set Theory, American Mathematical Society, U.C.L.A., pp. IV-0-1 - IV-0-12.
1967	"On the Application of Boolean-Valued Models to Solutions of Problems in Boolean Algebra"	Summaries of Talks Prepared in Connection with the Summer Institute on Axiomatic Set Theory, American Mathematical Society, U.C.L.A. (1967), pp. IV-T-1 through IV-T-7.
1967	"Deduction-preserving Recursive Isomorphisms between Theories" (with Marian Boykan Pour-El)	Fundamenta Mathematicae 61:141-163.
1971	"Identity and Necessity"	Identity and Individuation, edited by M. K. Munitz. New York: New York University Press.
1972 (1980)	"Naming and Necessity"	Semantics of Natural Language, edited by D. Davidson and G. Harman. Dordrecht; Boston: Reidel.
1975	"Outline of a Theory of Truth"	Journal of Philosophy 72:690–716. Philosophical Troubles. Collected Papers Vol. I, Oxford University Press에 재수록.
1976	"Is There a Problem about Substitutional Quantification?"	Truth and Meaning: Essays in Semantics, edited by Gareth Evans and John McDowell. Oxford: Oxford University Press.
1976	"A Theory of Truth I. Preliminary Report," abstract	Journal of Symbolic Logic, Vol. 41, No. 2, pp. 556.
1976	"A Theory of Truth II. Preliminary Report," abstract	Journal of Symbolic Logic, Vol. 41, No. 2, pp. 556–557.
1977	"Speaker's Reference and Semantic Reference"	Midwest Studies in Philosophy 2:255–276. Philosophical Troubles. Collected Papers Vol. I, Oxford University Press에 재수록.
1979	"A Puzzle about Belief"	Meaning and Use, edited by A. Margalit. Dordrecht and Boston: Reidel. Philosophical Troubles. Collected Papers Vol. I, Oxford University Press에 재수록.
1982	"Nonstandard Models of Peano Arithmetic" (with S. Kochen)	Logic and Algorithmics: International Symposium Held in Honor of Ernst Specker, H. Läuchli (ed.), University of Geneva: 277-295.
1986	"A Problem in the Theory of Reference: the Linguistic Division of Labor and the Social Character of Naming"	Philosophy and Culture (Proceedings of the XVIIth World Congress of Philosophy), Montreal, Editions Montmorency: 241-247.
1992	"Summary: Individual Concepts: Their Logic, Philosophy, and Some of Their Uses."	Proceedings and Addresses of the American Philosophical Association 66: 70-73
2005	"Russell's Notion of Scope"	Mind 114:1005–1037. Philosophical Troubles. Collected Papers Vol. I, Oxford University Press에 재수록.
2008	"Frege's Theory of Sense and Reference: Some Exegetical Notes"	Theoria 74:181-218. Philosophical Troubles. Collected Papers Vol. I, Oxford University Press에 재수록.
2009	"Presupposition and Anaphora: Remarks on the formulation of the projection problem"	Linguistic Inquiry 40(3):367-386. Philosophical Troubles. Collected Papers Vol. I, Oxford University Press에 재수록.
2009	"The Collapse of the Hilbert Program," (Abstract)	Bulletin of Symbolic Logic 15(2):229-231.
2011	"The First Person"	Philosophical Troubles. Collected Papers Vol. I, Oxford University Press.
2011	"Two Paradoxes of Knowledge"	Philosophical Troubles. Collected Papers Vol. I, Oxford University Press.
2011	"Nozick on Knowledge"	Philosophical Troubles. Collected Papers Vol. I, Oxford University Press.
2011	"A Puzzle about Time and Thought"	Philosophical Troubles. Collected Papers Vol. I, Oxford University Press.
2011	"Vacuous Names and Fictional Entities"	Philosophical Troubles. Collected Papers Vol. I, Oxford University Press.
2011	"Unrestricted Exportation and Some Morals for the Philosophy of Language"	Philosophical Troubles. Collected Papers Vol. I, Oxford University Press.
2013	"The Church-Turing Thesis as a Special Corollary of Gödel's Completeness Theorem"	Computability: Turing, Gödel, Church, and Beyond, Copeland, B. J., Posy, C., and Shagrir, O. (eds), Cambridge, Mass., MIT Press.
1980	이름과 필연성(Naming and Necessity)
1985	『명칭과 필연성──양상의 형이상학과 심신 문제』	야기사와 케이・노이에 케이이치 역, 산업도서
1982	규칙과 사적 언어에 대한 비트겐슈타인(Wittgenstein on Rules and Private Language)
1983 (2022)	『비트겐슈타인의 역설──규칙・사적 언어・타인의 마음』	쿠로사키 히로시 역, 산업도서/치쿠마 학예 문고
1976	대체적 수량화에 대한 문제는 있는가?(Is There a Problem about Substitutional Quantification?)	Truth and Meaning pp.325-419/edi. EVANS and McDOWELL/Oxford
1967	Marian Boykan Pour-El and Saul Kripke, Deduction-preserving "recursive isomorphisms" between theories	Fundamenta Mathematicae. 61 (1967) pp.141-163

5. 수상 및 영예

연도	내용
1962년 - 1963년	풀브라이트 장학금
1963년 - 1966년	하버드 대학교 연구 펠로우
1977년	네브래스카 대학교 명예 인문학 박사 학위
1978년 -	미국 예술 과학 아카데미 회원
1985년 -	영국 아카데미 통신 회원
1988년	프린스턴 대학교 하워드 베르만 상
1993년 -	Academia Scientiarum et Artium Europaea 회원
1997년	존스 홉킨스 대학교 명예 인문학 박사 학위
1998년	하이파 대학교 명예 인문학 박사 학위
2000년 -	노르웨이 과학 아카데미 회원
2001년	스웨덴 왕립 과학 아카데미 쇼크상 (논리학 및 철학)
2005년	펜실베이니아 대학교 명예 인문학 박사 학위
2005년 -	미국 철학 학회 회원

6. 솔 크립키 센터

뉴욕 시립 대학교 대학원에 위치한 솔 크립키 센터는 크립키의 연구를 보존하고 장려하는 데 전념하고 있다. 센터 책임자는 로미나 파드로이다. 솔 크립키 센터는 크립키의 연구와 관련된 행사를 개최하고 있으며, 1950년대부터의 크립키의 강연, 강의 노트, 서신 등 이전에 출판되지 않은 기록의 디지털 아카이브를 구축하고 있다.^[31]

참조

_[1] 백과사전 Names https://plato.stanfo[...] Metaphysics Research Lab, Stanford University 2013-03-19
_[2] 학술지 "''A Priori'' Knowledge in Perspective: (II) Naming, Necessity and the Analytic A Posteriori" 1987-12
_[3] 서적 Minding the Brain: A Guide to Philosophy and Neuroscience Palgrave
_[4] 서적 Understanding the Nature of Law: A Case for Constructive Conceptual Explanation Edward Elgar Publishing 2015
_[5] 문서 Rigid Designation and the Contingent A Priori: The Meter Stick Revisited Notre Dame 1986
_[6] 간행물 Water's water everywhere http://www.lrb.co.uk[...] London Review of Books 2004-10-21
_[7] 기타 Quine versus Kripke on the Metaphysics of Modality https://ruor.uottawa[...]
_[8] 기타 What the Tortoise said to Kripke https://academicwork[...]
_[9] 서적 Philosophical Troubles: Collected Papers Volume 1 Oxford University Press
_[10] 뉴스 Philosopher, 65, Lectures Not About 'What Am I?' but 'What Is I?' https://www.nytimes.[...] The New York Times 2008-01-23
_[11] 서적 'A Companion to Analytic Philosophy (Blackwell Companions to Philosophy)'
_[12] 웹사이트 Saul Kripke – The Graduate Center, CUNY https://web.archive.[...] 2019-08-18
_[13] 뉴스 Philosopher, 65, Lectures Not About 'What Am I?' but 'What Is I?' https://www.nytimes.[...] The New York Times 2006-01-28
_[14] 웹사이트 x.com https://twitter.com/[...] 2024-06-15
_[15] 웹사이트 'Saul Kripke | Life, Philosophy, Works, & Facts | Britannica' https://www.britanni[...] 2023-03-13
_[16] 웹사이트 Fellows of the British Academy https://www.thebriti[...] 2023-03-13
_[17] 웹사이트 Kungl. Vetenskapsakademien https://web.archive.[...] 2018-01-07
_[18] 웹사이트 Saul Aaron Kripke (1940-2022) – Saul Kripke Center https://saulkripkece[...] 2022-09-16
_[19] 뉴스 Saul Kripke, Philosopher Who Found Truths in Semantics, Dies at 81 https://www.nytimes.[...] The New York Times 2022-09-21
_[20] 웹사이트 Saul Kripke (1940-2022) https://dailynous.co[...] 2022-09-16
_[21] 학술지 A completeness theorem in modal logic 1959-03
_[22] 학술지 Modal logics with several operators and provability interpretations 1986-02
_[23] 문서 Histories of Narrative Theory: From Structuralism to Present Blackwell Publishing, MA 2005
_[24] 서적 The Conscious Mind Oxford University Press 1996
_[25] 학술지 Marcus, Kripke, and the Origin of the New Theory of Reference https://web.archive.[...] 2007-05-28
_[26] 학술지 No Plagiarism Here https://web.archive.[...] 2009-11-13
_[27] 문서 Marcus, Kripke, and Names
_[28] 문서 1980
_[29] 서적 "Wittgenstein's Philosophical Investigations: An Introduction" Cambridge University Press 2006
_[30] 백과사전 Self-Reference https://plato.stanfo[...] Metaphysics Research Lab, Stanford University 2017-08-31
_[31] 웹사이트 Saul Kripke Center website https://saulkripkece[...]
_[32] 학술지 Review of Philosophical Troubles: Collected Papers, Volume 1 http://ndpr.nd.edu/n[...] Notre Dame Philosophical Reviews 2013-10-30
_[33] 웹사이트 Big Bang Theory: Who is Barry Kripke really named after? Real-life inspiration revealed https://www.express.[...] 2022-01-23
_[34] 트윗 We mourn the passing but celebrate the life and achievements of Saul Aaron Kripke (Nov. 13, 1940–Sep. 15, 2022). His family and friends ask for privacy at this time. 2022-09-17
_[35] 뉴스 Philosopher, 65, Lectures Not About 'What Am I?' but 'What Is I?' https://www.nytimes.[...] The New York Times 2006-01-28
_[36] 웹사이트 Saul Kripke Center website http://kripkecenter.[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com