양상 논리
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
양상 논리는 와 와 같은 양상 연산자를 사용하여 필연성, 가능성, 의무, 지식 등의 개념을 표현하는 논리 체계이다. 명제 논리의 언어를 확장하여 정의되며, 통사론적으로는 두 기호 와 를 추가하여 사용하고, 의미론적으로는 크립키 모형을 통해 가능 세계와 접근 가능성 관계를 기반으로 해석된다. 양상 논리는 진리 양상, 인식 논리, 시간 논리, 의무 논리, 도속 논리 등 다양한 분야에 적용되며, 형이상학적 문제와 철학적 논쟁의 대상이 된다. 아리스토텔레스 시대로부터 시작되어 현대에 이르기까지 발전해 왔으며, 크립키 의미론의 등장으로 획기적인 발전을 이루었다. 컴퓨터 과학, 인문학, 종교철학 등 다양한 분야에서 응용되고 있다.
더 읽어볼만한 페이지
- 양상 - 솔 크립키
솔 크립키는 양상 논리, 언어 철학, 수학기초론에 기여한 미국의 철학자이자 논리학자로, 크립키 의미론 창시, 《이름과 필연》에서의 고유명사 이론 전개, '크립켄슈타인' 해석, 진리 이론 연구 등으로 알려져 있다. - 양상 - 가능세계론
가능세계론은 현실 세계 외에 다른 가능한 세계들이 존재한다는 철학 이론이며, 명제의 참/거짓, 가능성, 필연성을 설명하는 데 사용되고 양상 논리, 반사실 조건문 분석 등 다양한 분야에서 활용된다. - 양상 논리 - 본질
본질은 사물이나 개념의 근본적인 성질이나 특징을 의미하는 철학적 개념으로, 아리스토텔레스에서 유래하여 다양한 철학 사상과 종교에서 논의되었으며, 특히 실존주의는 "존재가 본질에 앞선다"는 관점으로 새로운 해석을 제시하였다. - 양상 논리 - 인식 논리
인식 논리는 지식과 믿음 같은 인식 상태를 형식적으로 추론하는 양상 논리의 분야로, '안다'를 나타내는 양상 연산자 K를 사용하여 지식을 표현하고 공통 지식과 분배 지식 같은 개념을 다루며, 가능 세계 모델에 기반한 크립키 구조로 형식화되어 지식 추론을 탐구한다. - 논리학 - 모순
모순은 논리학, 철학, 과학 등 다양한 분야에서 사용되는 개념으로, 서로 상반되는 두 가지 주장이나 사실이 동시에 존재하는 상태를 의미하며, 특히 헤겔과 마르크스의 변증법적 유물론에서 사물의 내재적 대립으로서 역사 발전의 원동력으로 간주된다. - 논리학 - 특수
특수는 철학에서는 개별적이고 구체적인 존재를, 언어학에서는 눈에 띄는 또는 예외적인 의미를 가지며, 사회적으로 특별함이 중요하게 여겨지기도 한다.
| 양상 논리 | |
|---|---|
| 개요 | |
| 유형 | 형식 논리 |
| 연구 대상 | 필연, 가능성, 믿음 등 |
| 주요 분야 | 철학, 언어학, 컴퓨터 과학, 인공지능, 게임 이론 |
| 역사 | |
| 기원 | 고대 그리스 (아리스토텔레스) |
| 발전 | 중세 논리학, 현대 논리학 |
| 주요 학자 | 아리스토텔레스 C.I. 루이스 솔 크립키 |
| 기본 개념 | |
| 가능 세계 | 명제의 참/거짓이 평가되는 가상적인 상황 또는 상태 |
| 접근 관계 | 가능 세계 간의 관계 (예: 인식 가능성, 시간적 선후 관계) |
| 필연 | 모든 가능 세계에서 참인 명제 |
| 가능성 | 적어도 하나의 가능 세계에서 참인 명제 |
| 양상 연산자 | |
| 종류 | 필연 연산자 (□) 가능성 연산자 (◇) |
| 의미 | □P: "P는 필연적이다" 또는 "P는 반드시 참이다" ◇P: "P는 가능하다" 또는 "P는 참일 수 있다" |
| 주요 시스템 | |
| 기본 양상 논리 (K) | 가장 기본적인 공리 체계를 가진 양상 논리 |
| T 시스템 | K에 반사 공리 (□P → P)를 추가한 시스템 |
| S4 시스템 | T에 전이 공리 (□P → □□P)를 추가한 시스템 |
| S5 시스템 | S4에 유클리드 공리 (◇P → □◇P)를 추가한 시스템 |
| 응용 분야 | |
| 철학 | 형이상학 (필연성, 가능성) 인식론 (믿음, 지식) 윤리학 (의무, 허용) |
| 언어학 | 양상 부사, 시제, 양상 동사 분석 |
| 컴퓨터 과학 | 프로그램 검증 지식 표현 및 추론 인공지능 |
| 게임 이론 | 게임 전략 분석, 에이전트 기반 모델링 |
| 관련 논리 | |
| 시간 논리 | 시간의 흐름에 따른 명제의 변화를 다루는 논리 |
| 인식 논리 | 지식과 믿음을 형식화하는 논리 |
| 의무 논리 | 의무, 허용, 금지 등의 개념을 다루는 논리 |
| 동적 인식 논리 | 정보 변화와 지식 갱신을 다루는 논리 |
| 다치 논리 | 참과 거짓 외에 다른 진리값을 허용하는 논리 |
| 참고 문헌 | |
| 주요 서적 | 패트릭 블랙번, 마르턴 더 리커, 이데 베네마, Modal Logic (2001) 요한 반 벤템, Modal Logic for Open Minds (2010) |
| 관련 항목 | |
| 논리학 | 수리 논리학 비고전 논리 술어 논리 |
| 철학 | 형이상학 인식론 |
2. 정의
양상 논리는 기존 명제 논리에 필연성을 나타내는 연산자와 가능성을 나타내는 연산자를 추가하여 확장한 논리 체계이다. 는 "필연적으로"라고 읽으며, 는 "가능하게"라고 읽는다.
양상 논리는 진리론적(형이상학적, 논리적) 양상을 다루는 데 주로 사용된다. 예를 들어, "설인은 존재할 리가 없다"는 주장은 인식론적이지만, "설인이 존재할 가능성은 있다"는 주장은 진리론적이다.
이 외에도 "내일 비가 올지는 정해져 있지 않다"와 같은 시간적 양상, "∼해서는 안 된다"와 같은 의무 관련 양상 등도 양상 논리로 다룰 수 있다. 의무 표현을 다루는 양상 논리는 의무론리라고 불린다.
양상 논리에는 다양한 공리계가 있으며, 어떤 공리계가 타당한지는 논쟁의 대상이다. 모든 공리계에서 공통적으로 나타나는 것은 두 양상 연산자 사이의 드 모르간 법칙적인 관계이다.
즉, "필연적으로 참"은 "거짓일 가능성이 없다"와 같으며, "참일 가능성이 있다"는 "필연적으로 거짓인 것은 아니다"와 같다.
최소한의 공리계 E는 고전 명제 논리에 다음 추론 규칙을 추가한다.
- 추론 규칙: 가 성립한다면, 도 성립한다.
E보다 "강한" 모든 공리계를 Classical 공리계라고 한다.
하지만, 직관적으로 참으로 인정해야 할지 명확하지 않은 논리식도 많이 만들 수 있다. 예를 들어, (필연적으로 참이라면 필연적으로 '필연적으로 참'이다)가 성립하는지 여부는 확실하지 않다. 이러한 정리를 인정하는지 여부에 따라 다양한 공리계가 생겨난다.
필연화 규칙을 만족하는 공리계(Normal 공리계) 중에서 가장 "작은" 공리계는 크립키가 제시한 K 공리계이다.[40]
2. 1. 통사론
양상 논리는 일반 명제 논리의 기호(, , , 등) 외에 와 라는 두 가지 기호를 사용한다.[40] 이 두 기호는 다음과 같은 관계를 갖는다.이 두 기호는 여러 가지로 해석될 수 있지만, 일반적인 진리 양상 논리에서는 다음과 같이 해석한다.
- : 명제 는 필연적으로 참이다. 즉, 는 모든 가능한 세계에서 참이다.
- : 명제 는 개연적으로 참이다. 즉, 가 참인 세계가 존재한다.
이 밖에도 다음과 같이 다르게 해석할 수 있다.
- 증명가능성 논리(provability logic영어)
- : 명제 는 증명할 수 있다.
- : 명제 는 반증할 수 없다.
- 인식론적 논리(epistemic logic영어)
- : 명제 가 참인 것을 안다.
- : 명제 가 거짓인 것을 알지 못한다.
- 의무론적 논리 (deontological logic영어)
- : 명제 를 만족시킬 의무가 있다.
- : 명제 를 만족시키는 것이 허용된다.
양상 논리는 및 와 같은 양상 연산자를 사용한다는 점에서 다른 종류의 논리와 다르다. 는 일반적으로 "필연적으로"라고 읽으며, 도덕적 또는 법적 의무, 지식, 역사적 필연성과 같은 개념을 표현하는 데 사용될 수 있다. 는 일반적으로 "가능하게"라고 읽히며, 허가, 능력, 증거와의 양립 가능성 등의 개념을 표현하는 데 사용될 수 있다.[40]
양상 논리의 잘 정돈된 공식에는 와 같은 비양상 공식이 포함되지만, , , 등과 같은 양상 공식도 포함된다.[40]
기본적인 명제 논리의 언어 는 다음과 같이 재귀적 정의될 수 있다.
1. 만약 가 원자 공식이라면, 는 의 공식이다.
2. 만약 가 의 공식이라면, 도 마찬가지이다.
3. 만약 와 가 의 공식이라면, 도 마찬가지이다.
4. 만약 가 의 공식이라면, 도 마찬가지이다.
5. 만약 가 의 공식이라면, 도 마찬가지이다.
양상 연산자는 위의 4 및 5와 유사한 규칙을 도입하여 다른 종류의 논리에 추가할 수 있다. 양상 술어 논리는 와 같은 공식을 포함하는 널리 사용되는 변형 중 하나이다. 와 가 쌍대인 양상 논리 시스템에서, 는 의 약어로 간주될 수 있으며, 따라서 이를 도입하기 위한 별도의 구문 규칙이 필요하지 않다. 그러나 두 연산자가 상호 정의 불가능한 시스템에서는 별도의 구문 규칙이 필요하다.[40]
일반적인 표기 변형에는 지식을 나타내는 데 사용되는 양상 논리 시스템에서 및 와 믿음을 나타내는 데 사용되는 시스템에서 및 와 같은 기호가 포함된다. 이러한 표기법은 여러 양상 연산자를 동시에 사용하는 시스템에서 특히 일반적이다. 예를 들어, 결합된 인식-의무 논리는 "나는 P가 허용됨을 안다"로 읽히는 공식 를 사용할 수 있다. 양상 논리 시스템은 인덱스(예: , , 등)로 구별되는 무한히 많은 양상 연산자를 포함할 수 있다.[40]
2. 2. 공리계
명제 논리의 공리 및 전건 긍정 외에도, 양상 논리 고유의 공리들이 있다. 가장 기본적인 양상 논리 '''K'''는 명제 논리에 다음 두 공리를 추가하여 만들어진다.이 외에도 다음과 같은 공리들을 추가할 수 있다.
- '''T'''공리:
- '''4번 공리''':
- '''5번 공리''':
- '''B'''공리:
- '''D'''공리:
- '''GL'''공리:
'''K'''에 이 공리들 가운데 일부를 추가하면 다음과 같은 양상 논리들을 얻는다.
| 논리 체계 | 추가되는 공리 |
|---|---|
| T | K + T공리 |
| K4 | K + 4번 공리 |
| S4 | K + T공리 + 4번 공리 |
| S5 | K + T공리 + 5번 공리 |
| D | K + D공리 |
| D45 | K + D공리 + 4번 공리 + 5번 공리 |
| GL | K + GL공리 |
양상 논리의 의미론은 주로 크립키 의미론(가능세계 의미론)을 통해 설명된다. 크립키 의미론은 존재할 수 있는 세계인 '가능세계'를 가정하는 가능세계론에 기반한다.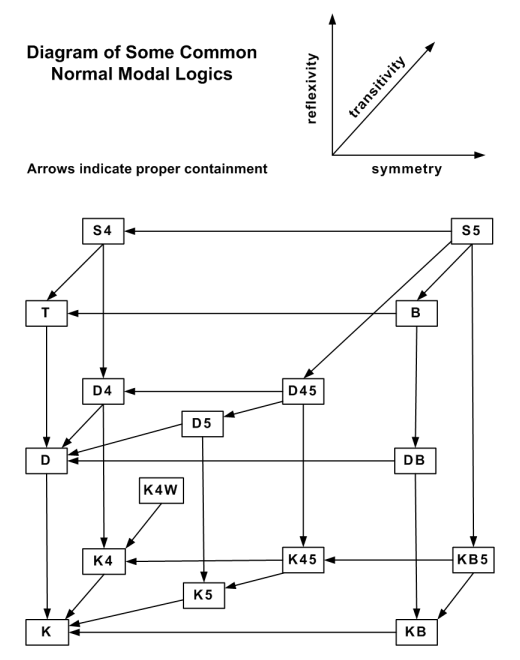
3. 의미론
솔 크립키에 의해 주어진 크립키 의미론은 양상 논리의 의미론 체계이며, 가능 세계론과 관련된 아이디어를 제공한다. 가능 세계 사이의 이항 관계로 정의되는 도달 가능성의 개념을 통해 공리계의 변형을 파악할 수 있다.
명제 양상 논리의 의미론에서 ''W''는 공집합이 아닌 집합으로, 개개의 가능 세계 전체의 집합을 나타낸다. ''W''상의 이항 관계 ''R''을 통해 가능 세계 간의 도달 관계를 정의하고, 양상 연산자가 붙은 논리식의 참/거짓에 영향을 미치도록 한다. 또한 명제 변수 전체의 집합 ''PV''와 함수 V를 통해 원자 명제에 대한 해석을 정의한다.
해석 ''V''는 논리식 전체로 재귀적으로 확장되며, 명제 논리의 결합자에 관해서는 고전 명제 논리와 같지만, 양상 연산자에 관해서는 가능 세계와 도달 관계를 고려해야 한다.
"비정규 세계"(non-normal worlds)를 도입하여 비정규 양상 논리에서의 해석을 정의할 수 있다. 비정규 세계에서는 정의적으로 모든 가능 명제가 참이고, 모든 필연 명제가 거짓이다.
공리계 S4의 위상적 의미론에서는 원자 명제들을 위상 공간 안의 도형으로 해석하고, 양상 연산자는 개핵 작용소와 폐포 작용소로 해석된다. 대수적 의미론에서는 원자 명제들을 위상 부울 대수의 원소로 해석한다.
3. 1. 크립키 의미론
크립키 모형(Kripke model)은 양상 논리에서 가장 많이 사용되는 의미론으로, 가능한 세계를 가정하는 가능세계론에 기반한다.
일반적인 양상 논리 의미론에서는 순서쌍 이 정의된다. 여기서 G는 가능 세계들의 집합이고, R은 가능 세계들 간의 이항 관계인 접근가능성 관계이다. 예를 들어 w R u는 세계 u가 세계 w로부터 접근 가능함을 의미한다. 현실 세계는 G 속의 한 불변항 로 나타낼 수 있다.
가능 세계들과 양의 문자들 간의 관계 v는 G 속의 각 세계에서 모든 명제들의 진리값을 특정하여 모형을 확장한다. 만약 인 세계 w가 존재하면, P는 w에서 참이다. 이에 따라 모형은 가 된다.
모형 안에서 세계 속의 논리식의 참은 다음과 같이 재귀적으로 정의된다(iff는 필요충분조건):
양상 논리에서 명제의 참 여부는 가능 세계 w 안에서만 결정될 수 있는 상대적 특성을 가진다. w에 접근 가능한 모든 세계에서 참이면 w에서 필연적으로 참이고, w에 접근 가능한 일부 세계에서 참이면 w에서 참임이 가능하다.
양상 논리의 체계들은 접근가능성 관계의 특성에 따라 구분된다. 접근가능성 관계는 다음과 같은 특성을 가질 수 있다.
이러한 조건들에 의해 양상 공리 체계들을 설명하면 다음과 같다.
S4의 경우, 위상 공간으로서 의미론을 정의할 수 있으며, 이 때의 대응성은 다음과 같다.
S4의 공리들은 내부와 폐포의 성질로 해석할 수 있다.
관계 의미론은 양상 논리의 표준 의미론이며, 공식의 진리 값은 가능 세계를 기준으로 결정된다. 양상 연산자를 포함하는 공식의 경우, 그 진리 값은 접근 가능한 세계에서 참인 것에 따라 달라질 수 있다. 관계 의미론은 모형 을 사용하여 양상 논리의 공식을 해석한다.[5] 여기서,
1. 는 가능 세계의 집합이다.
2. 은 에 대한 이항 관계이다.
3. 는 원자 공식과 세계의 각 쌍에 진리 값을 할당하는 평가 함수이다(즉, , 여기서 는 원자 공식의 집합이다).
는 전체 집합이라고도 불린다. 이항 관계 은 접근 관계라고 불리며, 어떤 세계가 서로를 "볼" 수 있는지 제어한다. 예를 들어, 는 세계 가 세계 에서 접근 가능하다는 것을 의미한다. 즉, 로 알려진 사태는 에 대한 현실적인 가능성이다. 함수 는 평가 함수라고 알려져 있으며, 어떤 원자 공식이 어떤 세계에서 참인지 결정한다.
모형 에서 세계 에서 공식의 진리 값은 다음과 같이 재귀적으로 정의된다.
- iff
- iff
- iff and
- iff 의 모든 원소 에 대해, 만약 이면
- iff 의 어떤 원소 에 대해, 이고 가 성립한다
이 의미론에 따르면, 공식은 세계 에서 접근 가능한 모든 세계에서 성립하는 경우 세계 에 대해 필요하며, 에서 접근 가능한 어떤 세계에서 성립하는 경우 가능하다. 가능성은 접근 관계 에 의존하며, 이를 통해 가능성의 상대적 본성을 표현할 수 있다.
3. 1. 1. 프레임과 완전성
크립키 모형(Kripke model)에서 평가 함수를 제외한 관계 모델의 일부인 ''프레임''은 쌍으로 표현된다. 여기서 는 가능한 세계의 집합이고, 은 에 대한 이진 관계이다.[5]모달 논리의 서로 다른 시스템은 ''프레임 조건''을 사용하여 정의된다. 주요 프레임 조건은 다음과 같다.
- '''반사적''': 모든 ''w'' in ''G''에 대해 ''w R w''
- '''대칭적''': 모든 ''w''와 ''u'' in ''G''에 대해 ''w R u''이면 ''u R w''
- '''추이적''': 모든 ''w'', ''u'', ''q'' in ''G''에 대해 ''w R u''와 ''u R q''이면 ''w R q''
- '''직렬적''': 모든 ''w'' in ''G''에 대해 ''w R u''가 성립하는 ''u'' in ''G''가 존재
- '''유클리드적''': 모든 ''u'', ''t'', ''w''에 대해, ''w R u''와 ''w R t''이면 ''u R t'' (대칭성에 의해, 이것은 또한 ''t R u''와 ''t R t'' 및 ''u R u''를 함축)
이러한 프레임 조건에서 파생된 논리는 다음과 같다.
- ''K'' := 조건 없음
- ''D'' := 직렬
- ''T'' := 반사적
- ''B'' := 반사적 및 대칭적
- ''S4'' := 반사적 및 추이적
- ''S5'' := 반사적 및 유클리드적
유클리드 속성은 반사성과 함께 대칭성과 추이성을 낳는다. 따라서 접근 관계 ''R''이 반사적이고 유클리드적인 경우, ''R''은 증명 가능한 대칭적 및 추이적이다. S5 모델의 경우, ''R''은 동치 관계이다.
이러한 프레임이 모든 세계가 ''W''의 다른 모든 세계를 볼 수 있는 프레임과 동일한 유효 문장 집합을 생성한다는 것을 증명할 수 있다.
3. 2. 위상 의미론
S4 양상 논리는 위상 공간을 통해 의미론을 정의할 수 있다. S4 양상 논리와 위상수학의 대응 관계는 다음과 같다.
이 경우, S4의 공리들은 내부와 폐포의 성질로 해석할 수 있다.
양상 논리는 위상 구조를 사용하여 해석될 수도 있다. 예를 들어, ''내부 의미론''은 양상 논리의 공식을 다음과 같이 해석한다.
''위상 모델''은 튜플 이며, 여기서 는 위상 공간이고 는 각 원자 공식에 의 부분 집합을 매핑하는 평가 함수이다. 기본적인 내부 의미론은 양상 논리의 공식을 다음과 같이 해석한다.
- iff
- iff
- iff and
- iff for some we have both that and also that for all
위상적 접근 방식은 관계적 접근 방식을 포함하며, 비정규 양상 논리를 허용한다. 이 방식은 또한 자신의 신념에 대한 증거 또는 정당화와 같은 특정 개념을 모델링하는 투명한 방법을 제공한다. 위상 의미론은 형식적 인식론의 최근 연구에서 널리 사용되며, 데이비드 루이스와 안젤리카 크라처의 반사실적 조건문에 대한 논리와 같은 초기 연구에서 그 기원을 찾을 수 있다.
4. 철학에서의 양상 논리
고전적 양상 논리에서 명제는 다음과 같이 정의된다.
- '''가능적'''인 것은 ''반드시 거짓은 아닌'' 경우이다(실제로 참인지 거짓인지와 관계없이).
- '''필연적'''인 것은 ''가능적으로 거짓이 아닌'' 경우이다(즉, 참이고 필연적으로 참인 경우).
- '''우연적'''인 것은 ''필연적으로 거짓이 아니고'' ''필연적으로 참이지도 않은'' 경우이다(즉, 가능하지만 필연적으로 참은 아님).
- '''불가능적'''인 것은 ''가능적으로 참이 아닌'' 경우이다(즉, 거짓이고 필연적으로 거짓인 경우).
따라서 고전적 양상 논리에서는 가능성 또는 필연성 중 하나의 개념을 기본으로 취할 수 있으며, 다른 개념들은 드 모르간의 이중성의 방식으로 이를 통해 정의된다. 직관주의적 양상 논리는 가능성과 필연성을 완벽하게 대칭적인 것으로 취급하지 않는다.
예를 들어, 편의점에 가는 길에 프리드리히의 집을 지나갔는데 불이 꺼져 있는 것을 보았다고 가정해 보자. 돌아오는 길에 불이 켜져 있는 것을 보았다.
- "누군가 또는 무언가가 불을 켰다"는 것은 ''필연적''이다.
- "프리드리히가 불을 켰다", "프리드리히의 룸메이트 맥스가 불을 켰다", "아돌프라는 강도가 프리드리히의 집에 침입해서 불을 켰다"는 것은 ''우연적''이다.
- 위의 모든 진술은 ''가능적''이다.
- 소크라테스(2천 년 이상 전에 사망)가 불을 켰다는 것은 ''불가능''하다.
어떤 것이 가능하지만 참이 아닌 개념을 이해하는 데 어려움을 겪는 사람들을 위해 이러한 용어의 의미는 여러 "가능 세계"(라이프니츠의 의미에서) 또는 "대체 우주"를 생각함으로써 더 이해하기 쉬울 수 있다. "필연적"인 것은 모든 가능 세계에서 참이고, "가능적"인 것은 적어도 하나의 가능 세계에서 참이다.
물리적으로, 또는 규범적으로 가능하다는 것은 물리 법칙에 의해 허용되는 경우를 의미한다. 예를 들어, 현재 이론은 그러한 원자가 존재하지 않더라도 원자 번호가 126인 원자가 존재할 수 있도록 허용하는 것으로 생각된다.[7] 반면에, 광속을 초과하여 가속하는 것은 논리적으로 가능하지만,[8] 현대 과학은 물질 입자나 정보에 대해서는 물리적으로 불가능하다고 규정한다.[9]
4. 1. 진리 양상 논리
고전적 양상 논리에서 명제는 다음과 같이 정의된다.- '''가능적'''인 것은 ''반드시 거짓은 아닌'' 경우이다(실제로 참인지 거짓인지와 관계없이).
- '''필연적'''인 것은 ''가능적으로 거짓이 아닌'' 경우이다(즉, 참이고 필연적으로 참인 경우).
- '''우연적'''인 것은 ''필연적으로 거짓이 아니고'' ''필연적으로 참이지도 않은'' 경우이다(즉, 가능하지만 필연적으로 참은 아님).
- '''불가능적'''인 것은 ''가능적으로 참이 아닌'' 경우이다(즉, 거짓이고 필연적으로 거짓인 경우).
따라서 고전적 양상 논리에서는 가능성 또는 필연성 중 하나의 개념을 기본으로 취할 수 있으며, 다른 개념들은 드 모르간의 이중성의 방식으로 이를 통해 정의된다. 직관주의적 양상 논리는 가능성과 필연성을 완벽하게 대칭적인 것으로 취급하지 않는다.
예를 들어, 편의점에 가는 길에 프리드리히의 집을 지나갔는데 불이 꺼져 있는 것을 보았다고 가정해 보자. 돌아오는 길에 불이 켜져 있는 것을 보았다.
- "누군가 또는 무언가가 불을 켰다"는 것은 ''필연적''이다.
- "프리드리히가 불을 켰다", "프리드리히의 룸메이트 맥스가 불을 켰다", "아돌프라는 강도가 프리드리히의 집에 침입해서 불을 켰다"는 것은 ''우연적''이다.
- 위의 모든 진술은 ''가능적''이다.
- 소크라테스(2천 년 이상 전에 사망)가 불을 켰다는 것은 ''불가능''하다.
어떤 것이 가능하지만 참이 아닌 개념을 이해하는 데 어려움을 겪는 사람들을 위해 이러한 용어의 의미는 여러 "가능 세계"(라이프니츠의 의미에서) 또는 "대체 우주"를 생각함으로써 더 이해하기 쉬울 수 있다. "필연적"인 것은 모든 가능 세계에서 참이고, "가능적"인 것은 적어도 하나의 가능 세계에서 참이다.
물리적으로, 또는 규범적으로 가능하다는 것은 물리 법칙에 의해 허용되는 경우를 의미한다. 예를 들어, 현재 이론은 그러한 원자가 존재하지 않더라도 원자 번호가 126인 원자가 존재할 수 있도록 허용하는 것으로 생각된다.[7] 반면에, 광속을 초과하여 가속하는 것은 논리적으로 가능하지만,[8] 현대 과학은 물질 입자나 정보에 대해서는 물리적으로 불가능하다고 규정한다.[9]
4. 2. 인식 논리
인식론적 논리에서 인식 양상은 문장의 ''확실성''을 다룬다.[12] 연산자는 "x는 ...을 확신한다"로 번역되고, 연산자는 "x가 아는 모든 것에 대해, ...이 사실일 수 있다"로 번역된다.[12]일상 대화에서 형이상학적 양상과 인식적 양상은 종종 비슷한 단어로 표현된다. 예를 들어 존스라는 사람은 다음과 같이 말할 수 있다.
# "아니, 빅풋이 존재할 가능성은 ''없어''; 나는 그것을 매우 확신해."
# "물론, 빅풋이 존재할 ''가능성''은 있어."
(1)에서 존스는 모든 사용 가능한 정보를 고려했을 때 빅풋의 존재 여부에 대한 질문이 남아 있지 않다는 인식적 주장을 하는 것이다. (2)에서 존스는 빅풋이 ''존재할 수 있다''는 ''형이상학적'' 주장을 하는 것이다.
인식적 가능성은 형이상학적 가능성과는 다르게 실제 세계에 영향을 미친다. 형이상학적 가능성은 세상이 ''어떻게 변했을지''에 대한 영향을 미치지만, 인식적 가능성은 세상이 ''어떻게 될지''(우리가 아는 모든 것에 대해)에 대한 영향을 미친다.[13]
인식 양상 논리의 몇 가지 특징은 논쟁 중에 있다. 예를 들어 ''x''가 ''p''를 알고 있다면, ''x''는 자신이 ''p''를 안다는 것을 아는가? 즉, 가 이러한 시스템의 공리가 되어야 하는가? 이 질문에 대한 답은 명확하지 않지만,[12] 적어도 하나의 공리는 일반적으로 인식 양상 논리에 포함된다.[13]
진리 양상과 인식 양상이 서로 구별되어야 하는지에 대한 의문이 제기되었다.[13] 한 연구에서는 진리 양상과 인식 양상이 문법적 분위기와 같은 수단으로 형식적으로 구별되는 언어를 찾지 못했다.[14]
4. 3. 시간 논리
시간 논리는 시제를 가진 표현, 즉 언제에 대한 수식어를 가진 표현의 의미론에 대한 접근 방식이다. 예를 들어 '2 + 2 = 4'와 같은 명제는 항상 참이지만, '존은 행복하다'와 같은 시제를 가진 표현은 때때로만 참이다.시간 논리에서 시제 구조는 모달리티(Modality) 측면에서 처리되며, 시간을 형식화하는 표준 방법은 과거와 미래에 대한 양상 연산자 쌍을 사용하는 것이다. 예를 들면 다음과 같다.
- '''F'''''P'' : 때때로 ''P''가 사실일 것이다.
- '''G'''''P'' : 항상 ''P''가 사실일 것이다.
- '''P'''''P'' : 언젠가 ''P''가 사실이었다.
- '''H'''''P'' : 항상 ''P''가 사실이었다.
이 연산자들을 사용하여 다양한 모달 논리 체계를 만들 수 있다. 예를 들어 다음과 같이 정의할 수 있다.
: = ''P''는 시간 ''t''에 사실이다.
: = ''P''는 모든 시간 ''t''에 사실이다.
또는 미래(또는 과거)만 다루는 연산자를 정의할 수도 있다.
: = '''F'''''P''
: = '''G'''''P''
혹은 다음과 같이 정의할 수도 있다.
: = ''P'' 및/또는 '''F'''''P''
: = ''P'' 및 '''G'''''P''
'''F'''와 '''G''' 연산자는 처음에는 생소하게 보일 수 있지만, 이들은 정규 모달 시스템을 생성한다. '''F'''''P''는 ¬'''G'''¬''P''와 같다. 이러한 연산자들을 결합하여 복잡한 명제를 만들 수 있다. 예를 들어, '''P'''''P'' → □'''P'''''P''는 "과거에 참이었던 모든 것은 필연적이다"라는 의미를 나타낸다.
시간의 흐름에 따라 명제의 참, 거짓이 변하는 것을 고려할 때, 과거는 고정되어 있지만 미래는 그렇지 않다는 우연적 필연성 문제가 발생한다. 예를 들어, 어제 비가 왔다는 사실은 바꿀 수 없지만, 내일 비가 올지 안 올지는 아직 결정되지 않았다. 이러한 개념은 미래 우연성의 문제와도 연결된다. 아리스토텔레스는 미래에 대한 단언에 대해 이원론의 원리를 거부하기도 했다.
선형 템포럴 논리에서는 이진 연산자를 추가적으로 사용하기도 한다.
시간 논리는 컴퓨터 과학에서 컴퓨터 작동을 모델링하고 정리를 증명하는 데 사용될 수 있다. 예를 들어, ◇''P''는 "컴퓨터 계산의 미래 시간에 P가 참이 되는 컴퓨터 상태가 가능함"을 의미하고, □''P''는 "컴퓨터 계산의 모든 미래 시간에 P가 참이 됨"을 의미하는 방식으로 사용될 수 있다.
4. 4. 의무 논리
의무론적 논리(deontological logic영어)는 "해야 한다", "해도 된다"와 같은 의무와 허가에 관련된 명제를 다룬다. 이러한 표현들은 "필요하다", "가능하다"와 같은 진리 양상과 유사한 구조를 가진다. 의무 논리는 그리스어 ''의무''에서 유래하여 ''의무적'' 논리라고도 불린다.[15]일반적인 명제 논리 기호 외에, 의무 논리는 다음 두 가지 양상 기호를 사용한다.
- : 명제 를 만족시킬 의무가 있다.
- : 명제 를 만족시키는 것이 허용된다.
이 두 기호는 다음과 같은 관계를 가진다.
:
:
의무 논리는 크립키 의미론에서 접근성 관계의 반사성을 나타내는 공리 '''T''' ()를 일반적으로 갖지 않는다. '''T'''는 모든 의무가 참이라고 해석될 수 있는데, 예를 들어 살인이 도덕적으로 금지되어 있다면, '''T'''는 사람들이 실제로 살인을 하지 않는다는 결론을 내리게 된다. 이는 명백히 거짓이다.[15]
대신, 크립키 의미론을 통해 우리 세계가 모든 의무를 실현하지는 않지만, 접근 가능한 이상화된 세계에서는 '''T'''가 성립한다고 설명한다. 즉, 우리 세계에 관해 ''P''가 의무적이라는 것은 우리 세계에 접근 가능한 모든 이상화된 세계에서 ''P''가 성립한다는 것이다.[15]
또 다른 원리 ''D'' ()는 접근성 관계의 직렬성에 해당하며, "해야 한다면 할 수 있다"는 칸트의 사상을 나타낸다.[15]
표준 양상 논리로 윤리를 형식화할 때 몇 가지 문제점이 발생한다. 예를 들어, "돈을 훔쳤다면 소액이어야 한다"를 표현할 때, (K: 돈을 훔쳤다, Q: 소액을 훔쳤다)는 당신이 소액을 훔쳐야 한다는 잘못된 결론을 도출한다. 역시 "훔치지 말아야 한다"는 가설에서 "훔쳤다면 거액이어야 한다"는 명제를 도출하는 문제를 야기한다.[16]
4. 5. 도속 논리
'''도속 논리'''는 (어떤 집단의) 믿음에 대한 논리이다. "도속(doxastic)"이라는 용어는 "믿음"을 의미하는 고대 그리스어 ''doxa''에서 파생되었다. 일반적으로, 도속 논리는 기호를 사용하며, 종종 "B"로 표기하여 "다음이 믿어진다"는 의미로 사용하거나, 특정 에이전트 s에 상대화하여 "s가 다음을 믿는다"는 의미로 사용한다.5. 형이상학적 문제
철학자들은 대상이 과학적 법칙에 의해 규정되지 않은 속성을 갖는지에 대해 논쟁한다. 솔 크립키는 모든 사람은 필연적으로 그들이 가진 부모를 가진다고 주장했다. 다른 부모를 가진 사람은 동일한 사람이 아닐 것이다.[10]
양상 논리에서 "논리적으로 가능한 세계"를 고려한다. 어떤 진술이 모든 가능 세계에서 참이라면, 그것은 필연적 진리이다. 만약 어떤 진술이 우리의 세계에서 참이지만, 모든 가능 세계에서 참이 아니라면, 그것은 우연적 진리이다. 어떤 가능 세계(반드시 우리 자신의 세계가 아님)에서 참인 진술은 가능한 진리라고 불린다.
이 "가능 세계 표현"에 따르면, 빅풋의 존재가 가능하지만 실제는 아니라고 주장하려면, "빅풋이 존재하는 어떤 가능 세계가 있다; 그러나 실제 세계에서는 빅풋이 존재하지 않는다"라고 말한다. 그러나 이 주장이 우리에게 무엇을 요구하는지는 불분명하다. 우리는 정말로 우리의 실제 세계만큼이나 현실적인 가능 세계의 존재를 주장하는가, 단지 실제가 아닐 뿐인가? 솔 크립키는 '가능 세계'가 일종의 오해라고 생각한다. 즉, '가능 세계'라는 용어는 가능성의 개념을 시각화하는 유용한 방법일 뿐이다.[17] 그에게 있어서 "당신은 6 대신 4를 굴릴 수 있었다"라는 문장과 "당신이 4를 굴린 가능 세계가 있지만, 실제 세계에서는 6을 굴렸다"라는 문장은 크게 다르지 않은 진술이며, 어느 쪽도 우리에게 가능 세계의 존재를 요구하지 않는다.[18] 반면에, 데이비드 루이스는 모든 단순한 가능 세계가 우리 세계만큼이나 현실적이며, 우리 세계를 '실제'로 구별하는 것은 단순히 그것이 우리 세계라는 점, 즉 '이' 세계라는 점을 주장하여 스스로 악명이 높아졌다.[19] 그 입장은 "양상적 실재론"의 주요 원칙이다.
6. 역사
아리스토텔레스는 그의 저서 『전(前) 분석론』에서 양상 삼단논법을 개발했으며, 테오프라스토스가 이를 개선하려 시도했다.[24] 헬레니즘 시대에, 논리학자 크로노스의 디오도루스, 변증법가 필론, 스토아 학파의 크리시포스는 각각 가능성과 필연성의 상호 정의 가능성을 설명하고, 공리 '''T'''(아래 참조)를 수용하며, 주 논변을 해결하기 위해 양상 논리와 시간 논리의 요소를 결합한 양상 체계를 개발했다.[25] 가장 초기의 형식 양상 논리 체계는 아비세나에 의해 개발되었으며, 그는 궁극적으로 "시간적 양상" 삼단논법 이론을 개발했다.[26] 오컴의 윌리엄과 던스 스코투스와 같은 스콜라 철학자들은 주로 본질과 부수적 성질에 대한 명제를 분석하기 위해 비형식적으로 양상적 방식으로 추론했다.
C. I. 루이스는 1912년 "함축과 논리의 대수"를 시작으로 일련의 학술 논문을 통해 현대 양상 논리를 창시했다.[28][29] 루이스는 고전 논리가 물질적 함축의 역설과 같은 진공 진리 원칙을 허용한다는 근거에 따라 양상 논리, 특히 엄격한 함축을 발명하게 되었다.[30] 이 연구는 1932년 그의 저서 『기호 논리학』(C. H. 랭포드 공저)으로 절정에 달했으며, 여기에서 다섯 개의 체계 ''S1''에서 ''S5''까지가 소개되었다.
루스 C. 바칸(후일 루스 바칸 마르쿠스)은 양화된 양상 논리의 최초의 공리적 체계를 개발했다. - 루이스의 ''S2'', ''S4'', ''S5''의 일차 및 이차 확장.[34][35][36]
솔 크립키는 1959년에 현재 표준으로 사용되는 양상 논리에 대한 크립키 의미론(가능 세계 의미론)을 도입했다.[37]
A. N. 프라이어는 1957년에 양상 논리와 밀접하게 관련된 현대 시간 논리를 만들었다. 보언 프랫은 1976년에 동적 논리를 도입했다. 1977년, 아미르 프누엘리는 지속적으로 작동하는 병행 프로그래밍의 동작을 형식화하기 위해 시간 논리를 사용할 것을 제안했다.
7. 추가 응용
양상 논리는 문학, 시, 예술, 역사와 같은 인문학 분야에서 사용되기 시작했다.[21][22] 종교철학에서는 양상 논리가 신의 존재에 대한 논증에 일반적으로 사용된다.[23]
참조
[1]
서적
Modal Logic
https://books.google[...]
Cambridge University Press
2001
[2]
서적
Modal Logic for Open Minds
https://pdfs.semanti[...]
CSLI
2010
[3]
논문
The set-theoretic multiverse
2012
[4]
논문
Dynamic Epistemic Logics of Diffusion and Prediction in Social Networks.
2019
[5]
서적
First-Order Modal Logic
https://books.google[...]
Kluwer Academic Publishers
1998
[6]
뉴스
Press release: Superheavy Element 114 Confirmed: A Stepping Stone to the Island of Stability
http://newscenter.lb[...]
Lawrence Berkeley National Laboratory
2009-09-24
[7]
논문
Possibility of Faster-Than-Light Particles
[8]
논문
Zur Elektrodynamik bewegter Körper
http://sedici.unlp.e[...]
1905-06-30
[9]
웹사이트
Physicalism
http://plato.stanfor[...]
2014-12-16
[10]
문서
Naming and Necessity
Harvard University Press
1980
[11]
서적
Content and Modality : Themes from the Philosophy of Robert Stalnaker
https://books.google[...]
Oxford University Press
2014-12-16
[12]
문서
Blindsight and Subliminal perception
[13]
서적
The Expression of Modality
https://books.google[...]
Mouton de Gruyter
2010-01-03
[14]
서적
Epistemic Modality, Language, and Conceptualization: A Cognitive-pragmatic Perspective
John Benjamins Publishing Co
2000-11
[15]
논문
Ideal Worlds—Wishful Thinking in Deontic Logic
[16]
웹사이트
Logic for Philosophy
http://tedsider.org/[...]
[17]
서적
Naming and Necessity
Harvard UP
1980
[18]
서적
Naming and Necessity
Harvard UP
1980
[19]
서적
On the Plurality of Worlds
Blackwell
1986
[20]
논문
Theories of Actuality
https://www.jstor.or[...]
1974-09
[21]
웹사이트
Dickens Universe
http://www.estherled[...]
[22]
논문
Lives Unled in Realist Fiction
The Regents of the University of California
2007
[23]
뉴스
Modal Ontological Arguments
https://compass.onli[...]
2023-08
[24]
웹사이트
Ancient Logic
[25]
문서
"Chrysippus' Modal Logic and its Relation to Philo and Diodorus"
1993
[26]
웹사이트
History of logic: Arabic logic
https://www.britanni[...]
[27]
논문
The Venn-MacColl Dispute in Nature
[28]
논문
Implication and the Algebra of Logic.
1912
[29]
웹사이트
Modern Origins of Modal Logic
https://plato.stanfo[...]
2020-08-30
[30]
논문
The issues concerning material implication.
1917
[31]
서적
Symbolic Logic
Dover Publications
[32]
서적
Bertrand Russell Memorial Volume
George Allen and Unwin
[33]
논문
Ontological Foundations of Russell's Theory of Modality
http://www.members.t[...]
2012-10-22
[34]
논문
A Functional Calculus of First Order Based on Strict Implication
1946-03
[35]
논문
The Deduction Theorem in a Functional Calculus of First Order Based on Strict Implication
1946-12
[36]
논문
The Identity of Individuals in a Strict Functional Calculus of Second Order
1947-03
[37]
서적
Modalities: Philosophical Essays
Oxford University Press
1993
[38]
논문
A Solution of the Decision Problem for the Lewis Systems S2 and S4, with an Application to Topology
[39]
간행물
Mathematical Modal Logic: A view of its evolution
http://www.mcs.vuw.a[...]
[40]
서적
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com