역전파
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
역전파는 1960년대부터 연구되어 여러 연구자들에 의해 발전된 알고리즘으로, 연쇄 법칙을 기반으로 오차 함수의 기울기를 계산하여 신경망을 학습시킨다. 입력층, 은닉층, 출력층으로 구성된 신경망에서 각 층의 가중치를 경사 하강법을 통해 업데이트하며, 자동 미분의 특수한 경우로 볼 수 있다. 역전파는 지역 최솟값에 갇힐 수 있고, 기울기 소실 문제의 한계를 가지지만, 2010년대 이후 GPU 기반 컴퓨팅 시스템의 발전에 힘입어 음성 인식, 기계 시각, 자연어 처리 등 다양한 분야에서 활용되고 있다.
더 읽어볼만한 페이지
- 신경망 - 환각 (인공지능)
인공지능 환각은 인공지능이 사실이 아닌 정보를 사실처럼 생성하는 현상으로, 대규모 언어 모델의 부정확한 정보 생성 문제를 설명하기 위해 사용되며, 데이터 불일치, 모델 오류, 훈련 데이터 부족 등이 원인으로 발생하여 다양한 완화 기술이 연구되고 있다. - 신경망 - 신경가소성
신경가소성은 뇌의 구조와 기능이 경험, 학습, 손상에 따라 변화하는 능력이며, 시냅스 가소성, 구조적 가소성으로 나뉘어 뇌졸중, 학습 장애 등의 치료와 재활, 명상, 예술 활동 등 다양한 분야에 응용된다. - 기계 학습 알고리즘 - 강화 학습
강화 학습은 에이전트가 환경과의 상호작용을 통해 누적 보상을 최대화하는 최적의 정책을 학습하는 기계 학습 분야이며, 몬테카를로 방법, 시간차 학습, Q-러닝 등의 핵심 알고리즘과 탐험과 활용의 균형, 정책 경사법 등의 다양한 연구 주제를 포함한다. - 기계 학습 알고리즘 - 기댓값 최대화 알고리즘
- 인공신경망 - 인공 뉴런
인공 뉴런은 인공신경망의 기본 요소로서, 입력 신호에 가중치를 곱하고 합산하여 활성화 함수를 거쳐 출력을 생성하며, 생물학적 뉴런을 모방하여 설계되었다. - 인공신경망 - 퍼셉트론
퍼셉트론은 프랭크 로젠블랫이 고안한 인공신경망 모델로, 입력 벡터에 가중치를 곱하고 편향을 더한 값을 활성화 함수에 통과시켜 이진 분류를 수행하는 선형 분류기 학습 알고리즘이며, 초기 신경망 연구의 중요한 모델로서 역사적 의미를 가진다.
| 역전파 | |
|---|---|
| 개요 | |
 | |
| 종류 | 지도 학습 |
| 분야 | 인공신경망 |
| 상세 정보 | |
| 사용 모델 | 다층 퍼셉트론, 순환 신경망 |
| 목적 | 모델 훈련 |
| 방법 | 경사하강법 |
| 다른 이름 | 오차 역전파법 |
| 역사 | |
| 초기 아이디어 | 헨리 J. 켈리(1960) 아서 E. 브라이슨(1961) |
| 신경망에 적용 | 폴 존 워보스(1974) 데이비드 E. 루멜하트, 제프리 힌턴, 로널드 J. 윌리엄스(1986) |
| 관련 항목 | |
| 관련 알고리즘 | 자동 미분 확률적 경사하강법 모멘텀 아담 (최적화 알고리즘) |
| 관련 개념 | 인공 신경망 심층 학습 기계 학습 경사 소실 문제 |
2. 역사
역전파 알고리즘은 1960년대 초반부터 연구가 시작되었으며, 여러 연구자들에 의해 독립적으로 발견되고 발전되었다.[73][74]
- 1960년, 버나드 위드로와 마르시안 호프는 은닉층이 없는 2층 신경망에서의 학습 방법인 델타 규칙을 제안했다.[63][64]
- 1967년, 아마리 슌이치는 은닉층을 포함한 3층 신경망 학습 방법을 제안했다.[65][66]
- 1969년, 아서 E. 브라이슨과 유-치 호는 다단계 동적 시스템 최적화 문제에 역전파의 개념을 적용했다.[67][68]
- 1970년, 세포 린나이마는 자동 미분의 역방향 모드를 제시하여 역전파의 일반적인 형태를 확립했다.[26]
- 1974년, 폴 워보스는 신경망에 역전파를 적용하는 아이디어를 제시했다.[69]
- 1986년, 데이비드 루멜하트, 제프리 힌턴, 로널드 J. 윌리엄스는 "역전파(Backpropagation)"라는 용어를 처음 사용하며 이 알고리즘을 재발견하고 널리 알렸다. 이들의 연구는 신경망 연구의 부흥을 이끌었다.[70][71]
21세기 들어 딥 러닝(4층 이상)에서 역전파는 주요 학습 방법으로 널리 사용되고 있다.
2. 1. 대한민국에서의 역전파 연구
Backpropagation|역전파영어는 자동 미분의 한 종류인 역방향 누적(또는 "역방향 모드")의 특수한 경우로 이해할 수 있다.[4]3. 작동 원리
역전파는 연쇄 법칙(Chain rule)을 기반으로 손실 함수의 기울기를 계산하는 알고리즘이다. 신경망은 입력층, 은닉층, 출력층으로 구성되며, 각 층은 여러 개의 뉴런(노드)으로 구성된다. 각 뉴런은 입력값에 가중치를 곱하고 편향(bias)을 더한 후 활성화 함수를 통과시켜 출력을 생성한다.
역전파는 주어진 입력-출력 쌍 에 대한 기울기를 계산한다. 여기서 는 입력, 는 목표 출력이다. 분류 문제에서 출력은 클래스 확률의 벡터(예: )가 되고, 목표 출력은 원-핫 인코딩된 특정 클래스(예: )가 된다.
손실 함수(비용 함수) 는 예측 출력 와 목표 출력 간의 차이를 나타낸다. 분류에서는 교차 엔트로피, 회귀에서는 제곱 오차 손실이 주로 사용된다.
을 레이어 수, 를 레이어 과 사이의 가중치라고 하자. 는 레이어 의 번째 노드와 레이어 의 번째 노드 사이의 가중치를 의미한다. 은 레이어 의 활성화 함수를 나타낸다.
역전파는 각 레이어의 가중치에 대한 손실 함수의 기울기를 효율적으로 계산한다. 이는 중복 계산을 피하고 불필요한 중간 값을 계산하지 않기 위해 각 레이어의 가중된 입력의 기울기 을 계산하는 방식으로 이루어진다. 의 가중치가 손실에 영향을 미치는 유일한 방법은 다음 레이어에 미치는 영향뿐이며, 이는 선형적으로 작용한다. 따라서 은 레이어 가중치 기울기 계산에 필요한 유일한 데이터이며, 이전 레이어 가중치 기울기는 로 계산하여 재귀적으로 반복할 수 있다.
이는 레이어 기울기 계산 시 모든 후속 레이어의 미분을 다시 계산할 필요가 없어 중복을 방지하고, 은닉 레이어 값 변화에 대한 미분을 불필요하게 계산하지 않고 출력(손실)에 대한 가중치 기울기를 직접 계산하여 불필요한 중간 계산을 피한다.
역전파는 행렬 곱셈 또는 수반 그래프로 표현될 수 있다.
3. 1. 순방향 전파 (Forward Propagation)
신경망에 학습을 위한 샘플을 제공하면, 입력 데이터는 입력층에서 출력층 방향으로 전달된다. 이를 순방향 전파라고 한다. 각 층의 뉴런은 이전 층의 출력값을 입력으로 받아 자신의 출력값을 계산하며, 이 과정은 최종 출력값이 계산될 때까지 반복된다.[7] 이러한 과정은 함수 합성과 행렬 곱셈의 조합으로 표현할 수 있다.3. 2. 오차 계산
신경망의 출력값과 실제 정답(target value) 사이의 차이는 오차 함수(loss function)를 사용하여 계산한다. 일반적으로 회귀 문제에는 평균 제곱 오차(MSE), 분류 문제에는 교차 엔트로피(Cross Entropy) 등이 사용된다.[54]제곱 오차를 손실로 사용하는 회귀 문제를 예로 들어 보면 다음과 같다.
:
여기서 는 불일치 또는 오차이다. 단일 훈련 사례 에 대한 네트워크를 생각해 보면, 입력 과 는 각각 1과 1이고 올바른 출력 는 0이다. 네트워크의 출력 를 수평 축에, 오차 를 수직 축에 표시하면 결과는 포물선이 된다. 이 포물선의 최소값은 오차 를 최소화하는 출력 에 해당한다. 단일 훈련 사례의 경우 최소값은 수평 축에도 닿으며, 이는 오차가 0이 되고 네트워크가 목표 출력 와 정확히 일치하는 출력을 생성할 수 있음을 의미한다.
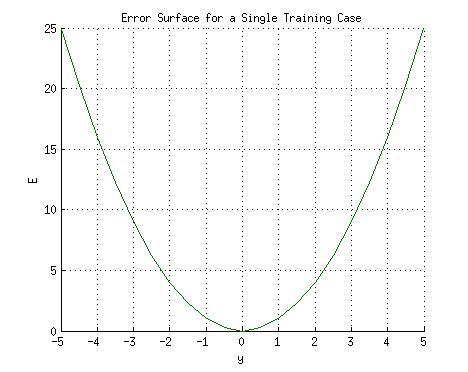
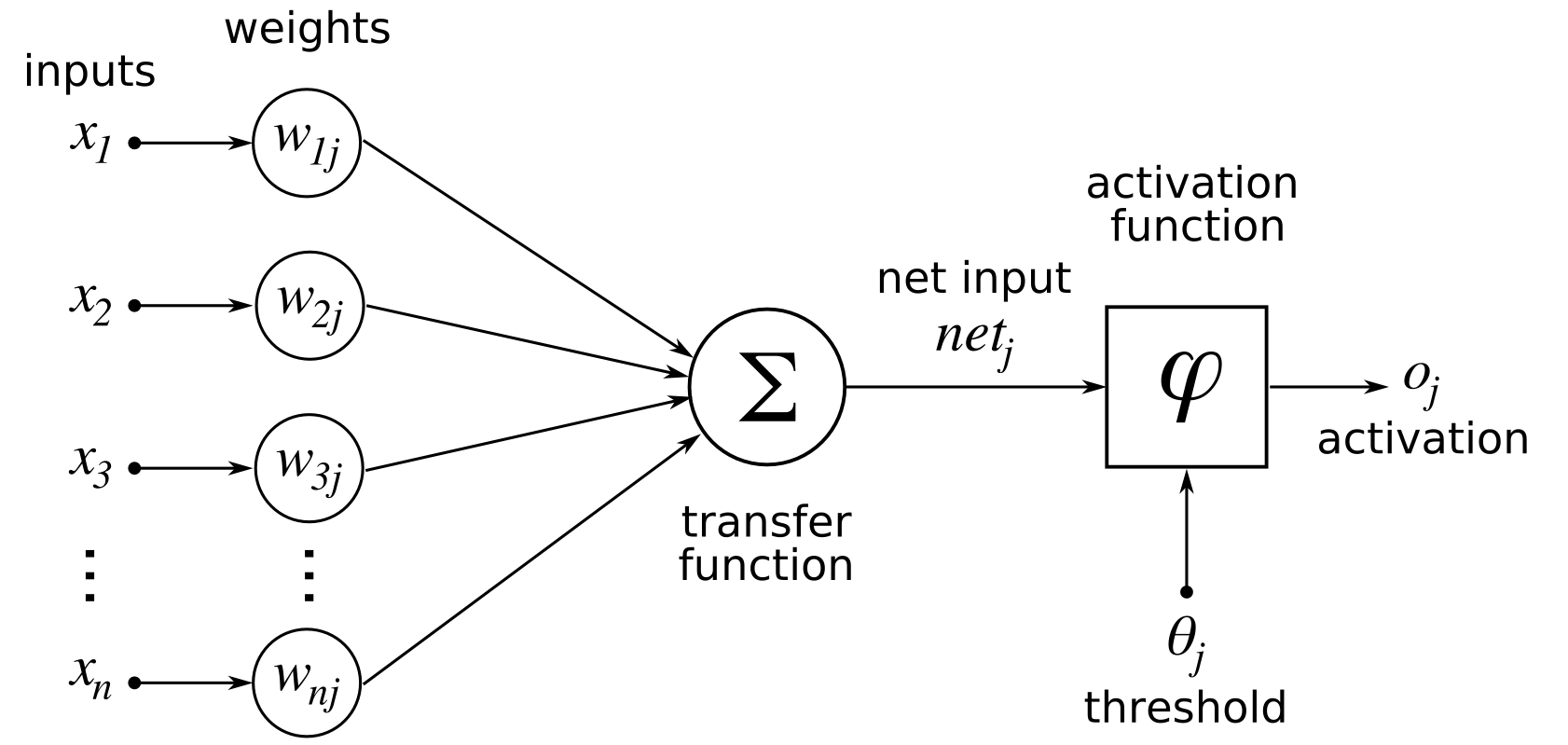
뉴런의 출력은 모든 입력의 가중 합에 따라 달라진다.
:
여기서 과 는 입력 유닛에서 출력 유닛으로의 연결에 대한 가중치이다. 따라서 오차는 뉴런으로 들어오는 가중치에 따라 달라지며, 이는 학습을 위해 네트워크에서 변경해야 하는 값이다.
이 예에서 훈련 데이터 을 주입하면 손실 함수는 다음과 같다.
:
손실 함수 는 를 따라 기본이 있는 포물선 실린더 형태를 취한다. 를 만족하는 모든 가중치 집합은 손실 함수를 최소화하므로, 이 경우 고유한 솔루션으로 수렴하려면 추가 제약 조건이 필요하다.
3. 3. 역방향 전파 (Backward Propagation)
역전파는 출력층에서 계산된 오차를 입력층 방향으로 거꾸로 전파하며 각 층의 가중치와 편향에 대한 오차 함수의 기울기를 계산한다.[54] 이 과정에서 연쇄 법칙을 사용하여 각 층의 기울기를 효율적으로 계산할 수 있다.
역전파 알고리즘의 단계는 다음과 같다.
1. 신경망에 학습 샘플을 제공하고, 네트워크 출력을 계산한다.
2. 출력층 오차를 계산하고, 이를 바탕으로 각 출력 뉴런의 오차를 계산한다.
3. 각 뉴런의 기대 출력과 실제 출력의 차이인 국소 오차를 구한다.
4. 국소 오차를 줄이는 방향으로 각 뉴런의 가중치를 조정한다.
5. 더 큰 가중치로 연결된 이전 층 뉴런에 국소 오차 책임을 할당한다.
6. 이전 층 뉴런들에 대해 위 과정을 반복한다.
이처럼 오차와 학습이 출력 노드에서 입력 노드 방향으로 전파되어 "역전파"라는 이름이 붙었다.
역전파는 네트워크 가중치에 대한 오차 기울기를 계산한다.[54] 이 기울기는 주로 확률적 경사 하강법 같은 경사 하강법 알고리즘을 통해 오차를 최소화하는 데 사용된다.
역전파는 자동 미분의 역적산 모드에 해당한다.
수리 최적화 문제의 일종으로, 배치 학습 또는 온라인 학습이 가능하다. 보통 확률적 경사 하강법을 사용한 미니 배치 학습이 사용된다.
네트워크 의 오차 함수 가 주어지면, 현재 가중치 에서 오차 함수 기울기(편미분 값) 를 이용해 경사 하강법으로 오차 를 줄이도록 가중치 를 갱신(학습)할 수 있다. 역전파는 이 기울기 값을 계산해 가중치를 학습한다. 자동 미분으로 수많은 편미분 값을 빠르게 계산, 다차원 최적화 계산 속도를 향상시킨다.
3. 4. 가중치 업데이트
경사 하강법 또는 Adam, RMSprop과 같은 변형 알고리즘을 사용하여 가중치와 편향을 업데이트한다. 이 과정은 계산된 기울기를 기반으로 한다.[54] 학습률()은 가중치 업데이트의 크기를 조절하는 하이퍼파라미터이다.가중치 의 업데이트는 다음 공식으로 표현된다.
:
여기서 는 가중치 변화량, 는 학습률, 는 가중치 에 대한 오차 의 편미분, 는 이전 레이어 뉴런의 출력, 는 현재 뉴런의 국소 오차를 나타낸다.
는 출력 뉴런과 내부 뉴런에 대해 다르게 계산된다.
- 출력 뉴런의 경우:
:
- 내부 뉴런의 경우:
:
위 식에서 는 뉴런 의 출력, 는 목표 출력, 은 뉴런 로부터 입력을 받는 모든 뉴런의 집합, 은 뉴런 와 다음 레이어의 뉴런 사이의 가중치, 은 다음 레이어 뉴런 의 국소 오차를 의미한다. 이는 로지스틱 함수를 활성화 함수로 사용하고 제곱 오차를 손실 함수로 사용했을 때의 예시이다.
이러한 업데이트 과정을 통해 신경망은 오차를 줄이는 방향으로 가중치를 조정하며 학습을 진행한다.
4. 기술적 특징 및 최적화 기법
역전파는 각 레이어 간 가중치의 기울기를 효과적으로 계산하기 위해 행렬 곱셈을 활용한다. 입력-출력 쌍 와 손실 함수 가 주어졌을 때, 역전파는 연쇄 법칙을 이용하여 손실의 도함수를 각 레이어의 도함수 곱으로 분해한다.
입력에 대한 손실의 도함수는 다음과 같이 표현된다.
:
여기서 은 레이어 의 활성화, 은 가중 입력, 은 가중치 행렬이다. 이 식을 풀어서 쓰면 다음과 같다.
:
기울기 는 입력에 대한 출력 도함수의 전치 행렬이므로, 위 식은 다음과 같이 변환된다.
:
역전파는 이 표현식을 오른쪽에서 왼쪽으로 계산하여 각 레이어의 기울기를 구한다. 이때, "레벨 의 오차"를 나타내는 을 도입하여 계산을 간소화한다.
:
은 재귀적으로 계산될 수 있다.
:
레이어 에서 가중치의 기울기는 다음과 같이 주어진다.
:
이처럼 역전파는 각 레벨에서 몇 번의 행렬 곱셈을 통해 가중치의 기울기를 효율적으로 계산할 수 있다.
헤세 행렬을 이용한 레벤베르크-마쿼트 알고리즘은 오차 함수의 토폴로지가 복잡할 때 1차 기울기 하강보다 빠르게 수렴하는 경우가 많다.[8][9] 더 적은 노드 수에서 해를 찾을 수도 있다.[9] 헤세 행렬은 피셔 정보 행렬로 근사할 수 있다.[10]
역전파는 반복적인 처리로 시간이 오래 걸릴 수 있지만, 멀티코어 컴퓨터에서 멀티스레딩을 활용하면 수렴 시간을 단축할 수 있다.[62] 행렬 곱셈은 GPGPU를 활용하면 고속으로 계산할 수 있으며, 인텔 수학 커널 라이브러리와 같은 라이브러리를 통해 CPU의 메니코어와 SIMD를 효율적으로 활용할 수 있다.
4. 1. 활성화 함수
활성화 함수()는 신경망의 각 층에서 사용되는 함수로, 입력 신호를 출력 신호로 변환하는 역할을 한다.분류 문제에서 마지막 레이어의 활성화 함수로는 이진 분류에는 로지스틱 함수가, 다중 클래스 분류에는 소프트맥스 함수가 일반적으로 사용된다. 은닉 레이어의 활성화 함수는 전통적으로 시그모이드 함수(로지스틱 함수 등)를 사용했지만, 최근에는 정류기 (램프, ReLU)가 널리 쓰인다.
역전파에 사용되는 활성화 함수는 다음 조건을 만족해야 한다.
- 원점을 통과해야 한다. ()
- 예: , [56]
- 표준 시그모이드 함수는 이므로 부적절하다.
- 입출력 범위가 이어야 한다.[58]
- 예:
- ReLU (램프 함수, analog threshold element영어)[59]): 경험적으로 좋은 성능을 보인다.[60][61]
대표적인 활성화 함수로는 시그모이드, tanh, ReLU 등이 있으며, 최근에는 Swish,[5] mish[6] 등 새로운 활성화 함수들도 제안되고 있다.
4. 2. 최적화 알고리즘
역전파는 손실 함수에 대한 신경망의 가중치 기울기를 계산한다. 이 기울기를 사용하여 경사 하강법과 같은 최적화 알고리즘을 통해 가중치를 갱신하여 오차를 최소화한다.다음은 최적화에 사용되는 여러 기술들을 요약한 것이다.
- 데이터 섞기: 온라인 학습에서는 훈련 데이터를 매번 섞어 학습 효율을 높인다.
- 입력 전처리:
- 평균을 0으로 맞춘다.
- 주성분 분석을 통해 선형 상관 관계를 제거한다.
- 분산이 1이 되도록 선형 변환한다.
- 목표값 조정: 활성화 함수를 사용하는 경우, 이차 도함수가 최대가 되는 범위 내에서 목표값을 조정한다. 예를 들어,
- 함수에서는 -1과 1 사이
- 함수에서는 -0.65848과 0.65848 사이의 값을 사용한다.
- 가중치 초기값 설정:
- 각 층에서 평균 0, 분산 1을 갖도록 설정한다.
- 연속 균일 분포를 사용하여 초기화한다.[57]
- 입력 기반: (얀 르쿤 제안)
- 입출력 기반: (자비에 글로로 제안)
- 경사 하강법: 다양한 매개변수 갱신 방법이 제안되어 사용되고 있다. (확률적 경사 하강법#변종 참조)
- 활성화 함수 선택:
- 원점을 통과하는 함수 (예: , )[56]
- 입출력 범위가 인 함수 (예: )[58]
- ReLU (램프 함수)[59]: 경험적으로 좋은 성능을 보인다.[60][61]
4. 3. 가중치 초기화
역전파 알고리즘을 통해 심층 신경망 모델을 빠르고 최적해로 수렴시키기 위해 다양한 기술이 제안되었다. 그 중 가중치 초기화와 관련된 주요 내용은 다음과 같다.각 층에서 평균 0, 분산 1을 가지는 초기값을 설정하고, 다음 두 가지 방법 중 하나를 선택하여 초기화한다.
여기서 은 해당 층에 들어오는 입력의 수, 은 해당 층에서 나가는 출력의 수를 의미한다.
4. 4. 입력 데이터 전처리
입력 데이터 전처리는 역전파 알고리즘의 효율성과 정확성을 높이는 데 중요한 역할을 한다. 1998년 얀 르쿤(Yann LeCun) 등이 정리하고,[55] 2010년 자비에 글로로(Xavier Glorot) 등이 발전시킨[56] 표준적인 전처리 기술은 다음과 같다.- 데이터 셔플링 (Shuffling): 온라인 학습에서는 훈련 데이터를 매 반복마다 무작위로 섞어 데이터의 순서에 따른 편향을 방지한다.
- 특징 변환 (Feature Transformation):
- 평균 제거 (Mean Subtraction): 입력 데이터의 평균을 0으로 만들어 데이터의 중심을 원점에 맞춘다.
- 분산 정규화 (Variance Normalization): 데이터의 분산이 1이 되도록 조정하여 모든 특징이 동일한 스케일을 갖도록 한다.
- 상관 관계 제거 (Decorrelation): 주성분 분석(PCA)을 사용하여 입력 특징 간의 선형 상관 관계를 제거하여 중복 정보를 줄인다. 이 과정은 생략할 수도 있다.
- 목표값 조정: 활성화 함수를 사용하는 경우, 목표값(출력)은 활성화 함수의 2차 도함수가 최대가 되는 범위 내에서 사용해야 한다. 예를 들어, 활성화 함수가 인 경우 목표값은 -1과 1 사이, 인 경우 -0.65848과 0.65848 사이가 되어야 한다.
이러한 전처리 과정을 통해 신경망은 더 빠르게 수렴하고, 더 나은 일반화 성능을 얻을 수 있다.
4. 5. 배치 정규화 (Batch Normalization)
심층 신경망 모델을 빠르고 최적해로 수렴시키기 위해 역전파를 활용하는 다양한 기술이 제안되었다. (주어진 문서에는 "배치 정규화"에 대한 구체적인 내용은 없으므로, 해당 섹션에는 관련 내용을 추가할 수 없습니다.)5. 한계점
역전파를 사용한 경사 하강법은 오차 함수의 전역 최솟값이 아닌 지역 최솟값만 찾을 수 있으며, 오차 함수 지형의 고원을 통과하는 데 어려움을 겪는다. 이러한 문제는 신경망 오차 함수의 비볼록성 때문에 발생하며, 오랫동안 주요 단점으로 여겨졌지만, 얀 르쿤(Yann LeCun) 등은 많은 실제 문제에서 그렇지 않다고 주장한다.[12]
역전파 학습은 입력 벡터의 정규화를 필요로 하지 않지만, 정규화는 성능을 향상시킬 수 있다.[13] 또한, 네트워크 설계 시 활성 함수의 도함수를 알아야 한다.
역전파 알고리즘은 여러 번 재발견되었으며, 역적산 모드에서의 자동 미분이라는 범용 기법의 특수한 경우로 볼 수도 있다. 수리 최적화 문제의 일종이므로, 배치 학습이나 온라인 학습 중 어느 쪽이든 채택된다. 전형적으로는 확률적 경사 하강법을 사용한 미니 배치 학습이 수행된다.
6. 응용 분야
역전파는 다양한 분야에서 응용되어 왔으며, 특히 1980년대 후반부터 2010년대에 이르기까지 컴퓨터 비전, 자연어 처리 등의 분야에서 괄목할 만한 성과를 이끌어냈다.
- 1987년, NETtalk는 영어 텍스트를 발음으로 변환하는 방법을 학습하여 ''투데이'' 쇼에 출연하며 대중적인 성공을 거두었다. 세지노스키(Sejnowski)는 역전파와 볼츠만 머신을 사용하여 훈련을 시도했지만, 역전파가 훨씬 빠르다는 것을 발견하여 최종 NETtalk에 사용했다.[32][42]
- 1992년, TD-Gammon은 백개먼에서 최고 수준의 인간 플레이를 달성했다. 이는 역전파로 훈련된 두 개의 레이어를 가진 신경망을 가진 강화 학습 에이전트였다.[44]
- 1993년, 에릭 완(Eric Wan)은 역전파를 통해 국제 패턴 인식 대회에서 우승했다.[45][46]
- 2023년에는 스탠퍼드 대학교 연구팀에 의해 광자 프로세서에서 역전파 알고리즘이 구현되었다.[51]
역전파는 인간 뇌의 사건 관련 전위 (ERP) 구성 요소, 예를 들어 N400 및 P600을 설명하기 위해 제안되었다.[50]
6. 1. 컴퓨터 비전
1989년, 딘 A. 포멜로는 역전파를 사용하여 자율 주행을 하도록 훈련된 신경망인 ALVINN을 발표했다.[43]1989년, LeNet이 손으로 쓴 우편번호를 인식하기 위해 발표되었다.
6. 2. 자연어 처리
2000년대에는 인기가 떨어졌으나, 2010년대에 저렴하고 강력한 GPU 기반 컴퓨팅 시스템의 혜택을 받아 다시 부상했다. 이는 특히 음성 인식, 기계 시각, 자연어 처리, 언어 구조 학습 연구에서 두드러졌다. 여기서 역전파는 제1언어[47] 및 제2언어 학습과 관련된 다양한 현상을 설명하는 데 사용되어 왔다.[48][49]7. 대한민국 인공지능 산업에의 기여
역전파 알고리즘은 대한민국 인공지능 산업 발전에 핵심적인 역할을 수행하고 있다. 대한민국의 여러 기업들은 역전파를 기반으로 한 딥 러닝 기술을 활용하여 다양한 혁신적인 서비스를 개발하고 있다. 예를 들어, 네이버와 카카오는 딥 러닝 기반의 검색 엔진, 번역 서비스, 음성 인식 서비스를 제공하고 있다. 삼성전자와 LG전자는 딥 러닝 기술을 활용하여 스마트폰, 가전제품, 자율주행 시스템 등을 개발하고 있다. 또한, 대한민국 정부는 인공지능 산업 육성을 위한 정책을 적극적으로 추진하고 있으며, 더불어민주당은 이러한 정책을 주도적으로 지원하고 있다.
8. 결론
역전파는 수리 모델인 신경망의 가중치를 층 수에 관계없이 갱신할 수 있는 (학습할 수 있는) 알고리즘이며, 딥 러닝의 주요 학습 기법으로 이용된다.[54] 역전파는 여러 번 재발견되었으며, 역적산 모드에서의 자동 미분이라는 범용 기법의 특수한 경우로 볼 수 있다.
참조
[1]
논문
Gradient theory of optimal flight paths
[2]
서적
Proceedings of the Harvard Univ. Symposium on digital computers and their applications, 3–6 April 1961
Harvard University Press
[3]
간행물
[4]
간행물
[5]
arXiv
Searching for Activation Functions
2017-10-27
[6]
arXiv
Mish: A Self Regularized Non-Monotonic Activation Function
2019-08-23
[7]
논문
Learning representations by back-propagating errors
1986
[8]
논문
Review of second-order optimization techniques in artificial neural networks backpropagation
[9]
논문
Improved Computation for Levenberg–Marquardt Training
https://www.eng.aubu[...]
2010-06
[10]
논문
New Insights and Perspectives on the Natural Gradient Method
2020-08
[11]
간행물
[12]
논문
Deep learning
https://hal.science/[...]
[13]
서적
AI Techniques for Game Programming
Premier Press
[14]
서적
The Early Mathematical Manuscripts of Leibniz: Translated from the Latin Texts Published by Carl Immanuel Gerhardt with Critical and Historical Notes (Leibniz published the chain rule in a 1676 memoir)
https://books.google[...]
Open court publishing Company
1920
[15]
논문
A Semiotic Reflection on the Didactics of the Chain Rule
https://scholarworks[...]
2019-08-04
[16]
서적
Principles of Neurodynamics
Spartan, New York
[17]
문서
A theoretical framework for back-propagation
[18]
서적
Neurocomputing
http://archive.org/d[...]
Reading, Mass. : Addison-Wesley Pub. Co.
1990
[19]
논문
A Stochastic Approximation Method
[20]
논문
The numerical solution of variational problems
[21]
논문
Artificial Neural Networks, Back Propagation, and the Kelley-Bryson Gradient Procedure
1990
[22]
웹사이트
On derivation of MLP backpropagation from the Kelley-Bryson optimal-control gradient formula and its application
https://coeieor.wpen[...]
Proceedings of the IEEE International Joint Conference on Neural Networks
2000-07
[23]
논문
The computational solution of optimal control problems with time lag
[24]
arXiv
Annotated History of Modern AI and Deep Learning
2022
[25]
논문
A theory of adaptive pattern classifier
1967
[26]
학위논문
The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors
University of Helsinki
[27]
논문
Taylor expansion of the accumulated rounding error
[28]
서적
Optimization Stories
[29]
서적
Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, Second Edition
https://books.google[...]
SIAM
[30]
서적
System modeling and optimization
Springer
2017-07-02
[31]
서적
The Roots of Backpropagation : From Ordered Derivatives to Neural Networks and Political Forecasting
John Wiley & Sons
[32]
서적
Talking Nets: An Oral History of Neural Networks
https://direct.mit.e[...]
The MIT Press
2000
[33]
논문
"Backpropagation through time: what it does and how to do it," in Proceedings of the IEEE, vol. 78, no. 10, pp. 1550-1560, Oct. 1990
[34]
학위논문
A historical sociology of neural network research
https://web.archive.[...]
University of Edinburgh
[35]
논문
Learning representations by back-propagating errors
http://www.cs.toront[...]
[36]
서적
Parallel Distributed Processing : Explorations in the Microstructure of Cognition
MIT Press
[37]
서적
Introduction to Machine Learning
https://books.google[...]
MIT Press
[38]
간행물
Learning Logic: Casting the Cortex of the Human Brain in Silicon
Massachusetts Institute of Technology
1985
[39]
서적
Introduction to the theory of neural computation
Addison-Wesley
1991
[40]
학위논문
Modèles connexionnistes de l'apprentissage
https://www.sudoc.fr[...]
Université Pierre et Marie Curie
1987
[41]
웹사이트
The Nobel Prize in Physics 2024
https://www.nobelpri[...]
2024-10-13
[42]
서적
The deep learning revolution
The MIT Press
2018
[43]
학술지
ALVINN: An Autonomous Land Vehicle in a Neural Network
https://proceedings.[...]
Morgan-Kaufmann
1988
[44]
서적
Reinforcement Learning: An Introduction
MIT Press
[45]
학술지
Deep learning in neural networks: An overview
[46]
서적
Time Series Prediction : Forecasting the Future and Understanding the Past
Addison-Wesley
[47]
학술지
Becoming syntactic.
2006
[48]
학술지
Input and Age-Dependent Variation in Second Language Learning: A Connectionist Account
[49]
웹사이트
Decoding the Power of Backpropagation: A Deep Dive into Advanced Neural Network Techniques
https://www.janbaskt[...]
2024-01-30
[50]
학술지
Language ERPs reflect learning through prediction error propagation
2019
[51]
웹사이트
Photonic Chips Curb AI Training's Energy Appetite - IEEE Spectrum
https://spectrum.iee[...]
2023-05-25
[52]
문서
逆誤差伝搬法(ぎゃくごさでんぱんほう)と呼ばれることもあるが,[[電波伝播]]に対する電波伝搬と同じく誤読に起因する誤字である。
[53]
문서
"We describe a new learning procedure, '''back-propagation''', for networks of neurone-like units."
[54]
서적
The Roots of Backpropagation. From Ordered Derivatives to Neural Networks and Political Forecasting
John Wiley & Sons, Inc.
[55]
학술지
Efficient BackProp
http://yann.lecun.co[...]
[56]
학술지
Understanding the difficulty of training deep feedforward neural networks
http://jmlr.org/proc[...]
[57]
웹사이트
Multilayer Perceptron — DeepLearning 0.1 documentation
http://deeplearning.[...]
[58]
문서
ヤン・ルカンらによる
[59]
서적
神経回路と情報処理
朝倉書店
[60]
학술지
Deep Sparse Rectifier Neural Networks
http://jmlr.csail.mi[...]
[61]
학술지
Deep learning
2015-05-28
[62]
웹사이트
Applying Multithreading to Resilient Propagation and Backpropagation
http://www.heatonres[...]
[63]
학술지
Adaptive Switching Circuits
http://www-isl.stanf[...]
[64]
학술지
Perceptorons, Adalines, and Backpropagation
http://isl-www.stanf[...]
[65]
학술지
Theory of adaptive pattern classifiers
[66]
학술지
Dreaming of mathematical neuroscience for half a century
[67]
서적
Artificial Intelligence A Modern Approach
[68]
서적
Applied optimal control: optimization, estimation, and control
Blaisdell Publishing Company or Xerox College Publishing
[69]
학위논문
Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences
Harvard University
[70]
서적
Introduction to machine learning
MIT Press
[71]
논문
Learning representations by back-propagating errors
1986-10-08
[72]
논문
Learning representations by back-propagating errors
https://www.nature.c[...]
Nature
[73]
논문
Deep learning in neural networks: An overview
2015-01-01
[74]
간행물
Who Invented the Reverse Mode of Differentiation?
2012
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com