인공 뉴런

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 구조
- 2.1. 인공 뉴런
- 2.2. 매컬럭-피츠 뉴런 (McCulloch–Pitts neuron)
3. 생물학적 모델
- 3.1. 부호화 (Encoding)
4. 물리적 인공 세포
5. 활성화 함수
6. 역사
7. 의사 코드 알고리즘
참조

1. 개요

인공 뉴런은 인공신경망의 기본 구성 요소로, 여러 개의 뉴런이 연결된 형태를 갖는다. 각 뉴런은 입력 신호에 가중치를 곱하고, 이를 모두 합산하여 활성화 함수를 거쳐 출력을 내보내는 방식으로 작동한다. 이 모델은 선형 변환과 비선형 변환을 반복하는 것을 의미하며, 생물학적 뉴런을 모방하여 설계되었다. 최초의 인공 뉴런은 1943년에 제안되었으며, 이후 다양한 활성화 함수와 학습 알고리즘이 개발되었다.

더 읽어볼만한 페이지

인공신경망 - 퍼셉트론
퍼셉트론은 프랭크 로젠블랫이 고안한 인공신경망 모델로, 입력 벡터에 가중치를 곱하고 편향을 더한 값을 활성화 함수에 통과시켜 이진 분류를 수행하는 선형 분류기 학습 알고리즘이며, 초기 신경망 연구의 중요한 모델로서 역사적 의미를 가진다.
인공신경망 - 순환 신경망
순환 신경망(RNN)은 시계열 데이터나 순차 데이터 처리에 특화된 인공 신경망으로, 내부 상태를 유지하며 이전 시점의 정보를 반영하여 시퀀스 데이터의 시간적 의존성을 모델링하고, LSTM, GRU 등의 발전과 함께 음성 인식, 기계 번역 등 다양한 분야에서 활용되지만 기울기 소실 문제 해결을 위한 연구가 진행 중이다.
미국의 발명품 - 텔레비전
텔레비전은 움직이는 영상과 소리를 전기 신호로 변환하여 전송하고 수신 측에서 다시 영상과 소리로 바꾸는 기술을 이용한 매체로, 닙코프 원판을 이용한 초기 기계식 방식에서 음극선관 발명을 통해 전자식으로 발전하여 디지털 기술과 다양한 디스플레이 기술 발전을 거쳐 현재에 이르렀으며 사회, 문화, 경제적으로 큰 영향을 미치지만 건강 문제 및 부정적 콘텐츠 노출 등의 부작용도 존재한다.
미국의 발명품 - 태양 전지
태양전지는 빛 에너지를 전기 에너지로 변환하는 장치로, 기술 발전을 거듭하여 발전 효율이 크게 향상되었고 다양한 분야에 응용되고 있으며, 고집광 태양전지와 페로브스카이트 태양전지 등의 새로운 기술 개발과 투자가 지속적으로 요구되는 지속 가능한 에너지원이다.

인공 뉴런
개요
인공 뉴런 모식도
유형	수학적 함수
목적	신경망 모델링 생물학적 뉴런의 동작을 모방
설명	생물학적 뉴런의 단순화된 모델로, 입력 신호를 받아 가중치를 적용하고 활성화 함수를 통해 출력을 생성함
특징
입력	여러 입력 신호 (각각 가중치가 곱해짐)
가중치	각 입력 신호의 중요도를 조절하는 값
합산	가중치가 적용된 입력 신호를 모두 더함
활성화 함수	합산된 결과를 비선형적으로 변환하여 최종 출력 결정
활성화 함수
종류	시그모이드 함수 하이퍼볼릭 탄젠트 함수 ReLU 함수 계단 함수
역할	비선형성 도입 출력 범위 제한 모델 학습 능력 향상
응용 분야
주요 활용	인공 신경망 심층 학습 패턴 인식 기계 학습 제어 시스템
기타	뉴로모픽 컴퓨팅 신경 인터페이스 회로 설계
추가 정보
모델	단순화된 생물학적 뉴런 모델 호지킨-헉슬리 모델과 같은 더 복잡한 모델의 기본 구성 요소
정보 처리	가중치와 활성화 함수를 통해 입력 정보 처리
발전	초기 모델에서 복잡한 모델로 발전
중요성	인공지능 분야의 핵심 구성 요소
제약 사항	생물학적 뉴런의 복잡성을 완전히 반영하지 못함 특정 작업에 대한 과적합 문제 발생 가능성
참고 자료
학술 자료	Rami A. Alzahrani, Alice C. Parker, Neuromorphic Circuits With Neural Modulation Enhancing the Information Content of Neural Signaling A. K. Maan, D. A. Jayadevi, A. P. James, A Survey of Memristive Threshold Logic Circuits F. C. Hoppensteadt and E. M. Izhikevich, Weakly connected neural networks

2. 구조

인공신경망의 기본 구성 요소인 인공 뉴런은 입력 신호에 연결 가중치를 곱하고, 그 값들을 모두 더한 후 활성화 함수를 적용하여 출력을 계산한다. 정보는 연결 가중치 벡터에 저장된다고 볼 수 있다.

인공 뉴런의 출력 y는 다음과 같은 식으로 계산된다.

:

y = f \left ( \sum_{i=1}^n x_n \cdot w_n - \theta \cdot w_0 \right )

여기서 f는 비선형 함수인 활성화 함수(전달 함수)이다. θ는 뉴런의 임계값(threshold) 또는 바이어스(bias)로, Σ(xi·wi) 값이 임계치보다 작을 때 뉴런이 활성화되지 않도록 한다.

인공 뉴런의 구조와 작동 방식에 대한 더 자세한 내용은 #인공 뉴런 및 #매컬럭-피츠 뉴런 (McCulloch–Pitts neuron) 하위 섹션을 참조하면 된다.

2. 1. 인공 뉴런

인공 뉴런은 인간의 사고와 인지에 관심을 가진 인지과학자와 새로운 계산 모형에 관심을 가진 학자들이 신경해부학적 사실을 바탕으로 고안한 처리기(processor)이다. 이는 생물학적 뉴런의 기능을 수학적으로 모델링한 것으로, 단순한 연산 기능을 갖는 수많은 인공 뉴런들이 서로 연결되어 정보를 저장하고 처리하는 기본 개념을 갖고 있다.

주어진 인공 뉴런

k

는

x_0

부터

x_m

까지의 신호와

w_{k0}

부터

w_{km}

까지의 가중치를 갖는

m+1

개의 입력을 받는다. 일반적으로 입력

x_0

에는 +1의 값이 할당되며, 이는

w_{k0} = b_k

인 바이어스 입력이 된다. 따라서 뉴런에는

m

개의 입력(

x_1

부터

x_m

)만 남는다.

k

번째 뉴런의 출력은 다음과 같이 계산된다.

:

y_k = \varphi \left(\sum_{j=0}^m w_{kj} x_j \right)

여기서

\varphi

(phi)는 활성화 함수이다.

출력은 생물학적 뉴런의 축삭돌기와 유사하며, 그 값은 시냅스를 통해 다음 계층의 입력으로 전달된다. 출력 벡터의 일부로 시스템을 빠져나갈 수도 있다.

인공 뉴런 자체는 학습 과정을 가지고 있지 않으며, 활성화 함수의 가중치는 계산되고 임계값은 미리 결정된다.

MCP 뉴런(McCulloch–Pitts neuron)은 제한적인 인공 뉴런의 일종으로, 이산적인 시간 단계에서 동작한다. 각 뉴런은 0개 이상의 입력을 가지며(

x_1, ..., x_n

), 하나의 출력(

y

)을 갖는다. 각 입력은 '흥분성(excitatory)' 또는 '억제성(inhibitory)'일 수 있으며, 출력은 '무반응(quiet)' 또는 '발화(firing)'일 수 있다. MCP 뉴런은 임계값

b \in \{0, 1, 2, ...\}

을 갖는다.

MCP 신경망에서 모든 뉴런은

t = 0, 1, 2, 3, ...

의 동기식 이산 시간 단계에서 동작한다. 시간

t+1

에서 발화하는 흥분성 입력의 수가 임계값 이상이고 억제성 입력이 발화하지 않는 경우 뉴런의 출력은

y(t+1) = 1

이며, 그렇지 않으면

y(t+1)=0

이다.

각 출력은 자기 자신을 포함하여 임의의 수의 뉴런에 대한 입력이 될 수 있지만, 단일 뉴런과 한 번 이상 연결될 수는 없다.

간단한 예로, 임계값이 0이고 단일 억제성 자기 루프를 가진 단일 뉴런은 "시계" 역할을 하며 매 단계마다 0과 1 사이에서 진동한다.

모든 유한 상태 기계는 MCP 신경망으로 시뮬레이션될 수 있으며,^[4] 무한 테이프를 갖춘 MCP 신경망은 모든 튜링 기계를 시뮬레이션할 수 있다.^[5]

뉴런과 수초가 있는 축색돌기. 신호는 수상돌기의 입력에서 축색돌기 종말의 출력으로 흐른다.

인공 뉴런은 생물학적 뉴런의 여러 측면을 모방하도록 설계되었지만, 성능 차이가 존재한다. 특히, XOR 함수를 학습할 수 있는 진동 활성화 함수를 가진 인간 뇌의 단일 생물학적 뉴런이 발견되었다.^[6]

수상돌기: 생물학적 뉴런에서 입력 벡터 역할을 하며, 많은 수의 인접 뉴런으로부터 신호를 받을 수 있게 한다. 각 수상돌기는 "가중치 값"으로 "곱셈"을 수행할 수 있는데, 이는 시냅스 신경 전달 물질에 대한 반응으로 수상돌기에 도입된 신호 화학 물질에 대한 시냅스 신경 전달 물질의 비율을 조절함으로써 이루어진다.
세포체: 생물학적 뉴런에서 합산 함수 역할을 한다. 수상돌기에서 양극 및 음극 신호가 세포체에 도착하면 양이온과 음이온이 혼합되어 효과적으로 합산된다.
축색돌기: 세포체 내부에서 발생하는 합산 동작으로부터 신호를 받아 다른 인공 뉴런에 연결하는 기능을 한다. 세포체가 특정 전위에 도달하면 축색돌기는 전체 신호 펄스를 전달한다.

대부분의 인공 뉴런과 달리 생물학적 뉴런은 불연속 펄스로 발화한다. 세포체 내부의 전기적 전위가 특정 임계값에 도달하면 펄스가 축색돌기를 따라 전달되며, 이러한 펄싱은 연속적인 값으로 변환될 수 있다.

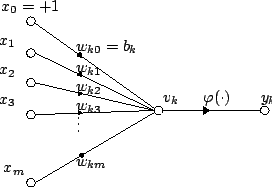
잘 연구된 인공뉴런의 한 유형은 다음과 같다.

m개의 입력(

x_1

부터

x_m

), 가중치(

w_1

부터

w_m

), 바이어스 항(

b

), 활성화 함수(

\varphi

)를 사용한다.

k번째 인공 신경의 출력은 다음과 같이 표현된다.

:

y_k =  \varphi_k \left( \sum_{i=1}^m w_{ki} x_i + b_k \right)

개략도는 다음과 같다.

:400px

이 모델은 선형 변환과

\varphi

(비선형을 포함한 어떤 변환)을 번갈아 반복하는 것을 의미하며, 어떤 임의의 함수 변환도 표현할 수 있다.

2. 2. 매컬럭-피츠 뉴런 (McCulloch–Pitts neuron)

MCP 뉴런(McCulloch–Pitts neuron)은 1943년 워런 매컬럭과 월터 피츠가 제안한 초기 인공신경망 모델이다.^[4] MCP 뉴런은 이산적인 시간 단계에서 동작하는 제한적인 인공 뉴런의 일종으로, 각 뉴런은 0개 이상의 입력(

x_1, ..., x_n

)과 하나의 출력(

y

)을 갖는다. 각 입력은 '흥분성(excitatory)' 또는 '억제성(inhibitory)'일 수 있으며, 출력은 '무반응(quiet)' 또는 '발화(firing)'일 수 있다. 또한 MCP 뉴런은 임계값

b \in \{0, 1, 2, ...\}

을 갖는다.

MCP 신경망에서 모든 뉴런은

t = 0, 1, 2, 3, ...

와 같이 동기화된 이산 시간 단계에서 동작한다. 시간

t+1

에서, 발화하는 흥분성 입력의 수가 임계값 이상이고 억제성 입력이 발화하지 않는 경우 뉴런의 출력은

y(t+1) = 1

이 되고, 그렇지 않으면

y(t+1)=0

이 된다.

각 뉴런의 출력은 자기 자신을 포함하여 임의의 수의 뉴런에 대한 입력이 될 수 있다(즉, 자기 루프 허용). 그러나 출력은 단일 뉴런과 한 번 이상 연결될 수 없다. 신경망이 동기식 이산 시간 단계에서 동작하므로 자기 루프는 모순을 일으키지 않는다.

임계값이 0이고 단일 억제성 자기 루프를 가진 단일 뉴런의 경우, 그 출력은 "시계"처럼 매 단계마다 0과 1 사이를 오간다.

모든 유한 상태 기계는 MCP 신경망으로 시뮬레이션될 수 있으며,^[4] 무한 테이프를 갖춘 MCP 신경망은 모든 튜링 기계를 시뮬레이션할 수 있다.^[5]

매컬럭과 피츠의 제안은 생물학적 신경 세포 모방보다는 계산 이론에서의 계산 모델로서의 성질을 검토하는 데 중점을 두었다.

3. 생물학적 모델

인공 뉴런은 생물학적 뉴런의 여러 측면을 모방하도록 설계되었지만, 둘 사이에는 상당한 성능 차이가 존재한다. 예를 들어, XOR 함수를 학습할 수 있는 진동 활성화 함수를 가진 인간 뇌의 단일 생물학적 뉴런이 발견되었다.^[6]

생물학적 뉴런의 주요 구성 요소는 다음과 같다.

수상돌기: 입력 벡터 역할을 하며, 수많은 인접 뉴런으로부터 신호를 받을 수 있게 한다. 각 수상돌기는 "가중치 값"으로 "곱셈"을 수행할 수 있는데, 이는 시냅스 신경 전달 물질의 비율을 조절하여 이루어진다. 음의 곱셈 효과는 신호 억제제를 전달함으로써 가능하다.
세포체: 수상돌기에서 들어오는 양극 및 음극 신호(흥분성 및 억제성)를 합산하는 역할을 한다. 세포체 내 용액에 양이온과 음이온이 혼합되면서 신호가 합산된다.
축색돌기: 세포체에서 합산된 신호를 받아 다른 뉴런으로 전달하는 역할을 한다. 세포체가 특정 전위에 도달하면 축색돌기는 전체 신호 펄스를 전달한다.

대부분의 인공 뉴런과 달리 생물학적 뉴런은 불연속 펄스로 발화한다. 세포체 내부의 전기적 전위가 특정 임계값에 도달하면 펄스가 축색돌기를 따라 전달된다. 이러한 펄스 빈도는 인접 세포에 신호 이온이 도입되는 속도로 변환될 수 있다. 이러한 변환 덕분에 컴퓨터 과학자와 수학자들은 생물학적 신경망을 시뮬레이션할 수 있게 되었다.

매컬럭은 1943년 인공신경망 연구의 시초로 여겨지는 논문 "신경 활동에 내재된 사상의 논리적 계산(A Logical Calculus of the Ideas Immanent in Nervous Activity)"의 공저자 중 한 명이다. 그는 신경생리학자였지만, 그들의 제안은 생물 신경 세포를 모방하기보다는 계산 이론에서 계산 모델로서의 성질을 검토하는 데 있었다.

이후 1957년에 제안된 퍼셉트론이나, 결합주의 연구가 확산되었지만, 생물학적 실제 신경 세포 모델인지에 대한 의문은 인지과학 등에서 지속적으로 제기되었다. 그러나 "소뇌 퍼셉트론설"과 같은 가설이 지지되는 등, 2020년 현재로서는 완전히 무관하지 않다는 것이 일반적인 견해이다.

3. 1. 부호화 (Encoding)

연구에 따르면 일진법 코딩이 새소리 생성을 담당하는 신경 회로에서 사용된다는 것이 밝혀졌다.^[7]^[8] 생물학적 네트워크에서 일진법이 사용되는 것은 이 코딩의 고유한 단순성 때문일 것이다. 또 다른 요인으로는 일진법 코딩이 어느 정도의 오류 수정 기능을 제공한다는 점을 들 수 있다.^[9]

4. 물리적 인공 세포

일부 인공 신경 세포는 도파민(전기 신호가 아닌 신경 전달 물질)을 수용 및 방출하고 자연 쥐 근육 및 뇌세포와 통신할 수 있으며, 뇌-컴퓨터 인터페이스(BCI)/보철에 사용될 가능성이 있다.^[1]

저전력 생체 적합성 멤리스터는 생물학적 활동 전위의 전압에서 작동하는 인공 신경 세포를 구축하는 데 사용될 수 있으며, 신경 형태 컴퓨팅 및/또는 생물학적 신경 세포와의 직접 통신을 위해 생체 센싱 신호를 직접 처리하는 데 사용될 수 있다.^[2]

폴리머로 만들어지고 이온이 풍부한 젤로 코팅되어 실제 신경 세포처럼 전하를 운반할 수 있는 유기적 신경 형태 회로는 로봇에 내장되어 시뮬레이션이나 가상 환경이 아닌 실제 세계에서 감각 운동 학습을 가능하게 했다.^[3] 또한, 연성 물질(폴리머)로 만들어진 인공 스파이킹 신경 세포는 생물학적으로 관련된 환경에서 작동할 수 있으며 인공 영역과 생물학적 영역 간의 시너지 효과를 낼 수 있는 통신을 가능하게 한다.^[4]

5. 활성화 함수

인공신경망에서 인공 뉴런은 입력 신호에 연결 가중치를 곱하고 그 값들을 더한 뒤, 비선형 함수를 적용한다. 여기서 사용되는 비선형 함수 f를 '''활성함수'''(activation function) 또는 '''전달함수'''(transfer function)라고 부른다. 활성화 함수는 네트워크의 성능을 향상시키거나 단순화하는 속성을 가지도록 선택된다. 예를 들어, 선형 활성화 함수만 사용하는 다층 퍼셉트론은 단일 계층 네트워크와 동일하기 때문에, 다층 네트워크의 장점을 얻기 위해서는 비선형 함수가 필요하다.

뉴런의 활성화 함수는 입력 신호의 가중치 합에 적용된다. n개의 입력에 대한 가중치 합 u는 다음과 같이 계산된다.

: $u = \sum_{i=1}^n w_i x_i$

여기서 w는 가중치 벡터, x는 입력 벡터이다.

m개의 입력을 받는 k번째 인공 뉴런의 출력은 활성화 함수 φ를 사용하여 다음과 같이 표현된다.

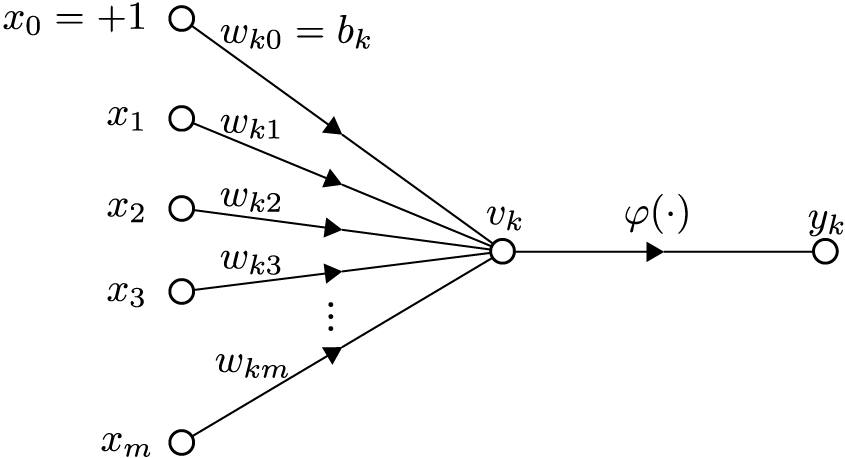
: $y_k = \varphi_k \left( \sum_{i=1}^m w_{ki} x_i + b_k \right)$

이 모델은 선형 변환과 비선형 변환 φ를 번갈아 반복하여, 어떤 임의의 함수 변환도 표현할 수 있다.

5. 1. 계단 함수 (Step function)

인공신경망을 구성하는 인공 뉴런은 입력 신호에 연결 가중치를 곱하고 그 값들을 더한 뒤 비선형 함수를 적용하는데, 이때 쓰이는 함수를 '''활성함수''' 또는 '''전달함수'''라고 한다. 활성화 함수의 출력

y

는 입력이 특정 임계값

\theta

(세타)를 넘는지에 따라 결정된다. 임계값을 넘으면 출력이 1이 된다.

:

y = \begin{cases} 1 & \text{if }u \ge \theta \\ 0 & \text{if }u < \theta \end{cases}

이 함수는 퍼셉트론에서 사용되며, 공간을 초평면으로 나누어 입력을 이진 분류하는 네트워크의 마지막 계층에서 유용하다.

5. 2. 선형 결합 (Linear combination)

인공 뉴런은 입력 신호

x_1

부터

x_m

까지에 각각의 가중치

w_1

부터

w_m

까지를 곱한 값을 모두 더하고, 여기에 바이어스 항

b

를 더한다. 이러한 연산을 선형 결합이라고 한다. k번째 인공 뉴런의 출력(

y_k

)은 다음과 같이 표현된다.

:

y_k =  \varphi_k \left( \sum_{i=1}^m w_{ki} x_i + b_k \right)

여기서

\varphi

는 활성화 함수를 나타낸다.

여러 선형 뉴런은 입력 벡터에 대한 선형 변환을 수행하며, 조화 분석과 같이 선형 모델을 기반으로 하는 분석 도구를 사용할 수 있다. 바이어스 항은 데이터에 대한 아핀 변환을 가능하게 한다.^[1]

5. 3. 시그모이드 함수 (Sigmoid function)

활성함수의 일종인 시그모이드 함수는 로지스틱 함수와 같이 비교적 단순한 비선형 함수이며, 미분값을 쉽게 계산할 수 있다는 장점이 있다. 이는 네트워크에서 가중치 업데이트를 계산할 때 중요하며, 네트워크를 수학적으로 더욱 쉽게 조작할 수 있게 해준다. 따라서 시뮬레이션의 계산 부하를 최소화해야 했던 초기 컴퓨터 과학자들에게 매력적인 선택지였다. 이전에는 다층 퍼셉트론에서 흔히 사용되었다. 그러나 최근 연구에 따르면 시그모이드 뉴런은 렐루(Rectified Linear Unit) 뉴런보다 효과가 떨어지는 것으로 나타났다. 그 이유는 역전파 알고리즘에 의해 계산된 기울기가 시그모이드 뉴런의 층을 통과하면서 0에 가까워지는 경향이 있어, 여러 층의 시그모이드 뉴런을 사용하는 신경망을 최적화하기 어렵기 때문이다.

5. 4. 렐루 (ReLU, Rectified Linear Unit)

인공 신경망에서 '''렐루'''(ReLU, Rectified Linear Unit, 정류 선형 유닛)는 입력 값의 양수 부분으로 정의되는 활성화 함수이다.

:

f(x) = x^+ = \max(0, x),

여기서

x

는 뉴런의 입력이다. 이것은 램프 함수로도 알려져 있으며, 전기 공학의 반파 정류와 유사하다. 이 활성화 함수는 2000년 Hahnloser 등이 ''네이처''^[25]에 발표한 논문에서 강력한 생물학적 동기와 수학적 정당성^[26]을 바탕으로 동적 네트워크에 처음 소개되었다. 2011년에는 로지스틱 시그모이드와 쌍곡탄젠트보다 깊은 네트워크 학습을 향상시키는 것으로 입증되었다.^[27]^[28]

ReLU 활성화 함수의 변형으로, 유닛이 활성화되지 않을 때 작은 양수 기울기를 허용하는 Leaky ReLU가 있다.

:

f(x) = \begin{cases}x & \text{if } x > 0, \\ax & \text{otherwise}.\end{cases}

여기서

x

는 뉴런의 입력이고

a

는 작은 양수 상수(원 논문에서는 0.01로 설정)이다.^[29]

6. 역사

1943년 워런 매컬럭과 월터 피츠는 "신경 활동에 내재된 사상의 논리적 계산(A logical calculus of the ideas immanent in nervous activity)"^[21]에서 최초의 인공 뉴런 모델인 임계 논리 단위(TLU) 또는 선형 임계 단위를 제안했다.^[22] 이 모델은 뇌의 "신경망"에 대한 계산 모델을 목표로 했으며, 활성화 함수로는 헤비사이드 계단 함수와 동등한 임계값을 사용했다. 초기에는 이진 입력 및 출력, 가중치 제약, 유연한 임계값을 가진 단순한 모델만 고려되었다. 그러나 AND 함수와 OR 함수를 구현하고, 이들을 합취적 또는 결합 표준 형식에서 사용하여 모든 부울 함수를 이러한 장치 네트워크로 구현할 수 있다는 점이 이미 알려졌다.

연구자들은 뉴런을 통한 피드백을 가진 순환 네트워크가 메모리를 가진 동적 시스템을 정의할 수 있다는 것을 곧 깨달았지만, 대부분의 연구는 더 쉬운 순전파 네트워크에 집중되었다.

프랭크 로젠블랫이 개발한 퍼셉트론은 선형 임계 함수를 사용한 중요하고 선구적인 인공 신경망 중 하나이다. 이 모델은 뉴런에서 더 유연한 가중치 값을 고려했으며, 적응 능력을 가진 기계에 사용되었다. 1960년 버나드 위드로는 임계값을 바이어스 항으로 표현하는 방법을 소개했다. ( ADALINE 참조)

1980년대 후반, 신경망 연구가 다시 활기를 띠면서 더 연속적인 형태의 뉴런이 고려되기 시작했다. 활성화 함수를 미분할 수 있다는 것은 가중치 조정을 위해 경사 하강법 및 기타 최적화 알고리즘을 직접 사용할 수 있게 했다. 신경망은 또한 일반적인 함수 근사 모델로 사용되기 시작했다. 가장 잘 알려진 훈련 알고리즘인 역전파는 여러 번 재발견되었지만, 최초 개발은 폴 워보스의 연구로 거슬러 올라간다.^[23]^[24]

7. 의사 코드 알고리즘

다음은 단일 임계값 논리 유닛(TLU)의 간단한 의사 코드 구현이다.^[1] 이는 부울 입력(참 또는 거짓)을 받아 활성화될 때 단일 부울 출력을 반환한다. 객체 지향 모델이 사용된다.

'''클래스''' TLU '''정의:'''

'''데이터 멤버''' 임계값 '':'' 숫자
'''데이터 멤버''' 가중치 '':'' 크기가 X인 숫자의 '''목록'''

'''함수 멤버''' fire(입력 '':'' 크기가 X인 부울의 '''목록''') '':'' 부울 '''정의:'''
* '''변수''' T '':'' 숫자
* T '''←''' 0
* '''각''' i '''에 대해''' 1 '''부터''' X '''까지'''
** '''만약''' 입력(i) '''이''' 참 '''이라면'''

T '''←''' T + 가중치(i)

** '''만약 끝'''
* '''각 끝'''
* '''만약''' T > 임계값 '''이라면'''
** '''반환''' 참
* '''그렇지 않으면:'''
** '''반환''' 거짓
* '''만약 끝'''
'''함수 끝'''

'''클래스 끝'''

참조

_[1] 논문 Neuromorphic Circuits With Neural Modulation Enhancing the Information Content of Neural Signaling Association for Computing Machinery
_[2] 논문 A Survey of Memristive Threshold Logic Circuits 2016-01-01
_[3] 서적 Weakly connected neural networks Springer
_[4] 서적 Computation: Finite and Infinite Machines Prentice Hall 1967-01-01
_[5] 논문 A logical calculus of the ideas immanent in nervous activity https://doi.org/10.1[...] 1943-12-01
_[6] 논문 Dendritic action potentials and computation in human layer 2/3 cortical neurons 2020-01-03
_[7] 서적 Neural network models of birdsong production, learning, and coding https://clm.utexas.e[...] Elservier 2015-04-12
_[8] 논문 Motor pathway convergence predicts syllable repertoire size in oscine birds
_[9] 논문 Error Correction Capacity of Unary Coding 2014-11-26
_[10] 뉴스 Making computer chips act more like brain cells https://knowablemaga[...] 2022-08-25
_[11] 논문 A biohybrid synapse with neurotransmitter-mediated plasticity https://research.tue[...] 2020-09-01
_[11] 뉴스 Researchers develop artificial synapse that works with living cells https://medicalxpres[...] 2022-09-23
_[12] 뉴스 Artificial neuron swaps dopamine with rat brain cells like a real one https://www.newscien[...] 2022-09-16
_[13] 논문 A chemically mediated artificial neuron https://www.research[...] 2022-08-08
_[14] 뉴스 Scientists create tiny devices that work like the human brain https://www.independ[...] 2020-04-20
_[15] 뉴스 Researchers unveil electronics that mimic the human brain in efficient learning https://phys.org/new[...] 2020-05-17
_[16] 논문 Bioinspired bio-voltage memristors 2020-04-20
_[17] 뉴스 Lego Robot with an Organic 'Brain' Learns to Navigate a Maze https://www.scientif[...] 2022-02-01
_[18] 논문 Organic neuromorphic electronics for sensorimotor integration and learning in robotics 2021-12-01
_[19] 논문 An organic artificial spiking neuron for in situ neuromorphic sensing and biointerfacing 2022-11-07
_[20] 논문 Artificial neurons emulate biological counterparts to enable synergetic operation https://www.nature.c[...] 2022-11-10
_[21] 서적 Discrete Mathematics of Neural Networks: Selected Topics https://books.google[...] SIAM 2001-01-01
_[22] 서적 Data Classification: Algorithms and Applications https://books.google[...] CRC Press 2014-07-25
_[23] 논문 Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences Harvard University
_[24] 논문 Backpropagation through time: what it does and how to do it https://zenodo.org/r[...]
_[25] 논문 Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit
_[26] 논문 Permitted and Forbidden Sets in Symmetric Threshold-Linear Networks
_[27] 논문 Deep sparse rectifier neural networks http://jmlr.org/proc[...]
_[28] 백과사전 Efficient BackProp http://yann.lecun.co[...] Springer
_[29] 논문 Rectifier Nonlinearities Improve Neural Network Acoustic Models https://ai.stanford.[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com