폰 망골트 함수

3. 성질

폰 망골트 함수는 수론적 함수이지만, 곱셈적 함수는 아니다. 산술의 기본 정리에 의해 다음이 성립한다.^[1]

:$\backslash log\; n\; =\; \backslash sum\_\{d|n\}\; \backslash Lambda(d)$

예를 들어 $n=12=2^2\; \backslash times\; 3$인 경우를 들 수 있다.

체비쇼프 함수는 폰 망골트 함수를 이용하여 간단하게 정의할 수 있다.^[5]

:$\backslash psi(x)\; =\; \backslash sum\_\{n\; \backslash le\; x\}\; \backslash Lambda(n)$

모든 $x\; \backslash ge\; 1$에 대해 다음이 성립한다.

:$\backslash sum\_\{n\backslash le\; x\}\backslash frac\{\backslash Lambda(n)\}\{n\}=\backslash log\; x+O(1).$

3. 1. 뫼비우스 반전 공식과의 관계

4. 디리클레 급수와의 관계

폰 망골트 함수는 디리클레 급수 이론, 특히 리만 제타 함수에서 중요한 역할을 한다. 예를 들어, 리만 제타 함수의 로그는 다음과 같은 디리클레 급수로 표현할 수 있다. (Re(s) > 1)

:$\backslash log\; \backslash zeta(s)=\backslash sum\_\{n=2\}^\backslash infty\; \backslash frac\{\backslash Lambda(n)\}\{\backslash log(n)\}\backslash ,\backslash frac\{1\}\{n^s\}$

리만 제타 함수의 로그 도함수는 다음과 같다.^[6][17]

:$\backslash frac\; \{\backslash zeta^\backslash prime(s)\}\{\backslash zeta(s)\}\; =\; -\backslash sum\_\{n=1\}^\backslash infty\; \backslash frac\{\backslash Lambda(n)\}\{n^s\}.$

4. 1. 일반적인 디리클레 급수와의 관계

5. 체비쇼프 함수

파프누티 체비쇼프가 소개한 두 번째 체비쇼프 함수 ''ψ''(''x'')는 폰 망골트 함수의 총합 함수이다.^[7]

:$\backslash psi(x)\; =\; \backslash sum\_\{p^k\backslash le\; x\}\backslash log\; p=\backslash sum\_\{n\; \backslash leq\; x\}\; \backslash Lambda(n)\; \backslash \; .$

이 함수는 소수 계량 함수 $\backslash pi(x)$의 정확한 순서가 $x/\backslash log\; x$임을 보이는 데 사용되었다. 폰 망골트는 리만 제타 함수의 비자명 영점들의 합을 포함하는 ''ψ''(''x'')에 대한 명시적 공식의 엄밀한 증명을 제공했는데, 이는 소수 정리의 첫 번째 증명의 중요한 부분이었다.

체비쇼프 함수의 멜린 변환은 페론 공식을 적용하여 구할 수 있다.

:$\backslash frac\{\backslash zeta^\backslash prime(s)\}\{\backslash zeta(s)\}\; =\; -\; s\backslash int\_1^\backslash infty\; \backslash frac\{\backslash psi(x)\}\{x^\{s+1\}\}\backslash ,dx$

이는 $Re(s)\; >\; 1$에 대해 성립한다.^[18]

6. 지수 급수

하디와 리틀우드는 다음 급수를 연구했다.^[8][19]

:$F(y)=\backslash sum\_\{n=2\}^\backslash infty\; \backslash left(\backslash Lambda(n)-1\backslash right)\; e^\{-ny\}$

극한에서. 리만 가설을 가정하면, 그들은 다음을 증명했다.

:$F(y)=O\backslash left(\backslash frac\{1\}\{\backslash sqrt\{y\}\}\backslash right)\backslash quad\; \backslash text\{and\}\backslash quad\; F(y)=\backslash Omega\_\backslash pm\backslash left(\backslash frac\{1\}\{\backslash sqrt\{y\}\}\backslash right)$

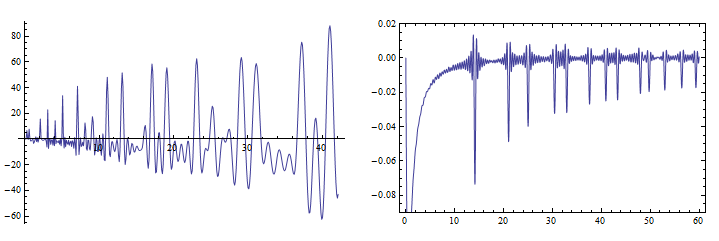
특히 이 함수는 발산하는 진동과 함께 진동한다. 즉, 다음 부등식이 모두 성립하는 값이 존재한다.

:

0의 모든 근방에서 무한히 자주. 오른쪽 그림은 이러한 동작이 처음에는 수치적으로 명확하지 않다는 것을 나타낸다. 즉, 급수가 1억 개 이상의 항으로 합산될 때까지 진동이 명확하게 보이지 않으며, 일 때만 쉽게 볼 수 있다.

7. 리스 평균

폰 망골트 함수의 리스 평균은 다음과 같이 주어진다.

:$\backslash begin\{align\}$

\sum_{n\le \lambda} \left(1-\frac{n}{\lambda}\right)^\delta \Lambda(n) &= -\frac{1}{2\pi i} \int_{c-i\infty}^{c+i\infty}

\frac{\Gamma(1+\delta)\Gamma(s)}{\Gamma(1+\delta+s)} \frac{\zeta^\prime(s)}{\zeta(s)} \lambda^s ds \\

&= \frac{\lambda}{1+\delta} + \sum_\rho \frac{\Gamma(1+\delta)\Gamma(\rho)}{\Gamma(1+\delta+\rho)} + \sum_n c_n \lambda^{-n}.

\end{align}

여기서, $\backslash lambda$와 $\backslash delta$는 리스 평균을 특징짓는 숫자이다. $c\; >\; 1$이어야 한다. $\backslash rho$에 대한 합은 리만 제타 함수의 영점에 대한 합이며,

:$\backslash sum\_n\; c\_n\; \backslash lambda^\{-n\}\backslash ,$

는 $\backslash lambda\; >\; 1$에 대해 수렴하는 급수로 나타낼 수 있다.

8. 리만 제타 함수의 영점을 이용한 근사

참조

_[1] 서적 Apostol (1976) p.32
_[2] 서적 Tenenbaum (1995) p.30
_[3] 서적 Apostol (1976) p.33
_[4] 서적 Number theory in science and communication. With applications in cryptography, physics, digital information, computing, and self-similarity Springer-Verlag
_[5] 서적 Apostol (1976) p.88
_[6] 서적 Hardy & Wright (2008) §17.7, Theorem 294
_[7] 서적 Apostol (1976) p.246
_[8] 학술지 Contributions to the Theory of the Riemann Zeta-Function and the Theory of the Distribution of Primes http://www.ift.uni.w[...] 2014-07-03
_[9] 학술지 The Riemann hypothesis http://www.ams.org/n[...] 2003-03
_[10] 기타 E. Landau, Über die Nullstellen der Zetafunktion, Math. Annalen 71 (1911 ), 548-564.
_[11] 간행물 Opera de cribro American Mathematical Society 2010
_[12] 서적 Apostol (1976) p.32
_[13] 서적 Tenenbaum (1995) p.30
_[14] 서적 Tenenbaum (1995) p.30
_[15] 서적 Apostol (1976) p.33
_[16] 서적 Number theory in science and communication. With applications in cryptography, physics, digital information, computing, and self-similarity Springer-Verlag
_[17] 서적 Hardy & Wright (2008) §17.7, Theorem 294
_[18] 서적 Apostol (1976) p.246
_[19] 학술지 Contributions to the Theory of the Riemann Zeta-Function and the Theory of the Distribution of Primes http://www.ift.uni.w[...] 2014-07-03
_[20] 학술지 The Riemann hypothesis http://www.ams.org/n[...] 2003-03