맨위로가기

포획 이온 양자컴퓨터

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

포획 이온 양자 컴퓨터는 전자기장으로 이온을 가두어 양자 정보를 저장하고 처리하는 방식으로 작동한다. 1995년 제어-NOT 게이트 구현 방식이 제안된 이후, 이온 트랩 기술은 양자 계산 분야의 주요 후보로 발전해 왔다. 파울 이온 트랩은 대전 입자를 가두는 데 사용되며, 큐비트 초기화, 측정, 단일 큐비트 회전, 2 큐비트 얽힘 게이트와 같은 양자 계산의 핵심 요건을 충족해야 한다. 확장 가능한 트랩 설계를 통해 큐비트 수를 늘릴 수 있지만, 결어긋남과 같은 구현 과제가 존재한다. 한국에서는 2020년대 초부터 정부 주도로 이온 트랩 양자 컴퓨터 연구가 활발히 진행되고 있다.

더 읽어볼만한 페이지

  • 양자정보과학 - 양자 컴퓨터
    양자 컴퓨터는 양자역학적 현상을 이용하여 정보를 처리하는 컴퓨터로, 큐비트를 통해 0과 1을 동시에 표현하여 특정 연산에서 기존 컴퓨터보다 빠른 속도를 보이며 암호 해독, 신약 개발 등 다양한 분야에 혁신을 가져올 것으로 기대된다.
  • 양자정보과학 - 벨 부등식
    벨 부등식은 양자역학과 국소적 숨은 변수 이론의 모순을 보이는 부등식으로, 실험 결과는 벨 부등식의 위반을 통해 양자역학의 비국소성을 시사하며 양자 정보 과학에 중요한 함의를 가진다.
포획 이온 양자컴퓨터
기본 정보
이온 트랩 양자 컴퓨터의 다이어그램
이온 트랩 양자 컴퓨터의 다이어그램
유형양자 컴퓨터
비트 유형큐비트
큐비트 기술이온 트랩
세부 정보
설명전자기장을 사용하여 개별적으로 대전된 이온을 가두고 조작하여 양자 정보를 저장하는 양자 컴퓨터이다.
구현
특징높은 충실도
긴 코히어런스 시간
모든 대 모든 연결
일반적인 이온이트륨
바륨
칼슘
수은
마그네슘
스트론튬
인듐
개발 중인 기술CCD 양자 컴퓨터
이온 트랩 위에 금속-절연체-금속 장치를 통합
주요 개발 및 연구 그룹
연구 그룹인스브루크 대학교
미시간 대학교
메릴랜드 대학교
옥스포드 대학교
아이온큐
하니웰 양자 솔루션
샌디아 국립 연구소
라이퀴스
아르곤 국립 연구소
참고 자료
참고양자 컴퓨팅
양자 컴퓨터
큐비트
이온 트랩

2. 역사

1995년, 이그나시오 시라크와 페터 촐러는 제어-NOT 양자 게이트의 첫 번째 구현 방식을 제안했는데,[2] 특히 포획 이온 시스템에 적합했다. 같은 해, 제어-NOT 게이트의 핵심 단계가 국립 표준 기술 연구소(NIST) 이온 저장 그룹에서 실험적으로 구현되었고, 양자 컴퓨팅 연구가 전 세계적으로 시작되었다.[26]

380px


2021년, 인스브루크 대학교 연구원들은 두 개의 19인치 서버 랙 안에 들어가는 양자 컴퓨팅 데몬스트레이터를 발표했는데, 이는 세계 최초의 품질 기준을 충족하는 소형 포획 이온 양자 컴퓨터였다.[3][4]

지난 10년간 이온 트랩은 양자 계산의 주요 후보로 남아있을 정도로 엄청난 발전을 이루었다.

한국에서는 2020년대 초부터 정부 주도의 양자 컴퓨팅 연구 개발 투자가 본격화되면서, 이온 트랩 양자 컴퓨터 연구가 활발히 진행되고 있다.

3. 파울 이온 트랩

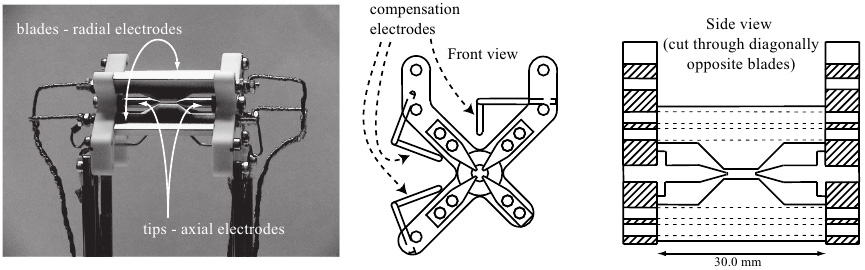
볼프강 파울이 1950년대에 발명한 전기역학적 이온 트랩은 포획된 이온 양자컴퓨팅 연구에 사용된다.[47] 언쇼 정리에 따라 대전 입자는 정전기력만으로는 3차원 공간에 포획될 수 없다. 따라서 무선 주파수(RF)에서 진동하는 전기장이 적용되어 회전하는 안장 형태의 퍼텐셜을 형성한다. 적절한 파라미터를 갖는 RF 장에서 대전 입자는 복원력에 의해 안장점에서 매튜 방정식으로 기술되는 운동을 하며 효율적으로 포획된다.[48]

일련의 칼슘 이온을 위한 인스브루크의 고전적인 선형 파울 트랩.


이 안장점은 퍼텐셜 장 안에 있는 이온들의 에너지 규모 \left\vert E(\vec{x}) \right\vert가 최소가 되는 지점이다.[49] 파울 트랩은 이온을 2차원 평면에 가두고, z축 방향으로는 가두지 않는 조화 퍼텐셜 우물로 표현된다. 다중 이온이 안장점에 있고 계가 평형 상태일 때, 이온들은 z축 방향으로만 자유롭게 움직인다. 이온들은 서로 반발하여 z축에서 수직적 구성을 만든다.[50] 많은 이온들이 동일한 덫에서 초기화되면, 복잡성 증가의 쿨롱 상호작용은 더욱 뒤얽힌 이온 구성을 만들 것이다.[48] 더불어 추가된 이온들의 추가적 진동이 초기화와 계산을 더욱 어렵게 만드는 양자 시스템을 상당히 복잡하게 만든다.[50]

포획된 이온들은 람-디케 영역에 도달할 정도로 충분히 냉각되어야 한다. 이는 도플러 냉각과 분해된 사이드밴드 냉각을 통해 달성할 수 있다. 극저온에서 이온 트랩 내부의 진동 에너지는 음자(phonon)로 양자화된다. 단일 음자의 에너지는 \hbar\omega_z 관계에 의해 주어진다. 이러한 양자 상태는 포획된 이온들이 외부로부터 완전히 고립되어 함께 진동할 때 발생한다. 이온들이 완전히 고립되지 않으면, 외부 전자기장과 상호작용하여 잡음이 발생하고 양자화된 에너지 상태가 붕괴될 수 있다.[48]

3. 1. 작동 원리

볼프강 파울이 1950년대에 발명한 전기역학적 이온 덫은 포획된 이온 양자컴퓨팅 연구에 사용된다.[47] 언쇼 정리에 따라 대전 입자는 정전기력만으로는 3차원 공간에 포획될 수 없다. 따라서 무선주파수(RF)에서 진동하는 전기장이 적용되어 회전하는 안장 형태의 퍼텐셜을 형성한다. 적절한 파라미터를 갖는 RF 장에서 대전 입자는 복원력에 의해 안장점에서 매튜 방정식으로 기술되는 운동을 하며 효율적으로 포획된다.[48]

이 안장점은 퍼텐셜 장 안에 있는 이온들의 에너지 규모 \left\vert E(\vec{x}) \right\vert가 최소가 되는 지점이다.[49] 파울 트랩은 이온을 2차원 평면에 가두고, z축 방향으로는 가두지 않는 조화 퍼텐셜 우물로 표현된다. 다중 이온이 안장점에 있고 계가 평형 상태일 때, 이온들은 z축 방향으로만 자유롭게 움직인다. 이온들은 서로 반발하여 z축에서 수직적 구성을 만든다.[50]

포획된 이온들은 램-디케 영역(Lamb Dicke regime)에 도달할 정도로 충분히 냉각되어야 한다. 이는 도플러 냉각과 분해된 측파대 냉각을 통해 달성할 수 있다. 극저온에서 이온 트랩 내부의 진동 에너지는 음향양자(phonon)로 양자화된다. 단일 음자의 에너지는 \hbar\omega_z 관계에 의해 주어진다. 이러한 양자 상태는 포획된 이온들이 외부로부터 완전히 고립되어 함께 진동할 때 발생한다. 이온들이 완전히 고립되지 않으면, 외부 전자기장과 상호작용하여 잡음이 발생하고 양자화된 에너지 상태가 붕괴될 수 있다.[48]

4. 양자 계산의 요건



기능을 갖춘 양자 컴퓨터에 대한 모든 요구 사항이 완전히 알려져 있지는 않지만, 일반적으로 받아들여지는 많은 요구 사항이 있다. 데이비드 디빈첸조는 이러한 양자 컴퓨팅 기준 중 몇 가지를 제시했다.[11]

양자 컴퓨터의 완전한 기능 요건은 불분명하지만, 일반적으로 받아들여지는 다수의 요건이 있으며, 이는 디빈첸조에 의해 개략적으로 설명되었다.[27]

4. 1. 큐비트 (Qubits)

어떤 두 준위 양자 시스템이든 큐비트를 형성할 수 있으며, 이온의 전자 상태를 사용하여 큐비트를 형성하는 두 가지 주요 방법이 있다.[10][28]

  • 초미세 큐비트: 두 개의 바닥 상태 초미세 준위를 이용한다. 수명이 매우 길고(수천 년에서 수백만 년) 위상/주파수가 안정적이다.[10][28]
  • 광학 큐비트: 바닥 상태 준위와 들뜬 준위를 이용한다. 논리 게이트 작동 시간(마이크로초)에 비해 비교적 긴 수명(약 1초)을 가진다.[10][28]


각 유형의 큐비트를 사용하는 것은 실험실에서 고유한 과제를 제기한다.

4. 2. 초기화 (Initialization)

이온 큐비트 상태는 광 펌핑 과정을 통해 특정 큐비트 상태로 준비될 수 있다. 이 과정에서 레이저는 이온을 일부 여기 상태에 결합시키고, 이온은 결국 레이저와 결합되지 않은 하나의 상태로 붕괴된다. 이온이 해당 상태에 도달하면, 해당 레이저가 존재하는 동안에는 결합할 수 있는 여기 레벨이 없으므로 해당 상태에 유지된다. 이온이 다른 상태 중 하나로 붕괴되면, 레이저는 이온이 레이저와 상호 작용하지 않는 상태로 붕괴될 때까지 계속해서 이온을 여기시킨다. 이 초기화 과정은 많은 물리학 실험에서 표준으로 사용되며, 매우 높은 충실도 (>99.9%)로 수행할 수 있다.[12][29]

따라서 양자 계산을 위한 시스템의 초기 상태는 초미세 및 운동 바닥 상태의 이온으로 설명할 수 있으며, 그 결과 |0\rangle (0개 포논)의 초기 질량 중심 포논 상태, 제로 포논 상태가 된다.[11][29]

4. 3. 측정 (Measurement)

이온에 저장된 큐비트의 상태 측정은 레이저를 이용한다. 레이저는 큐비트 상태 중 하나에만 결합하도록 설정되어 이온에 조사된다. 측정 과정에서 이온이 특정 상태로 붕괴되면 레이저에 의해 여기되고, 이온이 다시 붕괴하면서 광자를 방출한다. 이온은 레이저에 의해 지속적으로 여기되어 반복적으로 광자를 방출하게 된다. 이 광자는 광전자 증배관 (PMT) 또는 전하 결합 소자 (CCD) 카메라로 수집할 수 있다.[13][30]

이온이 다른 큐비트 상태로 붕괴되면 레이저와 상호 작용하지 않아 광자가 방출되지 않는다. 수집된 광자 수를 세어 이온의 상태를 매우 높은 정확도(>99.99%)로 결정할 수 있다.[13][30]

4. 4. 단일 큐비트 회전 (Arbitrary single qubit rotation)

단일 큐비트의 상태를 일관성 있게 변경하는 것은 보편적인 양자 컴퓨터의 필수 요건이다.[11][31] 포획 이온 시스템에서는 자기 쌍극자 전이 또는 유도 라만 전이를, 광학 큐비트에 대해 전기 사중극 전이를 이용하여 이 작업을 수행한다.[11] "회전"이라는 용어는 큐비트 순수 상태의 블로흐 구 표현을 의미한다.[11][31] 게이트 충실도는 99% 이상이 될 수 있다.[11][31]

회전 연산자 R_x(\theta)와 R_y(\theta)는 외부 전자기장의 주파수를 조작하고 특정 시간 동안 이온을 해당 장에 노출시켜 개별 이온에 적용할 수 있다.[11][31] 이러한 제어는 H_I^i=\hbar\Omega/2(S_+\exp(i\phi)+S_-\exp(-i\phi)) 형태의 해밀토니안을 생성한다. 여기서, S_+와 S_-는 스핀의 올림 및 내림 연산자이다 (사다리 연산자 참조).[11][31] 이러한 회전은 양자 컴퓨팅에서 단일 큐비트 게이트를 위한 보편적인 구성 요소이다.[11][31]

이온-레이저 상호 작용에 대한 해밀토니안을 얻으려면, 제인스-커밍스 모형을 적용한다.[11][32] 해밀토니안을 찾으면 양자 시간 진화의 원리를 사용하여 큐비트에 수행된 유니타리 연산에 대한 공식을 도출할 수 있다. 이 모델은 회전파 근사를 사용하지만, 포획 이온 양자 컴퓨팅의 목적에 효과적인 것으로 입증되었다.[11][32]

4. 5. 2 큐비트 얽힘 게이트 (Two qubit entangling gates)

시라크와 졸러가 제안한 제어-NOT 게이트 외에도, 다양하고 견고한 방식들이 제안되고 실험적으로 구현되었다.[14][33] JJ. 가르시아-리폴, 시라크, 졸러의 최근 이론 연구에 따르면 얽힘 게이트 속도에는 근본적인 제한이 없지만, 1 마이크로초보다 빠른 게이트는 아직 실험적으로 시연되지 않았다.[14] 이러한 구현의 충실도는 99% 이상이다.[14][33]

5. 확장 가능한 트랩 설계

양자 컴퓨터는 어려운 계산 문제를 해결하기 위해 많은 큐비트를 한 번에 초기화, 저장 및 조작할 수 있어야 한다. 그러나 앞서 논의했듯이, 각 트랩에는 계산 능력을 유지하면서 유한한 수의 큐비트만 저장할 수 있다. 따라서 정보를 한 트랩에서 다른 트랩으로 전송할 수 있는 상호 연결된 이온 트랩을 설계하는 것이 필요하다. 이온은 동일한 상호 작용 영역에서 개별 저장 영역으로 분리하여 내부 상태에 저장된 양자 정보를 잃지 않고 다시 함께 가져올 수 있다. 또한 이온을 "T"자형 접합부에서 방향을 바꾸도록 만들어 2차원 트랩 배열 설계를 가능하게 한다.[15] 반도체 제조 기술 또한 새로운 세대의 트랩을 제조하는 데 사용되어 '칩 위의 이온 트랩'을 현실로 만들었다. 예로는 D. Kielpinski, 크리스토퍼 몬로(Christopher Monroe)와 데이비드 와이널드(David J. Wineland)가 설계한 양자 전하 결합 소자(QCCD)가 있다.[15] QCCD는 큐비트를 저장하고 조작하기 위한 지정된 영역이 있는 전극의 미로와 유사하다.

전극에 의해 생성된 가변 전위는 특정 영역에 이온을 가두고 수송 채널을 통해 이동시킬 수 있으며, 이는 모든 이온을 단일 트랩에 포함해야 할 필요성을 없앤다. QCCD의 메모리 영역에 있는 이온은 모든 작업으로부터 격리되어 있으므로 해당 상태에 포함된 정보는 나중에 사용하기 위해 보존된다. 두 개의 이온 상태를 얽히게 하는 게이트를 포함한 게이트는 이 문서에서 이미 설명한 방법으로 상호 작용 영역의 큐비트에 적용된다.[15]

5. 1. 확장 가능한 트랩에서의 결어긋남 (Decoherence in scalable traps)

이온이 상호 연결된 트랩의 영역 사이에서 이동하고 불균일한 자기장에 노출되면, 제만 효과에 의해 다음과 같은 형태의 양자 데코히어런스(결어긋남)가 발생할 수 있다.[15][36]

:\left|\uparrow\right\rangle + \left|\downarrow\right\rangle\longrightarrow \exp(i\alpha)\left|\uparrow\right\rangle + \left|\downarrow\right\rangle

이는 양자 상태의 상대 위상을 효과적으로 변경한다. 여기서 위쪽 화살표와 아래쪽 화살표는 일반적인 중첩 큐비트 상태, 이 경우 이온의 바닥 상태와 들뜬 상태를 나타낸다.

추가적인 상대 위상은 트랩의 물리적 움직임이나 의도하지 않은 전기장의 존재로 인해 발생할 수 있다. 사용자가 매개변수 α를 결정할 수 있다면, 상대 위상을 수정하기 위한 알려진 양자 정보 프로세스가 존재하므로 이 결어긋남을 고려하는 것은 비교적 간단하다.[11][37] 그러나 자기장과의 상호 작용으로 인한 α는 경로 의존적이므로 문제는 매우 복잡하다.

이온 트랩에서 상대 위상의 결어긋남이 도입될 수 있는 여러 가지 방법을 고려하여, 결어긋남을 최소화하는 새로운 기저로 이온 상태를 재구성하는 것이 문제를 해결하는 방법이 될 수 있다. 결어긋남에 대처하는 한 가지 방법은 데코히어런스-프리 부분 공간(DFS)을 이용하는 것이다. DFS의 기저 상태는 \left|\uparrow\downarrow\right\rangle 및 \left|\downarrow\uparrow\right\rangle이다. DFS는 실제로 두 이온 상태의 부분 공간으로, 두 이온 모두 동일한 상대 위상을 얻으면 DFS의 전체 양자 상태가 영향을 받지 않는다.[15][38]

6. 구현 과제 및 한국의 현황

포획 이온 양자 컴퓨터는 이론적으로 양자 컴퓨팅을 위한 모든 디빈첸조의 기준을 충족하지만, 시스템 구현은 매우 어려울 수 있다. 주요 과제는 이온의 운동 상태 초기화와 비교적 짧은 음향자 상태 수명이다.[11] 또한, 큐비트가 원치 않게 외부 환경과 상호 작용할 때 발생하는 결 어긋남을 제거하는 것도 어려운 과제로 입증되었다.[2]

제어 NOT 게이트(CNOT 게이트)는 모든 양자 게이트가 CNOT 게이트와 단일 큐비트 회전의 조합으로 생성될 수 있기 때문에 양자 컴퓨팅의 중요한 구성 요소이다.[10] 포획 이온 양자 컴퓨터는 다음 세 가지 요구 사항을 충족하여 이 연산을 수행할 수 있어야 한다.


  • 포획 이온 양자 컴퓨터는 큐비트에 대한 임의 회전을 수행할 수 있어야 한다.
  • 양자 논리 게이트 참조) 제어 위상 반전 게이트 또는 제어 ''X'' 게이트에서 포논 큐비트가 |1\rangle 상태에 있으면 작동 큐비트의 위상이 뒤집힌다.
  • 이온 상태와 포논 상태 모두에 작용하는 SWAP 게이트를 구현해야 한다.[11]


CNOT 게이트를 나타내는 두 가지 대체 방식은 마이클 닐슨과 아이작 좡의 ''양자 계산 및 양자 정보''와 시라크와 졸러의 ''냉각 포획 이온을 이용한 양자 계산''에 제시되어 있다.[11][2]

참조

[1] 논문 A Race-Track Trapped-Ion Quantum Processor https://link.aps.org[...] 2023-12-18
[2] 논문 Quantum Computations with Cold Trapped Ions 1995-05-15
[3] 뉴스 Quantum computer is smallest ever, claim physicists https://physicsworld[...] Physics World 2021-07-07
[4] 논문 Compact Ion-Trap Quantum Computing Demonstrator https://journals.aps[...] 2021-06-17
[5] 웹사이트 The Nobel Prize in Physics 1989 http://nobelprize.or[...] 2005-06-22
[6] 웹사이트 Introduction to Ion Trap Quantum Computing {{!}} University of Oxford Department of Physics https://www2.physics[...] 2018-11-05
[7] 논문 Observation of ordered structures of laser-cooled ions in a quadrupole storage ring https://link.aps.org[...] 1992-03-30
[8] 논문 Ionic crystals in a linear Paul trap https://link.aps.org[...] 1992-05-01
[9] 논문 Multiple-shell structures of laser-cooled 24Mg+ ions in a quadrupole storage ring https://doi.org/10.1[...] 1992-05-28
[10] 논문 Quantum Computing with Trapped Ion Hyperfine Qubits 2004
[11] 서적 Quantum computation and quantum information Cambridge University Press 2010
[12] 논문 A quantum information processor with trapped ions http://stacks.iop.or[...] 2018-12-04
[13] 논문 High Fidelity State Preparation and Measurement of Ion Hyperfine Qubits with $I>\frac{1}{2}$ https://link.aps.org[...] 2022-09-19
[14] 논문 Fast and robust two-qubit gates for scalable ion trap quantum computing 2003-10-07
[15] 논문 Architecture for a large-scale ion-trap quantum computer https://deepblue.lib[...] 2019-09-26
[16] 서적 Quantum computation and quantum information Cambridge University Press 2010
[17] 논문 Observation of Entangled States of a Fully Controlled 20-Qubit System 2018-04-10
[18] 논문 14-Qubit Entanglement: Creation and Coherence 2011-03-31
[19] 논문 Electromagnetic traps for charged and neutral particles 1990-07-01
[20] URL http://nobelprize.or[...]
[21] 서적 Quantum computation and quantum information Cambridge University Press 2010
[22] 웹사이트 Introduction to Ion Trap Quantum Computing {{!}} University of Oxford Department of Physics https://www2.physics[...] 2018-11-05
[23] 논문 Quantum Computing with Trapped Ion Hyperfine Qubits 2004
[24] 서적 Quantum computation and quantum information Cambridge University Press 2010
[25] 서적 Quantum computation and quantum information Cambridge University Press 2010
[26] 논문 Quantum Computations with Cold Trapped Ions 1995-05-15
[27] 서적 Quantum computation and quantum information Cambridge University Press 2010
[28] 논문 Quantum Computing with Trapped Ion Hyperfine Qubits 2004
[29] 논문 A quantum information processor with trapped ions http://stacks.iop.or[...] 2013
[30] 기타
[31] 서적 Quantum computation and quantum information Cambridge University Press 2010
[32] 서적 Quantum computation and quantum information Cambridge University Press 2010
[33] 논문 Fast and robust two-qubit gates for scalable ion trap quantum computing 2018-10-25
[34] 논문 Architecture for a large-scale ion-trap quantum computer https://deepblue.lib[...] 2002-06
[35] 논문 Architecture for a large-scale ion-trap quantum computer https://deepblue.lib[...] 2002-06
[36] 논문 Architecture for a large-scale ion-trap quantum computer https://deepblue.lib[...] 2002-06
[37] 서적 Quantum computation and quantum information Cambridge University Press 2010
[38] 논문 Architecture for a large-scale ion-trap quantum computer https://deepblue.lib[...] 2002-06
[39] 서적 Quantum computation and quantum information Cambridge University Press 2010
[40] 논문 Quantum Computations with Cold Trapped Ions 1995-05-15
[41] 서적 Quantum computation and quantum information Cambridge University Press 2010
[42] 서적 Quantum computation and quantum information Cambridge University Press 2010
[43] 논문 Quantum Computations with Cold Trapped Ions 1995-05-15
[44] 저널 Observation of Entangled States of a Fully Controlled 20-Qubit System https://link.aps.org[...] 2018-04-10
[45] 저널 14-Qubit Entanglement: Creation and Coherence https://link.aps.org[...] 2011-03-31
[46] 저널 Electromagnetic traps for charged and neutral particles https://link.aps.org[...] 1990-07-01
[47] 웹인용 null http://nobelprize.or[...] null null
[48] 서적 인용 Quantum computation and quantum information https://www.worldcat[...] 2010
[49] 웹인용 Introduction to Ion Trap Quantum Computing {{!}} University of Oxford Department of Physics https://www2.physics[...] 2019-06-08
[50] 저널 Quantum Computing with Trapped Ion Hyperfine Qubits http://link.springer[...] 2004-10


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com