백분위수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 정규 분포와 백분위수
4. 응용
5. 계산 방법
참조

1. 개요

백분위수는 데이터 집합에서 특정 값보다 작거나 같은 값의 비율을 나타내는 통계적 개념이다. 정규 분포에서 백분위수는 평균을 중심으로 한 표준 편차의 간격과 관련되며, 68-95-99.7 규칙을 통해 특정 범위 내에 포함되는 데이터의 비율을 알 수 있다.

백분위수는 다양한 분야에서 활용된다. 인터넷 서비스 제공업체는 대역폭 요금 부과 시, 의사는 어린이의 성장 평가를 위해, 도로에서는 제한 속도 설정을 위해 사용한다. 또한, 금융 분야에서는 위험 가치를 평가하는 데 활용된다.

백분위수는 가장 가까운 순위 방법과 선형 보간 방법을 포함하여 다양한 방식으로 계산할 수 있으며, 가중치를 고려한 가중 백분위수 방법도 존재한다.

더 읽어볼만한 페이지

통계량 - 제곱평균제곱근
제곱평균제곱근(RMS)은 값들의 크기를 나타내는 통계량으로, 이산 데이터의 경우 각 값의 제곱의 평균의 제곱근, 연속 함수의 경우 함수 제곱의 적분 평균의 제곱근으로 정의되며, 전기공학, 물리학 등 다양한 분야에서 활용되고 표준편차와 밀접한 관련이 있다.
통계량 - 최빈값
최빈값은 데이터 집합에서 가장 자주 나타나는 값으로, 확률 분포의 중심 경향을 나타내는 척도이며 이상치에 둔감하고 명목형 데이터에도 적용 가능하다.

백분위수
통계적 위치
일반적인 의미
정의	백분위수는 데이터 집합을 100개의 동일한 부분으로 나누는 값이다.
용도	데이터 내에서 특정 값의 상대적 위치를 나타내는 데 사용된다.
계산	정렬된 데이터 집합에서 특정 백분위수에 해당하는 값을 찾는다.
예시	90번째 백분위수는 데이터의 90%가 그 값 아래에 있음을 의미한다.
세부 사항
기원	백분위수의 개념은 19세기에 프랜시스 골턴에 의해 소개되었다.
활용 분야	시험 점수 인구 통계 소득 분배 기타 여러 분야에서 널리 사용된다.
장점	데이터의 분포를 이해하는 데 도움을 준다. 이상치를 식별하는 데 유용하다. 서로 다른 데이터 집합을 비교하는 데 사용될 수 있다.
단점	데이터 집합의 크기에 따라 민감하게 변할 수 있다. 데이터의 정확성에 의존한다.
관련 개념	사분위수: 데이터 집합을 4개의 동일한 부분으로 나눈다. 십분위수: 데이터 집합을 10개의 동일한 부분으로 나눈다. 중앙값: 데이터 집합의 중앙값 (50번째 백분위수).
추가 정보
주의사항	백분위수는 데이터의 분포를 설명하는 데 유용한 도구이지만, 데이터의 전체적인 그림을 제공하지는 않는다.
참고 자료	통계학 교재, 온라인 통계 자료

2. 정의

백분위수에 대한 표준 정의는 없지만,^[1]^[2]^[3] 모든 정의는 관측치의 수가 매우 많고 확률 분포가 연속적일 때 유사한 결과를 생성한다.^[4] 표본 크기가 무한대에 접근함에 따라, 100''p''^번째 백분위수(0<''p''<1)는 ''p''가 누적 분포 함수(CDF)에 근사할 때, 형성된 누적 분포 함수의 역함수를 ''p''에서 평가한 값에 근사한다. 이는 글리벤코-칸텔리 정리의 결과로 볼 수 있다.

3. 정규 분포와 백분위수

3-시그마 규칙의 표현. 어두운 파란색 영역은 평균 (μ)에서 양쪽으로 1 표준 편차 (σ) 이내의 관측치를 나타내며, 이는 전체 인구의 약 68.3%를 차지한다. 평균에서 2 표준 편차(어두운 파란색과 중간 파란색)는 약 95.4%를 차지하고, 3 표준 편차(어두운 파란색, 중간 파란색, 밝은 파란색)는 약 99.7%를 차지한다.

일반적으로 정규 분포를 따르는 매우 큰 모집단의 경우, 백분위수는 종종 정규 곡선 도표를 참조하여 나타낼 수 있다. 정규 분포는 표준 편차 또는 시그마(σ) 단위를 기준으로 눈금이 매겨진 축을 따라 플롯된다. 수학적으로 정규 분포는 왼쪽으로 음의 무한대까지, 오른쪽으로 양의 무한대까지 확장된다. 그러나 모집단의 개인 중 매우 작은 비율만이 -3σ에서 +3σ 범위를 벗어난다는 점에 유의해야 한다. 예를 들어, 인간의 키의 경우 +3σ 키 수준을 초과하는 사람은 거의 없다.

백분위수는 정규 곡선 아래의 영역을 나타내며, 왼쪽에서 오른쪽으로 증가한다. 각 표준 편차는 고정된 백분위수를 나타낸다. 따라서 소수점 둘째 자리까지 반올림하면 -3σ는 0.13 백분위수, -2σ는 2.28 백분위수, -1σ는 15.87 백분위수, 0σ는 50 백분위수(분포의 평균과 중앙값 모두), +1σ는 84.13 백분위수, +2σ는 97.72 백분위수, +3σ는 99.87 백분위수이다. 이는 68-95-99.7 규칙 또는 3-시그마 규칙과 관련이 있다. 이론적으로 0 백분위수는 음의 무한대에, 100 백분위수는 양의 무한대에 해당하지만, 시험 결과와 같은 많은 실제 응용 분야에서는 자연적인 하한 및/또는 상한이 적용된다는 점에 유의해야 한다.

4. 응용

인터넷 서비스 제공업체(ISP)는 "버스터블" 인터넷 대역폭 요금을 청구할 때 95번째 또는 98번째 백분위수를 사용한다. 이는 대역폭 최고치 상위 5% 또는 2%를 제외하고 가장 가까운 요율로 청구하는 방식이다. 흔치 않은 최고 사용량을 무시하여 고객에게 더 공정한 요금을 부과한다. 95번째 백분위수는 사용량의 95%가 이 값보다 낮다는 것을 의미하며, 나머지 5%의 시간 동안 사용량이 그 값보다 높다는 것을 뜻한다.

의사들은 유아와 어린이의 체중과 키를 성장 도표의 전국 평균 및 백분위수와 비교하여 성장을 평가한다.

도로의 교통 속도 85번째 백분위수는 제한 속도 설정의 지침으로 사용된다.^[5]^[6]

금융에서 위험 가치는 주어진 기간과 신뢰 값을 바탕으로 포트폴리오 가치가 특정 수준 이하로 떨어지지 않을 것으로 예상되는 수량을 평가하는 표준 척도이다.

5. 계산 방법

백분위수를 계산하는 방법에는 여러 가지가 있으며, 크게 가장 가까운 순위 방법과 선형 보간 방법으로 나눌 수 있다. 백분위수에 대한 표준 정의는 없지만,^[1]^[2]^[3] 모든 정의는 관측치의 수가 매우 많고 확률 분포가 연속적일 때 유사한 결과를 생성한다.^[4]

Hyndman과 Fan^[1]은 백분위수 점수를 구하는 공식이나 알고리즘^[7] 9가지를 식별했으며, 대부분의 통계 및 스프레드시트 소프트웨어는 그들이 설명한 방법 중 하나를 사용한다.^[11] 알고리즘은 점수 집합에 존재하는 점수 값을 반환(가장 가까운 순위 방법)하거나 기존 점수 간을 보간하며, 배타적이거나 포괄적이다.

다음 표는 10점수 분포를 기준으로, 가장 가까운 순위 방법과 보간 방법으로 계산된 백분위수 값을 비교하여 보여준다.

백분위수 계산 방법 비교 (10점수 분포 기준)
	지정된 백분위수 (PC)	0.10	0.25	0.50	0.75	0.90
가장 가까운 순위 방법	점수 개수 (N)	10	10	10	10	10
	순위 = PC × N	1	2.5	5	7.5	9
	순위: >OR / ≥OR	2/1	3/3	6/5	8/8	10/9
	순위에서의 점수 (배타적/포괄적)	2/1	3/3	4/3	5/5	7/5
보간 방법	점수 개수 (N)	10	10	10	10	10
	OR: PC×(N+1) / PC×(N−1)+1	1.1/1.9	2.75/3.25	5.5/5.5	8.25/7.75	9.9/9.1
	LoRank: OR 절사	1/1	2/3	5/5	8/7	9/9
	HiRank: OR 올림	2/2	3/4	6/6	9/8	10/10
	LoScore: LoRank에서의 점수	1/1	2/3	3/3	5/4	5/5
	HiScore: HiRank에서의 점수	2/2	3/3	4/4	5/5	7/7
	차이: HiScore − LoScore	1/1	1/0	1/1	0/1	2/2
	보간된 점수 (배타적/포괄적) = LoScore + Mod × 차이	1.1/1.9	2.75/3	3.5/3.5	5/4.75	6.8/5.2

가장 가까운 순위 방법은 분포에서 점수를 반환하는 가장 간단한 방법이지만, 보간 방법에 비해 결과가 다소 조잡할 수 있다. 반면 보간 방법은 분포의 점수 사이에 있는 점수를 반환할 수 있어, 통계 프로그램에서 주로 사용된다. Microsoft Excel의 percentile.exc 및 percentile.inc 함수가 보간 방법을 사용한다.

5. 1. 가장 가까운 순위 방법 (The nearest-rank method)

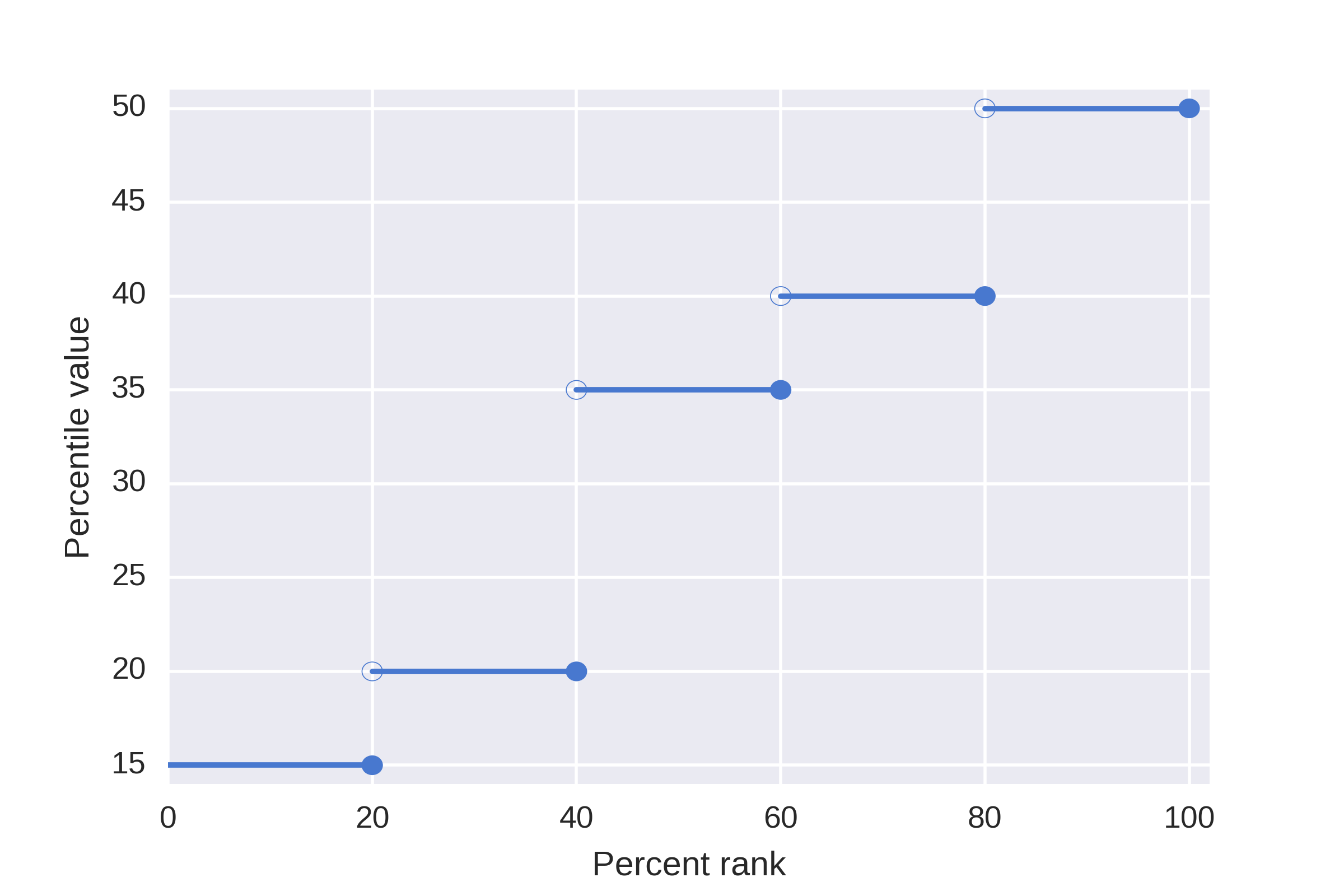
백분위수의 한 가지 정의는, 종종 교과서에서 제시되는데, 정렬된 ''N''개의 값(최소에서 최대 순으로 정렬됨)의 ''P''번째 백분위수(0 < P ≤ 100)는 데이터의 ''P'' 퍼센트 이하가 해당 값보다 엄격하게 작고, 데이터의 최소 ''P'' 퍼센트가 해당 값보다 작거나 같은 목록에서 가장 작은 값이다. 이는 먼저 서수 순위 ''n''을 다음 공식을 사용하여 계산한다.

:

n =  \left \lceil \frac{P}{100} \times N  \right \rceil.

계산된 순위 ''n''에 해당하는 정렬된 목록에서 값을 가져온다.

100개 미만의 고유한 값을 가진 목록에 대해 가장 가까운 순위 방법을 사용하면 여러 백분위수에 대해 동일한 값이 사용될 수 있다.
가장 가까운 순위 방법을 사용하여 계산된 백분위수는 항상 원래 정렬된 목록의 구성원일 것이다.
100번째 백분위수는 정렬된 목록에서 가장 큰 값으로 정의된다.

5. 2. 선형 보간 방법 (The linear interpolation between closest ranks method)

다양한 응용 분야에서 사용되는 반올림의 대안은 인접한 순위 간의 선형 보간법을 사용하는 것이다.

순서 통계량이 다음과 같이 주어졌을 때:

:

\{v_i,i=1,2,\ldots,N : v_{i+1}\ge v_i,\forall i=1,2,\ldots,N-1\},

점

(v_i,i)

를 통과하는 선형 보간 함수는 다음과 같이 구할 수 있다.

:

v(x) = v_{\lfloor x\rfloor} + (x \bmod 1)(v_{\lfloor x\rfloor+1}-v_{\lfloor x\rfloor}),\forall x\in[1,N] : v(i)=v_i \text{, for } i=1,2,\ldots,N,

여기서

\lfloor x\rfloor

는 바닥 함수를 사용하여 양수의 정수 부분을 나타내고,

x\bmod 1

는 모듈로 함수를 사용하여 소수 부분(1로 나눈 나머지)을 나타낸다.

x

는 첨자

i

의 연속적인 버전이며, 인접한 노드 사이에서

v

를 선형 보간한다.

변형 접근 방식은 "순위"

x

, "백분율 순위"

P=100p

, 그리고 표본 크기

N

의 함수인 상수 사이의 선형 관계에서 차이가 있다.

:

x=f(p,N)=(N+c_1)p+c_2.

중앙값에 해당하는 범위

(1,N)

의 중간점이

p=0.5

에서 발생해야 한다는 추가 요구 사항이 있다.

:

\begin{align} f(0.5,N)&=\frac{N+c_1}{2}+c_2=\frac{N+1}{2}\\ \therefore 2c_2+c_1&=1 \end{align},

따라서 수정된 함수는 다음과 같이 하나의 자유도만 가진다.

:

x=f(p,N)=(N+1-2C)p+C.

p

의

[0,1]

범위의 가장자리 근처에서 함수의 정의에 따라 변형이 달라지기도 한다.

f(p,N)

은

[1,N]

범위 내에서 결과를 생성하거나 강제로 생성해야 하는데, 이는 더 넓은 영역에서 일대일 대응이 없을 수 있음을 의미한다.

5. 3. 가중 백분위수 (The weighted percentile method)

총 가중치를 사용하여 백분율을 계산하는 ''가중 백분위수''도 있다. 가중 백분위수에 대한 표준 함수는 없다. 한 가지 방법은 위의 방식을 자연스럽게 확장하는 것이다.

정렬된 ''N''개의 표본 값에 각각 양의 가중치 $w_1, w_2, w_3, \dots, w_N$가 있다고 가정한다.

$S_N = \sum_{k=1}^N w_k,$

는 가중치의 합이다. 그러면 위의 공식은 다음과 같이 일반화된다.

: $p_n = \frac{1}{S_N}\left(S_n - \frac{w_n}{2}\right)$ ($C=1/2$일 때)

또는

: $p_n = \frac{S_n - Cw_n}{S_N +(1-2C)w_n}$ (일반 $C$에 대해)

그리고

: $v = v_k + \frac{P - p_k}{p_{k + 1} - p_k}(v_{k + 1} - v_k)$.

50% 가중 백분위수는 가중 중앙값으로 알려져 있다.

참조

_[1] 논문 Sample Quantiles in Statistical Packages https://www.research[...] American Statistical Association 1996-11
_[2] 웹사이트 Percentiles http://cnx.org/conte[...] 2007-09-15
_[3] 웹사이트 Statistical flaws in Excel http://nestor.covent[...] 2013-03-25
_[4] 논문 Estimation of population percentiles
_[5] 서적 Elementary Statistics https://books.google[...] Cengage Learning
_[6] 웹사이트 Rational Speed Limits and the 85th Percentile Speed http://www.lsp.org/p[...] Louisiana State Police 2018-10-28
_[7] 웹사이트 Percentiles in Free Statistics Software http://www.wessa.net[...] Office for Research Development and Education 2021-11-13
_[8] 웹사이트 Matlab Statistics Toolbox – Percentiles http://www.mathworks[...] 2006-09-15
_[9] 논문 Quartiles in Elementary Statistics 2006
_[10] 웹사이트 NumPy 1.12 documentation https://docs.scipy.o[...] SciPy 2017-03-19
_[11] 웹사이트 Engineering Statistics Handbook: Percentile http://www.itl.nist.[...] NIST 2009-02-18

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com