누적 분포 함수

1. 개요

누적 분포 함수(CDF)는 확률 변수의 확률 분포를 나타내는 함수로, 주어진 값보다 작거나 같은 값을 가질 확률을 의미한다. 실수 값 확률 변수의 경우, CDF는 확률 변수가 특정 값 이하일 확률을, 확률 벡터의 경우 각 변수가 특정 값 이하일 확률을 나타낸다. CDF는 확률 변수 또는 확률 벡터의 확률 분포를 유일하게 결정하며, 이산, 연속, 특이 확률 변수의 특성을 나타낸다. CDF는 여(상보) 누적 분포 함수, 분위 함수, 접힌 누적 분포 함수, 경험적 분포 함수 등 다양한 파생 함수를 가지며, 통계적 분석에서 누적 빈도 분석, 콜모고로프-스미르노프 검정, 카이퍼 검정 등에 활용된다.

2. 정의

확률 공간 $(\backslash Omega,\backslash mathcal\; F,\backslash operatorname\{Pr\})$ 위의 실수 값을 갖는 확률 변수 $X\backslash colon\backslash Omega\backslash to(\backslash mathbb\; R,\backslash mathcal\; B(\backslash mathbb\; R))$의 (우연속) 누적 분포 함수(Cumulative Distribution Function, CDF) $F\_X\backslash colon\backslash mathbb\; R\backslash to\backslash mathbb\; R$는 확률 변수 $X$가 특정 값 $x$보다 작거나 같은 값을 가질 확률로 정의된다. 수학적으로는 다음과 같이 표현한다.
:$F\_X(x)\; =\; \backslash operatorname\{P\}(X\; \backslash leq\; x)\; =\; \backslash operatorname\{Pr\}(X\backslash in(-\backslash infty,x])\backslash qquad\backslash forall\; x\backslash in\backslash mathbb\; R$

보다 일반적으로, 확률 공간 $(\backslash Omega,\backslash mathcal\; F,\backslash operatorname\{Pr\})$ 위의 $n$차원 실수값 확률 벡터 $X=(X\_1,\backslash dots,X\_n)\backslash colon\backslash Omega\backslash to(\backslash mathbb\; R^n,\backslash mathcal\; B(\backslash mathbb\; R^n))$의 (우연속) 누적 분포 함수 $F\_X\backslash colon\backslash mathbb\; R^n\backslash to\backslash mathbb\; R$는 각 성분 $X\_i$가 해당 값 $x\_i$보다 작거나 같을 확률로 정의된다.
:$F\_X(x\_1,\backslash dots,x\_n)=\backslash operatorname\{Pr\}(X\_1\backslash in(-\backslash infty,x\_1],\backslash dots,X\_n\backslash in(-\backslash infty,x\_n])\backslash qquad\backslash forall(x\_1,\backslash dots,x\_n)\backslash in\backslash mathbb\; R^n$

위 정의에서 확률을 계산하는 구간 $(-\backslash infty,\; x]$ (또는 $(-\backslash infty,\; x\_i]$) 대신 열린구간 $(-\backslash infty,\; x)$ (또는 $(-\backslash infty,\; x\_i)$)를 사용하면, 즉 (또는 각 성분에 대해 )를 사용하면 좌연속 누적 분포 함수가 정의된다. 일반적으로 통계학에서는 별다른 언급이 없으면 우연속 누적 분포 함수를 의미한다.

2.1. 확률 변수의 누적분포함수

확률 공간 $(\backslash Omega,\backslash mathcal\; F,\backslash operatorname\{Pr\})$ 위의 실수 값을 갖는 확률 변수 $X$의 (우연속) 누적 분포 함수(Cumulative Distribution Function, CDF) $F\_X:\backslash mathbb\; R\; \backslash to\; [0,\; 1]$는 다음과 같이 정의된다.
:$F\_X(x)\; =\; \backslash operatorname\{P\}(X\backslash leq\; x)$
여기서 우변은 확률 변수 $X$가 실수 $x$보다 작거나 같은 값을 가질 확률을 나타낸다. 이 확률은 하측 확률(lower-tail probability)이라고도 불린다.

누적 분포 함수를 이용하면 확률 변수 $X$가 반닫힌 구간 $(a,\; b]$ ()에 속할 확률을 다음과 같이 계산할 수 있다.
:

위 정의에서 "≤" 기호를 사용하는 것이 일반적인 관례이지만, 모든 문헌에서 통용되는 것은 아니다 (예를 들어, 헝가리 문헌에서는 "<"를 사용하기도 한다). 이 구분은 특히 이산 분포에서 중요하다. 예를 들어 이항 분포나 푸아송 분포의 확률표를 올바르게 사용하려면 이 관례를 따라야 한다. 또한 폴 레비의 특성 함수에 대한 역 공식과 같은 중요한 공식들도 "이하(≤)" 형태의 정의에 기반한다.

여러 확률 변수 $X,\; Y,\; \backslash dots$ 등을 다룰 때는 각 변수를 나타내는 문자를 아래 첨자로 사용하여 $F\_X,\; F\_Y$ 등으로 표기하고, 하나의 확률 변수만 다룰 때는 아래 첨자를 생략하기도 한다. 누적 분포 함수는 일반적으로 대문자 $F$로 표기하며, 이는 확률 밀도 함수(PDF)나 확률 질량 함수(PMF)를 소문자 $f$로 표기하는 것과 구별된다. 특정 분포는 자체적인 표기법을 가지기도 하는데, 예를 들어 정규 분포의 누적 분포 함수와 확률 밀도 함수는 각각 $\backslash Phi$와 $\backslash phi$로 표기하는 경우가 많다.

연속 확률 변수 $X$의 누적 분포 함수 $F\_X(x)$는 확률 밀도 함수 $f\_X(t)$가 존재할 경우, 이를 적분하여 표현할 수 있다.
:$F\_X(x)\; =\; \backslash int\_\{-\backslash infty\}^x\; f\_X(t)\; \backslash ,\; dt$
반대로, 누적 분포 함수 $F\_X(x)$가 미분 가능하면, 미적분학의 기본 정리에 따라 이를 미분하여 확률 밀도 함수 $f\_X(x)$를 얻을 수 있다.
:$f\_X(x)\; =\; \backslash frac\{dF\_X(x)\}\{dx\}$

만약 확률 변수 $X$의 분포가 특정 값 $b$에서 이산적인 성분을 가진다면 (즉, $X=b$일 확률이 0보다 크다면), 이 확률은 누적 분포 함수의 좌극한과 함숫값의 차이로 계산할 수 있다.
:$\backslash operatorname\{P\}(X=b)\; =\; F\_X(b)\; -\; \backslash lim\_\{x\; \backslash to\; b^-\}\; F\_X(x)$
만약 누적 분포 함수 $F\_X$가 $b$에서 연속이라면, 이 값은 0이 되며, 이는 $b$에서 이산적인 성분이 없음을 의미한다.

위 정의에서 반닫힌구간 $(-\backslash infty,\; x]$ 대신 열린구간 $(-\backslash infty,\; x)$를 사용하면 좌연속 누적 분포 함수가 정의된다. 일반적으로는 우연속 누적 분포 함수를 사용한다.

보다 일반적으로, 확률 공간 $(\backslash Omega,\backslash mathcal\; F,\backslash operatorname\{Pr\})$ 위의 $n$차원 실수값 확률 벡터 $X=(X\_1,\backslash dots,X\_n)$의 (우연속) 누적 분포 함수 $F\_X\backslash colon\backslash mathbb\; R^n\backslash to[0,\; 1]$는 다음과 같이 정의된다.
:$F\_X(x\_1,\backslash dots,x\_n)=\backslash operatorname\{Pr\}(X\_1\backslash in(-\backslash infty,x\_1],\backslash dots,X\_n\backslash in(-\backslash infty,x\_n])\backslash qquad\backslash forall(x\_1,\backslash dots,x\_n)\backslash in\backslash mathbb\; R^n$

2.2. 확률 벡터의 누적분포함수

확률 공간 $(\backslash Omega,\backslash mathcal\; F,\backslash operatorname\{Pr\})$ 위의 실숫값 확률 벡터 $X=(X\_1,\backslash dots,X\_n)\backslash colon\backslash Omega\backslash to(\backslash mathbb\; R^n,\backslash mathcal\; B(\backslash mathbb\; R^n))$의 (우연속) 누적분포함수 $F\_X\backslash colon\backslash mathbb\; R^n\backslash to\backslash mathbb\; R$는 다음과 같다.
:$F\_X(x\_1,\backslash dots,x\_n)=\backslash operatorname\{Pr\}(X\_1\backslash in(-\backslash infty,x\_1],\backslash dots,X\_n\backslash in(-\backslash infty,x\_n])\backslash qquad\backslash forall(x\_1,\backslash dots,x\_n)\backslash in\backslash mathbb\; R^n$

위 정의에 등장하는 반닫힌구간들을 열린구간으로 대체하면 좌연속 누적분포함수의 정의를 얻는다.

2.3. 좌연속 및 우연속 누적분포함수

확률 변수 $X$의 누적 분포 함수(Cumulative Distribution Function, CDF)는 일반적으로 확률 변수가 특정 값 $x$보다 작거나 같을 확률, 즉 $\backslash operatorname\{P\}(X\; \backslash le\; x)$로 정의된다. 이 정의에 따른 누적 분포 함수는 우연속이다.

확률 공간 $(\backslash Omega,\backslash mathcal\; F,\backslash operatorname\{Pr\})$ 위의 실숫값 확률 변수 $X\backslash colon\backslash Omega\backslash to(\backslash mathbb\; R,\backslash mathcal\; B(\backslash mathbb\; R))$의 우연속 누적분포함수 $F\_X\backslash colon\backslash mathbb\; R\backslash to\backslash mathbb\; R$는 다음과 같이 정의된다.
:$F\_X(x)=\backslash operatorname\{Pr\}(X\backslash in(-\backslash infty,x])\; =\; \backslash operatorname\{P\}(X\backslash leq\; x)\backslash qquad\backslash forall\; x\backslash in\backslash mathbb\; R$

이 정의에서 사용된 부등호 "≤"는 일반적인 관례이지만, 모든 문헌에서 보편적으로 사용되는 것은 아니다. 예를 들어, 헝가리 문헌 등 일부에서는 "<" 기호, 즉 를 사용하여 누적 분포 함수를 정의하기도 한다. 이 경우 누적 분포 함수는 좌연속이 된다. 즉, 우연속 정의에 등장하는 반닫힌구간 $(-\backslash infty,\; x]$를 열린구간 $(-\backslash infty,\; x)$로 대체하면 좌연속 누적분포함수의 정의를 얻게 된다.

좌연속 정의와 우연속 정의의 차이는 이산 분포에서 특히 중요하다. 확률 변수 $X$가 특정 값 $b$를 가질 확률 $\backslash operatorname\{P\}(X=b)$는 우연속 누적분포함수 $F\_X(x)$를 사용하여 다음과 같이 표현할 수 있다.
:$\backslash operatorname\{P\}(X=b)\; =\; F\_X(b)\; -\; \backslash lim\_\{x\; \backslash to\; b^-\}\; F\_X(x)$
여기서 $\backslash lim\_\{x\; \backslash to\; b^-\}\; F\_X(x)$는 $x$가 $b$보다 작은 쪽에서 $b$로 접근할 때의 좌극한을 의미하며, 이는 좌연속 누적분포함수의 $b$에서의 값 와 동일하다. 만약 누적분포함수 $F\_X$가 $b$에서 연속이라면, 우극한과 좌극한값이 함수값과 모두 같으므로 $F\_X(b)\; =\; \backslash lim\_\{x\; \backslash to\; b^-\}\; F\_X(x)$가 되어 $\backslash operatorname\{P\}(X=b)=0$이 된다. 이는 연속 확률 변수의 경우에 해당한다.

대부분의 확률론 및 통계학 분야에서는 우연속 정의($\backslash operatorname\{P\}(X\backslash leq\; x)$)를 표준으로 채택하고 있다. 이항 분포나 푸아송 분포와 같은 이산 분포의 확률표나 폴 레비의 특성 함수에 대한 역 공식 등 많은 중요한 결과들이 이 우연속 정의를 기반으로 한다. 따라서 특정 문헌이나 자료를 참고할 때는 어떤 정의(좌연속 또는 우연속)를 사용하고 있는지 명확히 확인하는 것이 중요하다.

3. 성질

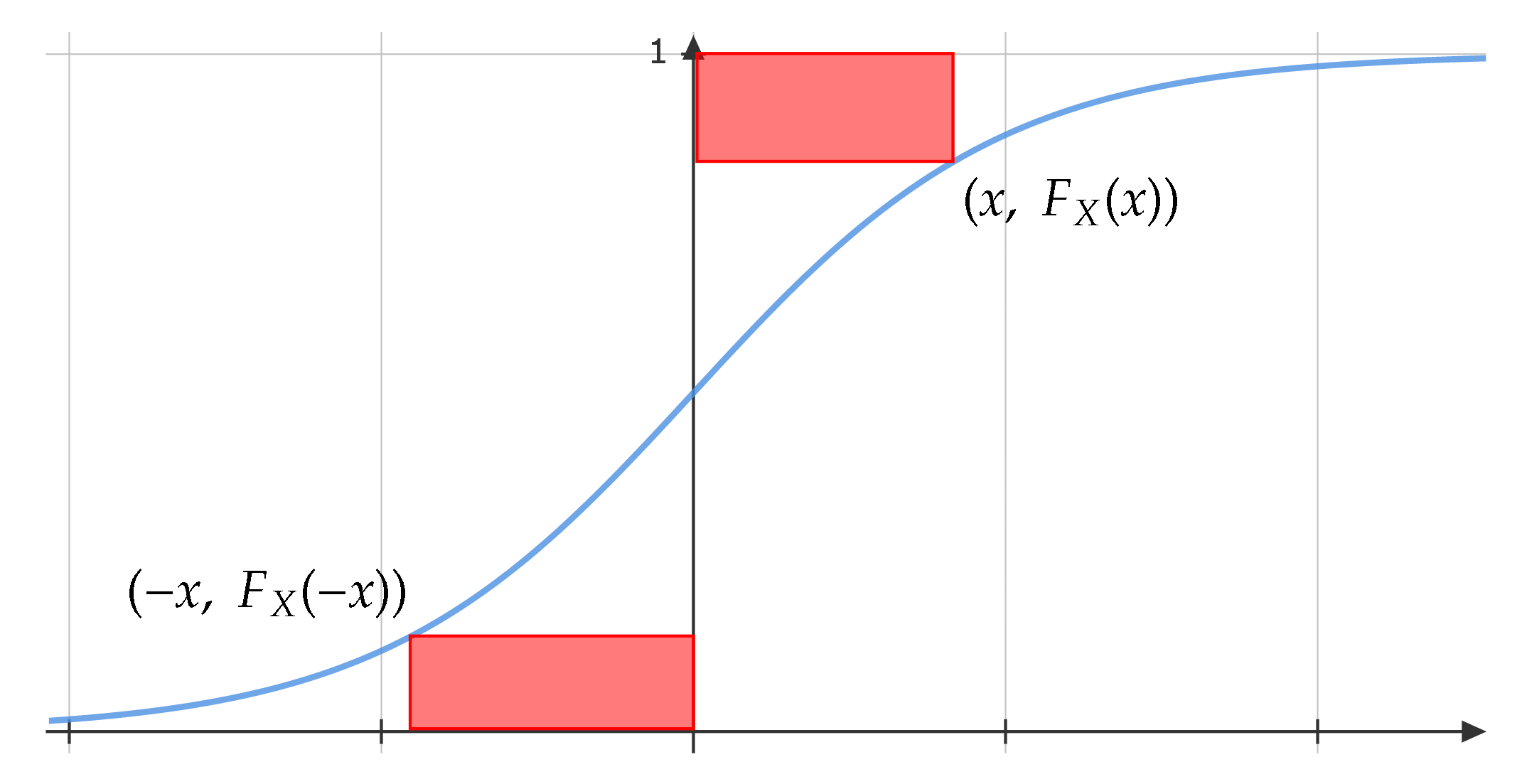
모든 누적 분포 함수(CDF) $F\_X$는 기본적으로 몇 가지 중요한 성질을 공유한다. 첫째, 함수값이 감소하지 않는 [[단조 증가]] 함수이다. 둘째, 그래프가 오른쪽에서 이어지는 [[우연속 함수|우연속]] 함수이다. 이 두 성질 때문에 CDF는 càdlàg 함수의 한 종류가 된다. 셋째, 음의 무한대로 갈 때의 극한값은 0이고, 양의 무한대로 갈 때의 극한값은 1이다.
$$\backslash lim\_\{x\; \backslash to\; -\backslash infty\}\; F\_X(x)\; =\; 0,\; \backslash quad\; \backslash lim\_\{x\; \backslash to\; +\backslash infty\}\; F\_X(x)\; =\; 1.$$
이 세 가지 기본 성질(단조 증가, 우연속성, 특정 극한값)을 만족하는 모든 함수는 어떤 확률 변수의 누적 분포 함수가 될 수 있다.

확률 변수 $X$의 종류에 따라 누적 분포 함수의 형태가 달라진다. 예를 들어, $X$가 순수하게 이산 확률 변수라면, 누적 분포 함수 $F\_X$는 특정 값들($x\_i$)에서 불연속적인 계단 형태를 보일 수 있다. 반면, $X$의 누적 분포 함수 $F\_X$가 연속 함수라면, $X$는 연속 확률 변수이다. 만약 $F\_X$가 절대 연속이라면, 확률 밀도 함수 $f\_X(x)$가 존재하며, 누적 분포 함수는 이 밀도 함수의 르베그 적분으로 표현될 수 있다.

누적 분포 함수는 확률 변수의 기댓값과도 밀접한 관련이 있다. 만약 확률 변수 $X$가 유한한 L1-노름을 가진다면 (즉, $|X|$의 기댓값이 유한하다면), 기댓값 $\backslash mathbb\; E[X]$는 리만-스틸티어스 적분을 사용하여 다음과 같이 계산할 수 있다.
$$$$
\mathbb E[X] = \int_{-\infty}^\infty t\,dF_X(t)

또한, 누적 분포 함수와 기댓값 사이에는 다음과 같은 유용한 부등식이 성립한다.
모든 $x\; \backslash geq\; 0$에 대해,
$$$$
x (1-F_X(x)) \leq \int_x^{\infty} t\,dF_X(t)

그리고,
$$$$
x F_X(-x) \leq \int_{-\infty}^{-x} (-t)\,dF_X(t)

이러한 관계는 오른쪽 그림에서 시각적으로 확인할 수 있다. 이 부등식들로부터 다음과 같은 극한 관계도 유도된다.
$$$$
\lim_{x \to -\infty} x F_X(x) = 0, \quad \lim_{x \to +\infty} x (1-F_X(x)) = 0.

3.1. 함수로서의 성질

임의의 함수 $F\backslash colon\backslash mathbb\; R\backslash to\backslash mathbb\; R$가 어떤 확률 변수의 누적분포함수(CDF)가 되기 위한 필요충분조건은 다음 세 가지 성질을 만족하는 것이다.

1. [[증가 함수|단조 증가]]: 함수값이 감소하지 않는다. 즉, 모든 실수 $x,\; y$에 대해 $x\; \backslash le\; y$이면 $F(x)\; \backslash le\; F(y)$이다.
2. [[우연속 함수|우연속성]]: 함수의 그래프에서 오른쪽으로 접근할 때 극한값이 함숫값과 같다. 즉, 모든 실수 $x$에 대해 $\backslash lim\_\{y\; \backslash to\; x^+\}\; F(y)\; =\; F(x)$이다. 단조 증가와 우연속성 때문에 누적 분포 함수는 càdlàg 함수이다.
3. 극한값: 음의 무한대로 갈 때 극한값은 0이고, 양의 무한대로 갈 때 극한값은 1이다.
$$\backslash lim\_\{x\; \backslash to\; -\backslash infty\}\; F(x)\; =\; 0,\; \backslash quad\; \backslash lim\_\{x\; \backslash to\; +\backslash infty\}\; F(x)\; =\; 1.$$

이 세 가지 성질을 만족하는 모든 함수 $F$에 대해, $F$를 누적 분포 함수로 가지는 확률 변수를 정의할 수 있다.

확률 변수의 종류에 따라 누적 분포 함수의 형태가 달라진다.

* 만약 $X$가 순수하게 이산 확률 변수이고, 값 $x\_1,\; x\_2,\; \backslash ldots$를 각각 확률 $p\_i\; =\; \backslash operatorname\{P\}(X=x\_i)$로 가진다면, $X$의 누적 분포 함수 $F\_X$는 각 $x\_i$ 지점에서 불연속이며, 그 지점에서 위로 점프한다. 이 경우 누적 분포 함수는 다음과 같이 계산된다.
$$F\_X(x)\; =\; \backslash operatorname\{P\}(X\backslash leq\; x)\; =\; \backslash sum\_\{x\_i\; \backslash leq\; x\}\; \backslash operatorname\{P\}(X\; =\; x\_i)\; =\; \backslash sum\_\{x\_i\; \backslash leq\; x\}\; p(x\_i).$$
즉, $x$보다 작거나 같은 모든 $x\_i$ 값들에 대한 확률의 합이다.

* 만약 실수 값을 가지는 확률 변수 $X$의 누적 분포 함수 $F\_X$가 연속 함수라면, $X$는 연속 확률 변수이다. 더 나아가 $F\_X$가 절대 연속이면, 르베그 적분이 가능한 함수 $f\_X(x)$가 존재하여 모든 실수 $a,\; b$ ()에 대해 다음이 성립한다.

이 함수 $f\_X$는 $X$ 분포의 확률 밀도 함수라고 불리며, 거의 어디서나 $F\_X$의 미분과 같다.

이러한 성질을 통해 누적 분포 함수는 확률 변수의 분포를 완전히 나타낼 수 있다.

더 나아가, 다차원 확률 변수, 즉 확률 벡터의 누적 분포 함수도 유사한 성질을 만족한다. 임의의 함수 $F\backslash colon\backslash mathbb\; R^n\backslash to\backslash mathbb\; R$가 어떤 확률 벡터의 누적분포함수이기 위한 필요충분조건은 다음과 같다.

* 증가 조건: 만약 $x,y\backslash in\backslash mathbb\; R^n$이며 모든 $i\backslash in\backslash \{1,\backslash dots,n\backslash \}$에 대해 $x\_i\backslash le\; y\_i$이라면, 다음 부등식이 성립해야 한다.
$\backslash textstyle\backslash sum\_\{t\backslash in\backslash \{x\_1,y\_1\backslash \}\backslash times\backslash cdots\backslash times\backslash \{x\_n,y\_n\backslash \}\}(-1)^$

👆

좌우로 밀어서 보기

📌 열 고정 해제

F(t)\ge 0.
(이 조건과 아래 세 번째 조건은 $F$가 각 변수에 대해 증가 함수임을 함의한다.)
* [[우연속 함수|우연속성]]: 임의의 $x\backslash in\backslash mathbb\; R^n$에 대하여, $F(x^+)=F(x)$이다. 여기서 $F(x^+)=\backslash lim\_\{y\_1\backslash to\; x\_1^+,\backslash dots,y\_n\backslash to\; x\_n^+\}F(y)$이다.
* 극한값 (0): 임의의 $i\backslash in\backslash \{1,\backslash dots,n\backslash \}$ 및 $x\_1,\backslash dots,x\_\{i-1\},x\_\{i+1\},\backslash dots,x\_n\backslash in\backslash mathbb\; R$에 대하여, $F(x\_1,\backslash dots,x\_\{i-1\},-\backslash infty,x\_\{i+1\},\backslash dots,x\_n)=0$이다. 여기서 $F(x\_1,\backslash dots,x\_\{i-1\},-\backslash infty,x\_\{i+1\},\backslash dots,x\_n)=\backslash lim\_\{x\_i\backslash to-\backslash infty\}F(x)$이다.
* 극한값 (1): $F(\backslash infty,\backslash dots,\backslash infty)=1$이다. 여기서 $F(\backslash infty,\backslash dots,\backslash infty)=\backslash lim\_\{x\_1\backslash to\backslash infty,\backslash dots,x\_n\backslash to\backslash infty\}F(x)$이다.

3.2. 확률 분포와의 관계

확률 변수 또는 확률 벡터의 누적분포함수는 그 확률 분포를 유일하게 결정한다. 이는 누적분포함수에 대한 르베그-스틸티어스 측도와 일치한다. 그러나 누적분포함수가 확률 변수 자체를 유일하게 결정하지는 않는다.

확률 변수 $X$가 구간 $(a,b]$에 속할 확률과 특정 실수 $x\backslash in\backslash mathbb\; R$를 취할 확률은 누적분포함수 $F\_X$를 통해 각각 다음과 같이 나타낼 수 있다.
:$\backslash operatorname\{P\}(X\backslash in(a,b])=F\_X(b)-F\_X(a)$
:$\backslash operatorname\{P\}(X=x)=F\_X(x)-F\_X(x^-)$

보다 일반적으로, 확률 벡터 $X=(X\_1,\backslash dots,X\_n)$가 $(a\_1,b\_1]\backslash times\backslash cdots\backslash times(a\_n,b\_n]$에 속할 확률과 특정 값 $x=(x\_1,\backslash dots,x\_n)\backslash in\backslash mathbb\; R^n$을 취할 확률은 각각 다음과 같다.
:$\backslash operatorname\{P\}(X\_1\backslash in(a\_1,b\_1],\backslash dots,X\_n\backslash in(a\_n,b\_n])=\backslash sum\_\{t\backslash in\backslash \{a\_1,b\_1\backslash \}\backslash times\backslash cdots\backslash times\backslash \{a\_n,b\_n\backslash \}\}(-1)^$

👆

좌우로 밀어서 보기

📌 열 고정 해제

F_X(t)
:$\backslash operatorname\{P\}(X\_1=x\_1,\backslash dots,X\_n=x\_n)=\backslash lim\_\{\backslash epsilon\backslash to\; 0^+\}\backslash sum\_\{t\backslash in\backslash \{x\_1-\backslash epsilon,x\_1\backslash \}\backslash times\backslash cdots\backslash times\backslash \{x\_n-\backslash epsilon,x\_n\backslash \}\}(-1)^$

👆

좌우로 밀어서 보기

📌 열 고정 해제

F_X(t)

3.3. 이산성·연속성·특이성과의 관계

모든 누적 분포 함수(CDF) $F\_X$는 단조 증가 함수이며 우연속 함수이다. 이는 CDF가 càdlàg 함수임을 의미한다. 또한 다음 극한값을 만족한다.
:$\backslash lim\_\{x\; \backslash to\; -\backslash infty\}\; F\_X(x)\; =\; 0,\; \backslash quad\; \backslash lim\_\{x\; \backslash to\; +\backslash infty\}\; F\_X(x)\; =\; 1.$
이 세 가지 속성(단조 증가, 우연속, 위 극한값 만족)을 가진 모든 함수는 어떤 확률 변수의 CDF가 될 수 있다.

확률 변수 $X$의 누적분포함수 $F\_X$의 형태는 $X$의 성질(이산성, 연속성, 특이성 등)과 밀접한 관련이 있다.

이산 확률 변수
확률 변수 $X$에 대하여, 다음 두 조건은 서로 동치이다.
* $X$는 이산 확률 변수이다. (즉, 확률의 총합이 1이 되는 가산 집합 $A$ 위에 확률 질량이 분포한다: $\backslash operatorname\{Pr\}(X\backslash in\; A)=1$)
* $X$의 CDF $F\_X$에서 모든 불연속점에서의 점프 크기(좌극한과 함숫값의 차이)의 합이 1이다: $\backslash textstyle\backslash sum\_\{x\backslash in\backslash mathbb\; R\}\backslash left(F\_X(x)-\backslash lim\_\{y\backslash to\; x^-\}F\_X(y)\backslash right)=1$
특히, 계단 함수 형태의 누적분포함수를 갖는 확률 변수는 이산 확률 변수이다. 그러나 그 역은 성립하지 않을 수 있다. (예: 오른쪽 그림처럼 가산 무한 개의 불연속점을 갖는 경우)
$X$가 순수하게 이산적인 확률 변수이고 확률 $p\_i\; =\; \backslash operatorname\{P\}(X=x\_i)$로 값 $x\_1,x\_2,\backslash ldots$을 가진다면, $X$의 CDF는 각 $x\_i$에서 불연속이며, 다음과 같이 표현된다.
:$F\_X(x)\; =\; \backslash operatorname\{P\}(X\backslash leq\; x)\; =\; \backslash sum\_\{x\_i\; \backslash leq\; x\}\; \backslash operatorname\{P\}(X\; =\; x\_i)\; =\; \backslash sum\_\{x\_i\; \backslash leq\; x\}\; p\_i.$

연속 확률 변수
확률 변수 $X$에 대하여, 다음 두 조건은 서로 동치이다.
* $X$는 연속 확률 변수이다. (즉, 임의의 한 점 $x\backslash in\backslash mathbb\; R$에서 확률이 0이다: $\backslash operatorname\{P\}(X=x)=0$)
* $X$의 CDF $F\_X$는 연속 함수이다.

절대 연속 확률 변수
연속 확률 변수 중 특별한 경우로, 확률 변수 $X$에 대하여 다음 두 조건은 서로 동치이다.
* $X$는 절대 연속 확률 변수이다. (즉, $X$의 확률 분포 $\backslash operatorname\{Pr\}(X\backslash in\backslash bullet)$가 르베그 측도에 대해 절대 연속 측도이거나, 동등하게 $X$가 확률 밀도 함수 $f\_X(x)$를 갖는다.)
* $X$의 CDF $F\_X$는 임의의 닫힌구간에서 절대 연속 함수이다.
이 경우, 모든 실수 $a$와 $b$ ()에 대해 다음 관계가 성립한다.
:
여기서 적분은 르베그 적분이다. 함수 $f\_X$는 거의 어디서나 $F\_X$의 미분과 같으며, $X$ 분포의 확률 밀도 함수라고 불린다.

특이 확률 변수
연속 확률 변수 중 절대 연속이 아닌 경우도 있다. 확률 변수 $X$에 대하여, 다음 두 조건은 서로 동치이다.
* $X$는 특이 확률 변수이다. (즉, $X$의 확률 분포 $\backslash operatorname\{Pr\}(X\backslash in\backslash bullet)$와 르베그 측도가 서로 특이 측도이다.)
* $X$의 CDF $F\_X$는 연속 함수이지만, 르베그 측도 기준으로 거의 어디서나 그 미분값이 0이다: $F\_X\text{'}(x)=0$ a.e. (예: 칸토어 분포)

누적분포함수의 분해
르베그 분해 정리에 따라, 임의의 누적분포함수 $F$는 이산 부분($F\_\{\backslash operatorname\{disc\}\}$), 절대 연속 부분($F\_\{\backslash operatorname\{a.c.\}\}$), 특이 연속 부분($F\_\{\backslash operatorname\{s.c.\}\}$)의 합으로 유일하게 표현될 수 있다. 각 부분은 CDF이며, 이들의 가중치 합으로 원래 CDF를 나타낸다.
:$F=c\_\{\backslash operatorname\{disc\}\}F\_\{\backslash operatorname\{disc\}\}+c\_\{\backslash operatorname\{a.c.\}\}F\_\{\backslash operatorname\{a.c.\}\}+c\_\{\backslash operatorname\{s.c.\}\}F\_\{\backslash operatorname\{s.c.\}\}$
여기서 가중치 $c\_\{\backslash operatorname\{disc\}\},\; c\_\{\backslash operatorname\{a.c.\}\},\; c\_\{\backslash operatorname\{s.c.\}\}\; \backslash ge\; 0$ 이고 $c\_\{\backslash operatorname\{disc\}\}+c\_\{\backslash operatorname\{a.c.\}\}+c\_\{\backslash operatorname\{s.c.\}\}=1$ 이다. 이는 어떤 확률 변수라도 이산형, 절대 연속형, 특이 연속형 확률 변수의 볼록 결합으로 생각할 수 있음을 의미한다. 예를 들어, 위 그림 중 세 번째는 이산 부분($c\_\{\backslash operatorname\{disc\}\}>0$)과 연속 부분($c\_\{\backslash operatorname\{a.c.\}\}>0$)을 모두 갖는 경우($c\_\{\backslash operatorname\{s.c.\}\}=0$)를 보여준다.

3.4. 독립성과의 관계

같은 확률 공간 위에 있는 확률 변수 또는 확률 벡터들의 집합 $\backslash mathcal\; X$가 주어졌을 때, 이들이 서로 독립일 필요충분조건은 누적 분포 함수를 이용하여 다음과 같이 표현할 수 있다.

다음 두 조건은 서로 동치이다.
* 집합 $\backslash mathcal\; X$에 속한 확률 변수 또는 확률 벡터들은 서로 독립이다.
* 집합 $\backslash mathcal\; X$에서 임의로 선택한 서로 다른 확률 변수(또는 벡터) $X\_1,\; \backslash dots,\; X\_n$와 각각의 값 $x\_i\; \backslash in\; \backslash operatorname\{dom\}F\_\{X\_i\}$ ($i=1,\backslash dots,n$)에 대하여, 결합 누적 분포 함수가 각 확률 변수(또는 벡터)의 누적 분포 함수의 곱과 같다. 즉, 다음 식이 성립한다:
$F\_\{(X\_1,\backslash dots,X\_n)\}(x\_1,\backslash dots,x\_n)\; =\; F\_\{X\_1\}(x\_1)\; \backslash cdots\; F\_\{X\_n\}(x\_n)$

증명.

첫 번째 조건(독립성)이 성립하면 두 번째 조건(누적 분포 함수의 곱)은 정의상 자명하게 성립한다. 이제 두 번째 조건이 성립한다고 가정하고 첫 번째 조건(독립성)을 증명해 보자. 설명을 위해 유한 개의 확률 변수
:$\backslash mathcal\; X=\backslash \{X\_1,\backslash dots,X\_n\backslash \}$
:$X\_i\backslash colon(\backslash Omega,\backslash mathcal\; F,\backslash operatorname\{Pr\})\backslash to(\backslash mathbb\; R,\backslash mathcal\; B(\backslash mathbb\; R))$
의 경우만 다루지만, 일반적인 경우도 유사하게 증명할 수 있다.

먼저, 구간들의 집합 $\backslash mathcal\; C\; =\; \backslash \{(-\backslash infty,\; x]\; \backslash colon\; x\; \backslash in\; \backslash mathbb\; R\backslash \}$를 정의하자. 이 집합 $\backslash mathcal\; C$는 교집합에 대해 닫혀 있는 π계이며, 실수 상의 보렐 시그마 대수 $\backslash mathcal\; B(\backslash mathbb\; R)$는 $\backslash mathcal\; C$를 포함하는 가장 작은 시그마 대수이다.

이제 다음과 같은 집합 $\backslash mathcal\; L\_n$을 생각하자:
:$\backslash mathcal\; L\_n\; =\; \backslash \{B\_n\; \backslash in\; \backslash mathcal\; B(\backslash mathbb\; R)\; \backslash mid\; \backslash forall\; B\_1,\; \backslash dots,\; B\_\{n-1\}\; \backslash in\; \backslash mathcal\; C\; \backslash colon\; \backslash operatorname\{Pr\}(X\_1\; \backslash in\; B\_1,\; \backslash dots,\; X\_n\; \backslash in\; B\_n)\; =\; \backslash operatorname\{Pr\}(X\_1\; \backslash in\; B\_1)\; \backslash cdots\; \backslash operatorname\{Pr\}(X\_n\; \backslash in\; B\_n)\backslash \}$
가정에 의해, 모든 $(-\backslash infty,\; x\_n]$ 형태의 구간은 $\backslash mathcal\; L\_n$에 속하므로, $\backslash mathcal\; C\; \backslash subseteq\; \backslash mathcal\; L\_n$이다. 또한, $\backslash mathcal\; L\_n$이 λ계의 조건들(전체 공간 포함, 여집합에 대해 닫힘, 서로소인 가산 합집합에 대해 닫힘)을 만족함을 보일 수 있다. 딘킨 π-λ 정리에 따르면, π계를 포함하는 λ계는 그 π계가 생성하는 시그마 대수 전체를 포함해야 하므로, $\backslash mathcal\; L\_n\; =\; \backslash mathcal\; B(\backslash mathbb\; R)$가 된다.

다음으로, 비슷한 방식으로 집합 $\backslash mathcal\; L\_\{n-1\}$을 정의한다:
:$\backslash mathcal\; L\_\{n-1\}\; =\; \backslash \{B\_\{n-1\}\; \backslash in\; \backslash mathcal\; B(\backslash mathbb\; R)\; \backslash mid\; \backslash forall\; B\_1,\; \backslash dots,\; B\_\{n-2\}\; \backslash in\; \backslash mathcal\; C,\; B\_n\; \backslash in\; \backslash mathcal\; B(\backslash mathbb\; R)\; \backslash colon\; \backslash operatorname\{Pr\}(X\_1\; \backslash in\; B\_1,\; \backslash dots,\; X\_n\; \backslash in\; B\_n)\; =\; \backslash operatorname\{Pr\}(X\_1\; \backslash in\; B\_1)\; \backslash cdots\; \backslash operatorname\{Pr\}(X\_n\; \backslash in\; B\_n)\backslash \}$
앞선 결과($\backslash mathcal\; L\_n\; =\; \backslash mathcal\; B(\backslash mathbb\; R)$)로부터 $\backslash mathcal\; C\; \backslash subseteq\; \backslash mathcal\; L\_\{n-1\}$임을 알 수 있고, $\backslash mathcal\; L\_\{n-1\}$ 역시 λ계임을 보일 수 있다. 따라서 딘킨 π-λ 정리에 의해 $\backslash mathcal\; L\_\{n-1\}\; =\; \backslash mathcal\; B(\backslash mathbb\; R)$이다.

이 과정을 $n-1$번 반복하면, 결국 임의의 보렐 집합 $B\_1,\; \backslash dots,\; B\_n\; \backslash in\; \backslash mathcal\; B(\backslash mathbb\; R)$에 대하여 다음 식이 성립함을 알 수 있다:
:$\backslash operatorname\{Pr\}(X\_1\; \backslash in\; B\_1,\; \backslash dots,\; X\_n\; \backslash in\; B\_n)\; =\; \backslash operatorname\{Pr\}(X\_1\; \backslash in\; B\_1)\; \backslash cdots\; \backslash operatorname\{Pr\}(X\_n\; \backslash in\; B\_n)$
이는 확률 변수들 $\backslash \{X\_1,\; \backslash dots,\; X\_n\backslash \}$이 서로 독립이라는 정의와 정확히 일치한다.

증명 끝.

4. 파생 함수

누적 분포 함수(CDF)로부터 여러 가지 유용한 함수들을 파생시킬 수 있다. 이러한 함수들은 특정 확률적 질문에 답하거나 데이터의 특성을 파악하는 데 도움을 준다.

* 여누적 분포 함수 (Complementary CDF): 확률 변수가 특정 값 x보다 클 확률, 즉 P(X > x)를 나타낸다. 이는 생존 분석에서의 생존 함수나 신뢰성 공학에서의 신뢰성 함수와 같은 개념으로 사용된다.
* 분위 함수 (Quantile Function): 누적 분포 함수의 역함수에 해당한다. 특정 누적 확률 p에 대응하는 확률 변수의 값 x를 찾는 데 사용되며, 역변환 표본 추출 등에 활용된다.
* 접힌 누적 분포 (Folded CDF): 누적 분포 함수의 그래프를 특정 지점(주로 중앙값에 해당하는 확률 0.5)을 기준으로 접어서 만든 그래프이다. 분포의 대칭성이나 퍼짐 정도를 시각적으로 파악하는 데 유용하다.
* 경험적 분포 함수 (Empirical CDF): 실제 관측된 표본 데이터를 이용하여 모집단의 누적 분포 함수를 추정한 것이다. 표본 크기가 커짐에 따라 실제 모집단의 누적 분포 함수에 수렴한다.

각 파생 함수에 대한 자세한 정의와 속성은 해당 하위 섹션에서 설명한다.

4.1. 여(상보) 누적분포함수 (꼬리 분포)

때로는 확률 변수가 특정 값보다 클 확률, 즉 P(X > x)를 아는 것이 유용할 때가 있다. 이를 여누적 분포 함수(complementary cumulative distribution function, CCDF) 또는 간단히 꼬리 분포(tail distribution), 초과 확률(exceedance probability), 상측 확률(upper-tail probability)이라고 부른다. 정의는 다음과 같다.
$$\backslash bar\; F\_X(x)\; =\; \backslash operatorname\{P\}(X\; >\; x)\; =\; 1\; -\; F\_X(x)$$

여누적 분포 함수는 여러 분야에서 활용된다. 예를 들어 통계학적 가설 검정에서는 관찰된 검정 통계량보다 더 극단적인 값이 나올 확률, 즉 p-값을 계산하는 데 사용된다. 검정 통계량 T가 연속적인 분포를 가질 때, 관찰된 값 $t$에 대한 일방 p-값은 다음과 같이 여누적 분포 함수로 간단히 표현된다.
$$p\; =\; \backslash operatorname\{P\}(T\; \backslash ge\; t)\; =\; \backslash operatorname\{P\}(T\; >\; t)\; =\; 1\; -\; F\_T(t)$$

생존 분석 분야에서는 여누적 분포 함수를 생존 함수(survival function)라고 부르며 $S(x)$로 표기한다. 공학, 특히 신뢰성 공학에서는 이를 "신뢰성 함수"(reliability function)라고 부르기도 한다.

속성
* 기댓값($\backslash operatorname\{E\}(X)$)을 갖는 음이 아닌 연속 확률 변수 X의 경우, 마르코프 부등식에 따라 다음이 성립한다.
$$\backslash bar\; F\_X(x)\; \backslash leq\; \backslash frac\{\backslash operatorname\{E\}(X)\}\{x\}$$
* x가 무한대로 갈 때 ($x\; \backslash to\; \backslash infty$), 여누적 분포 함수 값은 0으로 수렴한다 ($\backslash bar\; F\_X(x)\; \backslash to\; 0$). 만약 기댓값 $\backslash operatorname\{E\}(X)$가 유한하다면, $\backslash bar\; F\_X(x)\; =\; o(1/x)$ 관계가 성립한다. 즉, $1/x$보다 빠르게 0으로 수렴한다.
증명: $X$가 밀도 함수 $f\_X$를 갖는다고 가정하면, 모든 $c\; >\; 0$에 대해
$$\backslash operatorname\{E\}(X)\; =\; \backslash int\_0^\backslash infty\; x\; f\_X(x)\; \backslash ,\; dx\; \backslash geq\; \backslash int\_0^c\; x\; f\_X(x)\; \backslash ,\; dx\; +\; c\backslash int\_c^\backslash infty\; f\_X(x)\; \backslash ,\; dx$$
$\backslash bar\; F\_X(c)\; =\; \backslash int\_c^\backslash infty\; f\_X(x)\; \backslash ,\; dx$임을 이용하여 항을 재배열하면,
$$0\; \backslash leq\; c\backslash bar\; F\_X(c)\; \backslash leq\; \backslash operatorname\{E\}(X)\; -\; \backslash int\_0^c\; x\; f\_X(x)\; \backslash ,\; dx\; \backslash to\; 0\; \backslash text\{\; as\; \}\; c\; \backslash to\; \backslash infty$$
가 된다.
* 기댓값을 갖는 확률 변수의 경우, 기댓값은 다음과 같이 계산할 수 있다.
$$\backslash operatorname\{E\}(X)\; =\; \backslash int\_0^\backslash infty\; \backslash bar\; F\_X(x)\; \backslash ,\; dx\; -\; \backslash int\_\{-\backslash infty\}^0\; F\_X(x)\; \backslash ,\; dx$$
만약 확률 변수가 음이 아닌 값만 갖는다면, 두 번째 항($\backslash int\_\{-\backslash infty\}^0\; F\_X(x)\; \backslash ,\; dx$)은 0이 된다. 확률 변수가 음이 아닌 정수 값만 가질 수 있다면, 기댓값은 다음과 같이 급수로 표현된다.
$$\backslash operatorname\{E\}(X)\; =\; \backslash sum\_\{n=0\}^\backslash infty\; \backslash bar\; F\_X(n)$$

4.2. 분위 함수 (역함수)

누적 분포 함수(CDF) F가 엄격하게 증가하고 연속적이면, $F^\{-1\}(\; p\; ),\; p\; \backslash in\; [0,1],$는 $F(x)\; =\; p$를 만족하는 유일한 실수 $x$이다. 이 $F^\{-1\}$를 [[분위 함수]](quantile function) 또는 역 분포 함수라고 부른다. 역변환 표본 추출 등에서 사용된다.

모든 분포가 고유한 역함수를 갖는 것은 아니다. 예를 들어, 특정 구간 $(a,\; b)$에서 확률 밀도 함수 $f\_X(x)=0$이라면, 해당 구간에서 누적 분포 함수 $F\_X$는 상수값을 가지므로 역함수가 유일하게 정의되지 않는다. 이런 경우에는 다음과 같이 정의되는 일반화된 역 분포 함수를 사용할 수 있다.
:$$
F^{-1}(p) = \inf \{x \in \mathbb{R}: F(x) \geq p \}, \quad \forall p \in [0,1].

여기서 $\backslash inf$는 하한을 의미한다. 이 일반화된 정의를 사용하면 모든 누적 분포 함수에 대해 역함수를 정의할 수 있다.

* 예시 1: 중앙값은 $F^\{-1\}(\; 0.5\; )$이다.
* 예시 2: $\backslash tau\; =\; F^\{-1\}(\; 0.95\; )$로 두면, $\backslash tau$는 95번째 백분위수라고 부른다.

역 CDF(일반화된 역 분포 함수 포함)는 다음과 같은 유용한 속성을 가진다.

# $F^\{-1\}$는 감소하지 않는다.
# $F^\{-1\}(F(x))\; \backslash leq\; x$
# $F(F^\{-1\}(p))\; \backslash geq\; p$
# $F^\{-1\}(p)\; \backslash leq\; x$는 $p\; \backslash leq\; F(x)$와 동치이다.
# 만약 확률 변수 $Y$가 구간 [0, 1]에서의 균등 분포($U[0,\; 1]$)를 따른다면, $F^\{-1\}(Y)$는 누적 분포 함수 $F$를 따르는 분포를 가진다. 이 속성은 역변환 표본 추출 방법을 사용하여 난수 생성에 활용된다.

CDF의 역함수인 분위 함수는 균등 분포에서 얻은 결과를 다른 분포로 변환하는 데 사용될 수 있다. 특히 정규 분포의 분위 함수는 프로빗이라고도 불린다.

4.3. 접힌 누적분포

누적 분포 $F$의 그래프는 보통 S자 모양을 갖지만, 그래프의 상반부(누적 확률이 0.5를 넘는 부분)를 아래로 접어서 표현하는 방식도 있다. 이를 접힌 누적 분포 또는 산 모양 그림이라고 부른다.

수학적으로는 다음과 같이 정의된다.
:$F\_\backslash text\{fold\}(x)=F(x)1\_\{\backslash \{F(x)\backslash leq\; 0.5\backslash \}\}+(1-F(x))1\_\{\backslash \{F(x)>0.5\backslash \}\}$
여기서 $1\_\{\backslash \{A\backslash \}\}$는 특정 조건을 만족할 때만 1이 되고, 그렇지 않으면 0이 되는 지시 함수를 의미한다. 즉, 누적 분포 $F(x)$가 0.5 이하일 때는 원래 값을 그대로 사용하고, 0.5보다 클 때는 $1-F(x)$ 값을 사용한다. $1-F(x)$는 생존 함수라고도 불린다.

이런 방식으로 그래프를 그리면 산봉우리 모양이 되며, 누적 확률 0.5를 기준으로 올라가는 부분과 내려오는 부분에 대해 각각 다른 눈금을 사용한다. 접힌 누적 분포 그래프는 분포의 중앙값, 분산 (특히 중앙값으로부터의 평균 절대 편차) 및 왜도(분포가 얼마나 비대칭적인지)를 시각적으로 파악하는 데 유용하다.

4.4. 경험적 분포 함수

표본 누적 분포 함수는 표본 내 점들을 생성한 누적 분포 함수의 추정치이다. 이는 확률 1로 해당 기본 분포로 수렴한다. 표본 누적 분포 함수가 기본 누적 분포 함수로 수렴하는 속도를 정량화하기 위한 다수의 결과가 존재한다.

5. 예시

예시로, $X$가 단위 구간 $[0,1]$에서 균등 분포를 따른다고 가정해 보자.

그러면 $X$의 CDF는 다음과 같다.
$$F\_X(x)\; =\; \backslash begin\{cases\}$$
0 &:\ x < 0\\
x &:\ 0 \le x \le 1\\
1 &:\ x > 1
\end{cases}

대신 $X$가 0과 1의 이산 값만 동일한 확률로 갖는다고 가정해 보자.

그러면 $X$의 CDF는 다음과 같다.
$$F\_X(x)\; =\; \backslash begin\{cases\}$$
0 &:\ x < 0\\
1/2 &:\ 0 \le x < 1\\
1 &:\ x \ge 1
\end{cases}

$X$가 지수 분포를 따른다고 가정해 보자. 그러면 $X$의 CDF는 다음과 같다.
$$F\_X(x;\backslash lambda)\; =\; \backslash begin\{cases\}$$
1-e^{-\lambda x} & x \ge 0, \\
0 & x < 0.
\end{cases}

여기서 $\backslash lambda\; >\; 0$는 분포의 매개변수이며, 종종 속도 매개변수라고 한다.

$X$가 정규 분포를 따른다고 가정해 보자. 그러면 $X$의 CDF는 다음과 같다.
$$F(t;\backslash mu,\backslash sigma)\; =\; \backslash frac\{1\}\{\backslash sigma\backslash sqrt\{2\backslash pi\}\}\; \backslash int\_\{-\backslash infty\}^t\; \backslash exp\; \backslash left(\; -\backslash frac\{(x\; -\; \backslash mu)^2\}\{2\backslash sigma^2\}\; \backslash right)\backslash ,\; dx.$$

여기서 매개변수 $\backslash mu$는 분포의 평균 또는 기댓값이고, $\backslash sigma$는 표준 편차이다.

표준 정규 분포의 CDF 표는 통계적 응용 분야에서 자주 사용되며, 표준 정규 분포표, 단위 정규 분포표, 또는 Z표라고 한다.

$X$가 이항 분포를 따른다고 가정해 보자. 그러면 $X$의 CDF는 다음과 같다.
$$F(k;n,p)\; =\; \backslash Pr(X\backslash leq\; k)\; =\; \backslash sum\; \_\{i=0\}^\{\backslash lfloor\; k\backslash rfloor\; \}\{n\; \backslash choose\; i\}\; p^\{i\}\; (1-p)^\{n-i\}$$

여기서 $p$는 성공 확률이고, 함수는 $n$개의 독립적인 실험 시퀀스에서 성공 횟수의 이산 확률 분포를 나타내며, $\backslash lfloor\; k\backslash rfloor$는 $k$보다 작거나 같은 최대 정수인 $k$의 "바닥"을 나타낸다.

6. 다변수 누적분포함수

둘 이상의 확률 변수를 동시에 다룰 때는 각 변수가 특정 값 이하일 확률을 함께 고려하는 결합 누적 분포 함수(Joint Cumulative Distribution Function)를 정의하여 사용한다. 예를 들어, 두 확률 변수 $X$와 $Y$에 대한 결합 누적 분포 함수는 $X$가 특정 값 $x$보다 작거나 같은 값을 가지면서 동시에 $Y$가 특정 값 $y$보다 작거나 같은 값을 가질 확률을 나타낸다. 이러한 개념은 두 개를 넘어 여러 개의 확률 변수에 대해서도 동일하게 확장하여 적용할 수 있다.

6.1. 두 확률 변수에 대한 정의

둘 이상의 확률 변수를 동시에 다룰 때는 결합 누적 분포 함수(Joint Cumulative Distribution Function)를 정의할 수 있다. 예를 들어, 두 확률 변수 $X,Y$에 대한 결합 누적 분포 함수 $F\_\{XY\}$는 다음과 같이 주어진다.

$$F\_\{X,Y\}(x,y)\; =\; \backslash operatorname\{P\}(X\backslash leq\; x,Y\backslash leq\; y)$$

여기서 우변은 확률 변수 $X$가 $x$보다 작거나 같은 값을 취하고 그리고 $Y$가 $y$보다 작거나 같은 값을 취할 확률을 나타낸다.

결합 누적 분포 함수의 예시는 다음과 같다.

* 두 개의 연속 확률 변수 X와 Y의 경우, 특정 구간에 속할 확률은 다음과 같이 계산할 수 있다.

여기서 $f(x,y)$는 결합 확률 밀도 함수이다.

* 두 개의 이산 확률 변수의 경우, 각 X와 Y 값에 대한 결합 확률 질량 함수를 표로 나타내고, 이를 이용해 결합 누적 분포 함수를 계산할 수 있다. 예를 들어, 다음과 같은 결합 확률 질량 함수가 주어졌다고 가정하자.

👆

좌우로 밀어서 보기

📌 열 고정 해제

결합 확률 질량 함수 예시

	Y = 2	Y = 4	Y = 6	Y = 8
X = 1	0	0.1	0	0.1
X = 3	0	0	0.2	0
X = 5	0.3	0	0	0.15
X = 7	0	0	0.15	0

이 표를 바탕으로, 각 X와 Y의 특정 값보다 작거나 같을 누적 확률을 계산하여 다음과 같은 결합 누적 분포 함수 테이블을 만들 수 있다. 예를 들어, $F\_\{X,Y\}(3,\; 6)\; =\; \backslash operatorname\{P\}(X\backslash leq\; 3,\; Y\backslash leq\; 6)$는 $X\; \backslash le\; 3$이고 $Y\; \backslash le\; 6$인 모든 칸의 확률 값을 더한 값이다 ($0+0.1+0+0+0+0.2\; =\; 0.3$).

👆

좌우로 밀어서 보기

📌 열 고정 해제

결합 누적 분포 함수 예시

	Y < 2	Y ≤ 2	Y ≤ 4	Y ≤ 6	Y ≤ 8 (모든 Y)
X < 1	0	0	0	0	0
X ≤ 1	0	0	0.1	0.1	0.2
X ≤ 3	0	0	0.1	0.3	0.4
X ≤ 5	0	0.3	0.4	0.6	0.85
X ≤ 7 (모든 X)	0	0.3	0.4	0.75	1

6.2. 두 개 이상의 확률 변수에 대한 정의

$N$개의 확률 변수 $X\_1,\; \backslash ldots,\; X\_N$에 대해, 결합 누적 분포 함수 $F\_\{X\_1,\; \backslash ldots,\; X\_N\}$는 다음과 같이 정의된다.

$F\_\{X\_1,\backslash ldots,X\_N\}(x\_1,\backslash ldots,x\_N)\; =\; \backslash operatorname\{P\}(X\_1\; \backslash leq\; x\_1,\backslash ldots,X\_N\; \backslash leq\; x\_N)$

$N$개의 확률 변수를 확률 벡터 $\backslash mathbf\{X\}\; =\; (X\_1,\; \backslash ldots,\; X\_N)^T$로 생각하면 다음과 같이 더 간결하게 표기할 수 있다.

$F\_\{\backslash mathbf\{X\}\}(\backslash mathbf\{x\})\; =\; \backslash operatorname\{P\}(X\_1\; \backslash leq\; x\_1,\backslash ldots,X\_N\; \backslash leq\; x\_N)$

6.3. 다변수 누적분포함수의 성질

모든 다변수 누적 분포 함수(CDF)는 다음과 같은 특성을 갖는다.

# 각 변수에 대해 단조 감소하지 않는다.
# 각 변수에 대해 오른쪽 연속이다.
# 함수의 값은 0과 1 사이에 있다: $0\backslash leq\; F\_\{X\_1\; \backslash ldots\; X\_n\}(x\_1,\backslash ldots,x\_n)\backslash leq\; 1$
# 모든 변수가 양의 무한대로 갈 때 극한값은 1이고, 어느 한 변수라도 음의 무한대로 갈 때 극한값은 0이다: $$\backslash lim\_\{x\_1,\backslash ldots,x\_n\; \backslash rightarrow+\backslash infty\}F\_\{X\_1\; \backslash ldots\; X\_n\}(x\_1,\backslash ldots,x\_n)=1$$ 이고, 모든 $i$에 대해 $\backslash lim\_\{x\_i\backslash rightarrow-\backslash infty\}F\_\{X\_1\; \backslash ldots\; X\_n\}(x\_1,\backslash ldots,x\_n)=0$ 이다.

하지만 위의 네 가지 속성을 모두 만족하는 함수라고 해서 반드시 다변수 CDF인 것은 아니다. 이는 단일 변수 CDF의 경우와 다르다. 예를 들어, 또는 또는 일 경우 $F(x,y)=0$이고, 그렇지 않은 경우 $F(x,y)=1$인 함수를 생각해보자. 이 함수는 위 네 조건을 만족하지만 CDF는 아니다. 만약 CDF라면, 아래에서 설명하는 확률 계산 방식에 따라 값이 음수가 되어 모순이 발생하기 때문이다.

다변수 CDF를 이용하여 어떤 점이 특정 초직육면체에 속할 확률은 1차원 경우와 유사한 방식으로 계산할 수 있다:

7. 복소수 누적분포함수

실수에서 복소 확률 변수로의 누적 분포 함수를 일반화하는 것은 간단하지 않다. 왜냐하면 복소수 사이에는 명확한 대소 관계가 없으므로 $P(Z\; \backslash leq\; 1+2i)$와 같은 표현은 의미를 정의하기 어렵기 때문이다. 하지만 복소수의 실수부와 허수부는 각각 실수이므로, $P(\backslash Re\{(Z)\}\; \backslash leq\; 1,\; \backslash Im\{(Z)\}\; \backslash leq\; 3)$와 같은 형태의 표현은 의미를 가질 수 있다.

따라서 복소 확률 변수 $Z$의 누적 분포 함수 $F\_Z(z)$는 $Z$의 실수부($\backslash Re\{(Z)\}$)와 허수부($\backslash Im\{(Z)\}$)의 결합 확률 분포를 이용하여 다음과 같이 정의한다.
$$F\_Z(z)\; =\; F\_\{\backslash Re\{(Z)\},\backslash Im\{(Z)\}\}(\backslash Re\{(z)\},\backslash Im\{(z)\})\; =\; P(\backslash Re\{(Z)\}\; \backslash leq\; \backslash Re\{(z)\}\; ,\; \backslash Im\{(Z)\}\; \backslash leq\; \backslash Im\{(z)\}).$$

이 정의는 복소 확률 벡터 $\backslash mathbf\{Z\}\; =\; (Z\_1,\backslash ldots,Z\_N)^T$로 확장될 수 있다. 복소 확률 벡터 $\backslash mathbf\{Z\}$의 누적 분포 함수 $F\_\{\backslash mathbf\{Z\}\}(\backslash mathbf\{z\})$는 각 성분 $Z\_k$의 실수부와 허수부 모두가 특정 값($\backslash Re\{(z\_k)\}$, $\backslash Im\{(z\_k)\}$)보다 작거나 같을 확률로 정의된다.
$$F\_\{\backslash mathbf\{Z\}\}(\backslash mathbf\{z\})\; =\; F\_\{\backslash Re\{(Z\_1)\},\backslash Im\{(Z\_1)\},\; \backslash ldots,\; \backslash Re\{(Z\_n)\},\backslash Im\{(Z\_n)\}\}(\backslash Re\{(z\_1)\},\; \backslash Im\{(z\_1)\},\backslash ldots,\backslash Re\{(z\_n)\},\; \backslash Im\{(z\_n)\})\; =\; \backslash operatorname\{P\}(\backslash Re\{(Z\_1)\}\; \backslash leq\; \backslash Re\{(z\_1)\},\backslash Im\{(Z\_1)\}\; \backslash leq\; \backslash Im\{(z\_1)\},\backslash ldots,\backslash Re\{(Z\_n)\}\; \backslash leq\; \backslash Re\{(z\_n)\},\backslash Im\{(Z\_n)\}\; \backslash leq\; \backslash Im\{(z\_n)\})$$

8. 통계적 분석에서의 활용

누적 분포 함수의 개념은 통계 분석에서 크게 두 가지 방식으로 활용된다. 하나는 누적 빈도 분석이며, 다른 하나는 경험적 분포 함수를 이용한 통계적 가설 검정이다. 이러한 접근 방식들은 데이터의 분포 특성을 파악하고 통계적 추론을 수행하는 데 중요한 역할을 한다.

8.1. 누적 빈도 분석

누적 빈도 분석은 특정 현상의 값이 기준 값보다 작은 경우의 발생 빈도에 대한 분석이다. 이는 누적 분포 함수의 개념이 통계 분석에서 나타나는 한 가지 방식이다.

8.2. 콜모고로프-스미르노프 검정 및 카이퍼 검정

누적 분포 함수는 통계 분석에서 중요한 역할을 하며, 특히 경험적 분포 함수는 누적 분포 함수를 직접 추정한 것으로 다양한 통계적 가설 검정의 기초가 된다. 이러한 검정들은 주어진 데이터 표본이 특정 분포에서 나왔는지, 또는 두 개의 데이터 표본이 동일한 모집단 분포에서 나왔는지 등을 평가하는 데 사용될 수 있다.

콜모고로프-스미르노프 검정은 누적 분포 함수를 기반으로 하는 대표적인 통계적 가설 검정 방법이다. 이 검정은 두 개의 경험적 분포 함수가 서로 다른지, 또는 특정 경험적 분포 함수가 이론적으로 기대되는 이상적인 분포와 다른지를 비교하는 데 사용된다.

카이퍼 검정은 콜모고로프-스미르노프 검정과 밀접하게 관련된 검정 방법이다. 특히 카이퍼 검정은 분포의 영역이 요일이나 월과 같이 순환적인 특징을 가질 때 유용하게 활용될 수 있다. 예를 들어, 연중 특정 시기에 토네이도 발생 빈도가 달라지는지, 혹은 특정 제품의 판매량이 요일이나 월별로 주기적인 변화를 보이는지 등을 검정하는 데 카이퍼 검정을 사용할 수 있다.