테일러 소용돌이
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
테일러 소용돌이는 회전하는 동축 실린더 사이의 유체 흐름인 테일러-쿠에트 흐름에서 테일러 수가 임계값을 초과할 때 형성되는 와류이다. 흐름의 안정성은 레일리의 기준과 테일러 수에 의해 결정되며, 테일러 와류가 형성되면 새로운 흐름 패턴이 나타난다. 골럽-스위니 실험은 테일러-쿠에트 흐름의 난류 전이를 연구했으며, 이는 유체역학적 시스템의 난류 전환 이해에 기여했다.
더 읽어볼만한 페이지
- 소용돌이 - 사이클론
사이클론은 저기압성 순환을 보이는 대기 현상으로, 규모와 형성과정에 따라 다양한 유형으로 나뉘며, 북반구는 반시계 방향, 남반구는 시계 방향으로 회전하는 특징을 갖고, 열대 사이클론은 해수면 온도, 대기 불안정, 습도 등의 조건에서 형성되고 강도에 따라 여러 단계로 구분되며, 지구 외 다른 행성에서도 관측된다. - 소용돌이 - 허리케인
허리케인은 시속 119km 이상의 강풍과 눈을 동반하는 열대성 저기압으로, 대서양 북부 등에서 주로 발생하며 강도에 따라 등급이 나뉘고, 다양한 요인에 의해 경로가 결정되며, 심각한 피해를 일으키므로 대비가 중요하다. - 유체역학 - 양력
양력은 유체 속에서 물체가 받는 수직 방향의 힘이며, 받음각, 익형, 공기 밀도 등에 따라 달라지며 항공기 날개, 헬리콥터, 선박 프로펠러 등에서 활용된다. - 유체역학 - 무인 항공기
무인 항공기는 조종사 없이 자율 또는 원격 조종으로 비행하는 동력 비행체로, 다양한 기준으로 분류되어 군사 및 민간용으로 활용되지만 안전 및 보안 위협, 사이버 공격, 악의적 사용 가능성 등의 문제점도 존재한다.
2. 흐름 특성
간단한 테일러-쿠에트 흐름은 회전하는 무한히 긴 동축 실린더 사이에서 생성되는 정상 흐름이다.[3] 실린더 길이가 무한히 길기 때문에 흐름은 본질적으로 정상 상태에서 단방향이다. 안쪽 실린더의 반지름을 반지름/Radius영어 ''R''1이라 하고, 일정한 각속도 ''Ω''1으로 회전하며, 바깥 실린더의 반지름을 ''R''2라 하고 일정한 각속도 ''Ω''2으로 회전한다고 하면, 방위각 속도 성분은 다음과 같다.[4]
:''v''θ = ''Ar'' + ''B''/''r'', ''A'' = ''Ω''1 (''μ'' - ''η''2) / (1 - ''η''2), ''B'' = ''Ω''1 ''R''12 (1 - ''μ'') / (1 - ''η''2)
여기서
:''μ'' = ''Ω''2 / ''Ω''1, ''η'' = ''R''1 / ''R''2.
2. 1. 기본 흐름
간단한 테일러-쿠에트 흐름은 회전하는 무한히 긴 동축 실린더 사이에서 생성되는 정상 흐름이다.[3] 실린더 길이가 무한히 길기 때문에 흐름은 본질적으로 정상 상태에서 단방향이다. 안쪽 실린더의 반지름을 반지름/Radius영어 이라 하고, 일정한 각속도 으로 회전하며, 바깥 실린더의 반지름을 라 하고 일정한 각속도 으로 회전한다고 하면, 방위각 속도 성분은 다음과 같다.[4]:
여기서
:
3. 안정성 기준
레일리 경[5][6]은 비점성 가정을 사용하여, 즉 오일러 방정식을 섭동하여 문제의 안정성을 연구했다. 이 기준은 다음과 같다. ''점성이 없는 경우, 방위각 속도 의 분포가 안정하기 위한 필요 충분 조건은''[7]
:
''구간의 모든 곳에서 성립해야 하며, 가 구간 내의 어느 곳에서든 감소하면 분포는 불안정하다.'' 는 회전축에 대한 유체 요소의 단위 질량당 각운동량을 나타내므로, 이 기준을 다르게 표현하면 다음과 같다. ''축에 대한 각운동량의 층화는 밖으로 단조롭게 증가하는 경우에만 안정하다.''
이 기준을 테일러-쿠에트 흐름에 적용하면, 흐름은 일 때 안정하다는 것을 알 수 있다. 즉, 안정성을 위해서는 외부 실린더가 내부 실린더의 각속도의 배보다 더 큰 각속도로 (같은 방향으로) 회전해야 한다. 레일리의 기준은 일 때 전체 유체에서 위반()된다. 반면에, 실린더가 반대 방향으로 회전할 때, 즉 일 때, 레일리의 기준은 내부 영역에서만 위반된다. 즉, for
4. 테일러 와류
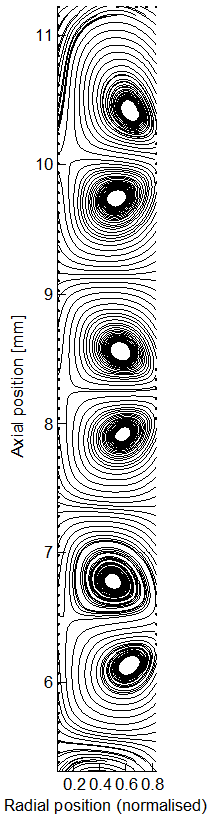
제프리 잉그램 테일러 경의 이름을 따서 명명된 테일러 와류는 회전하는 테일러-쿠에트 흐름에서 테일러 수(
흐름이
:
인 경우 흐름의 불안정성이 존재하지 않는다. 즉, 흐름에 대한 교란은 점성력에 의해 감쇠되고 흐름은 정상 상태이다. 그러나
이상적인 수학적 문제는
4. 1. 테일러 와류 발생 조건
제프리 잉그램 테일러 경의 이름을 따서 명명된 테일러 와류는 회전하는 테일러-쿠에트 흐름에서 테일러 수(흐름이
4. 2. 테일러 와류 이후의 흐름 변화
회전하는 테일러-쿠에트 흐름에서 흐름의 테일러 수(
흐름이
5. 골럽-스위니 실험
1975년, J. P. 골럽과 H. L. 스위니는 회전하는 유체의 난류 발생에 관한 논문을 발표했다.[12] 테일러-쿠에트 흐름 시스템에서 회전 속도가 증가함에 따라 유체가 일련의 "유체 도넛"으로 층을 이루는 것을 관찰했다. 회전 속도가 더 증가하면 도넛이 진동하고 꼬이다가 마침내 난류가 된다. 그들의 연구는 난류에서 뤼엘-타켄스 시나리오를 확립하는 데 기여했으며,[13] 이는 유체역학적 시스템이 안정적인 흐름 패턴에서 난류로 어떻게 전환되는지 이해하는 데 중요한 공헌이다. 이 전환의 주요 지배 요인은 레이놀즈 수이지만, 흐름이 열린 흐름(측면 상류 및 하류가 존재)인지 닫힌 흐름(흐름이 측면으로 제한됨, 예: 회전)인지, 그리고 경계가 있는 흐름(벽 효과의 영향을 받음)인지 경계가 없는 흐름(벽 효과의 영향을 받지 않음)인지에 따라 다른 중요한 영향 요인이 존재한다. 이러한 분류에 따르면 테일러-쿠에트 흐름은 닫힌 경계 흐름 시스템에서 형성되는 흐름 패턴의 예이다.
6. 한국의 연구 동향
참조
[1]
논문
Stability of a viscous liquid contained between two rotating cylinders
[2]
논문
Flow regimes in a circular Couette system with independently rotating cylinders
[3]
서적
Hydrodynamic Stability
Cambridge University Press
[4]
논문
The growth of Taylor vortices in flow between rotating cylinders
[5]
간행물
"On the stability or instability of certain fluid motions. Scientific Papers, 3."
Rayleigh, Lord
1880
[6]
간행물
"On the dynamics of revolving fluids."
Rayleigh, Lord
1917
[7]
서적
Hydrodynamic and hydromagnetic stability
Courier Corporation
2013
[8]
논문
Delaying Transition in Taylor–Couette Flow with Axial Motion of the Inner Cylinder
[9]
논문
Quasi-Periodic State and Transition to Turbulence in a Rotating Couette System
[10]
논문
Velocity field for Taylor–Couette flow with an axial flow
[11]
논문
A Periodically Forced Flow Displaying Symmetry Breaking Via a Three-Tori Gluing Bifurcation and Two-Tori Resonances
[12]
논문
Onset of turbulence in a rotating fluid
http://scholarship.h[...]
[13]
서적
Dynamical System and Chaos
Springer Berlin
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
