양력

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

양력은 물체가 유체 내에서 움직일 때 발생하는 힘으로, 항공기, 헬리콥터, 풍력 터빈 등 다양한 분야에서 활용된다. 양력은 받음각, 에어포일 형상, 공기 밀도, 속도 등 여러 요소에 의해 영향을 받으며, 뉴턴의 운동 법칙과 베르누이 방정식 등을 통해 설명할 수 있다. 실속, 마그누스 효과, 지면 효과 등 양력과 관련된 다양한 현상들이 존재하며, 항공기 설계 및 운용에 중요한 영향을 미친다.

더 읽어볼만한 페이지

힘 - 전기장
전기장은 공간의 각 지점에서 단위 전하가 받는 힘으로 정의되는 벡터장으로, 전하 또는 시간에 따라 변하는 자기장에 의해 발생하며, 전기력선으로 표현되고 맥스웰 방정식으로 기술되는 전자기장의 한 요소이다.
힘 - 복원력
복원력은 변화나 환경에 적응하여 원래 상태로 회복하거나 새로운 균형을 찾는 능력이다.
유체역학 - 무인 항공기
무인 항공기는 조종사 없이 자율 또는 원격 조종으로 비행하는 동력 비행체로, 다양한 기준으로 분류되어 군사 및 민간용으로 활용되지만 안전 및 보안 위협, 사이버 공격, 악의적 사용 가능성 등의 문제점도 존재한다.
유체역학 - 점도계
점도계는 유체의 점도를 측정하는 장치로, 오스트왈트 점도계, 낙하구 점도계, U자관 점도계 등 다양한 종류가 있으며 측정 대상 유체의 종류와 특성에 따라 적절한 점도계를 선택하여 사용하는 것이 중요하다.

양력
개요
힘의 종류	공기역학적 힘
방향	유체 흐름에 수직
발생 원인	에어포일 또는 다른 물체가 유체 흐름을 변경할 때 발생
정의
유체 흐름	유체 흐름에 의해 물체에 작용하는 힘
방향	유체 흐름에 수직
양력 생성 원리	베르누이 원리 또는 코안다 효과
양력 발생	날개 프로펠러 로터 돛
양력과 항력
관계	양력은 항력과 함께 공기역학적 힘의 두 가지 주요 구성 요소
항력	유체 흐름 방향으로 작용하는 힘
양력	유체 흐름에 수직으로 작용하는 힘
양력의 활용
항공	항공기의 비행을 가능하게 함
선박	돛단배의 추진력을 제공
기타	회전익 항공기의 로터 풍력 발전기 수중익선 경주용 자동차
양력 계산
공식	L = 1/2 * ρ * v² * S * Cl
L	양력
ρ (rho)	유체의 밀도
v	유체의 속도
S	양력면의 면적
Cl	양력 계수
양력 발생 메커니즘
비대칭 날개	날개 위쪽의 공기 흐름이 빠르고 아래쪽의 공기 흐름은 느림 (베르누이 원리)
날개 각도	날개의 각도를 변경하여 양력 조절 가능
코안다 효과	유체가 물체 표면을 따라 흐르는 경향을 이용하여 양력 생성
주의사항
실속	날개의 각도가 너무 커지면 양력이 급격히 감소
항력 증가	양력이 증가하면 항력도 증가
추가 정보
참고 자료	NASA Glenn Research Center - What is Lift?

2. 역사적 배경

양력은 유동 방향에 수직인 항력의 성분으로 정의되며, 항력은 유동 방향과 평행한 성분이다.

양력에 대한 이해는 항공기 개발의 역사와 밀접하게 관련되어 있다. 초기 항공기 설계자들은 새의 날개 모양을 모방하여 양력을 발생시키려고 노력했으며, 다양한 시행착오를 거쳐 효율적인 날개 형태를 개발해왔다.

20세기 초, 쿠타-주코프스키 정리Kutta–Joukowski theorem|쿠타-주코프스키 정리^영어^[84]^[112]^[113]는 2차원 익형에서 발생하는 양력을 순환과 연관시켜 설명하는 데 중요한 역할을 했다.^[117] 이 정리는 익형이 정지 상태에서 움직이기 시작할 때 시작 와류가 만들어지고, 이것이 익형 주변의 순환을 형성하는 과정을 통해 양력을 설명한다.^[114]^[115]^[116] 하지만 쿠타-주코프스키 모델은 실제로 2차원 익형에서 얼마나 많은 순환이나 양력이 생성되는지 예측하지는 않는다. 실제 익형에서 발생하는 양력은 날개 설계, 전진 속도, 받음각, 공기 밀도와 같은 비행 조건에 따라 달라진다.

2. 1. 초기 역사

고체 물체 표면 주위를 흐르는 유체는 그 물체에 힘을 작용한다. 물체가 정지된 유체를 통과하거나, 유체가 물체 주위를 움직이거나, 둘 다 움직이는 경우 모두 힘이 작용한다. '''양력'''은 이 힘 중에서 다가오는 유동 방향에 수직인 성분이다.^[1] 양력에는 항상 항력이 수반되는데, 이는 유동 방향과 평행한 표면력의 성분이다.

양력은 주로 고정익 항공기의 날개와 관련이 있지만, 프로펠러, 연, 헬리콥터 로터, 경주용 자동차 날개, 해상 돛, 풍력 터빈, 요트 용골, 선박 타륜, 수중익선 등 유선형의 다양한 물체에서도 발생한다. 양력은 조류, 박쥐, 곤충 등 비행 및 활강 동물과 특정 나무 씨앗과 같은 식물계에서도 사용된다.^[2]

"lift"라는 단어는 양력이 무게에 반대한다는 의미를 내포하지만, 양력은 유동 방향을 기준으로 정의되므로 중력과 관계없이 어떤 방향이든 될 수 있다. 항공기가 직선 및 수평 비행으로 순항하는 경우 양력은 중력에 반대하지만, 상승, 하강, 경사 선회하는 경우에는 수직 방향에 대해 기울어진다.^[3] 양력은 곡예 비행 루프 상단의 고정익 항공기 날개와 항공기 수평 안정판에서 다운포스로 작용하거나, 범선처럼 주로 수평 방향으로 작용할 수도 있다.

이 문서에서 논의되는 양력은 주로 익형과 관련이 있다. 해양 수중익선과 프로펠러는 밀도, 압축성, 점도 등 공기와 물의 차이에도 불구하고 동일한 물리적 원리를 공유하며 같은 방식으로 작동한다.

2. 2. 20세기 초

익형이 양력을 발생시킬 때, 익형 주변의 공기는 순환하는 듯한 움직임을 보인다. 이러한 순환은 익형 앞의 상향류, 위쪽의 가속된 흐름, 아래쪽의 감속된 흐름, 그리고 뒤쪽의 하향류 등이 합쳐져서 나타난다.

쿠타-주코프스키 정리는 2차원 익형에서 발생하는 양력을 이러한 순환과 연관시켜 설명한다.Kutta–Joukowski theorem|쿠타-주코프스키 정리^영어^[84]^[112]^[113] 이 정리는 익형이 정지 상태에서 움직이기 시작할 때 시작 와류가 만들어지고, 이것이 익형 주변의 순환을 형성하는 과정을 통해 양력을 설명하는 데 중요한 역할을 한다.^[114]^[115]^[116] 쿠타-주코프스키 정리는 이러한 과정을 수학적으로 표현하여 양력을 추론한다.^[117]

하지만 쿠타-주코프스키 모델은 2차원 익형이 실제로 얼마나 많은 순환이나 양력을 생성하는지 예측하지는 않는다. 이 모델을 사용하여 양력을 계산하려면 순환 값을 미리 알고 있어야 한다. 특히, 후류 침체점이 익형 후미 가장자리에 위치하고 그곳에 계속 붙어있는 쿠타 조건이 만족되면, 등각 사상 방법을 통해 양력을 이론적으로 계산할 수 있다.

실제 익형에서 발생하는 양력은 날개의 설계와 전진 속도, 받음각, 공기 밀도와 같은 비행 조건에 따라 달라진다. 예를 들어, 경계층 분출이나 분출 플랩과 같이 순환을 인위적으로 증가시키는 방법을 통해 양력을 높일 수 있다. 플레트너 로터의 경우에는 익형 전체가 원형으로 되어 있고, 스팬 방향 축을 중심으로 회전하면서 순환을 만들어낸다.

3. 양력 발생 원리

일반적으로 유체 내에서 움직이는 모든 물체는 항력을 받고, 물체의 모양이 비대칭일 경우 유체의 흐름에 수직하는 양력을 받는다.^[147] 익형(翼型)은 항력보다 훨씬 큰 양력을 발생시키도록 특별히 고안된 형태이다.^[147] 추력, 항력, 양력, 중력은 익형에 작용하는 대표적인 힘이다.^[146]

고정익 항공기의 날개 뿐만 아니라 헬리콥터의 로터, 범선의 돛, 요트의 킬, 경주용 자동차의 날개, 터빈의 날개 등 유체가 있는 곳이라면 어디서든 양력이 발생한다.

익형에서 발생하는 양력은 뉴턴의 운동 법칙과 베르누이 방정식을 이용하여 설명할 수 있다. 양력은 압력 차이로도 설명 가능한데, 압력은 단위 면적에 작용하는 변형력을 뜻한다. 유체 속에 놓인 익형에 전달되는 변형력의 알짜힘은 각 부분마다 다르다. 이 때문에 힘의 편향이 일어나 익형의 볼록한 부분은 압력이 낮고 오목한 쪽은 압력이 높아져 양력이 발생한다. 비행기 날개의 위쪽은 유체 속력이 빨라 압력이 낮고, 아래쪽은 유체 속력이 느려 압력이 높기 때문에 위쪽으로 힘을 받게 된다.^[156]

1754년 레온하르트 오일러는 뉴턴 운동 법칙의 제2법칙을 응용하여 압력차 계산 공식을 정리하였다.^[157]

:

\frac{\operatorname{d}p}{\operatorname{d}R}= \rho \frac{v^2}{R}

위 식에서 R은 곡률의 반지름, p는 압력, ρ는 밀도, v는 속도를 나타낸다. 곡률의 반지름이 커져 유체의 흐름이 평탄해지면(R → ∞) 압력차(즉, 양력)는 0으로 수렴한다.

받음각은 익형의 익현과 다가오는 기류 사이의 각도이다. 대칭형 익형은 받음각이 0일 때 양력을 발생시키지 않지만, 받음각이 증가하면 공기가 더 큰 각도로 굴절되고 기류 속도의 수직 성분이 증가하여 양력이 증가한다. 작은 각도의 경우, 대칭형 익형은 받음각에 거의 비례하는 양력을 발생시킨다.^[63]^[64]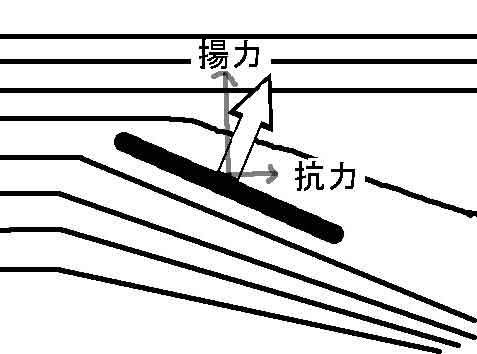

받음각이 증가함에 따라 양력은 어떤 각도에서 최대값에 도달한다. 이 임계 받음각을 넘어 받음각을 증가시키면 상면 흐름이 날개에서 분리되고, 아래쪽으로의 굴절이 감소하여 익형이 발생시키는 양력이 감소한다. 이때 익형은 실속 상태라고 한다.^[65]

3. 1. 베르누이 방정식

베르누이 방정식은 유체의 속도와 압력 사이의 관계를 나타내는 방정식이다. 이 방정식에 따르면 유체의 속도가 증가하면 압력이 감소하고, 속도가 감소하면 압력이 증가한다.^[159] 이는 압력에너지와 운동에너지의 합이 일정하다는 것을 보여준다.

:

{p \over \rho} + {v^2 \over 2} + gh  = \mbox{constant}

$v$ 는 유선 내 한 점에서의 유동 속도
$g$ 는 중력 가속도
$h$ 는 기준면에 대한 그 점의 높이
$p$ 는 그 점에서의 압력
$\rho$ 는 유체의 밀도

날개 윗면은 아랫면보다 공기가 더 빠르게 흐르도록 설계되어 있다. 속도가 다른 두 흐름의 전체 에너지 합계는 베르누이 방정식에 따라 일정하므로, 속도가 빠른 익형 윗부분의 압력이 낮아지게 된다. 이와 같은 익형의 위아래 압력차가 양력 발생의 주요 원인이 된다. 실제 고정익기의 날개가 받는 양력은 날개 각 지점의 단면이 이루는 익형에서 발생하는 양력을 전체 날개의 면적으로 곱하여 계산할 수 있다.^[159]

3. 2. 뉴턴의 운동 법칙

뉴턴의 운동 법칙에 따르면, 물체에 힘이 작용하면 가속도가 발생한다. 날개는 공기의 흐름을 아래로 밀어내고, 이에 대한 반작용으로 위로 향하는 양력을 받는다. 이는 작용-반작용의 법칙으로 설명할 수 있다.^[153]^[154]

날개가 양력을 발생시키면 공기를 아래쪽으로 휘게 하고, 이렇게 하려면 공기에 아래쪽 힘을 가해야 한다. 뉴턴의 제3법칙에 따라 공기는 날개에 위쪽으로 같은 크기의 힘을 가해야 한다.

익형은 공기가 지나갈 때 아래쪽으로 힘을 가함으로써 양력을 발생시킨다. 뉴턴의 제3법칙에 따라 공기는 익형에 크기가 같고 방향이 반대인 (위쪽으로 향하는) 힘, 즉 양력을 가해야 한다.^[15]^[16]^[17]^[18]

공기 흐름이 익형에 접근할 때 위쪽으로 휘어지지만, 익형을 지나면 방향이 바뀌어 아래쪽으로 휘어진 경로를 따른다. 뉴턴의 제2법칙에 따라 이러한 흐름 방향의 변화에는 익형에 의해 공기에 가해지는 아래쪽 힘이 필요하다. 그러면 뉴턴의 제3법칙에 따라 공기는 익형에 위쪽으로 힘을 가해야 한다. 따라서 방향 변화와 반대되는 반작용, 즉 양력이 발생한다. 비행기 날개의 경우, 날개는 공기에 아래쪽 힘을 가하고 공기는 날개에 위쪽 힘을 가한다.^[19]^[20]^[21]^[22]^[23]^[24]

3. 3. 받음각

받음각은 유체의 흐름과 익형의 시위선이 이루는 각이다.^[158] 받음각이 변하면 유체의 흐름도 변하고, 결국 양력의 크기도 변한다.

날개나 세일 등에서는 받음각이 어느 정도 작을 때에는 받음각에 비례하여 양력의 크기가 변한다. 받음각의 절대값이 커지면 물체 표면에서 흐름이 박리되어 양력의 크기는 작아지고 항력이 급격히 증대되는데, 이러한 현상을 실속이라고 한다.^[136]^[137]

항공기의 날개는 대부분 양력각을 갖도록 기체에 고정되어 있으며, 기체가 수평이더라도 최소한의 양력을 발생시킨다. 많은 여객기 설계에서는 순항 중 필요한 양력을 확보하기 위해 기체를 1~2도 정도 상향으로 기울이기도 한다(단, 항력은 약간 증가한다).

더 많은 양력이 필요한 상태(저속 시, 상승 시)에서는 기체를 더 크게 상향으로 기울여야 한다. 이착륙 시에는 플랩을 사용하여 양력을 더욱 증가시킨다.

3. 4. 익형 (Airfoil)

익형(翼型)은 항공기 날개의 단면 형상을 의미하며, 양력 발생에 최적화된 형태로 설계된다. 윗면은 곡률이 크고, 아랫면은 비교적 평평한 형태를 가지는 것이 일반적이다.^[148] 익형으로 된 날개는 항력보다 훨씬 큰 양력을 발생시킨다.^[149]

익형은 항력보다 훨씬 더 큰 양력을 발생시킬 수 있는 유선형이다.^[10] 평평한 판도 양력을 발생시킬 수 있지만, 유선형 익형만큼 크지 않고 항력이 다소 더 크다.

일반적으로 유체 내에서 움직이는 모든 물체는 항력을 받고, 물체의 모양이 비대칭일 경우 유체의 흐름에 수직하는 양력을 받게 된다.^[147] 익형은 양력의 발생을 극대화하기 위해 특별히 고안된 형태로^[147] 추력, 항력, 양력, 중력이 작용한다.^[146]

익형에서 발생하는 양력에 대해서는 다양한 수준의 이론으로 설명이 가능하다. 익형의 위쪽의 길이가 길고 아랫쪽은 짧기 때문에 유체가 양쪽을 같은 시간에 지나게 되면 상대적으로 경로가 긴 위쪽의 흐름이 빨라져 압력이 낮아지므로 양력이 발생하게 된다고 설명하는 것이 대표적이다.^[152]

뉴턴의 운동 법칙과 베르누이 방정식을 이용하여 양력의 발생을 설명할 수 있다.

양력의 발생은 압력의 차이로도 설명이 가능하다. 압력은 단위 면적에 작용하는 변형력을 뜻한다. 유체 속에 놓인 익형에게 전달되는 변형력의 알짜힘은 각 부분마다 다르다. 이 때문에 힘의 편향이 일어나게 되고, 각 부분이 받는 압력 역시 달라지게 된다. 그 결과 익형의 볼록한 부분은 상대적으로 압력이 적은 상태가 되고 오목한 쪽은 압력이 높아져 양력이 발생한다. 비행기의 날개에서 위쪽은 유체속력이 빨라서 압력이 낮고, 아래쪽은 유체속력이 느려 압력이 높기 때문에 힘을 윗쪽으로 받게 된다.^[156]

1754년 레온하르트 오일러는 뉴턴 운동 법칙의 제2법칙을 응용하여 아래와 같은 압력차 계산 공식을 정리하였다.^[157]

:

\frac{\operatorname{d}p}{\operatorname{d}R}= \rho \frac{v^2}{R}

위 식에서 R은 곡률의 반지름, p는 압력, ρ는 밀도, v는 속도를 나타낸다. 곡률의 반지름이 커져 유체의 흐름이 평탄해지면(R → ∞) 압력차(즉, 양력)은 0으로 수렴한다.

받음각은 익형의 익현과 다가오는 기류 사이의 각도이다. 대칭형 익형은 받음각이 0일 때 양력을 발생시키지 않는다. 하지만 받음각이 증가함에 따라 공기는 더 큰 각도로 굴절되고 기류 속도의 수직 성분이 증가하여 양력이 증가한다. 작은 각도의 경우, 대칭형 익형은 받음각에 거의 비례하는 양력을 발생시킨다.^[63]^[64]

받음각이 증가함에 따라 양력은 어떤 각도에서 최대값에 도달한다. 이 임계 받음각을 넘어 받음각을 증가시키면 상면 흐름이 날개에서 분리되고, 아래쪽으로의 굴절이 감소하여 익형이 발생시키는 양력이 감소한다. 이때 익형은 실속 상태라고 한다.^[65]

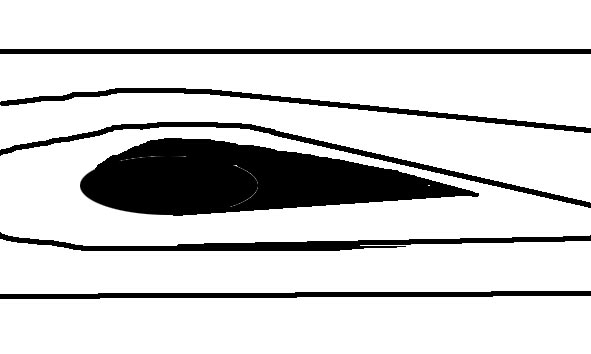
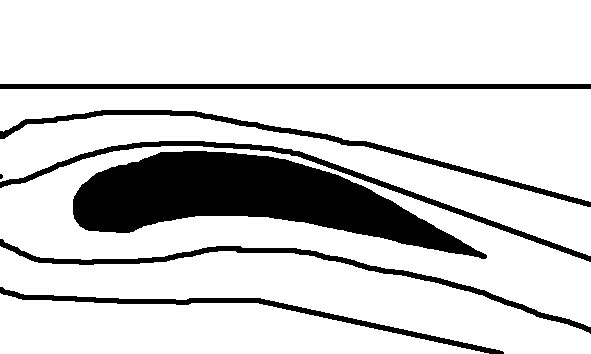
기본적으로 앞쪽 끝이 둥글고 뒤쪽 끝이 뾰족한 소위 “물방울 모양” 또는 그것을 굽히거나 비틀어 만든 형상이다. 항공기의 경우에는 날개 내부의 부피를 크게 하는 것도 요구되어, 날개 형상 설계에 영향을 미친다.

운용 시 받음각(迎え角)이 일정하지 않다는 것을 전제로, 앞전 부근은 박리(剥離)를 방지하기 위해 둥글게 하고 곡률을 작게 한다. 날개 아랫면의 흐름이 뒤쪽 끝에서 날개로부터 떨어지기 때문에 뒤쪽 끝은 곡률을 크게 하고 뾰족하게 한다.

초기의 비행기에는 굽은 형상이 사용되었다. 이러한 형상에서는 날개 아랫면 기류가 앞전 부분을 피한 후에 더욱 뒤쪽 끝 부분을 피하게 되어, 항력이 크다. 1960년대 이후 널리 채택되고 있는 초임계익은 저항력과 곡률을 양립시키고 있다.

초음속 용도에서는 앞쪽 끝도 뾰족하게 한 형상이 일반적이다.

4. 양력에 영향을 미치는 요소

일반적으로 유체 내에서 움직이는 모든 물체는 항력을 받으며, 물체의 모양이 비대칭일 경우 유체의 흐름에 수직하는 양력을 받게 된다.^[147] 익형(날개 단면)으로 된 날개는 항력보다 훨씬 큰 양력을 발생시킨다.^[148]^[149] 익형은 양력 발생을 극대화하기 위해 특별히 고안된 형태이다.^[147]

양력은 고정익 항공기의 날개뿐만 아니라 프로펠러, 연, 헬리콥터 로터, 경주용 자동차 날개, 풍력 터빈 등 다양한 물체에서 발생한다. 비행 및 활강 동물과 곤충, 심지어 특정 나무의 씨앗과 같은 식물계에서도 양력을 사용한다.^[2]

받음각은 유체의 흐름과 익형의 시위선이 이루는 각으로,^[158] 받음각이 변하면 양력의 크기도 변한다. 양력은 압력 차이에 의해 발생하며, 받음각, 에어포일 형상, 공기 밀도, 속도에 따라 달라진다.

헬리콥터의 로터, 범선의 돛, 요트 바닥의 킬, 자동차 경주용 자동차 날개, 터빈 날개 등 유체가 있는 곳이라면 어디서든 양력을 포함한 네 가지 힘(추력, 항력, 중력)이 작용한다. 보통 양력은 중력을 거슬러 떠오르게 하는 힘을 의미하지만, 유체 역학에서는 유체 흐름에 수직 방향으로 작용하는 힘을 말한다.^[151]

"lift"(양력)라는 단어는 양력이 무게에 반대된다는 뜻을 내포하지만, 양력은 유동 방향을 기준으로 정의되므로 어떤 방향이든 될 수 있다. 항공기가 직선 및 수평 비행으로 순항하는 경우 양력은 중력에 반대되지만, 상승, 하강 또는 경사 선회하는 경우 양력은 수직 방향에 대해 기울어진다.^[3]

해양 수중익선과 프로펠러는 공기와 물의 차이에도 불구하고 동일한 물리적 원리를 공유하고 동일한 방식으로 작동한다. 양력 익형 주위의 흐름은 유체 역학 현상으로, 수학적 이론과 물리적 설명으로 이해할 수 있다.^[11]

양력을 발생시키는 에어포일 주변의 유선과 유관. 흐름은 2차원이며 에어포일은 무한한 스팬을 갖는다.

대부분의 단순화된 설명은 뉴턴의 운동 법칙 또는 베르누이 정리 중 하나에 기반한다.^[11]^[12]^[13]^[14] "장애물" 또는 "유관 수축" 설명은 상부 표면 위의 흐름이 하부 표면 위의 흐름보다 빠르다고 주장하지만, 속도 차이의 이유는 다르게 설명한다. 이 설명은 곡선 상부 표면이 흐름에 대한 장애물 역할을 하여 유선이 더 가까이 모이게 하고 유관을 더 좁게 만들어 속도 차이가 발생한다고 주장한다.^[52]

장애물 설명은 유관 수축 발생 원인, 상부 표면과 하부 표면의 차이, 평평한 판, 대칭 에어포일, 범선의 돛, 거꾸로 비행하는 에어포일의 양력 발생 원리, 수축 또는 장애물 양에 따른 양력 계산 시 실험 결과 예측 불가 등의 결함이 있다.^[54]^[55]^[56]^[57] 또한 질량 보존 법칙은 흐름 가속의 물리적 이유가 될 수 없다.^[58]

4. 1. 날개 모양

주어진 속도에서 날개가 발생시킬 수 있는 최대 양력은 날개의 형상, 특히 익형 곡률(윗면이 아랫면보다 더 볼록한 곡률)의 양에 따라 달라진다. 일반적으로 익형 곡률을 증가시키면 주어진 속도에서 최대 양력이 증가한다.^[66]^[67]

곡률이 있는 날개는 받음각이 0일 때도 양력을 발생시킨다. 현(chord line)이 수평일 때, 후연(trailing edge)은 아래쪽 방향을 향하고 공기는 후연을 따라 흐르므로 아래쪽으로 편향된다.^[68] 곡률이 있는 날개를 거꾸로 뒤집으면 받음각을 조절하여 양력이 위쪽으로 향하게 할 수 있다. 이것이 비행기가 거꾸로 비행할 수 있는 이유를 설명한다.^[69]^[70]

물체에 작용하는 양력은 정미 동압과 그것이 작용하는 면적에 의존하는 양으로 생각되기 때문에, 일반적으로 다음 식으로 나타낼 수 있다.

:

L = {1 \over 2} \rho V^2 S C_{\rm L}

$C_{\rm L}$ 는 양력계수(Coefficient of Lift)
ρ는 유체의 밀도(해수면 고도의 대기 중이라면 1.293 kg/m³)
V는 물체와 주류(익과의 상대속도가 균일하다고 간주될 정도로 익에서 떨어진 곳의 유체 요소와 익의 상대속도)
S는 물체의 대표 면적, 보통은 익면적(Surface)
L은 발생하는 양력 (Lift)

항력과 동일한 형식이지만 항력의 S는 전방 투영 면적으로 하는 경우가 있다. 이 때문에 CL/CD는 양항비와 일치한다고는 할 수 없다.

{1 \over 2} \rho V^2

는 주류 속도로부터 환산되는 동압이다.

양력계수

C_{\rm L}

는 정압과 양력의 비([무차원수])이다. 물체의 형상과 진행 방향, 받음각, 유체의 물성, 유속(레이놀즈 수) 및 마하 수 등에 따라 변화한다.

날개나 세일 등에서는 받음각이 어느 정도 작을 때에는 받음각에 비례하여 변화한다. 받음각의 절대값이 커지면 물체 표면에서 흐름이 박리되어 양력계수의 절대값은 작아지고 항력이 급격히 증대한다.^[136]^[137] 이 현상을 실속이라고 한다.
날개체의 고도가 낮고 지면이나 수면 근처를 비행할 때는 고고도에 비해 양력계수가 커진다. 이것을 지면 효과라고 한다.
어떤 형상에 대한 양력계수는 실제로 양력을 측정(수치 시뮬레이션으로 구해도 좋다)하여 위 식에 적용함으로써 얻을 수 있다.
실무상으로는 형상과 레이놀즈 수에 대해 각각 동일하다고 간주되는 경우에는 양력계수도 동일하다고 간주하는 경우가 있다.

4. 2. 공기 밀도

양력은 공기 밀도에 비례한다. 즉, 공기 밀도가 높을수록 양력은 증가한다. 그러나 고도가 높아질수록 공기 밀도는 낮아진다. 따라서 항공기는 고도가 높아질수록 동일한 양력을 얻기 위해 더 빠른 속도로 비행해야 한다.^[92]

공기 밀도(

\rho

)는 다음 공식에서 확인할 수 있듯이 양력(

L

)에 직접적인 영향을 준다.

:

L = \tfrac12\rho v^2 S C_L

여기서,

$v$ 는 속도 또는 대기 속도
$S$ 는 평면형(투영) 날개 면적
$C_L$ 은 원하는 받음각, 마하 수, 및 레이놀즈 수에서의 양력 계수이다.^[93]

일반적으로 항공기가 비행할 때 주변 유동 조건에는 유체의 밀도, 점도 및 유속이 양력에 영향을 미친다. 밀도는 온도와 매질의 음속, 즉 압축성 효과에 의해 영향을 받는다.

4. 3. 속도

양력은 공기 밀도에 비례하고, 유속의 제곱에 거의 비례하여 증가한다. 또한 양력은 날개의 크기에 따라 달라지며, 일반적으로 양력 방향으로 투영된 날개 면적에 비례한다.^[92]

:

L = \tfrac12\rho v^2 S C_L

여기서

$L$ 은 양력이다.
$\rho$ 는 공기 밀도이다.
$v$ 는 속도 또는 대기 속도이다.
$S$ 는 평면형(투영) 날개 면적이다.
$C_L$ 은 원하는 받음각, 마하 수, 및 레이놀즈 수에서의 양력 계수이다.^[93]

따라서 항공기는 이륙 시 충분한 양력을 얻기 위해 높은 속도로 활주한다.

5. 양력과 관련된 현상

양력은 유체 속을 움직이는 물체에 작용하는 힘 중 하나로, 유동 방향에 수직인 힘의 성분을 말한다.^[1] 고정익 항공기의 날개뿐만 아니라 프로펠러, 연, 헬리콥터 로터, 경주용 자동차 날개, 돛, 풍력 터빈 등 다양한 유선형 물체에서 발생한다. 조류, 박쥐, 곤충과 같은 동물이나 특정 나무의 씨앗에서도 양력이 활용된다.^[2]

일반적으로 양력은 무게에 반대되는 힘으로 생각되지만, 유동 방향을 기준으로 정의되기 때문에 중력과 관계없이 어떤 방향으로든 작용할 수 있다. 예를 들어, 항공기가 수평 비행할 때는 양력이 중력에 반대되지만, 상승, 하강, 경사 선회할 때는 수직 방향에 대해 기울어진다.^[3] 곡예 비행 루프 상단의 항공기 날개나 수평 안정판에서는 다운포스로 작용할 수도 있고, 범선에서는 수평 방향으로 작용하기도 한다.

; 익 표면상의 압력과 속도장

: 유체가 물체에 미치는 힘은 물체 표면의 압력과 마찰을 표면 전체에서 적분한 양이다. 양력은 주로 압력으로 설명되며, 양력이 위쪽 방향일 때 물체 윗면은 저압, 아랫면은 고압 경향을 보인다. 익 표면 압력이 상부에서 저압이면, 대응하는 속도는 물체의 상측에서 고속, 하측에서 저속의 분포이다. 따라서 익형 경계선에서 순환을 추정하면 유한값을 취한다.

: 또한, 물체에 양력이 작용하고 있을 때, 양력에 대한 반작용으로 양력과 반대 방향의 운동이 물체 주위 유체의 어딘가에 반드시 발생한다. 익체의 상배면에서 익 후단의 후방에 걸쳐 현저한 하향의 흐름은, 주로 항공기 공학 분야에서 “다운워시”라고 불린다.

; 익 주위의 와류

: 다운워시는 익 후연(뒷날개)이 가로지른 직사각형 영역에 발생한다. 이 직사각형의 선은 하강류와 상승류의 경계이며, 전단 즉 와도가 집중하고, 와류가 발생한다. 그러나 직사각형의 전방측은 익체에 의해 차단되어 있기 때문에 익 주위의 순환이 와류의 역할을 한다. 다운워시는 익 후연과 두 개의 익단 와류와 출발 와류로 둘러싸인 형태가 된다.

; 다운포스

: 레이싱카 등에서는 하향 양력을 '''다운포스'''라고 부르는 경우가 있다. 범선의 돛에 작용하는 양력은 거의 수평 방향을 향하고 있다. 풍차나 터빈에서는 주방향, 프로펠러에서는 회전축 방향이 대략적인 양력의 방향이 된다.

; 스포츠

: 탁구, 야구를 비롯한 구기에서는 물체의 회전에 의해 발생하는 양력(마그누스 효과)이 이용된다.

: 수영에서는 양력을 강조한 팔 동작을 취하면 장시간 편안하게 수영할 수 있다.

; 양력을 이용하는 예

: 양력은 식물의 종자, 곤충의 날개, 수성 동물의 지느러미, 조류의 날개, 연, 비행기의 고정익, 헬리콥터의 회전익, 수중익선의 수중익, 선박의 돛(종익)과 키, 노, 프로펠러, 팬, 터빈 등에서 이용된다.

; 칼만 와류와 양력

: 물체 후류에는 칼만 와류라고 불리는 와류열이 주기적으로 발생하고, 유체력은 진동하는 경우가 많다. 따라서 회전 없이 받음각 없이 순 양력이 0으로 여겨지는 형상이라도 순간적인 양력이 발생하는 경우가 있다.

; 양력에 대한 간이적인 설명

날개 주위의 흐름과 양력에 대한 일반적인 간이 설명은 다음과 같다.

설명	내용	타당성
칼만 와류와의 대비	단순한 원통이나 구 주위 흐름에서 칼만 와류가 발생할 때 순간적인 양력이 발생한다. 이는 물체 전후 정체점, 박리 위치, 물체 상하좌우 유속에 자유도와 순환 의존성이 있고, 초기값 의존성이나 히스테리시스가 발생하는 현상이다.	야구공 솔기와 같은 돌기가 있으면 정체점이나 박리점이 고정되어 시간 평균했을 때 순 양력이 나타날 수 있다.
주류에 대한 편향판 (다운워시의 반작용)	주류 방향을 바꾸는 편향판으로 설명한다. 물체 형상에 따라 국소적인 유동 방향이 변하고, 날개 주위나 뒤에서 아래쪽 흐름이 발생한다. 전체적으로 흐름 방향이 아래쪽으로 편향되고, 그 반작용으로 날개는 위쪽으로 향한다.		날개에 따른 움직임 설명은 밀도 변화를 연상시켜 비압축 흐름 설명으로는 충분하지 않다. 특히 날개 아랫면에서는 실제 현상과 맞지 않다.
지상을 미끄러지는 물체의 양력	차량처럼 지면 바로 위를 이동하는 반원형 물체 등을 가정하여 설명한다. 위쪽이 고속이고 저압이 되는 것과 순환을 설명하기 쉽다.		물체 아래면을 고려할 필요가 없어 간단하다.
돌 튀기기 설	물수제비에 비유하여, 날개체 아래면에 공기가 부딪혀 고압 영역이 형성된다고 해석한다.		압축성(초음속) 흐름 현상에 가깝고, 일상 현상과는 일치하지 않는다. 공기가 수면처럼 날개체 아래면에 계속 부딪히는 일은 없으며, 부딪혀도 유체는 수축하지 않고 유로가 좁아져 압력이 오히려 내려간다. 초음속기 날개 원리로는 타당하다.
순환설	날개 주위 순환(회전 성분, 날개 상하 속도차와 유사)으로 설명 가능하다. 쿠타-주코프스키 정리를 중시하며, 날개 상하류 합류가 날개 후연에서 어긋나는 상태는 불안정하여 나타나지 않으므로 쿠타 조건을 만족하는 것이 전제이다.	쿠타-주코프스키 정리는 마그누스 효과의 해석해이며,^[138] 양력이 유속 제곱과 유체 밀도에 비례하는 식^[139]이다. 날개 배면을 따라 움직이는 이유는 안정해이기 때문이라는 정도의 설명이다.
등시간 통과설(동착설)	날개 앞전에서 상하로 갈라진 기류는 등시간으로 통과하여 후연에서 만난다. 따라서 날개 아래면보다 윗면 팽창이 크면, 거리가 긴 윗면 쪽 유속이 빨라 정압이 낮아진다.	윗면 압력 적분량이 아랫면 적분량보다 작을 때 위쪽 양력이 된다.	동착은 관측 수단 부족 시대의 해석으로 오류^[140]^[141]이다. 윗면과 아랫면 유속 차이로 양력이 발생한다는 부분은 옳다.^[142].
유선 곡률의 정리에 기반한 설명	유선 곡률의 정리에 의해, 물체 위아래면에서 유선이 비대칭으로 굽으면 압력차가 된다. 유선이 있을 때 양력 설명 방법 중 하나이다.	시각적으로 알기 쉽다.
앤더슨의 작용·반작용설	날개 윗면의 국소적 고속 공기는 날개 형상에 따라 흐르며 주위 유체나 벽면을 끌어들인다. 유체는 아래쪽으로 향한다(분류의 코안다 효과와 같다는 해석). 날개 배면 흐름이 후연까지 부착하는 것, 쿠타 조건 원인을 설명한다.	결점이 지적되었고^[145], 분류 외에 코안다 효과를 가져올 필요가 없다는 지적^[142]이 있다. 경계층 부착에 코안다 효과를 도입할 필요가 없다.

5. 1. 실속 (Stall)

주어진 공기 속도에서 에어포일의 최대 양력은 경계층 분리에 의해 제한된다. 받음각이 증가함에 따라 경계층이 더 이상 상면에 부착될 수 없는 지점에 도달한다. 경계층이 분리되면 위 그림처럼 상면 위에 재순환 흐름 영역이 남는데, 이것을 ''실속''이라고 한다. 실속 이상의 받음각에서는 양력이 크게 감소하지만 0으로 떨어지지는 않는다. 양력 계수 측면에서 실속 전에 달성할 수 있는 최대 양력은 단일 요소 에어포일의 경우 일반적으로 1.5 미만이며, 고양력 슬롯 플랩과 전연 장치가 배치된 에어포일의 경우 3.0을 초과할 수 있다.^[76]

날개나 세일 등에서는 받음각이 어느 정도 작을 때에는 받음각에 비례하여 양력계수가 변화한다. 받음각의 절대값이 커지면 물체 표면에서 흐름이 박리되어 양력계수의 절대값은 작아지고 항력이 급격히 증대한다.^[136]^[137] 이 현상을 실속이라고 한다.

5. 2. 마그누스 효과 (Magnus Effect)

회전하는 물체 주위의 공기 흐름은 비대칭적으로 변한다. 이로 인해 물체에 양력이 발생하는데, 이를 마그누스 효과(Magnus Effect)라고 한다. 이 효과는 야구공의 변화구, 축구공의 프리킥 등 구기 종목에서 활용된다.

5. 3. 지면 효과 (Ground Effect)

Ground effect^영어는 항공기가 지면에 가까이 비행할 때, 날개와 지면 사이의 공기 흐름이 압축되어 양력이 증가하고 항력이 감소하는 현상이다.

일반적으로 날개는 공기를 아래로 밀어내는 힘을 발생시킨다. 뉴턴의 제3법칙에 따라 공기는 날개에 같은 크기의 반대 방향(위쪽) 힘을 가하게 되는데, 이것이 바로 양력이다.^[17]

날개 주변의 공기는 압력 차이에 의해 힘을 받는다. 날개 윗면은 압력이 낮아지고, 아랫면은 압력이 높아진다. 이때 아랫면의 높은 압력이 윗면의 낮은 압력보다 더 강하게 밀어 올리면서 양력이 발생한다.^[82]

익형 주위의 흐름: 점들은 흐름과 함께 움직인다. 검은 점들은 시간 슬라이스에 있으며, 앞전에서 두 부분(윗부분과 아랫부분)으로 나뉜다. 윗면과 아랫면 유선 사이의 현저한 속도 차이는 이미지 애니메이션에서 가장 분명하게 나타나며, 윗면 마커가 아랫면 마커보다 훨씬 빨리 후면에 도착한다. 점의 색상은 유선을 나타낸다.

날개는 넓은 범위의 공기 흐름에 영향을 주는데, 이를 ''속도장''이라고 한다. 날개가 양력을 만들 때, 날개 앞의 공기는 위로, 날개 위아래 공기는 아래로 향하게 된다. 이때 날개 윗면의 공기는 속도가 빨라지고, 아랫면은 느려진다. 이렇게 아래로 향하는 공기 흐름과 속도 변화는 넓은 영역에 걸쳐 나타나며, 날개에 가까울수록 더 뚜렷하게 나타난다.^[84]^[85]

익형 주변의 압력장. 선은 등압선(isobar)을 나타내며, 화살표는 고압(빨강)에서 저압(파랑)으로의 압력 차이, 따라서 공기가 그 방향으로 가속되는 순 힘을 보여준다.

날개 주변에는 ''압력장''이라는 불균일한 압력 패턴이 형성된다. 날개 윗면은 낮은 압력 영역이, 아랫면은 높은 압력 영역이 나타난다. 이러한 압력 차이는 날개 표면에 작용하는 힘의 일부일 뿐이다.^[86]

불균일한 압력은 공기에 힘을 가하여 고압에서 저압으로 이동시킨다. 날개 윗면의 공기는 저압 영역 중심으로 밀리고, 아랫면 공기는 고압 영역 바깥쪽으로 밀려난다.

뉴턴의 제2법칙에 따르면, 힘은 공기를 가속시킨다. 따라서 날개 위아래 공기는 아래쪽으로 가속되며, 이는 비균일 압력이 공기 흐름을 아래로 휘게 하는 원인임을 나타낸다. 이러한 흐름을 만들기 위해서는 날개가 양의 받음각을 가지거나 충분한 캠버를 가져야 한다. 코안다 효과를 언급하는 일부 설명에서는 점성이 아래쪽 방향 전환에 중요한 역할을 한다고 제안하지만, 이것은 잘못된 것이다.

날개 앞뒤의 공기 흐름도 영향을 받는다. 날개 앞 공기는 위로, 날개 뒤 공기는 아래로 향했다가 다시 위로 향한다. 또한, 날개 윗면의 저압 영역을 통과하는 공기는 속도가 빨라졌다가 느려지고, 아랫면의 고압 영역을 통과하는 공기는 느려졌다가 빨라진다. 이는 베르누이 원리와 일치한다.

이처럼 공기 흐름의 방향과 속도 변화는 비균일 압력에 의해 발생한다. 하지만 이 관계는 일방적인 것이 아니라 상호작용이다. 공기 흐름은 압력 차이에 영향을 받고, 압력 차이는 공기 흐름에 의해 유지된다.^[87] 압력 차이는 밀어낼 대상이 있어야 존재할 수 있는데, 공기역학적 흐름에서는 공기의 관성이 그 역할을 한다.^[88]

날개 표면에 양력을 작용하는 압력 차이를 유지하려면 넓은 영역에서 비균일 압력 패턴이 유지되어야 한다. 이를 위해 수직 및 수평 방향 모두에서 압력 차이가 필요하며, 베르누이 원리에 따라 흐름의 아래쪽 방향 전환과 속도 변화가 함께 나타난다. 압력 차이와 흐름 변화는 상호 작용하며 서로를 유지한다. 압력 차이는 뉴턴의 제2법칙과 날개 표면을 따라 흐르는 공기가 주로 아래쪽으로 기울어진 윤곽을 따른다는 사실에서 자연스럽게 발생하며, 공기의 질량이 이 상호 작용에 중요한 역할을 한다.^[89]

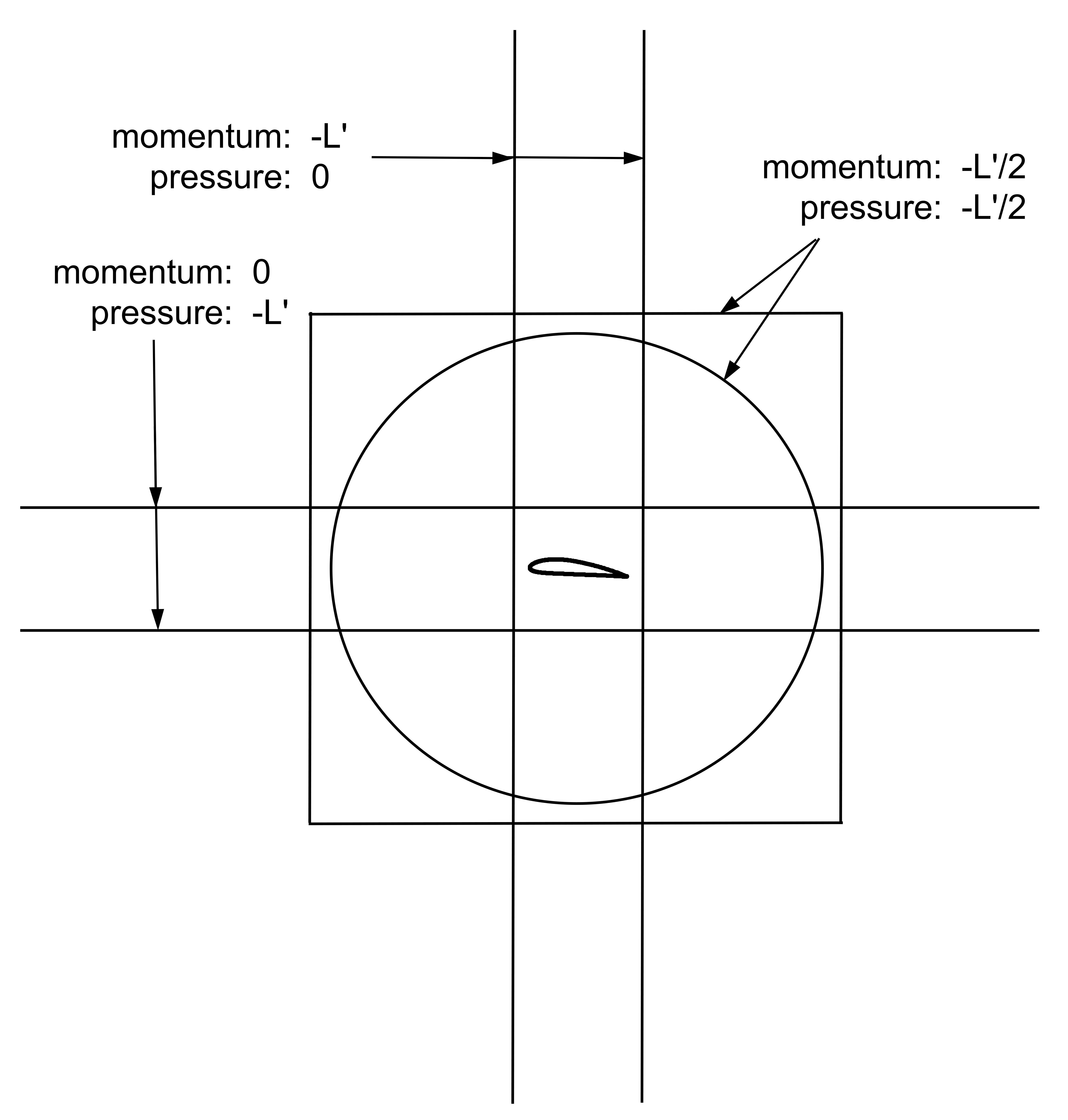
양력을 발생시키는 에어포일 주변 2차원 유동의 운동량 균형을 분석하는 데 사용된 다양한 모양의 제어 체적. 에어포일은 단위 스팬당 공기에 -L'의 하향력을 작용하는 것으로 가정하며, 그 힘이 외곽 경계에서 운동량 플럭스와 압력 차이로 나타나는 비율은 제어 체적의 모양에 따라 다르게 표시되어 있다.

양력을 발생시키는 날개 주변의 흐름은 뉴턴의 제2법칙(운동량 보존 법칙)을 만족해야 한다. 이는 국소적으로, 그리고 넓은 영역에 걸쳐 통합된 의미로 모두 적용된다. 넓은 영역에서는 뉴턴의 제2법칙이 '제어 체적에 대한 운동량 정리' 형태로 나타난다. 제어 체적은 분석을 위해 선택된 유동 영역이다. 운동량 정리는 제어 체적 경계에 작용하는 통합된 힘이 유체 덩어리의 운동량의 통합된 시간 변화율과 같다는 것을 의미한다. 정상 유동의 경우, 이는 경계를 통한 운동량 플럭스의 순 면적분으로 표현할 수 있다.^[130]

2차원 날개 주변의 양력 흐름은 날개를 완전히 둘러싸는 제어 체적에서 분석된다. 제어 체적의 내부 경계는 날개 표면이며, 여기서 단위 스팬당 하향력

-L'

이 날개가 유체에 작용한다. 외부 경계는 일반적으로 큰 원 또는 큰 직사각형이다. 날개에서 멀리 떨어진 외부 경계에서 속도와 압력은 균일한 흐름과 와류가 결합된 형태로 나타나며, 점성 응력은 무시할 수 있다. 따라서 외부 경계에서 적분해야 하는 유일한 힘은 압력이다.^[131]^[132]^[133] 자유 유동 속도는 수평으로, 양력은 수직 상향으로 작용한다고 가정하면, 수직 운동량이 관심 대상이다.

지면이 없는 자유 공기의 경우, 날개가 유체에 작용하는 힘

-L'

은 운동량 플럭스와 외부 경계의 압력 차이로 부분적으로 나타난다. 높이보다 훨씬 긴 수평 직사각형의 경우, 앞면과 뒷면의 수직 운동량 플럭스는 무시되며, 양력은 위쪽과 아래쪽의 통합된 압력 차이로만 설명된다.^[131] 정사각형이나 원의 경우, 운동량 플럭스와 압력 차이는 각각 양력의 절반을 차지한다.^[131]^[132]^[133] 폭보다 훨씬 높은 수직 직사각형의 경우, 위쪽과 아래쪽의 불균형 압력은 무시되며, 양력은 전적으로 운동량 플럭스로 설명된다. 앞면을 통해 들어오는 상향 운동량 플럭스가 양력의 절반, 뒷면을 통해 나가는 하향 운동량 플럭스가 나머지 절반을 차지한다.^[131]

위의 모든 제어 체적 분석 결과는 쿠타-주코프스키 정리와 일치한다. 높은 직사각형과 원형 제어 체적 모두 정리 유도에 사용되었다.^[132]^[133]

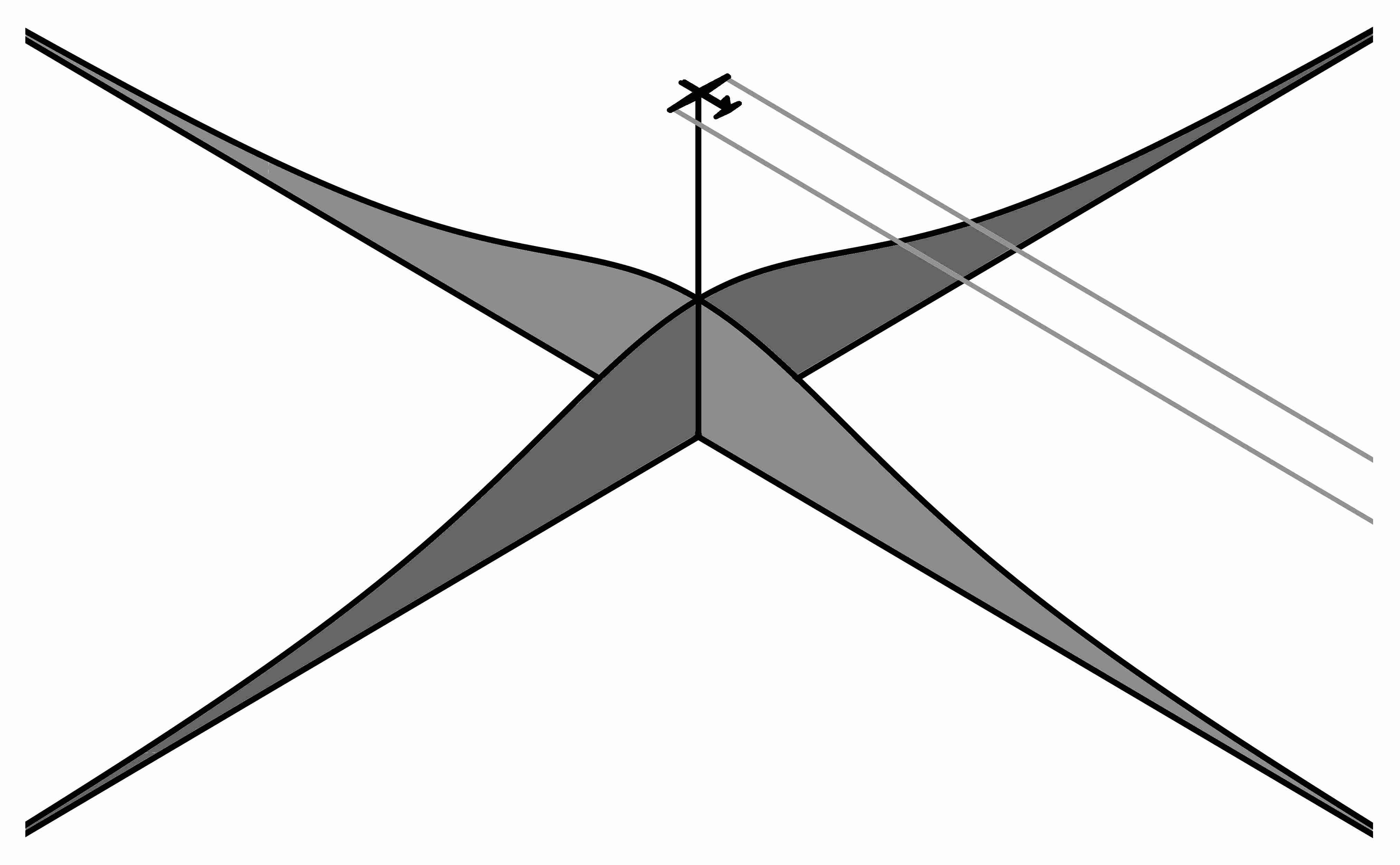
날개는 주변 공기에 압력장을 생성한다. 이 압력장은 거리가 멀어질수록 점차 감소하지만, 완전히 사라지지는 않는다. 항공기 아래쪽에서는 압력장이 지면에 도달하는 양의 압력 교란으로 지속되어, 지면에 약간 주변보다 높은 압력 패턴을 형성한다.^[134] 항공기 아래쪽 먼 곳에서는 압력 차이가 매우 작지만, 넓은 면적에 걸쳐 분포되어 상당한 힘으로 합산된다. 안정적인 수평 비행의 경우, 압력 차이로 인한 적분된 힘은 항공기의 총 공기역학적 양력 및 무게와 같다. 뉴턴의 제3법칙에 따라, 공기가 지면에 가하는 압력은 지면이 공기에 가하는 같은 크기의 반대 방향 힘에 의해 상쇄되며, 이는 항공기가 공기에 가하는 모든 하향력을 상쇄한다. 따라서 양력으로 인한 순 힘은 대기 전체에 작용하여 0이 되므로, 대기의 수직 운동량이 누적되지 않는다.

5. 4. 다운포스 (Downforce)

"장애물" 또는 "유관 수축" 설명은 윗면의 흐름이 아랫면보다 빠르다고 주장하지만, 그 이유는 다르게 설명한다. 이 설명은 윗면이 흐름을 방해하여 유선이 모이고 유관이 좁아져 속도 차이가 생긴다고 주장한다. 유관이 좁아지면 질량 보존 법칙에 따라 유속이 증가해야 한다.^[52] 베르누이 원리에 의해 윗면의 압력이 낮아져 위쪽으로 양력이 발생한다. 때때로 윗면이 흐름을 수축시키는 벤투리 노즐처럼 작용한다고 비유하기도 한다.^[53]

하지만 이 설명은 유관 수축이 어떻게 발생하는지, 또는 왜 윗면에서 아랫면보다 더 큰 유관 수축이 일어나는지 설명하지 못한다. 바닥이 평평하고 윗면이 굽은 일반적인 날개에서는 이것이 어느 정도 직관적으로 이해되지만, 평평한 판, 대칭 에어포일, 범선의 돛 또는 거꾸로 비행하는 일반적인 에어포일이 어떻게 양력을 발생시키는지 설명하지 못하며, 수축 또는 장애물의 양에 따라 양력을 계산하려는 시도는 실험 결과를 예측하지 못한다.^[54]^[55]^[56]^[57] 또 다른 결함은 질량 보존 법칙이 흐름이 빨라지는 만족스러운 물리적 이유가 아니라는 것이다. 물체의 가속을 효과적으로 설명하려면 물체를 가속시키는 힘을 확인해야 한다.^[58]

6. 양력의 응용

양력은 고정익 항공기의 날개, 헬리콥터의 로터, 범선의 돛, 요트 바닥에 설치된 킬, 자동차 경주용 자동차의 날개, 터빈 날개 등 유체가 있는 곳이라면 어디서든 작용한다.^[151] 유체 역학에서는 유체의 흐름에 수직 방향으로 작용하는 힘을 양력이라고 정의한다.^[151]

양력은 프로펠러, 연, 헬리콥터 로터, 경주용 자동차 날개, 해상 돛, 풍력 터빈, 물 속의 요트 용골, 선박 타륜, 수중익선 등에서도 광범위하게 발생한다.^[2] 비행 및 활강 동물 (특히 조류, 박쥐, 곤충)은 물론, 특정 나무 씨앗과 같은 식물계에서도 양력이 활용된다.^[2]

레이싱카의 다운포스는 하향 양력을 의미한다. 범선 돛에 작용하는 양력은 거의 수평 방향이며, 풍차나 터빈에서는 주 방향, 프로펠러에서는 회전축 방향이 양력의 방향이 된다.^[151]

양력은 식물 종자, 곤충 날개, 수성 동물 지느러미, 조류 날개, 연, 비행기 고정익, 헬리콥터 회전익, 수중익선 수중익, 선박 돛(종익)과 키, 노, 프로펠러, 팬, 터빈 등에 이용된다.

탁구, 야구 등 구기 종목에서는 물체의 회전에 의해 발생하는 마그누스 효과를 이용하며, 수영에서는 양력을 강조한 팔 동작으로 장시간 편안하게 수영할 수 있다.

6. 1. 항공기

고정익 항공기는 날개에서 발생하는 양력을 이용하여 비행한다. 날개는 양력 발생에 최적화된 형태로 설계되며, 받음각, 플랩 등을 조절하여 양력을 제어한다. 항공기의 날개는 대부분 양력각을 갖도록 기체에 고정되어 있어, 기체가 수평이더라도 최소한의 양력을 발생시킨다. 많은 여객기 설계에서는 순항 중 필요한 양력을 확보하기 위해 기체를 1~2도 정도 상향으로 기울이기도 한다(단, 항력은 약간 증가한다).^[119]

더 많은 양력이 필요한 상태(저속 시, 상승 시)에서는 기체를 더 크게 상향으로 기울여야 한다. 이착륙 시에는 플랩을 사용하여 양력을 더욱 증가시킨다. 한편, 프로펠러기의 프로펠러에도 마찬가지 원리가 적용되지만, 날개와는 사정이 다르다. 가변 피치(可変ピッチ) 기구를 가진 프로펠러의 경우, 이착륙 시나 최고 속도 영역에서는 피치, 즉 회전 방향에 대한 받음각을 작게 하고, 한편으로 프로펠러의 회전수를 높인다. 피치각을 작게 하여 항력을 줄이고 프로펠러의 효율을 최대한 높이기 위해서이다. 한편, 순항 시에는 피치각을 크게 하고 엔진의 회전수를 낮춘다. 프로펠러 자체의 효율을 생각하면 항력이 커지는 만큼 악화되지만, 엔진의 회전수를 낮춤으로써 연비 효율이 높아지는 효과가 더 크기 때문이다.

헬리콥터의 경우, 로터(회전익)의 각도 조절은 매우 중요하다. 헬리콥터가 전진할 때, 회전하는 로터 블레이드의 한쪽은 기체와 같은 방향으로 회전하여 대기와의 상대 속도가 크고, 다른 한쪽은 기체와 반대 방향으로 회전하기 때문에 상대 속도가 작다. 따라서 로터 블레이드의 좌우에 양력의 차이가 발생한다. 따라서 회전축이 고정된 싱글 로터 헬리콥터에는 좌우 로터 블레이드가 발생시키는 양력을 같게 하기 위해 받음각을 조절하는 장치가 필수적이다.

7. 결론

양력은 유체 속에서 움직이는 물체에 작용하는 중요한 힘으로, 고정익 항공기의 날개, 헬리콥터 로터, 경주용 자동차 날개, 풍력 터빈 등에서 발생한다. 특히 항공기 비행의 핵심 원리이며, 조류, 박쥐, 곤충과 같은 동물들도 양력을 사용한다.^[2]

양력은 항력과 함께 발생하는데, 항력은 유동 방향과 평행한 힘의 성분이다. 항공기가 직선 및 수평 비행을 할 때는 양력이 중력에 반대되지만, 상승, 하강, 경사 선회할 때는 양력이 수직 방향에 대해 기울어진다.^[3]

양력은 유체 역학 현상에 대한 수학적 이론과 물리적 설명으로 이해할 수 있다. 수학적 이론은 정확하지만 방정식을 풀어야 하고, 물리적 설명은 덜 엄격하지만 인과 관계가 미묘하여 포괄적인 설명이 복잡하다.^[11]

양력은 운동량 보존 법칙, 질량 보존 법칙, 에너지 보존 법칙과 같은 물리학의 기본 원리에 따라 발생한다.^[97] 나비어-스톡스 방정식은 양력 이론을 가장 정확하게 제공하지만, 실제로는 레이놀즈 평균 나비어-스톡스 방정식을 사용해야 한다.^[101] 더 간단하지만 정확도가 떨어지는 오일러 방정식과 퍼텐셜 유동 이론도 사용된다.

쿠타-주코프스키 정리는 2차원 익형의 양력을 유동의 순환 성분과 관련짓는 핵심 요소이다.^[84]^[112]^[113]

3차원 날개 주변의 유동은 날개 끝과 관련하여 추가적인 문제를 포함하며, 특히 델타 날개와 같이 종횡비가 낮은 날개는 3차원 유동 효과가 지배적일 수 있다.^[118]

양력에 대한 지속적인 연구와 기술 개발은 항공우주공학, 기계공학, 유체역학 등 다양한 분야에서 중요하게 다루어지며, 더욱 효율적이고 안전한 항공기 개발에 기여하고 있다.

참조

_[1] 웹사이트 What is Lift? https://www1.grc.nas[...] NASA Glenn Research Center 2023-02-09
_[2] 논문 2010
_[3] 서적 Aerodynamics
_[4] 간행물 Aerodynamic Lift, Part 1: The Science 2018-11
_[5] 웹사이트 Incorrect lift theory #1 https://www.grc.nasa[...] NASA 2000-08-16
_[6] 간행물 Quibbles, Misunderstandings, and Egregious Mistakes – Survey of High-School Physics Texts http://aapt.scitatio[...] 1999-05
_[7] 웹사이트 The Aerodynamics of Sail Interaction https://web.archive.[...] Proceedings of the Third AIAA Symposium on the Aero/Hydronautics of Sailing 1971 2011-07-12
_[8] 간행물 A comparison of explanations of the aerodynamic lifting force 1987-01-01
_[9] 웹사이트 Archived copy – Tom Benson Interview https://web.archive.[...] NASA's Glenn Research Center 2012-07-26
_[10] 서적 Aerodynamics
_[11] 간행물 Aerodynamic Lift, Part 2: A comprehensive Physical Explanation 2018-11
_[12] 서적 Understanding Aerodynamics: Arguing from the Real Physics John Wiley & Sons 2012
_[13] 간행물 An Aerodynamicist's View of Lift, Bernoulli, and Newton https://web.archive.[...] 2002-03
_[14] 웹사이트 Bernoulli Or Newton: Who's Right About Lift? https://web.archive.[...] 2011-01-14
_[15] 서적 Fundamentals of Physics 3rd Ed. John Wiley & Sons
_[16] 논문 2001
_[17] 서적 1944
_[18] 서적 Sailing Aerodynamics Adlard Coles Limited
_[19] 웹사이트 Lift from Flow Turning https://www.grc.nasa[...] NASA Glenn Research Center 2000-05-27
_[20] 간행물 Flight Physics for Beginners: Simple Examples of Applying Newton's Laws https://archive.toda[...] 2011-09
_[21] 서적 Stick and Rudder
_[22] 간행물 Flight without Bernoulli http://www.df.uba.ar[...] 1998-11
_[23] 서적 Aerodynamics Pitman 1975
_[24] 논문 Bernoulli and Newton in Fluid Mechanics 1972
_[25] 웹사이트 Incorrect Theory #2 https://www1.grc.nas[...] Glenn Research Center NASA
_[26] 간행물 An Aerodynamicist's View of Lift, Bernoulli, and Newton http://www.df.uba.ar[...] 2002-03
_[27] 웹사이트 Airfoil Behavior: Pressure Distribution over a Clark Y-14 Wing https://www.jove.com[...] College of Engineering, Technology, and Aeronautics (CETA), Southern New Hampshire University
_[28] 간행물 Bernoulli Or Newton: Who's Right About Lift? 2016-02
_[29] 논문 Why Aircraft Fly 2000
_[30] 웹사이트 Fallacious Model of Lift Production https://web.archive.[...] 2008-08-18
_[31] 논문 Report on the first European Mechanics Colloquium, on the Coanda effect 1965
_[32] 웹사이트 How Airplanes Fly: A Physical Description of Lift http://www.allstar.f[...] 2008-06-04
_[33] 웹사이트 Coanda Effect: Understanding Why Wings Work http://jef.raskincen[...] 1994
_[34] 논문 2000
_[35] 논문 1996
_[36] 논문
_[37] 서적 Fluid Mechanics McGraw Hill
_[38] 논문 Section 7.3.2
_[39] 논문 Section 7.3.1.7
_[40] 서적 Encyclopædia of aviation Pitman
_[41] 서적 The Pilot's Handbook of Aeronautical Knowledge McGraw-Hill
_[42] 서적 Aircraft engineering principles Elsevier Butterworth-Heinemann
_[43] 논문 Bernoulli and Newton in Fluid Mechanics http://scitation.aip[...] 2018-01-01 #dead link
_[44] 논문 Stop Abusing Bernoulli
_[45] 논문 Bernoulli and Newton in Fluid Mechanics http://tpt.aapt.org/[...] 2012-03-17 #dead link
_[46] 서적 Understanding Flight McGraw-Hill
_[47] 서적 Introduction to Flight McGraw-Hill Higher Education
_[48] 뉴스 Cambridge scientist debunks flying myth - Telegraph https://www.telegrap[...] UK Telegraph 2012-06-30 #dead link
_[49] 비디오 Flow Visualization http://web.mit.edu/h[...] National Committee for Fluid Mechanics Films/Educational Development Center 2009-01-21
_[50] 논문 An Aerodynamicist's View of Lift, Bernoulli, and Newton http://www.df.uba.ar[...] 2009-04-11 #dead link
_[51] 웹사이트 Incorrect Lift Theory #1 https://www.grc.nasa[...] NASA 2021-06-27
_[52] 서적 Introduction to Flight
_[53] 웹사이트 Incorrect Theory #3 https://www1.grc.nas[...] NASA Glenn Research Center 2023-02-09 #dead link
_[54] 웹사이트 Incorrect lift theory #3 https://www.grc.nasa[...] NASA Glenn Research Center 2021-06-27
_[55] 논문 Quest for an Improved Explanation of Lift http://corsair.flugm[...] American Institute of Aeronautics and Astronautics 2012-12-07 #dead link
_[56] 논문 An Aerodynamicist's View of Lift, Bernoulli, and Newton http://www.df.uba.ar[...] 2009-04-11 #dead link
_[57] 서적 Bernoulli's Law and Aerodynamic Lifting Force http://scitation.aip[...] 2018-01-01 #dead link
_[58] 서적 Understanding Aerodynamics Wiley
_[59] 웹사이트 How Airplanes Fly: A Physical Description of Lift http://www.allstar.f[...] 2016-01-26
_[60] 서적 An Introduction to Fluid Dynamics Cambridge University Press
_[61] 논문 How do wings work? 2003-11
_[62] 논문 A comparison of explanations of the aerodynamic lifting force http://aapt.scitatio[...] 2021-04-28 #dead link
_[63] 웹사이트 Angle of Attack for Airfoil http://hyperphysics.[...] Georgia State University Dept. of Physics and Astronomy 2012-10-14 #dead link
_[64] 논문 A comparison of explanations of the aerodynamic lifting force
_[65] 논문 A comparison of explanations of the aerodynamic lifting force
_[66] 논문
_[67] 논문
_[68] 논문 A comparison of explanations of the aerodynamic lifting force
_[69] 논문 Mechanics of Flight http://iopscience.io[...]
_[70] 웹사이트 http://hyperphysics.[...] GSU Dept. of Physics and Astronomy 2012-07-08 #dead link
_[71] 서적
_[72] 서적
_[73] 서적
_[74] 서적
_[75] 서적
_[76] 서적
_[77] 논문 Vortex-induced vibrations
_[78] 서적 Hydrodynamics around cylindrical structures World Scientific
_[79] 서적 Flow around circular cylinders Oxford University Press
_[80] 서적 Aerodynamics
_[81] 서적
_[82] 서적
_[83] 서적
_[84] 서적
_[85] 서적
_[86] 서적
_[87] 서적
_[88] 서적
_[89] 서적
_[90] 서적 Understanding Aerodynamics: Arguing from the Real Physics John Wiley & Sons
_[91] 서적
_[92] 서적 Introduction to Flight McGraw-Hill
_[93] 웹사이트 Mach Number & Similarity Parameters http://www.aerospace[...] Aerospaceweb.org 2003-12-28
_[94] 서적
_[95] 서적
_[96] 서적
_[97] 논문 An Aerodynamicist's View of Lift, Bernoulli, and Newton http://www.df.uba.ar[...]
_[98] 서적
_[99] 서적
_[100] 서적
_[101] 서적 Elsevier Science Publishers
_[102] 서적
_[103] 서적
_[104] 서적
_[105] 서적 Understanding Aerodynamics
_[106] 웹사이트 Faculty Web Directory https://web.archive.[...] 2012-07-26
_[107] 서적 Section 2.7 1967
_[108] 서적 Section 3.31 1966
_[109] 서적 Section 4.8 1975
_[110] 서적 Section 4.5 1991
_[111] 서적 Sections 8.1–8 1975
_[112] 서적 Section VIII.2 1959
_[113] 서적 Section 3.15 1991
_[114] 서적 1934
_[115] 서적 Section 6.7 1967
_[116] 서적 2006
_[117] 서적 Section 7.2.1 2012
_[118] 서적 Section 12.3 1966
_[119] 서적 Section 8.1.3 2012
_[120] 서적 Section 8.1.1 2012
_[121] 서적 Aerodynamics for Naval Aviators 1965
_[122] 서적 1907
_[123] 서적 Section 10.1 1966
_[124] 서적 Section 8.9 1975
_[125] 서적 Section 5.2 1991
_[126] 서적 Section 2.4 1967
_[127] 서적 Section 9.3 1966
_[128] 서적 Section III.2 1932
_[129] 서적 Section 8.1 2012
_[130] 서적 Section 1.5, equation 1.15 1953
_[131] 서적 Lift in thin slices: the two dimensional case 1996
_[132] 서적 Sections B.V.6, B.V.7 1932
_[133] 서적 Section 6.4, p. 407 1967
_[134] 서적 Figure 150 1934
_[135] 서적 Sections 5 and 112 1907
_[136] 웹사이트 NACA 2412 (naca2412-il) http://airfoiltools.[...] 2022-06-17
_[137] 기타
_[138] 웹사이트 クッタ‐ジューコフスキの定理 https://kotobank.jp/[...] 2020-05-20
_[139] 웹사이트 クッタ‐ジュコフスキーの定理 https://kotobank.jp/[...] 2020-05-18
_[140] 웹사이트 翼の原理 http://www.jsme-fed.[...]
_[141] 웹사이트 Incorrect Lift Theory https://www.grc.nasa[...] NASA(미국항공우주국) 2019-05-04
_[142] 웹사이트 飛行機はなぜ飛ぶのかはまだ分からない?? - NPO法人知的人材ネットワーク・あいんしゅたいん http://jein.jp/jifs/[...]
_[143] 웹사이트 航空実用辞典 http://www.jal.co.jp[...] 일본항공
_[144] 웹사이트 how wings work? Smoke streamlines around an airfoil https://www.youtube.[...] 2018-10-24
_[145] 웹사이트 新しい航空学　デビッド・アンダーソン氏の新理論 http://www.wetwing.c[...] 2011-11-19
_[146] 웹사이트 What is Lift http://www.grc.nasa.[...] NASA 2009-03-09
_[147] 서적 유체역학 교보문고 2010
_[148] 간행물 표준국어대사전 국립국어원
_[149] 서적 Aerodynamics Pitman Publishing Limited 1975
_[150] 웹사이트 Drag of Blunt Bodies and Streamlined Bodies http://www.efluids.c[...]
_[151] 서적 Aerodynamics Pitman Publishing Limited 1975
_[152] 웹인용 Incorrect Lift Theory http://www.grc.nasa.[...] 2014-02-16
_[153] 웹사이트 Physics of Flight – reviewed http://user.uni-fran[...] 2011-07-19
_[154] 서적 The Feynman Lectures on Physics Addison-Wesley 1963
_[155] 웹사이트 Lift from Flow Turning http://www.grc.nasa.[...] NASA Glenn Research Center 2009-07-07
_[156] 서적 An Introduction to Fluid Dynamics Cambridge University Press 1967
_[157] 웹사이트 A comparison of explanations of the aerodynamic lifting force http://scitation.aip[...]
_[158] 서적 항공역학 성안당 2012
_[159] 서적 항공역학 성안당 2012

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com