곡선의 길이

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 역사
- 3.1. 고대
- 3.2. 17세기
4. 적분을 이용한 호의 길이 계산
- 4.1. 수치 적분
- 4.2. 다양한 좌표계에서의 호의 길이
5. 간단한 경우
- 5.1. 원호
6. 무한 길이 곡선
7. (유사-) 리만 다양체로의 일반화
참조

1. 개요

곡선의 길이는 곡선 상의 두 점 사이의 거리를 측정한 값이다. 유클리드 공간 또는 거리 공간에서 연속 함수로 표현될 수 있으며, 구간을 분할하여 다각형 경로로 근사할 수 있다. 곡선이 매끄러울 경우, 분할을 무한히 세분화하면 적분을 통해 호의 길이를 정의할 수 있다. 17세기에는 미적분학의 발달과 함께 호의 길이를 계산하는 방법이 발전했으며, 현대에는 적분을 이용하여 계산한다. 극좌표, 구면 좌표, 원통 좌표 등 다양한 좌표계에서 호의 길이를 계산하는 공식이 존재하며, 대부분의 경우 닫힌 형식으로 해를 구할 수 없어 수치 적분을 사용한다. 일부 곡선은 무한 길이를 가지며, 유사 리만 다양체로 일반화하여 정의할 수 있다.

더 읽어볼만한 페이지

수학 개념 - 차원
차원은 수학, 물리학, 컴퓨터 과학에서 객체의 특성을 나타내는 핵심 개념으로, 수학에서는 객체 위의 점이 움직일 수 있는 자유도의 수, 물리학에서는 시공간, 컴퓨터 과학에서는 기하 기본 요소 정의나 문자 코드 묶음 수를 나타내는 데 사용된다.
수학 개념 - 무차원량
무차원량은 물리량의 차원이 1인 값으로, 동일 종류 물리량의 비율이나 물리 상수 정규화로 얻어지며, 물리 법칙의 단위계 독립성을 나타내는 버킹엄 π 정리에 의해 중요성이 강조되고 과학 및 공학 분야에서 널리 활용된다.
미적분학 정리 - 연쇄 법칙
연쇄 법칙은 둘 이상의 미분 가능한 함수 합성의 미분법을 제공하며, z의 y에 대한 순간적인 변화율과 y의 x에 대한 순간적인 변화율을 곱하여 z의 x에 대한 순간적인 변화율을 계산하는 직관적인 아이디어를 바탕으로 실변수 함수, 다변수 함수 등 다양한 경우에 적용된다.
미적분학 정리 - 미적분학의 기본 정리
미적분학의 기본 정리는 미분과 적분 사이의 관계를 설명하는 미적분학의 핵심 정리로서, 제1 기본 정리와 제2 기본 정리로 구성되며, 17세기에 발전되어 르베그 적분 등으로 일반화된다.
곡선 - 선적분
선적분은 스칼라장이나 벡터장의 곡선에 대한 적분으로, 함수의 종류와 곡선의 표현 방식에 따라 다양하게 정의되며, 물리학과 공학 등에서 활용된다.
곡선 - 아스트로이드
아스트로이드는 별 모양의 곡선으로, `x^2/3 + y^2/3 = a^2/3` (a는 상수)로 표현되는 6차 실수 대수곡선이며, 매개변수 방정식, 페달 방정식 등 다양한 수학적 표현으로 나타낼 수 있고, 면적은 (3/8)πa², 둘레는 6a이며, 원 내부에서 작은 원이 구르며 생기는 자취로도 설명된다.

곡선의 길이
정의
정의	곡선의 길이는 곡선의 주어진 두 점 사이의 호의 길이이다.
역사적 용어	곡선의 정량화
공식
미분 가능한 함수	y = f(x), a ≤ x ≤ b 곡선의 길이 L = ∫ab √(1 + (dy/dx)2) dx
매개변수 방정식	x = x(t), y = y(t), a ≤ t ≤ b 곡선의 길이 L = ∫ab √((dx/dt)2 + (dy/dt)2) dt
극좌표	r = f(θ), α ≤ θ ≤ β 곡선의 길이 L = ∫αβ √(r2 + (dr/dθ)2) dθ
3차원 공간	곡선의 길이 L = ∫ab \|r'(t)\| dt, 여기서 r'(t)는 속도 벡터이다.
추가 정보
관련 개념	미분 기하학 곡률 측지선

2. 정의

여러 개의 선형 세그먼트로 곡선을 근사하는 방법, 곡선의 ''교정''이라고 한다.

평면의 곡선은 곡선상의 점들을 (직선) 선분으로 연결하여 다각형 경로를 생성하여 근사할 수 있다. 각 선분의 길이는 (예를 들어, 유클리드 공간에서 피타고라스 정리를 사용하여) 쉽게 계산할 수 있으므로 근사의 총 길이는 각 선분의 길이를 합산하여 구할 수 있으며, 이 근사는 ''(누적) 현 거리''라고 알려져 있다.^[1]

곡선이 이미 다각형 경로가 아닌 경우, 점차 더 많은 수의 짧은 선분을 사용하면 곡선 길이를 더 잘 근사할 수 있다. 곡선을 연결된 (직선) 선분으로 근사하여 곡선 길이를 결정하는 것을 곡선의 ''교정''이라고 한다. 연속적인 근사의 길이는 감소하지 않고 무한정 증가할 수 있지만, 매끄러운 곡선의 경우 선분의 길이가 임의로 작아지면 유한한 극한에 가까워진다.

일부 곡선의 경우, 모든 다각형 근사(교정)의 길이에 대한 상한인 가장 작은 수

L

이 존재한다. 이러한 곡선을 '''가선'''이라고 하며, '''호의 길이'''는 숫자

L

로 정의된다.

'''부호 있는 호의 길이'''는 곡선에서 원점으로 간주되는 기준점에 대한 방향 또는 "방향" 감각을 전달하도록 정의할 수 있다(참고: 곡선 방향 및 부호 있는 거리).^[2]

f\colon[a,b]\to\R^n

을 단사이고 연속 미분 가능 (즉, 도함수가 연속 함수임) 함수라고 하자.

f

로 정의된 곡선의 길이는 세그먼트 수가 무한대에 가까워질 때

[a,b]

의 정규 분할에 대한 선형 세그먼트 길이의 합의 극한으로 정의될 수 있다. 이는 다음을 의미한다.

L(f) = \lim_{N\to\infty}\sum_{i=1}^N \bigg|f(t_i) - f(t_{i-1})\bigg|

여기서

t_i = a + i(b - a)/N = a + i\Delta t

이고

\Delta t = \frac{b-a}{N} = t_i - t_{i-1}

(

i = 0, 1, \dotsc, N

). 이 정의는 호의 표준 정의와 동등하다.

L(f) = \lim_{N\to\infty} \sum_{i=1}^N \bigg|f(t_i) - f(t_{i-1})\bigg| = \lim_{N\to\infty}\sum_{i=1}^N \left|\frac{f(t_i) - f(t_{i-1})}{\Delta t}\right|\Delta t = \int_a^b \Big|f'(t)\Big|\ dt.

마지막 등식은 다음 단계로 증명된다.

# 미적분학의 제2 기본 정리는 다음을 보여준다.

f(t_i) - f(t_{i-1}) = \int_{t_{i-1}}^{t_i} f' (t)\ dt = \Delta t \int_0^1 f' (t_{i-1} + \theta(t_i - t_{i-1}))\ d\theta

여기서

t = t_{i-1} + \theta(t_i - t_{i-1})

는

\theta \in [0,1]

에서

[t_{i-1},t_i]

로 매핑되고

dt = (t_i - t_{i-1}) \, d \theta = \Delta t \, d \theta

이다. 아래 단계에서 다음의 동등한 표현이 사용된다.

\frac{f(t_i) - f(t_{i-1})}{\Delta t} = \int_0^1 f' (t_{i-1} + \theta(t_i - t_{i-1}))\ d\theta.

# 함수

\left|f'\right|

는 닫힌 구간

[a,b]

에서 실수 집합으로의 연속 함수이므로, 하이네-칸토어 정리에 따라 균등 연속이므로, 양의 실수

\varepsilon

에 대한 양의 실수이자 단조 감소하지 않는 함수

\delta(\varepsilon)

가 존재하여

\Delta t < \delta(\varepsilon)

이면

\left|\left|f'(t_{i-1} + \theta(t_i - t_{i-1}))\right| - \left|f'(t_i)\right|\right| < \varepsilon

여기서

\Delta t = t_i - t_{i-1}

이고

\theta \in [0,1]

이다. 다음 수식의 극한

N \to \infty

를 고려해보자.

\sum_{i=1}^N \left|\frac{f(t_i) - f(t_{i-1})}{\Delta t}\right|\Delta t - \sum_{i=1}^N \left|f'(t_i)\right|\Delta t.

위 단계의 결과를 사용하여, 다음이 된다.

\sum_{i=1}^N \left|\int_0^1 f' (t_{i-1} + \theta(t_i - t_{i-1}))\ d\theta \right|\Delta t - \sum_{i=1}^N \left|f'(t_i)\right|\Delta t.

항들을 재배열하면 다음이 된다.

\begin{align}& \Delta t \sum_{i=1}^N \left( \left|\int_0^1 f' (t_{i-1} + \theta(t_i - t_{i-1}))\ d\theta \right| - \int_0^1 \left|f'(t_i)\right| d\theta \right) \\&\qquad \leqq \Delta t \sum_{i=1}^N \left( \int_0^1 \left| f' (t_{i-1} + \theta(t_i - t_{i-1})) \right| \ d\theta  - \int_0^1 \left|f'(t_i)\right| d\theta \right) \\&\qquad = \Delta t\sum _{i=1}^{N}\int _{0}^{1}\left|f'(t_{i-1}+\theta (t_{i}-t_{i-1}))\right|-\left|f'(t_{i})\right|\ d\theta\end{align}

여기서 가장 왼쪽에 있는

\left|f'(t_i)\right| = \int_0^1 \left|f'(t_i)\right| d \theta

가 사용된다.

\Delta t < \delta(\varepsilon)

에 의해, 다음이 된다.

\Delta t \sum_{i=1}^N \left( \left|\int_0^1 f' (t_{i-1} + \theta(t_i - t_{i-1}))\ d\theta \right| - \left|f'(t_i)\right| \right) < \varepsilon N \Delta t

\left|f'(t_i)\right| = \int_0^1 \left|f'(t_i)\right| d \theta

,

\varepsilon N \Delta t = \varepsilon (b - a)

를 사용하여, 극한

N \to \infty

에서

\delta(\varepsilon) \to 0

이므로

\varepsilon \to 0

이므로, 왼쪽이

0

에 접근한다. 즉,

\sum_{i=1}^N \left|\frac{f(t_i) - f(t_{i-1})}{\Delta t}\right|\Delta t = \sum_{i=1}^N \left|f'(t_i)\right|\Delta t

이고, 이 등식의 오른쪽은

\left|f'(t)\right|

에 대한 리만 적분이다. 이 호의 길이 정의는 연속 미분 가능한 함수

f: [a, b] \to \R^n

로 표현된 곡선의 길이가

[a, b]

에서 항상 유한하다는 것을 보여준다. 즉, 가장 길이를 잴 수 있다.

도함수의 노름의 적분으로 매끄러운 곡선의 호의 길이 정의는 다음 정의와 동등하다.

L(f) = \sup\sum_{i=1}^N \bigg|f(t_i) - f(t_{i-1})\bigg|

여기서 상한은

[a, b]

의 모든 가능한 분할

a = t_0 < t_1 < \dots < t_{N-1} < t_N = b

에 대해 취해진다.^[3] 이 정의는

f

가 미분 가능하지 않고 단순히 연속적인 경우에도 유효하다.

곡선은 무한히 많은 방식으로 매개변수화될 수 있다.

\varphi: [a, b] \to [c, d]

를 임의의 연속 미분 가능한 전단사라고 하자. 그러면

g = f\circ\varphi^{-1}: [c, d] \to \R^n

은 처음에

f

로 정의된 곡선의 다른 연속 미분 가능한 매개변수화이다. 곡선의 호의 길이는 곡선을 정의하는 데 사용된 매개변수화에 관계없이 동일하다.

\begin{align}L(f) &= \int_a^b \Big|f'(t)\Big|\ dt = \int_a^b \Big|g'(\varphi(t))\varphi'(t)\Big|\ dt \\&= \int_a^b \Big|g'(\varphi(t))\Big|\varphi'(t)\ dt \quad \text{경우 }\varphi\text{가 감소하지 않음} \\&= \int_c^d \Big|g'(u)\Big|\ du \quad \text{치환 적분 사용}\\&= L(g).\end{align}

유클리드 공간이나 더 일반적인 거리 공간에서 곡선 는 실수 직선 내의 닫힌 구간 에서 거리 공간으로의 연속 사상 의 상이다.

구간 에 대한 구간의 분할

:

a=t_{0}

을 고려하면, 곡선 위에 유한 개의 점 를 취할 수 있다. 에서 까지의 거리를 각각 , 로 나타내면, 이것은 이 두 점을 잇는 선분의 길이이다.

곡선 의 '''호의 길이''' 는

:

L(C) = \sup_{a=t_0 < t_1 < \cdots < t_n = b} \sum_{i = 0}^{n - 1} d(f(t_i), f(t_{i+1}))

로 주어진다. 단, 상한 은 구간 의 분할 개수 을 얼마든지 크게 하여 만들 수 있는 모든 분할에 걸쳐 취한다.

호의 길이 은 유한하거나 무한할 수 있는데, 이면 는 '''유한장'''(rectifiable^영어; 구장 가능), 즉 길이를 잴 수 있다고 하며, 그렇지 않으면 '''무한장'''(non-rectifiable^영어; 구장 불가능)이라고 한다. 이 호의 길이 정의에서, 는 미분가능 함수 로 정의될 필요는 없다. 사실, 일반적인 거리 공간에서 생각할 경우, 미분 가능성을 정의하는 것은 일반적으로 기대할 수 없다.

곡선은 다양한 방법으로 매개변수 표시될 수 있다. 따라서 곡선 가 정의 사상 외에 매개변수 표시 를 갖는 경우를 고려한다. 및 가 단사일 때, 연속 단조 사상 가 존재하여 가 성립하고, 역 사상 이 존재한다. 분명히, 임의의

:

\sum_{i = 0}^{n - 1} d(f(t_i), f(t_{i+1}))

형태의 합은, 라고 하면,

:

\sum_{i = 0}^{n - 1} d(g(u_i), g(u_{i+1}))

형태의 합과 같으며, 그 역도 마찬가지이다. 따라서 호의 길이는, 매개변수 선택에 의존하지 않는다는 의미에서, 곡선에 내재된 성질임을 알 수 있다.

곡선에 대한 이 호의 길이 정의는, 실수값 함수에 대한 전변동의 정의와 유사하다.

3. 역사

아르키메데스는 고갈법을 통해 곡선 아래 면적을 구하는 방법을 개척했다. 사람들은 곡선 안에 다각형을 새겨 넣어 변의 길이를 계산함으로써 곡선 길이의 근사값을 구했다. 더 많은 선분을 사용하고 각 선분의 길이를 줄이면 더 정확한 근사값을 얻을 수 있었다. 특히, 많은 변을 가진 다각형을 원에 새겨 넣어 π의 근사값을 구할 수 있었다.^[6]^[7]

17세기에는 소진법을 바탕으로 여러 초월 곡선의 길이를 구하는 기하학적 방법이 개발되었다. 1645년 에반젤리스타 토리첼리는 로그 나선의 길이를 구했고, 1658년 크리스토퍼 렌은 사이클로이드의 길이를, 1691년 고트프리트 라이프니츠는 현수선의 길이를 구했다.^[8]

1659년, 존 월리스는 윌리엄 네일이 반입방 포물선의 길이를 구하는 방법을 발견했다고 발표했다.^[8]

미적분학이 발전하기 전에, 헨드릭 판 호라트와 피에르 드 페르마는 호의 길이 결정 문제를 적분 문제로 변환하는 방법을 독립적으로 발견했다. 1659년 판 호라트는 호 길이 결정 문제를 곡선 아래 면적(즉, 적분) 결정 문제로 변환할 수 있음을 보여주는 구성을 발표했다. 그는 포물선 아래 면적을 구해야 하는 반입방 포물선의 호 길이를 결정했다.^[9] 1660년, 페르마는 ''De linearum curvarum cum lineis rectis comparatione dissertatio geometrica'' (직선과 비교한 곡선에 대한 기하학적 논문)에서 동일한 결과를 포함하는 더 일반적인 이론을 발표했다.^[10]

페르마는 곡선의 길이를 구하기 위해, x = a 에서의 접선을 구하고, a를 작은 양만큼 증가시켜 곡선의 길이를 근사하는 방법을 사용했다. 그는 피타고라스 정리를 사용하여 짧은 선분의 길이를 구하고, 이 선분들을 합산하여 호의 길이를 근사했다.

3. 1. 고대

대부분의 기간 동안 위대한 수학자들조차 불규칙한 호의 길이를 계산하는 것을 불가능하다고 생각했지만, 아르키메데스는 고갈법으로 곡선 아래 면적을 구하는 방법을 개척했다. 사람들은 곡선 안에 다각형을 새겨 넣어 변의 길이를 계산하여 길이의 근사값을 구했다. 더 많은 선분을 사용하고 각 선분의 길이를 줄임으로써 점점 더 정확한 근사값을 얻을 수 있었다. 특히, 많은 변을 가진 다각형을 원에 새겨 넣음으로써 π의 근사값을 구할 수 있었다.^[6]^[7]

3. 2. 17세기

17세기에는 소진법을 바탕으로 여러 초월 곡선의 길이를 구하는 기하학적 방법이 개발되었다. 1645년 에반젤리스타 토리첼리는 로그 나선(일부 자료에서는 1650년대 존 월리스)의 길이를 구했고, 1658년 크리스토퍼 렌은 사이클로이드의 길이를, 1691년 고트프리트 라이프니츠는 현수선의 길이를 구했다.^[8]

1659년, 월리스는 윌리엄 네일이 반입방 포물선의 길이를 구하는 방법을 발견했다고 인정했다.^[8]

미적분학이 발전하기 전에, 헨드릭 판 호라트와 피에르 드 페르마는 호의 길이 결정 문제를 적분 문제로 변환하는 방법을 독립적으로 발견했다.

1659년, 판 호라트는 호 길이 결정 문제를 곡선 아래 면적(즉, 적분) 결정 문제로 변환할 수 있음을 보여주는 구성을 발표했다. 그는 포물선 아래 면적을 구해야 하는 반입방 포물선의 호 길이를 결정했다.^[9] 1660년, 페르마는 ''De linearum curvarum cum lineis rectis comparatione dissertatio geometrica'' (직선과 비교한 곡선에 대한 기하학적 논문)에서 동일한 결과를 포함하는 더 일반적인 이론을 발표했다.^[10]

페르마는 다음 곡선을 사용했다.

:

y = x^\frac{3}{2} \,

이 곡선의 ''x'' = ''a''에서의 접선은 기울기가

:

{3 \over 2} a^\frac{1}{2}

이므로 접선은 다음 방정식을 갖는다.

:

y = {3 \over 2} a^\frac{1}{2}(x - a) + f(a).

다음으로, 그는 ''a''를 작은 양인 ''a'' + ''ε''로 증가시켜 세그먼트 ''AC''가 ''A''에서 ''D''까지의 곡선 길이에 대한 비교적 좋은 근사치를 만들었다. 세그먼트 ''AC''의 길이를 구하기 위해 그는 피타고라스 정리를 사용했다.

:

\begin{align}AC^2 &= AB^2 + BC^2 \\&= \varepsilon^2 + {9 \over 4} a \varepsilon^2 \\&= \varepsilon^2 \left(1 + {9 \over 4} a\right)\end{align}

이것을 풀면

:

AC = \varepsilon \sqrt{1 + {9 \over 4} a \,}.

호 길이를 근사하기 위해, 페르마는 짧은 세그먼트들의 시퀀스를 합산했다.

4. 적분을 이용한 호의 길이 계산

평면의 곡선은 곡선상의 점들을 (직선) 선분으로 연결하여 다각형 경로를 생성하여 근사할 수 있다. 각 선분의 길이는 (예를 들어, 유클리드 공간에서 피타고라스 정리를 사용하여) 쉽게 계산할 수 있으므로, 근사의 총 길이는 각 선분의 길이를 합산하여 구할 수 있다. 이 근사는 ''(누적) 현 거리''라고 알려져 있다.^[1]

곡선이 이미 다각형 경로가 아닌 경우, 점차 더 많은 수의 짧은 선분을 사용하면 곡선 길이를 더 잘 근사할 수 있다. 곡선을 연결된 (직선) 선분으로 근사하여 곡선 길이를 결정하는 것을 곡선의 ''교정''이라고 한다. 연속적인 근사의 길이는 감소하지 않고 무한정 증가할 수 있지만, 매끄러운 곡선의 경우 선분의 길이가 임의로 작아지면 유한한 극한에 가까워진다.

일부 곡선의 경우, 모든 다각형 근사(교정)의 길이에 대한 상한인 가장 작은 수 $L$ 이 존재한다. 이러한 곡선을 잴 수 있는 곡선이라고 하며, 호의 길이는 숫자 $L$ 로 정의된다.

$f\colon[a,b]\to\R^n$ 을 단사이고 연속 미분 가능 (즉, 도함수가 연속 함수) 함수라고 하자. $f$ 로 정의된 곡선의 길이는 세그먼트 수가 무한대에 가까워질 때 $[a,b]$ 의 정규 분할에 대한 선형 세그먼트 길이의 합의 극한으로 정의될 수 있다. 이는 다음을 의미한다.

: $L(f) = \lim_{N\to\infty}\sum_{i=1}^N \bigg|f(t_i) - f(t_{i-1})\bigg|$

여기서 $t_i = a + i(b - a)/N = a + i\Delta t$ 이고 $\Delta t = \frac{b-a}{N} = t_i - t_{i-1}$ for $i = 0, 1, \dotsc, N.$ 이 정의는 호의 표준 정의와 동등하다.

: $L(f) = \lim_{N\to\infty} \sum_{i=1}^N \bigg|f(t_i) - f(t_{i-1})\bigg| = \lim_{N\to\infty}\sum_{i=1}^N \left|\frac{f(t_i) - f(t_{i-1})}{\Delta t}\right|\Delta t = \int_a^b \Big|f'(t)\Big|\ dt.$

연속 미분 가능한 함수 $f: [a, b] \to \R^n$ 로 표현된 곡선의 길이는 $[a, b]$ 에서 항상 유한하다.

도함수의 노름의 적분으로 매끄러운 곡선의 호의 길이 정의는 다음 정의와 동등하다.

: $L(f) = \sup\sum_{i=1}^N \bigg|f(t_i) - f(t_{i-1})\bigg|$

여기서 상한은 $[a, b]$ 의 모든 가능한 분할 $a = t_0 < t_1 < \dots < t_{N-1} < t_N = b$ 에 대해 취해진다.^[3] 이 정의는 $f$ 가 미분 가능하지 않고 단순히 연속적인 경우에도 유효하다.

곡선은 무한히 많은 방식으로 매개변수화될 수 있다. $\varphi: [a, b] \to [c, d]$ 를 임의의 연속 미분 가능한 전단사라고 하자. 그러면 $g = f\circ\varphi^{-1}: [c, d] \to \R^n$ 은 처음에 $f$ 로 정의된 곡선의 다른 연속 미분 가능한 매개변수화이다. 곡선의 호의 길이는 곡선을 정의하는 데 사용된 매개변수화에 관계없이 동일하다.

: $사용}\\&= L(g).\end{align}$

$\R^2$ 에서 평면 곡선이 $y = f(x)$ 방정식으로 정의되고, 여기서 $f$ 가 연속 미분 가능하면, 이는 $x = t$ 및 $y = f(t)$ 인 매개변수 방정식의 특별한 경우이다. 각 무한소 호 세그먼트의 유클리드 거리는 다음과 같다.

: $\sqrt{dx^2 + dy^2} = \sqrt{1 + \left(\frac{dy}{dx}\right)^2 \,}dx.$

호의 길이는 다음과 같다.

: $s=\int_a^b \sqrt{1 + \left(\frac{dy}{dx}\right)^2 \,}dx.$

호의 길이에 대한 폐쇄 형식의 해가 있는 곡선에는 현수선, 원, 사이클로이드, 로그 나선, 포물선, 절반 입방 포물선 및 직선이 포함된다. 타원 및 쌍곡선 호의 길이에 대한 폐쇄 형식 해가 없다는 것은 타원 적분의 개발로 이어졌다.

4. 1. 수치 적분

대부분의 경우, 단순한 곡선을 포함하여 호의 길이에 대한 폐쇄형 해가 없으므로 수치 적분이 필요하다.^[1] 호 길이 적분의 수치 적분은 대개 매우 효율적이다.^[1] 예를 들어, 호 길이 적분을 수치 적분하여 단위 원의 1/4 길이를 구하는 문제를 고려해 보자.^[1] 단위 원의 윗부분은

y = \sqrt{1 - x^2}.

로 매개변수화할 수 있다.^[1] 구간

x \in \left[-\sqrt{2}/2, \sqrt{2}/2\right]

는 원의 1/4에 해당한다.^[1]

dy/dx = -x \big/ \sqrt{1 - x^2}

이고

1 + (dy/dx)^2 = 1\big/\left(1 - x^2\right),

이므로, 단위 원의 1/4 길이는 다음과 같다.^[1]

:

\int_{-\sqrt{2}/2}^{\sqrt{2}/2} \frac{dx}{\sqrt{1 - x^2}}\, .

^[1]

이 적분에 대한 15점 가우스-크론로드 규칙 추정값은 1.570796326808177이고, 실제 길이

:

\arcsin x\bigg|^{\sqrt{2}/2}_{-\sqrt{2}/2} = \frac{\pi}{2}

와 1.3e-11만큼 차이가 나고, 16점 가우스 구적법 규칙 추정값 1.570796326794727은 실제 길이와 1.7e-13만큼 차이가 난다.^[1] 즉, 16번의 피적분 함수 계산만으로 이 적분을 거의 머신 엡실론에 가깝게 계산할 수 있다.^[1]

4. 2. 다양한 좌표계에서의 호의 길이

극좌표, 구면 좌표, 원통 좌표 등 다양한 좌표계에서 곡선의 길이를 구하는 방법을 살펴본다.

극좌표는 평면 위의 점을 거리와 각도로 나타내는 좌표계이며, 구면 좌표는 3차원 공간에서 점을 거리, 극각, 방위각으로 나타내는 좌표계이다. 원통 좌표는 3차원 공간에서 점을 거리, 각도, 높이로 나타내는 좌표계이다. 이러한 좌표계들에서 곡선의 길이는 각각 다르게 표현된다.^[1]

4. 2. 1. 극좌표

극좌표로 표현된 곡선 '''C''''(t) = (r(t), θ(t))가 주어졌다고 가정한다. 극좌표에서 직교 좌표로 변환하는 공식은 다음과 같다.

'''x''''(r, θ) = (rcos|코스^영어θ, rsin|사인^영어θ).

호의 길이 적분식의 피적분 함수는

\left|\left(\mathbf{x}\circ\mathbf{C}\right)'(t)\right|

이다. 벡터장의 연쇄 법칙에 따르면

D(\mathbf{x} \circ \mathbf{C}) = \mathbf{x}_r r' + \mathbf{x}_{\theta} \theta'.

이므로, 호의 길이 적분식의 제곱된 피적분 함수는 다음과 같다.

\left(\mathbf{x_r}\cdot\mathbf{x_r}\right)\left(r'\right)^2 + 2\left(\mathbf{x}_r\cdot\mathbf{x}_{\theta}\right)r'\theta' + \left(\mathbf{x}_{\theta}\cdot\mathbf{x}_{\theta}\right)\left(\theta'\right)^2 = \left(r'\right)^2 + r^2\left(\theta'\right)^2.

따라서 극좌표로 표현된 곡선의 호의 길이는 다음과 같이 계산할 수 있다.

:

\int_{t_1}^{t_2} \sqrt{\left(\frac{dr}{dt}\right)^2 + r^2\left(\frac{d\theta}{dt}\right)^2 \,} dt =\int_{\theta(t_1)}^{\theta(t_2)} \sqrt{\left(\frac{dr}{d\theta}\right)^2 + r^2 \,} d\theta.

두 번째 식은 t=θ로 매개변수화된 극좌표 그래프 r = r(θ)에 대한 식이다.

4. 2. 2. 구면 좌표

\mathbf{C}(t) = (r(t), \theta(t), \phi(t))

를

\theta

가 양의

z

축에서 측정된 극각이고

\phi

가 방위각인 구면 좌표로 표현된 곡선이라고 하자. 구면 좌표에서 직교 좌표로 변환하는 매핑은 다음과 같다.

:

\mathbf{x}(r, \theta, \phi) = (r \sin\theta \cos\phi, r\sin\theta \sin\phi, r\cos\theta).

연쇄 법칙을 사용하면

D(\mathbf{x}\circ\mathbf{C}) = \mathbf{x}_r r' + \mathbf{x}_{\theta}\theta' + \mathbf{x}_{\phi}\phi'.

임을 알 수 있다.

i

와

j

가 다른 모든 점곱

\mathbf{x}_i \cdot \mathbf{x}_j

는 0이므로, 이 벡터의 제곱된 노름은 다음과 같다.

:

\left(\mathbf{x}_r \cdot \mathbf{x}_r\right)\left(r'^2\right) + \left(\mathbf{x}_{\theta} \cdot \mathbf{x}_{\theta}\right)\left(\theta'\right)^2 + \left(\mathbf{x}_{\phi} \cdot \mathbf{x}_{\phi}\right)\left(\phi'\right)^2 = \left(r'\right)^2 + r^2\left(\theta'\right)^2 + r^2 \sin^2\theta \left(\phi'\right)^2.

따라서 구면 좌표로 표현된 곡선의 호의 길이는 다음과 같이 계산할 수 있다.^[1]

:

\int_{t_1}^{t_2} \sqrt{\left(\frac{dr}{dt}\right)^2 + r^2\left(\frac{d\theta}{dt}\right)^2 + r^2\sin^2\theta \left(\frac{d\phi}{dt}\right)^2 \,} dt.

4. 2. 3. 원통 좌표

원통 좌표로 표현된 곡선의 호의 길이는 다음과 같이 계산할 수 있다.

:

\int_{t_1}^{t_2} \sqrt{\left(\frac{dr}{dt}\right)^2 + r^2\left(\frac{d\theta}{dt}\right)^2 + \left(\frac{dz}{dt}\right)^2 \,} dt.

5. 간단한 경우

원의 반지름을 r이라고 할 때, 원주의 길이는 $C = 2\pi r$로 표현된다. 반원의 경우 호의 길이는 $s = \pi r$이다. 중심각 $\theta$가 라디안이면 $s = r\theta$로 간단히 나타낼 수 있다. 현수선, 사이클로이드, 로그 나선, 포물선, 반입방 포물선 등은 닫힌 형태로 호의 길이를 표현할 수 있다. 반면 타원과 쌍곡선의 호의 길이는 닫힌 형태로 표현할 수 없어 타원 적분으로 나타낸다.

5. 1. 원호

호의 길이는 라틴어로 길이(또는 크기)를 뜻하는 단어 ''spatium''이기 때문에 ''s''로 표기한다.

다음에서

r

은 원의 반지름,

d

는 지름,

C

는 원주,

s

는 원의 호의 길이,

\theta

는 호가 원의 중심에서 이루는 각도를 나타낸다. 거리

r, d, C,

및

s

는 동일한 단위로 표현된다.

$C = 2\pi r,$ 는 $C = \pi d.$ 와 같다. 이 방정식은 $\pi.$ 의 정의이다.
호가 반원인 경우 $s = \pi r.$ 이다.
임의의 원형 호의 경우:
$\theta$ 가 라디안인 경우 $s = r\theta.$ 이다. 이는 라디안의 정의이다.
$\theta$ 가 도인 경우 $s = \frac{\pi r \theta}{180^\circ},$ 는 $s = \frac{C \theta}{360^\circ}.$ 와 같다.
$\theta$ 가 그라드인 경우(100 그라드, 또는 등급, 또는 그래디언트는 한 직각) $s = \frac{\pi r \theta}{200\text{ grad}},$ 는 $s = \frac{C\theta}{400\text{ grad}}.$ 와 같다.
$\theta$ 가 회전인 경우(한 회전은 완전한 회전 또는 360°, 또는 400 그라드, 또는 $2\pi$ 라디안) $s = C\theta/1\text{ turn}$ 이다.

6. 무한 길이 곡선

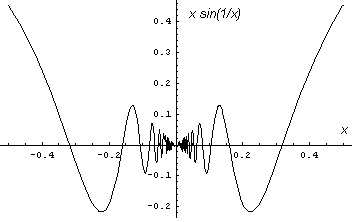
이미 언급했듯이, 일부 곡선은 꺾은선 근사의 길이에 상계가 없어 길이를 얼마든지 크게 할 수 있다. 이러한 곡선은 길이가 무한하다고 표현한다. 곡선 위의 임의의 호(적어도 두 점 이상을 포함하는)가 무한 길이를 갖는 연속 곡선이 존재한다. 그러한 곡선의 예시로는 코흐 곡선과 0을 한쪽 끝으로 하는 임의의 열린 구간에서 f(x) = x \cdot \sin(1/x) 이고 f(0) = 0으로 정의되는 함수의 그래프 등이 있다. 이러한 무한 길이 곡선의 크기를 측정하기 위해 하우스도르프 차원이나 Hausdorff measure|하우스도르프 측도^영어가 사용되기도 한다.

7. (유사-) 리만 다양체로의 일반화

M^영어을 유사 리만 다양체, g^영어를 (유사-) 계량 텐서라고 하고, γ:[0,1]→M^영어을 M^영어의 곡선으로, n^영어개의 매개변수 방정식으로 정의하면 다음과 같다.

: $\gamma(t)=[\gamma^1(t), \dots, \gamma^n(t)],\quad t\in [ 0,1]$

: $\gamma(0) = \mathbf x, \,\,\gamma(1) = \mathbf y$

γ^영어의 길이는 다음과 같이 정의된다.

: $\ell(\gamma) = \int\limits_0^1 ||\gamma'(t)||_{\gamma(t)} dt$

또는 국소 좌표 x^영어를 선택하면 다음과 같다.

: $\ell(\gamma) = \int\limits_0^1 \sqrt{\pm \sum_{i,j=1}^n g_{ij}(x(\gamma(t)))\frac{dx^i(\gamma(t))}{dt}\frac{dx^j(\gamma(t))}{dt}}dt$

여기서 $\gamma'(t) \in T_{\gamma(t)} M$ 는 t^영어에서 γ^영어의 접선 벡터이다. 제곱근의 부호는 주어진 곡선에 대해 제곱근이 실수인지 확인하기 위해 한 번 선택된다. 시공간 곡선에 대해 양의 부호가 선택되고, 유사-리만 다양체에서는 시간꼴 곡선에 대해 음의 부호가 선택될 수 있다. 따라서 곡선의 길이는 음이 아닌 실수이다. 일반적으로 일부는 공간꼴이고 일부는 시간꼴인 곡선은 고려되지 않는다.

상대성 이론에서 시간꼴 곡선(세계선)의 호의 길이는 세계선을 따라 경과된 고유 시간이며, 공간꼴 곡선의 호의 길이는 곡선을 따른 고유 거리이다.

참조

_[1] 서적 The Theory of Splines and Their Applications https://archive.org/[...] Academic Press 1967
_[2] 논문 Arc length as a global conformal parameter for analytic curves Elsevier BV
_[3] 서적 Principles of Mathematical Analysis https://archive.org/[...] McGraw-Hill, Inc.
_[4] 웹사이트 Special Publication 811 http://www.physics.n[...] 2009-07-02
_[5] 간행물 CRC Handbook of Chemistry and Physics
_[6] 논문 Circular Reasoning: Who First Proved That C Divided by d Is a Constant? 2015-05
_[7] 논문 The Lengths of Curves 1953-02
_[8] 서적 Tractatus Duo. Prior, De Cycloide et de Corporibus inde Genitis… http://gallica.bnf.f[...] University Press 1659
_[9] 서적 Renati Des-Cartes Geometria https://books.google[...] Louis & Daniel Elzevir 1659
_[10] 서적 De Linearum Curvarum cum Lineis Rectis Comparatione Dissertatio Geometrica https://books.google[...] Arnaud Colomer 1660
_[11] 서적 解析学序説上巻裳華房 1981-02-01

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com