꼬임군 (위상수학)

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

꼬임군은 n개의 가닥을 꼬는 연산을 연구하는 수학적 구조로, 유한 생성군이며 꼬임이라고 불리는 원소들로 구성된다. 꼬임군은 꼬임들의 연결을 통해 군 연산을 수행하며, 땋임 관계식을 통해 호모토피적 동치 관계를 정의한다. 꼬임군은 매듭 이론, 양자 물리학, 유체 역학 등 다양한 분야에 응용되며, 대칭군과의 관계, 꼬임군의 표현, 꼬임 지수 등의 개념을 포함한다. 꼬임군은 3차 꼬임군이 모듈러 군의 중심 확대와 동형이며, 꼬임의 분류, 꼬임의 매듭 표현, 단어 문제 해결 등 계산적 측면에서도 연구된다.

더 읽어볼만한 페이지

매듭 이론 - 천-사이먼스 이론
천-사이먼스 이론은 천싱선과 제임스 해리스 사이먼스가 정의한 3차 천-사이먼스 형식을 기반으로 3차원 다양체에서 정의되는 위상 양자장론으로, 양자장론, 매듭 이론, 끈 이론 등 다양한 분야와 연관되어 있으며 존스 다항식, 베스-추미노-위튼 모형, 분수 양자 홀 효과 설명 등에 활용된다.
매듭 이론 - 소 매듭
소 매듭은 방향에 의존하지 않고 더 이상 분해할 수 없는 매듭의 기본 요소로, 유한 개의 유향 소 매듭들의 연결합으로 모든 유향 매듭을 표현할 수 있으며, 교차수에 따라 분류되어 세잎 매듭과 8자 매듭 등이 있다.

꼬임군 (위상수학)
개요
분야	수학, 추상대수학, 군론
정의	매듭 이론에서 꼬임을 대수적으로 나타내는 군
역사
창시자	에밀 아르틴
발표 연도	1925년
기본 성질
생성원	σ1, σ2, ..., σn-1 (여기서 n은 꼬임 가닥의 수)
관계	σiσj = σjσi (만약 \|i - j\| ≥ 2) σiσi+1σi = σi+1σiσi+1
군 연산	꼬임의 합성 (braid composition)
응용
관련 분야	매듭 이론, 위상수학, 수학, 끈 이론
응용 예시	평면 대수 곡선의 모노드로미 표현

2. 정의

n^영어가닥의 꼬임군( $\operatorname{Braid}(n)$ )은 표시를 갖는 유한생성군이다. 꼬임군의 원소는 꼬임(braid^영어)이라고 한다. 꼬임군은 다음과 같이 정의된다.

: $\operatorname{Braid}(n)= \left \langle \sigma_1,\ldots,\sigma_{n-1}| \sigma_i\sigma_{i+1}\sigma_i=\sigma_{i+1}\sigma_i\sigma_{i+1}, \sigma_i\sigma_j=\sigma_j\sigma_i \right \rangle$

여기서 첫 번째 관계식은 $i=1,2,\dots,n-2$ 이고, 두 번째 관계식은 $|i-j|\ge2$ 이다. $\sigma_i$ 는 $i$ 번째 가닥과 $i+1$ 번째 가닥을 한 번 꼬는 것을 의미한다. 군 연산은 꼬임들을 서로 연결하는 것이다.

: $\sigma_i\sigma_{i+1}\sigma_i=\sigma_{i+1}\sigma_i\sigma_{i+1}$

: $\sigma_i\sigma_j=\sigma_j\sigma_i\qquad(|i-j|\ge2)$

위 관계식은 꼬임 합성의 호모토피적 동치 관계이다.

4가닥 꼬임군( $B_4$ )을 예로 들어 설명하면 다음과 같다.

탁자 위에 4개의 물건이 수직으로 배열되어 일렬로 놓여 있다고 가정한다. (아래 그림에서 검은색 점). 각 물건을 다른 물건과 잇는 네 개의 끈을 사용하여, 각 집합의 항목이 다른 집합의 항목과 일대일 대응이 되도록 연결한다. 이러한 연결을 ''꼬임''이라고 한다. 끈은 다른 끈 위나 아래로 지나갈 수 있으며, 이는 꼬임의 중요한 특징이다.

와

는 서로 다른 꼬임이다. 그러나 끈을 당겨서 동일하게 만들 수 있다면 같은 꼬임으로 간주한다.

- 는
시그마 1⁻¹의 또 다른 표현
과 동일하다.

과 같이 매듭은 꼬임으로 간주되지 않는다. 모든 가닥은 왼쪽에서 오른쪽으로 이동해야 한다.

두 꼬임을 결합하려면 첫 번째 꼬임 옆에 두 번째 꼬임을 놓고 가운데 네 개의 항목을 연결한다.

-|]]|]] 와 --|]]|]]를 결합하면 --|]]가 된다.

-|]] 와 --|]]를 결합하면 --|]]가 된다.

꼬임 σ와 τ의 결합은 στ로 표기한다.

B_4

는 위에서 설명한 꼬임 결합을 연산으로 하는 군이다. 항등원은 네 개의 평행한 수평 가닥으로 구성된 꼬임이고, 역원은 첫 번째 꼬임이 한 것을 "되돌리는" 꼬임이다.

꼬임군은 대수적 위상수학의 호모토피 개념을 사용하여 배치 공간의 기본군으로 정의할 수도 있다.

n

차원 다양체

X

의

n

개 복사본의 대칭 곱은

X^n

의 몫으로, 좌표의 지수에 작용하는

n

가닥에 대한 대칭군의 순열 작용에 의한

X

의

n

겹 데카르트 곱이다. 순서가 있는

n

-튜플은 재정렬된 버전과 같은 궤도에 있다.

n

겹 대칭 곱에서의 경로는

X

의

n

개 점을 비순서화된

n

-튜플로 간주하여,

n

개의 끈을 추적한다. 끈이 서로 지나가지 않도록, 구별되는 점들의

n

-튜플의 궤도인 대칭 곱의 부분 공간

Y

로 이동한다. 즉,

x_i = x_j

(

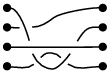
1\le i)로 정의된 X^n 의 모든 부분 공간을 제거한다. 이는 대칭군에 불변이며, Y 는 제외되지 않은 n -튜플의 대칭군에 의한 몫이다. Y 는 연결되어 있다.

'''

n

개의 끈을 가진

X

의 꼬임군'''은

Y

의 기본군으로 정의된다 (기저점 선택은 동형사상까지 잘 정의됨).

X

가 유클리드 평면인 경우가 아르틴의 원래 경우이다.

Y

의 더 높은 호모토피 군은 자명하다.

n=4

일 때, 4개의 점이 두 쌍으로 일렬로 늘어서 있고, 그 사이를 잇는 평행한 끈 4개가 있는 그림과 같은 상황을 생각한다.

]]|]]

e

옆 끈을 교차시키는 3가지 연산 $\sigma_1, \sigma_2, \sigma_3$ 를 고려한다.

]]|]]

\sigma_1

]]

\sigma_2

]]

\sigma_3

$\sigma_1, \sigma_2, \sigma_3$ 및 그 교차의 상하를 반전시킨 연산을 반복하여 하나의 끈 상태를 만든다. 이를 '''브레이드''' 또는 '''땋은 끈'''이라고 한다.

두 브레이드 a, b의 곱 ab는 a 오른쪽에 b를 연결하고 a의 왼쪽 끝점과 b의 오른쪽 끝점을 새 끝점으로 하는 브레이드이다.

$B_4$ 는 $\sigma_1, \sigma_2, \sigma_3$ 를 생성원으로 하는 군이며, 기본 관계식은 다음과 같다.

# $\sigma_1 \sigma_3 = \sigma_3 \sigma_1$

# $\sigma_1 \sigma_2 \sigma_1 = \sigma_2 \sigma_1 \sigma_2$

# $\sigma_2 \sigma_3 \sigma_2 = \sigma_3 \sigma_2 \sigma_3$

이는 얽힘이 같은 브레이드에 관한 등식이며, 1은 공통 끈이 없는 교차 연산은 가환임을, 2와 3은 라이데마이스터 이동 III형의 동치성에 해당한다.

2. 1. 꼬임군의 표현

n^영어가닥의 꼬임군

\operatorname{Braid}(n)

은 다음과 같은 생성원과 관계식을 갖는 유한생성군으로 표현될 수 있다.^[13]^[14] 꼬임군의 원소들을 꼬임(braid^영어)이라고 한다.

:

\operatorname{Braid}(n)= \left \langle \sigma_1,\ldots,\sigma_{n-1}| \sigma_i\sigma_{i+1}\sigma_i=\sigma_{i+1}\sigma_i\sigma_{i+1}, \sigma_i\sigma_j=\sigma_j\sigma_i \right \rangle

여기서 첫 번째 관계식은

i=1,2,\dots,n-2

이고, 두 번째 관계식은

|i-j|\ge2

이다.

생성원

\sigma_i

는 i번째 가닥과 i+1번째 가닥을 한 번 꼬는 것을 나타낸다. 예를 들어, 4가닥의 꼬임군(

\operatorname{Braid}(4)

)의 생성원은 다음과 같다.

σ₁	σ₂	σ₃
	σ₂	σ₃

꼬임군에서의 연산은 꼬임들을 서로 연결하는 것이다. 예를 들어

꼬임의 연산 예시
--	·	--	=	σ₃σ₂

위에서 제시된 관계식

: $\sigma_i\sigma_{i+1}\sigma_i=\sigma_{i+1}\sigma_i\sigma_{i+1}$

: $\sigma_i\sigma_j=\sigma_j\sigma_i\qquad(|i-j|\ge2)$

는 꼬임 합성의 호모토피적 동치 관계를 나타낸다. 즉, 꼬임을 어떻게 변형하더라도 꼬임의 연결 관계가 변하지 않으면 같은 꼬임으로 간주한다는 의미이다.

이러한 관계식은 양-바스터 방정식 이론에서 중요한 역할을 한다.

2. 2. 무한 꼬임군

꼬임군 사이에는 다음과 같은 포함 관계가 존재한다.

:

\operatorname{Braid}(n)\hookrightarrow\operatorname{Braid}(n+1)

:

\sigma_i^{(n)}\mapsto\sigma_i^{(n+1)}

이렇게 하여, 귀납적 극한을 취하면 '''무한 꼬임군'''

\operatorname{Braid}(\infty)

을 얻는다.

:

\operatorname{Braid}(\infty)=\varinjlim_n\operatorname{Braid}(n)

무한 가닥으로 이 개념을 일반화하는 방법은 많다. 가장 간단한 방법은 꼬임군들의 직접 극한을 취하는 것인데, 이때 결합 사상

f \colon B_n \to B_{n+1}

는

B_{n}

의

n-1

개의 생성자를

B_{n+1}

의 처음

n-1

개의 생성자로 보낸다(즉, 자명한 가닥을 부착함으로써). 그러나 이 군은 연속성을 유지하면서 거리화 가능한 위상을 허용하지 않는다.

폴 페이블(Paul Fabel)은 결과적인 군에 부과될 수 있는 두 개의 위상이 있으며, 각각의 완비가 다른 군을 생성한다는 것을 보였다.^[17] 첫 번째는 매우 온순한 군이며, 무한히 구멍 뚫린 원반—원반의 경계로 수렴하는 이산적인 구멍 집합—의 사상 클래스 군과 동형이다.

두 번째 군은 유한 꼬임군과 동일하게 생각할 수 있다. 각 점

(0, 1/n)

에 가닥을 놓고, 꼬임—꼬임은 함수가 종점에서의 순열을 생성하도록

(0, 1/n, 0)

에서

(0, 1/n, 1)

까지의 경로들의 모음으로 정의됨—의 집합은 이 더 거친 군과 동형이다. 흥미로운 사실은 이 군에서의 순수 꼬임군은 유한 순수 꼬임군

P_n

의 역 극한과 힐베르트 큐브에서 집합

:

\{(x_i)_{i\in \mathbb{N}} \mid x_i=x_j\text{ for some }i\ne j\}.

을 뺀 공간의 기본군과 동형이라는 것이다.

2. 3. 드오르누아 순서

꼬임군

\operatorname{Braid}(n)

위에는 '''드오르누아 순서'''(Dehornoy order^영어)라는 전순서가 존재하며, 이는 군의 왼쪽 작용에 대하여 불변이다. 구체적으로, 드오르누아 순서에서 양인 원소는

\sigma_1,\dots,\sigma_{n-1}

들과 이들의 역원의 곱으로 만든 문자열 가운데 적어도 한

i\in\{1,\dots,n-1\}

가 다음 세 조건을 모두 만족시키는 것이다.

문자열은 $\sigma_i$ 를 포함한다.
모든 $j 에 대하여, 문자열은 \sigma_j 를 포함하지 않는다.$
모든 $j\le i$ 에 대하여, 문자열은 $\sigma_j^{-1}$ 를 포함하지 않는다.

이러한 원소들의 집합을

P

라고 하면,

PP\subseteq P

이며, 꼬임군은

:

\operatorname{Braid}(n)=P\sqcup P^{-1}\sqcup\{1\}

이다.

3. 성질

꼬임군의 모든 원소는 항등원을 제외하고 무한한 차수를 갖는다. n ≥ 2일 때, Bₙ은 두 개의 원소로 생성되는 자유군을 부분군으로 갖는다.

꼬임군 $B_1$ 은 자명군이며, $B_2$ 는 무한 순환군 $\Z$ 이고, $B_3$ 는 매듭군 중 세잎 매듭의 매듭군과 동형이며, 특히 무한 비가환군이다.
$n$ -가닥 꼬임군 $B_n$ 은 처음 $n$ 개의 가닥을 교차하지 않는 추가 가닥을 더함으로써 $(n+1)$ -가닥 꼬임군 $B_{n+1}$ 의 부분군으로 포함된다. 모든 $n \ge 1$ 에 대한 꼬임군의 증가하는 합집합은 '''무한 꼬임군''' $B_{\infty}$ 이다.
$B_n$ 의 모든 비항등원은 무한 차수를 가진다. 즉, $B_n$ 은 꼬임이 없는 군이다.
$B_n$ 에는 Dehornoy 순서라고 불리는 좌불변 선형 순서가 존재한다.
$n\ge 3$ 에 대해, $B_n$ 은 두 개의 생성원에 대한 자유군과 동형인 부분군을 포함한다.
$\sigma_i \mapsto 1$ 에 의해 정의된 군 준동형사상 $B_n \to \Z$ 가 존재한다. 예를 들어, 꼬임 $\sigma_2\sigma_3\sigma_1^{-1}\sigma_2\sigma_3$ 은 $1 + 1 - 1 + 1 + 1 = 3$ 으로 매핑된다. 이 맵은 꼬임군의 가환화에 해당한다. $\sigma_i^k \mapsto k$ 이므로, $\sigma_i^k$ 는 $k=0$ 일 때만 항등원이 된다. 이것은 생성원이 무한 차수를 갖는다는 것을 증명한다.

3. 1. 몫군

꼬임군의 아벨화는 무한 순환군이다. 구체적으로는 다음과 같다.

:

\sigma_i\mapsto 1\qquad(i=1,\dots,n-1)

:

\sigma_i^{-1}\mapsto -1\qquad(i=1,\dots,n-1)

꼬임군은 대칭군을 다음과 같이 몫군으로 갖는다.

:

\operatorname{Braid}(n)\twoheadrightarrow\operatorname{Sym}(n)=\operatorname{Sym}(\{1,2,\dots,n\})

:

\sigma_i\mapsto(i,i+1)\qquad(i=1,\dots,n-1)

:

\sigma_i^{-1}\mapsto(i,i+1)\qquad(i=1,\dots,n-1)

3. 2. 중심

n \ge 3

일 때, 꼬임군

\operatorname{Braid}(n)

의 중심은 다음과 같은 원소로 생성되는 무한 순환군이다.^[24]

:

\left(\sigma_1(\sigma_2\sigma_1)\cdots(\sigma_{n-1}\sigma_{n-2}\cdots\sigma_1)\right)^2

n \le 2

일 경우, 꼬임군은 아벨 군이므로 군 전체가 중심이다.

4. 예

꼬임군	동형인 군
$\operatorname{Braid}(0)$	자명군
$\operatorname{Braid}(1)$	자명군
$\operatorname{Braid}(2)$	무한 순환군 $\mathbb Z$
$\operatorname{Braid}(3)$	세잎매듭의 매듭군 $\pi_1(S^3\setminus 3_1)$ , 모듈러 군의 중심 확대

3차 꼬임군은 가장 낮은 가닥 수의 비가환 꼬임군이다.

4. 1. 3차 꼬임군

3가닥 꼬임군

\operatorname{Braid}(3)

은 가장 낮은 가닥 수의 비가환 꼬임군이다. 이 군은 세잎매듭 3₁의 매듭군

\pi_1(S^3\setminus 3_1)

과 동형이며, 모듈러 군

\operatorname{PSL}(2;\mathbb Z)

의 중심 확대이다. 이 관계는 다음과 같은 가환그림으로 나타낼 수 있다.

-|]]|]]

여기서

\overline{\operatorname{SL}(2;\mathbf R)}

은

\operatorname{SL}(2;\mathbb R)

의 범피복군이다. 모듈러 군은 중심이 없으므로, 모듈러 군은

\operatorname{Braid}(n)

의 중심에 대한 몫군과 동형이다.

:

\operatorname{PSL}(2;\mathbb Z)=\operatorname{Braid}(n)/\operatorname Z(\operatorname{Braid}(n))

브레이드 군 B₃는 모듈러 군

\Gamma

의 중심 확대이다. 즉,

B_3

의 중심을

Z(B_3)

로 나타낼 때, 다음의 짧은 완전열을 만족한다.^[1]

:

1 \to Z(B_3) \to B_3 \to \Gamma \to 1

따라서

\Gamma \cong B_3/Z(B_3)

이다.^[1]

5. 응용

꼬임군 이론은 유체 역학, 특히 유체 흐름의 혼돈 혼합 분야에 적용되었다. 물리적 막대, 주기 궤도 등의 운동으로 형성된 시공간 궤도의 꼬임은 닐센-서스턴 분류를 사용하여 여러 유체 시스템의 위상 엔트로피를 추정하는데 사용되었다.^[3]^[4]^[5]

양자 물리학에서 꼬임군 및 관련 위상 개념은 애니온 이론 및 양자 컴퓨터 연구에 응용된다. 애니온은 오류 정정 양자 컴퓨터의 기반을 형성할 수 있으며, 양자 정보에서 중요하다.

5. 1. 꼬임 지수

J. W. 알렉산더의 정리에 따르면 모든 매듭은 꼬임의 "폐쇄"로 얻어질 수 있다.^[6] 1935년에 안드레이 마르코프 주니어는 해당 닫힌 꼬임에서 동치를 생성하는 꼬임 다이어그램에 대한 두 가지 움직임을 설명했다.^[6] 마르코프 정리는 두 꼬임의 닫힘이 동등한 매듭이 되는 데 필요한 충분 조건을 제공한다.^[8]

꼬임 지수는 매듭의 닫힌 꼬임 표현을 만들기 위해 필요한 최소 끈의 수이다.^[9] 이는 매듭의 모든 투영에서 자이페르트 원의 최소 수와 같다.^[9]

6. 역사

꼬임군은 1925년 에밀 아르틴에 의해 명시적으로 소개되었지만, 1974년 빌헬름 마그누스가 지적했듯이^[10] 이미 1891년 아돌프 후르비츠의 모노드로미에 관한 연구에 암묵적으로 나타나 있었다.

1947년 에밀 아르틴은 꼬임군을 명시적인 표현으로 설명했다.^[11] 꼬임군은 특정 배치 공간의 기본군으로 이해할 수도 있다.^[11]

마그누스는 후르비츠가 꼬임군을 배치 공간의 기본군으로 해석했으며(cf. 꼬임 이론), 이러한 해석은 1962년 랄프 폭스와 리 노이워스에 의해 재발견되기 전까지 잊혀졌다고 말했다.^[12]

7. 추가 성질

는 자명군이고, 는 무한 순환군 이며, 는 세잎 매듭의 매듭군과 동형이다.
에 대해, 은 두 개의 생성원을 갖는 자유군과 동형인 부분군을 포함한다. 따라서 이 군들은 가환군이 아닌 무한군이다.
단위원을 제외한 모든 의 원소는 그 위수가 무한이다. 즉, 은 꼬임이 없다.
위에는 라고 불리는 좌불변인 전순서가 존재한다.
은 1개의 새로운 끈을 최초의 개의 끈 중 어느 것과도 교차하지 않도록 추가함으로써, -가닥의 땋임군 의 부분군으로서 매립할 수 있다.

8. 상호 관계

꼬임군은 대칭군, 순수 꼬임군, 모듈러 군, 사상류군 등 다양한 군들과의 관계를 맺고 있다.

대칭군 및 순수 꼬임군과의 관계: 꼬임의 교차를 무시하면, *n*개의 가닥에 대한 모든 꼬임은 *n*개의 원소에 대한 순열을 결정한다. 이는 꼬임군에서 대칭군으로의 전사적 군 준동형사상 $B_n → S_n$을 정의하며, 이 준동형사상의 핵은 순수 꼬임군 $P_n$이다. 순수 꼬임군은 각 끈의 시작점과 종점이 같은 위치에 있는 꼬임들로 구성된다.^[13]

모듈러 군과의 관계: 3가닥 꼬임군($B_3$)은 모듈러 군 $\operatorname{PSL}(2, \mathbb Z)$의 보편적 중심 확대이며, $B_3$를 그 중심 $Z(B_3)$로 나눈 몫군은 모듈러 군과 동형이다.^[13]

사상류군과의 관계: 꼬임군 $B_n$은 $n$개의 구멍이 뚫린 원판의 사상류군과 동형이다. 이를 통해 각 꼬임은 주기적, 가약 또는 유사 아노소프로 분류할 수 있다.^[13]

8. 1. 대칭군 및 순수 꼬임군과의 관계

꼬임의 교차를 무시하면, *n*개의 가닥에 대한 모든 꼬임은 *n*개의 원소에 대한 순열을 결정한다. 이는 꼬임군에서 대칭군으로의 전사적 군 준동형사상 *B_n* → *S_n*을 정의한다. 꼬임 σ_*i* ∈ *B_n*의 이미지는 전위 *s_i* = (*i*, *i*+1) ∈ *S_n*이다.

이 준동형사상 *B_n* → *S_n*의 핵은 *n*개의 가닥에 대한 순수 꼬임군이라 불리며 *P_n*으로 표기되는 *B_n*의 부분군이다. 순수 꼬임군은 다음 짧은 완전열을 만족한다.

:1→F_n-1→P_n→P_n-1→1.

이 수열은 분리되므로 순수 꼬임군은 자유군의 반복적인 반직접곱으로 구성된다.

기하학적으로 순수 꼬임군은 각 끈의 시작점과 종점이 같은 위치에 있는 꼬임들로 구성되어, 단일 치환으로 사상되는 원소들이다.

8. 2. B₃와 모듈러 군의 관계

3가닥 꼬임군(

B_3

)은 모듈러 군

\operatorname{PSL}(2,\mathbb Z)

의 보편적 중심 확대이다. 모듈러 군은 자명한 중심을 가지므로,

B_3

를 그 중심

Z(B_3)

로 나눈 몫군과 동형이다. 이는

B_3

의 내부 자기 동형의 군과 동형이다.

다음은 이 동형 사상에 대한 설명이다.

:

a = \sigma_1 \sigma_2 \sigma_1, \quad b = \sigma_1 \sigma_2

라고 정의하면, 꼬임 관계로부터

a^2 = b^3

가 성립한다. 이 마지막 곱을

c

로 표시하면, 꼬임 관계로부터 다음이 성립한다.

:

\sigma_1 c \sigma_1^{-1} = \sigma_2 c \sigma_2^{-1}=c

이는

c

가

B_3

의 중심에 있음을 의미한다.

C

를

c

에 의해 생성된

B_3

의 부분군으로 나타내면,

C \subset Z(B_3)

이므로, 이는 정규 부분군이며 몫군

B_3/C

를 취할 수 있다.

B_3/C \cong \operatorname{PSL}(2,\mathbb Z)

이며, 이 동형 사상은 다음과 같이 주어진다. 잉여류

\sigma_1 C

및

\sigma_2 C

는 다음으로 매핑된다.

:

\sigma_1C \mapsto R=\begin{bmatrix}1 & 1 \\ 0 & 1 \end{bmatrix} \qquad \sigma_2C \mapsto L^{-1}=\begin{bmatrix}1 & 0 \\ -1 & 1 \end{bmatrix}

여기서

L

및

R

은 슈테른-브로코 트리의 표준 좌/우 이동이며, 이러한 이동은 모듈러 군을 생성한다.

모듈러 군의 일반적인 표현 중 하나는 다음과 같다.

:

\langle v,p\, |\, v^2=p^3=1\rangle

여기서

:

v=\begin{bmatrix}0 & 1 \\ -1 & 0 \end{bmatrix}, \qquad p=\begin{bmatrix}0 & 1 \\ -1 & 1 \end{bmatrix}.

a

를

v

로,

b

를

p

로 매핑하면 전사 군 준동형사상

B_3 \to \operatorname{PSL}(2,\mathbb Z)

가 생성된다.

B_3

의 중심은

C

와 같으며, 이는

c

가 중심에 있다는 사실, 모듈러 군이 자명한 중심을 갖는다는 사실, 그리고 위의 전사 준동형사상이 핵

C

를 갖는다는 사실의 결과이다.

8. 3. 사상류군과의 관계 및 꼬임의 분류

꼬임군 $B_n$은 $n$개의 구멍이 뚫린 원판의 매핑 클래스 군과 동형이다. 이는 각 구멍이 원판의 경계와 끈으로 연결되어 있다고 상상하면 시각적으로 이해하기 쉽다. 두 구멍을 치환하는 각 매핑 준동형은 끈의 호모토피, 즉 끈들의 꼬임으로 볼 수 있다.

이러한 꼬임의 매핑 클래스 군 해석을 통해, 각 꼬임은 주기적, 가약 또는 유사 아노소프로 분류할 수 있다.

n=4인 경우를 예로 들어보자. 일렬로 늘어선 4개의 점이 두 쌍으로 있고, 그 사이를 잇는 평행한 끈이 4개 있는 상황을 생각할 수 있다.

이러한 끈에 대해, 옆 끈을 교차시키는 세 가지 연산 $\sigma_1, \sigma_2, \sigma_3$를 생각할 수 있다.

끈의 교차에서는 상하를 구별하며, 예를 들어 다음은 $\sigma_1$과는 다른 연산으로 간주된다. (이는 $\sigma_1$의 역원인 $\sigma_1^{-1}$으로 간주할 수 있다.)

-|]]

$\sigma_1, \sigma_2, \sigma_3$ 및 그 교차의 상하를 반전시킨 연산을 반복하여 얻어지는 하나의 구체적인 끈의 상태를 '''브레이드''' 또는 '''땋은 끈'''이라고 부른다.

두 개의 브레이드 a, b가 있을 때, a의 오른쪽에 b를 연결하고 a의 원래 왼쪽 끝점과 b의 오른쪽 끝점을 새로운 끝점으로 하는 브레이드를 a와 b의 곱 ab로 정의한다. 곱셈의 예시는 아래 표와 같다.

곱셈의 예
	a	b	ab
예1	]] $\sigma_3$	]] $\sigma_2$	]] $\sigma_3 \sigma_2$
예2	]] $\sigma_1^{-1} \sigma_3^{-1}$	]] $\sigma_1 \sigma_3^{-1}$	]] $\sigma_3^{-2}$

임의의 브레이드와, 맨 앞의 브레이드 $e$의 곱은 원래 브레이드를 변경하지 않는다. 또한 임의의 브레이드에 대해, 그 오른쪽 끝의 모든 점을 통과하는 세로선을 축으로 하여 경면 반전시킨 브레이드와의 곱을 취하면 $e$가 되므로, 항상 역원이 존재한다. 따라서 브레이드는 위의 곱에 관해 군이 되며, 이 군이 $B_4$이다.

$B_4$를 $\sigma_1, \sigma_2, \sigma_3$를 생성원으로 하는 군으로 볼 때, 그 기본 관계식은 아래와 같다.

# $\sigma_1 \sigma_3 = \sigma_3 \sigma_1$

# $\sigma_1 \sigma_2 \sigma_1 = \sigma_2 \sigma_1 \sigma_2$

# $\sigma_2 \sigma_3 \sigma_2 = \sigma_3 \sigma_2 \sigma_3$

위의 관계식 1은 대상에 공통 끈이 없는 교차 연산은 가환임을 나타내는 조건이고, 2 및 3은 라이데마이스터 이동 III형의 동치성에 상당한다.

브레이드 군 $B_n$은 $n$개의 구멍을 가진 원판의 사상류군과 동형이다. 이는 사상류군의 각 원소가 구멍끼리 서로 바꾸므로, 원래 작용 전후의 같은 위치에 있는 구멍을 잇는 끈의 집합을 브레이드로 간주함으로써 브레이드와 대응시킬 수 있기 때문이다.

사상류군의 원소에 관한 닐센-써스턴 분류에 따라 브레이드를 주기적, 가약적, 의사 아노소프의 세 종류로 분류할 수 있다.

9. 매듭 이론과의 연관성

꼬임의 양 끝을 연결하면 고리 또는 매듭을 얻을 수 있다. 알렉산더 정리에 따르면, 모든 매듭과 고리는 적어도 하나의 꼬임으로부터 이러한 방식으로 발생한다.^[8] 꼬임은 생성자에서의 단어로 구체적으로 주어질 수 있기 때문에, 이것은 종종 매듭을 컴퓨터 프로그램에 입력하는 데 선호되는 방법이다.

바운 존스는 원래 자신의 존스 다항식을 꼬임 불변량으로 정의한 다음, 닫힌 꼬임의 클래스에만 의존한다는 것을 보였다. 1935년에 마르코프는 해당 닫힌 꼬임에서 동치를 생성하는 꼬임 다이어그램에 대한 두 가지 움직임을 설명했다.^[6] 마르코프 정리는 두 꼬임의 닫힘이 동등한 매듭이 되는 데 필요한 충분 조건을 제공한다.^[8]

10. 계산적 측면

단어 문제는 효율적으로 해결 가능하며 생성자 σ|σ^영어, ..., σ에 대한 ''B''}}의 원소에 대한 정규 형식이 존재한다. 자유 GAP 컴퓨터 대수 시스템은 원소가 이러한 생성자를 기준으로 주어지는 경우 ''B''}}에서 계산을 수행할 수 있다. 또한 꼬임군을 특별히 지원하는 GAP3용 ''CHEVIE''라는 패키지도 있다. 단어 문제는 로렌스-크래머 표현을 통해 효율적으로 해결된다.^[15]

단어 문제 외에도 꼬임군을 구현할 수 있는 몇 가지 어려운 계산 문제가 알려져 있으며 암호화 분야에서 적용될 수 있다고 제안되었다.^[23]

11. 작용

대칭군의 순열에 의한 작용과 유사하게, 다양한 수학적 설정에서 꼬임군은 "꼬임"을 포함하는 대상의 ''n''-튜플 또는 ''n''-겹 텐서 곱에 자연스러운 작용을 한다. 임의의 군 ''G''를 고려하고 ''X''를 ''G''의 원소의 모든 ''n''-튜플의 집합으로 정의하며, 곱이 ''G''의 항등원이 되도록 한다. 그러면 ''B_n''은 다음과 같은 방식으로 작용한다.

: $\sigma_i \left (x_1,\ldots,x_{i-1},x_i, x_{i+1},\ldots, x_n \right)= \left (x_1,\ldots, x_{i-1}, x_{i+1}, x_{i+1}^{-1}x_i x_{i+1}, x_{i+2},\ldots,x_n \right ).$

따라서 원소 ''x_i''와 ''x''_''i''+1''은 자리를 바꾸고, 추가적으로 ''x_i''는 ''x''_''i''+1''에 해당하는 내부 자기 동형에 의해 꼬인다. 이는 ''x''의 구성 요소의 곱이 항등원으로 유지되도록 한다. 꼬임군 관계가 만족하는지 확인할 수 있으며, 이 공식은 실제로 ''B_n''의 ''X''에 대한 군 작용을 정의한다. 또 다른 예로, 꼬임 모노이드 범주는 꼬임군 작용을 갖는 모노이드 범주이다. 이러한 구조는 현대 수리 물리학에서 중요한 역할을 하며, 양자 매듭 불변량으로 이어진다.

12. 표현

꼬임군 ''B_n''의 원소는 행렬로 더 구체적으로 표현될 수 있다. 이러한 고전적인 표현 중 하나는 행렬 요소가 단일 변수 로랑 다항식인 부라우 표현이다. 부라우 표현이 충실한 표현인지에 대한 오랜 질문이 있었지만, ''n'' ≥ 5에 대해 부정적인 것으로 밝혀졌다.

1990년, 루스 로렌스는 여러 매개변수에 의존하는 보다 일반적인 "로렌스 표현"의 집합을 설명했다. 2001년경 스티븐 비글로우와 단 크라머는 모든 꼬임군이 선형군임을 독립적으로 증명했다. 그들의 연구는 변수 q^영어와 t^영어에 의존하는 차원 $n(n-1)/2$ 의 로렌스-크라머 표현을 사용했다. 이러한 변수를 적절하게 특수화함으로써 꼬임군 $B_n$ 은 복소수에 대한 일반 선형군의 부분군으로 실현될 수 있다.

브레이드 군 ''B_n''^영어의 선형 표현으로 고전적인 Burau 표현|en|Burau representation^한국어이나, Lawrence-Krammer(-Bigelow) 표현|en|Lawrence–Krammer representation^한국어이 알려져 있다.

Burau 표현은 1변수 정수 계수 로랑 다항식환의 일반 선형군으로 간주될 수 있다.

: $B_n \to GL_{n-1}(\Z[\Z]).$

Burau 표현이 충실한지 여부는 오랫동안 문제였지만, $n \ge 5$ 에 대해서는 그렇지 않다는 것이 밝혀졌다.

Lawrence-Krammer(-Bigelow) 표현은 2변수 정수 계수 로랑 다항식환의 일반 선형군으로 간주될 수 있다.

: $B_n \to GL_{\binom n2}(\Z[\Z^2]).$

1996년, C. 나약(C. Nayak)과 프랭크 윌첵은 SO(3)^영어의 사영 표현의 유사점으로 브레이드 군의 사영 표현이 분수 양자 홀 효과에 관한 준입자에 관한 물리적 의미를 갖는다고 제창했다.^[22]

13. 무한 생성 꼬임군

무한 가닥으로 꼬임군을 일반화하는 방법은 여러 가지이다. 가장 간단한 방법은 꼬임군들의 직접 극한을 취하는 것이지만, 이 군은 연속성을 유지하면서 거리화 가능한 위상을 허용하지 않는다.

폴 페이블(Paul Fabel)은 서로 다른 두 위상을 통해 완비가 되는 서로 다른 군을 생성할 수 있음을 보였다.^[17] 첫 번째 군은 매우 온순하며, 무한히 구멍 뚫린 원반—원반의 경계로 수렴하는 이산적인 구멍 집합—의 사상 클래스 군과 동형이다.

두 번째 군은 유한 꼬임군과 비슷하게 생각할 수 있다. 각 점 $(0, 1/n)$ 에 가닥을 놓고, 꼬임(함수가 종점에서의 순열을 생성하도록 $(0, 1/n, 0)$ 에서 $(0, 1/n, 1)$ 까지의 경로들의 모음으로 정의됨)의 집합은 이 더 거친 군과 동형이다. 이 군에서의 순수 꼬임군은 유한 순수 꼬임군 $P_n$ 의 역 극한과 힐베르트 큐브에서 특정 집합을 뺀 공간의 기본군과 동형이다.

14. 코호몰로지

군 코호몰로지 $G$ 의 코호몰로지는 해당 Eilenberg–MacLane 분류 공간 $K(G, 1)$ 의 코호몰로지로 정의되며, 이 공간은 $G$ 에 의해 호모토피까지 고유하게 결정되는 CW 복합체이다. 꼬임군 $B_n$ 의 분류 공간은 평면( $\R^2$ )에서 서로 다른 $n$ 개의 점들의 모든 집합의 공간(번째 정렬되지 않은 배치 공간)이다.^[18]

: $\operatorname{UConf}_n(\R^2) = \{ \{u_1, ..., u_n\} : u_i \in \R^2, u_i \neq u_j \text{ for } i \neq j \}$ .

계수가 $\Z/2\Z$ 인 계산은 Fuks (1970)에서 찾을 수 있다.^[19]

마찬가지로 순수 꼬임군 $P_n$ 의 분류 공간은 평면( $\R^2$ )의 번째 ''정렬된'' 배치 공간 $\operatorname{Conf}_n(\R^2)$ 이다. 1968년 블라디미르 아르놀트(Vladimir Arnold)는 순수 꼬임군 $P_n$ 의 정수 코호몰로지가 다음 관계식을 만족하는 차수 1인 클래스 $\omega_{ij} \; \; 1 \leq i < j \leq n$ 의 모음으로 생성된 외대수의 몫이라고 밝혔다:^[20]

: $\omega_{k,\ell} \omega_{\ell,m} + \omega_{\ell,m} \omega_{m,k} + \omega_{m,k} \omega_{k,\ell} =0.$

참조

_[1] 웹사이트 Braid Group http://mathworld.wol[...]
_[2] 논문 The Braid Monodromy of Plane Algebraic Curves and Hyperplane Arrangements 1997
_[3] 간행물 Topological fluid mechanics of stirring http://www.math.ufl.[...]
_[4] 간행물 Topological mixing with ghost rods
_[5] 간행물 Topological chaos and periodic braiding of almost-cyclic sets
_[6] 간행물 Über die freie Äquivalenz der geschlossenen Zöpfe http://mi.mathnet.ru[...]
_[7] 간행물 Markov's theorem in 3-manifolds
_[8] 서적 Braids, links, and mapping class groups Princeton University Press
_[9] 웹사이트 Braid Index http://mathworld.wol[...] MathWorld – A Wolfram Web Resource 2014-08
_[10] 서적 Proceedings of the Second International Conference on the Theory of Groups Springer
_[11] 논문 Theory of Braids 1947
_[12] 논문 The braid groups
_[13] arXiv BRAIDS: A SURVEY 2004
_[14] 웹사이트 Introduction to Braid Groups https://www.math.uch[...]
_[15] arXiv Braid Group Cryptography 2009
_[16] 간행물 "{{math|2''n''}} Quasihole States Realize {{math|2^''n''-1}}-Dimensional Spinor Braiding Statistics in Paired Quantum Hall States" 1996
_[17] 간행물 Completing Artin's braid group on infinitely many strands
_[18] 서적 Braids World Scientific 2009-12-01
_[19] 논문 Cohomology of the braid group mod 2
_[20] 논문 The cohomology ring of the colored braid group http://www.pdmi.ras.[...]
_[21] 서적 Proceedings of the Second International Conference on the Theory of Groups Springer
_[22] 간행물 "{{math|2''n''}} Quasihole States Realize {{math|2^''n''-1}}-Dimensional Spinor Braiding Statistics in Paired Quantum Hall States" 1996
_[23] arXiv Braid Group Cryptography 2009
_[24] 저널 Basic results on braid groups

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com

	a	b	ab
예1	]] \(\sigma_3\)	]] \(\sigma_2\)	]] \(\sigma_3 \sigma_2\)
예2	]] \(\sigma_1^{-1} \sigma_3^{-1}\)	]] \(\sigma_1 \sigma_3^{-1}\)	]] \(\sigma_3^{-2}\)