원환면

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 기하학적 특성
3. 위상수학적 특성
4. 응용 분야
5. 기타
- 5.1. 어원
- 5.2. 대수적 표현
참조

1. 개요

원환면은 3차원 공간에서 원을 회전시켜 얻는 도형으로, 기하학적, 위상수학적 특성을 가지며 다양한 분야에 응용된다. 기하학적으로는 매개변수 방정식으로 표현되며, 부피와 겉넓이를 계산할 수 있다. 원환면은 링 토러스, 혼 토러스, 스핀들 토러스 등 다양한 형태로 나타나며, 종횡비에 따라 형태가 결정된다. 위상수학적으로는 두 원의 곱공간으로 정의되며, 기본군과 호몰로지 군을 갖는다. 원환면은 고차원으로 일반화되어 n차원 토러스로 확장되며, 색칠 문제, 자르기 문제, 음악 이론, 핵융합, 드 브루인 토러스 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

다양체 - 짜임새 공간
짜임새 공간은 위상 공간 위의 점들의 위치 관계를 연구하는 공간으로, 위상 공간 $X$ 위의 $n$ 개의 점들의 짜임새 공간 $\operatorname{Conf}^nX$ 은 $X$ 속의, $n$ 개 이하의 원소들을 갖는 부분 집합들의 집합으로 정의되며, 위상수학, 응용수학, 물리학 등 다양한 분야에서 활용된다.
다양체 - 대수 다양체
대수 다양체는 대수기하학에서 연구되는 기하학적 대상이며, 타원 곡선과 그라스마니안이 그 예시이다.

원환면

2. 기하학적 특성

원환면은 3차원 공간에서 원을 회전시켜 얻어지는 도형이다.

원환면의 형상과 크기는 큰 원의 반지름인 ''R''(큰 반지름)과 작은 원의 반지름인 ''r''(작은 반지름) (''R'' > ''r'')의 두 가지 값으로 나타낼 수 있다. 여기서 작은 원은 회전체의 단면이 되는 원이고, 큰 원은 작은 원의 중심이 그리는 원으로, 원환면의 '''중심 곡선'''이라고도 한다.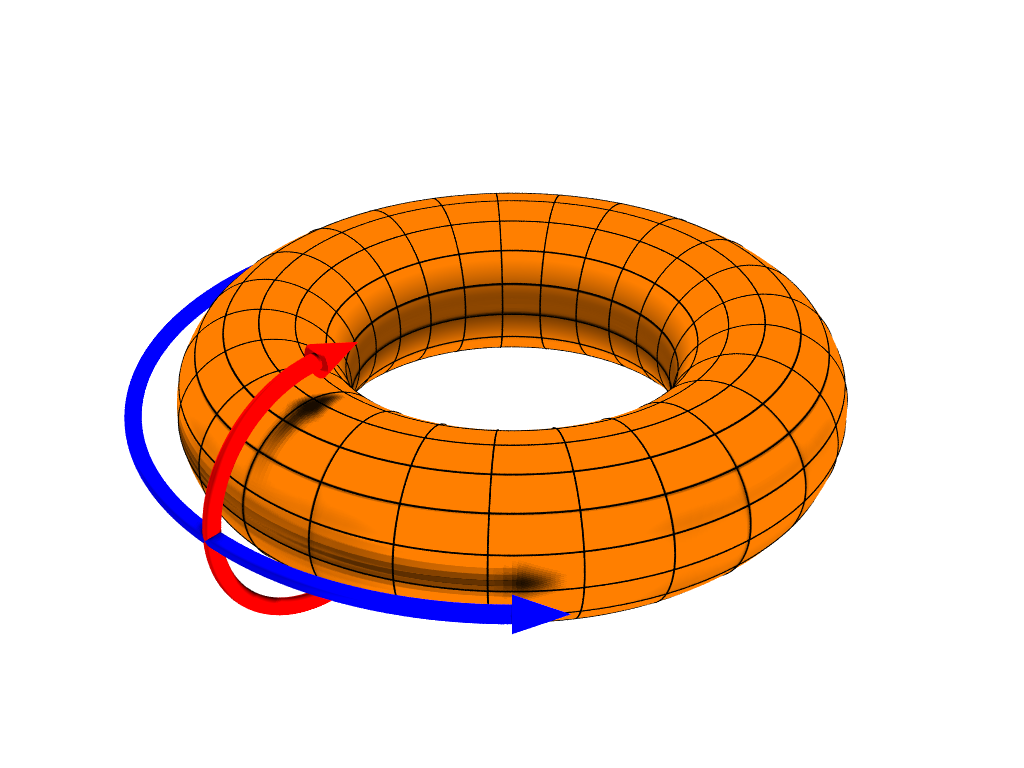

원환면은 ''R''과 ''r'' 값에 따라 여러 가지 형태로 나타낼 수 있으며, 매개변수 방정식이나 음함수 방정식으로 표현할 수 있다.^[2]

2. 1. 좌표계 표현

원환면은 매개변수 방정식 또는 음함수 방정식으로 표현할 수 있다.^[2]

3차원 공간에서 회전하는 원환면은 다음과 같은 매개변수 방정식으로 나타낼 수 있다.

\begin{align}x(\theta, \varphi) &= (R + r \cos \theta) \cos{\varphi}\\y(\theta, \varphi) &= (R + r \cos \theta) \sin{\varphi}\\z(\theta, \varphi) &= r \sin \theta\\\end{align}

여기서

\theta, \varphi \in [0,2\pi)

는 각각 튜브 주위의 회전과 원환면 회전축 주위의 회전을 나타낸다. ''R''은 튜브 중심에서 원환면 중심까지의 거리(주요 반경)이고, ''r''은 튜브의 반경(부반경)이다.^[3]

R/r

비율은 원환면의 ''종횡비''라고 한다. 일반적인 도넛의 종횡비는 약 3:2이다.

z

-좌표축을 중심으로 하는 원환면의 음함수 방정식은 다음과 같다.

{\textstyle \bigl(\sqrt{x^2 + y^2} - R\bigr)^2} + z^2 = r^2.

제곱근을 대수적으로 제거하면 다음과 같은 사차 방정식을 얻는다.

\left(x^2 + y^2 + z^2 + R^2 - r^2\right)^2 = 4R^2\left(x^2+y^2\right).

원환면은 ''R''과 ''r'' 값에 따라 세 가지 형태로 나뉜다.

R과 r의 관계	종류	설명
R > r	링 토러스 (앵커 링)	가장 흔한 형태로, 구멍이 있는 도넛 모양이다.
R = r	호른 토러스	구멍이 없는 형태이다.
R < r	스핀들 토러스	자기 교차하는 형태이며, 안쪽은 레몬, 바깥쪽은 사과 모양이다.

''R'' = 0 이면, 원환면은 반지름이 ''r''인 구가 된다.
''r'' = 0 이면, 원환면은 반지름이 ''R''인 원이 된다.

원환면은 두 원의 곱으로 나타낼 수 있으므로, 구면 좌표계의 수정된 버전을 사용하기도 한다.^[5]

''R'': 좌표계 중심으로부터의 거리
''θ'': 폴로이달 방향 각도 (''r''의 중심으로 이동)
''φ'': 토로이달 방향 각도 (구면 좌표계와 동일)

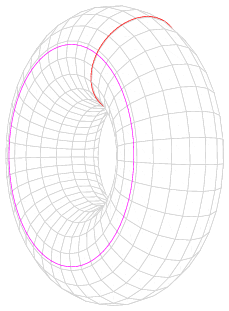
매개변수 ''t''를 일정하게 했을 때 원환면 위의 닫힌 곡선을 '''메리디안'''(경선)이라고 하며, ''p''를 일정하게 했을 때 닫힌 곡선을 '''롱지튜드'''(위선)라고 한다.

2. 2. 부피와 겉넓이

원환체(torus^영어)의 부피와 겉넓이는 파푸스 중점 정리를 사용하여 쉽게 계산할 수 있다.^[4] 원환체의 중심에서 튜브 중심까지의 거리가

R

이고 튜브의 반지름이

r

인 원환체의 부피는

2 \pi^2 r^2 R

이고, 겉넓이는

4 \pi^2 rR

이다.

이 공식은 작은 원의 평면을 따라 튜브를 자르고 튜브 중심을 따라 달리는 선을 직선화하여 풀어서 얻은 길이

2\pi R

및 반경

r

인 원기둥과 같다. 튜브 안쪽의 표면적 및 부피 손실은 바깥쪽의 이득을 정확히 상쇄한다.

토러스 표면의 가장 바깥쪽 점과 중심 사이의 거리

p

와 가장 안쪽 점과 중심 사이의 거리

q

로 표면적과 부피를 표현하면 (

R = \frac{p+q}{2}

및

r = \frac{p-q}{2}

), 다음과 같다.

:

\begin{align}A &= 4 \pi^2 \left(\frac{p+q}{2}\right) \left(\frac{p-q}{2}\right) = \pi^2 (p+q) (p-q), \\[5mu]V &= 2 \pi^2 \left(\frac{p+q}{2}\right) \left(\frac{p-q}{2}\right)^2 = \tfrac14 \pi^2 (p+q) (p-q)^2.\end{align}

2. 3. 다양한 형태

3차원 공간에서 회전 원환면은 다음과 같이 매개변수 방정식으로 표현할 수 있다.^[2]

:

\begin{align}x(\theta, \varphi) &= (R + r \cos \theta) \cos{\varphi}\\y(\theta, \varphi) &= (R + r \cos \theta) \sin{\varphi}\\z(\theta, \varphi) &= r \sin \theta\\\end{align}

각 좌표

\theta, \varphi \in [0,2\pi),

는 튜브 주위의 회전과 원환면 회전축 주위의 회전을 각각 나타낸다. 여기서 ''주반경''

R

은 튜브 중심에서 원환면 중심까지의 거리이고, ''부반경''

r

은 튜브의 반경이다.^[3]

R/r

은 원환면의 ''종횡비''라고 한다.

z

-좌표축을 중심으로 하는 원환면에 대한 음함수 방정식은 다음과 같다.

:

{\textstyle \bigl(\sqrt{x^2 + y^2} - R\bigr)^2} + z^2 = r^2.

제곱근을 대수적으로 제거하면 다음과 같은 사차 방정식이 얻어진다.

:

\left(x^2 + y^2 + z^2 + R^2 - r^2\right)^2 = 4R^2\left(x^2+y^2\right).

R^영어과 r^영어 사이의 종횡비에 따라 세 가지 표준 원환면이 존재한다.

형태	조건	설명
링 토러스 (Ring torus)	R > r	일반적인 링 모양 또는 앵커 링 형태이다.
혼 토러스 (Horn torus)	R = r	"구멍"이 없는 원환면이다.
스핀들 토러스 (Spindle torus)	R < r	자기 교차하는 형태이다. 안쪽 껍질은 레몬, 바깥쪽 껍질은 사과와 유사하다.
구 (Sphere)	R = 0	반경 r인 구로 축퇴된다.
원	r = 0	반경 R인 원으로 축퇴된다.

$R \ge r$ 인 경우, 이 원환면의 내부

: ${\textstyle \bigl(\sqrt{x^2 + y^2} - R\bigr)^2} + z^2 < r^2$

는 미분동형이며 위상동형이다. 또한 데카르트 곱과 원의 유클리드 열린 원판이다. 이 입체 원환면(Solid torus)의 부피와 원환면의 표면적은 파푸스 중점 정리를 사용하여 쉽게 계산할 수 있으며, 다음과 같다.^[4]

: $\begin{align}A &= \left( 2\pi r \right) \left(2 \pi R \right) = 4 \pi^2 R r, \\[5mu]V &= \left ( \pi r^2 \right ) \left( 2 \pi R \right) = 2 \pi^2 R r^2.\end{align}$

원환면 표면의 가장 바깥쪽 점과 중심 사이의 거리 ''p''와 가장 안쪽 점과 중심 사이의 거리 ''q''로 표면적과 부피를 표현하면 ( 및 ), 다음과 같다.

: $\begin{align}A &= 4 \pi^2 \left(\frac{p+q}{2}\right) \left(\frac{p-q}{2}\right) = \pi^2 (p+q) (p-q), \\[5mu]V &= 2 \pi^2 \left(\frac{p+q}{2}\right) \left(\frac{p-q}{2}\right)^2 = \tfrac14 \pi^2 (p+q) (p-q)^2.\end{align}$

원환면은 두 원의 곱이므로 구면 좌표계의 수정된 버전을 사용하기도 한다. 전통적인 구면 좌표에는 세 가지 측정이 있다. ''R''은 좌표계 중심으로부터의 거리이고, ''θ''와 ''φ''는 중심점에서 측정된 각도이다.

원환면은 효과적으로 두 개의 중심점을 가지므로 각도의 중심점이 이동한다. ''φ''는 구면 시스템에서와 동일한 각도를 측정하지만 "토로이드" 방향으로 알려져 있다. ''θ''의 중심점은 ''r''의 중심으로 이동하며, "폴로이달" 방향으로 알려져 있다. 이러한 용어는 지구의 자기장에 대한 논의에서 처음 사용되었으며, 여기서 "폴로이달"은 "극 방향"을 나타내는 데 사용되었다.^[5] 현대적인 사용법에서 토로이드 및 폴로이달은 자기 제한 핵융합 장치를 논의하는 데 더 일반적으로 사용된다.

가장 흔한 원환면은 원(둘레)의 바깥쪽에 회전축을 놓고 얻을 수 있는 회전체로, 대표적인 도넛 모양 중 하나인 "링 도넛" 형태이다.

원환면의 형상과 크기를 나타내기 위해서는 큰 원의 반지름인 큰 반지름 ''R''과 작은 원의 반지름인 작은 반지름 ''r'' (''R'' > ''r'')의 두 가지 값이 필요하다(그림). 작은 원은 회전체의 단면인 원, 큰 원은 작은 원의 중심이 이루는 원이다. 큰 원은 원환면의 '''중심 곡선'''이라고도 한다.

위 그림과 같이 매개변수 ''t'', ''p'' (0≦''t''≦2π, 0≦''p''≦2π)를 사용하면 다음과 같이 표현할 수 있다.

: $\begin{align}x &= R\cos{t} + r\cos{p}\cos{t}\\y &= R\sin{t} + r\cos{p}\sin{t}\\z &= r \sin{p}\end{align}$

여기서 매개변수 ''t''를 일정하게 했을 때의 원환면 위의 닫힌 곡선을 '''메리디안'''(meridian) 또는 '''경선'''이라고 하며, ''p''를 일정하게 했을 때의 원환면 위의 닫힌 곡선을 '''롱지튜드'''(longitude) 또는 '''위선'''이라고 한다.

3. 위상수학적 특성

위상수학적으로, 원환면은 두 원의 곱 ''S''¹ × ''S''¹으로 정의되는 닫힌 곡면이다. 이는 '''C'''²에 놓인, 반지름이 √2인 3-구 ''S''³의 부분 집합으로 볼 수 있으며, 클리포드 원환면이라고도 불린다.^[6]

원환면은 2차원 평면에서 정수만큼 평행이동하여 겹치는 점들을 동치 관계로 묶어 묘사할 수 있다. 즉,

:( ''x'' , ''y'' ) ~ ( ''x''+1, ''y'' ) ~ ( ''x'' , ''y''+1).

이는 몫

: $(x,y) \sim (x+1,y) \sim (x,y+1), \,$

또는 반대쪽 모서리를 붙여 만든 단위 정사각형의 몫( 기본 다각형 ''ABA''⁻¹''B''⁻¹)으로도 표현된다.

원환면에 구멍을 내면 안팎을 뒤집을 수 있는데, 이때 튜브를 감싸는 원은 가운데 빈 구멍을 둘러 돌아가는 원이 되고, 그 역도 성립한다.

3. 1. 기본군과 호몰로지 군

원환체의 기본군은 원의 기본군의 곱집합이다. 즉,

:

\pi_1(\mathbb{T}^2) = \pi_1(S^1) \times \pi_1(S^1) \cong \mathbb{Z} \times \mathbb{Z}.

^[7]

직관적으로 설명하면, 원환면의 "구멍"을 도는 닫힌 경로(예: 특정 위도를 따라가는 원)와 원환면의 "몸체"를 도는 경로(예: 특정 경도를 따라가는 원)는 몸체를 돌고 구멍을 도는 경로로 변형될 수 있다는 것이다. 따라서, 엄격한 '위도' 경로와 엄격한 '경도' 경로는 서로 교환 가능하다. 이는 두 개의 끈이 서로 통과한 다음 풀고 다시 감는 것으로 비유할 수 있다.

원환면의 첫 번째 호몰로지 군은 기본군과 동형 사상이다(이는 기본군이 아벨 군이므로 후레비츠 정리에서 따름).

3. 2. 고차원 원환면

원환면은 n차원으로 일반화될 수 있으며, n차원 원환면은 n개의 원의 곱집합으로 정의된다. 즉, 다음과 같다.

:

\mathbb{T}^n = \underbrace{S^1 \times S^1 \times \cdots \times S^1}_n.

1차원 원환면은 원

\mathbb{T}^{1}=\mathbb{S}^{1}

이다. 2차원 원환면은

\mathbb{T}^2

이다. n차원 원환면

\mathbb{T}^{n}

은 모든 좌표에서 정수 이동 하에서

\mathbb{R}^{n}

의 몫으로 설명될 수 있다. 다시 말해, n차원 원환면은 정수 격자

\mathbb{Z}^{n}

의 작용에 대한

\mathbb{R}^{n}

의 몫 공간이다. n차원 원환면은 n차원 초입방체에서 마주보는 면을 붙여서 얻을 수도 있다.

n차원 원환면의 기본군은 랭크 n의 자유 아벨 군이다. n차원 원환면의 k차 호몰로지 군은 랭크 n 이항 계수 k를 선택하는 자유 아벨 군이다. 따라서 n차원 원환면의 오일러 지표는 모든 n에 대해 0이다. 코호몰로지 환 ''H''^•(

\mathbb{T}^{n}

, '''Z''')는 '''Z'''-가군

\mathbb{Z}^{n}

의 외대수로 식별될 수 있다.

4차원에서 간단한 회전을 수행하는 클리포드 토러스의 입체 투영 (xz 평면을 통해)

''n''-토러스는 원의 ''n''-겹 곱이므로, ''n''-토러스는 원 위의 순서가 정해진 ''n''개의 점의 배치 공간이다. 기호로

\mathbb{T}^{n}= (\mathbb{S}^{1})^{n}

이다. 순서가 정해지지 않은 점들의 배치 공간은 오비폴드

\mathbb{T}^{n} / \mathbb{S}_{n}

이며, 이는 ''n''개의 문자에 대한 대칭군에 의한 토러스의 몫이다.

n=2인 경우 몫은 뫼비우스 띠이다. n=3인 경우, 이 몫은 단면이 정삼각형인 솔리드 토러스로 묘사될 수 있다.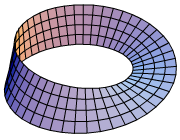

원 위의 두 점의 배치 공간은 2-토러스, '''T'''²/''S''₂의 오비폴드 몫이며, 이는 뫼비우스 띠이다.

3. 3. 평면 토러스

평면 토러스는 곡률이 0인 원환면으로, 4차원 유클리드 공간에 임베딩될 수 있다.^[17] 평면 토러스는 직사각형 또는 평행사변형의 반대쪽 변을 붙여서 만들 수 있다. 예를 들어, 가정용 게임 드래곤 퀘스트 시리즈와 같은 컴퓨터 RPG에서 세계 지도의 오른쪽 끝과 왼쪽 끝, 상단과 하단이 연결된 세계는 지구와 같은 구면이 아닌 평면 토러스이다.^[17]

평면 토러스는

\mathbb{R}^{2}

/'''L'''의 몫으로 표현할 수 있다. 여기서 '''L'''은

\mathbb{Z}^{2}

와 동형인

\mathbb{R}^{2}

의 이산 부분군이다. 가장 간단한 예는 '''L''' =

\mathbb{Z}^{2}

인 경우로,

\mathbb{R}^{2}/\mathbb{Z}^{2}

는 (''x'', ''y'') ~ (''x'' + 1, ''y'') ~ (''x'', ''y'' + 1)과 같이 데카르트 평면으로 설명할 수 있다. 이 "정사각형" 평면 토러스는 유클리드 4차원 공간에 임베딩될 수 있으며, 모든 곳에서 가우스 곡률이 0이다.

직사각형 평면 토러스의 4차원 유클리드 임베딩은 다음과 같이 표현할 수 있다.

:

(x,y,z,w) = (R\cos u, R\sin u, P\cos v, P\sin v)

여기서 ''R''과 ''P''는 종횡비를 결정하는 양의 상수이다.

입체 투영에서 볼 때, 4차원 ''평면 토러스''는 3차원으로 투영되어 고정된 축에서 회전할 수 있다.

3차원에서 직사각형을 토러스로 구부릴 수 있지만, 이렇게 하면 체커 무늬의 왜곡에서 볼 수 있듯이 표면을 따라 측정된 거리에 필연적으로 영향을 미친다.

$C^1$ $\mathbb R^3$ 에서 평면 토러스의 등거리 임베딩, 주름살

평면 토러스는 원기둥 면을 평탄한 채로 구부려 양쪽 끝을 맞춰 붙여서 얻을 수 있다. "평탄"이란 "곡률 0"이라는 의미이다. 3차원 공간 내에서 원기둥 면을 구부리면 도넛 모양 밖에 만들 수 없지만, 평탄 토러스를 만들려면 4차원 공간이 필요하다.

평행사변형으로도 평탄 토러스를 만들 수 있다. 예를 들어, 이중 주기를 가진 타원 함수는 두 개의 기본 주기가 그리는 평행사변형으로 구성된 평탄 토러스 위에서 자연스럽게 정의되는 함수로 해석된다.

다음은 평면 토러스를 만드는 과정을 시각적으로 나타낸 것이다.

--
A와 A, B와 B (또는 B와 B, A와 A)를 연결한다.

4. 응용 분야

원환면은 수학, 물리학, 공학 등 다양한 분야에서 활용된다.

4. 1. 색칠 문제

사색문제와 비슷한 문제를 2차원 원환면 위에서 생각해 볼 수 있다. 원환면에 임의의 영역이 나뉘어 있을 때, 인접한 영역을 다른 색으로 항상 색칠가능한 최소의 색의 개수는 7개이다. 평면에서는 네 가지 색으로 충분하다.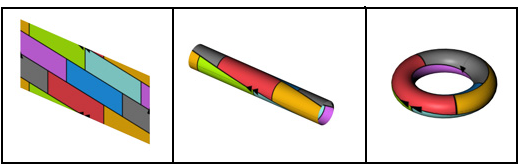

이러한 구성을 통해 경계를 구별하는데 최소한 일곱개의 색이 필요함을 알 수 있다.

원환면의 Heawood 수는 7인데, 이는 원환면에 매립될 수 있는 모든 그래프가 최대 7의 채색수를 갖는다는 것을 의미한다. (완전 그래프

\mathsf{K_7}

이 원환면에 매립될 수 있고,

\chi (\mathsf{K_7}) = 7

이므로, 상한은 정확하다.) 다른 표현으로는, 원환면이 영역으로 나뉘어 있을 때, 인접한 영역이 같은 색을 갖지 않도록 7개 이하의 색을 사용하여 영역을 채색하는 것이 항상 가능하다. (평면에 대한 사색 정리와 비교해 보라.)

4. 2. 자르기 문제

표준적인 2차원 원환면을 ''n''개의 평면으로 자를 경우 최대

\frac{1}{6}\left(n^3+3n^2+8n\right)

개의 조각이 만들어진다.^[16]

회전체의 원환면은 ''n'' (> 0)개의 평면에 의해 최대

:

\begin{pmatrix}n+2 \\ n-1\end{pmatrix} +\begin{pmatrix}n \\ n-1\end{pmatrix} = \tfrac{1}{6}(n^3 + 3n^2 + 8n)

개의 조각으로 잘릴 수 있다.^[16] (단, 조각들은 재배열될 수 없고 모든 절단에 대해 제자리에 있어야 한다.)

0 ≤ ''n'' ≤ 10에 대한 조각의 처음 11개의 수는 다음과 같다.

: 1, 2, 6, 13, 24, 40, 62, 91, 128, 174, 230, ...

4. 3. 음악 이론

'''톤네츠'''는 음악 이론에서 토러스의 한 예시이다.
톤네츠는 변성 동음 이의를 가정하여 반복된 평행사변형의 오른쪽 가장자리의 (F♯-A♯) 세그먼트를 왼쪽 가장자리의 (G♭-B♭) 세그먼트와 동일시해야만 진정한 토러스가 된다.

드미트리 티모츠코와 펠리페 포사다, 마이클 콜리나스 등의 협력자들은 음악 이론 연구에서 오비폴드를 화음 모델링에 응용하였다.^[9]^[10]

4. 4. 드 브루인 토러스

조합론 수학에서, '''드 브루인 토러스'''는 모든 ''m''×''n'' 행렬을 정확히 한 번 포함하는 알파벳(종종 0과 1)의 기호 배열이다. 가장자리가 랩어라운드로 간주되므로 토러스이다. 그 이름은 ''n''이 1(1차원)인 특수한 경우로 간주될 수 있는 드 브루인 수열에서 유래했다.

STL 모델 드 브루인 토러스 ''(16,32;3,3)₂'' (1은 패널, 0은 메쉬의 구멍으로 표현) – 일관된 방향으로 모든 3×3 행렬이 정확히 한 번 나타남

5. 기타

대수기하학에서 사용되는 개념으로 Algebraic torus|대수적 토러스^영어가 있다.

$T^1 = S^1$ 는 2차원 특수 직교군 $\mathrm{SO}(2)=\mathrm{O}(2)\cap\mathrm{SL}(2,\mathbf R)=\left\{\begin{pmatrix} x & -y \\ y & x\end{pmatrix} \,\mid \,x,y \in \mathbf R, x^2+y^2=1 \right\}$ 과 동일시할 수 있어, $\mathbf R$ 위에 정의된 대수군으로 간주할 수 있다. 그 복소화 $\mathrm{SO}(2,\mathbf C)$ 는 0이 아닌 복소수 전체의 곱셈군 $\mathbf C^\times$ 과 동형이다. 일반적으로, 완전체 $F$ 위에 정의된 대수군 ''T''가 랭크 $r\ge 1$ 의 토러스라는 것은, $F$ 의 대수적 폐포 $\bar F$ 위에서 ''T''가 $(F^\times)^r$ 과 동형이 되는 것을 말한다.

예를 들어, 일반 선형군 $\mathrm{GL}(n,\mathbf R)$ 에 속하는 대각 행렬 전체로 이루어진 군은 랭크 $n$ 의 토러스이지만, $\mathbf R$ 위에서 $(\mathbf R^\times)^n$ 과 동형이 된다. 이러한 성질을 가진 토러스를 분열 토러스라고 한다. 첫 번째 예의 $T^1 = S^1$ 는 분열 토러스가 아니다.

5. 1. 어원

'''토러스'''는 "둥근, 부풀어 오른, 솟아오른, 돌출된"을 뜻하는 라틴어 단어이다.^[1]

5. 2. 대수적 표현

Algebraic torus|대수적 토러스^영어는 대수기하학에서 사용되는 개념이다.

T^1 = S^1

는 2차원의 특수 직교군

:

\mathrm{SO}(2)=\mathrm{O}(2)\cap\mathrm{SL}(2,\mathbf R)=\left\{\begin{pmatrix} x & -y \\ y & x\end{pmatrix} \,\mid \,x,y \in \mathbf R, x^2+y^2=1 \right\}

과 동일시할 수 있으므로,

\mathbf R

위에 정의된 대수군으로 간주할 수 있다. 그 복소화

\mathrm{SO}(2,\mathbf C)

는 0이 아닌 복소수 전체의 곱셈군

\mathbf C^\times

과 동형이다. 일반적으로, 완전체

F

위에 정의된 대수군 ''T''가 랭크

r\ge 1

의 토러스라는 것은,

F

의 대수적 폐포

\bar F

위에서 ''T''가

(F^\times)^r

과 동형이 되는 것을 말한다.

예를 들어, 일반 선형군

\mathrm{GL}(n,\mathbf R)

에 속하는 대각 행렬 전체로 이루어진 군은 랭크

n

의 토러스이지만,

\mathbf R

위에서

(\mathbf R^\times)^n

과 동형이 된다. 이러한 성질을 가진 토러스를 분열 토러스라고 한다. 첫 번째 예의

T^1 = S^1

는 분열 토러스가 아니다.

참조

_[1] 서적 A Guide to the Classification Theorem for Compact Surfaces Springer, Heidelberg
_[2] 웹사이트 Equations for the Standard Torus http://www.geom.uiuc[...] Geom.uiuc.edu 1995-07-06
_[3] 웹사이트 Torus http://doc.spatial.c[...] Spatial Corp. 2014-11-16
_[4] MathWorld Torus https://mathworld.wo[...]
_[5] 웹사이트 poloidal http://dictionary.oe[...] Oxford University Press 2007-08-10
_[6] 간행물 Applications of the Clifford torus to material textures https://journals.iuc[...] 2024-03-07
_[7] 문서 "FUNDAMENTAL GROUPS: MOTIVATION, COMPUTATION METHODS, AND APPLICATIONS" https://math.uchicag[...] REA Program, Uchicago 2014
_[8] 웹사이트 Torus https://mathworld.wo[...] 2021-07-27
_[9] 간행물 The Geometry of Musical Chords http://www.brainmusi[...] 2006-07-07
_[10] 웹사이트 Take on Math in the Media http://www.ams.org/m[...] American Mathematical Society 2006-10
_[11] 간행물 Doc Madhattan: A flat torus in three dimensional space http://docmadhattan.[...] 2012-07-21
_[12] 웹사이트 Mathematicians Produce First-Ever Image of Flat Torus in 3D http://www.sci-news.[...] 2012-04-18
_[13] 웹사이트 Mathematics: first-ever image of a flat torus in 3D – CNRS Web site – CNRS http://www2.cnrs.fr/[...]
_[14] 웹사이트 Flat tori finally visualized! http://math.univ-lyo[...] Math.univ-lyon1.fr 2012-04-18
_[15] 웹사이트 The Tortuous Geometry of the Flat Torus http://www.science4a[...] 2016
_[16] MathWorld Torus Cutting https://mathworld.wo[...]
_[17] 서적 空想科学大学宝島社
_[18] 서적 http://www.perseus.t[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com