유한 상태 기계

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 표현 방법
4. 예시
- 4.1. 수리 기계와 인식기
- 4.2. 변환기
  - 4.2.1. 무어 모델 (Moore Model)
  - 4.2.2. 밀리 모델 (Mealy Model)
5. 역사
6. 유한 오토마타와 인공 생명
- 6.1. 인공 생명 (Artificial Life)
- 6.2. 인공 생명과 관련된 분야들
7. 사용되는 곳
- 7.1. 하드웨어적 응용
- 7.2. 소프트웨어적 응용
참조

1. 개요

유한 상태 기계(FSM)는 시스템의 상태와 상태 간의 전이를 수학적으로 모델링하는 데 사용되는 개념이다. 시작 상태, 수용 상태, 전이, 동작 등의 구성 요소로 이루어져 있으며, 현재 상태와 입력에 따라 다음 상태와 출력이 결정된다. FSM에는 결정적 유한 오토마타(DFA)와 비결정적 유한 오토마타(NFA)가 있으며, NFA는 DFA로 변환될 수 있다. FSM은 회전문, 수리 기계, 변환기 등 다양한 형태로 표현될 수 있으며, 상태/이벤트 표, UML 상태 기계, SDL 상태 기계 등 여러 표현 방법이 존재한다. FSM은 전기 공학, 컴퓨터 과학, 언어학 등 다양한 분야에서 활용되며, 하드웨어 및 소프트웨어 응용 프로그램 설계, 프로그래밍 언어 컴파일러, 패리티 비트 생성 등에 사용된다. 또한, 인공 생명 및 인공 지능 연구에도 중요한 역할을 한다.

더 읽어볼만한 페이지

유한 상태 기계 - 정규 언어
정규 언어는 주어진 알파벳으로 구성된 문자열 집합으로, 클레이니 스타, 합집합, 문자열 연결 연산을 통해 확장되며, 정규 표현식, 유한 상태 기계 등으로 표현 가능하다.
유한 상태 기계 - Lex
Lex는 마이크 레스크와 에릭 슈미트가 개발한 어휘 분석기 생성기로, 정규 표현식을 기반으로 입력 텍스트를 분석하여 토큰을 식별하고 컴파일러 개발 등에 활용된다.
오토마타 이론 - 튜링 기계
튜링 기계는 앨런 튜링이 제시한 계산 모델로, 테이프 위에서 기계적으로 작동하며, 유한한 상태, 테이프, 헤드, 명령 표를 통해 작동하고, 계산 가능성과 알고리즘의 한계를 연구하는 데 사용된다.
오토마타 이론 - 형식 문법
형식 문법은 문자열 변환 규칙의 집합으로, 시작 기호로부터 규칙을 적용하여 문자열을 생성하며, 촘스키 위계에 따라 분류되고 생성 규칙을 통해 문자열을 변환한다.

유한 상태 기계
개요
유형	수학적 계산 모델
설명	입력, 출력, 상태를 갖는 추상 기계 상태 전이를 통해 다음 상태를 결정 현재 상태와 입력에 따라 다음 상태가 결정되는 시스템 컴퓨터 과학, 수학, 언어학 등 다양한 분야에서 사용
정의 및 특징
정의	내부 상태(state)들을 가지고 있는 시스템 입력에 따라 상태를 변경하는 시스템 내부 상태는 유한개로 정의
상태 전이	현재 상태와 입력에 의해 다음 상태로 이동 전이 함수(transition function)에 의해 정의
입력	외부에서 시스템으로 들어오는 신호 또는 데이터
출력	시스템이 외부로 내보내는 신호 또는 데이터
유한성	상태의 개수가 유한함 입력의 종류가 유한함
결정론적/비결정론적	결정론적(Deterministic): 각 상태에서 특정 입력에 대한 다음 상태가 단 하나로 결정 비결정론적(Nondeterministic): 각 상태에서 특정 입력에 대한 다음 상태가 여러 개일 수 있음
표현 방법
상태 다이어그램	원으로 상태를 표현하고 화살표로 전이를 나타냄 원 안에 상태 이름 표기, 화살표 위에 입력 표기
상태 테이블	행은 현재 상태, 열은 입력으로 구성 각 셀은 다음 상태를 나타냄
전이 함수	수학적 함수로 상태 전이를 표현 (현재 상태, 입력) → 다음 상태
활용 분야
컴퓨터 과학	컴파일러의 어휘 분석기 프로토콜 구현 텍스트 분석 패턴 매칭
전자 공학	디지털 논리 회로 설계 임베디드 시스템 설계 컨트롤러 설계
언어학	자연어 처리 형태소 분석 구문 분석
기타	게임 인공지능 로봇 제어 생물학 (세포 모델링)
종류
결정적 유한 오토마타 (DFA)	각 상태에서 특정 입력에 대한 다음 상태가 하나
비결정적 유한 오토마타 (NFA)	각 상태에서 특정 입력에 대한 다음 상태가 여러 개 가능
입실론-비결정적 유한 오토마타 (ε-NFA)	입력 없이 상태 변경이 가능
무어 머신	출력이 현재 상태에만 의존
밀리 머신	출력이 현재 상태와 입력에 의존
관련 개념
오토마타 이론	유한 상태 기계를 포함한 계산 모델 연구
정규 언어	유한 상태 기계로 인식 가능한 언어 집합
상태 공간	유한 상태 기계가 가질 수 있는 모든 상태의 집합
기타
다른 이름	유한 오토마톤 (Finite automaton) 유한 상태 오토마톤 (Finite-state automaton)
로마자 표기	yuhan sangtae gigye

2. 정의

시작 상태(start state)는 유한 오토마타가 입력값을 처리하기 전의 상태이다. 받아들여지는 상태(accept states 또는 final states)는 유한 오토마타가 모든 입력값을 처리했을 때의 상태가 받아들여질 경우 이 상태의 집합을 의미한다. 받아들여지는 상태는 한개 또는 여러개일 수 있으며 이는 동치이다. 일반적으로 받아들여지는 상태는 이중 원으로 표현한다.

상태(state)는 전이(transition)를 기다리는 시스템의 상태를 설명하는 것이다. 전이는 조건이 충족되거나 이벤트가 수신될 때 실행될 일련의 동작이다.^[24] 전이는 조건이 충족되거나 이벤트를 수신했을 때 실행되는 동작의 집합이다.^[29]

예를 들어, 오디오 시스템을 사용하여 라디오를 듣는 경우(시스템이 "라디오" 상태임), "다음" 자극을 받으면 다음 방송국으로 이동한다. 시스템이 "CD" 상태인 경우 "다음" 자극은 다음 트랙으로 이동하는 결과를 가져온다. 동일한 자극이 현재 상태에 따라 다른 동작을 트리거한다.

일부 유한 상태 기계 표현에서는 상태에 동작을 연결하는 것도 가능하다.

진입 동작(entry action): 상태에 ''진입할 때'' 수행되고,
탈출 동작(exit action): 상태에서 ''나갈 때'' 수행된다.

유한 오토마타(유한 상태 기계=FSM)의 다음 상태와 출력은 입력과 현재 상태에 따라 결정된다. 그림 8에 FSM 논리를 나타낸다.

일반적인 분류에 따라 다음과 같은 형식적인 정의를 찾을 수 있다.

==== 구성 요소 ====

유한 오토마타는 다음 요소들로 구성된다.^[30]

상태: 전이를 시작하기 위해 대기하고 있는 시스템의 행동적 노드를 의미한다. 상태는 전이를 기다리는 시스템의 상태를 설명하는 것이다. 예를 들어, 자동차 오디오에서 라디오를 듣고 있을 때(''라디오 "상태"'') "다음" 버튼을 누르면(''다음 "유발점"'') 다른 방송국으로 넘어가지만, CD를 듣고 있을 때(''CD "상태"'') "다음" 버튼을 누르면 다음 곡을 재생한다. 이처럼 같은 유발점이 현재 상태에 따라 다른 동작을 보일 수 있다.^[30]
전이: 어떤 조건이 만족되거나 이벤트가 발생하였을 때 수행되는 일련의 동작을 의미한다.
동작: 일부 유한 상태 기계 표현에서는 상태에 동작을 연결하는 것도 가능하다.^[30]
진입 동작: 상태에 ''진입'' 할 때 수행되는 동작
퇴장 동작: 상태로부터 ''퇴장'' 할 때 수행되는 동작
초기 상태: 일반적으로 어떤 곳에서도 화살표로 가리키지 않는 상태이다.^[30]
수용 상태: 기계가 절차를 성공적으로 완료한 상태이다. 일반적으로 이중 원으로 표현된다.^[30]

==== 결정적 유한 오토마타 (DFA) ====

'''결정적 유한 오토마타'''(Deterministic Finite-State Machine, DFSM) 또는 '''결정적 유한 상태 수용기'''(Deterministic Finite-State Acceptor)는 다음과 같은 5튜플(quintuple)

(\Sigma, S, s_0, \delta, F)

이다.

$\Sigma$ : 입력 알파벳(유한한 비어 있지 않은 기호 집합)
$S$ : 유한한 비어 있지 않은 상태 집합
$s_0$ : 초기 상태, $S$ 의 원소
$\delta$ : 상태 전이 함수: $\delta: S \times \Sigma \rightarrow S$ (비결정적 유한 오토마타에서는 $\delta: S \times \Sigma \rightarrow \mathcal{P}(S)$ 가 된다. 즉, $\delta$ 는 상태 집합을 반환한다.)
$F$ : 종료 상태 집합, $S$ 의 (비어 있을 수 있는) 부분 집합

결정적 및 비결정적 FSM 모두에서

\delta

가 부분 함수가 되도록 허용하는 것이 일반적이다. 즉, 모든

s \isin S

와

x \isin \Sigma

의 조합에 대해

\delta(s, x)

가 정의될 필요는 없다. 만약 FSM

M

이 상태

s

에 있고 다음 기호가

x

이며

\delta(s, x)

가 정의되지 않으면

M

은 오류를 알릴 수 있다(즉, 입력을 거부한다). 이것은 일반적인 상태 기계의 정의에 유용하지만 기계를 변환할 때는 덜 유용하다. 기본 형태의 일부 알고리즘은 전 함수를 필요로 할 수 있다.

유한 상태 기계는 그 헤드가 "읽기" 작업만 수행하고 항상 왼쪽에서 오른쪽으로 이동해야 하는 것으로 제한된 튜링 기계와 동일한 계산 능력을 갖는다. 즉, 유한 상태 기계가 수용하는 각 형식 언어는 이러한 종류의 제한된 튜링 기계에 의해 수용되고 그 반대도 마찬가지다.^[15]

==== 비결정적 유한 오토마타 (NFA) ====

비결정적 유한 오토마타(NFA)는 한 상태에서 동일한 입력에 대해 여러 개의 다음 상태로 전이가 가능하거나, 입력 없이 전이(ε-전이)가 가능한 오토마타이다. 수학적으로 5-튜플 (Q, Σ, s₀, δ, F)로 표현된다.

''Q''는 상태의 공집합이 아닌 유한 집합이다.
''Σ''는 입력 문자이다. (유한하며, 비어있지 않은 기호의 집합이다).
''S''는 유한하며, 비어있지 않은 상태의 집합이다.
''δ''는 상태 전이 함수이다: $\delta: Q \times \left(\Sigma \cup \left\{\epsilon \right\} \right) \rightarrow \mathcal{P}(Q)$
''s₀''는 초기 상태이며, ''Q''의 원소이다.
''F''는 최종 상태의 집합이며, ''Q''의 원소이다.

비결정적 유한 오토마타는 결정적 유한 오토마타와는 다르게 입력 기호에 대해서

\epsilon

-transition 에 의해 0개 이상의 이동이 가능하다. 만약 가능한 다음 상태의 경우가 없다면, 기계는 입력을 거부한다.

결정적 유한 오토마타에서 모든 상태는 각각의 가능한 입력에 대해 정확히 하나의 변환된 상태를 가질 수 있다. 비 결정적 유한 오토마타에서 입력은 주어진 상태에 대해 한 가지 또는 여러 가지의 변환된 상태를 가지게 할 수 있다. 여러 알고리즘(멱집합 구성 등)을 사용하여 어떠한 NFA라도 동일한 기능을 가지는 DFA로 변환할 수 있다.

결정적 유한 오토마타(DFA)와 비결정적 유한 오토마타(NFA), 일반화된 비결정적 유한 오토마타(GNFA)는 결정적 오토마타에서는 각 상태에 대해 가능한 모든 입력에 대해 정확히 하나의 전이가 존재한다는 점에서 구별된다. 비결정적 오토마타에서는 주어진 상태에 대해 하나의 입력이 하나 이상 또는 전혀 전이를 일으키지 않을 수 있다.

==== 비결정적 유한 오토마타의 결정적 유한 오토마타로의 변환 ====

멱집합 구성 알고리즘을 통해 임의의 비결정적 오토마타를 동일한 기능을 가진 (일반적으로 더 복잡한) 결정적 오토마타로 변환할 수 있다.

멱집합 구성(부분집합 구성) 방식은 유한 오토마타 변환의 표준적인 방법이다. 이 방식을 통해 정규 언어를 인식하는 비결정적 유한 오토마타(NFA)는 결정적 유한 오토마타(DFA)로 변환된다. NFA가 더 유연함에도 불구하고, DFA가 인식하지 못하는 어떠한 언어도 인지할 수 없다는 점이 이 이론의 핵심이다. NFA를 DFA로 변환하는 주된 이유는, 더 쉽게 구성되는 NFA를 컴퓨터에서 효율적으로 실행할 수 있는 DFA로 바꾸기 위함이다. 하지만 NFA가 ''n''개의 상태를 가지고 있다면, 변환된 DFA는 최대 2^''n'' 개의 상태를 가질 수 있어, 복잡도가 지수적으로 증가한다. 따라서 큰 NFA에 대해 이 변환은 비실용적일 수 있다.^[10]

==== 비결정적 유한 오토마타와 결정적 유한 오토마타의 항등성 ====

비결정적 유한 오토마타와 결정적 유한 오토마타는 서로 변환 가능한데, 그 이유는 서로 항등(equivalence) 관계에 있기 때문이다.

''M''₁=<''Q'', ''Σ'', ''q''_1,0, ''δ''₁, ''A''₁>가 언어 L을 인식하는 비결정적 유한 오토마타라고 하고, 변환을 통해 얻어진 결정적 유한 오토마타를 ''M''₂=<''Q'', ''Σ'', ''q''_2,0, ''δ''₂, ''A''₂> 라고 하자. 모든 문자열 ''w''에 대하여, δ₁*(''q''_1,0, ''w'') = δ₂*(''q''_2,0, ''w'') 임을 귀납법에 의해 보이면 다음과 같다.

기초 단계 :

w = Λ일 때,

δ₂*(''q''_2,0, ''Λ'') = ''q''_2,0 (δ₂*의 정의에 의하여)

={q_1,0} (결정적 유한 오토마타 M₂의 정의에 의하여)

=δ₁*(''q''_1,0, ''q''_2,0 ) (δ₁*의 정의에 의하여)

귀납 단계 :

어떤 문자열 w에 대하여 δ₁*(''q''_1,0, ''w'') = δ₂*(''q''_2,0, ''w'') 라고 가정하자.

이때 문자열 w 와 Σ의 기호 a에 대해,

δ₁*(''q''_1,0, wa) = ∪_{p∈δ₁*(''q''_1,0, ''w'')}''δ''_1,0(p,a)

=''δ''₂ ( ''δ''₁*(''q''_1,0, ''w''),a)

=''δ''₂*( ''q''_2,0, wa)

그러므로, 어떤 문자열 w에 대해서도 δ₁*(''q''_1,0, ''w'') = δ₂*(''q''_2,0, ''w'')이다.

결정적 유한 오토마타(DFA)와 비결정적 유한 오토마타(NFA), 일반화된 비결정적 유한 오토마타(GNFA)는 결정적 오토마타에서는 각 상태에 대해 가능한 모든 입력에 대해 정확히 하나의 전이가 존재한다는 점에서 구별된다. 비결정적 오토마타에서는 주어진 상태에 대해 하나의 입력이 하나 이상 또는 전혀 전이를 일으키지 않을 수 있다. 멱집합 구성 알고리즘을 통해 임의의 비결정적 오토마타를 동일한 기능을 가진 (일반적으로 더 복잡한) 결정적 오토마타로 변환할 수 있다.

더 세분화된 분류 방법으로는 '''결정적 유한 오토마타'''(DFA)와 '''비결정적 유한 오토마타'''(NFA, GNFA)가 있다. 결정적 유한 오토마타에서는 각 상태의 모든 가능한 입력에 대해 다음 상태가 유일하게 결정된다. 비결정적 유한 오토마타에서는 어떤 상태에서 특정 입력이 있을 때 전이가 어떻게 될지 결정되지 않는다(전이가 없을 수도 있고, 여러 전이가 대응될 수도 있다). 각 오토마타가 표현할 수 있는 동작은 같으며, 임의의 NFA를 등가의(하지만 더 큰) DFA로 변환하는 알고리즘(Powerset construction)이 존재한다.

==== 유한 상태 변환기 ====

'''유한 상태 변환기'''(Finite-State Transducer)는 다음과 같은 6튜플(sextuple)

(\Sigma, \Gamma, S, s_0, \delta, \omega)

이다.

$\Sigma$ : 입력 알파벳(유한한 비어 있지 않은 기호 집합)
$\Gamma$ : 출력 알파벳(유한한 비어 있지 않은 기호 집합)
$S$ : 유한한 비어 있지 않은 상태 집합
$s_0$ : 초기 상태, $S$ 의 원소
$\delta$ : 상태 전이 함수: $\delta: S \times \Sigma \rightarrow S$
$\omega$ : 출력 함수

출력 함수가 상태와 입력 기호에 따라 달라지는 경우(

\omega: S \times \Sigma \rightarrow \Gamma

) 해당 정의는 ''밀리 모델''(Mealy model)에 해당하며 밀리 기계(Mealy machine)로 모델링할 수 있다. 출력 함수가 상태에만 따라 달라지는 경우(

\omega: S \rightarrow \Gamma

) 해당 정의는 ''무어 모델''(Moore model)에 해당하며 무어 기계(Moore machine)로 모델링할 수 있다. 출력 함수가 없는 유한 상태 기계는 반자동 기계(semiautomaton) 또는 전이 시스템(transition system)으로 알려져 있다.

무어 기계의 첫 번째 출력 기호

\omega(s_0)

를 무시하면, 모든 밀리 전이의 출력 함수(즉, 모든 간선에 레이블 지정)를 대상 무어 상태의 출력 기호로 설정하여 출력이 동등한 밀리 기계로 쉽게 변환할 수 있다. 역변환은 밀리 기계 상태가 들어오는 전이(간선)에 대해 서로 다른 출력 레이블을 가질 수 있기 때문에 덜 간단하다. 이러한 각 상태는 들어오는 각 출력 기호에 대해 여러 무어 기계 상태로 분할되어야 한다.^[16]

2. 1. 구성 요소

유한 오토마타는 다음 요소들로 구성된다.^[30]

상태: 전이를 시작하기 위해 대기하고 있는 시스템의 행동적 노드를 의미한다. 상태는 전이를 기다리는 시스템의 상태를 설명하는 것이다. 예를 들어, 자동차 오디오에서 라디오를 듣고 있을 때(''라디오 "상태"'') "다음" 버튼을 누르면(''다음 "유발점"'') 다른 방송국으로 넘어가지만, CD를 듣고 있을 때(''CD "상태"'') "다음" 버튼을 누르면 다음 곡을 재생한다. 이처럼 같은 유발점이 현재 상태에 따라 다른 동작을 보일 수 있다.^[30]
전이: 어떤 조건이 만족되거나 이벤트가 발생하였을 때 수행되는 일련의 동작을 의미한다.
동작: 일부 유한 상태 기계 표현에서는 상태에 동작을 연결하는 것도 가능하다.^[30]
진입 동작: 상태에 ''진입'' 할 때 수행되는 동작
퇴장 동작: 상태로부터 ''퇴장'' 할 때 수행되는 동작
초기 상태: 일반적으로 어떤 곳에서도 화살표로 가리키지 않는 상태이다.^[30]
수용 상태: 기계가 절차를 성공적으로 완료한 상태이다. 일반적으로 이중 원으로 표현된다.^[30]

2. 2. 결정적 유한 오토마타 (DFA)

결정적 유한 오토마타(DFA)는 모든 상태에서 각 입력에 대해 다음 상태가 유일하게 결정되는 오토마타이다.^[6]^[10] DFA는 수학적으로 5-튜플

(Q, \Sigma, s_0, \delta, F)

로 표현되며, 다음과 같이 정의된다.^[6]

$Q$ : 상태의 공집합이 아닌 유한 집합
$\Sigma$ : 입력 알파벳(유한하며, 비어있지 않은 기호의 집합)
$\delta$ : 상태 전이 함수: $\delta: Q \times \Sigma \rightarrow Q$ (비결정적 유한 오토마타에서는 $\delta: S \times \Sigma \rightarrow \mathcal{P}(S)$ 가 된다. 즉, $\delta$ 는 상태 집합을 반환한다.)
$s_0$ : 초기 상태이며, $Q$ 의 원소
$F$ : 최종 상태의 집합이며, $Q$ 의 (비어 있을 수 있는) 부분 집합

DFA에서 모든 상태는 각각의 가능한 입력에 대해 정확히 하나의 변환된 상태를 가진다.^[6] 비 결정적 유한 오토마타(NFA)와 달리, DFA는 주어진 상태에서 특정 입력에 대해 유일한 다음 상태로 전이한다.^[6]^[10]

유한 상태 기계는 튜링 기계와 동일한 계산 능력을 가지지만, 헤드가 "읽기" 작업만 수행하고 항상 왼쪽에서 오른쪽으로 이동해야 한다는 제한이 있다.^[15]^[35]

일반적으로

\delta

가 부분 함수가 되도록 허용되는데, 이는 모든 상태와 입력 기호의 조합에 대해

\delta(s, x)

가 정의될 필요는 없음을 의미한다. 정의되지 않은 경우, FSM은 오류를 알리고 입력을 거부한다.^[15]^[35]

2. 3. 비결정적 유한 오토마타 (NFA)

비결정적 유한 오토마타(NFA)는 한 상태에서 동일한 입력에 대해 여러 개의 다음 상태로 전이가 가능하거나, 입력 없이 전이(ε-전이)가 가능한 오토마타이다. 수학적으로 5-튜플 (Q, Σ, s₀, δ, F)로 표현된다.

''Q''는 상태의 공집합이 아닌 유한 집합이다.
''Σ''는 입력 문자이다. (유한하며, 비어있지 않은 기호의 집합이다).
''S''는 유한하며, 비어있지 않은 상태의 집합이다.
''δ''는 상태 전이 함수이다: $\delta: Q \times \left(\Sigma \cup \left\{\epsilon \right\} \right) \rightarrow \mathcal{P}(Q)$
''s₀''는 초기 상태이며, ''Q''의 원소이다.
''F''는 최종 상태의 집합이며, ''Q''의 원소이다.

비결정적 유한 오토마타는 결정적 유한 오토마타와는 다르게 입력 기호에 대해서

\epsilon

-transition 에 의해 0개 이상의 이동이 가능하다. 만약 가능한 다음 상태의 경우가 없다면, 기계는 입력을 거부한다.

결정적 유한 오토마타에서 모든 상태는 각각의 가능한 입력에 대해 정확히 하나의 변환된 상태를 가질 수 있다. 비 결정적 유한 오토마타에서 입력은 주어진 상태에 대해 한 가지 또는 여러 가지의 변환된 상태를 가지게 할 수 있다. 여러 알고리즘(멱집합 구성 등)을 사용하여 어떠한 NFA라도 동일한 기능을 가지는 DFA로 변환할 수 있다.

결정적 유한 오토마타(DFA)와 비결정적 유한 오토마타(NFA), 일반화된 비결정적 유한 오토마타(GNFA)는 결정적 오토마타에서는 각 상태에 대해 가능한 모든 입력에 대해 정확히 하나의 전이가 존재한다는 점에서 구별된다. 비결정적 오토마타에서는 주어진 상태에 대해 하나의 입력이 하나 이상 또는 전혀 전이를 일으키지 않을 수 있다. 멱집합 구성 알고리즘을 통해 임의의 비결정적 오토마타를 동일한 기능을 가진 (일반적으로 더 복잡한) 결정적 오토마타로 변환할 수 있다.

2. 3. 1. 비결정적 유한 오토마타의 결정적 유한 오토마타로의 변환

멱집합 구성(부분집합 구성) 방식은 유한 오토마타 변환의 표준적인 방법이다. 이 방식을 통해 정규 언어를 인식하는 비결정적 유한 오토마타(NFA)는 결정적 유한 오토마타(DFA)로 변환된다. NFA가 더 유연함에도 불구하고, DFA가 인식하지 못하는 어떠한 언어도 인지할 수 없다는 점이 이 이론의 핵심이다. NFA를 DFA로 변환하는 주된 이유는, 더 쉽게 구성되는 NFA를 컴퓨터에서 효율적으로 실행할 수 있는 DFA로 바꾸기 위함이다. 하지만 NFA가 ''n''개의 상태를 가지고 있다면, 변환된 DFA는 최대 2^''n'' 개의 상태를 가질 수 있어, 복잡도가 지수적으로 증가한다. 따라서 큰 NFA에 대해 이 변환은 비실용적일 수 있다.^[10]

멱집합 구성 알고리즘은 임의의 비결정적 오토마타를 동일한 기능을 가진 (일반적으로 더 복잡한) 결정적 오토마타로 변환할 수 있다.

2. 3. 2. 비결정적 유한 오토마타와 결정적 유한 오토마타의 항등성

비결정적 유한 오토마타와 결정적 유한 오토마타는 서로 변환 가능한데, 그 이유는 서로 항등(equivalence) 관계에 있기 때문이다.

''M''₁=<''Q'', ''Σ'', ''q''_1,0, ''δ''₁, ''A''₁>가 언어 L을 인식하는 비결정적 유한 오토마타라고 하고, 변환을 통해 얻어진 결정적 유한 오토마타를 ''M''₂=<''Q'', ''Σ'', ''q''_2,0, ''δ''₂, ''A''₂> 라고 하자. 모든 문자열 ''w''에 대하여, δ₁*(''q''_1,0, ''w'') = δ₂*(''q''_2,0, ''w'') 임을 귀납법에 의해 보이면 다음과 같다.

기초 단계 :

w = Λ일 때,

δ₂*(''q''_2,0, ''Λ'') = ''q''_2,0 (δ₂*의 정의에 의하여)

={q_1,0} (결정적 유한 오토마타 M₂의 정의에 의하여)

=δ₁*(''q''_1,0, ''q''_2,0 ) (δ₁*의 정의에 의하여)

귀납 단계 :

어떤 문자열 w에 대하여 δ₁*(''q''_1,0, ''w'') = δ₂*(''q''_2,0, ''w'') 라고 가정하자.

이때 문자열 w 와 Σ의 기호 a에 대해,

δ₁*(''q''_1,0, wa) = ∪_{p∈δ₁*(''q''_1,0, ''w'')}''δ''_1,0(p,a)

=''δ''₂ ( ''δ''₁*(''q''_1,0, ''w''),a)

=''δ''₂*( ''q''_2,0, wa)

그러므로, 어떤 문자열 w에 대해서도 δ₁*(''q''_1,0, ''w'') = δ₂*(''q''_2,0, ''w'')이다.

결정적 유한 오토마타(DFA)와 비결정적 유한 오토마타(NFA), 일반화된 비결정적 유한 오토마타(GNFA)는 결정적 오토마타에서는 각 상태에 대해 가능한 모든 입력에 대해 정확히 하나의 전이가 존재한다는 점에서 구별된다. 비결정적 오토마타에서는 주어진 상태에 대해 하나의 입력이 하나 이상 또는 전혀 전이를 일으키지 않을 수 있다. 멱집합 구성 알고리즘을 통해 임의의 비결정적 오토마타를 동일한 기능을 가진 (일반적으로 더 복잡한) 결정적 오토마타로 변환할 수 있다.

더 세분화된 분류 방법으로는 '''결정적 유한 오토마타'''(DFA)와 '''비결정적 유한 오토마타'''(NFA, GNFA)가 있다. 결정적 유한 오토마타에서는 각 상태의 모든 가능한 입력에 대해 다음 상태가 유일하게 결정된다. 비결정적 유한 오토마타에서는 어떤 상태에서 특정 입력이 있을 때 전이가 어떻게 될지 결정되지 않는다(전이가 없을 수도 있고, 여러 전이가 대응될 수도 있다). 각 오토마타가 표현할 수 있는 동작은 같으며, 임의의 NFA를 등가의(하지만 더 큰) DFA로 변환하는 알고리즘(Powerset construction)이 존재한다.

3. 표현 방법

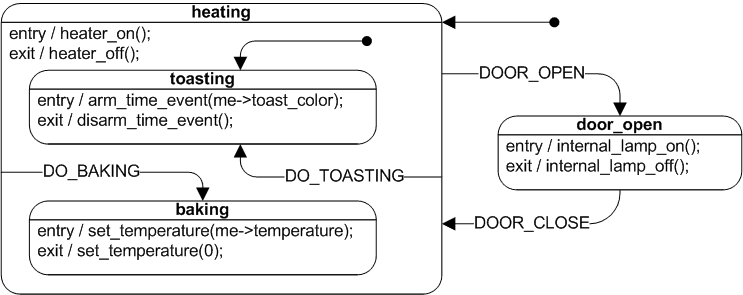
유한 상태 기계(FSM)를 나타내는 방법에는 매우 다양한 변형이 존재한다.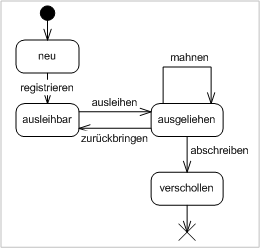

유한 오토마톤은 여러 가지 표현 방법이 있으며, 예를 들어 그림 3도 그중 하나이다.

유한 오토마톤을 표현하는 다른 의미론도 존재한다. 예를 들어, 임베디드 컨트롤러용 논리 회로를 모델링 및 설계하는 도구가 있다.^[31] 계층적인 상태 기계, 플로우 그래프, 진리표를 하나의 언어에 통합하여 서로 다른 형식적 방법과 의미론의 집합을 생성한다.^[32] Harel의 독자적인 상태 머신 다이어그램^[33] 등은 계층적인 중첩 상태, 직교 영역, 상태 동작, 전이 동작 등을 지원한다.^[34]

==== 상태/이벤트 표 (상태 전이표) ====

상태/이벤트 표는 현재 상태와 입력에 따른 다음 상태를 표 형태로 나타낸 것으로, 전이 규칙을 명확하게 보여주는 장점이 있다. 몇 가지 종류의 상태 전이 표가 사용된다. 가장 흔히 쓰이는 표현 방법은 다음과 같다. 현재 상태(예: B)와 입력값(예: Y)의 조합은 다음 상태(예: C)를 나타낸다.

상태 전이 표
현재 상태 → 입력 값 ↓	상태 A	상태 B	상태 C
입력값 X	...	...	...
입력값 Y	...	상태 C	...
입력값 Z	...	...	...

전체 동작 정보는 표에서 직접 표현되지 않고, 각주를 이용하여서 추가하는 것만 가능하다. 전체 동작 정보를 포함하는 유한 상태 기계는 가상 유한 상태 기계(Virtual finite-state machine)의 상태 표를 이용하여 정의 가능하다. 유한 오토마타(有限オートマトン)의 동작을 그래프 이론·그래프 (데이터 구조)의 그림으로 나타낸 것이 상태 천이도이다.

==== UML 상태 기계 ====

통합 모델링 언어(UML)는 상태 기계를 나타내는 표기법을 제공한다. UML 상태 기계는 고전적인 유한 상태 기계의 장점을 유지하면서, 계층적으로 중첩된 상태와 직교 영역 등의 개념을 도입하여 한계를 극복한다. UML 상태 기계는 밀리 모델과 무어 모델의 특징을 모두 가진다. 상태와 트리거링 이벤트에 의존하는 액션(동작)을 지원하여 밀리 모델과 유사하고, 상태에 진입하거나 탈출할 때 실행되는 액션(동작)을 지원하여 무어 모델과 유사하다.

상태 머신을 나타내는 다른 의미 체계 집합도 존재한다. 임베디드 컨트롤러의 논리를 모델링하고 설계하기 위한 도구들은 계층적 상태 머신, 흐름 그래프, 진리표를 결합한 언어를 사용한다.^[11]^[12] 이러한 차트는 데이비드 하렐의 원래 상태 머신과 유사하게 계층적으로 중첩된 상태, 직교 영역, 상태 동작 및 전이 동작을 지원한다.^[13]^[14]

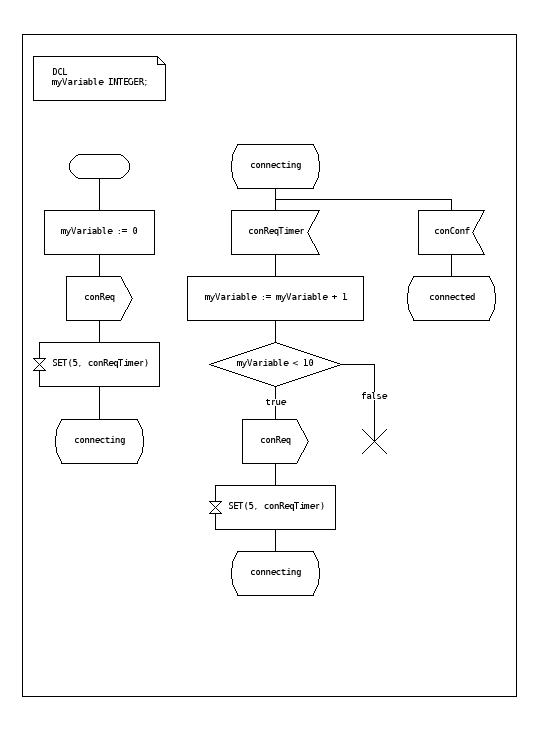
==== SDL 상태 기계 ====

기술 표준언어(SDL)는 ITU의 표준 규격이며, 전이 과정에서의 동작을 설명하는 그래픽 기호를 포함한다.

이벤트 송신
이벤트 수신
타이머 시작
타이머 취소
다른 병렬 동작하는 상태 머신 시작
판단

SDL에는 추상 데이터 유형(Abstract Data Types)이라고 불리는 기본 데이터 유형, 동작 언어, 유한 상태 머신을 실행 가능하게 하는 실행 의미론을 포함한다.

3. 1. 상태/이벤트 표 (상태 전이표)

상태/이벤트 표는 현재 상태와 입력에 따른 다음 상태를 표 형태로 나타낸 것으로, 전이 규칙을 명확하게 보여주는 장점이 있다. 몇 가지 종류의 상태 전이 표가 사용된다. 가장 흔히 쓰이는 표현 방법은 다음과 같다. 현재 상태(예: B)와 입력값(예: Y)의 조합은 다음 상태(예: C)를 나타낸다.

상태 전이 표
현재 상태 → 입력 값 ↓	상태 A	상태 B	상태 C
입력값 X	...	...	...
입력값 Y	...	상태 C	...
입력값 Z	...	...	...

전체 동작 정보는 표에서 직접 표현되지 않고, 각주를 이용하여서 추가하는 것만 가능하다. 전체 동작 정보를 포함하는 유한 상태 기계는 가상 유한 상태 기계(Virtual finite-state machine)의 상태 표를 이용하여 정의 가능하다. 유한 오토마타(有限オートマトン)의 동작을 그래프 이론·그래프 (데이터 구조)의 그림으로 나타낸 것이 상태 천이도이다.

3. 2. UML 상태 기계

통합 모델링 언어(UML)는 상태 기계를 나타내는 표기법을 제공한다. UML 상태 기계는 고전적인 유한 상태 기계의 장점을 유지하면서, 계층적으로 중첩된 상태와 직교 영역 등의 개념을 도입하여 한계를 극복한다. UML 상태 기계는 밀리 모델과 무어 모델의 특징을 모두 가진다. 상태와 트리거링 이벤트에 의존하는 액션(동작)을 지원하여 밀리 모델과 유사하고, 상태에 진입하거나 탈출할 때 실행되는 액션(동작)을 지원하여 무어 모델과 유사하다.

상태 머신을 나타내는 다른 의미 체계 집합도 존재한다. 임베디드 컨트롤러의 논리를 모델링하고 설계하기 위한 도구들은 계층적 상태 머신, 흐름 그래프, 진리표를 결합한 언어를 사용한다.^[11]^[12] 이러한 차트는 데이비드 하렐의 원래 상태 머신과 유사하게 계층적으로 중첩된 상태, 직교 영역, 상태 동작 및 전이 동작을 지원한다.^[13]^[14]

3. 3. SDL 상태 기계

기술 표준언어(SDL)는 ITU의 표준 규격이며, 전이 과정에서의 동작을 설명하는 그래픽 기호를 포함한다.

이벤트 송신
이벤트 수신
타이머 시작
타이머 취소
다른 병렬 동작하는 상태 머신 시작
판단

SDL에는 추상 데이터 유형(Abstract Data Types)이라고 불리는 기본 데이터 유형, 동작 언어, 유한 상태 머신을 실행 가능하게 하는 실행 의미론을 포함한다.

4. 예시

상태 머신으로 모델링할 수 있는 간단한 메커니즘의 예로는 회전문이 있다.^[4]^[5] 지하철이나 놀이공원 놀이기구의 출입을 통제하는 데 사용되는 회전문은 허리 높이에 회전하는 세 개의 팔이 있는 문으로, 하나는 입구를 가로막고 있다. 처음에는 팔이 잠겨 입구가 막히고 이용객이 통과하는 것을 막는다. 회전문의 슬롯에 동전이나 토큰을 넣으면 팔의 잠금이 해제되어 단일 고객이 통과할 수 있다. 고객이 통과한 후에는 동전을 다시 넣을 때까지 팔이 다시 잠긴다.

상태 머신으로 간주하면 회전문에는 "잠김"과 "잠금 해제"의 두 가지 상태가 있다.^[4] 상태에 영향을 미치는 두 가지 입력이 있다. 슬롯에 동전을 넣는 것("동전")과 팔을 미는 것("밀기")이다. 잠긴 상태에서는 팔을 밀어도 효과가 없다. "밀기" 입력을 몇 번이나 주어도 잠긴 상태로 유지된다. 동전을 넣는 것, 즉 머신에 "동전" 입력을 주면 상태가 "잠김"에서 "잠금 해제"로 바뀐다. 잠금 해제 상태에서는 추가 동전을 넣어도 효과가 없다. 즉, 추가 "동전" 입력을 제공해도 상태가 바뀌지 않는다. 고객이 팔을 밀면 "밀기" 입력이 주어지고 상태가 "잠김"으로 재설정된다.

회전문 상태 머신은 상태 전이표로 나타낼 수 있으며, 각 가능한 상태에 대해 (머신에 주어진 입력을 기반으로) 상태 간의 전이와 각 입력의 결과로 생성되는 출력을 보여준다.

::

현재 상태	입력	다음 상태	출력
잠김	동전	잠금 해제	회전문의 잠금을 해제하여 고객이 통과할 수 있도록 합니다.
잠김	밀기	잠김	없음
잠금 해제	동전	잠금 해제	없음
잠금 해제	밀기	잠김	고객이 통과하면 회전문의 잠금이 걸립니다.

회전문 상태 머신은 방향 그래프인 상태 다이어그램으로도 나타낼 수 있다. (위 그림 참조) 각 상태는 노드("원")로 표시된다. 에지("화살표")는 한 상태에서 다른 상태로의 전이를 보여준다. 각 화살표에는 해당 전이를 트리거하는 입력이 표시되어 있다. 상태 변경을 일으키지 않는 입력(예: "잠금 해제" 상태의 "동전" 입력)은 원래 상태로 돌아가는 원형 화살표로 표시된다. 검은 점에서 "잠김" 노드로 들어가는 화살표는 초기 상태임을 나타낸다.

4. 1. 수리 기계와 인식기

수리 기계(acceptors)와 인식기(recognizers)는 입력값이 기계에서 받아들여졌는지 이진값인 '예 또는 아니오'로 결과를 출력한다.^[9] 유한 오토마타의 모든 상태는 받아들여지는지 또는 받아들여지지 않는지에 대한 값을 가지고 있다. 모든 입력이 처리되었을때, 만약 현재 상태가 받아들여질 수 있는 상태라면 그 입력값은 기계에 의해 받아들여진 것이다. 반대로 현재 상태가 받아들여질 수 없는 상태라면 그 입력값은 거부된 것이다.

그림 5 수용 상태의 예. 이 유한 오토마톤은 입력 수열 내의 "0"의 개수가 짝수인지 여부를 판단한다. ''S''₁은 0이 짝수일 때의 수용 상태이다.

유한 오토마타는 언어를 정의하는 데에도 사용될 수 있다. 받아들여지는 모든 단어를 포함하고 그 문법으로 기계를 구성할 수도 있다. 이렇게 유한 오토마타로 구성이 가능한 언어를 "유한 오토마타가 받아들일 수 있는 언어"라고 한다. 정의에 의해 유한 오토마타가 받아들일 수 있는 모든 언어는 정규 표현식이다. 또한 역도 성립한다. 즉, 모든 정규 표현식은 유한 오토마타가 받아들일 수 있다.^[6]

수용기의 예로, 결정적 유한 오토마타(DFA)는 이진수 입력 문자열에 0이 짝수 개 있는지 감지한다. ''S''₁(시작 상태이기도 함)은 0이 짝수 개 입력된 상태를 나타내며 수용 상태이다. 이 수용기는 이진 문자열에 0이 짝수 개 있는 경우(0이 없는 이진 문자열 포함) 수용 상태에서 종료된다. 이 수용기가 수용하는 문자열의 예는 ε( 빈 문자열) 1, 11, 11..., 00, 010, 1010, 10110 등이다.

4. 2. 변환기

유한 상태 변환기는 상태와 주어진 입력값에 기반하여 출력값을 생성한다.^[41] 전산언어학 분야에서 응용 프로그램을 제어하는 데 사용된다.^[41] 유한 상태 변환기는 다음과 같이 두 종류가 있다.

무어 모델(Moore model)

:이 종류의 유한 상태 오토마타는 오직 진입 동작만을 사용한다. 즉 출력값은 오직 현재 상태에 따라서만 결정된다. 무어 기계의 장점은 행위를 단순화시킬 수 있다는 것이다. 엘리베이터 문을 예시로 들자면 유한 상태 기계는 “문을 열어라”와 “문을 닫으라” 라는 상태를 변경해 주는 두 명령어를 인식할 수 있다. “열리는 중”의 상태에 있는 진입 동작은 모터를 돌려 문을 열기 시작하는 것이고 “닫히는 중”의 상태에 있는 진입 동작은 모터를 반대로 돌려 문을 닫는 것이다. “열림”과 “닫힘”의 상태는 완전히 열리거나 닫힌 상태에서 모터를 정지시킨다.

:무어 모델은 수학적으로 (''S'', ''S''₀, Σ, Λ, ''T'', ''G'')으로 구성된 6-튜플로 정의된다.

:* ''S''는 상태의 유한 집합이다.

:* ''S''₀는 초기 상태이며 ''S''의 원소이다.

:* Σ는 입력 값의 유한 집합이다.

:* Λ는 출력 값의 유한 집합이다.

:* ''T''는 현재 상태와 입력 값을 기반으로 다음 상태값을 반환하는 상태 전이 함수이다: ''S'' × Σ → ''S''

:* ''G''는 현재 상태를 기반으로 출력 값을 반환하는 상태 전이 함수이다: ''S'' → Λ

밀리 모델(Mealy model)

:이 종류의 유한 상태 오토마타는 오직 입력값만을 사용한다. 즉 출력 값은 입력 값과 현재 상태 모두에 의존한다. 밀리 기계는 일반적으로 상태의 수를 줄이는데 사용한다. 앞의 무어 기계와 같은 엘리베이터 문을 예시로 들자면 무어 모델과 달리 중간의 “열리는 중”과 “닫히는 중”의 상태가 없다. 또한 진입 동작이 아니라, 다음과 같이 현재 상태와 입력 값에 모두 영향을 받는 두 종류의 입력 행위가 있다. “만약 문을 열어라 라는 입력 값이 들어온다면 문을 열기 위해 모터를 작동시킨다”와 “만약 문을 닫아라 라는 입력 값이 들어온다면 문을 닫기 위해 모터를 반대 방향으로 작동시킨다”라는 두 입력 행위가 존재한다.

:밀리 모델은 수학적으로 (''S'', ''S''₀, Σ, Λ, ''T'', ''G'')으로 구성된 6-튜플로 정의된다.

:* ''S''는 상태의 유한 집합이다.

:* ''S''₀는 초기 상태이며 ''S''의 원소이다.

:* Σ는 입력값의 유한 집합이다.

:* Λ는 출력값의 유한 집합이다.

:* ''T''는 현재 상태와 입력값을 기반으로 다음 상태값을 반환하는 상태 전이 함수이다: ''S'' × Σ → ''S''

:* ''G''는 현재 상태와 입력값을 기반으로 출력값을 반환하는 상태 전이 함수이다: ''S'' × Σ → Λ

4. 2. 1. 무어 모델 (Moore Model)

무어 기계는 출력값이 현재 상태에만 의존하는 유한 상태 오토마타이다.^[55] 무어 모델은 동작의 단순화라는 장점을 가진다.

무어 모델은 유한 상태 변환기의 한 종류로, 다음과 같은 6-튜플로 정의된다.^[16]^[36]

:

(\Sigma, \Gamma, S, s_0, \delta, \omega)

여기서,

$\Sigma$ : 입력 알파벳(유한한 비어 있지 않은 기호 집합)
$\Gamma$ : 출력 알파벳(유한한 비어 있지 않은 기호 집합)
$S$ : 유한한 비어 있지 않은 상태 집합
$s_0$ : 초기 상태, $S$ 의 원소
$\delta$ : 상태 전이 함수: $\delta: S \times \Sigma \rightarrow S$
$\omega$ : 출력 함수: $\omega: S \rightarrow \Gamma$ (출력 함수가 상태에만 의존)

Edward F. Moore는 1956년 논문 ''Gedanken-experiments on Sequential Machines''에서 순차 기계를 유한 개의 상태, 입력 및 출력 기호를 가지는 유한 상태 기계로 정의하며, 출력값이 현재 상태에만 의존한다고 설명했다.^[55]

예를 들어, 엘리베이터 문을 제어하는 유한 상태 기계를 무어 모델로 구현할 수 있다. "Opening" 상태에서는 문을 여는 모터를 작동시키고, "Closing" 상태에서는 문을 닫는 모터를 작동시킨다. "Opened"와 "Closed" 상태에서는 모터를 정지시키고, 외부에는 "문이 열림", "문이 닫힘"과 같은 신호를 보낸다.^[57]

무어 기계는 밀리 기계와 달리 현재 상태만으로 출력값이 결정된다. 자동차가 빨간 신호등을 인식했을 때 바로 멈추는 것이 무어 기계의 예시이다.^[58]

무어 기계를 밀리 기계로 변환하는 것은 간단하지만, 그 반대는 복잡하다. 밀리 기계의 각 상태는 들어오는 전이에 대해 서로 다른 출력 레이블을 가질 수 있기 때문에, 각 상태는 들어오는 각 출력 기호에 대해 여러 무어 기계 상태로 분할되어야 한다.^[16]^[36]

4. 2. 2. 밀리 모델 (Mealy Model)

밀리 모델(Mealy model)은 출력 함수가 상태와 입력 기호에 따라 달라지는 경우(

\omega: S \times \Sigma \rightarrow \Gamma

)에 해당하며 밀리 기계(Mealy machine)로 모델링할 수 있다.^[16]^[36] 출력은 현재 상태와 현재 입력값에 의해 결정된다.^[58]

밀리 기계는 조지 H. 밀리(George H. Mealy)가 1955년 논문 ''A Method for Synthesizing Sequential Circuits''("순차 회로 합성 방법")에서 처음 제시했다.^[54] 순차 회로(sequential circuit)는 순차 논리(sequential logic) 회로, 즉 현재 입력값 뿐 아니라 과거 입력값에도 의존하는 논리 회로를 의미한다.

밀리 유한 상태 기계(FSM)의 사용은 종종 상태 수 감소로 이어진다. 그림 7은 무어 모델 예시와 동일한 동작을 구현하는 밀리 FSM을 보여준다. 두 가지 입력 동작(I:)이 있다. "command_close가 도착하면 문을 닫는 모터를 시작"과 "command_open이 도착하면 문을 여는 반대 방향으로 모터를 시작"이다.

유한 상태 변환기는 6-튜플(

\Sigma, \Gamma, S, s_0, \delta, \omega

)로 정의된다:

$\Sigma$ : 입력 알파벳(유한한 비어 있지 않은 기호 집합)
$\Gamma$ : 출력 알파벳(유한한 비어 있지 않은 기호 집합)
$S$ : 유한한 비어 있지 않은 상태 집합
$s_0$ : 초기 상태, $S$ 의 원소
$\delta$ : 상태 전이 함수: $\delta: S \times \Sigma \rightarrow S$
$\omega$ : 출력 함수

무어 기계는 모든 밀리 전이의 출력 함수를 대상 무어 상태의 출력 기호로 설정하여, 출력이 동등한 밀리 기계로 쉽게 변환할 수 있다. 그러나 역변환은 밀리 기계 상태가 들어오는 전이에 대해 서로 다른 출력 레이블을 가질 수 있기 때문에 덜 간단하다. 이러한 각 상태는 들어오는 각 출력 기호에 대해 여러 무어 기계 상태로 분할되어야 한다.^[16]

5. 역사

5. 1. 고대와 중세 (~16세기)

유한 오토마타의 기원은 오토마타(Automata), 즉 자동기계 개념에서 찾을 수 있다.^[43] 인류는 고대부터 자동기계에 관심을 가지고 개발해왔다. 헬레니즘 시대와 고대 그리스 시대에 이미 오토마타는 장난감, 종교적 신상, 과학 원리 증명 도구 등으로 만들어졌다. 고대 그리스 수학자 알렉산드리아의 헤론은 수력 오르간, 소화기, 사이펀 등 최초의 오토마타를 기록했고, 아르키메데스는 자동 천체 모형을 만들었다고 전해진다. 기원전 250년경 고대 그리스 과학자 크테시비우스는 자동인형이 부착된 최초의 자동물시계 '클렙시드라'를 만들었다.^[44]

고대 중국에서도 자동기계에 대한 기록이 있다. 주나라 무왕(1023-957 BC) 시절 얀시(Yan Shi)라는 기술자가 사람 크기의 기계를 만들었고, 사마천의 《사기》에는 자동 발사되는 기계장치 쇠뇌에 대한 기록이 있다.^[45]

중세 시대에는 이슬람에서 과학이 발전하며 많은 오토마타가 개발되었다. 8세기 중엽 바그다드에는 풍력으로 작동하는 동상이 만들어졌다. 12세기 이슬람 과학자 알 자자리는 자동인형, 자동문, 자동 악대 등을 개발했다.

레오나르도 다 빈치(Leonardo da Vinci, 1452-1519)는 가슴이 열리면 꽃이 나오는 사자 자동인형과 로봇 전투병 스케치를 남겼다.^[46] 조선의 장영실(1390?~1450?)은 자격루, 옥루, 일성정시의 등 자동시계를 제작했다. 중국에서는 11세기 북송시대 천문학자 소송이 자동물시계 시계탑인 '수운의상대(水運儀象臺)'를 만들었다.^[47]

5. 2. 근대 (16세기~19세기)

17세기 유럽에 유행한 르네 데카르트(1596~1650)의 기계론은 오토마타를 새로운 관점으로 보게 했으며, 오토마타에 대한 이론적, 철학적 토대를 마련하였다.^[48] 데카르트는 살아 있는 생명체가 사실상 복잡한 기계와 다를바 없다고 주장하였다.^[48] 그에 따라 자연과 사물을 비교하는 방식의 중심엔 외형 대신 작동 방식이 들어서게 되었고, 그에 따라 자동기계는 더 활발히, 대중적으로 연구되고 개발되었다.^[48] 오토마타는 18세기 유럽에서 번창했는데, 대표적인 사람으론 기계오리를 만든 프랑스 발명가 자크 드 보캉송, 자동체스인형을 고안한 헝가리 발명가 볼프강 폰 켐펠렌, 그리고 여러 자동인형을 만든 자크-드로즈 등이 있다.^[48]

한편 동양에서는 17세기 에도 시대에 일본으로 오토마타가 유럽으로부터 전해지기 시작했다.^[48] 일본에서는 오토마타를 '카라구리'라고 부르며, 중국 등에서 온 물시계 제작 기술들의 영향을 받아 태엽과 톱티바퀴로 움직이는 자동인형들이 만들어졌다.^[48]

5. 3. 현대 (20세기~)

현대에 들어서 오늘날까지도 여전히 오토마타 또는 자동기계는 하나의 예술 분야로서 폴 스푸너ㆍ피터 마키ㆍ아키오 니시다ㆍ키스 뉴스테와 같은 작가들에 의해 유지, 발전되고 있다.^[49]

그러나 유한 오토마타와 관련해서 현대에서 주목할 점은, 현대에 들어선 자동기계, 그리고 자동기계를 통해 생물을 모방, 창조하려는 시도가 컴퓨터 과학이라는 분야에서도 꽃피기 시작했고, 후에 컴퓨터 과학에서의 굳건한 분야로 자리잡았다는 점이다. 처음으로 유한 오토마타, 또는 유한 상태기계를 생각하게 된 사람들엔 생물학자들, 심리학자들, 수학자들, 공학자들, 그리고 최초의 컴퓨터 과학자들이 들어 있었다. 그들은, 이전의 자동기계들을 통해 본질적으로 구현해 내지 못한 인간의 특징인 '인간의 사고 과정(human thought process)'을 이론적 또는 실체적으로 구현해 내고자 수많은 시도를 하였다.^[50]

앨런 튜링(Alan Turing, 1912~1954)은 1936년 ''On Computable Numbers, with an Application to the Entscheidungsproblem''("결정 문제에 대한 응용을 포함한 계산 가능한 수에 관하여")이라는 논문에서 튜링 기계(Turing Machine)의 개념을 소개했다.^[51]

튜링 기계는 유한 오토마타를 포함하는 더 강력한 계산 모델이다. 유한 오토마타는 사실상 '머리'가 오른쪽으로만 움직일 뿐만 아니라, 읽을 수만 있고 쓸 수 없는 튜링 기계의 특별한 집합이다.^[51] 튜링 기계가 컴퓨터 과학 분야에서 중요한 이유는, 튜링 기계가 역사상 가장 정교하고 강력한 오토마타이기 때문이다.^[51]

존 폰 노이만(John von Neumann, 1903년 12월 28일 ~ 1957년 2월 8일)은 헝가리 미국 독일 유태계의 수학자로서 양자물리학, 함수해석학, 집합이론, 컴퓨터 과학, 경제학과 많은 수학분야에 중요한 공헌을 하였다.

그는 생명체를 일종의 기계로 보았기 때문에 무기물인 기계도 자가 복제가 가능할 것이라고 생각했다. 노이만은 적어도 자신과 같은 정도의 복잡한 것을 만들어 내는 것이 가능하다는 것을 다음과 같은 방법으로 1948년에 논리적으로 증명하는 데 성공하였다.

임의의 어떤 기계라도 만들 수 있는 만능제조 기계(Universal Machine) 을 설계한다.
UM 에 어떤 기계 M 을 만드는 프로그램을 담은 테이프 T(M) 을 넣는다면 UM 은 테이프 내용대로 기계 M 을 만들어 낼 것이다.
만약 테이프 내용이 UM 을 만들라는 것일 경우 만능기계인 UM 은 테이프 내용 그대로 자신과 똑같은 또 하나의 UM 을 만들어 낼 것이다.

이 증명에서의 한가지 문제는 자가 복제 기계의 존재성은 만능 제조 기계의 존재성을 전제로 한다는 것이다. 노이만은 이 문제를 해결하기 위해 독일의 컴퓨터 과학자 콘라드 주세 (Konrad Zuse, 1910 ~ 95)의 아이디어를 빌렸다. 노이만은 물리적 계의 이산모델로서 오토마타가 병렬로 연결된 계산공간을 고안해 낸다. 노이만은 결국 약 20만 개에 달하는 29개의 상태를 갖는 오토마타를 2 차원의 평면에 배열하여 자가 복제 기계를 만드는데 성공했다.

사후에 그의 공동연구자 아터 버크스가 논문으로 제작하여 출판하였고 (''Theory of Self Reproducing Automata'')^[52] 미국 IBM의 코드(E. F. Codd)에 의해 단순화되었고 실제로 구현되었다.

크리스토퍼 랭턴(1948~)은 유한 오토마타와 연관이 깊은 개념인 인공 생명(Artificial Life, Alife, AL)의 개념의 창시자라고 할 수 있다.

랭턴은 1987년 로스앨러모스 국립 연구소에서,"생명계의 합성과 시뮬레이션에 대한 워크샵"(Workshop on the Synthesis and Simulation of Living Systems, Artificial Life I)을 최초로 열었으며 이때 인공 생명이라는 단어를 만들었다.

랭턴은 인공 생명분야에 시뮬레이션과 계산적 모델, 그리고 철학적 문제까지 많은 부분 공헌하였다. 그는 정보, 계산과 번식에 관한 문제를 본질적으로 연관짓고, 기본적인 법칙을 정의하였다. 물리학의 법칙중 특히 상전이에 영감을 받아 셀룰러 오토마타의 몇가지 기본 개념과, 정량적 분석을 발전시켰다. 또, 특히 생물학에서, 정렬이 비정렬로부터 분리해 내는 임계점이 복잡계를 형성하는 데에 중요한 역할을 함을 제시하였다. 이런 그의 아이디어는, 비록 다른 근사법을 썼지만, Per Bak이나 James Crutchfield등에 의해서도 동시에 논의되었다.

워런 맥컬록(Warren McCulloch)와 월터 피츠(Walter Pitts)는 1943년 ''A Logical Calculus Immanent in Nervous Activity''("신경 활동에 내제된 논리적 고등 계산법")라는 논문을 통해 신경 네트워크 이론, 오토마타 이론, 그리고 컴퓨터 조작 및 인공두뇌학 이론에 큰 기여를 했다.^[53] 미주리 대학에서 철학, 심리학, 신경 과학 등을 연구하는 철학자 Gualtiero Piccinini는 그들의 논문에 대하여, 신경 과학과 컴퓨터 조작에서의 중요성에도 불구하고, 거의 역사적, 철학적 주목을 받지 못 했다고 평가한다. 1943년 당시 이미 신경 네트워크에 대한 수학적 연구를 하는 생물물리학자들의 집단이 존재했었고, McCulloch와 Pitt의 논문에서 참신했던 점은 신경 활동, 즉 정신적 활동을 이해하기 위한 논리와 계산이었다. 그들의 공헌은 유한 오토마타(컴퓨터 연산 이론에서 중요한 형식주의)의 개념을 도출, 논리 설계(현대 컴퓨터 디자인의 기초적인 부분)의 개념에 영감을 줌, 정신-육체 문제를 다루기 위한 최초의 컴퓨터 연산의 사용,정신과 뇌에 관한 최초의 현대적 컴퓨터 연산 이론을 포함한다.

George H. Mealy는 1955년 그의 논문 ''A Method for Synthesizing Sequential Circuits''("순차 회로 합성 방법")에서 밀리 기계(Mealy machine)라는 개념을 처음으로 발표했다.^[54] Edward F. Moore는 1956년 그의 논문 ''Gedanken-experiments on Sequential Machines''에서 무어 기계(Moore machine)의 개념을 소개했다.^[55]

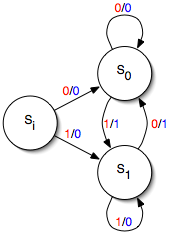
밀리 기계와 무어 기계는 둘 다 유한 오토마타에 속하는 기계인데, 차이점은 밀리 기계는 결과값이 현재 상태(current state)와 현재 입력값(current inputs)에 의해 결정되지만 무어 기계는 오로지 현재 상태에 의해서만 결정된다는 점이다.

예를 들어 자동차가 빨간 신호등을 인식했을 때 바로 멈추면 무어 기계인 것이고, 현재 진행 중이던 일을 마친 이후에 멈추면 밀리 기계인 것이다.^[58]

에이브럼 노엄 촘스키는 1956년에 촘스키 위계(Chomsky hierachy)이라는 것을 처음 서술하였다. 형식언어(Formal Language)를 생성하는 형식문법(Formal Grammar) 들을 분류해 놓은 계층구조이다.^[59]

Type-3 문법(정규 문법, RG, regular grammars)이 생성한 정규 언어(regular languages)는 유한 오토마타로 결정가능한 모든 언어들이다. 모든 유한 오토마타는 모든 정규 언어를 표현할 수 있으며 역으로 모든 정규 언어는 모든 유한 오토마타로 표현될 수 있다. 즉, 유한 오토마타의 집합과 정규 언어의 집합은 일치한다.^[59]

5. 3. 1. 앨런 튜링 (Alan Turing)

앨런 튜링(Alan Turing, 1912~1954)은 1936년 ''On Computable Numbers, with an Application to the Entscheidungsproblem''("결정 문제에 대한 응용을 포함한 계산 가능한 수에 관하여")이라는 논문에서 튜링 기계(Turing Machine)의 개념을 소개했다.^[51]

튜링 기계는 유한 오토마타를 포함하는 더 강력한 계산 모델이다. 유한 오토마타는 사실상 '머리'가 오른쪽으로만 움직일 뿐만 아니라, 읽을 수만 있고 쓸 수 없는 튜링 기계의 특별한 집합이다.^[51] 튜링 기계가 컴퓨터 과학 분야에서 중요한 이유는, 튜링 기계가 역사상 가장 정교하고 강력한 오토마타이기 때문이다.^[51]

5. 3. 2. 존 폰 노이만 (John Von Neumann)

2. UM 에 어떤 기계 M 을 만드는 프로그램을 담은 테이프 T(M) 을 넣는다면 UM 은 테이프 내용대로 기계 M 을 만들어 낼 것이다.

3. 만약 테이프 내용이 UM 을 만들라는 것일 경우 만능기계인 UM 은 테이프 내용 그대로 자신과 똑같은 또 하나의 UM 을 만들어 낼 것이다.}}

이 증명에서의 한가지 문제는 자가 복제 기계의 존재성은 만능 제조 기계의 존재성을 전제로 한다는 것이다. 노이만은 이 문제를 해결하기 위해 독일의 컴퓨터 과학자 콘라드 주세 (Konrad Zuse, 1910 ~ 95)의 아이디어를 빌렸다. 노이만은 물리적 계의 이산모델로서 오토마타가 병렬로 연결된 계산공간을 고안해 낸다. 노이만은 결국 약 20만 개에 달하는 29개의 상태를 갖는 오토마타를 2 차원의 평면에 배열하여 자가 복제 기계를 만드는데 성공했다.

사후에 그의 공동연구자 아터 버크스가 논문으로 제작하여 출판하였고 (''Theory of Self Reproducing Automata'')^[52] 미국 IBM의 코드(E. F. Codd)에 의해 단순화되었고 실제로 구현되었다.

5. 3. 3. 크리스토퍼 랭턴 (Christopher G. Langton)

크리스토퍼 랭턴(1948~)은 유한 오토마타와 연관이 깊은 개념인 인공 생명(Artificial Life, Alife, AL)의 개념의 창시자라고 할 수 있다.

랭턴은 1987년 로스앨러모스 국립 연구소에서,"생명계의 합성과 시뮬레이션에 대한 워크샵"(Workshop on the Synthesis and Simulation of Living Systems, Artificial Life I)을 최초로 열었으며 이때 인공 생명이라는 단어를 만들었다.

랭턴은 인공 생명분야에 시뮬레이션과 계산적 모델, 그리고 철학적 문제까지 많은 부분 공헌하였다. 그는 정보, 계산과 번식에 관한 문제를 본질적으로 연관짓고, 기본적인 법칙을 정의하였다. 물리학의 법칙중 특히 상전이에 영감을 받아 셀룰러 오토마타의 몇가지 기본 개념과, 정량적 분석을 발전시켰다. 또, 특히 생물학에서, 정렬이 비정렬로부터 분리해 내는 임계점이 복잡계를 형성하는 데에 중요한 역할을 함을 제시하였다. 이런 그의 아이디어는, 비록 다른 근사법을 썼지만, Per Bak이나 James Crutchfield등에 의해서도 동시에 논의되었다.

5. 3. 4. 워렌 맥컬럭(Warren McCulloch)과 월터 피츠(Walter Pitts)

워런 맥컬록(Warren McCulloch)와 월터 피츠(Walter Pitts)는 1943년 ''A Logical Calculus Immanent in Nervous Activity''("신경 활동에 내제된 논리적 고등 계산법")라는 논문을 통해 신경 네트워크 이론, 오토마타 이론, 그리고 컴퓨터 조작 및 인공두뇌학 이론에 큰 기여를 했다.^[53] 미주리 대학에서 철학, 심리학, 신경 과학 등을 연구하는 철학자 Gualtiero Piccinini는 그들의 논문에 대하여, 신경 과학과 컴퓨터 조작에서의 중요성에도 불구하고, 거의 역사적, 철학적 주목을 받지 못 했다고 평가한다. 1943년 당시 이미 신경 네트워크에 대한 수학적 연구를 하는 생물물리학자들의 집단이 존재했었고, McCulloch와 Pitt의 논문에서 참신했던 점은 신경 활동, 즉 정신적 활동을 이해하기 위한 논리와 계산이었다. 그들의 공헌은 유한 오토마타(컴퓨터 연산 이론에서 중요한 형식주의)의 개념을 도출, 논리 설계(현대 컴퓨터 디자인의 기초적인 부분)의 개념에 영감을 줌, 정신-육체 문제를 다루기 위한 최초의 컴퓨터 연산의 사용,정신과 뇌에 관한 최초의 현대적 컴퓨터 연산 이론을 포함한다.

5. 3. 5. G. H. Mealy와 E. F. Moore

George H. Mealy는 1955년 그의 논문 ''A Method for Synthesizing Sequential Circuits''("순차 회로 합성 방법")에서 밀리 기계(Mealy machine)라는 개념을 처음으로 발표했다.^[54] Edward F. Moore는 1956년 그의 논문 ''Gedanken-experiments on Sequential Machines''에서 무어 기계(Moore machine)의 개념을 소개했다.^[55]

밀리 기계와 무어 기계는 둘 다 유한 오토마타에 속하는 기계인데, 차이점은 밀리 기계는 결과값이 현재 상태(current state)와 현재 입력값(current inputs)에 의해 결정되지만 무어 기계는 오로지 현재 상태에 의해서만 결정된다는 점이다.

예를 들어 자동차가 빨간 신호등을 인식했을 때 바로 멈추면 무어 기계인 것이고, 현재 진행 중이던 일을 마친 이후에 멈추면 밀리 기계인 것이다.^[58]

5. 3. 6. 노엄 촘스키(Noam Chomsky)

에이브럼 노엄 촘스키는 1956년에 촘스키 위계(Chomsky hierachy)이라는 것을 처음 서술하였다. 형식언어(Formal Language)를 생성하는 형식문법(Formal Grammar) 들을 분류해 놓은 계층구조이다.^[59]

Type-3 문법(정규 문법, RG, regular grammars)이 생성한 정규 언어(regular languages)는 유한 오토마타로 결정가능한 모든 언어들이다. 모든 유한 오토마타는 모든 정규 언어를 표현할 수 있으며 역으로 모든 정규 언어는 모든 유한 오토마타로 표현될 수 있다. 즉, 유한 오토마타의 집합과 정규 언어의 집합은 일치한다.^[59]

6. 유한 오토마타와 인공 생명

기계론적 사고관과 이를 바탕으로 번성한 자동 기계들을 통해 사람들은 생명이란 무엇인가에 대해 의문을 가지게 되었다. 이러한 생각을 바탕으로, 유한 오토마타와 관련이 깊은 인공 생명(Artificial Life, Alife, AL)과 인공 지능(Artificial Intelligence, AI) 등의 개념들이 탄생하였다.

기계론적 사고관에선 자연에 존재하는 모든 물체들은 수학적, 역학적 법칙을 따라 외부의 원인에 의해서만 움직인다고 말한다. 이 자연관에 따르면 생명체와 비생명체, 유기체와 무기체의 구분은 무의미할 뿐이다. 자동 기계들은 생명체는 아니지만 생명체와 매우 비슷한 행동과 모습들을 보여주었다. 결국 이 둘은 사람들로 하여금 대중적으로 생명체라 여겨지지 않았던 것들도 생명체와 다를 바가 없다는 생각을 심어주었고, 이를 과학적으로 표현한 것이 바로 인공 생명과 인공 지능 등의 컴퓨터 과학 개념이라고 할 수 있다.

역사적, 기술적으로도 유한 오토마타와 인공 생명은 연관이 깊다. 미시간 대학의 전기 공학 및 컴퓨터 과학 교수 Arthur W. Burks의 말에 따르면, 인공 생명이란 "셀룰러 오토마타의 논리와 다른 전산화 가능한 진화학적 구조(computerizable evolutionary structures)로부터 발생한 창의적인 인간-기계 연구"라고 한다. 여기서 셀룰러 오토마타(Cellular Automata, CA)란 유한 오토마타의 한 종류로, 폰 노이만의 1948년 논문인 ''Theory of Self-reproducing Automata''("자가 복제 오토마타 이론")에서 스스로를 복제할 수 있는 로봇에 관하여 구상할 때 처음 나온 개념이다.(1948년에 내용을 완성했으나 출판된 것은 1966년이라고 한다.)

6. 1. 인공 생명 (Artificial Life)

인공생명은 크리스토퍼 랭턴(Christopher G. Langton, 1948~)이 1987년에 처음 제창한 개념으로, "생명이라 할 수 있는 생명(life as it could be)"을 추구한다.^[60] 1948년 폰 노이만의 셀룰러 오토마타^[60] 이론과 노버트 위너(Norbert Wiener)의 항상성(homeostasis) 연구^[60]는 인공생명 연구의 초기 발전에 기여했다.

인공 생명에는 크게 세 가지 종류가 있다.^[61]

Soft Artificial Life('부드러운' 인공 생명): 소프트웨어 프로그램 상으로 존재하는 인공 생명이다. 셀룰라 오토마타(Cellular Automata, CA)와 신경 네트워크(Neural Network)가 주로 사용된다.^[61] 랭턴의 개미(Langton's Ant)와 랭턴의 루프(Langton's Loop) 등이 대표적인 예시이다.

Hard Artificial Life('딱딱한' 인공 생명): 실제 세계에서 작동하는 로봇과 자동기계(automaton)를 의미한다.^[61]
Wet Artificial Life('젖은' 인공 생명): 유기물질 등으로 외형을 갖춘 인공 생명이다.^[61]

인공 생명과 연관된 분야로는 인공 지능(Artificial Intelligence, AI), 인공 화학(Artificial Chemistry), 진화 알고리즘(Evolutionary Algorithms), 진화 예술(Evolutionary Art), 진화 음악(Evolutionary Music), 자연발생론(Abiogenesis) 등이 있다.

6. 2. 인공 생명과 관련된 분야들

6. 2. 1. 인공 지능 (Artificial Intelligence)

'''인공지능'''(人工知能)은 철학적으로 인간이나 지성을 갖춘 존재, 혹은 시스템에 의해 만들어진 지능, 즉 인공적인 지능을 뜻한다. 일반적으로 범용 컴퓨터에 적용한다고 가정한다. 이 용어는 또한 그와 같은 지능을 만들 수 있는 방법론이나 실현 가능성 등을 연구하는 과학 분야를 지칭하기도 한다.

인공지능이란 분야를 처음 인식하기 시작한 것은 1943년 McCulloch 와 Pitts에 의해서 시작되었으며 그 동기는 뇌에 있어서 뉴런의 기능과 작용에 대한 연구와 명제 논리 그리고 튜링 테스트 연구였다. 뉴런으로 연결된 네트워크 학습의 개념이 필요함을 주장하였으면 인간의 사고 과정을 최초로 연결망을 통해 모델화했다는 점에서 인공지능 역사상 의의가 매우 크다고 볼 수 있다.

1956년 여름 다트마우스(Dartmouth) 대학의 캠퍼스에 '생각하는 기계', 즉 지적인 행동을 하는 컴퓨터에 관해 토론하기 위해서 많은 사람들이 모였으며(수학자,심리학자,전기기술자,대학의 연구자 기업가 등등) 이들은 디지털 계산기를 '생각하는 기계'로 만들 수 있다는 신념을 가지고 있었고 이 회의가 인공지능(artificial intelligence: AI)이란 단어를 탄생시킨 계기가 되었다. 이 회의는 공식적으로 '다트마우스 하기 인공지능 연구계획'이라 불리며 그 뒤의 10년간을 지배한 여러 연구성과를 냈다. 이것이 제1차 인공지능 연구의 시작이었다.

인공지능에 대한 연구는 강한 인공지능과 약한 인공지능으로 나뉘는데, 강한 인공지능은 어떤 문제를 실제로 사고하고 해결할 수 있는 컴퓨터 기반의 인공적인 지능을 만들어 내는 것에 관한 연구다. 즉, 인공지능의 강한 형태는, 지각력이 있고, 스스로를 인식하는 것이라고 말할 수 있다.

반면 약한 인공지능은 어떤 문제를 실제로 사고하거나 해결할 수는 없는 컴퓨터 기반의 인공적인 지능을 만들어 내는 것에 관한 연구다. 그와 같은 시스템은 진짜 지능이나 지성을 갖추고 있지는 못하지만, 어떤 면에서 보면 지능적인 행동을 보일 것이다.

여기서 강한 인공지능이 존재할 수 있는지에 관한 철학적인 논쟁이 발생하였다. 강한 인공지능이 존재한다고 주장하는 사람들은 다음과 같은 4가지 논리를 든다.

# 인간의 마음은 유한 오토마타(Finite Automata)이고, 따라서 처치-튜링 명제는 뇌에 적용 가능하다.

# 인간의 마음은 소프트웨어이다(유한 상태 기계의 일종이다).

# 뇌는 순수한 하드웨어이다(말하자면 고전적인 컴퓨터처럼 동작한다).

# 인간의 마음은 오로지 뇌를 통해서만 존재한다.

그러나 로저 펜로즈를 포함한 몇몇 사람들은 처치-튜링 명제의 적용이 가능하지 않다고 논박한다. 어떤 이들은 인간의 마음은 물리적인 속성을 뛰어넘는 무엇이 있다고 이야기한다.

6. 2. 2. 인공 화학 (Artificial Chemistry)

인공 화학은 3-튜플 (S,R,A)로 일반적으로 정의된다. 어떤 경우에는 튜플 (S,I)로도 정의된다.

S는 가능한 분자의 집합이다. S={s₁...,s_n} 이고, n은 무한일 가능성을 내포하는 원소의 개수이다.
R는 S에 속한 분자에 대한 n진법 연산이며, 반응 규칙 R={r₁...,r_n} 을 의미한다. 각각의 규칙, r_i의 화학적 반응은 a+b+c->a*+b*+c* 와 같은 방식으로 기술된다. (단, r_i는 연산자임에 주의)
A는 규칙 R을 어떻게 부분집합 P $\subset$ S 에 적용할지에 대한 알고리즘이다.
I는 S의 분자들의 상호 작용에 대한 규칙이다.

인공 화학은 인공생명의 하위 분야이며, 구체적으로는 딱딱한 인공 생명의 하위 분야이다. 이 분야에 깔려있는 아이디어는, 살아있는 것을 구성하기 위해서는, 살아있지 않은 독립체로 이루어져야 한다는 것이다. 예컨대, 세포는 살아있지만, 살아 있지 않은 분자들로 이루어져있다. 인공 화학은, 극도로 '''기초 부터의 접근'''이 강조된 인공 생명이라고 볼 수 있다.

6. 2. 3. 진화 알고리즘 (Evolutionary Algorithm)

미시간 대학의 John Holland는 1975년에 게임 이론과 공학에서의 문제를 포함한 다양한 문제에 유전학적 선택을 적용하는 방법론을 개발하였다. 진화 알고리즘(Evolutionary Algorithm) 또는 유전 알고리즘(Genetic Algorithm)이라고 불리는 이 과정은 다음과 같은 규칙에 따라 작동한다.^[63]

# 적당한 환경에서 몇가지 유전자형의 집단으로 시작한다.

# 표현형에서 성공적인 유전자형 짝들을 선택한다.

# 가장 성공적인 설계에 대응하는 유전자형들을 번식시킨다.

# 새 후손으로 가장 덜 성공적인 유전자형을 대체하고 2단계로 돌아가서 사이클을 되풀이한다.

이 규칙에서도 알 수 있듯이 진화 알고리즘 또는 유전자 알고리즘은 19세기의 찰스 다윈(Charles Darwin, 1809~1882)이 주장한 진화론에서의 자연선택과 적자생존에 기반을 둔, 자연에서의 진화 현상을 컴퓨터적, 알고리즘적으로 응용하여 문제를 푸는 과정이다. 진화 알고리즘에서 쓰는 용어는 아래와 같다.

문제에 대한 각각의 가능한 해 → 유기체(organism) 또는 개체(individual)
가능한 해의 집합 → 개체군(population)
각각의 해의 특징을 구성하는 요소 → 염색체(chromosome)
염색체를 변형하는 연산자 → 유전연산자(genetic operator)

진화 알고리즘에는 여러 가지 종류가 있다.

# 유전 알고리즘(GA),

# 진화 전략(ES),

# 진화 프로그래밍(EP),

# 유전자 프로그래밍(GP)

이들은 주로 3가지의 진화적 프로세스, 즉 선택(selection), 돌연변이(mutation), 생식(reproduction)을 사용한다. 이러한 각각의 진화적 접근에는 세 가지 공통적인 요소들이 있다.

# 적응도(fitness): 개체가 다음 세대에 얼마나 영향을 주는지를 결정한다.

# 생식 연산자(reproduction operator): 개체가 다음 세대에 자손을 만들게 한다.

# 유전 연산자(genetic operator): 부모의 정보를 통해 자손의 정보를 결정한다.

이러한 진화 알고리즘의 중요한 장점으론, 단순히 병렬적으로 나열된 가능한 해 중 진짜 해를 찾아나가는 것보다 더 효율적으로, 복수 개체 사이의 상호 협력(선택과 교배)을 통해 해를 찾아나갈 수 있다는 점이다. 뿐만 아니라 신경 네트워크(neural network) 등에서는 작업을 위해 평가 함수의 미분값이 필요할 때가 있는데, 이와 달리 진화 알고리즘은 현재 상태로만 판단하기 때문에 단순하고 쉬운 알고리즘이며 불연속적인 평가 함수에 대해서도 적용이 가능하다. 하지만 진화 알고리즘의 단점으론 어떤 문제를 진화 알고리즘을 이용해서 푸는 일반적인 방법이 없다는 점과 진화 과정에서 고려해야 하는 변수들이 많다는 점들이 있다.^[64]

진화 알고리즘의 예로는 개미를 키우는 MICROANTS가 있다.

6. 2. 4. 진화 예술 (Evolutionary Art)

'''진화 예술'''은 컴퓨터에 의해 만들어지는 예술의 한 형태로, 진화 디자인 가운데 예술적 창의성을 가장 큰 특징으로 갖는다. 진화 예술의 기본 배경은 사용자가 자연선택과 유사한 방식인 '선택'메커니즘을 통해 자신이 선호하는 작품을 만들고자 하는 것이다. 모든 진화 예술에서는 하나 이상의 부모 작품이 돌연변이 및 교배되어 다수의 자손 작품을 발생하게 되며, 적합도 평가에 기초해서 다음 세대를 구성할 작품이 선택된다. 가령, 미적인 이미지를 만드는 진화 예술 시스템은 임의의 값으로 초기화된 이미지 집단을 컴퓨터 화면에 보인다. 예술성을 평가할 기준을 컴퓨터 프로그램으로 만드는 데에는 아직 한계가 있기 때문에, 진화 예술가가 직접 이미지를 선택함으로써 자신이 선호하는 작품이 생존해서 더 좋은 작품으로 진화하도록 한다.

진화 예술 시스템은 평가를 통해 선택된 이미지들을 돌연변이해서 다음 세대의 이미지를 만들어낸다. 이렇게 만들어진 이미지는 이전 세대의 것 보다는 미적으로 개선된 것이다. 진화 예술가는 다시 평가에 참여하고 진화계산에 의해 새로운 세대의 이미지가 발생한다. 이런 과정은 원하는 이미지가 만들어질 때까지 반복될 수 있다. 물론, 초기 집단에서 임의로 만들어진 이미지 대신에 이전에 만들었던 작품이나 아직 완성되지 않은 작품을 사용할 수도 있다. 진화 예술에서 진화 알고리즘은 끊임없이 새로운 것을 발생시키기 위해 사용된다. 본질적으로 적합도를 평가할 수 있는 기준이 존재한다면 문자열로 표현할 수 있는 모든 것을 진화알고리즘에 의해 진화시킬 수 있다. 예술성을 평가할 기준을 컴퓨터 프로그램으로 만드는 데는 아직 한계가 있기 때문에, 진화 예술에서 작품에 대한 적합도 평가는 사용자가 한다. 즉, 프로그램이 다수의 예술작품을 발생하고 사용자가 자신의 선호도에 따라 작품을 선택하면, 재결합을 통해 새로운 세대의 작품이 발생하게 된다.

6. 2. 5. 진화 음악 (Evolutionary Music)

'''진화 음악'''은 진화 예술에서 소리를 다루는 부분이다. 진화 음악은 진화 알고리즘으로부터 생성되는 알고리즘적인 음악이다. 진화 음악은 개인, 또는 여러 사람이 만들어낸 소리(멜로디 등)나 그 소리의 일부분을 사용하거나 완전히 랜덤하게 시작된다. 그 다음 계산적인 생물학적 과정(예를 들어 자연선택, 돌연변이, 재결합)을 사용하여 생산된 소리가 더 음악적이 되도록 만든다.

진화 음악의 합성은 소리를 생성하거나 악기를 종합하는 기술과도 연관되어 있다. 진화 음악은 사용자나 청중들에게 음악의 기능이 적합하도록 만들어주는 상호작용적인 진화 알고리즘을 사용하지만, 아직 계산적으로 음악의 품질을 측정하기는 어려움이 있다. 그러나 음악의 품질에 대한 자동 계산의 정확성을 높이는 것에 대한 연구도 현재 이루어지고 있다. 진화 계산 기술은 조화나 반주 작업에도 사용된다. 이러한 진화 연산 작업을 구현하는 기술로는 유전 알고리즘이나 유전 프로그래밍이 있다.

6. 2. 6. 자연발생론 (Abiogenesis)

'''자연발생설'''(自然發生說, 아바이오제네시스/Abiogenesis^영어)은 생명체가 부모 없이 스스로 생길 수 있다는 가설이지만, 인공생명에서 다루는 '''자연발생론'''이란 생명의 기원에 대한 알고리즘적 시뮬레이션을 의미한다.

7. 사용되는 곳

여기에서 제시된 반응 시스템 모델링 외에도, 유한 상태 기계는 전기 공학, 언어학, 컴퓨터 과학, 철학, 생물학, 수학, 비디오 게임 프로그래밍 및 논리학을 포함한 많은 분야에서 중요한 역할을 한다. 유한 상태 기계는 오토마타 이론과 계산 이론에서 연구되는 오토마타의 한 종류이다.

컴퓨터 과학에서 유한 상태 기계는 애플리케이션 동작 모델링(제어 이론), 하드웨어 디지털 시스템 설계, 소프트웨어 공학, 컴파일러, 네트워크 프로토콜 및 전산 언어학에 널리 사용된다.

여기에서 보이는 반응 시스템 설계뿐만 아니라, 유한 오토마타(有限オートマトン)는 전기 공학, 언어학, 컴퓨터 과학, 철학, 생물학, 수학, 논리학 등 다양한 분야에서 활용된다. 유한 오토마타는 오토마타 이론과 계산 이론에서 연구되는 일종의 오토마타이다. 정보 공학과 컴퓨터 과학에서는 애플리케이션 동작의 모델링, 디지털 시스템의 하드웨어 설계, 소프트웨어 공학, 컴파일러 설계, 통신 프로토콜 설계, 계산과 언어에 관한 연구 등에 폭넓게 활용되고 있다.

7. 1. 하드웨어적 응용

디지털 회로에서 유한 오토마타는 설계 가능 논리 소자, 프로그래머블 로직 컨트롤러, 논리 회로, 플립플롭 또는 전자계전기를 사용하여 구축될 수 있다.^[21]^[22]^[40] 하드웨어적 응용에는 상태 변수를 저장할 프로세서 레지스터, 상태 전이 함수를 결정할 여러 가지 논리들과 유한 오토마타의 출력을 결정할 논리들이 필요하다. 고전적인 하드웨어 구현 중 하나는 리차드 컨트롤러이다.

''메드베데프 머신''에서는 출력이 상태 플립플롭에 직접 연결되어 플립플롭과 출력 사이의 시간 지연을 최소화한다. 저전력을 위한 상태 인코딩을 통해 상태 머신을 최적화하여 전력 소비를 최소화할 수 있다.

7. 2. 소프트웨어적 응용

유한 상태 기계는 응용 프로그램 설계, 텍스트 필터링, 컴파일러 설계, 패리티 비트 생성 등에 사용된다.^[65]

오토마타 기반 프로그래밍
가상 유한 상태 기계

유한 오토마타는 미래의 상태에 대한 출력값이 이전 상태에 의존하는 특성을 가지며, 이는 키보드, 마우스, 타이머, 네트워크 활동 등 컴퓨터 내/외적 요소에서 발생하는 다양한 이벤트에 응답하는 데 유용하다. 이러한 특성으로 인해 자바스크립트, C# 등을 사용한 응용 프로그램 설계에 사용된다.^[65]

자바나 C#, SQL 등의 프로그래밍 언어에서 결정적 유한 오토마타를 사용하여 이메일 주소와 같은 문자열의 형식이 올바른지 판별할 수 있다. 정규 문법을 사용한 코드는 각 프로그래밍 언어의 컴파일러에 의해 자동으로 결정적 유한 오토마타로 변환된다.

프로그래밍 언어 컴파일러는 특정 프로그래밍 언어로 쓰여 있는 문서를 다른 프로그래밍 언어로 옮기는 프로그램으로, 어휘 분석 과정에 유한 오토마타가 사용된다. 어휘 분석기는 입력된 코드를 자유 문맥 언어의 의미 단위로 나누는데, 이 의미 단위는 대부분 정규집합으로 표현 가능하다.

대부분의 어휘 분석기 생성기는 정규 표현의 순열을 입력으로 받아 ε-전이를 가진 비결정적 유한 오토마타로 변환 후, 부분집합을 이용하여 결정적 유한 오토마타를 구성한다. 예를 들어, 파스칼 언어에서 변수(identifier)는 문자로 시작하여 문자나 숫자가 혼용되어 사용될 수 있는데, 이러한 변수인지 확인하는 과정에서 결정적 유한 오토마타가 사용된다.

'''패리티 비트'''(Parity bit)는 정보 전달 과정에서 오류 검사를 위해 추가된 비트로, 오류 검출 부호의 가장 간단한 형태이다. 짝수 패리티는 전체 비트에서 1의 개수가 짝수가 되도록, 홀수 패리티는 홀수가 되도록 패리티 비트를 정하며, 이러한 패리티 비트를 출력하는 과정에 유한 오토마타가 사용된다.

오른쪽 그림은 패리티 비트를 출력하는 유한 오토마타를 나타낸다. A는 짝수 패리티, B는 홀수 패리티 상태를 나타내며, 입력에 따라 상태가 전이되면서 패리티 비트가 출력된다. 예를 들어, 입력이 010011일 경우 출력은 011101이 된다.

유한 오토마타는 프로그래밍 언어 컴파일러의 프런트 엔드에서 자주 사용된다. 어휘 분석기와 파서는 프로그래밍 언어 문법의 정규 및 맥락 자유 부분을 처리한다.^[23]

다음은 유한 상태 기계를 이용한 소프트웨어 애플리케이션 구축에 흔히 사용되는 개념들이다.

이벤트 기반 유한 상태 기계
가상 유한 상태 기계
오토마타 기반 프로그래밍
상태 패턴

참조

_[1] 서적 Formal Methods in Computer Science CRC Press
_[2] 웹사이트 Finite State Machines – Brilliant Math & Science Wiki https://brilliant.or[...] 2018-04-14
_[3] 서적 Encyclopedia of Computer Science and Technology https://books.google[...] CRC Press
_[4] 서적 Discrete Mathematics With Applications https://books.google[...] Academic Press
_[5] 웹사이트 Finite State Machines https://web.archive.[...] David R. Wright website, N. Carolina State Univ. 2012-07-14
_[6] 서적 Computer Science: Abstraction to Implementation http://www.cs.hmc.ed[...] Harvey Mudd College
_[7] 서적 Generic Inference: A Unifying Theory for Automated Reasoning John Wiley & Sons
_[8] 웹사이트 Algebraic path problems https://web.archive.[...] 2008-06
_[9] 서적 Quality Measures in Data Mining - Studies in Computational Intelligence Springer, Berlin, Heidelberg
_[10] 간행물 Structural Division Procedure for Efficient IC Analysis http://arrow.dit.ie/[...] IET Irish Signals and Systems Conference (ISSC 2008) 2008-06-18/2008-06-19
_[11] 웹사이트 Tiwari, A. (2002). Formal Semantics and Analysis Methods for Simulink Stateflow Models. http://www.csl.sri.c[...] 2018-04-14
_[12] 학회 A Denotational Semantics for Stateflow ACM
_[13] 웹사이트 Harel, D. (1987). A Visual Formalism for Complex Systems. Science of Computer Programming, 231–274. https://web.archive.[...] 2011-06-07
_[14] 웹사이트 Alur, R., Kanade, A., Ramesh, S., & Shashidhar, K. C. (2008). Symbolic analysis for improving simulation coverage of Simulink/Stateflow models. International Conference on Embedded Software (pp. 89–98). Atlanta, GA: ACM. https://web.archive.[...] 2011-07-15
_[15] 웹사이트 Finite State Machine https://web.archive.[...] U.S. National Institute of Standards and Technology 2008-05-12
_[16] 서적 Automata theory with modern applications https://books.google[...] Cambridge University Press
_[17] 보고서 An ''n'' log ''n'' algorithm for minimizing states in a finite automaton ftp://reports.stanfo[...] Stanford Univ.
_[18] 보고서 On the performance of automata minimization algorithms https://web.archive.[...] Porto Univ.
_[19] 학술지 Gedanken-Experiments on Sequential Machines Princeton University Press
_[20] 학술지 Minimization of Acyclic automata in Linear Time 1992
_[21] 서적 Digital Integrated Circuit Design: From VLSI Architectures to CMOS Fabrication Cambridge University Press
_[22] 웹사이트 Synchronous Finite State Machines; Design and Behaviour http://users.etech.h[...] University of Applied Sciences Hamburg
_[23] 서적 Compilers: Principles, Techniques, and Tools Addison-Wesley
_[24] 용어
_[25] 용어
_[26] 용어
_[27] 용어
_[28] 용어
_[29] 용어
_[30] 서적
_[31] 웹사이트 Formal Semantics and Analysis Methods for Simulink Stateflow Models http://www.csl.sri.c[...]
_[32] 학회 A Denotational Semantics for Stateflow http://citeseerx.ist[...] ACM 2005
_[33] 웹사이트 A Visual Formalism for Complex Systems http://www.inf.ed.ac[...]
_[34] 웹사이트 Symbolic analysis for improving simulation coverage of Simulink/Stateflow models http://drona.csa.iis[...] ACM
_[35] 학술지 Finite State Machine http://www.nist.gov/[...] U.S. National Institute of Standards and Technology 2008-05-12
_[36] 서적 Automata theory with modern applications https://books.google[...] Cambridge University Press 2006
_[37] 논문 An n log n algorithm for minimizing states in a finite automaton ftp://reports.stanfo[...] 2017-10
_[38] 논문 On the performance of automata minimization algorithms http://www.dcc.fc.up[...] 2007
_[39] 논문 Minimization of Acyclic automata in Linear Time Elsevier 1992
_[40] 웹사이트 FSM: Medvedev http://www.vhdl-onli[...] 2010-07-10
_[41] 웹사이트 Moore or Mealy model? http://www.statework[...]
_[42] 웹사이트 http://www.cs.odu.ed[...]
_[43] 웹인용 Basics of Automata Theory http://www-cs-facult[...] Standford University, Sophomore College 2012-04-29
_[44] 웹인용 컬쳐뉴스 공식 블로그-인간의 아주 오래된 꿈, 오토마타(Automata) http://culturenews.t[...] 컬쳐뉴스 2012-05-06
_[45] 웹인용 아직도 밝히지 못한 진시황릉의 비밀-오마이뉴스 http://www.ohmynews.[...] 오마이뉴스 2012-04-29
_[46] 웹인용 Public Domain Photos and Images: A robot based on drawings by Leonardo da Vinci http://public-domain[...] 2012-04-29
_[47] 웹인용 오토마타 공작소 I Love Automata http://www.iloveauto[...] 2012-05-06
_[48] 웹인용 오토마타 공작소 I Love Automata http://www.iloveauto[...] 2012-05-06
_[49] 웹인용 컬쳐뉴스 공식 블로그-인간의 아주 오래된 꿈, 오토마타(Automata) http://culturenews.t[...] 컬쳐뉴스 2012-05-06
_[50] 웹인용 Basics of Automata Theory http://www-cs-facult[...] Standford University, Sophomore College 2012-04-22
_[51] 서적 이산수학 2012
_[52] 서적 Theory of Self-Reproducing Automata https://web.archive.[...] Univ. of Illinois Press 2012-04-25
_[53] 웹인용 The First Computational Theory of Mind and Brain: A Close Look At McCulloch and Pitt's "Logical Calculus of Ideas Immanent in Nervous Activity" http://www2.fiit.stu[...] Kluwer Academic Publishers 2012-04-22
_[54] 저널 A Method for Synthesizing Sequential Circuits 1955-09
_[55] 저널 Gedanken-experiments on Sequential Machines Princeton University Press 1956
_[56] 웹인용 Automata Studies-Gedanken-experiments on Sequential Machines(129-130) http://books.google.[...] Princeton University Press 2012-05-05
_[57] 웹인용 Automata Studies-Gedanken experiment on sequential machines(129-132) http://books.google.[...] Princeton University Press 2012-05-05
_[58] 웹인용 Mealy Machine과 Moore Machine http://www.jmjs.com/[...] 2012-05-04
_[59] 웹사이트 http://www.aistudy.c[...]
_[60] 웹인용 인공생명(A-Life)과 생물학의 철학 http://bric.postech.[...]
_[61] 웹인용 Artificial Life http://people.reed.e[...] 2012-05-04
_[62] 웹인용 Artificial Life paper http://people.reed.e[...] 2012-05-04
_[63] 웹인용 인공생명의 개념 http://www.aistudy.c[...] 2012-05-06
_[64] 웹인용 유전자 알고리즘 http://www.aistudy.c[...] 2012-05-17
_[65] 웹사이트 http://www.ibm.com/d[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com