음정
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
- 1. 개요
- 2. 계산 원리
- 3. 계산법의 종류
- 4. 장/단, 완전의 구분
- 5. 그 외 명칭
- 6. 평균율 음정 기억법
- 7. 음정의 크기
- 8. 주요 음정
- 9. 음정 번호와 성질 (Interval Number and Quality)
- 10. 전위 (Inversion)
- 11. 분류 (Classification)
- 12. 미분음 (Minute Intervals)
- 13. 복합 음정 (Compound Intervals)
- 14. 화음의 음정 (Intervals in Chords)
- 15. 다양한 조율 시스템에서의 음정 크기 (Size of Intervals Used in Different Tuning Systems)
- 16. 음정 근음 (Interval Root)
- 17. 음정 순환 (Interval Cycles)
- 18. 대체 음정 명명 규칙 (Alternative Interval Naming Conventions)
- 19. 라틴어 명명법 (Latin Nomenclature)
- 20. 비온음계적 음정 (Non-diatonic Intervals)
- 21. 음고류 음정 (Pitch-class Intervals)
- 22. 일반 음정과 특정 음정 (Generic and Specific Intervals)
- 23. 일반화 및 비음고 사용 (Generalizations and Non-pitch Uses)
- 참조
1. 개요
음정은 두 음 사이의 높이 차이를 의미하며, 오선보에서의 간격으로 명칭이 결정된다. 1옥타브 이하의 음정은 단음정, 그 이상은 겹음정으로 구분된다. 음정은 도수와 성질을 가지며, 도수는 음이름 순서에 따라, 성질은 장(Major), 단(minor), 완전(Perfect), 증(Augmented), 감(diminished) 등으로 구분된다. 음정 계산에는 계이름, 음이름, 반음 개수 계산법 등이 사용되며, 음정의 크기는 주파수 비율 또는 센트로 나타낸다. 주요 음정으로는 유니즌, 반음, 온음, 셋온음, 옥타브 등이 있으며, 음정은 선율적/화성적, 온음계적/반음계적, 협화/불협화, 단순/복합, 순차/도약, 이명동음 등으로 분류될 수 있다.
더 읽어볼만한 페이지
- 음정 - 옥타브
옥타브는 음악에서 주파수 비율 2:1로 표현되는 음정 간격으로, 특정 음과 그 두 배 또는 절반 주파수를 갖는 다른 음 사이의 관계를 나타내며, 옥타브 등가성 개념에 따라 여러 문화권에서 동등하게 인식된다. - 음정 - 센트 (음악)
센트는 음악에서 음높이 간격을 나타내는 로그 척도 단위로, 두 주파수 비율 측정에 사용되며 균등 조율에서 반음은 100센트, 옥타브는 1200센트에 해당하고 청각적 현상과도 관련된다. - 음악 용어 - 리듬
리듬은 음악, 무용, 언어 등에서 나타나는 시간적 패턴으로, 음악에서는 펄스, 비트, 마디 등의 시간 단위가 결합하여 형성되며, 언어학에서는 강세, 음절 등을 기준으로 분류된다. - 음악 용어 - 오디오 신호
오디오 신호는 소스에서 스피커 또는 녹음 장치로 이동하는 경로를 따라 흐르는 신호이며, 대역폭, 레벨 등의 매개변수로 특징지어지고 다양한 형태로 전송된다. - 음악에 관한 - 리듬
리듬은 음악, 무용, 언어 등에서 나타나는 시간적 패턴으로, 음악에서는 펄스, 비트, 마디 등의 시간 단위가 결합하여 형성되며, 언어학에서는 강세, 음절 등을 기준으로 분류된다. - 음악에 관한 - 악보
악보는 음의 높낮이와 길이, 악기, 연주법 등을 시각적으로 표현하는 기호 체계로, 오선, 음표, 쉼표 등 다양한 기호를 사용하여 음악을 기록하고 전달하는 매체이다.
| 음정 | |
|---|---|
| 음정 | |
| 정의 | |
| 종류 | |
| 음정의 크기 | |
| 음정의 종류 (수식어 기준) | |
| 음정의 방향 | |
| 겹음정 | |
| 협화음정 및 불협화음정 | |
| 딴이름 음정 (enharmonic interval) | |
2. 계산 원리
음정은 두 음 사이의 간격을 나타내며, 도수와 성질을 통해 표현된다. 음정의 크기는 주파수 비율 또는 센트로 나타낼 수 있다.
음정 명칭은 오선보에서의 간격으로 결정되며, "◯도"와 같이 표현한다. 1옥타브 이하의 음정은 '''단음정''', 그 이상은 '''겹음정'''이라고 한다. 13 반음 이상, 즉 1 옥타브보다 크게 벌어진 음정은 '''복음정'''이라고 부르며, "3 옥타브와 완전 4도"와 같이 옥타브 수와 단음정을 조합하여 나타낸다. 다만, "9도와 같은 약간의 복음정은 화성의 특징적인 요소이므로, 큰 쪽의 수로 불리는 것이 보통이다"[35] (예: "1 옥타브와 단 3도" → "단 10도").
두 음 중 높은 음을 1옥타브 내리는 것을 '''전위'''(転回)라고 한다. 예를 들어 "C"와 "E"가 있을 때, 높은 음 E를 "1옥타브 낮은 E"와 (원래 옥타브와 같은) "C"로 바꾸면 전위된 음정이 된다. 전위로 생긴 음정을 '''전위 음정'''(転回音程)이라고 한다.[32] 높은 음을 1옥타브 내리는 대신 낮은 음을 1옥타브 올려도 같은 전위 음정을 얻을 수 있다.[39]
두 음이 n 반음 떨어져 있을 때, 전위된 음정은 (12-n) 반음만큼 떨어져 있다. 전위 음정은 다음과 같이 구할 수 있다.
| 원래 음정 | 전위 음정 |
|---|---|
| 완전 1도 | 완전 8도 |
| 단 2도 | 장 7도 |
| 장 2도 | 단 7도 |
| 단 3도 | 장 6도 |
| 장 3도 | 단 6도 |
| 완전 4도 | 완전 5도 |
전위 음정의 전위는 원래 음정으로 돌아온다. 전위 음정의 명칭은 다음과 같이 결정된다.
- 원래 음정이 m도이면, 전위 음정은 (9-m)도이다.
- '''장'''↔'''단''', '''증'''↔'''감''', '''겹증'''↔'''겹감'''으로 바뀐다.
- '''완전''' 음정은 전위하여도 '''완전''' 음정이다.
전위는 한쪽 음을 1옥타브 올리거나 내리는 것으로, 주파수 비율이 a:b인 음 쌍을 전위하면 주파수 비율은 b:2a가 된다.
2. 1. 도수
도수는 음이름에 따라 결정되는데, C D E F G A B C, E F G A B C D E와 같이 순서에 따라 정해진다.- C, E를 기준으로 했을 때, C, E는 첫 번째 순번이자 같은 음이므로 C - C, E - E의 도수는 1도이다.
- C, E를 기준으로 했을 때, D, F는 두 번째 순번이므로 C - D, E - F의 도수는 2도이다.
- C, E를 기준으로 했을 때, E, G는 세 번째 순번이므로 C - E, E - G의 도수는 3도이다.
- C, E를 기준으로 했을 때, F, A는 네 번째 순번이므로 C - F, E - A의 도수는 4도이다.
- C, E를 기준으로 했을 때, G, B는 다섯 번째 순번이므로 C - G, E - B의 도수는 5도이다.
- C, E를 기준으로 했을 때, A, C는 여섯 번째 순번이므로 C - A, E - C의 도수는 6도이다.
- C, E를 기준으로 했을 때, B, D는 일곱 번째 순번이므로 C - B, E - D의 도수는 7도이다.
- C, E를 기준으로 했을 때, (한 옥타브 위) C, (한 옥타브 위) E는 여덟 번째 순번이므로 C - (한 옥타브 위) C, E - (한 옥타브 위) E의 도수는 8도이다.
예를 들어 B-D는 B, C, D 세 개의 음 이름을 포함하므로 3도이다.[32]
2. 2. 성질
도수를 기반으로 음정의 정확한 간격을 나타내기 위해 장(Major), 단(minor), 완전(Perfect), 증(Augmented), 감(diminished) 등의 성질을 사용한다. 장음계의 계이름을 기준으로 두 음 모두 ♯이나 ♭이 붙지 않았을 경우, 2, 3, 6, 7도 간격에는 장(Major) 성질을, 1, 4, 5, 8도 간격에는 완전(Perfect) 성질을 붙여 표기한다.[32]기준음이나 비교 대상 음에 ♯이나 ♭이 붙어 음 사이 간격이 변하면, 도수는 그대로이나 성질은 변화한다. 장(Major) 음정은 단(minor), 감(diminished), 증(Augmented)으로, 완전(Perfect) 음정은 감(diminished), 증(Augmented)으로 변화한다.[32]

- 도 - 미: 3도, ♯이나 ♭ 없음, 장(Major) (장3도)
- 도 - 미♭: 장3도에서 반음만큼 좁아짐, 단(minor) (단3도)
- 도♯ - 미♭: 단3도에서 반음만큼 더 좁아짐, 감(diminished) (감3도)
- 도 - 솔: 5도, ♯이나 ♭ 없음, 완전(Perfect) (완전5도)
- 도 - 솔♯: 완전5도에서 반음만큼 넓어짐, 증(Augmented) (증5도)
- 도♭ - 솔♯: 증5도에서 반음만큼 더 넓어짐, 겹증(Doubly Augmented) (겹증5도)
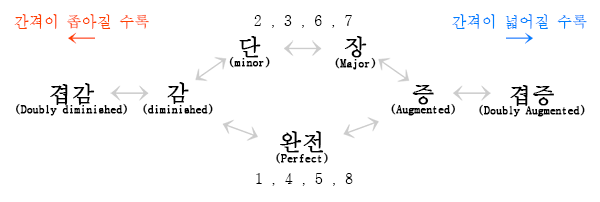
증진된 음정은 완전 또는 장 음정보다 반음 넓고, 감소된 음정은 완전 또는 단 음정보다 반음 좁다. 예를 들어 증진된 6도는 장 6도보다 반음 넓고, 감소된 6도는 단 6도보다 반음 좁다.
증4도('''A4''')와 감5도('''d5''')는 으뜸음계에서 나타나는 유일한 증∙감 음정이다.
1옥타브 이하 음정은 '''단음정''', 그 이상은 '''겹음정'''이라 한다. 음정에는 "단", "장", "완전", "증", "감"과 같은 접두사를 붙인다.
미~파와 시~도는 반음이고, 그 외는 온음이다. 전자는 '''단2도''', 후자는 '''장2도'''이다.[32]
마찬가지로 3도에서는 미~파와 시~도를 포함하는 레~파, 미~솔, 라~도는 3반음으로 좁고, 포함하지 않는 도~미, 파~라, 솔~시는 4반음으로 넓어 전자는 '''단3도''', 후자는 '''장3도'''이다.
6도, 7도도 같은 이유로 좁은 쪽에 "단", 넓은 쪽에 "장"을 붙인다. 4도와 5도는 완전 협화 음정을 포함하여 "완전", "증", "감" 접두사를 사용한다.
- 4도: 다-파, 라-솔 등 5반음은 "'''완전 4도'''", 파-시 6반음은 "'''증 4도'''"이다.[32]
- 5도: 시-파 6반음은 "'''감 5도'''", 다-솔 등 7반음은 "'''완전 5도'''"이다.[32]
1도와 8도는 완전 협화 음정 한 종류만 있어, 1도는 "'''완전 1도'''"(유니즌이라고도 함), 8도는 "'''완전 8도'''"이다.[32]
"증4도"와 "감5도"는 12음 평균율에서 6반음으로 같지만, 악보상 다르다. 예를 들어 이 둘은 트라이톤이라고도 한다.
- '''장''' 또는 '''완전'''보다 반 음 넓으면 '''증'''(増), 2반음 넓으면 '''중증'''(重増) 접두사를 붙인다(예: 증7도, 중증5도).
- '''단''' 또는 '''완전'''보다 반 음 좁으면 '''감'''(減), 2반음 좁으면 '''중감'''(重減) 접두사를 붙인다.
올림표나 내림표 등 변화 기호가 붙으면, 예를 들어 "증2도"와 "단3도"는 12 평균율에서 3반음으로 같지만, 악보상 "2도"와 "3도"로 달라 "증2도", "단3도"로 부른다.
| 0반음 | 1반음 | 2반음 | 3반음 | 4반음 | 5반음 | 6반음 | 7반음 | 8반음 | 9반음 | 10반음 | 11반음 | 12반음 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 완전1도 | 단2도 | 장2도 | 단3도 | 장3도 | 완전4도 | 감5도 증4도 | 완전5도 | 단6도 | 장6도 | 단7도 | 장7도 | 완전8도 |
두 음 중 높은 음을 1옥타브 내리는 것을 '''전위'''(転回)라 한다. 예를 들어 "C"와 "E"의 쌍에서 높은 E를 1옥타브 낮추면 원래 쌍의 전위가 된다. 전위로 생긴 음정을 '''전위 음정'''(転回音程)이라 한다.[32]
두 음을 1옥타브씩 옮겨도 음정은 같으므로, 높은 음을 1옥타브 내리는 대신 낮은 음을 1옥타브 올려도 전위이다.[39]
두 음의 쌍이 n 반음 떨어져 있을 때, 전위된 쌍은 (12-n) 반음 떨어져 있게 되므로, 다음과 같다.
| 원래 음정 | 전위 음정 |
|---|---|
| 완전 1도 | 완전 8도 |
| 단 2도 | 장 7도 |
| 장 2도 | 단 7도 |
| 단 3도 | 장 6도 |
| 장 3도 | 단 6도 |
| 완전 4도 | 완전 5도 |
전위 음정의 전위는 원래대로이다. 전위 음정 명칭은 다음과 같다.
- 원래 음정이 m도이면, 전위 음정은 (9-m)도이다.
- '''장'''←→'''단''', '''증'''←→'''감''', '''겹증'''←→'''겹감'''으로 바꾼다.
- 원래 음정이 "'''완전'''"이면 전위 음정도 "'''완전'''"이다.
전위는 한쪽 음을 1옥타브 올리거나 내리는 행위로, 주파수비가 a:b인 음 쌍을 전위하면 주파수비가 b:2a가 된다.
온음계 내 음정은 '''온음계적 음정''', 아니면 '''반음계적 음정'''이다. 완전, 장, 단음정과 증4도, 감5도가 '''온음계적 음정'''이고, 나머지는 '''반음계적 음정'''이다.
장음계에 나타나는 음정 일람이다.
| 아래 음\위 음 | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| C | 완전 8도 | 장2도 | 장3도 | 완전 4도 | 완전 5도 | 장6도 | 장7도 |
| D | 단7도 | 완전 8도 | 장2도 | 단3도 | 완전 4도 | 완전 5도 | 장6도 |
| E | 단6도 | 단7도 | 완전 8도 | 단2도 | 단3도 | 완전 4도 | 완전 5도 |
| F | 완전 5도 | 장6도 | 장7도 | 완전 8도 | 장2도 | 장3도 | 증4도 |
| G | 완전 4도 | 완전 5도 | 장6도 | 단7도 | 완전 8도 | 장2도 | 장3도 |
| A | 단3도 | 완전 4도 | 완전 5도 | 단6도 | 단7도 | 완전 8도 | 장2도 |
| B | 단2도 | 단3도 | 완전 4도 | 감5도 | 단6도 | 단7도 | 완전 8도 |
음정을 계산하는 방법은 크게 세 가지가 있으며, 계산하는 사람의 음감(상대음감, 절대음감)에 따라 선호하는 계산법이 달라진다.
3. 계산법의 종류
어떤 방법을 사용하든, 음정의 명칭은 오선보에서의 간격을 기준으로 "◯도"로 결정된다. 1옥타브 이내의 음정은 '''단음정''', 그 이상은 '''겹음정'''이라고 한다. 두 음이 같은 높이에 있으면 "0도"가 아닌 "1도"(유니즌)가 된다. 예를 들어, 1옥타브 차이 나는 두 음은 악보상 7칸 떨어져 있으므로, 7+1 = "'''8도'''"가 된다.
12음 평균율에서 "증4도"와 "감5도"는 6반음으로 동일하지만, 악보 표기 상으로는 다르다. 위 그림에서 왼쪽은 4도이므로 "증4도", 오른쪽은 5도이므로 "감5도"이다. 이 두 음정은 '''트라이톤'''이라고도 불린다.
13반음 이상, 즉 1옥타브보다 크게 벌어진 음정은 '''복음정'''이라고 하며, "3옥타브와 완전 4도"와 같이 옥타브 수와 단음정의 조합으로 나타낸다. 다만, 9도와 같이 가까운 복음정은 화성의 특징적인 요소이므로, 큰 쪽의 수("단10도")로 불리는 것이 일반적이다.[35]
계이름이나 음이름으로 계산할 때, 계이름과 음이름의 차이를 이해하지 못하면 음정의 성질을 잘못 계산할 수 있으므로 주의해야 한다.[43]
3. 1. 계이름 계산법
상대음감을 가진 사람들은 계이름에 의존하여 음정을 계산하는 경우가 많다. 기준음을 '도' 또는 '미'로 보고 음정을 계산한다.
장음계는 다음과 같이 구성된다.
여기서 1-2음과 5-6음 사이는 반음이고, 나머지는 온음이다.
음정에는 "단", "장", "완전", "증", "감"과 같은 접두사를 붙여 나타낸다.
오른쪽 그림과 같이 으뜸음 위의 2도 음 쌍은 7쌍이 있지만, '''미~파와 시~도는 반음'''이고, '''그 외의 쌍은 2반음 = 온음'''이다. 전자를 '''단2도''', 후자를 '''장2도'''라고 부른다.[32]
마찬가지로 으뜸음 위의 3도에서는 '''미~파와 시~도'''라는 반음 구간을 포함하는 '''레~파, 미~솔, 라~도는 3반음으로 좁고, 반음 구간을 포함하지 않는 도~미, 파~라, 솔~시는 4반음으로 넓'''기 때문에, 전자를 '''단3도''', 후자를 '''장3도'''라고 부른다.
6도, 7도도 같은 이유로 좁은 쪽에 "단", 넓은 쪽에 "장"이라는 접두사를 붙인다. 4도와 5도는 완전 협화 음정을 포함하기 때문에 "완전", "증", "감"의 접두사를 사용한다.
이러한 명칭은 올림표나 내림표 등의 변화 기호가 붙었을 때 사용한다. 예를 들어 "증2도"와 "단3도"는 모두 12 평균율에서는 3반음으로 동일한 음정이지만, 악보상에서는 왼쪽은 "2도"이고 오른쪽은 "3도"이므로, 왼쪽을 "증2도"라고 부르고 오른쪽을 "단3도"라고 부른다.
| 0반음 | 1반음 | 2반음 | 3반음 | 4반음 | 5반음 | 6반음 | 7반음 | 8반음 | 9반음 | 10반음 | 11반음 | 12반음 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 완전1도 | 단2도 | 장2도 | 단3도 | 장3도 | 완전4도 | 감5도 증4도 | 완전5도 | 단6도 | 장6도 | 단7도 | 장7도 | 완전8도 |
음정에는 온음계 내에 나타나는 음정과 그렇지 않은 음정이 있으며, 전자를 '''온음계적 음정''', 후자를 '''반음계적 음정'''이라고 부르기도 한다. 모든 완전 음정, 장음정, 단음정과 증4도, 감5도가 '''온음계적 음정'''이며, 그 외는 '''반음계적 음정'''이다.
아래는 장음계에 나타나는 각 음정의 일람이다.
| 아래 음\위 음 | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| C | 완전 8도 | 장2도 | 장3도 | 완전 4도 | 완전 5도 | 장6도 | 장7도 |
| D | 단7도 | 완전 8도 | 장2도 | 단3도 | 완전 4도 | 완전 5도 | 장6도 |
| E | 단6도 | 단7도 | 완전 8도 | 단2도 | 단3도 | 완전 4도 | 완전 5도 |
| F | 완전 5도 | 장6도 | 장7도 | 완전 8도 | 장2도 | 장3도 | 증4도 |
| G | 완전 4도 | 완전 5도 | 장6도 | 단7도 | 완전 8도 | 장2도 | 장3도 |
| A | 단3도 | 완전 4도 | 완전 5도 | 단6도 | 단7도 | 완전 8도 | 장2도 |
| B | 단2도 | 단3도 | 완전 4도 | 감5도 | 단6도 | 단7도 | 완전 8도 |
3. 2. 음이름 계산법
절대음감을 가진 사람들은 음정을 계산할 때 음이름에 의존하는 경우가 많다. 이들은 기준음을 계이름 '도', '미'로 생각하기보다 음이름 그대로 계산하는 것을 선호한다.예를 들어 다음과 같이 각 조(Key)의 음계(Scale)를 기준으로 음정 간격을 파악한다.
- C - E를 기준으로 할 때: C Major Key (다장조)는 C - D - E - F - G - A - B - C 이므로 E - F - G - A - B - C - D - E
- D♭ - F를 기준으로 할 때: D♭ Major Key (내림라장조)는 D♭ - E♭ - F - G♭ - A♭ - B♭ - C - D♭ 이므로 F - G♭ - A♭ - B♭ - C - D♭ - E♭ - F
- D - F♯를 기준으로 할 때: D Major Key (라장조)는 D - E - F♯ - G - A - B - C♯ - D 이므로 F♯ - G - A - B - C♯ - D - E - F♯
- E♭ - G를 기준으로 할 때: E♭ Major Key (내림마장조)는 E♭ - F - G - A♭ - B♭ - C - D - E♭ 이므로 G - A♭ - B♭ - C - D - E♭ - F - G
- E - G♯를 기준으로 할 때: E Major Key (마장조)는 E - F♯ - G♯ - A - B - C♯ - D♯ - E 이므로 G♯ - A - B - C♯ - D♯ - E - F♯ - G♯
- F - A를 기준으로 할 때: F Major Key (바장조)는 F - G - A - B♭ - C - D - E - F 이므로 A - B♭ - C - D - E - F - G - A
- F♯ - A♯를 기준으로 할 때: F♯ Major Key (올림바장조)는 F♯ - G♯ - A♯ - B - C♯ - D♯ - E♯ - F♯ 이므로 A♯ - B - C♯ - D♯ - E♯ - F♯ - G♯ - A♯
- G♭ - B♭를 기준으로 할 때: G♭ Major Key (내림사장조)는 G♭ - A♭ - B♭ - C♭ - D♭ - E♭ - F - G♭ 이므로 B♭ - C♭ - D♭ - E♭ - F - G♭ - A♭ - B♭
- G - B를 기준으로 할 때: G Major Key (사장조)는 G - A - B - C - D - E - F♯ - G 이므로 B - C - D - E - F♯ - G - A - B
- A♭ - C를 기준으로 할 때: A♭ Major Key (내림가장조)는 A♭ - B♭ - C - D♭ - E♭ - F - G - A♭ 이므로 C - D♭ - E♭ - F - G - A♭ - B♭ - C
- A - C♯를 기준으로 할 때: A Major Key (가장조)는 A - B - C♯ - D - E - F♯ - G♯ - A 이므로 C♯ - D - E - F♯ - G♯ - A - B - C♯
- B♭ - D를 기준으로 할 때: B♭ Major Key (내림나장조)는 B♭ - C - D - E♭ - F - G - A - B♭ 이므로 D - E♭ - F - G - A - B♭ - C - D
- B - D♯를 기준으로 할 때: B Major Key (나장조)는 B - C♯ - D♯ - E - F♯ - G♯ - A♯ - B 이므로 D♯ - E - F♯ - G♯ - A♯ - B - C♯ - D♯
음정에는 "단", "장", "완전", "증", "감"과 같은 접두사를 붙여 나타낸다.
"단", "장"과 같은 접두사를 붙이는 이유는 다음과 같다.
위 그림과 같이, 으뜸음 위의 2도의 음의 쌍은 7쌍이 있지만, '''미~파와 시~도는 반음'''이고, '''그 외의 쌍은 2반음 = 온음''' 떨어져 있다. 전자를 '''단2도''', 후자를 '''장2도'''라고 부른다[32]。
마찬가지로, 으뜸음 위의 3도에서는 '''미~파와 시~도'''라는 반음 구간을 포함하는 '''레~파, 미~솔, 라~도는 3반음으로 좁고, 반음 구간을 포함하지 않는 도~미, 파~라, 솔~시는 4반음으로 넓'''기 때문에, 전자를 '''단3도''', 후자를 '''장3도'''라고 부른다.
6도, 7도도 같은 이유로, 으뜸음 위에는 반음 다른 크고 작은 2종류의 음정이 있으므로, 좁은 쪽에 "단" · 넓은 쪽에 "장"이라는 접두사를 붙인다.
4도와 5도 또한 기본 음정 위에서 두 종류의 음정이 있지만, 완전 협화 음정을 포함하기 때문에 "완전", "증", "감"의 접두사를 사용한다.
- 4도의 경우, 다(도) - 파, 라(레) - 솔(소) 등, 반음 구간을 포함하며 완전 협화 음정인 5반음의 경우를 "'''완전 4도'''", 반음 구간을 포함하지 않는 파 - 시(si)의 6반음의 경우를 "'''증 4도'''"라고 부른다[32]。
- 5도의 경우, 반음 구간을 2번 포함하며 6반음인 시 - 파를 "'''감 5도'''", 그 외의 반음 구간을 1번만 포함하는 다(도) - 솔(소) 등 완전 협화 음정인 7반음의 경우를 "'''완전 5도'''"라고 부른다[32]。
앞서 언급했듯이 "증4도"와 "감5도"는 모두 12음 평균율에서는 6반음으로 동일한 음정이지만, 악보상에서는 다르다. 예를 들어, 위 그림의 두 쌍의 음은 모두 6반음 차이지만, 악보상에서 왼쪽은 4도이므로 "증4도", 오른쪽은 5도이므로 "감5도"라고 부른다. '''트라이톤'''(tritone)이라고도 부른다.
- '''장''' 또는 '''완전'''보다 반 음 넓은 음정에 '''증'''(増, 조), 2반음 넓은 음정에 '''중증'''(重増, 주조)이라는 접두사를 붙여 부른다(예: 증7도, 중증7도, 증5도, 중증5도).
- '''단''' 또는 '''완전'''보다 반 음 좁은 음정에 '''감'''(減, 겐), 2반음 좁은 음정에 '''중감'''(重減, 주겐)이라는 접두사를 붙여 부른다.
이러한 명칭은 예를 들어 올림표나 내림표 등의 변화 기호가 붙었을 때 사용한다.
예를 들어 위 그림에서 "증2도"와 "단3도"는 모두 12 평균율에서는 3반음으로 동일한 음정이지만, 악보상에서는 왼쪽은 "2도"이고 오른쪽은 "3도"이므로, 왼쪽을 "증2도"라고 부르고 오른쪽을 "단3도"라고 부른다.
| 0반음 | 1반음 | 2반음 | 3반음 | 4반음 | 5반음 | 6반음 | 7반음 | 8반음 | 9반음 | 10반음 | 11반음 | 12반음 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 완전1도 | 단2도 | 장2도 | 단3도 | 장3도 | 완전4도 | 감5도 증4도 | 완전5도 | 단6도 | 장6도 | 단7도 | 장7도 | 완전8도 |
음정에는 온음계 내에 나타나는 음정과 그렇지 않은 음정이 있으며, 전자를 '''온음계적 음정''', 후자를 '''반음계적 음정'''이라고 부르기도 한다. 모든 완전 음정, 장음정, 단음정과 증4도, 감5도가 '''온음계적 음정'''이며, 그 외는 '''반음계적 음정'''이다.
아래는 장음계에 나타나는 각 음정의 일람이다.
| 아래 음\위 음 | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| C | 완전 8도 | 장2도 | 장3도 | 완전 4도 | 완전 5도 | 장6도 | 장7도 |
| D | 단7도 | 완전 8도 | 장2도 | 단3도 | 완전 4도 | 완전 5도 | 장6도 |
| E | 단6도 | 단7도 | 완전 8도 | 단2도 | 단3도 | 완전 4도 | 완전 5도 |
| F | 완전 5도 | 장6도 | 장7도 | 완전 8도 | 장2도 | 장3도 | 증4도 |
| G | 완전 4도 | 완전 5도 | 장6도 | 단7도 | 완전 8도 | 장2도 | 장3도 |
| A | 단3도 | 완전 4도 | 완전 5도 | 단6도 | 단7도 | 완전 8도 | 장2도 |
| B | 단2도 | 단3도 | 완전 4도 | 감5도 | 단6도 | 단7도 | 완전 8도 |
3. 3. 반음 개수 계산법
기준음과 비교 대상 음 사이의 반음 개수를 세어 음정을 계산하는 방법이다. 암기 능력과 속셈에 능숙한 사람들에게 유용하다.| 반음 개수 | 음정 |
|---|---|
| 0 | 완전1도 |
| 1 | 단2도 |
| 2 | 장2도 |
| 3 | 단3도 |
| 4 | 장3도 |
| 5 | 완전4도 |
| 6 | 증4도, 감5도 |
| 7 | 완전5도 |
| 8 | 단6도 |
| 9 | 장6도 |
| 10 | 단7도 |
| 11 | 장7도 |
| 12 | 완전8도 |
하지만 이 방법은 악보 표기 상의 음정과 차이가 있을 수 있다. 예를 들어 피아노 건반 상 C♯ - D♯은 장2도이지만, 악보에 C♯ - E♭으로 표기된 경우 감3도로 해석해야 한다.[42]
3. 4. 계산 시 주의점
계이름 계산법이나 음이름 계산법으로 음정을 계산할 때 계이름과 음이름의 차이를 이해하지 못하면 음정의 성질을 잘못 계산할 수 있다.[43]계이름은 조성에 따라 음이름이 달라진다. 다장조(C Major Key)에서 계이름 '도'는 음이름 'C'이지만, 사장조(G Major Key)에서 계이름 '도'는 음이름 'G'이다. 이처럼 조성에 관계없이 계이름은 으뜸음을 '도'부터 시작해서 부르는 것이 권장된다.[43]
예를 들어, 바장조(F Major Key)에서 계이름 '도 레 미 파 솔 라 시 도'는 음이름 'F G A B♭ C D E F'가 된다. 따라서 바장조에서 2, 3, 6, 7음을 반음 내린 계이름 '도 레♭ 미♭ 파 솔 라♭ 시♭ 도'는 음이름 'F G♭ A♭ B♭ C D♭ E♭ F'가 된다. 나장조(B Major Key)에서 계이름 '도 레 미 파 솔 라 시 도'는 음이름 'B C♯ D♯ E F♯ G♯ A♯ B'가 된다. 따라서 나장조에서 2, 3, 6, 7음을 반음 내린 계이름 '도 레♭ 미♭ 파 솔 라♭ 시♭ 도'는 음이름 'B C D E F♯ G A B'가 된다.
F - B는 도수상 4도이지만[44], 완전4도가 아니다. F와 B가 완전4도가 되려면 B가 B♭로, 또는 F가 F♯로 바뀌어야 한다. (F - B♭ 또는 F♯ - B) 마찬가지로 B - F는 도수상 5도이지만[45], 완전5도가 아니다. B와 F가 완전5도가 되려면 F가 F♯로, 또는 B가 B♭로 바뀌어야 한다. (B - F♯ 또는 B♭ - F)

| 음이름 기준 | 계이름 기준 | 음정 |
|---|---|---|
| F - F | 도 - 도, 미 - 미 | 완전1도 |
| F - G | 도 - 레, 미 - 파♯ | 장2도 |
| F - A | 도 - 미, 미 - 솔♯ | 장3도 |
| F - B | 도 - 파♯, 미 - 라♯ | 증4도 |
| F - C | 도 - 솔, 미 - 시 | 완전5도 |
| F - B♭ | 도 - 파, 미 - 라 | 완전4도 |
| F - D | 도 - 라, 미 - 도♯ | 장6도 |
| F - E | 도 - 시, 미 - 레♯ | 장7도 |
| B - B | 도 - 도, 미 - 미 | 완전1도 |
| B - C | 도 - 레♭, 미 - 파 | 단2도 |
| B - D | 도 - 미♭, 미 - 솔 | 단3도 |
| B - E | 도 - 파, 미 - 라 | 완전4도 |
| B - F | 도 - 솔♭, 미 - 시♭ | 감5도 |
| B - F♯ | 도 - 솔, 미 - 시 | 완전5도 |
| B - G | 도 - 라♭, 미 - 도 | 단6도 |
| B - A | 도 - 시♭, 미 - 레 | 단7도 |
4. 장/단, 완전의 구분
음정에는 장/단, 완전의 구분이 있다. 1, 4, 5, 8도 음정은 "완전"으로, 2, 3, 6, 7도 음정은 "장/단"으로 구분한다.[46] 이는 음의 조화로운 울림에 영향을 미치는 배음과 관련이 있다.
사인파를 제외한 모든 음은 실제로 여러 개의 음이 같이 울리는데, 이를 배음이라고 한다. 인간은 배음 중 가장 잘 들리는 1배음을 주로 듣기 때문에 하나의 음으로 인식한다.[46]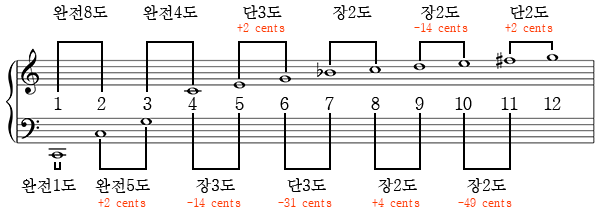
배음을 근음(1배음)부터 12배음까지 나열하여 각 배음의 음정을 살펴보면 다음과 같다.
- 근음 C2와 1배음 C2는 완전1도이다.
- 1배음 C2와 2배음 C3는 완전8도이다.
- 2배음 C3와 3배음 G3는 완전5도이다. (실제 3배음은 G3보다 +2 센트 높은 음이다.)
- 3배음 G3와 4배음 C4는 완전4도이다.
- 4배음 C4와 5배음 E4는 장3도이다. (실제 5배음은 E4보다 -14 센트 낮은 음이다.)
- 5배음 E4와 6배음 G4는 단3도이다. (실제 6배음은 G4보다 +2 센트 높은 음이다.)
- 6배음 G4와 7배음 Bb4는 단3도이다. (실제 7배음은 Bb4보다 -31 센트 낮은 음이다.)
- 7배음 Bb4와 8배음 C5는 장2도이다.
- 8배음 C5와 9배음 D5는 장2도이다. (실제 9배음은 D5보다 +4 센트 높은 음이다.)
- 9배음 D5와 10배음 E5는 장2도이다. (실제 10배음은 E5보다 -14 센트 낮은 음이다.)
- 10배음 E5와 11배음 F#5는 장2도이다. (실제 11배음은 F#5보다 -49 센트 낮은 음이다.)[47]
- 11배음 F#5와 12배음 G5는 단2도이다. (실제 12배음은 G5보다 +2 센트 높은 음이다.)
센트 (음악)는 단2도보다 더 좁은 간격, 즉 12음계를 벗어난 미세한 간격을 측정할 때 사용하는 단위이다.
일반적으로 인간은 5센트까지의 차이는 잘 구분하지 못한다. 따라서 4배음까지는 부조화를 느끼지 못해 완전한 울림으로, 5배음부터는 부조화를 느껴 완전 대신 장/단을 사용하기 시작한 것에서 유래되었다.[46]
5. 그 외 명칭
특정 음정은 "성질 + 도수" 표기법 외에 다른 명칭으로 불리기도 한다. 음정은 종종 완전 음정에는 '''P''', 단음정에는 '''m''', 장음정에는 '''M''', 감소 음정에는 '''d''', 증가 음정에는 '''A'''를 사용하여 줄여서 표기하며, 그 뒤에 음정 번호가 따라온다. M과 P 표시는 종종 생략된다.
예시:
- m2 (또는 min2): 단2도
- M3 (또는 maj3): 장3도
- A4 (또는 aug4): 증4도
- d5 (또는 dim5): 감5도
- P5 (또는 perf5): 완전5도
완전1도는 유니즌, 단2도는 반음, 장2도는 온음, 증4도와 감5도는 셋온음, 완전8도는 옥타브라고 부른다.
| 0반음 | 1반음 | 2반음 | 3반음 | 4반음 | 5반음 | 6반음 | 7반음 | 8반음 | 9반음 | 10반음 | 11반음 | 12반음 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 완전1도 | 단2도 | 장2도 | 단3도 | 장3도 | 완전4도 | 감5도 증4도 | 완전5도 | 단6도 | 장6도 | 단7도 | 장7도 | 완전8도 |
음정에는 온음계 내에 나타나는 음정과 그렇지 않은 음정이 있으며, 전자를 '''온음계적 음정''', 후자를 '''반음계적 음정'''이라고 부르기도 한다. 모든 완전 음정, 장음정, 단음정과 증4도, 감5도가 온음계적 음정이며, 그 외는 반음계적 음정이다.
아래는 장음계에 나타나는 각 음정의 일람이다.
| 아래 음\위 음 | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| C | 완전 8도 | 장2도 | 장3도 | 완전4도 | 완전5도 | 장6도 | 장7도 |
| D | 단7도 | 완전 8도 | 장2도 | 단3도 | 완전4도 | 완전5도 | 장6도 |
| E | 단6도 | 단7도 | 완전 8도 | 단2도 | 단3도 | 완전4도 | 완전5도 |
| F | 완전5도 | 장6도 | 장7도 | 완전 8도 | 장2도 | 장3도 | 증4도 |
| G | 완전4도 | 완전5도 | 장6도 | 단7도 | 완전 8도 | 장2도 | 장3도 |
| A | 단3도 | 완전4도 | 완전5도 | 단6도 | 단7도 | 완전 8도 | 장2도 |
| B | 단2도 | 단3도 | 완전4도 | 감5도 | 단6도 | 단7도 | 완전 8도 |
5. 1. 유니즌 (Unison)
완전1도는 유니즌(Unison)이라고 부른다.[32] 1도는 "동도"라고도 부른다.[32]5. 2. 반음 (Semitone, half tone, half step)
단2도는 반음(Semitone, half tone, half step)이라고 부른다.[48]으뜸음 위의 2도의 음의 쌍은 7쌍이 있지만, 미~파와 시~도는 반음이고, 그 외의 쌍은 2반음 = 온음(Tone, whole tone, whole step) 떨어져 있다. 전자를 단2도, 후자를 장2도라고 부른다.[32]
5. 3. 온음 (Tone, whole tone, whole step)
장2도(Major 2nd)는 온음(Tone, whole tone, whole step)이라고 부른다.[48]whole tone영어 또는 whole step영어이라고도 한다.
오른쪽 그림과 같이, 으뜸음 위의 2도의 음의 쌍은 7쌍이 있지만, '''미~파와 시~도는 반음'''이고, '''그 외의 쌍은 2반음 = 온음''' 떨어져 있다. 전자를 '''반음(단2도)''', 후자를 '''온음(장2도)'''라고 부른다.[32]
5. 4. 셋온음 (Tritone)
몇 가지 음정의 경우에는 "성질 + 도수" 표기법을 벗어나 하나의 단어로 바꿔 부르기도 하는데, 증4도와 감5도가 이에 해당한다. 이 두 음정은 도수의 해석은 다르나 음과 음 사이의 실제 간격은 같다고 볼 수 있는데, 이 음정을 셋온음(Tritone)이라고 부른다.[48]12음 평균율에서는 증4도와 감5도는 모두 6반음으로 동일한 음정이지만, 악보상에서는 다르다. 예를 들어, 아래 그림과 같이 두 쌍의 음은 모두 6반음 차이지만, 악보상에서 왼쪽은 4도이므로 "증4도", 오른쪽은 5도이므로 "감5도"라고 부른다.
트라이톤(tritone)이라고도 부른다.
5. 5. 옥타브 (Octave)
완전8도는 옥타브(Octave)라고 부른다.[32] 1도와 8도의 경우, 으뜸음 위에 완전 협화 음정 한 종류(1도는 0반음, 8도는 12반음)밖에 없으므로, 1도의 쌍(같은 음)을 "완전 1도", 8도 떨어진 쌍을 "완전 8도"라고 한다.[32]6. 평균율 음정 기억법
| 음정 | 높아짐 | 낮아짐 |
|---|---|---|
| 단2도 | 신세계 교향곡 4악장, 모차르트의 자장가 (잘자라 우리아기) | 엘리제를 위하여, 아침 이슬 |
| 장2도 | 생일 축하합니다, 학교종, 아리랑, 고요한 밤, 루돌프 | 고드름, 군밤타령, 비행기, 개똥벌레 |
| 단3도 | 따르릉, 봄(엄마엄마 이리와) | 개나리, 산토끼, 나비야, 설날, 그대로 멈춰라, 뽀뽀뽀 |
| 장3도 | 딩동댕 종소리, 똑같아요, 바둑이 방울, 우리들은 일학년, 곰 세 마리 | 운명 교향곡, 수업 종소리 |
| 완전4도 | 애국가, 결혼행진곡, 고기잡이, 어린 음악대, 과수원 길 | 산중호걸, 파란마음 하얀마음(우리들 마음에 빛이 있다면), 경찰차 싸이렌 |
| 트라이톤 | 더 심슨 주제곡, 마리아 (웨스트 사이드 스토리) | |
| 완전5도 | 반짝반짝 작은별, 스타워즈 메인 테마 | 바흐 미뉴에트(솔 도레미파 솔 도 도), 플린스톤, 슈퍼맨 |
| 단6도 | 러브스토리, 엔터테이너 | |
| 장6도 | 오빠 생각, 등대지기, 스승의 은혜, 코끼리 아저씨, 징글벨(흰 눈 사이로), 새싹들이다, 이히 리베 디히 | 청혼 (이소라) |
| 단7도 | 스타트랙, 난 행복해, 금지된 사랑 | |
| 장7도 | 노라 존스의 Don't know why' | |
| 완전8도 | 썸웨어 오버 더 레인보우 | 레이지 어게인스트 더 머신의 Bulls on Parade 기타 리프. |
7. 음정의 크기
음정의 크기(너비 또는 높이라고도 함)는 주파수 비율 또는 센트로 나타낼 수 있으며, 각각 다른 맥락에 적합하다.
전통적인 음정 명칭 외에, 음정을 정량적으로 정의하는 단위로 센트가 있다. 센트는 1옥타브가 1200센트가 되도록 정의된다. 평균율의 반음은 그 1/12이므로 100센트가 된다.
센트는 엄밀하게는 주파수의 대수로 정의된다. 두 음의 주파수비가 일 때, 그 두 음의 음정의 센트는 다음과 같이 정의된다.[40]
:
7. 1. 주파수 비율
두 음 사이의 음정 크기는 해당 음의 주파수 비율로 측정할 수 있다. 순정율 조율 시스템을 사용하여 악기를 조율할 때, 주요 음정의 크기는 1:1 (일치), 2:1 (옥타브), 5:3 (장6도), 3:2 (완전5도), 4:3 (완전4도), 5:4 (장3도), 6:5 (단3도)와 같은 작은 정수 비율로 표현될 수 있다. 작은 정수 비율을 가진 음정은 종종 ''순정 음정'' 또는 ''깨끗한 음정''이라고 불린다.그러나 오늘날 대부분의 악기는 12음 평균율이라는 다른 조율 시스템을 사용하여 조율된다. 결과적으로, 대부분의 평균율 음정의 크기는 작은 정수 비율로 표현될 수 없지만, 해당 순정 음정의 크기와 매우 가깝다. 예를 들어, 평균율 완전5도는 27/12:1의 주파수 비율을 가지며, 이는 대략 1.498:1 또는 2.997:2 (3:2에 매우 가깝다)와 같다.
7. 2. 센트 (Cents)
센트는 로그 척도의 음정 측정 단위이다. 12음 평균율에서 한 반음은 100센트이다. 따라서 12음 평균율에서 센트는 반음의 100분의 1로 정의될 수 있다.[40]주파수 ''f''1에서 주파수 ''f''2까지의 음정 크기(센트)는 다음 공식으로 계산된다.[40]
:
순정율 조율 시스템을 사용하는 악기에서 주요 음정의 크기는 작은 정수 비율로 표현될 수 있다. 예를 들어 1:1 (일치), 2:1 (옥타브), 5:3 (장6도) 등이 있다. 그러나 오늘날 대부분의 악기는 12음 평균율로 조율되므로, 대부분의 평균율 음정 크기는 작은 정수 비율로 표현하기 어렵지만 순정 음정의 크기와 매우 가깝다.
8. 주요 음정
반음계의 음 사이 간격에 대한 가장 널리 사용되는 전통적인 이름은 다음 표와 같다. 완전 협화음(완전 기본음이라고도 함)[5]은 두 개의 동일한 음으로 형성되며, 크기는 0 센트이다. 반음은 반음계의 두 인접한 음 사이의 간격이며, 온음은 두 반음을 포함하는 간격(예: 장2도)이다. 트라이톤은 세 개의 음, 즉 여섯 개의 반음을 포함하는 간격(예: 증4도)이다.
| 반음 수 | 단, 장, 또는 완전 간격 | 약어 | 증 또는 감 간격 | 약어 | 널리 사용되는 대안적 이름 | 약어 | 오디오 |
|---|---|---|---|---|---|---|---|
| 0 | 완전 협화음 | P1 | 감2도 | d2 | |||
| 1 | 단2도 | m2 | 증1도 | A1 | 반음, 하프 톤, 하프 스텝 | S | |
| 2 | 장2도 | M2 | 감3도 | d3 | 온음, 전체 톤, 전체 스텝 | T | |
| 3 | 단3도 | m3 | 증2도 | A2 | |||
| 4 | 장3도 | M3 | 감4도 | d4 | |||
| 5 | 완전4도 | P4 | 증3도 | A3 | |||
| 6 | rowspan="2" colspan="2"| | 감5도 | d5 | 트라이톤 | TT | ||
| 증4도 | A4 | ||||||
| 7 | 완전5도 | P5 | 감6도 | d6 | |||
| 8 | 단6도 | m6 | 증5도 | A5 | |||
| 9 | 장6도 | M6 | 감7도 | d7 | |||
| 10 | 단7도 | m7 | 증6도 | A6 | |||
| 11 | 장7도 | M7 | 감8도 | d8 | |||
| 12 | 완전 옥타브 | P8 | 증7도 | A7 |
9. 음정 번호와 성질 (Interval Number and Quality)
음정은 서양 음악 이론에서 '수'(number)와 '품질'(quality)에 따라 이름이 붙여진다.[6][7] 예를 들어 '장3도'(major third, M3)는 '장'(major, M)은 음정의 품질, '3도'(third, 3)는 음의 수를 나타낸다. 음정 명칭은 오선보 간격으로 "◯도"로 결정되며, 1옥타브 이하 음정은 '''단음정''', 그 이상은 '''겹음정'''이라 한다.
음정에는 "단", "장", "완전", "증", "감"과 같은 접두사가 붙는다.
- "단", "장" 접두사: 으뜸음 위 2도, 3도, 6도, 7도는 반음 차이로 크기가 다른 두 종류가 있다. 좁은 쪽은 "단", 넓은 쪽은 "장"을 붙인다. (예: 미~파, 시~도는 반음 간격 '''단2도''', 나머지는 온음 간격 '''장2도''')[32]
- "완전", "증", "감" 접두사: 4도, 5도는 완전 협화 음정을 포함하여 "완전", "증", "감"을 쓴다. (예: 5반음 '''완전4도''', 6반음 '''증4도''', 6반음 '''감5도''', 7반음 '''완전5도''')[32] 1도, 8도는 완전 협화 음정 한 종류만 있어 '''완전1도'''(유니즌), '''완전8도'''이다.[32]
트라이톤(tritone)("증4도", "감5도")은 12음 평균율에서 6반음으로 같지만, 악보 표기는 다르다.
- "증"(増), "중증"(重増) 접두사: '''장''' 또는 '''완전'''보다 반음 넓으면 '''증''', 2반음 넓으면 '''중증'''이다.
- "감"(減), "중감"(重減) 접두사: '''단''' 또는 '''완전'''보다 반음 좁으면 '''감''', 2반음 좁으면 '''중감'''이다.
올림표, 내림표 등 변화 기호에 따라 음정 명칭이 달라진다. (예: 12평균율에서 "증2도", "단3도"는 모두 3반음이나, 악보 표기로 구분)
다음은 반음 수에 따른 음정 명칭이다.[33][34]
| 0반음 | 1반음 | 2반음 | 3반음 | 4반음 | 5반음 | 6반음 | 7반음 | 8반음 | 9반음 | 10반음 | 11반음 | 12반음 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 완전1도 | 단2도 | 장2도 | 단3도 | 장3도 | 완전4도 | 감5도 증4도 | 완전5도 | 단6도 | 장6도 | 단7도 | 장7도 | 완전8도 |
다음은 반음계 음 간격의 전통적 이름이다.
| 반음 수 | 단, 장, 완전 간격 | 약어 | 증, 감 간격 | 약어 | 대안적 이름 | 약어 | 오디오 |
|---|---|---|---|---|---|---|---|
| 0 | 완전 협화음 | P1 | 감2도 | d2 | -- | ||
| 1 | 단2도 | m2 | 증1도 | A1 | 반음 | S | -- |
| 2 | 장2도 | M2 | 감3도 | d3 | 온음 | T | -- |
| 3 | 단3도 | m3 | 증2도 | A2 | -- | ||
| 4 | 장3도 | M3 | 감4도 | d4 | -- | ||
| 5 | 완전4도 | P4 | 증3도 | A3 | -- | ||
| 6 | rowspan="2" colspan="2"| | 감5도 | d5 | 트라이톤 | TT | -- | |
| 증4도 | A4 | ||||||
| 7 | 완전5도 | P5 | 감6도 | d6 | -- | ||
| 8 | 단6도 | m6 | 증5도 | A5 | -- | ||
| 9 | 장6도 | M6 | 감7도 | d7 | -- | ||
| 10 | 단7도 | m7 | 증6도 | A6 | -- | ||
| 11 | 장7도 | M7 | 감8도 | d8 | -- | ||
| 12 | 완전 옥타브 | P8 | 증7도 | A7 | -- |
9. 1. 수 (Number)
음정의 수는 음이름 또는 오선 위치(선과 간)의 개수를 의미한다. 예를 들어 B-D는 B부터 D까지 음이름(B, C, D)이 세 개이고, B와 D의 위치를 포함하여 세 개의 연속된 오선 위치를 차지하기 때문에 셋째 음(m3)이다.[6][7] 온음계 음계 차수를 세어 결정할 수도 있다.오선 위치와 온음계 음계 차수 사이에는 일대일 대응이 있다. 음정 번호는 오선 위치 대신 온음계 음계를 세어 결정할 수 있는데, 이는 음정을 형성하는 두 음이 온음계 음계에서 나온다는 조건 하에 가능하다. 즉, B-D는 B와 D를 포함하는 모든 온음계 음계에서 B에서 D까지의 시퀀스에 세 개의 음이 포함되기 때문에 셋째 음이다.
음정을 형성하는 음에 임시표를 추가하면, 정의상 해당 음의 오선 위치는 변경되지 않는다. 결과적으로, 모든 음정은 임시표가 없는 동일한 음으로 형성된 해당 자연 음정과 동일한 음정 번호를 갖는다. 예를 들어, B-D(반음 4개)와 B-D(반음 2개) 음정은 자연 음정 B-D(반음 3개)와 마찬가지로 셋째 음이다.
음정 번호는 종점을 뺀 차이가 아니라, 포함된 오선 위치 또는 음 이름의 개수를 포함하는 방식으로 세는 것에 유의해야 한다. 즉, 낮은 음을 0이 아닌 1부터 세기 시작한다.
9. 2. 품질 (Quality)
서양 음악 이론에서 음정은 '수'(number, 또는 '음계적 수', '음정 크기'[6], '일반 음정'[7])와 '품질'(quality)에 따라 이름이 붙여진다. 예를 들어, '장3도'(major third, '''M3''')는 음정의 이름이며, 여기서 '장'(major, '''M''')은 음정의 품질을, '3도'(third, '''3''')는 음의 수를 나타낸다.완전 음정은 전통적으로 완벽하게 협화적인 것으로 간주되었기 때문에 그렇게 불린다.[9] 하지만 서양 고전 음악에서는 완전 사도가 때때로 덜 완벽한 협화음으로 여겨졌는데, 그 기능이 대위법적일 때였다. 반대로 단, 장, 증, 감 음정은 일반적으로 협화음보다 덜하다고 여겨지며, 전통적으로 보통 협화음, 불완전 협화음 또는 거의 불협화음으로 분류되었다.[9]
온음계 내에서 모든 일도 ('''P1''')와 팔도 ('''P8''')는 완전 음정이다. 대부분의 사도와 오도도 완전 음정 ('''P4'''와 '''P5''')이며, 각각 5개와 7개의 반음을 포함한다. 사도의 한 예는 증4도 ('''A4''')이고, 오도의 한 예는 감5도 ('''d5''')인데, 둘 다 6개의 반음을 포함한다.
완전 음정의 전위도 완전 음정이다. 전위는 두 음의 음높이 종류를 변경하지 않으므로, 그들의 협화도 수준 (그들의 배음의 일치)에 거의 영향을 미치지 않는다. 반대로, 다른 종류의 음정은 전위에 대해 반대되는 성질을 갖는다. 장 음정의 전위는 단 음정이고, 증 음정의 전위는 감 음정이다.
완전음정과 옥타브를 제외하고, 주어진 음정 번호의 온음계적 음정은 항상 두 가지 크기로 나타나며, 이는 반음 하나로 차이가 난다. 예를 들어, 5도 중 6개는 7 반음을 포함한다. 다른 하나는 6 반음을 포함한다. 3도 중 4개는 3 반음을 포함하고, 다른 3도는 4 반음을 포함한다. 두 버전 중 하나가 완전 음정인 경우, 다른 하나는 감(즉, 반음 하나 좁힘) 또는 증(즉, 반음 하나 넓힘)이라고 한다. 그렇지 않으면 더 큰 버전을 장, 더 작은 버전을 단이라고 한다. 예를 들어, 7 반음의 5도는 완전 음정('''P5''')이므로, 6 반음의 5도는 "감5도"('''d5''')라고 한다. 반대로, 두 종류의 3도 모두 완전 음정이 아니기 때문에, 더 큰 쪽은 "장3도"('''M3'''), 더 작은 쪽은 "단3도"('''m3''')라고 한다.
증진된 음정, 감소된 음정
thumb
증진된 음정은 완전 또는 장 음정보다 반음 하나만큼 넓으며, 같은 음정 번호를 갖는다. 반면에, 감소된 음정은 같은 음정 번호의 완전 또는 단 음정보다 반음 하나만큼 좁다.
음정은 종종 완전 음정에는 '''P''', 단음정에는 '''m''', 장음정에는 '''M''', 감소 음정에는 '''d''', 증가 음정에는 '''A'''를 사용하여 줄여서 표기하며, 그 뒤에 음정 번호가 따라온다. M과 P 표시는 종종 생략된다. 옥타브는 P8이고, 겹일치는 일반적으로 단순히 "겹일치"라고 하지만 P1으로 표기할 수도 있다. 증4도 또는 감5도인 트라이톤은 종종 '''TT'''로 표기한다. 음정의 종류는 '''perf''', '''min''', '''maj''', '''dim''', '''aug'''로 줄여서 표기할 수도 있다. 예시:
- m2 (또는 min2): 단2도,
- M3 (또는 maj3): 장3도,
- A4 (또는 aug4): 증4도,
- d5 (또는 dim5): 감5도,
- P5 (또는 perf5): 완전5도.
음정에 "단", "장", "완전", "증", "감"과 같은 접두사를 붙여 음정을 나타낸다.
4도와 5도 또한 기본 음정 위에서 두 종류의 음정이 있지만, 완전 협화 음정을 포함하기 때문에 "완전", "증", "감"의 접두사를 사용한다.
- '''장''' 또는 '''완전'''보다 반 음 넓은 음정에 '''증'''(増)이라는 접두사를 붙여 부른다.
- '''단''' 또는 '''완전'''보다 반 음 좁은 음정에 '''감'''(減)이라는 접두사를 붙여 부른다.
| 0반음 | 1반음 | 2반음 | 3반음 | 4반음 | 5반음 | 6반음 | 7반음 | 8반음 | 9반음 | 10반음 | 11반음 | 12반음 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 완전1도 | 단2도 | 장2도 | 단3도 | 장3도 | 완전4도 | 감5도 증4도 | 완전5도 | 단6도 | 장6도 | 단7도 | 장7도 | 완전8도 |
10. 전위 (Inversion)
단순 음정은 낮은 음을 옥타브만큼 높이거나 높은 음을 옥타브만큼 낮춰서 전위할 수 있다. 예를 들어 낮은 C에서 높은 F까지의 4도는 낮은 F에서 높은 C까지의 5도를 만들도록 전위될 수 있다.[10]
어떤 단순 음정의 전위의 수와 음질을 결정하는 두 가지 규칙이 있다.[10]
# 음정 번호와 그 전위의 번호를 더하면 항상 9가 된다(예: 4 + 5 = 9).
# 장음정의 전위는 단음정이고, 그 반대도 성립한다. 완전 음정의 전위도 완전 음정이다. 증음정의 전위는 감음정이고, 그 반대도 성립한다. 배증 음정의 전위는 배감 음정이고, 그 반대도 성립한다.
예를 들어, C에서 그 위의 E까지의 음정은 단3도이다. 방금 제시된 두 규칙에 따라, E에서 그 위의 C까지의 음정은 장6도여야 한다.
복합 음정은 옥타브보다 크므로 "어떤 복합 음정의 전위는 항상 그것이 합성된 단순 음정의 전위와 같다".[11]
비율로 식별되는 음정의 경우, 전위는 비율을 역전시키고 비율에 2를 곱하여 1보다 커질 때까지 결정된다. 예를 들어, 5:4 비율의 전위는 8:5 비율이다.
반음의 정수 번호로 식별되는 음정의 경우, 전위는 해당 숫자를 12에서 빼서 얻는다.
음정 클래스는 음정 정수와 그 전위 중에서 선택된 더 낮은 숫자이므로, 음정 클래스는 전위될 수 없다.
두 음의 쌍 중 높은 음을 1옥타브 내리는 것을 '''전위'''(転回, 텐카이)라고 한다. 예를 들어 "C"와 "E"의 쌍이 있을 때, 높은 음인 E를 "1옥타브 낮은 E"와 (원래 옥타브와 같은) "C"의 쌍이 원래 쌍의 전위가 된다. 음정을 전위함으로써 그 결과로 생기는 음정을 '''전위 음정'''(転回音程, 텐카이온테이)이라고 한다.[32]
두 음의 양쪽을 1옥타브씩 옮겨도 음정은 변하지 않으므로, 높은 음을 1옥타브 내리는 대신 낮은 음을 1옥타브 올려도 전위가 된다.[39]
두 음의 쌍이 반음 떨어져 있을 때, 전위된 쌍은 반음 떨어져 있게 되므로, 다음과 같다.
전위 음정의 전위 음정은 원래대로 돌아온다. 상술한 대응 관계에서 알 수 있듯이, 전위 음정의 명칭은 다음과 같이 구할 수 있다.
- 원래 음정이 도이면, 전위 음정은 도이다.
- '''장'''←→'''단''', '''증'''←→'''감''', '''겹증'''←→'''겹감'''으로 바꾼다.
- 원래 음정이 "'''완전'''"이면 전위 음정도 "'''완전'''"으로 한다.
전위는 쌍의 한쪽 음을 1옥타브 올리거나 내리는 행위이며, 1옥타브 올리는 것은 주파수를 2배로 하는 행위이므로, '''주파수비가 a:b인 음의 쌍을 전위하면 주파수비가 b:2a가 된다'''.
11. 분류 (Classification)
음정은 다양한 기준에 따라 설명, 분류하거나 서로 비교할 수 있다. 기본적으로 오선보에서의 간격으로 "◯도"라는 명칭이 결정되며, 1옥타브 이하의 음정을 '''단음정''', 그 이상을 '''겹음정'''이라고 한다.
- 단순 및 복합 (Simple and Compound): 옥타브를 기준으로 한 옥타브 이하의 음정은 단순 음정, 그 이상의 음정은 겹음정이라고 한다. 겹음정은 단순 음정에 하나 이상의 옥타브를 더하여 얻을 수 있다.[32] 예를 들어, 13반음 이상 차이 나는 경우는 복음정이라고 하며, "3 옥타브와 완전 4도"와 같이 옥타브 수와 단음정의 조합으로 나타낸다.[35]
- 이명동음 (Enharmonic Intervals): 표기법은 다르지만 동일한 음높이를 가지는 음정들을 말한다. 즉, 두 음정의 음표 자체가 이명동음 관계에 있는 경우이다. 예를 들어, 12음 평균율에서 "증2도"와 "단3도"는 모두 3반음으로 동일한 음정이지만, 악보상 표기는 다르다.
| 반음 수 | 음정 이름 | 악보 위치 | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 4 | 장3도 | F | A | ||
| 4 | 장3도 | G | B | ||
| 4 | 감4도 | F | B | ||
| 4 | 겹증2도 | G | A | ||
11. 1. 선율적 및 화성적 (Melodic and Harmonic)
두 음이 동시에 울리면 수직적 또는 화성적 음정이라고 하고, 두 음이 연속적으로 울리면 수평적, 선형적 또는 선율적 음정이라고 한다.[2] 선율적 음정은 낮은 음이 높은 음보다 먼저 나오는 '상행' 또는 그 반대인 '하행'일 수 있다.11. 2. 온음계적 및 반음계적 (Diatonic and Chromatic)
온음계 음정은 온음계의 두 음으로 형성된 음정이다. 반음계 음정은 반음계의 두 음으로 형성된 비온음계적 음정이다.[12]널리 사용되는 온음계의 정의에 따르면 완전, 장, 단 음정은 모두 온음계 음정이다. 반대로 증 음정이나 감 음정은 증4도와 감5도를 제외하고는 온음계 음정이 아니다.
온음계 음정과 반음계 음정의 구분은 맥락에 따라 민감할 수 있다. 예를 들어 C 장조 음계로 형성된 56개의 음정은 "C 장조의 온음계"라고 하며, 다른 모든 음정은 "C 장조의 반음계"라고 한다. 예를 들어, 완전 5도 A–E는 A과 E이 C 장조 음계에 포함되지 않기 때문에 C 장조의 반음계이다. 그러나 A 장조와 같이 다른 음계에서는 온음계 음정이다.
음정에는 온음계 내에 나타나는 음정과 그렇지 않은 음정이 있으며, 전자를 '''온음계적 음정''', 후자를 '''반음계적 음정'''이라고 부르기도 한다. 모든 완전 음정, 장음정, 단음정과 증4도, 감5도가 '''온음계적 음정'''이며, 그 외는 '''반음계적 음정'''이다.
다음은 장음계에 나타나는 각 음정의 일람이다.
| 아래 음\위 음 | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|
| C | 완전 8도 | 장2도 | 장3도 | 완전 4도 | 완전 5도 | 장6도 | 장7도 |
| D | 단7도 | 완전 8도 | 장2도 | 단3도 | 완전 4도 | 완전 5도 | 장6도 |
| E | 단6도 | 단7도 | 완전 8도 | 단2도 | 단3도 | 완전 4도 | 완전 5도 |
| F | 완전 5도 | 장6도 | 장7도 | 완전 8도 | 장2도 | 장3도 | 증4도 |
| G | 완전 4도 | 완전 5도 | 장6도 | 단7도 | 완전 8도 | 장2도 | 장3도 |
| A | 단3도 | 완전 4도 | 완전 5도 | 단6도 | 단7도 | 완전 8도 | 장2도 |
| B | 단2도 | 단3도 | 완전 4도 | 감5도 | 단6도 | 단7도 | 완전 8도 |
11. 3. 협화음과 불협화음 (Consonant and Dissonant)
헤르만 폰 헬름홀츠는 비트의 존재 유무를 통해 불협화음 발생을 이론화했다.[14] 두 음을 함께 연주하여 발생하는 거침은 초당 발생하는 비트의 수에 비례한다.[14] 또한, 하모닉 사운드의 상위 배음이 만들어내는 비트가 기본 주파수 사이의 비트를 생성하기에는 너무 멀리 떨어진 간격에 대한 불협화음의 원인이 된다고 보았다.[14]데이비드 코프는 배음열에서의 위치에 근접하는 정도로 결정되는 '''음정 강도''' 개념을 제안했다.[15]
이러한 분석들은 수직적(동시적) 음정에 대한 것이다.
협화음과 불협화음은 특정 음악적 효과의 안정성 또는 휴식 상태를 나타내는 상대적인 용어이다. 불협화음은 긴장을 유발하고 협화음으로 ''해결''되기를 원하는 간격이다.
이 용어들은 다양한 작곡 스타일에 따라 상대적이다.
- 15세기와 16세기 사용에서 완전 5도와 옥타브, 장3도와 단3도, 장6도는 화성적으로 협화음으로, 완전 4도를 포함한 다른 모든 음정은 불협화음으로 간주되었다. 1473년까지는 (요하네스 틴크토리스에 의해) 수직적인 음향의 상성부 사이를 제외하고는 불협화음으로 묘사되었다. (예를 들어, 아래에 3도를 지지하는 경우("6-3 화음").)[13]
- 고전주의 시대에는 협화음과 불협화음 화음에 대해 이야기하는 것이 더 합리적이며, 이전에 불협화음으로 간주되었던 특정 음정(예: 단7도)은 특정 맥락에서 허용되었다. 그러나 16세기 관행은 이 기간 동안 초보 음악가들에게 여전히 가르쳐졌다.
정수비의 단순함(협화)의 정도에 따라 음정을 다음과 같이 분류한다.[32]
| 구분 | 세부 구분 | 음정 | 주파수비 (순정율의 경우)[37][38] |
|---|---|---|---|
| 협화 음정 | 완전 협화 음정 | 완전 1도 | 1:1 |
| 완전 8도 | 1:2 | ||
| 완전 5도 | 2:3 | ||
| 완전 4도 | 3:4 | ||
| 불완전 협화 음정 | 장3도 | 4:5 | |
| 단3도 | 5:6 | ||
| 장6도 | 3:5 | ||
| 단6도 | 5:8 | ||
| 불협화 음정 | 그 외 | - | |
완전 1도, 완전 8도를 특히 '''절대 협화 음정'''이라고 한다.
11. 4. 단순 및 복합 (Simple and Compound)
단순 음정은 한 옥타브 이하의 음정이다. 한 옥타브 이상의 음정은 겹음정이라고 하며, 이는 단순 음정에 하나 이상의 옥타브를 더하여 얻을 수 있다.[32] 음정의 명칭은 기본적으로 오선보에서의 간격으로 "◯도"라는 명칭이 결정된다. 1옥타브 이하의 음정을 '''단음정'''이라고 부르고, 그 이상 떨어져 있을 때를 '''겹음정'''이라고 한다.
예를 들어 올림표나 내림표 등의 변화 기호가 붙었을 때, "증2도"와 "단3도"는 모두 12 평균율에서는 3반음으로 동일한 음정이지만, 악보상에서는 "2도"와 "3도"로 다르므로, 전자를 "증2도", 후자를 "단3도"라고 부른다.
2개의 음높이 차이가 13 반음 이상, 즉 1 옥타브보다 크게 떨어져 있는 경우를 '''복음정'''이라고 부르며, "3 옥타브와 완전 4도"와 같이 옥타브 수와 단음정의 조합으로 복음정을 나타낸다. 다만, 9도와 같은 약간의 복음정은 화성의 특징적인 요소이므로, 큰 쪽의 수로 불리는 것이 보통이다.[35] 예를 들어 "1 옥타브와 단 3도"를 "단 10도"라고 부른다.
11. 5. 순차 진행 및 도약 (Steps and Skips)
선율적 음정은 순차 진행 또는 도약으로 설명될 수 있다. 순차 진행은 음계의 두 연속 음 사이의 선형 음정이다.[17] 온음계에서 순차 진행은 단2도(반음) 또는 장2도(온음)이다.예를 들어 C에서 D (장2도)는 순차 진행이다.
일반적으로 순차 진행은 음악 선에서 더 작거나 좁은 음정이며, 도약은 더 넓거나 큰 음정이다. 음정의 순차 진행과 도약 분류는 사용된 조율 체계와 음고 공간에 의해 결정된다.
두 연속 음고 사이의 음정이 순차 진행을 넘지 않거나, 도약이 드문 선율 진행을 '순차적' 선율 진행이라고 하며, 도약이 빈번하게 나타나는 '도약적' 선율 진행과 대조된다.
11. 6. 이명동음 (Enharmonic Intervals)
두 음정은 서로 다른 표기법으로 표기되었지만 동일한 음높이를 포함하고 있다면 '''이명동음'''이라고 한다. 즉, 두 음정의 음표 자체가 이명동음 관계에 있는 경우이다. 이명동음 음정은 동일한 수의 반음을 포함한다.예를 들어, 아래 표에 나열된 네 개의 음정은 모두 이명동음 관계에 있다. F과 G 음표가 동일한 음높이를 나타내고, A와 B도 마찬가지이기 때문이다. 이 모든 음정은 4개의 반음을 포함한다.[32]
| 반음 수 | 음정 이름 | 악보 위치 | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 4 | 장3도 | F | A | ||
| 4 | 장3도 | G | B | ||
| 4 | 감4도 | F | B | ||
| 4 | 겹증2도 | G | A |
피아노 건반에서 고립된 화음으로 연주될 때, 이 음정들은 동일한 두 건반으로 연주되기 때문에 귀로는 구별할 수 없다. 그러나 음악적 맥락에서, 이 음정들이 포함하는 음표들의 조성 기능은 매우 다르다.
위의 논의는 널리 사용되는 조율 시스템인 12음 평균율(12-TET)의 사용을 가정한다. 그러나 다른 역사적인 중간음 조율에서는 F과 G와 같은 음표 쌍의 음높이가 반드시 일치하지 않을 수 있다. 이 두 음표는 12-TET에서는 이명동음이지만, 다른 조율 시스템에서는 그렇지 않을 수 있다. 이러한 경우, 그들이 형성하는 음정 또한 이명동음이 아닐 것이다. 예를 들어, 4분의 1 콤마 중간음 조율에서는 위 예시에 표시된 네 개의 음정이 모두 다를 것이다.
12. 미분음 (Minute Intervals)
크로매틱 스케일에서 발견되지 않거나 고유한 이름을 가진, 음정의 미세한 간격도 많이 있다. 이것들은 미분음으로 묘사될 수 있으며, 그 중 일부는 콤마로 분류될 수도 있는데, 이는 일부 조율 시스템에서 이명동음에 해당하는 음들 사이에서 관찰되는 작은 불일치를 설명하기 때문이다. 다음 목록에서 음정 크기는 센트 단위로 대략적으로 표시된다.
- ''피타고라스 콤마''는 12개의 순정 완전 5도와 7옥타브 사이의 차이이다. 이는 주파수 비율 531441:524288 (23.5센트)로 표현된다.
- ''신토닉 콤마''는 4개의 순정 완전 5도와 2옥타브 더하기 장3도 사이의 차이이다. 이는 비율 81:80 (21.5센트)으로 표현된다.
- ''셉티멀 콤마''는 64:63 (27.3센트)이며, 피타고라스 또는 3-리밋 "7도"와 "화성 7도" 사이의 차이이다.
- ''디에시스''는 일반적으로 3개의 순정 장3도와 1옥타브 사이의 차이를 의미한다. 이는 비율 128:125 (41.1센트)로 표현된다. 그러나 다른 작은 간격을 의미하는 데 사용되기도 한다. 자세한 내용은 디에시스를 참조하십시오.
- ''디아스키스마''는 3옥타브와 4개의 순정 완전 5도 더하기 2개의 순정 장3도 사이의 차이이다. 이는 비율 2048:2025 (19.6센트)로 표현된다.
- ''스키스마''(또는 스키스마)는 5옥타브와 8개의 순정 5도 더하기 1개의 순정 장3도 사이의 차이이다. 이는 비율 32805:32768 ()로 표현된다. 또한 피타고라스 콤마와 신토닉 콤마 사이의 차이이기도 하다. (스키스마 장3도는 순정 장3도와 다른 스키스마이며, 8개의 5도 아래와 5개의 옥타브 위, C에서 F이다.)
- ''클레이스마''는 6개의 단3도와 1개의 ''트리타브'' 또는 ''완전 12도'' (옥타브 더하기 완전 5도) 사이의 차이이며, 주파수 비율은 15625:15552 (8.1센트)이다.
- ''셉티멀 클레이스마''는 5:4의 두 장3도와 9:7의 셉티멀 장3도 또는 초장3도가 옥타브를 초과하는 양이다. 비율 225:224 (7.7센트)이다.
- ''4분음''은 반음 너비의 절반이며, 이는 온음 너비의 절반이다. 정확히 50센트와 같다.
13. 복합 음정 (Compound Intervals)
겹음정은 1옥타브보다 큰 음정을 말한다.[16] 예를 들어 장9도, 단10도와 같은 음정이 겹음정이다. 겹음정은 단순 음정에 옥타브를 더하여 얻을 수 있다.
일반적으로 겹음정은 어떤 종류의 단순 음정 두 개 이상으로 구성된 시퀀스 또는 "스택"으로 정의될 수 있다. 예를 들어, 장10도(1옥타브 위로 음자리표 2칸)는 1옥타브와 장3도를 포함하며, ''겹장3도''라고도 한다. 모든 겹음정은 항상 1옥타브 이상과 하나의 단순 음정으로 분해될 수 있다. 예를 들어, 장17도는 2옥타브와 장3도로 분해될 수 있다.
겹음정의 음정의 종류는 이를 기반으로 하는 단순 음정의 종류에 의해 결정된다. 예를 들어, 겹장3도는 장10도(1+(8−1)+(3−1) = 10) 또는 장17도(1+(8−1)+(8−1)+(3−1) = 17)이다.
2개의 음높이 차이가 13 반음 이상, 즉 1 옥타브보다 크게 떨어져 있는 경우를 '''복음정'''이라고 부르며, "3 옥타브와 완전 4도"와 같이 옥타브 수와 단음정의 조합으로 복음정을 나타낸다. 다만, "9도와 같은 약간의 복음정은 화성의 특징적인 요소이므로, 큰 쪽의 수로 불리는 것이 보통이다"[35], 따라서 예를 들어 "1 옥타브와 단 3도"를 "단 10도"라고 부른다.
14. 화음의 음정 (Intervals in Chords)
화음은 셋 이상의 음으로 구성된 집합이며, 근음이라고 하는 공통 음에서 시작하는 음정의 조합으로 정의된다.[19] 예를 들어 장3화음은 근음과 장3도, 완전5도 음정으로 구성된다. 때로는 단일 음정(2음 음정)도 화음으로 간주된다.[19] 화음은 화음을 정의하는 음정의 종류와 개수에 따라 분류된다.
주요 화음의 종류에는 장조, 단조, 증, 감소, 반감소, 속음이 있다. 화음 종류에 사용되는 기호는 음정 종류에 사용되는 기호와 유사하다.
코드 이름 또는 기호를 해석하는 주요 규칙은 다음과 같다.
# 3음 코드(3화음)의 경우, 장3도 또는 단3도는 항상 근음에서 위로의 3도 음정을 나타내며, 증5도 및 감5도는 항상 근음에서 위로의 5도 음정을 나타낸다.
# 반대되는 정보가 없는 경우, 장3도 음정과 완전5도 음정(장3화음)이 암시된다.
# 5도 음정이 감5도인 경우, 3도는 단3도여야 한다.
# 일반 음정 번호만 포함하는 이름과 기호(예: "세븐 코드") 또는 코드 근음과 숫자(예: "C 세븐" 또는 C7)는 다음과 같이 해석된다.
- 숫자가 2, 4, 6 등인 경우, 코드는 장부가음 코드이다.
- 숫자가 7, 9, 11, 13 등인 경우, 코드는 도미넌트이다.
- 숫자가 5인 경우, 코드는 파워 코드이다.
다음 표는 주요 코드에 포함된 음정과 이를 나타내는 기호를 보여준다.
| 주요 코드 | 구성 음정 | |||
|---|---|---|---|---|
| 이름 | 기호 예시 | 3도 | 5도 | 7도 |
| 장3화음 | C | M3 | P5 | |
| CM, 또는 Cmaj | M3 | P5 | ||
| 단3화음 | Cm, 또는 Cmin | m3 | P5 | |
| 증3화음 | C+, 또는 Caug | M3 | A5 | |
| 감3화음 | Cdim, 또는 Cdim | m3 | d5 | |
| 도미넌트 세븐 코드 | C7, 또는 Cdom7 | M3 | P5 | m7 |
| 단7화음 | Cm7, 또는 Cmin7 | m3 | P5 | m7 |
| 장7화음 | CM7, 또는 Cmaj7 | M3 | P5 | M7 |
| 증7화음 | C+7, Caug7, C7#5, 또는 C7aug5 | M3 | A5 | m7 |
| 감7화음 | Cdim7, 또는 Cdim7 | m3 | d5 | d7 |
| 반감7화음 | Cm7(♭5), 또는 Cm7dim5 | m3 | d5 | m7 |
15. 다양한 조율 시스템에서의 음정 크기 (Size of Intervals Used in Different Tuning Systems)
(음정비)
27:25
133
10:9
182
32:27
294
318
(울프) 269
384
(울프) 427
27:20
520
(울프) 522
(울프) 462
감5도
25:18
569
588
621
40:27
680
(울프) 678
(울프) 738
27:16
906
9:5
1018
50:27
1067