전신 방정식
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
전신 방정식은 1887년 올리버 헤비사이드가 전신선의 신호 왜곡 문제를 해결하기 위해 도입한 편미분 방정식이다. 이 방정식은 단위 길이당 전기 저항, 인덕턴스, 전도율, 전기 용량 등의 특성을 가진 전신선에서 전압과 전류의 관계를 나타낸다. 전신 방정식은 손실이 없는 경우 파동 방정식으로 단순화되며, 전송 선로의 신호 전파 속도를 계산하는 데 사용된다. 또한, 분산 소자 모델을 통해 전송 선로의 특성을 분석하고, 회로 소자로 활용될 수 있다. 전신 방정식은 도체 내 전자기장, 감쇠가 있는 현의 진동, 클라인-고든 방정식 등 다양한 물리 현상을 설명하는 데에도 적용된다.
올리버 헤비사이드가 1887년에 전신 기사로 일하면서 전신선의 신호 왜곡 문제를 해결하기 위해 전신 방정식을 도입하였다.[15]
전신 방정식은 전송 선로의 분포 정수 모델을 기반으로 한다. 전송 선로는 단위 길이당 저항(R), 인덕턴스(L), 컨덕턴스(G), 커패시턴스(C)를 가지는 무한히 작은 요소들로 구성된 것으로 간주된다.
2. 역사
3. 전개
24 게이지 전화 폴리에틸렌 절연 케이블(PIC)의 대표적인 파라미터 데이터는 다음과 같다 (약 21.1°C에서).[2]주파수 R L G C Hz 1 Hz 172.24 52.50 612.9 186.8 0.000 0.000 51.57 15.72 1 kHz 172.28 52.51 612.5 186.7 0.072 0.022 51.57 15.72 10 kHz 172.70 52.64 609.9 185.9 0.531 0.162 51.57 15.72 100 kHz 191.63 58.41 580.7 177.0 3.327 1.197 51.57 15.72 1 MHz 463.59 141.30 506.2 154.3 29.111 8.873 51.57 15.72 2 MHz 643.14 196.03 486.2 148.2 53.205 16.217 51.57 15.72 5 MHz 999.41 304.62 467.5 142.5 118.074 35.989 51.57 15.72
위 표에서 R과 L의 변화는 주로 표피 효과와 근접 효과 때문이다. 커패시턴스가 일정하게 유지되는 것은 의도적인 설계의 결과이다. G의 변화는 다음 함수 형태를 따른다.[4]
:
여기서 는 주파수의 함수로서의 전도율이고, , 과 는 모두 실수 상수이다. 는 1.0에 가깝다.
일반적으로 저항 손실은 에 비례하여 증가하고 유전 손실은 에 비례하여 증가하며, 여기서 이므로, 충분히 높은 주파수에서는 유전 손실이 저항 손실을 초과하게 된다. 실제로, 그 지점에 도달하기 전에 더 나은 유전체를 가진 전송선이 사용된다. 장거리 강성 동축 케이블에서는 매우 낮은 유전 손실을 얻기 위해 고체 유전체를 간격을 두고 플라스틱 스페이서로 대체하여 중심 도체를 축상에 유지할 수 있다.
공간 변수 ''x''와 시간 변수 ''t''의 실수 값 함수 ''u''( ''x'', ''t'' )에 대해,
:
로 주어지는 쌍곡형 2계 편미분 방정식을 '''전신 방정식'''이라고 한다. 특히 γ=0인 경우에는, 일반적인 파동 방정식에 해당한다.
n차원 공간 변수 '''x'''=(''x''1,…,''x''n)와 시간 변수 ''t''의 실수 값 함수 ''u''( ''x'', ''t'' )에 대해서도 다음과 같은 편미분 방정식을 전신 방정식이라고 한다.
:
단, ∇2는 n차원에서의 라플라스 연산자이다.
:
전신 방정식은 다음과 같은 표준형으로 표현되는 경우가 많다.
::
이러한 경우에도 다음과 같은 변환을 통해 위의 형식으로 귀착된다.
::
::
3. 1. 전신 방정식 유도
편의상 , 로 표기한다.
매우 가는 균일한 전신선이 단위 길이당 전기 저항 과 단위 길이당 인덕턴스 을 가진다고 하자. 또한, 전신선에서 전류가 단위 길이당 전도율 과 단위 길이당 전기 용량 를 통해 (병렬로) 샌다고 하자.
전신선 위의 전압 과 전류 는 다음과 같은 연립 1차 편미분 방정식을 따른다.
:
:
두 편미분 방정식 가운데 하나를 다른 하나에 대입하면 다음과 같이 하나의 2차 편미분 방정식을 얻는다.
:
:
이를 '''전신 방정식'''이라고 한다.
전신 방정식의 시간 영역 표현은 다음과 같다.
이들은 결합되어 각각 종속 변수가 하나인 두 개의 편미분 방정식을 얻을 수 있으며, 이는 또는 이다.
종속 변수( 또는 )를 제외하면, 공식은 동일하다.
3. 2. 전파 속도
편의상 전력 손실을 무시하여 R=0, G=0으로 놓으면 전신 방정식은 다음과 같이 파동 방정식이 된다.
:
:
이 방정식의 일반해는 다음과 같다.
:
따라서, 전신 선로를 통해 전달되는 신호의 속도는 임을 알 수 있다.
4. 분산 소자
전신 방정식은 맥스웰 방정식에서 파생된다. 실제로는 도체가 2포트 네트워크의 무한한 일련의 기본 구성 요소로 구성되어 있으며, 각 구성 요소는 전송 선로의 미소한 짧은 세그먼트를 나타낸다고 가정한다.
이 모델은 그림에 표시된 무한한 일련의 미소 요소로 구성되며, 구성 요소의 값은 ''단위 길이당'' 지정되므로 주의해야 한다. 이러한 값들은 1차 선로 상수로도 불리며, 특성 임피던스, 전파 상수, 감쇠 상수, 위상 상수와 같은 2차 선로 상수와 구별된다. 1차 선로 상수는 시간, 전압, 전류에 대해서는 일정하지만, 주파수에 따라 변할 수 있다.
각 구성 요소의 역할은 오른쪽 애니메이션을 통해 확인할 수 있다.
, , , 는 케이블 또는 피드라인 재료에 따라 달라지며, 주파수에 따라 변한다. 과 는 고주파에서 증가하는 경향이 있고, 과 는 감소하는 경향이 있다.
오른쪽 그림은 과 가 0인 손실 없는 전송 선로를 보여주는데, 이는 전신 방정식의 가장 단순한 형태이지만 다소 비현실적이다.
24 게이지 전화 폴리에틸렌 절연 케이블(PIC)의 대표적인 파라미터 데이터 (약 21.1°C에서)
| 주파수 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Hz | ||||||||
| 1 Hz | 172.24 | 52.50 | 612.9 | 186.8 | 0.000 | 0.000 | 51.57 | 15.72 |
| 1 kHz | 172.28 | 52.51 | 612.5 | 186.7 | 0.072 | 0.022 | 51.57 | 15.72 |
| 10 kHz | 172.70 | 52.64 | 609.9 | 185.9 | 0.531 | 0.162 | 51.57 | 15.72 |
| 100 kHz | 191.63 | 58.41 | 580.7 | 177.0 | 3.327 | 1.197 | 51.57 | 15.72 |
| 1 MHz | 463.59 | 141.30 | 506.2 | 154.3 | 29.111 | 8.873 | 51.57 | 15.72 |
| 2 MHz | 643.14 | 196.03 | 486.2 | 148.2 | 53.205 | 16.217 | 51.57 | 15.72 |
| 5 MHz | 999.41 | 304.62 | 467.5 | 142.5 | 118.074 | 35.989 | 51.57 | 15.72 |
과 의 변화는 주로 표피 효과와 근접 효과 때문이다. 커패시턴스가 일정하게 유지되는 것은 의도적인 설계 결과이다.[2]
의 변화는 "역률은... 주파수에 독립적인 경향이 있는데, 이는 각 주기 동안 손실되는 에너지의 비율이... 넓은 주파수 범위에서 초당 사이클 수에 실질적으로 독립적이기 때문이다."라는 Terman의 언급[3]에서 추론할 수 있다.
형태의 함수에서 는 1.0에 가깝고, 이는 Terman의 언급과 일치한다. Chen은 유사한 형태의 방정식을 제시한다.[4]
일반적으로 저항 손실은 에 비례하여 증가하고 유전 손실은 ()에 비례하여 증가하므로, 충분히 높은 주파수에서는 유전 손실이 저항 손실을 초과한다. 실제로, 그 지점에 도달하기 전에 더 나은 유전체를 가진 전송선이 사용된다. 장거리 강성 동축 케이블에서는 매우 낮은 유전 손실을 얻기 위해 고체 유전체를 간격을 둔 플라스틱 스페이서로 대체하여 중심 도체를 축상에 유지할 수 있다.
5. 손실 없는 전송
및 일 때, 전선의 저항과 절연 컨덕턴스는 무시할 수 있으며, 전송 선로는 이상적인 무손실 구조로 간주된다. 이 경우 모델은 및 요소에만 의존한다. 전신 방정식은 전송 선로 상의 전압 와 전류 사이의 관계를 설명하며, 각 값은 위치 와 시간 의 함수이다.
:
전송선 방정식은 한 쌍의 결합된 1차 편미분 방정식으로 구성된다. 첫 번째 방정식은 유도 전압이 케이블 인덕턴스를 통한 전류의 시간에 따른 변화율과 관련이 있음을 보여주고, 두 번째 방정식은 케이블 커패시턴스에 의해 소모되는 전류가 전압의 시간에 따른 변화율과 관련이 있음을 보여준다.
:
:
이 방정식들을 결합하면 전압 와 전류 에 대한 파동 방정식을 얻을 수 있다.
:
여기서 는 전송 선로를 통과하는 파동의 전파 속도이다. 이상적인 평행 도체로 만들어지고 그 사이에 진공이 있는 전송 선로의 경우, 이 속도는 빛의 속도와 같다.
손실이 없는 경우 , 전압에 대한 파동 방정식의 일반적인 해는 전진파와 후진파의 합으로 나타낼 수 있다.
:
여기서,
- 과 는 어떤 두 해석 함수도 될 수 있으며,
- 는 파형의 전파 속도 (''위상 속도''라고도 함)이다.
은 왼쪽에서 오른쪽(양의 방향)으로 진행하는 파동의 진폭 프로파일을 나타내고, 는 오른쪽에서 왼쪽으로 진행하는 파동의 진폭 프로파일을 나타낸다. 선상의 임의의 지점 에서의 순간 전압은 두 파동에 의한 전압의 합이다.
전신 방정식에 의해 주어진 전류 와 전압 관계를 사용하면,
:
와 같이 쓸 수 있다.
5. 1. 정현파 정상 상태
사인파 정상 상태(즉, 순수한 정현파 전압이 인가되고 과도 상태가 멈춘 경우)에서 전압과 전류는 다음과 같은 단일 톤 사인파 형태를 취한다.[5][6][7][8][9][10][11]:
여기서 는 정상 상태 파동의 각 주파수이다. 이 경우 전신 방정식은 다음과 같이 축소된다.
:
마찬가지로 파동 방정식은 다음과 같이 축소된다.
:
여기서 는 파수이다.
이 두 방정식 각각은 1차원 헬름홀츠 방정식의 형태이다.
6. 손실 있는 전송
손실 요소 과 를 무시하기 어려울 정도로 클 경우, 선로의 기본 세그먼트를 설명하는 미분 방정식은 다음과 같다.[13]
:
위의 두 방정식을 에 대해 미분하고 약간의 대수를 사용하면, 각각 하나의 미지수만 포함하는 한 쌍의 쌍곡선 편미분 방정식을 얻는다.[13]
:
이 방정식은 와 와 그들의 1차 도함수에 추가 항이 있는 균질 파동 방정식과 유사하다. 이러한 추가 항은 신호가 시간과 거리에 따라 감쇠하고 퍼지게 한다. 전송 선로에 손실이 약간만 있는 경우 ( 및 ) 신호 강도는 로 거리에 따라 감쇠하며, 여기서 이다.[13]
7. 전신 방정식의 해와 회로 소자
전신 방정식의 해는 회로 소자로 직접 삽입될 수 있다. 존슨(Johnson)은 ABCD 파라미터를 사용하여 2포트 네트워크로 표현할 수 있음을 보였다.[10]
ABCD 2포트 네트워크의 정의 방정식은 다음과 같다.[10]
여기서
이다. , , , 는 주파수의 함수일 수 있음을 강조하기 위해 로 아래 첨자화되어 있다.
과 은 와 의 함수로 제공된다. 전압과 전류 관계는 대칭이므로, 위 방정식에서 와 를 과 의 함수로 나타내도 동일한 관계를 얻는다. 이때 아래 첨자 "1"과 "2"가 반전되고, 항의 부호는 "1"←"2" 방향이 "2"→"1" 방향으로 반전되면서 변경된다.
동축 케이블과 같은 불균형 전송선의 경우, 아래 그림과 같은 등가 회로를 사용하여 모델링할 수 있다.[14]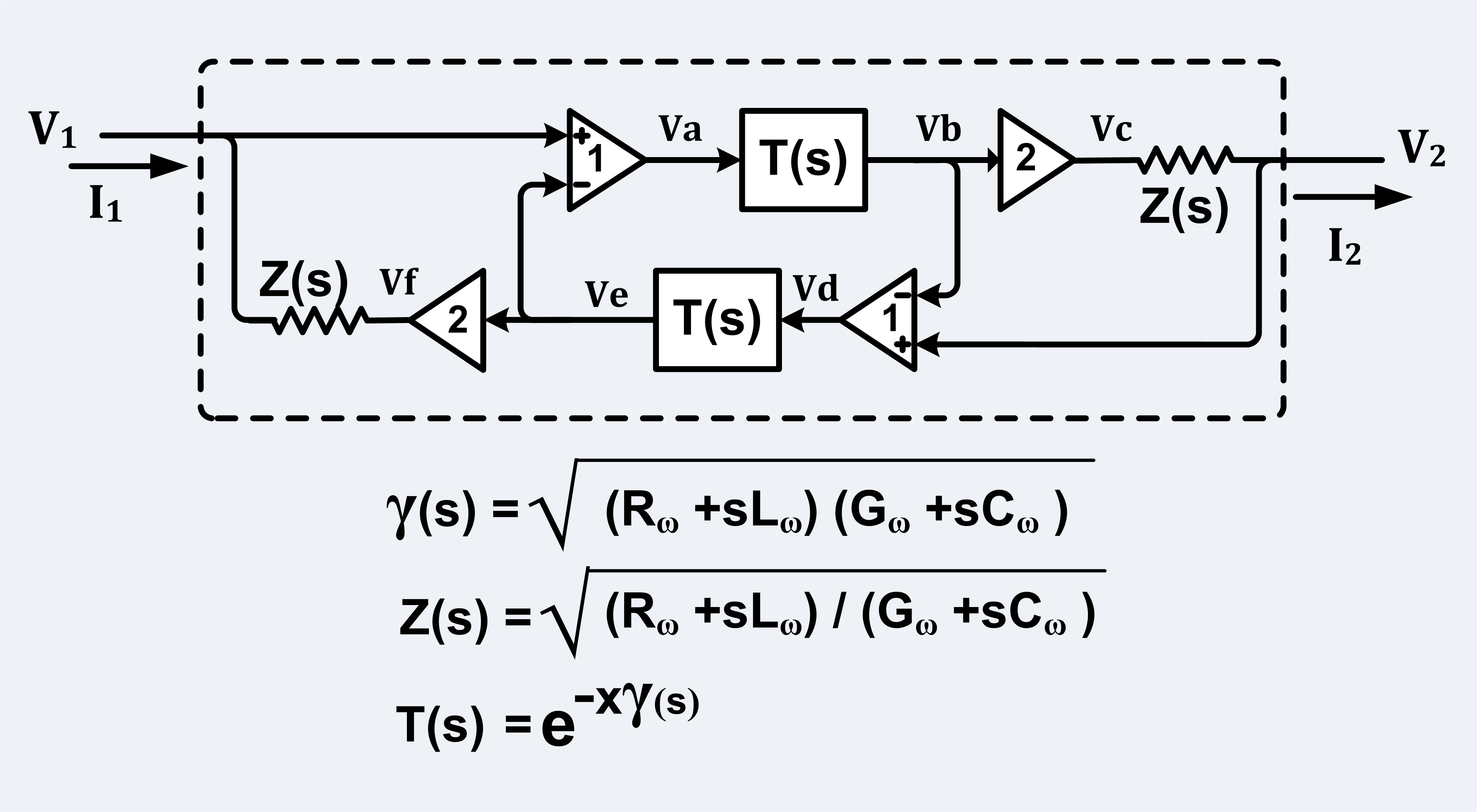
이 회로에서 전압 배가기, 차동 증폭기 및 임피던스 는 전송선과 외부 회로의 상호 작용을 설명한다.
분포 정수 회로인 전송선로에서 위치 ''x'', 시각 ''t''에서의 전압 , 전류 는 다음을 만족한다.
:
:
여기서 ''L''은 전송 선로의 인덕턴스, ''R''은 전송 선로의 저항, ''C''는 전송 선로의 용량, ''G''는 전송 선로의 누설 컨덕턴스이다. 좁은 의미에서 전신 방정식은 분포 정수 회로에서의 이 연립 미분 방정식 자체를 가리키는 경우가 많다.
위 식에서 서로의 변수를 소거하면,
:
:
을 얻는다.
8. 다양한 물리 현상과 전신 방정식
전신 방정식은 다양한 물리 현상을 설명하는 데 사용되는 쌍곡형 2계 편미분 방정식이다. 공간 변수 ''x''와 시간 변수 ''t''를 사용하는 실수 값 함수 ''u''(''x'', ''t'')에 대해 다음과 같이 표현된다.
:
여기서 γ=0인 경우에는 일반적인 파동 방정식에 해당한다.
n차원 공간 변수 '''x'''=(''x''1,…,''x''n)와 시간 변수 ''t''의 실수 값 함수 ''u''(''x'', ''t'')에 대해서는 다음과 같이 표현된다.
:
여기서 ∇2는 n차원에서의 라플라스 연산자이다.
전신 방정식은 시간 ''t''에 대한 1계 도함수나 물리적인 계수를 포함하는 형태로 표현될 수 있으며, 변환을 통해 위의 형식으로 귀착된다.
8. 1. 도체 내 전자기장
전기 전도율 σ, 유전율 ε, 투자율 μ인 도체 내에서 전장 '''E'''('''x''',''t''')와 자장 '''H'''('''x''',''t''')는 다음 형태의 전신 방정식을 만족한다.:
:
8. 2. 감쇠가 있는 현의 진동
감쇠가 있는 현의 진동에서 위치 ''x''와 시각 ''t''에서의 현의 변위를 ''u''(''x'', ''t'')라고 하면, ''u''(''x'', ''t'')는 다음의 전신 방정식을 만족한다.:
여기서, ''T''는 장력, ρ는 현의 선밀도, κ는 감쇠의 효과를 나타내는 비례 계수이다.
8. 3. 클라인-고든 방정식
양자장론에서 클라인-고든 장 φ('''x''',''t'' )이 만족하는 클라인-고든 방정식은 전신 방정식과 동일하며 다음과 같은 형태로 주어진다.:
여기서 ''c''는 빛의 속도, ''m''은 클라인-고든 장 입자의 질량이다.
참조
[1]
서적
The Maxwellians
Cornell University Press
2005
[2]
서적
Subscriber Loop Signaling and Transmission Handbook
https://archive.org/[...]
IEEE Press
1995
[3]
서적
Radio Engineers' Handbook
McGraw-Hill
1943
[4]
서적
Home Networking Basics
Prentice Hall
2004
[5]
서적
Electromagnetics
McGraw-Hill
[6]
서적
Engineering Electromagnetics
https://archive.org/[...]
McGraw-Hill
[7]
서적
Electromagnetic Concepts and Applications
Prentice-Hall
[8]
서적
Elements of Electromagnetics
Saunders College Publishing
[9]
서적
Time-Harmonic Electromagnetic Fields
McGraw-Hill
[10]
서적
Transmission lines and Filter Networks
Macmillan
[11]
서적
Transmission Lines with Pulse Excitation
Academic Press
[12]
서적
High Speed Signal Propagation
Prentice-Hall
[13]
서적
Transmission Lines and Lumped Circuits
Academic Press
2001
[14]
웹사이트
SPICE Simulation of Transmission Lines by the Telegrapher's Method
http://i.cmpnet.com/[...]
2010-06
[15]
서적
http://books.google.[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
