주사 터널링 현미경

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

주사 터널링 현미경(STM)은 양자 터널링 효과를 이용하여 원자 수준의 표면을 관찰하는 현미경이다. 탐침과 시료 사이에 전압을 가하면 전자가 얇은 진공 장벽을 통과하여 터널링 전류가 흐르며, 이 전류의 변화를 측정하여 표면의 전자 상태 밀도 분포를 이미지화한다. 1980년대 게르트 비니히와 하인리히 로러에 의해 개발되었으며, 표면 구조 분석, 원자 조작, 분광학적 측정 등 다양한 분야에 응용된다. STM을 기반으로 한 다양한 현미경 기술들이 개발되었으며, 반도체 산업 및 나노 기술 연구 등에서 활용된다.

더 읽어볼만한 페이지

주사 탐침 현미경 - 소년과 원자
"소년과 원자"는 주사 터널링 현미경으로 조작된 일산화 탄소 분자를 사용하여 제작된 스톱 모션 애니메이션 단편 영화로, 극저온 환경에서 원자 수준의 미세한 세계를 시각적으로 구현하여 '세계에서 가장 작은 스톱 모션 영화' 기네스 기록에 등재되었으며 과학 교육 자료로도 활용된다.
1981년 도입 - 노르딕 모바일 텔레폰
노르딕 모바일 텔레폰(NMT)은 1981년 스웨덴과 노르웨이에서 상용화된 아날로그 이동 통신 시스템으로, 450MHz와 900MHz 주파수 대역을 사용했으며 GSM 등장으로 쇠퇴했다.
1981년 도입 - 빠삐코
롯데제과에서 1974년 출시한 튜브형 아이스크림 빠삐코는 초기 화이트 사워 맛으로 인기를 얻었으며, 이후 초콜릿과 커피 맛을 결합한 제품과 스무디 형태 개선, 다양한 광고 모델을 통해 꾸준히 사랑받고 있다.
현미경 - 마이크로그라피아
로버트 훅의 마이크로그라피아는 현미경으로 관찰한 대상들의 정밀한 기록과 구리판화를 통해 미세 세계를 시각적으로 제시하며, 과학적 관심사와 사회에 큰 영향을 미친 책이다.
현미경 - 전자현미경
전자현미경은 전자선을 이용하여 광학 현미경의 분해능 한계를 넘어선 고배율 이미지를 얻는 현미경으로, 투과 전자 현미경, 주사 전자 현미경, 주사 투과 전자 현미경 등 다양한 종류가 있으며, 생물학, 재료공학 등 여러 분야에서 활용되지만 시료 준비, 장비 및 유지 비용, 진공 환경 등의 단점도 존재한다.

주사 터널링 현미경
개요
명칭	주사 터널링 현미경
영어 명칭	Scanning Tunneling Microscope (STM)
일본어 명칭	走査型トンネル顕微鏡 (Sōsa-gata tonneru kenbikyo)
원리 및 특징
작동 원리	양자 터널링 효과
특징	전도성 물질 표면의 원자 이미징 높은 분해능 (원자 수준) 국소적인 전자 구조 정보 획득 가능 실시간 표면 변화 관찰 가능 초고진공 환경 필요
구성 요소
탐침 (Probe)	텅스텐 또는 백금-이리듐 합금으로 만들어진 매우 뾰족한 바늘
압전 소자 (Piezoelectric element)	탐침의 위치를 정밀하게 제어
스캐너 (Scanner)	탐침을 표면 위에서 스캔
제어 장치 (Control unit)	탐침의 위치, 스캔 속도, 터널링 전류 등을 제어
진동 감쇠 장치 (Vibration isolation system)	외부 진동으로부터 장비 보호
작동 모드
정전류 모드 (Constant current mode)	탐침과 시료 사이의 거리를 조절하여 터널링 전류를 일정하게 유지
정 높이 모드 (Constant height mode)	탐침과 시료 사이의 거리를 고정하고 터널링 전류의 변화를 측정
활용 분야
표면 과학 (Surface science)	표면의 원자 구조 및 전자적 특성 연구
나노 기술 (Nanotechnology)	나노 구조체의 제작 및 분석
재료 과학 (Materials science)	새로운 재료의 개발 및 특성 평가
생물학 (Biology)	DNA, 단백질 등의 생체 분자 이미징
파생 기술
주사 터널링 분광법 (Scanning Tunneling Spectroscopy, STS)	특정 위치에서 전압을 변화시키며 전류를 측정하여 전자 구조를 분석
스핀 분해 주사 터널링 분광법 (Spin-Polarized STS)	스핀 의존적인 전자 구조 연구
단점
측정 환경	초고진공 또는 극저온 환경 필요
시료 제한	전도성 물질만 측정 가능
숙련도 요구	장비 작동 및 데이터 분석에 높은 숙련도 요구
기타 정보
발명	게르트 비니히, 하인리히 로러 (1981년)
노벨상 수상	1986년 노벨 물리학상 수상 (게르트 비니히, 하인리히 로러)

2. 원리

주사 터널링 현미경(STM)은 탐침과 시료 사이의 터널링 전류를 이용하여 작동한다. 탐침은 육안으로 관찰되는 조작 메커니즘을 통해 시료에 가까이 가져간다. 압전 스캐너 튜브는 제어 전압에 의해 길이가 변경될 수 있는데, 이를 통해 근접 거리에서 시료 표면에 대한 탐침 위치를 미세하게 제어한다.

시료와 탐침 사이에 바이어스 전압이 가해지면, 스캐너는 터널링 전류를 받기 시작할 때까지 점차 연장된다. 탐침-시료 간 거리 ''w''는 4–7 Å (0.4–0.7 nm) 범위로 유지된다. 이는 탐침이 반발 상호 작용을 경험하는 높이보다 약간 높지만, 여전히 인력 상호 작용이 존재하는 영역이다.^[5] 터널링 전류는 나노암페어 미만 범위이며, 스캐너에 가능한 한 가깝게 증폭된다. 터널링이 설정되면 실험 요구 사항에 따라 시료 바이어스와 탐침 위치가 변경된다.

탐침이 ''x''–''y'' 매트릭스에서 표면을 가로질러 이동할 때, 표면 높이와 전자 상태 밀도의 변화는 터널링 전류의 변화를 일으킨다. 표면의 디지털 이미지는 다음 두 가지 방식 중 하나로 형성된다.

정전류 모드: 터널링 전류의 변화가 직접 매핑된다. 피드백 전자 장치는 압전 높이 제어 메커니즘에 전압을 가하여 높이를 조정한다. 터널링 전류가 설정된 수준보다 낮으면 탐침이 시료 쪽으로 이동하고, 그 반대의 경우도 마찬가지이다. 이 모드는 상대적으로 느리다. 표면이 원자적으로 평평하면 ''z''-스캐너에 가해지는 전압은 주로 국소 전하 밀도의 변화를 반영한다. 원자 단계나 재구성으로 인해 표면이 휘어지면, 스캐너 높이도 전체 지형 때문에 변경되어야 한다. ''z''-스캐너 전압 이미지는 지형 및 전자 밀도 데이터를 모두 포함한다.
정전압 모드: ''z''-스캐너 전압이 일정하게 유지되고, 거리에 지수적으로 의존하는 터널링 전류가 매핑된다. 이 모드는 더 빠르지만, 거친 표면에서는 탐침이 충돌할 위험이 있다.

탐침의 래스터 스캔은 128×128에서 1024×1024(또는 그 이상) 매트릭스이며, 각 지점에 대해 단일 값이 얻어진다. STM 이미지는 그레이스케일이며, 후처리에서 색상이 추가된다.

주사 터널링 분광법 (STS)은 바이어스 전압을 스위핑하고 특정 위치에서 전류 변화를 측정하여 시료 내 지정된 위치의 전자 구조에 대한 정보를 얻는 방법이다.^[4] STM은 매우 국소적인 측정을 할 수 있다는 장점이 있다. 예를 들어, 불순물 위치에서의 상태 밀도를 주변 및 다른 위치와 비교할 수 있다.^[9]

탐침을 시료에 접근시키면 탐침과 시료가 충돌하기 전에 터널 효과에 의해 전류가 흐른다. 이 전류를 측정하며 시료 표면을 훑듯이 탐침을 이동시켜 시료 표면의 전자 상태 밀도를 관측한다. 압전 소자 액추에이터를 사용하여 탐침을 정밀하게 조작한다.

터널 전류는 탐침-표면 간 거리에 대해 지수 함수적으로 감소하지만, 표면에서 스며 나온 전자의 상태 파동 함수에 민감하게 영향을 받는다. 원자 한 개에서 수 개 정도의 거리에서도 터널 전류 양이 크게 변한다(0.1 nm = 1 Å 차이로 한 자릿수 변화). 탐침 최첨단 원자 하나가 표면 전자 상태와 측정 표면 상태를 가장 잘 감지하여 원자 수준 관측을 가능하게 한다. 관측되는 것은 파동 함수에서 스며 나온 터널 전류이며, 요철을 직접 관찰하는 것은 아니다. 전도성이 없는 시료는 관측할 수 없다.

관측 방법은 탐침과 표면 거리를 일정하게 유지하며 전류를 측정하는 정전류 모드와, 터널 전류를 일정하게 유지하며 탐침과 표면 거리를 측정하는 정전압 모드로 나뉜다. 대기 중이나 액체 중에서도 관측 가능하다. STM 터널 전류가 표면과 에너지를 주고받는 비탄성 전류는 표면 흡착 분자의 진동을 여기시키거나 결합을 절단할 수 있다.

2. 1. 양자 터널링 효과

전자의 양자 터널링은 주사 터널링 현미경(STM)의 작동 원리이며, 양자역학에서 나타나는 현상이다. 고전 물리학에서는 입자가 통과할 수 없는 에너지 장벽을 만나면 통과하지 못한다. 질량 ''m''_e인 전자가 전위 에너지 ''U''(''z'')를 갖는 ''z'' 방향으로 작용하는 전위에 의해 장벽이 주어질 때, 전자의 경로는 결정론적이며 운동 에너지와 전위 에너지의 합 ''E''는 항상 보존된다.

:

E = \frac{p^2}{2m_\text{e}} + U(z).

전자는 초기 에너지 ''E''가 ''U''(''z'')보다 큰 영역에서만 0이 아닌 운동량 ''p''를 가지며 존재할 수 있다. 그러나 양자 물리학에서는 전자가 고전적으로 금지된 영역을 통과할 확률이 존재한다. 이를 양자 터널링이라고 한다.^[5]

주사 터널링 현미경의 직사각형 포텐셜 장벽 모델에서 파동 함수의 실수부와 허수부

주사 터널링 현미경에서 시료와 탐침 사이의 터널링 현상을 설명하는 가장 간단한 모델은 직사각형 포텐셜 장벽 모델이다.^[15]^[5] 에너지 ''E''를 가진 전자가 폭 ''w''의 공간 영역에서 높이 ''U''의 에너지 장벽에 입사하는 상황을 가정한다. 전위 ''U''(''z'') 하에서 전자의 거동은 1차원적인 경우를 가정하여 파동 함수

\psi(z)

로 기술되며, 이 파동 함수는 다음 슈뢰딩거 방정식을 만족한다.

:

-\frac{\hbar^2}{2m_\text{e}} \frac{\partial^2\psi(z)}{\partial z^2} + U(z)\,\psi(z) = E\,\psi(z),

여기서 ''ħ''는 환산 플랑크 상수, ''z''는 위치, ''m''_e는 전자 질량이다. 장벽의 양쪽에 있는 0 포텐셜 영역에서 파동 함수는 다음과 같은 형태를 갖는다.

:

\psi_L(z) = e^{ikz} + r\,e^{-ikz}

for ''z'' < 0,

:

\psi_R(z) = t\,e^{ikz}

for ''z'' > ''w'',

여기서

k = \tfrac{1}{\hbar} \sqrt{2m_\text{e}E}

이다. 장벽 내부, 즉 ''E'' < ''U''인 경우, 파동 함수는 장벽의 한쪽에서 다른 쪽으로 감소하는 두 항의 중첩으로 표현된다.

:

\psi_B (z) = \xi e^{-\kappa z} + \zeta e^{\kappa z}

for 0 < ''z'' < ''w'',

여기서

\kappa = \tfrac{1}{\hbar} \sqrt{2m_\text{e}(U - E)}

이다.

계수 ''r''과 ''t''는 입사 전자 파동이 장벽에 의해 얼마나 반사 또는 투과되는지를 나타낸다. 즉, 전체 입사 입자 전류

j_i = \hbar k/m_\text{e}

중에서

j_t = |t|^2\, j_i

만이 투과된다. 이는 확률 전류 표현식을 통해 확인할 수 있다.

:

j_t = -i \frac{\hbar}{2m_\text{e}} \left\{\psi_R^* \frac{\partial}{\partial z}\psi_R - \psi_R \frac{\partial}{\partial z}\psi_R^*\right\},

이 식은

j_t = \tfrac{\hbar k}{m_\text{e}} \vert t \vert^2

로 계산된다. 투과 계수는 파동 함수와 그 도함수의 세 부분에 대한 연속성 조건을 ''z'' = 0 및 ''z'' = ''w''에서 적용하여 얻을 수 있다 (자세한 유도는 직사각형 포텐셜 장벽 문서 참조). 이를 통해

|t|^2 = \big[1 + \tfrac{1}{4} \varepsilon^{-1}(1 - \varepsilon)^{-1} \sinh^2\kappa w\big]^{-1},

를 얻으며, 여기서

\varepsilon = E/U

이다.

STM 실험에서 일반적인 장벽 높이는 물질 표면의 일함수 ''W''와 유사하며, 대부분의 금속에서 4 ~ 6 eV 사이의 값을 갖는다.^[15] 일함수는 점유된 에너지 준위(가장 높은 준위는 금속의 경우 ''T'' = 0 K에서 페르미 준위)에서 전자를 진공 준위로 이동시키는 데 필요한 최소 에너지이다. 전자는 한쪽의 점유된 상태에서 장벽 반대편의 비어있는 상태로만 터널링할 수 있다. 바이어스 전압이 없으면 페르미 에너지가 일치하여 터널링이 발생하지 않는다. 바이어스 전압은 한쪽 전극의 전자 에너지를 높여 다른 쪽에 동일한 에너지와 일치하는 전자가 없는 전자가 터널링할 수 있게 한다. 실험에서는 1 V의 작은 바이어스 전압이 사용되므로

\kappa

는 10 ~ 12 nm⁻¹ 정도이고, ''w''는 수 나노미터이다. 따라서 장벽은 강하게 감쇠된다. 투과 확률에 대한 표현식은

|t|^2 = 16\,\varepsilon(1 - \varepsilon)\,e^{-2\kappa w}.

로 간략화된다. 따라서 단일 레벨에서의 터널링 전류는 다음과 같다.^[15]

:

j_t = \left[\frac{4k\kappa}{k^2 + \kappa^2}\right]^2 \, \frac{\hbar k}{m_\text{e}}\,e^{-2\kappa w},

여기서 두 파동 벡터는 해당 레벨의 에너지 ''E''에 의존하며,

k = \tfrac{1}{\hbar} \sqrt{2m_\text{e}E},

이고

\kappa = \tfrac{1}{\hbar}\sqrt{2m_\text{e}(U - E)}.

이다.

터널링 전류는 시료와 탐침 사이의 거리에 지수적으로 의존하며, 간격이 1 Å (0.1 nm) 증가할 때마다 일반적으로 한 자릿수 감소한다.^[5] 이 때문에 터널링이 이상적으로 날카롭지 않은 탐침에서 발생하더라도 전류는 가장 돌출된 원자 또는 궤도에서 주로 발생한다.^[15]

음의 샘플 바이어스 ''V''는 전자 에너지 준위를 ''e⋅V''만큼 높인다. 샘플과 팁의 페르미 준위 사이에 있는 상태를 채우는 전자만 터널링을 할 수 있다.

장벽 한쪽의 점유된 에너지 준위에서 터널링이 일어나려면 장벽 반대쪽에 동일한 에너지의 빈 준위가 필요하다는 제약 때문에, 터널링은 주로 페르미 준위 근처의 전자에서 발생한다. 터널링 전류는 샘플에서 사용 가능한 또는 채워진 상태 밀도와 관련될 수 있다. 인가된 전압 ''V''에 의한 전류(터널링이 샘플에서 팁으로 발생한다고 가정)는 다음 두 가지 요인에 따라 달라진다. 1) 샘플에서 페르미 준위 ''E''_F와 ''E''_F − ''eV'' 사이의 전자 수, 2) 장벽 반대편 팁에서 터널링할 해당 자유 상태를 가진 전자 수.^[5] 터널링 영역에서 사용 가능한 상태 밀도가 높을수록 터널링 전류가 커진다. 일반적으로 양수 ''V''는 팁의 전자가 샘플의 빈 상태로 터널링하는 것을 의미하며, 음의 바이어스에서는 전자가 샘플의 점유된 상태에서 팁으로 터널링한다.^[5]

작은 바이어스 전압과 절대 영도 근처의 온도에서 터널링에 사용할 수 있는 주어진 부피 내의 전자 수(전자 농도)는 전자 상태 밀도 ''ρ''(''E''_F)와 두 페르미 준위 사이의 에너지 간격 ''eV''의 곱이다.^[5] 이 전자 중 절반은 장벽에서 멀어지고 있다. 나머지 절반은 전자 농도, 전하, 속도 ''v''의 곱으로 주어지는 장벽에 부딪히는 전류를 나타낸다(''I''_i = ''nev'').^[5]

:

I_i = \tfrac{1}{2} e^2 v\,\rho(E_\text{F})\,V.

터널링 전류는 부딪히는 전류의 작은 부분이며, 이 비율은 투과 확률 ''T''에 의해 결정된다.^[5]

:

I_t = \tfrac{1}{2} e^2v\,\rho(E_\text{F})\,V\,T.

직사각형 포텐셜 장벽의 가장 단순한 모델에서 투과 확률 계수 ''T''는 |''t''|²와 같다.

주사 터널링 현미경 모델에서 팁, 장벽 및 샘플 파동 함수. 장벽 너비는 ''w''. 팁 바이어스는 ''V''. 표면 일함수는 ''ϕ''.

두 전극에 대한 보다 현실적인 파동 함수를 기반으로 한 모델은 존 바딘이 금속-절연체-금속 접합 연구에서 고안했다.^[16] 그의 모델은 두 전극에 대한 두 개의 별개의 정규 직교 파동 함수 집합을 사용하고 시스템을 가깝게 배치할 때 시간 변화를 조사한다.^[5]^[15] 바딘의 방법은 두 하위 시스템의 상호 작용에서 섭동이 발생하는 시간 의존적 섭동 문제를 해결한다는 점에서 독창적이다.^[5]

샘플(S)과 팁(T)의 전자에 대한 각 파동 함수는 표면 일함수 크기와 대략 일치하는 표면 전위 장벽을 지난 후 진공으로 감소한다. 파동 함수는 전위 ''U''_S 및 ''U''_T에서 전자에 대한 두 개의 별도 슈뢰딩거 방정식의 해이다. 알려진 에너지

E^\text{S}_\mu

및

E^\text{T}_\nu

의 상태에 대한 시간 의존성이 제거되면 파동 함수는 다음과 같은 일반적인 형태를 갖는다.

:

\psi^\text{S}_\mu(t) = \psi^\text{S}_\mu \exp\left(-\frac{i}{\hbar} E^\text{S}_\mu t\right),

:

\psi^\text{T}_\nu(t) = \psi^\text{T}_\nu \exp\left(-\frac{i}{\hbar} E^\text{T}_\nu t\right).

두 시스템을 더 가깝게 배치했지만 여전히 얇은 진공 영역으로 분리하면 결합된 시스템에서 전자에 작용하는 전위는 ''U''_T + ''U''_S가 된다. 여기서 각 전위는 장벽 자체의 측면에 공간적으로 제한된다. 한 전극의 파동 함수의 꼬리가 다른 전극의 전위 범위 내에 있기 때문에, 어떤 상태가 시간이 지남에 따라 다른 전극의 상태로 진화할 유한한 확률이 있다.^[5] 샘플의 상태 ''μ''의 미래는

\psi^\text{S}_\mu(t)

및 모든

\psi^\text{T}_\nu(t)

의 시간 의존 계수를 갖는 선형 조합으로 쓸 수 있다.

:

\psi(t) = \psi^\text{S}_\mu(t) + \sum_\nu c_\nu(t) \psi^\text{T}_\nu(t)

초기 조건

c_\nu(0) = 0

으로.^[5] 새 파동 함수가 전위 ''U''_T + ''U''_S에 대한 슈뢰딩거 방정식에 삽입되면 얻어진 방정식은 각 개별

\psi^\text{T}_\nu

에 투영된다. 즉, 방정식은

{\psi^\text{T}_\nu}^*

로 곱해지고 전체 부피에 대해 적분된다. 계수

c_\nu.

를 추출하기 위해 모든

\psi^\text{S}_\mu

는 모든

\psi^\text{T}_\nu

에 대해 ''거의 직교''인 것으로 간주되며(겹침은 총 파동 함수의 작은 부분), 1차량만 유지된다. 결과적으로, 계수의 시간 변화는 다음과 같이 주어진다.

:

\frac{\mathrm{d}}{\mathrm{d}t} c_\nu(t) = -\frac{i}{\hbar} \int \psi^\text{S}_\mu \,U_\text{T}\, {\psi^\text{T}_\nu}^* \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z\,\exp\left[-\frac{i}{\hbar} (E^\text{S}_\mu - E^\text{T}_\nu) t\right].

전위 ''U''_T는 전극 표면에서 몇 개의 원자 직경 떨어진 거리에 0이므로, ''z''에 대한 적분은 장벽 내부의 점 ''z''₀에서 팁의 부피까지 수행할 수 있다(''z'' > ''z''₀).

터널링 행렬 요소가 다음과 같이 정의되면

:

M_{\mu\nu} = \int_{z > z_0} \psi^\text{S}_\mu \,U_\text{T}\, {\psi^\text{T}_\nu}^* \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z,

샘플의 상태 ''μ''가 시간 ''t''에 팁 ''ν''의 상태로 진화할 확률은 다음과 같다.

:

|c_\nu (t)|^2 = |M_{\mu\nu}|^2 \frac{4 \sin^2\big[\tfrac{1}{2\hbar}(E^\text{S}_\mu - E^\text{T}_\nu )t\big]}{(E^\text{S}_\mu - E^\text{T}_\nu)^2}.

많은 전자가 장벽에 부딪히는 시스템에서 이 확률은 성공적으로 터널링되는 전자의 비율을 제공한다. 시간 ''t''에 이 분율이

|c_\nu (t)|^2

였다면, 나중 시간 ''t'' + d''t''에

|c_\nu(t + \mathrm{d}t)|^2

의 총 분율이 터널링되었을 것이다. 따라서 각 인스턴스에서 터널링 전자의 "전류"는

|c_\nu(t + \mathrm{d}t)|^2 - |c_\nu(t)|^2

을

\mathrm{d}t

로 나눈 값에 비례하며, 이는

|c_\nu(t)|^2

의 시간 도함수이다.^[15]

:

\Gamma_{\mu \to \nu}\ \overset{\text{def}}{=}\ \frac{\mathrm{d}}{\mathrm{d}t} |c_\nu(t)|^2 = \frac{2\pi}{\hbar} |M_{\mu\nu}|^2\frac{\sin\big[(E^\text{S}_\mu - E^\text{T}_\nu) \tfrac{t}{\hbar}\big]}{\pi(E^\text{S}_\mu - E^\text{T}_\nu)}.

STM의 측정 시간 척도는 재료 내 전자의 프로세스의 전형적인 펨토초 시간 척도보다 훨씬 더 크며,

t/\hbar

는 크다. 공식의 분율 부분은

(E^\text{S}_\mu - E^\text{T}_\nu)

의 빠르게 진동하는 함수이며,

E^\text{S}_\mu = E^\text{T}_\nu

인 중심 피크에서 빠르게 감소한다. 즉, 가장 확률이 높은 터널링 과정은 전자의 에너지가 보존되는 탄성 과정이다. 위에서 작성된 분율은 델타 함수의 표현이므로,

:

\Gamma_{\mu \to \nu} = \frac{2\pi}{\hbar} |M_{\mu\nu}|^2 \delta(E^\text{S}_\mu - E^\text{T}_\nu).

고체 시스템은 일반적으로 불연속 에너지 레벨보다는 연속 에너지 레벨의 관점에서 설명된다. 용어

\delta(E^\text{S}_\mu - E^\text{T}_\nu)

는 에너지

E^\text{S}_\mu

에서 팁의 상태 밀도로 생각할 수 있다.

:

\Gamma_{\mu \to \nu} = \frac{2\pi}{\hbar} |M_{\mu\nu}|^2 \rho_\text{T}(E^\text{S}_\mu).

에너지

\varepsilon

와

\varepsilon + \mathrm{d}\varepsilon

사이의 샘플에 있는 에너지 레벨의 수는

\rho_\text{S}(\varepsilon)\,\mathrm{d}\varepsilon

이다. 점유되면 이러한 레벨은 스핀 축퇴되며(몇 가지 특수한 종류의 재료 제외) 각 스핀의 전하

2e \cdot \rho_\text{S}(\varepsilon)\,\mathrm{d}\varepsilon

을 포함한다. 샘플이 전압

V

로 바이어스되면 페르미-디랙 분포

f

에 의해 각 전극에 대해 주어진 점유가 동일하지 않은 상태 사이에서만 터널링이 발생할 수 있다. 즉, 하나 또는 다른 것이 점유되지만 둘 다 점유되지는 않는다. 즉,

f(E_\text{F} - eV + \varepsilon) - f(E_\text{F} + \varepsilon)

이 0이 아닌 모든 에너지

\varepsilon

에 해당한다. 예를 들어, 전자는 샘플의 에너지 레벨

E_\text{F} - eV

에서 팁의 에너지 레벨

E_\text{F}

로 터널링하고(

\varepsilon = 0

), 샘플의

E_\text{F}

에 있는 전자는 팁에서

E_\text{F} + eV

의 점유되지 않은 상태를 찾을 것이며(

\varepsilon = eV

), 그 사이의 모든 에너지도 마찬가지이다. 따라서 터널링 전류는 사용 가능한 전자를 나타내는

2e \cdot \rho_\text{S}(E_\text{F} - eV + \varepsilon)\,\mathrm{d}\varepsilon

, 터널링이 허용된 전자에 대한

f(E_\text{F} - eV + \varepsilon) - f(E_\text{F} + \varepsilon)

및 실제로 터널링될 전자에 대한 확률 인자

\Gamma

의 세 가지 요소의 곱의 모든 이러한 에너지에 대한 작은 기여의 합이다.

:

I_t = \frac{4 \pi e}{\hbar} \int_{-\infty}^{+\infty} [f(E_\text{F} - eV + \varepsilon) - f(E_\text{F} + \varepsilon)] \, \rho_\text{S}(E_\text{F} - eV + \varepsilon) \, \rho_\text{T}(E_\text{F} + \varepsilon) \, |M|^2 \, d \varepsilon.

일반적인 실험은 액체 헬륨 온도(약 4 K)에서 실행되며, 이 온도에서 전자 모집단의 페르미 레벨 컷오프는 1밀리전자볼트 미만이다. 허용된 에너지는 두 개의 단계별 페르미 레벨 사이의 에너지뿐이며, 적분은 다음과 같다.

:

I_t = \frac{4 \pi e}{\hbar} \int_0^{eV} \rho_\text{S}(E_\text{F} - eV + \varepsilon) \, \rho_\text{T}(E_\text{F} + \varepsilon) \, |M|^2 \, d \varepsilon.

바이어스가 작을 때 전자 파동 함수와 결과적으로 터널링 행렬 요소는 좁은 에너지 범위에서 크게 변경되지 않는다고 가정하는 것이 합리적이다. 그러면 터널링 전류는 단순히 샘플 표면과 팁의 상태 밀도의 컨볼루션이다.

:

I_t \propto \int_0^{eV} \rho_\text{S}(E_\text{F} - eV + \varepsilon) \, \rho_\text{T}(E_\text{F} + \varepsilon) \, d \varepsilon.

터널링 전류가 두 전극 사이의 거리에 어떻게 의존하는지는 터널링 행렬 요소에 포함되어 있다.

:

M_{\mu\nu} = \int_{z > z_0} \psi^\text{S}_\mu \,U_\text{T}\, {\psi^\text{T}_\nu}^* \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z.

이 공식은 전위에 대한 명시적 종속성이 유지되지 않도록 변환할 수 있다. 먼저,

U_\text{T}\, {\psi^\text{T}_\nu}^*

부분이 팁에 대한 슈뢰딩거 방정식에서 제거되고, 탄성 터널링 조건이 사용되므로

:

M_{\mu\nu} = \int_{z > z_0} \left({\psi^\text{T}_\nu}^* E_\mu \psi^\text{S}_\mu + \psi^\text{S}_\mu \frac{\hbar^2}{2m} \frac{\partial^2}{\partial z^2}{\psi^\text{T}_\nu}^*\right) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z.

이제

E_\mu\, {\psi^\text{S}_\mu}

는 샘플에 대한 슈뢰딩거 방정식에 존재하며,

\psi^\text{S}_\mu

에 작용하는 운동 에너지 연산자와 전위 연산자와 같다. 그러나 ''U''_S를 포함하는 전위 부분은 장벽의 팁 측면에서 거의 0이다. 남아있는 것은,

:

M_{\mu\nu} = -\frac{\hbar^2}{2m} \int_{z > z_0} \left({\psi^\text{T}_\nu}^* \frac{\partial^2}{\partial z^2}{\psi^\text{S}_\mu} - {\psi^\text{S}_\mu} \frac{\partial^2}{\partial z^2}{\psi^\text{T}_\nu}^*\right) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z,

괄호 안의 적분

\partial_z\left({\psi^\text{T}_\nu}^* \, \partial_z \psi^\text{S}_\mu - {\psi^\text{S}_\mu} \, \partial_z {\psi^\text{T}_\nu}^*\right).

이므로 ''z''에 대해 적분할 수 있다.

바딘의 터널링 행렬 요소는 두 평면 전극을 분리하는 표면에 대한 파동 함수와 기울기의 적분이다.

:

M_{\mu\nu} = \frac{\hbar^2}{2m} \int_{z = z_0} \left({\psi^\text{S}_\mu} \frac{\partial}{\partial z}{\psi^\text{T}_\nu}^* -{\psi^\text{T}_\nu}^* \frac{\partial}{\partial z}{\psi^\text{S}_\mu}\right) \,\mathrm{d}x\,\mathrm{d}y.

터널링 전류의 전극 분리에 대한 지수 의존성은 표면에서 전위 단계를 통해 "누출"되어 재료 외부의 고전적으로 금지된 영역으로 지수적으로 감소하는 바로 그 파동 함수에서 비롯된다.

터널링 행렬 요소는 상당한 에너지 의존성을 보이며, 이는 ''eV'' 간격의 상단에서 터널링이 바닥의 상태에서 터널링보다 거의 한 자릿수 더 가능하도록 한다. 샘플이 양으로 바이어스되면 팁의 상태 밀도가 페르미 레벨에 집중된 것처럼 점유되지 않은 레벨이 조사된다. 반대로, 샘플이 음으로 바이어스되면 점유된 전자 상태가 조사되지만 팁의 전자 상태 스펙트럼이 지배한다. 이 경우 팁의 상태 밀도가 가능한 한 평평한 것이 중요하다.^[5]

바딘의 결과와 동일한 결과는 두 전극의 단열적 접근을 고려하고 표준 시간 의존적 섭동 이론을 사용하여 얻을 수 있다.^[15] 이것은 위에서 주어진 형태의 전이 확률

\Gamma_{\mu \to \nu}

에 대한 페르미의 황금률로 이어진다.

바딘의 모델은 두 개의 평면 전극 사이의 터널링을 위한 것이며, 주사 터널링 현미경의 가로 해상도를 설명하지 않는다. 테르소프와 하만^[17]^[18]^[19]은 바딘의 이론을 사용하고 팁을 구조가 없는 기하학적 점으로 모델링했다.^[5] 이를 통해 팁의 특성(모델링하기 어려움)과 샘플 표면의 특성을 분리하는 데 도움이 되었다. 주요 결과는 터널링 전류가 구형 대칭 팁(''s''-파 팁 모델)의 곡률 중심 위치에서 취한 페르미 레벨에서 샘플의 국소 상태 밀도에 비례한다는 것이었다. 이러한 단순화를 통해, 그들의 모델은 피코미터 미만의 원자 규모 요철을 예측했음에도 불구하고 나노미터보다 큰 표면 특징의 이미지를 해석하는 데 유용했다. 이는 현미경의 검출 한계 미만이며, 실제로 실험에서 관찰된 값 미만이다.

서브 나노미터 해상도 실험에서는 팁과 샘플 표면 상태의 컨볼루션이 항상 중요하며, 동일한 스캔 내에서 관찰될 수 있는 원자 요철의 명백한 반전의 정도까지 영향을 미친다. 이러한 효과는 표면 및 팁 전자 상태를 모델링하고 두 전극이 제1 원리로부터 상호 작용하는 방식을 통해서만 설명할 수 있다.

2. 2. 터널링 전류와 상태 밀도

전자의 양자 터널링은 주사 터널링 현미경(STM) 작동의 핵심 개념이다. 고전적으로는 전자가 통과할 수 없는 장벽을 양자역학적으로 통과할 수 있는 현상을 양자 터널링이라고 한다.^[5]

STM에서 시료와 탐침 사이의 터널링은 직사각형 포텐셜 장벽 모델로 간단하게 설명할 수 있다.^[15]^[5] 에너지 ''E''를 가진 전자가 폭 ''w'', 높이 ''U''인 에너지 장벽에 입사할 때, 전자의 거동은 슈뢰딩거 방정식으로 설명된다.

장벽 내부에서 파동 함수는

\psi_B (z) = \xi e^{-\kappa z} + \zeta e^{\kappa z}

(0 < ''z'' < ''w'') 형태이며, 여기서

\kappa = \tfrac{1}{\hbar} \sqrt{2m_\text{e}(U - E)}

이다.

투과 계수 |''t''|²는

|t|^2 = \big[1 + \tfrac{1}{4} \varepsilon^{-1}(1 - \varepsilon)^{-1} \sinh^2\kappa w\big]^{-1}

로 주어지며, 여기서

\varepsilon = E/U

이다. STM 실험에서 일반적인 장벽 높이는 물질의 일함수 ''W''와 비슷하며, 대부분 금속에서 4~6 eV 정도이다.^[15] 작은 바이어스 전압(약 1 V)을 사용하면 투과 확률은

|t|^2 = 16\,\varepsilon(1 - \varepsilon)\,e^{-2\kappa w}

로 단순화된다. 따라서 단일 레벨에서의 터널링 전류는 다음과 같다.^[15]

:

j_t = \left[\frac{4k\kappa}{k^2 + \kappa^2}\right]^2 \, \frac{\hbar k}{m_\text{e}}\,e^{-2\kappa w},

여기서

k = \tfrac{1}{\hbar} \sqrt{2m_\text{e}E}

이고

\kappa = \tfrac{1}{\hbar}\sqrt{2m_\text{e}(U - E)}

이다.

터널링 전류는 시료와 탐침 간 거리에 지수적으로 의존하며, 거리가 1 Å (0.1 nm) 증가하면 전류는 일반적으로 한 자릿수 감소한다.^[5] 이 때문에 탐침이 이상적으로 날카롭지 않더라도 전류는 가장 돌출된 원자나 궤도에서 주로 발생한다.^[15]

터널링은 주로 페르미 준위 근처의 전자에서 발생하며, 터널링 전류는 시료에서 사용 가능한 상태 밀도와 관련된다. 인가된 전압 ''V''에 의한 전류는 샘플의 페르미 준위 ''E''_F와 ''E''_F − ''eV'' 사이의 전자 수와 장벽 반대쪽 탐침에서 터널링할 수 있는 자유 상태를 가진 전자 수에 따라 달라진다.^[5]

작은 바이어스와 절대 영도 근처 온도에서 터널링 전류는 다음과 같이 표현된다.^[5]

:

I_t = \tfrac{1}{2} e^2v\,\rho(E_\text{F})\,V\,T.

여기서 ''ρ''(''E''_F)는 전자 상태 밀도, ''V''는 전압, ''T''는 투과 확률이다.

존 바딘은 금속-절연체-금속 접합 연구에서 두 전극에 대한 별개의 정규 직교 파동 함수를 사용하는 모델을 고안했다.^[16] 그의 모델은 시간 의존적 섭동 문제를 해결하며, 터널링 행렬 요소를 다음과 같이 정의한다.

:

M_{\mu\nu} = \int_{z > z_0} \psi^\text{S}_\mu \,U_\text{T}\, {\psi^\text{T}_\nu}^* \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z,

바딘의 터널링 행렬 요소는 두 평면 전극을 분리하는 표면에 대한 파동 함수와 기울기의 적분이다.

:

M_{\mu\nu} = \frac{\hbar^2}{2m} \int_{z = z_0} \left({\psi^\text{S}_\mu} \frac{\partial}{\partial z}{\psi^\text{T}_\nu}^* -{\psi^\text{T}_\nu}^* \frac{\partial}{\partial z}{\psi^\text{S}_\mu}\right) \,\mathrm{d}x\,\mathrm{d}y.

터널링 전류는 샘플 표면과 팁의 상태 밀도의 컨볼루션에 비례한다.

:

I_t \propto \int_0^{eV} \rho_\text{S}(E_\text{F} - eV + \varepsilon) \, \rho_\text{T}(E_\text{F} + \varepsilon) \, d \varepsilon.

테르소프와 하만^[17]^[18]^[19]은 바딘의 이론을 사용하고 팁을 구조가 없는 기하학적 점으로 모델링하여 터널링 전류가 구형 대칭 팁의 곡률 중심 위치에서 취한 페르미 레벨에서 샘플의 국소 상태 밀도에 비례함을 보였다.^[5]

2. 3. 바딘의 형식

존 바딘은 금속-절연체-금속 접합 연구에서 두 전극에 대한 별개의 파동 함수를 이용한 모델을 고안했다.^[16] 이 모델은 두 전극에 대한 두 개의 별개의 정규 직교 파동 함수 집합을 사용하고 시스템을 가깝게 배치할 때 시간 변화를 조사한다.^[5]^[15] 바딘의 방법은 표준 레일리-슈뢰딩거 섭동 이론의 외부 전위가 아닌 두 하위 시스템의 상호 작용에서 섭동이 발생하는 시간 의존적 섭동 문제를 해결한다.^[5]

샘플(S)과 팁(T)의 전자에 대한 각 파동 함수는 표면 일함수 크기와 대략 일치하는 표면 전위 장벽을 친 후 진공으로 감소한다. 파동 함수는 전위 ''U''_S 및 ''U''_T에서 전자에 대한 두 개의 별도 슈뢰딩거 방정식의 해이다. 알려진 에너지

E^\text{S}_\mu

및

E^\text{T}_\nu

의 상태에 대한 시간 의존성이 제거되면 파동 함수는 다음과 같은 일반적인 형태를 갖는다.

:

\psi^\text{S}_\mu(t) = \psi^\text{S}_\mu \exp\left(-\frac{i}{\hbar} E^\text{S}_\mu t\right),

:

\psi^\text{T}_\nu(t) = \psi^\text{T}_\nu \exp\left(-\frac{i}{\hbar} E^\text{T}_\nu t\right).

두 시스템을 더 가깝게 배치하지만 여전히 얇은 진공 영역으로 분리되어 있으면 결합된 시스템에서 전자에 작용하는 전위는 ''U''_T + ''U''_S이다. 여기서 각 전위는 장벽 자체의 측면에 공간적으로 제한된다. 한 전극의 파동 함수의 꼬리가 다른 전극의 전위 범위 내에 있기 때문에, 어떤 상태가 시간이 지남에 따라 다른 전극의 상태로 진화할 유한한 확률이 있다.^[5] 샘플의 상태 ''μ''의 미래는

\psi^\text{S}_\mu(t)

및 모든

\psi^\text{T}_\nu(t)

의 시간 의존 계수를 갖는 선형 조합으로 쓸 수 있다.

:

\psi(t) = \psi^\text{S}_\mu(t) + \sum_\nu c_\nu(t) \psi^\text{T}_\nu(t)

(초기 조건

c_\nu(0) = 0

)^[5]

새 파동 함수가 전위 ''U''_T + ''U''_S에 대한 슈뢰딩거 방정식에 삽입되면 얻어진 방정식은 각 개별

\psi^\text{T}_\nu

에 투영된다. 즉, 방정식은

{\psi^\text{T}_\nu}^*

로 곱해지고 전체 부피에 대해 적분되어 계수

c_\nu

를 추출한다. 이때, 모든

\psi^\text{S}_\mu

는 모든

\psi^\text{T}_\nu

에 대해 ''거의 직교''인 것으로 간주되며(겹침은 총 파동 함수의 작은 부분), 1차항만 유지된다. 결과적으로, 계수의 시간 변화는 다음과 같이 주어진다.

:

\frac{\mathrm{d}}{\mathrm{d}t} c_\nu(t) = -\frac{i}{\hbar} \int \psi^\text{S}_\mu \,U_\text{T}\, {\psi^\text{T}_\nu}^* \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z\,\exp\left[-\frac{i}{\hbar} (E^\text{S}_\mu - E^\text{T}_\nu) t\right].

전위 ''U''_T는 전극 표면에서 몇 개의 원자 직경 떨어진 거리에 0이므로, ''z''에 대한 적분은 장벽 내부의 점 ''z''₀에서 팁의 부피까지 수행할 수 있다(''z'' > ''z''₀).

터널링 행렬 요소가 다음과 같이 정의되면

:

M_{\mu\nu} = \int_{z > z_0} \psi^\text{S}_\mu \,U_\text{T}\, {\psi^\text{T}_\nu}^* \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z,

샘플의 상태 ''μ''가 시간 ''t''에 팁 ''ν''의 상태로 진화할 확률은 다음과 같다.

:

|c_\nu (t)|^2 = |M_{\mu\nu}|^2 \frac{4 \sin^2\big[\tfrac{1}{2\hbar}(E^\text{S}_\mu - E^\text{T}_\nu )t\big]}{(E^\text{S}_\mu - E^\text{T}_\nu)^2}.

바딘의 터널링 행렬 요소는 두 평면 전극을 분리하는 표면에 대한 파동 함수와 기울기의 적분이다.

:

M_{\mu\nu} = \frac{\hbar^2}{2m} \int_{z = z_0} \left({\psi^\text{S}_\mu} \frac{\partial}{\partial z}{\psi^\text{T}_\nu}^* -{\psi^\text{T}_\nu}^* \frac{\partial}{\partial z}{\psi^\text{S}_\mu}\right) \,\mathrm{d}x\,\mathrm{d}y.

터널링 전류의 전극 분리에 대한 지수 의존성은 표면에서 전위 단계를 통해 "누출"되어 재료 외부의 고전적으로 금지된 영역으로 지수적으로 감소하는 바로 그 파동 함수에서 비롯된다.

3. 작동 방식

주사 터널링 현미경(STM)은 탐침과 시료 사이의 거리가 매우 가까울 때 발생하는 양자 터널링 효과를 이용한다. 탐침은 조작 메커니즘을 통해 시료에 가까이 접근시킨다. 근접 거리에서, 시료 표면에 대한 탐침 위치의 미세한 제어는 압전 스캐너 튜브에 의해 이루어지는데, 이 튜브는 제어 전압에 의해 길이가 변경될 수 있다. 시료와 탐침 사이에 바이어스 전압이 가해지고, 탐침이 터널링 전류를 받기 시작할 때까지 스캐너가 점차 연장된다. 탐침-시료 간 거리는 4–7 Å (0.4–0.7 nm) 범위 내로 유지된다.^[5] 터널링 전류는 나노암페어 미만 범위에서 증폭된다. 터널링이 설정되면, 실험의 요구 사항에 따라 시료 바이어스와 시료에 대한 탐침 위치가 변경된다.

STM은 주로 정전류 모드와 정전압 모드의 두 가지 방식으로 작동한다.

'''정전류 모드''': 터널링 전류를 일정하게 유지하면서 탐침의 높이 변화를 측정한다.
'''정전압 모드''': 탐침의 높이를 일정하게 유지하면서 터널링 전류의 변화를 측정한다.

탐침이 ''x''–''y'' 매트릭스에서 표면을 가로질러 이동함에 따라, 표면 높이와 전자 상태의 변화는 터널링 전류의 변화를 일으킨다.

시료를 가로질러 스캔하는 것 외에도, 바이어스 전압을 변화시키고 특정 위치에서 전류 변화를 측정하여 시료 내 지정된 위치에서 전자 구조에 대한 정보를 얻을 수 있다.^[4] 이러한 유형의 측정은 주사 터널링 분광법 (STS)이라고 하며, 일반적으로 시료 내 전자 에너지에 따른 국소 상태 밀도를 나타낸다. STM의 장점은 매우 국소적인 측정을 할 수 있다는 것이다. 예를 들어, 불순물 위치에서의 상태 밀도를 불순물 주변 및 표면의 다른 위치에서의 상태 밀도와 비교할 수 있다.^[9]

3. 1. 정전류 모드

정전류 모드에서는 피드백 전자 장치가 압전 높이 제어 메커니즘에 전압을 가하여 탐침의 높이를 조정한다. 터널링 전류가 설정된 수준보다 낮으면 탐침이 시료 쪽으로 이동하고, 그 반대의 경우도 마찬가지이다.^[5] 이 모드는 상대적으로 느린데, 전자 장치가 터널링 전류를 확인하고 표면의 각 측정 지점에서 피드백 루프에서 높이를 조정해야 하기 때문이다. 표면이 원자적으로 평평하면, ''z''-스캐너에 가해지는 전압은 주로 국소 전하 밀도의 변화를 반영한다. 그러나 원자 단계를 만나거나 재구성으로 인해 표면이 휘어지면, 스캐너의 높이도 전체 지형 때문에 변경되어야 한다. 탐침이 표면을 스캔하는 동안 터널링 전류를 일정하게 유지하는 데 필요한 ''z''-스캐너 전압의 이미지는 지형 데이터와 전자 밀도 데이터를 모두 포함한다. 어떤 경우에는 높이 변화가 어느 한쪽의 결과인지 명확하지 않을 수 있다.^[5]

3. 2. 정전압 모드

탐침의 높이를 일정하게 유지하면서 터널링 전류의 변화를 측정한다. 표면의 디지털 이미지는 정전류 모드가 아닌 정전압 모드로 형성되는데, 이 모드에서는 터널링 전류가 미리 결정된 수준으로 유지되는 동안 탐침의 높이(''z'')를 제어하는 전압이 기록된다.^[5]

이 작동 모드는 스캐너가 표면을 앞뒤로 움직일 때 ''z''-스캐너 전압이 일정하게 유지되고, 거리에 지수적으로 의존하는 터널링 전류가 매핑되기에 더 빠르다. 그러나 큰 흡착 분자가 존재하거나 능선과 홈이 있는 거친 표면에서는 탐침이 시료와 충돌할 위험이 있다.

탐침의 래스터 스캔은 128×128에서 1024×1024 (또는 그 이상) 매트릭스이며, 래스터의 각 지점에 대해 단일 값이 얻어진다. STM에 의해 생성된 이미지는 그레이스케일이며, 중요한 특징을 시각적으로 강조하기 위해 후처리에서 색상이 추가된다.

4. 장치 구성

주사 터널링 현미경(STM)은 팁, 압전 제어 ''z''축 및 ''x'', ''y''축 스캐너, 시료-팁 접근 메커니즘, 제어 시스템, 진동 방지 시스템으로 구성된다.^[5] 현미경은 전용 전자 장치와 컴퓨터로 제어된다.

4. 1. 탐침

STM의 탐침은 주로 텅스텐이나 백금-이리듐 합금 와이어로 만들어지며, 금도 사용된다.^[4] 텅스텐 탐침은 보통 전기화학적 에칭으로, 백금-이리듐 탐침은 기계적 전단으로 만들어진다. 이미지의 해상도는 탐침 끝의 곡률 반경에 의해 결정된다. 탐침 끝에 여러 개의 정점이 있으면 이미지에 결함이 생길 수 있는데, 특히 두 개의 정점이 터널링에 비슷하게 영향을 주는 '이중 팁 이미징'이 흔히 나타난다.^[4] 날카로운 탐침을 얻기 위한 여러 방법이 알려져 있지만, 탐침의 최종 품질은 진공 상태에서 터널링을 통해서만 확인할 수 있다. 때로는 탐침에 고전압을 가하거나, 표면에서 원자나 분자를 흡착시켜 탐침을 컨디셔닝하기도 한다.

초기에는 탐침 선단 반경이 100nm 정도였지만, 집속 이온 빔 등의 방법을 통해 더 날카로운 탐침을 제작할 수 있게 되었다. 2007년에는 탐침 끝의 직경이 약 10nm까지 작아졌다.

4. 2. 스캐너

주사 터널링 현미경(STM)의 주요 구성 요소는 주사 팁, 압전 제어 높이 (''z''축) 및 측면 (''x'' 및 ''y''축) 스캐너, 그리고 시료-팁 접근 메커니즘이다. 현미경은 전용 전자 장치와 컴퓨터로 제어되며, 진동 방지 시스템으로 지지된다.^[5]

대부분의 최신 설계에서 스캐너는 금속화된 표면을 가진, 방사형으로 편광된 압전체 중공 튜브이다. 외부 표면은 ''x'' 및 ''y'' 움직임 전극 역할을 하도록 네 개의 긴 사분면으로 나뉘며, 반대쪽에는 두 개의 극성을 가진 편향 전압이 적용된다. 튜브 재료는 약 5nm/볼트의 압전 상수를 가진 티탄산 지르콘산 납 세라믹이다. 팁은 튜브 중앙에 장착된다. 전극 간 일부 누화 및 고유한 비선형성으로 인해 움직임은 보정되며, 독립적인 ''x'', ''y'', ''z'' 움직임에 필요한 전압은 보정 테이블에 따라 적용된다.^[5]

4. 3. 제어 시스템

탐침의 움직임, 데이터 수집, 이미지 처리는 전용 전자 장치와 컴퓨터를 통해 제어된다.^[5] 주사 탐침 현미경용 소프트웨어를 사용하여 정량적 측정 및 이미지 처리를 수행한다.^[10]

일부 주사 터널링 현미경은 높은 프레임 속도로 이미지를 기록할 수 있다.^[11]^[12] 이러한 이미지로 제작된 비디오는 표면 확산^[13]을 보여주거나 표면에서의 흡착 및 반응을 추적할 수 있다. 비디오 속도 현미경에서는 팁의 높이를 조절하는 완벽하게 작동하는 피드백으로 80 Hz의 프레임 속도가 달성되었다.^[14]

4. 4. 진동 방지 시스템

외부 진동은 STM 이미지의 품질을 저하시키므로, 진동 방지 시스템이 필수적이다. 비니히(Gerd Binnig)와 로러(Heinrich Rohrer)의 첫 번째 STM에서는 자기 부상을 사용하여 STM을 진동으로부터 보호했다.^[5] 현재는 기계식 스프링 또는 가스 스프링 시스템이 주로 사용된다.^[5] 또한, 와전류를 사용하는 진동 감쇠 메커니즘이 구현되기도 한다.^[5]

극도의 안정성이 필요한 경우, STM은 실험실 내부의 진동 방지 장치 위에 자체적으로 부유하는 음향 및 전자기적 격리가 있는 전용 콘크리트실인 무반향실에 설치되기도 한다.

초기에는 냉각을 위해 1시간에 20L의 액체 헬륨을 필요로 하는 초전도체자기 부상 방식을 사용했지만, 이후 2단 매달기 스프링 기구와 와전류 방식의 영구 자석 진동 감쇠 장치로 변경되었다.

5. 역사

미국 국립표준기술연구소(NIST)의 R. 영, J. 워드, F. 스키어는 게르트 비니히와 하인리히 로러의 것과 유사한 ''토포그래피너''를 개발했다. 이는 전계 방출에 의존했다.^[21] 그러나 영은 노벨 위원회로부터 터널 효과를 사용하면 더 나은 해상도를 얻을 수 있다는 것을 깨달은 사람으로 인정받고 있다.^[22]

장치 완성 초기에는 장치의 성능과 원자 수준의 관측 결과에 회의적인 의견도 있었으나, 1983년 실리콘 (111) 표면의 7×7 재구성 구조(소위 DAS 모델)를 결정하는 중요한 단서를 STM의 관측 결과가 제공하면서 성능과 신뢰성이 인정받게 되었다.

기타 관련 특허에 대해서는 일본 국내에서 출원된 특허가 중심이지만, [http://www.inpit.go.jp/blob/katsuyo/pdf/chart/fippan19.pdf 프로브 현미경 기술]에 자세히 나와 있다.

5. 1. 초기 개발

1978년 IBM 취리히 연구소의 하인리히 로러는 조셉슨 접합 관련 절연성 박막의 국소적 성장 과정 및 전기적 특성 연구를 위해 볼프강 폰 괴테 대학교의 게르트 비니히를 채용했다. 이들은 10 nm 이하 좁은 범위에서 터널링 분광법을 관찰하는 장치를 개발했다.

처음에는 분광법 측정을 위해 10nm 이하 크기의 전극으로 시료를 끼우는 방식이 문제였다. 상부 전극을 금속 바늘로 하면 면적은 해결되지만, 접촉으로 인해 시료가 파괴될 수 있기 때문이었다. 비니히는 비접촉 방식인 터널링 효과를 이용, 금속 바늘을 수 Å 거리까지 접근시켜 국소 분광법 측정에 성공했다. 초기 공간 분해능은 4.5nm로 여겨졌으나,^[24] 1982년 CaIrSn₄(사주석화 칼슘 이리듐) 측정에서 원자 1개 단차를 측정, 더 높은 분해능을 확인했다.^[25]

5. 2. 실리콘 표면 연구와 노벨상

1983년, 주사 터널링 현미경(STM)의 관측 결과는 그 전까지 구조 해명이 이루어지지 않아 30년 가까이 논쟁의 대상이 되었던 실리콘 (111) 표면의 7x7 재구성 구조(소위 DAS 모델)를 결정하는 중요한 단서를 제공하면서 그 성능과 신뢰성이 인정받게 되었다.^[24] 게르트 비니히와 하인리히 로러는 STM 완성의 공적으로 1986년 노벨 물리학상을 수상했다.^[25]

5. 3. 특허

게르트 비니히와 하인리히 로러의 STM에 대한 특허(미국 특허 4343993)가 존재한다.^[26]

6. 응용 및 관련 기술

주사 터널링 현미경(STM)은 표면 과학, 재료 과학, 나노 기술 등 다양한 분야에 응용된다. 관련 기술로는 광자 주사 현미경(PSTM), 주사 터널링 전위법(STP), 스핀 편광 주사 터널링 현미경(SPSTM), 다중 팁 주사 터널링 현미경, 원자간력 현미경(AFM) 등이 있다.

6. 1. 표면 구조 분석

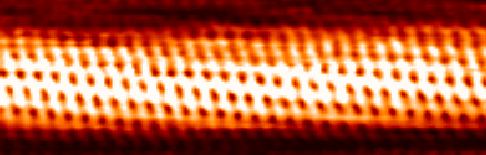
탄화 규소 (SiC) 결정 표면의 원자는 육각형 격자 형태로 배열되어 있으며 0.3nm 간격으로 떨어져 있음

6. 2. 관련 기술

광자 주사 현미경(PSTM)은 광학 팁을 사용하여 광자를 터널링하며,^[4] 주사 터널링 전위법(STP)은 표면을 가로지르는 전위를 측정한다.^[4] 스핀 편광 주사 터널링 현미경(SPSTM)은 강자성체 팁을 사용하여 스핀 편광 전자를 자기 샘플로 터널링한다.^[23] 다중 팁 주사 터널링 현미경은 나노 규모에서 전기적 측정을 수행할 수 있으며, 원자간력 현미경(AFM)은 팁과 샘플 사이의 상호 작용으로 인한 힘을 측정한다.

7. 한국의 STM 연구 및 활용

(주어진 원본 소스가 없으므로 내용을 작성할 수 없습니다.)

참조

_[1] 논문 Scanning tunneling microscopy
_[2] 논문 Scanning tunneling microscopy—from birth to adolescence 1987-07-01
_[3] 웹사이트 Press release for the 1986 Nobel Prize in physics http://nobelprize.or[...]
_[4] 서적 Scanning tunneling microscopy and its applications https://books.google[...] Springer Verlag
_[5] 서적 Introduction to Scanning Tunneling Microscopy http://www.columbia.[...] Oxford University Press
_[6] 웹사이트 STM 150 Aarhus – High Stability Temperature Control http://www.specs.de/[...] 2017-02-23
_[7] 간행물 Scanning Tunneling Spectroscopy (STS) https://doi.org/10.1[...] Springer 2020-10-15
_[8] 웹사이트 STM References – Annotated Links for Scanning Tunneling Microscope Amateurs http://www.e-basteln[...] 2012-07-13
_[9] 논문 Imaging the effects of individual zinc impurity atoms on superconductivity in Bi2Sr2CaCu2O8+delta 2000-02
_[10] 서적 Encyclopedia of Nanoscience and Nanotechnology http://www.lapshin.f[...] American Scientific Publishers
_[11] 논문 Scanning probe microscopy at video-rate
_[12] 논문 Fast-acting piezoactuator and digital feedback loop for scanning tunneling microscopes http://www.lapshin.f[...]
_[13] 논문 Direct measurement of surface diffusion using atom-tracking scanning tunneling microscopy https://zenodo.org/r[...] 1996-01
_[14] 논문 Scanning probe microscopes go video rate and beyond https://openaccess.l[...]
_[15] arXiv Theory of Scanning Tunneling Microscopy 2014-04-03
_[16] 논문 Tunneling from a many particle point of view
_[17] 논문 Theory and Application for the Scanning Tunneling Microscope 1983-06-20
_[18] 논문 Theory of the scanning tunneling microscope https://link.aps.org[...] 1985-01
_[19] 논문 Scanning tunneling microscopy https://aip.scitatio[...] 1987-01-15
_[20] 논문 Electronic structure of reconstructed Au(100): Two-dimensional and one-dimensional surface states 2012-07-18
_[21] 논문 The Topografiner: An Instrument for Measuring Surface Microtopography http://www.nanoworld[...]
_[22] 뉴스 The Topografiner: An Instrument for Measuring Surface Microtopography http://nvl.nist.gov/[...] NIST
_[23] 논문 Recent advances in spin-polarized scanning tunneling microscopy
_[24] 문서 C. F. Quate, ''Physics Today'', '''8''', 26 (1986)
_[25] 문서 G. Binning ''et al''., ''Phys. Rev. Lett.'', '''27''', 922 (1982)
_[26] 특허 US4,343,993 https://www.google.c[...]
_[27] 서적 Introduction to Scanning Tunneling Microscopy http://www.columbia.[...] Oxford University Press 2014-10-02
_[28] 웹인용 STM References - Annotated Links for Scanning Tunneling Microscope Amateurs http://www.e-basteln[...] 2012-07-13
_[29] 특허 US4,343,993 https://www.google.c[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com