맨위로가기

바스카라 2세

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

바스카라 2세는 1114년 인도에서 태어난 수학자이자 천문학자이다. 그는 아버지에게 수학을 배우고 우자인 천문대 책임자를 역임했으며, 저서 『싯단타 시로마니』를 통해 산술, 대수, 기하학, 삼각법 등 다양한 수학 분야에서 업적을 남겼다. 특히 2차, 3차, 4차 부정 방정식의 해법을 제시하고, 펠 방정식의 일반적인 정수 해법을 제시하는 등 대수학 발전에 기여했다. 또한 미분 계수의 근사치를 발견하고 롤의 정리의 초기 형태를 제시하는 등 미적분학의 초기 개념을 발전시켰다. 바스카라 2세는 항성년의 길이를 정확하게 정의했으며, 영구 기관의 초기 모델을 제시하는 등 공학 분야에서도 업적을 남겼다. 그의 업적은 인도뿐만 아니라 전 세계 수학 및 과학 발전에 큰 영향을 미쳤으며, 그의 이름을 딴 연구소와 위성이 존재한다.

더 읽어볼만한 페이지

  • 1110년대 출생 - 이오안네스 트제트제스
    이오안네스 트제트제스는 폭넓은 지식을 바탕으로 다양한 분야에서 저술 활동을 펼친 12세기 비잔틴 제국의 학자이자 작가로, 특히 고대 그리스 문학 연구에 기여했다.
  • 중세 인도의 수학자 - 닐라칸타 소마야지
    닐라칸타 소마야지는 케랄라 학파의 저명한 천문학자이자 수학자로, 《아리아바티야》 주석서에서 태양중심설 행성 모델을 제시하고 천문학과 수학을 다룬 대표작 《탄트라상그라하》를 저술했다.
  • 중세 인도의 수학자 - 샨카라 바리야르
    샨카라 바리야르는 16세기 인도의 수학자이자 천문학자로, 유크티바샤를 기반으로 한 탄트라상그라하 해설서인 유크티-디피카와 라구-비브리티, 그리고 바스카라 2세의 릴라바티 해설서인 크리야-크라마카리 등 다양한 수학 및 천문학 관련 저술을 남겼다.
바스카라 2세
지도
기본 정보
이름바스카라 2세
다른 이름바스카라차리야
출생일1114년경
출생지마하라슈트라 주 비자다비다 (아마도 파트나데비 또는 비드)
사망일1185년경
사망지우자인, 마디아프라데시 주
활동 시기샤카 시대
직업천문학자, 수학자
학문 분야
주요 관심사대수학, 산술, 삼각법
학문 분야수학자, 천문학자, 기하학자
주요 업적싯단타 시로마니
릴라바티
비자 가니타
카라나 쿠투할라
그라하가니타와 골라디야야
기타
로마자 표기Bhāskara

2. 생애와 배경

바스카라 2세는 1114년 인도 비자다비다(Vijjadavida)에서 태어났다. 그의 가문은 대대로 학자를 배출한 명문가였다. 아버지 마헤슈바라(Maheśvara)는 저명한 수학자이자 점성술사였으며, 바스카라 2세에게 수학을 가르쳤다.

바스카라 2세는 샤카력 1036년(서기 1114년)에 태어났고, 36세 때 『싯단타 시로마니』(Siddhānta Shiromani)를 저술했다고 밝혔다. 『싯단타 시로마니』는 서기 1150년에 완성되었으며, 69세(1183년) 때 『카라나 쿠투할라』(Karaṇa-kutūhala)라는 또 다른 저서를 저술했다.

바스카라 2세는 당시 인도의 주요 수학 중심지였던 우자인(Ujjain) 천문대의 책임자를 역임하면서 수학과 천문학 연구에 매진했다. 역사 기록에 따르면 그의 증조할아버지부터 아들 및 다른 후손들까지 궁정 학자직을 세습했다.[27] 그의 아들 로카삼무드라(Loksamudra)는 1207년에 바스카라 2세의 저술을 연구하기 위한 학교 설립을 도왔다.[27] 바스카라 2세는 1185년에 사망했다.

2. 1. 가문과 출생지 논란

바스카라는 데샤스타 리그베디 브라만(Deśastha Rigvedi Brahmin) 가문[10]에서 태어났으며, 그의 출생지인 비자다비다(Vijjadavida)의 정확한 위치에 대해서는 학자들 간에 이견이 있다.[3]

바스카라의 『싯단타 시로마니』 주석가인 무니슈바라(Munishvara, 17세기)는 그의 저서 『마리치 티카』(Marīci Tīkā)에서 비자다비다가 마하라슈트라주 비다르바 지역 근처, 고다바리 강변 근처에 위치한다고 설명했다. 그러나 정확한 위치에 대해서는 다음과 같은 다양한 주장이 제기되고 있다.

  • 찰리스가온 탈루카의 파탄 근처[11]
  • 현재의 비드 도시[1]
  • 카르나타카주의 비자푸르(Bijapur) 또는 비다르(Bidar)[12]
  • 텔랑가나주의 바사라(Basara)[13]

2. 2. 릴라바티 전설

바스카라 2세의 산술 책은 그의 딸 릴라바티를 위해 쓰였다는 전설이 있다. 페르시아어판 《릴라바티》에 실린 이야기는 다음과 같다. 바스카라 2세가 릴라바티의 점성술을 연구하여 점을 쳐 본 결과, 딸이 특정 시간에 결혼하지 않으면 남편이 결혼 후 얼마 지나지 않아 죽을 것이라는 결과가 나왔다. 딸에게 그 정확한 시간을 알려주기 위해, 바스카라 2세는 물이 담긴 용기를 놓고 그 위에 바닥에 작은 구멍이 뚫린 컵을 띄워 적절한 시간에 컵이 가라앉도록 설정했다. 그리고 릴라바티에게는 그것에 가까이 가지 말라고 경고했다. 하지만 딸은 이상하게 여겨 그것을 엿보았고, 코에 끼고 있던 진주가 컵에 떨어져 가라앉는 방식이 달라졌다. 그 때문에 결혼이 잘못된 시간에 치러졌고, 그녀는 곧 과부가 되었다.[28]

3. 주요 저서

바스카라 2세의 대표적인 저서는 1150년에 완성된 《싯단타 시로마니》이다. 이 책은 수학과 천문학에 관한 내용을 담고 있으며, 릴라바티, 비자가니타, 그라하가니타, 골라디야야의 네 부분으로 구성되어 있다. 바스카라 2세는 69세에 《카라나 쿠투할라》라는 저서도 저술했다.

3. 1. 릴라바티(Līlāvatī)

《릴라바티》(लीलावतीsa, Līlāvatī)는 바스카라 2세가 지은 책으로, 그의 딸의 이름을 따서 지어졌다. 277개의 구절로 구성되어 있으며, 계산, 급수, 측정, 순열 등 다양한 주제를 다룬다. 시와 같은 아름다운 구절들로 이루어져 있다.

《릴라바티》는 산술, 대수학, 기하학 등 다양한 수학 분야를 다루며, 다음과 같은 내용들을 포함한다.

《수리천문서론(Siddhānta Śiromaṇī)》의 첫 번째 권인 《릴라바티(Līlāvatī)》의 한 페이지. 모서리에 피타고라스 정리가 사용됨. 1650년 판


바스카라차리아의 피타고라스 정리 증명


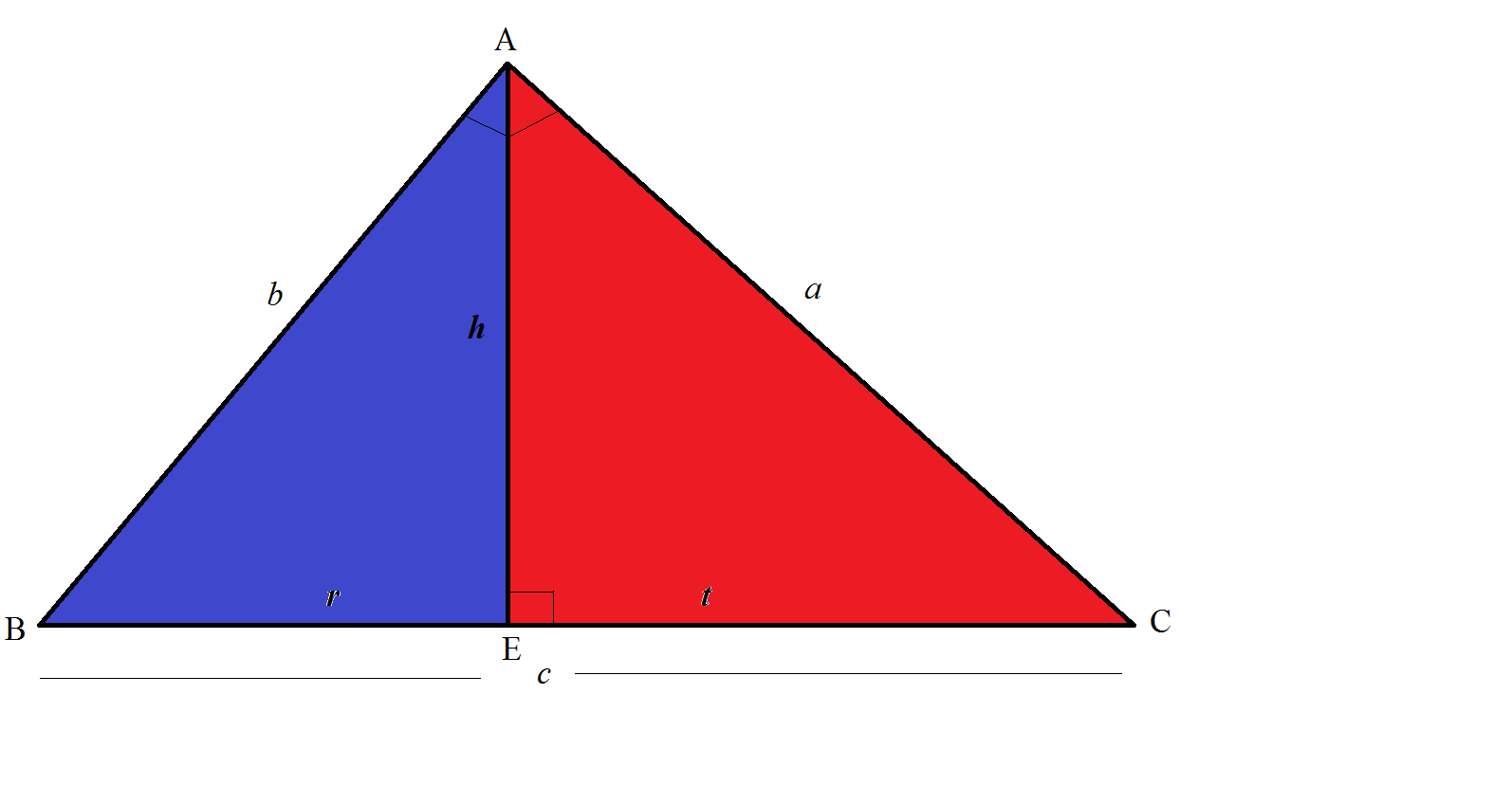
바스카라는 두 가지 다른 방법으로 같은 넓이를 계산하고 항을 소거하여 a2 + b2 = c2를 얻는 피타고라스 정리의 증명을 제시했다.[14]

그의 업적은 체계화, 개선된 방법, 그리고 그가 도입한 새로운 주제들로 인해 뛰어나다. 더욱이 『릴라바티』에는 훌륭한 문제들이 포함되어 있으며, 바스카라의 의도는 『릴라바티』를 배우는 학생들이 방법의 기계적인 적용에 관심을 가져야 한다는 것이었을 것이라고 생각된다.

3. 2. 비자가니타(Bījagaṇita)

《비자가니타》는 대수학을 다루는 책으로, 213개의 구절로 구성되어 있다. 이 책에서는 0, 무한대, 양수와 음수, 펠 방정식을 포함한 부정 방정식을 다룬다. 특히 바스카라는 61x^2 + 1 = y^2 문제를 꾸따꺼(Kuṭṭaka]]) 방법을 사용하여 풀었는데, 이 문제는 수세기 뒤에 페르마를 비롯한 유럽 수학자들이 풀지 못한 문제였다.[17]

《비자가니타》의 내용은 다음과 같다.

제목내용
양수와 음수양수 및 음수의 성질과 연산
0 (영)0의 개념과 성질
미지수미지수를 포함하는 식과 그 계산
미지수의 결정미지수의 값을 구하는 방법
무리수무리수와 그 제곱근을 구하는 방법
꾸따꺼(Kuṭṭaka)부정 방정식 및 디오판토스 방정식을 푸는 방법
단순 방정식2차, 3차, 4차의 부정 방정식
다변수를 포함하는 단순 방정식미지수가 둘 이상인 단순 방정식
부정 이차 방정식ax2 + b = y2 형태의 방정식
2차, 3차, 4차 부정 방정식의 해법다양한 차수의 부정 방정식 해법
이차 방정식이차 방정식의 해법
다변수를 포함하는 이차 방정식미지수가 둘 이상인 이차 방정식
다변수 곱셈 연산여러 미지수를 포함하는 곱셈 연산



바스카라 2세는 ax2 + bx + c = y 형태의 부정 이차 방정식을 푸는 순환적인 차크라발라 방법을 고안했다.[17] 또한, Nx2 + 1 = y2 형태의 펠 방정식 문제의 정수해를 구하는 방법을 제시했는데, 이 방법 역시 차크라발라 방법을 이용하며, 그 중요성이 높게 평가된다.

3. 3. 그라하가니타(Grahagaṇita)

《그라하가니타》는 행성의 운동을 다루는 책으로, 총 451개의 구절로 구성되어 있다. 이 책에서 바스카라 2세는 행성의 순간 속도를 고려했는데, 다음과 같은 근사값을 제시했다.

:\sin y' - \sin y \approx (y' - y) \cos y (y'가 y에 가까울 때)

현대 표기법으로는 다음과 같다.

: \frac{d}{dy} \sin y = \cos y .

이는 사인 함수의 미분값을 나타낸 것으로, 미적분학의 초기 개념에 해당한다. 이 결과는 문잘라차리아(Muñjalācārya) 마나삼(mānasam)이 사인표의 맥락에서 이미 관찰한 바 있다. 바스카라 2세는 또한 행성의 순간 속도가 최고점에서 0이 된다고 언급했다.

3. 4. 골라디야야(Golādhyāya)

주어진 소스는 《골라디야야》에 대한 내용이 아니므로, 요약만 남기고 삭제한다.

《골라디야야》는 구면 기하학과 천문학을 다루는 책이다. 구면 삼각법, 천구의 성질, 우주론, 지리학, 행성 운동 등 다양한 주제를 다룬다.

4. 수학적 업적

바스카라 2세는 대수학, 미적분학, 삼각법 등 다양한 분야에서 중요한 업적을 남겼다.


  • 피타고라스 정리 증명: 동일한 넓이를 두 가지 다른 방법으로 계산한 다음 항을 소거하여 ''a'' 2 + ''b'' 2 = ''c'' 2를 유도하였다.[37]
  • 방정식 해: 이차 방정식, 삼차 방정식, 사차 방정식의 해를 제시하였다.
  • 정수 해: 선형 및 이차 방정식에서 정수 해를 구하는 방법 (쿠타카법)을 제시하였다. 이는 17세기 르네상스 시대 유럽의 수학자들과 같은 방법이다.
  • 차크라발라법: ''ax'' 2 + ''bx'' + ''c'' = ''y''라는 형태의 방정식을 푸는 차크라발라법을 제시하였다.
  • 펠 방정식: 펠 방정식이라고 불리는 ''x'' 2 − ''ny'' 2 = 1이라는 형태의 방정식의 정수 해를 구하는 방법을 제시하였다.
  • 이차 방정식: 변수가 여러 개인 이차 방정식을 풀고, 음수와 무리수 해를 발견하였다.
  • 해석학: 해석학의 예비 개념을 제시하였다.
  • 미적분학: 미분법의 예비 개념과 적분법에 대한 기여와 함께 미분 계수를 발견하고 미분학을 구상하였다.
  • 롤의 정리 및 평균값 정리: 롤의 정리 및 평균값 정리의 흔적을 발견하였다.
  • 삼각함수: 삼각 함수 및 공식의 도함수 계산하였다.
  • 구면삼각법: ''싯단타-시로마니''에서 다른 삼각법 결과와 함께 구면 삼각법을 개발하였다.


바스카라 2세는 셋째 장 '그라하가니타(Grahagaṇita)'에서 행성의 운동을 다루면서, 행성의 순간 속도를 고려하여 다음과 같은 근사값을 얻었다.

:\sin y' - \sin y \approx (y' - y) \cos y (단, y'는 y에 가깝다)

현대적 표기법으로는 다음과 같다.

: \frac{d}{dy} \sin y = \cos y .

이 결과는 사인표(sine table)의 맥락에서 문잘라차리아(Muñjalācārya 또는 Mañjulācārya) 마나삼(mānasam)에 의해서도 이전에 관찰된 바 있다.

바스카라는 또한 행성의 순간 속도가 최고점에서 0이라고 명시했다.

4. 1. 대수학

바스카라 2세의 저서 ''비자가니타''(''Bījagaṇita,'' 대수학)는 12장으로 구성되어 있으며, 0과 무한대, 양수와 음수, 펠 방정식을 포함한 불확정 방정식을 ''꾸따꺼'' 방법을 사용하여 푸는 것에 대해 설명한다.[37] 특히, 61x² + 1 = y² 문제는 수세기 뒤에 페르마를 비롯한 유럽인들이 피한 문제였다.

바스카라 2세는 대수학에서 다음과 같은 중요한 업적을 남겼다.

  • 2차, 3차 및 4차 불확정 방정식의 해를 설명하였다.[38]
  • ''ax'' 2 + ''b'' = ''y'' 2 유형의 부정 이차 방정식의 해를 제시하였다.
  • 선형 및 이차 불확정 방정식의 정수 풀이법(''꾸따꺼'')을 제시하였는데, 이는 17세기 르네상스 유럽 수학자들의 풀이법과 동일하다.
  • ''ax'' 2 + ''bx'' + ''c'' = ''y'' 형식의 불확정 방정식을 푸는 순환 차크라발라 방법을 제시하였다.
  • Pell의 방정식 ''x'' 2 − ''ny'' 2 = 1의 해를 구하는 첫번째 일반적 방법을 제시하였다.
  • 61''x'' 2 + 1 = ''y'' 2과 같은 2차 디오판틴 방정식의 풀이법을 제시하였다. 이 풀이법은 18세기 오일러 시대까지 유럽에서 알려지지 않았다.[38]
  • 둘 이상의 미지수가 있는 이차 방정식을 풀고 음수와 무리수 해를 찾았다.

4. 2. 미적분학

바스카라 2세는 미분 계수의 근사치를 발견하고, 롤의 정리의 초기 형태를 제시하는 등 미적분학의 초기 개념을 발전시켰다. 그는 셋째 장 그라하가니타에서 행성의 순간 속도를 고찰하면서, x \approx y이면 \sin(y) - \sin(x) \approx (y - x)\cos(y)라는 결과를 제시하여 사인의 도함수를 찾았다. 이는 미분 및 미분 계수의 근사치를 발견한 것이었지만, 도함수의 개념을 개발하지는 않았다.[31]

바스카라는 이 결과를 사용하여 황도의 위치 각도를 계산하여 일식 시간을 정확하게 예측하는 데 필요한 양을 계산했다.[31] 행성의 순간 운동을 계산할 때, 행성의 연속적인 위치 사이의 시간 간격은 1트루티 또는 초보다 크지 않았고, 바스카라의 속도 측정은 이 무한한 시간 단위로 표현되었다.

바스카라는 변수가 최대값에 도달하면 그 미분이 사라진다는 것을 알고 있었다. 또한 행성이 지구에서 가장 멀거나 가장 가까이 있을 때 중심 방정식(행성이 움직일 것이라고 가정함으로써 예측되는 위치에서 행성이 얼마나 멀리 떨어져 있는지 측정)이 0이 됨을 보였다. 따라서 그는 어떤 중간 위치에 대해 중심 방정식의 미분이 0과 같다고 결론지었다. 이 결과에는 오늘날 일반적으로 롤의 정리에서 파생되는 분석에서 가장 중요한 정리 중 하나인 일반 평균값 정리의 자취가 있다.

그의 저서에는 초기 형태의 롤의 정리가 나타나 있는데, 롤의 정리의 현대 공식은 다음과 같다. f\left(a\right) = f\left(b\right) = 0 이면, a < x < b 인 어떤 x에 대해 f'\left(x\right) = 0 이다.

4. 3. 삼각법

바스카라 2세는 삼각법 분야에서 중요한 업적을 남겼다. 특히 사인 함수의 미분 공식을 유도하고, 구면 삼각법을 발전시켰다.[39]

:\sin y' - \sin y \approx (y' - y) \cos y (y'가 y에 가까울 때)

또는 현대 표기법으로 나타내면 다음과 같다.

: \frac{d}{dy} \sin y = \cos y .

이 결과는 먼절라카리아 머나삼(Muñjalācārya mānasam)이 ''사인 표의 맥락''에서 더 일찍 관찰하였다.

1150년에 쓰여진 『싯단타시로마니』는 바스카라의 삼각법 지식을 보여주는 저서로, 삼각함수표와 여러 삼각함수들 간의 관계를 포함하고 있다. 그는 18도와 36도의 사인 값을 계산하고, 다음과 같은 공식을 제시했다.[39]

: \sin\left(a + b\right) 및 \sin\left(a - b\right)

4. 4. 기타 업적


  • 넓이를 두 가지 다른 방법으로 계산한 다음 항을 소거하여 ''a'' 2 + ''b'' 2 = ''c'' 2를 얻는 피타고라스 정리 증명.[37]
  • 0의 성질(나누기 및 0이 있는 연산 규칙 포함).
  • π의 근사값 제시.
  • 이자 및 이자 계산과 관련된 문제 해결.

5. 천문학적 업적

브라마굽타가 7세기에 개발한 천문학적 모델을 사용하여, 바스카라 2세는 항성년의 길이를 365.2588일로 정확하게 정의했다. 이는 수랴싯단타와 동일한 값이다.[40] 현대 측정값은 365.25636일로, 3.5분밖에 차이가 나지 않는다.[19]

그의 수학 천문학 저서인 싯단타 시로마니는 수학 천문학에 관한 첫 번째 부분과 천구에 관한 두 번째 부분으로 구성되어 있다.

첫 번째 부분의 12장은 다음과 같은 주제를 다룬다.



두 번째 부분은 다음과 같은 13개의 장으로 구성되어 있다.

6. 공학적 업적

바스카라 2세는 1150년에 영원히 작동한다고 주장한 바퀴를 기술했는데, 이는 영구 기관의 초기 모델 중 하나이다.[32]

바스카라 2세는 '야슈티-얀트라(Yaṣṭi-yantra)'라고 불리는 측정 기구를 사용했다. 이 장치는 간단한 막대기부터 눈금이 매겨진 눈금자를 사용하여 각도를 결정하도록 특별히 설계된 V자형 지팡이까지 다양할 수 있다.[33]

7. 유산

바스카라 2세의 이름을 딴 인도의 여러 연구소와 대학이 있다. 푸네의 바스카라차르야 프라티슈타나(Bhaskaracharya Pratishthana), 델리의 바스카라차르야 응용과학대학(Bhaskaracharya College of Applied Sciences), 간디나가르의 바스카라차르야 우주응용 및 지리정보 연구소(Bhaskaracharya Institute For Space Applications and Geo-Informatics) 등이 있다.

1981년 11월 20일, 인도우주연구기구(ISRO)는 바스카라 2세를 기리기 위해 바스카라 II 위성을 발사했다.[41]

2015년, 인비스 멀티미디어(Invis Multimedia)는 바스카라차르야에 관한 인도 단편 다큐멘터리 영화 ''바스카라차르야(Bhaskaracharya)''를 공개했다.[25][26]

참조

[1] 서적 The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook https://books.google[...] Princeton University press 2021-08-10
[2] 간행물 Indian Journal of History of Science, Volume 35 National Institute of Sciences of India 2000
[3] 서적 Studies in Indology and Medieval History: Prof. G. H. Khare Felicitation Volume https://books.google[...] Joshi & Lokhande Prakashan
[4] 서적 Dr. G. S. Gai Felicitation Volume https://books.google[...] Agam Kala Prakashan
[5] 간행물 Proceedings, Indian History Congress, Volume 40 Indian History Congress 1979
[6] 서적 Cultural Leaders of India - Scientists Publications Division Ministry of Information & Broadcasting
[7] 서적 गणिती (Marathi term meaning Mathematicians) Manovikas 2013-12-23
[8] 서적 Mathematics in India Princeton University Press 2009
[9] 서적 Algebra with Arithmetic and Mensuration from the Sanscrit of Brahmegupta and Bhascara
[10] 서적 The Illustrated Weekly of India, Volume 95 https://books.google[...] Bennett, Coleman & Company, Limited, at the Times of India Press
[11] 간행물 Journal of the Royal Asiatic Society of Great Britain and Ireland https://books.google[...] 1865
[12] 기타
[13] 간행물 B.I.S.M. quarterly, Vol. 63, No. 1 Poona 1984
[14] 서적 Bijaganita
[15] 서적 Mathematical Achievements of Pre-modern Indian Mathematicians
[16] 서적 Students& Britannica India. 1. A to C
[17] 서적 50 Timeless Scientists
[18] 뉴스 The Great Bharatiya Mathematician Bhaskaracharya ll https://timesofindia[...] 2023-05-24
[19] 웹사이트 IERS EOP PC Useful constants http://hpiers.obspm.[...]
[20] 서적
[21] 서적
[22] 서적
[23] 서적
[24] 웹사이트 Bhaskara https://nssdc.gsfc.n[...] 2017-09-16
[25] 웹사이트 Anand Narayanan https://events.iist.[...] 2021-02-21
[26] 웹사이트 Great Indian Mathematician - Bhaskaracharya https://www.youtube.[...] indiavideodotorg 2015-09-22
[27] 서적 Mathematics in India
[28] 서적 数学の魔法の宝箱 ソフトバンク クリエイティブ
[29] 서적 Arithmetic and mensuration of Brahmegupta and Bhaskara 1817
[30] 학술지 Use of Calculus in Hindu Mathematics 1984
[31] 서적 The History of Mathematics: A Brief Course Wiley-Interscience
[32] 학술지 Tibet, India, and Malaya as Sources of Western Medieval Technology 1960-04
[33] 서적 Astronomical Instruments in India Springer
[34] 웹인용 [아빠와 함께 떠나는 스토리텔링 수학여행] 바스카라 2세의 독특한 뺄셈 http://www.daejonilb[...] 2022-08-21
[35] 서적 गणिती (Marathi term meaning Mathematicians) Manovikas 2013-12-23
[36] 서적 Mathematics in India Princeton University Press
[37] 서적 Bijaganita
[38] 서적 Mathematical Achievements of Pre-modern Indian Mathematicians
[39] 간행물 Students& Britannica India
[40] 웹사이트 IERS EOP PC Useful constants http://hpiers.obspm.[...]
[41] 웹사이트 Bhaskara https://nssdc.gsfc.n[...] 2017-09-16


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com