삼방사면체
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
삼방사면체는 데카르트 좌표로 표현되는 8개의 꼭짓점을 가진 다면체이다. 이 도형은 테타르토이드의 변형을 통해 얻을 수 있으며, 직교 투영 시 다양한 형태를 보인다. 삼각 뿔꼴 정사면체는 5-세포체의 전개도를 나타내며, 직각 이등변삼각형으로 구성될 경우 정육면체를 형성한다. 삼방사면체는 밀러의 규칙에 의해 허용되는 13개의 별붙이 중 하나이며, 관련 다면체 및 타일링과의 연관성을 갖는다. 또한, 삼각사면체를 구성하는 이등변삼각형의 각도와 변의 비율에 대한 정보를 제공한다.
더 읽어볼만한 페이지
- 카탈란의 다면체 - 마름모십이면체
마름모십이면체는 12개의 마름모로 이루어진 면추이 다면체이자 카탈란 다면체로서, 특정 비율의 대각선과 변을 가진 마름모로 구성되며, 공간을 채우는 평행다면체로서 벌집 구조, 광물 결정 구조, 우주선 반작용 휠 배치 등 다양한 분야에 응용되고, 정육면체, 정팔면체, 정팔포체, 정이십사포체와 관련이 있으며 초입방체의 투영으로 얻을 수 있다. - 카탈란의 다면체 - 마름모삼십면체
마름모삼십면체는 30개의 마름모 면으로 구성된 다면체로, 마름모의 대각선 길이 비율이 황금비를 따르며 정십이면체, 정이십면체와 관련이 있고 3차원 쌍곡 공간을 채울 수 있으며 디자인 등 다양한 분야에 활용된다.
| 삼방사면체 | |
|---|---|
| 개요 | |
 | |
| 종류 | 카탈란 입체, 십이면체 |
| 면의 수 | 12 |
| 면의 종류 | 이등변삼각형의 일종 |
| 면의 이미지 파일 | DU02 facets.png |
| 변의 수 | 18 |
| 꼭짓점의 수 | 8 |
| 대칭군 | Td |
| 쌍대 | 깎은 사면체 |
| 성질 | 볼록 집합 |
| 전개도 이미지 파일 | Triakistetrahedron net.png |
| 영어 명칭 | triakis tetrahedron |
| 치수 | |
| 면의 길이 비율 (짧은 변/긴 변) | sfrac|3|5 |
| 면의 길이 비율 (긴 변/짧은 변) | sfrac|5|3 |
| 관련 링크 | |
| 계산기 | 삼각첨가 사면체 - 기하 계산기 |
2. 데카르트 좌표
원점을 중심으로 하는 삼방사면체의 8개 꼭짓점에 대한 데카르트 좌표는 다음과 같다.
- 마이너스 부호가 짝수인 점 (±5/3, ±5/3, ±5/3)
- 마이너스 부호가 홀수인 점 (±1, ±1, ±1)
더 자세하게 나타내면 다음과 같다.
- (5/3, 5/3, 5/3), (5/3, −5/3, −5/3), (−5/3, 5/3, −5/3), (−5/3, −5/3, 5/3)
- (−1, 1, 1), (1, −1, 1), (1, 1, −1), (−1, −1, −1)
이 삼방사면체의 짧은 모서리의 길이는 2√2이다.
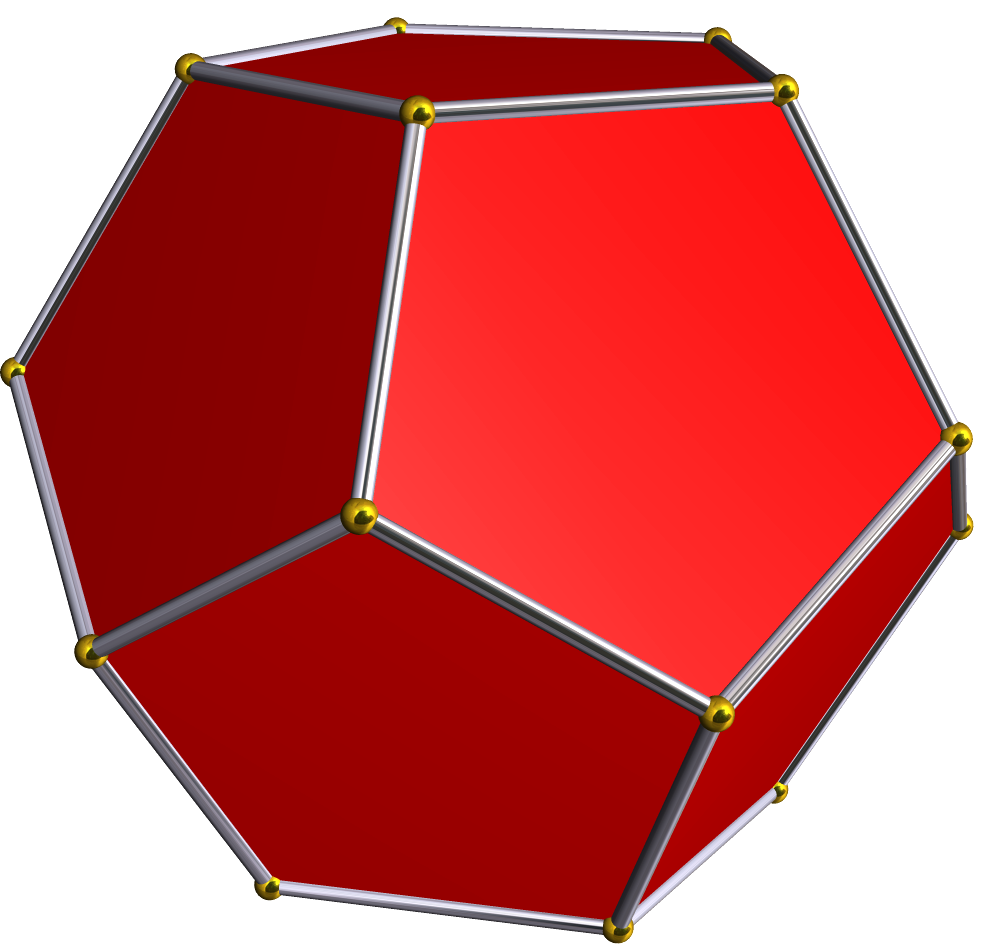
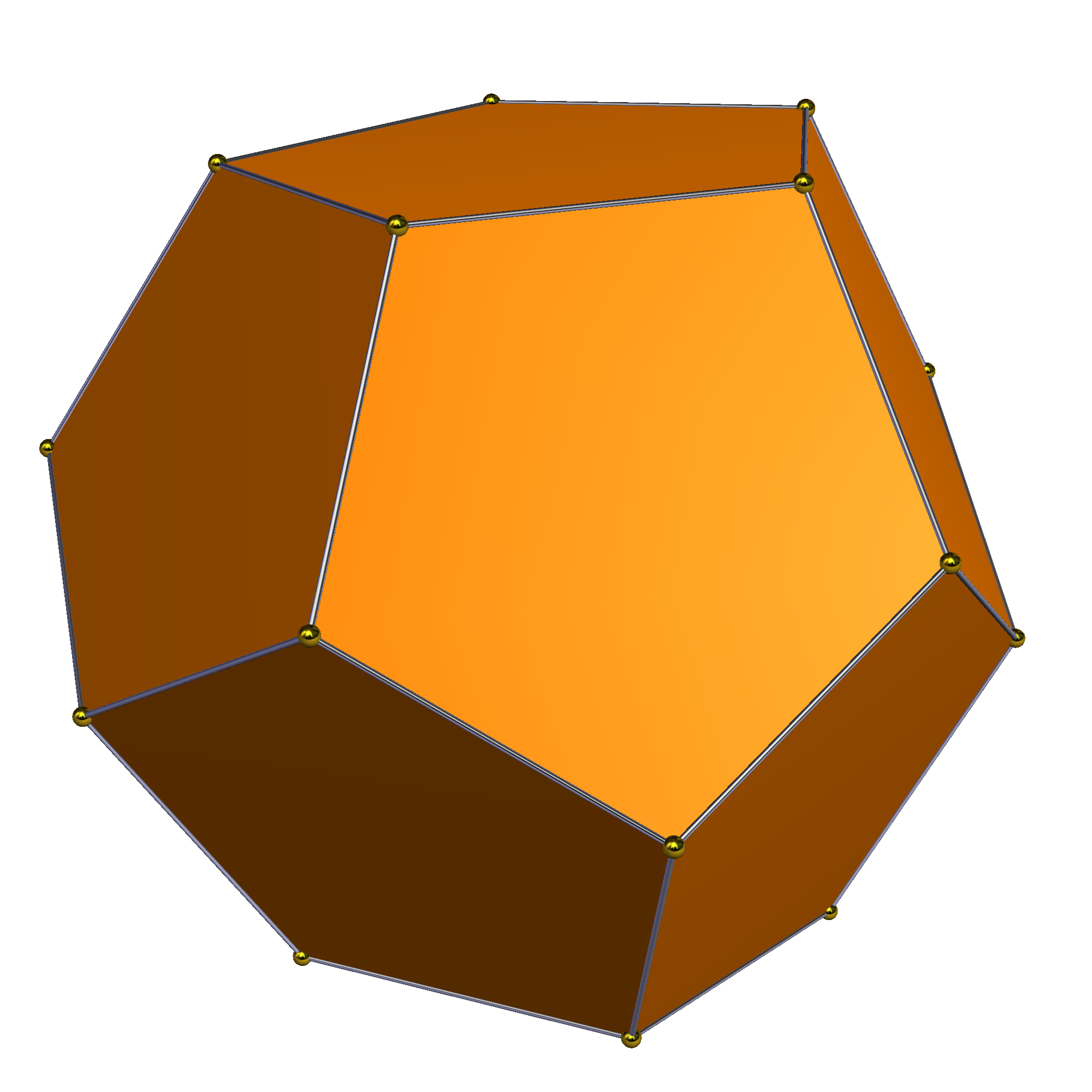
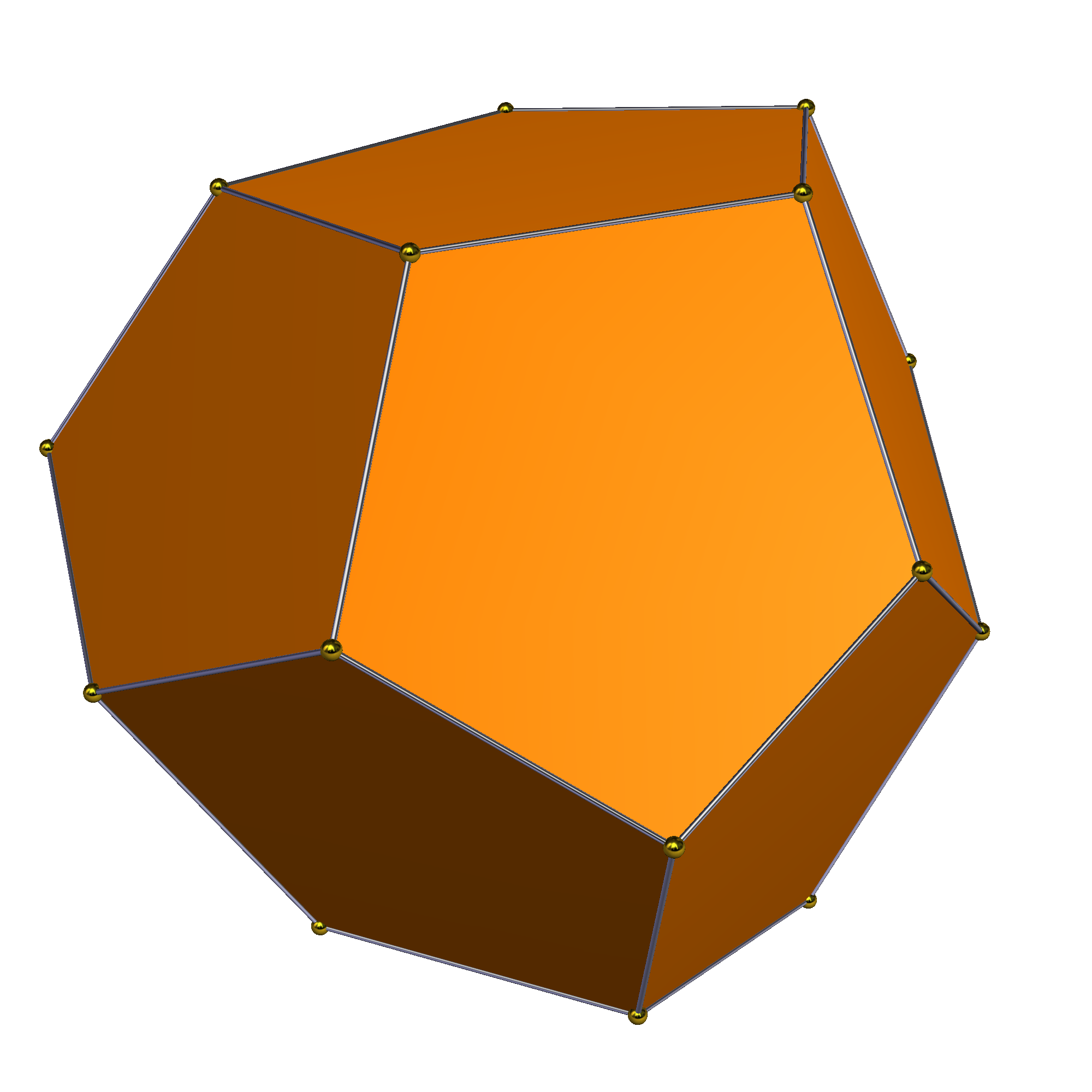
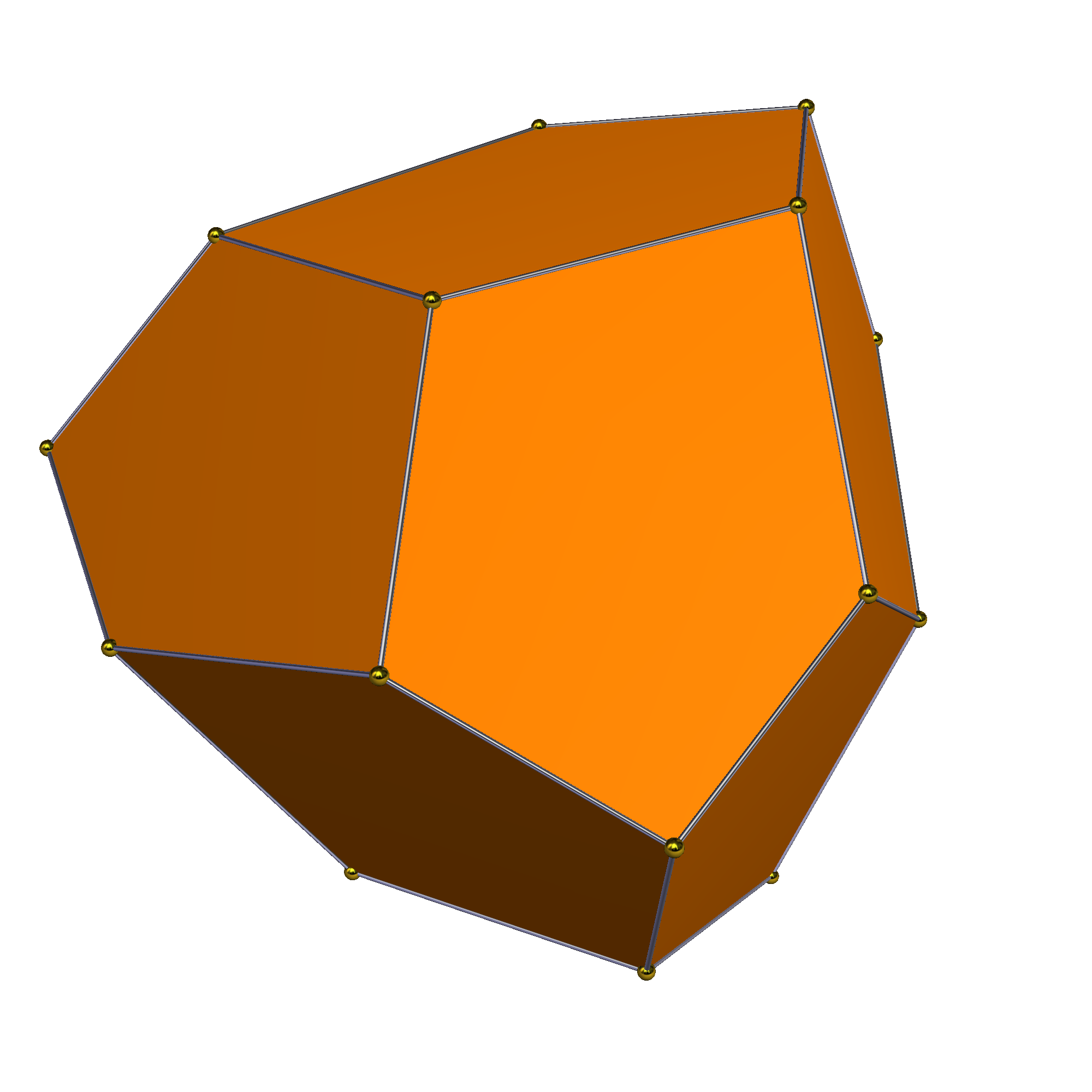
3. 테타르토이드 대칭
삼각사면체는 테타르토이드의 퇴화된 극한으로 만들 수 있다.
 |  |  |  |
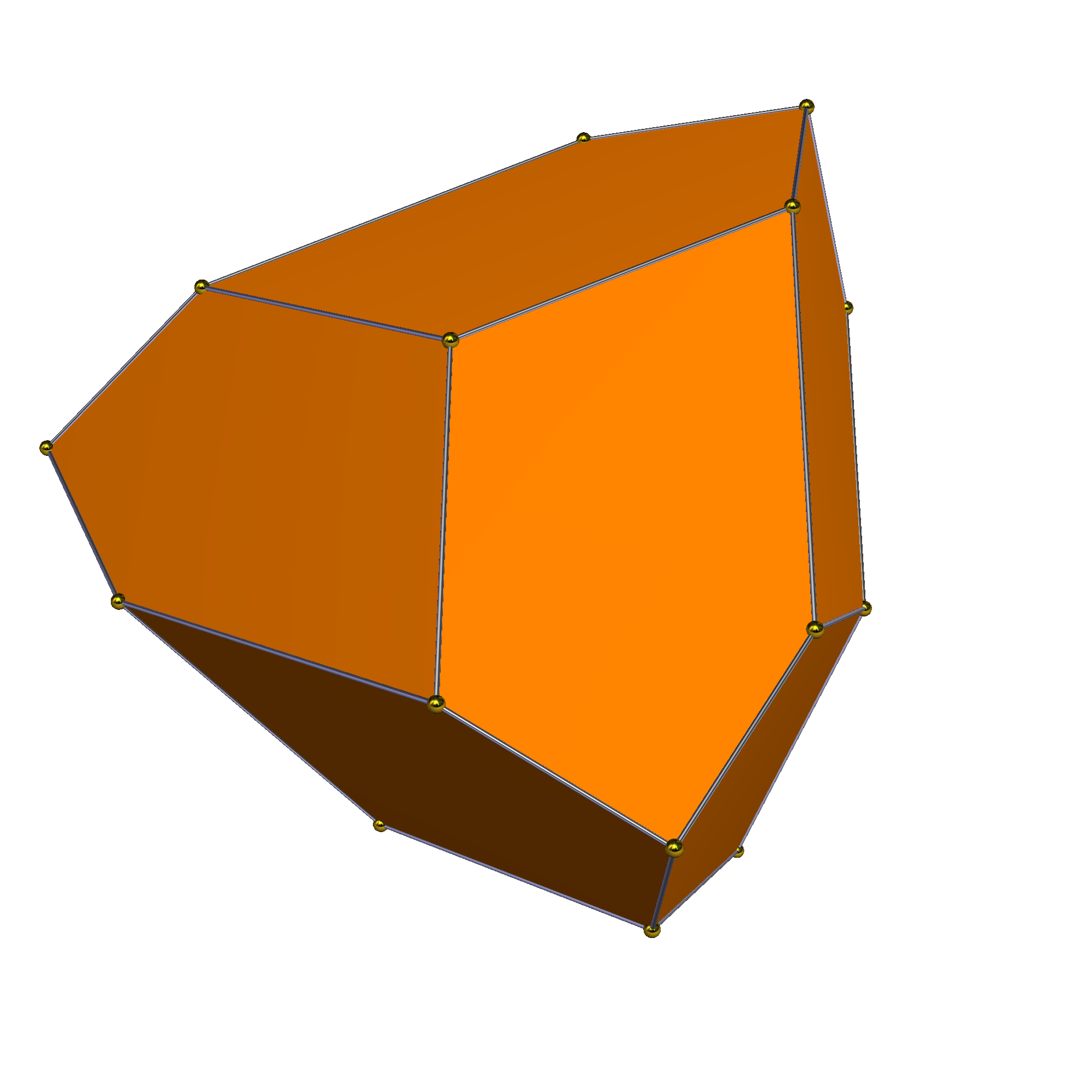 | 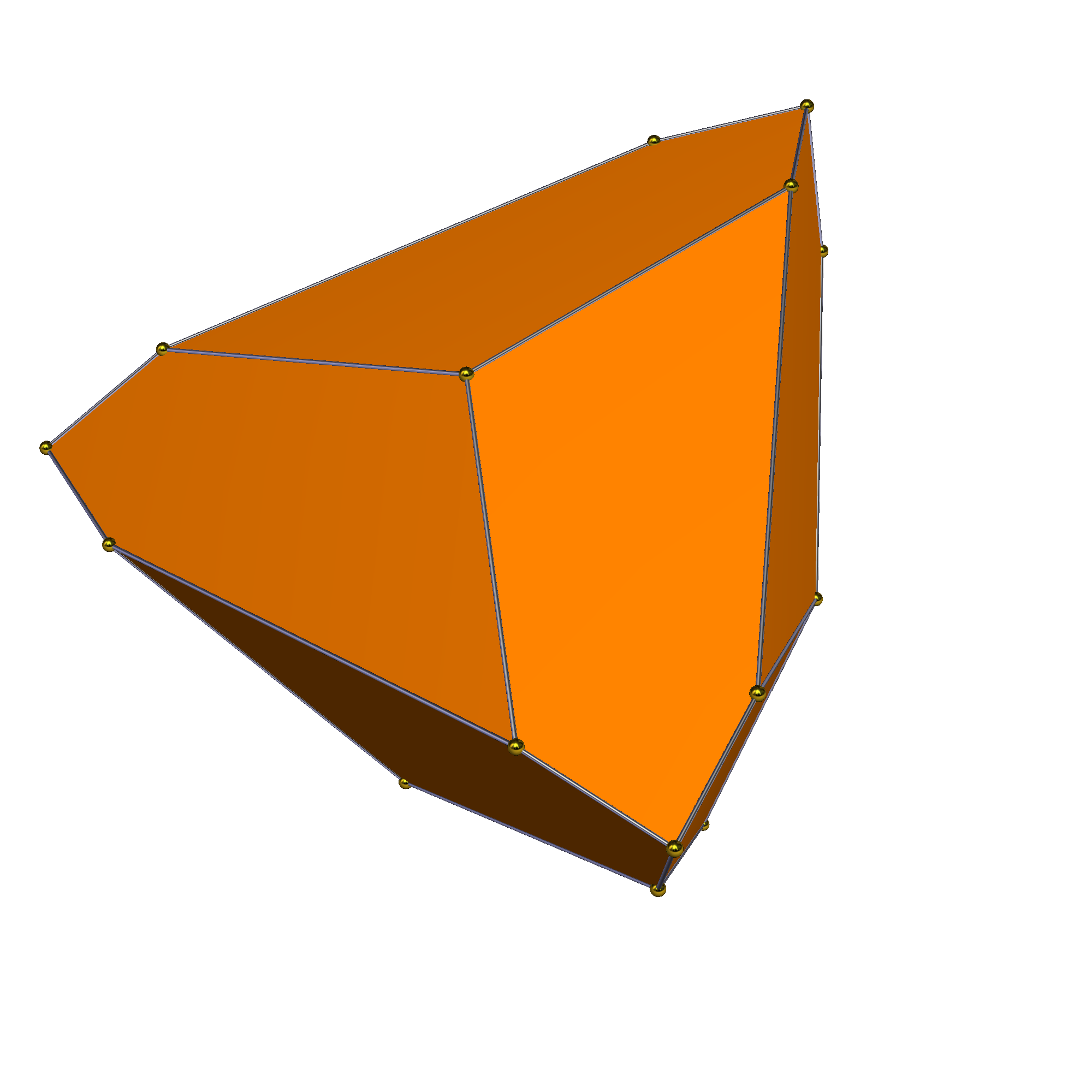 |  | 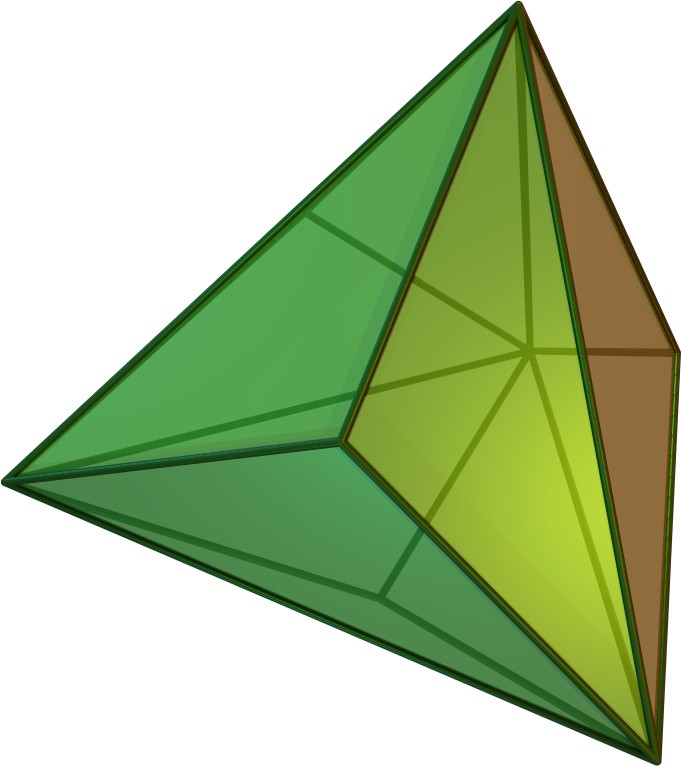 |
4. 직교 투영
삼각사면체를 여러 방향에서 직교 투영하면 다음과 같은 형태를 얻을 수 있다.
| 중심점 | 짧은 모서리 | 면 | 꼭짓점 | 긴 모서리 |
|---|---|---|---|---|
| 삼각 사면체 | 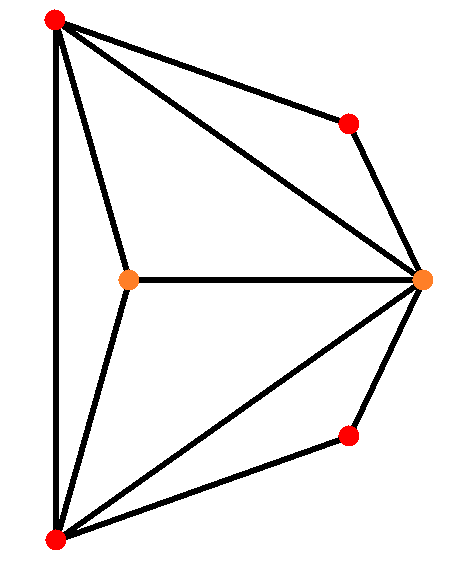 | 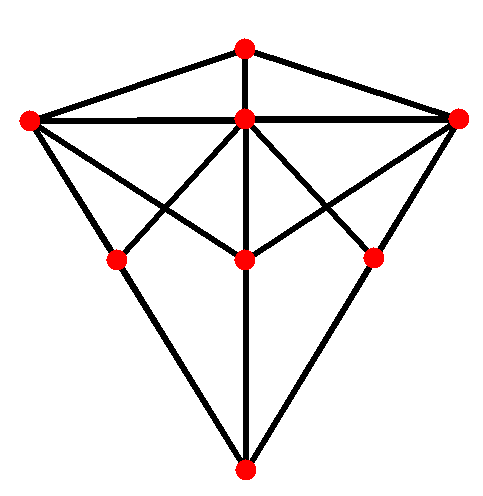 | 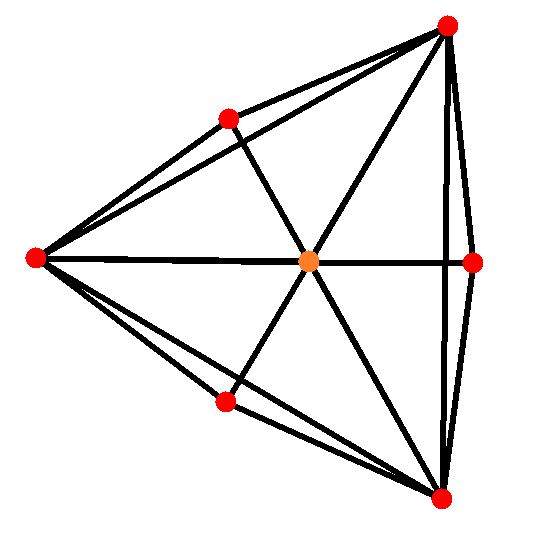 | 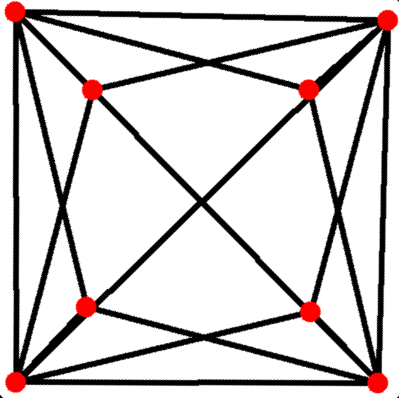 |
| (쌍대) 깎은 사면체 | 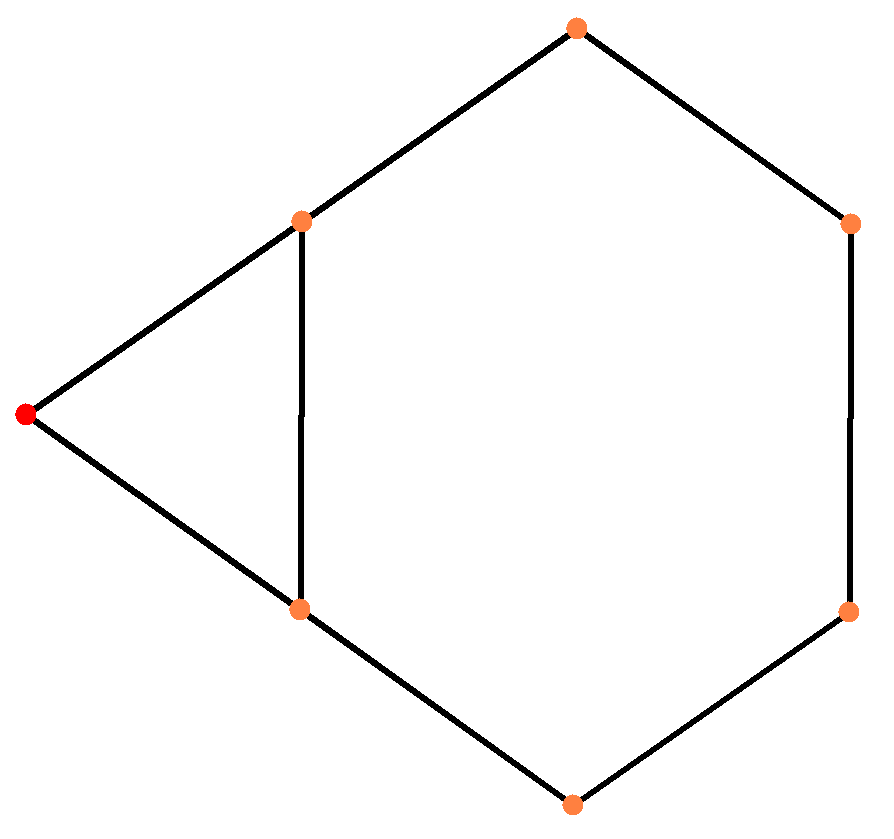 | 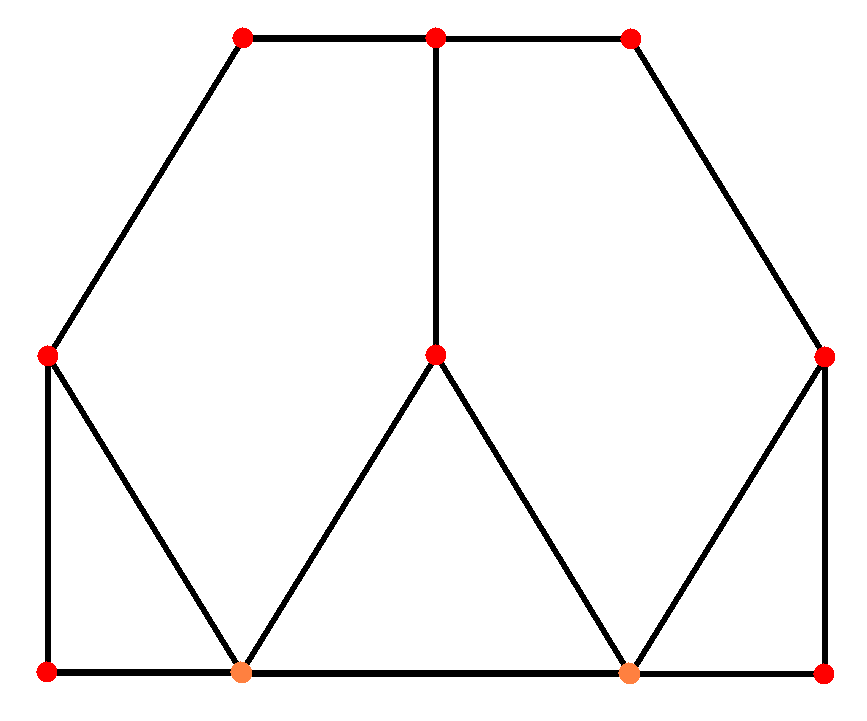 |  |  |
| 투영 대칭 | [1] | [3] | [4] | |
| 삼각 사면체 |  | 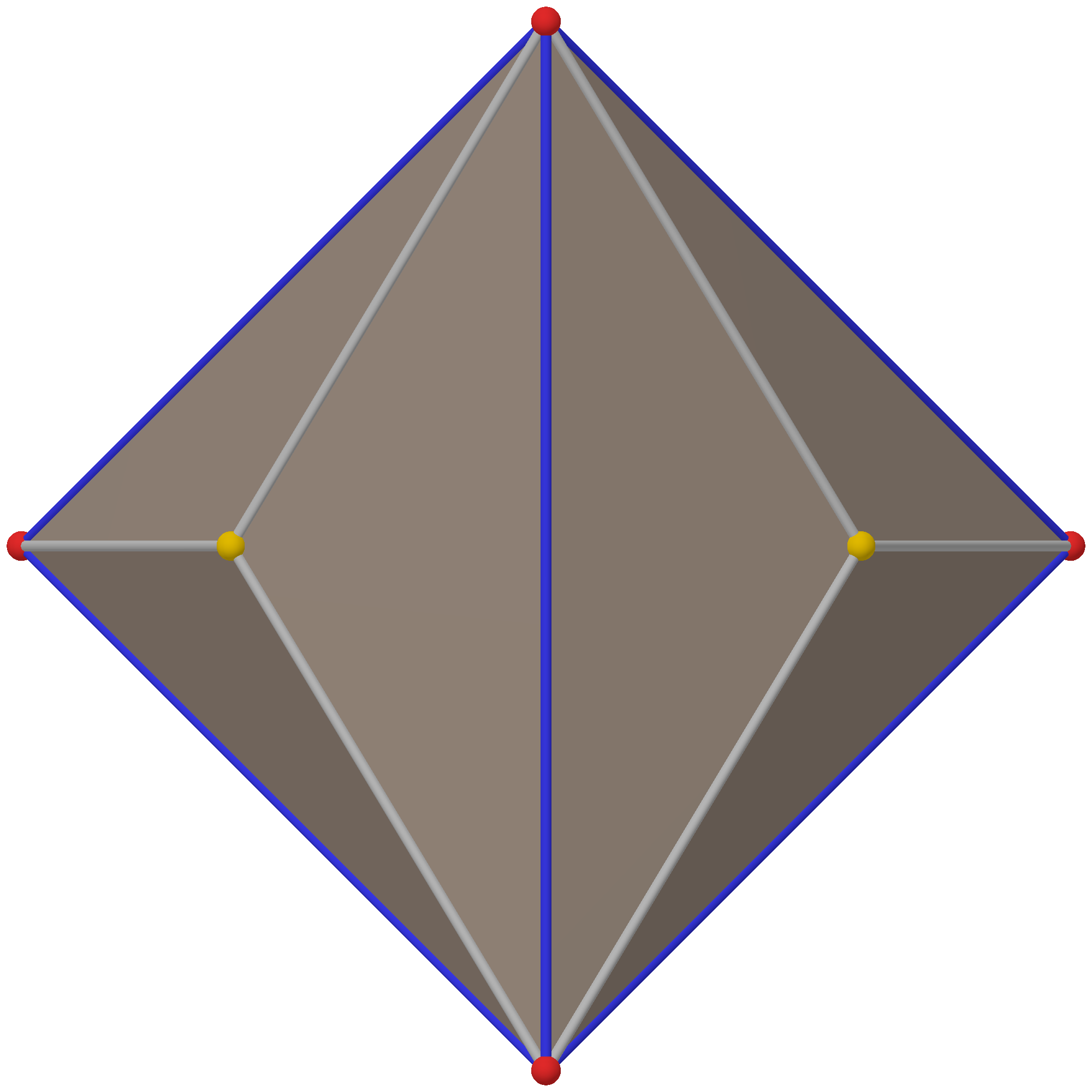 | 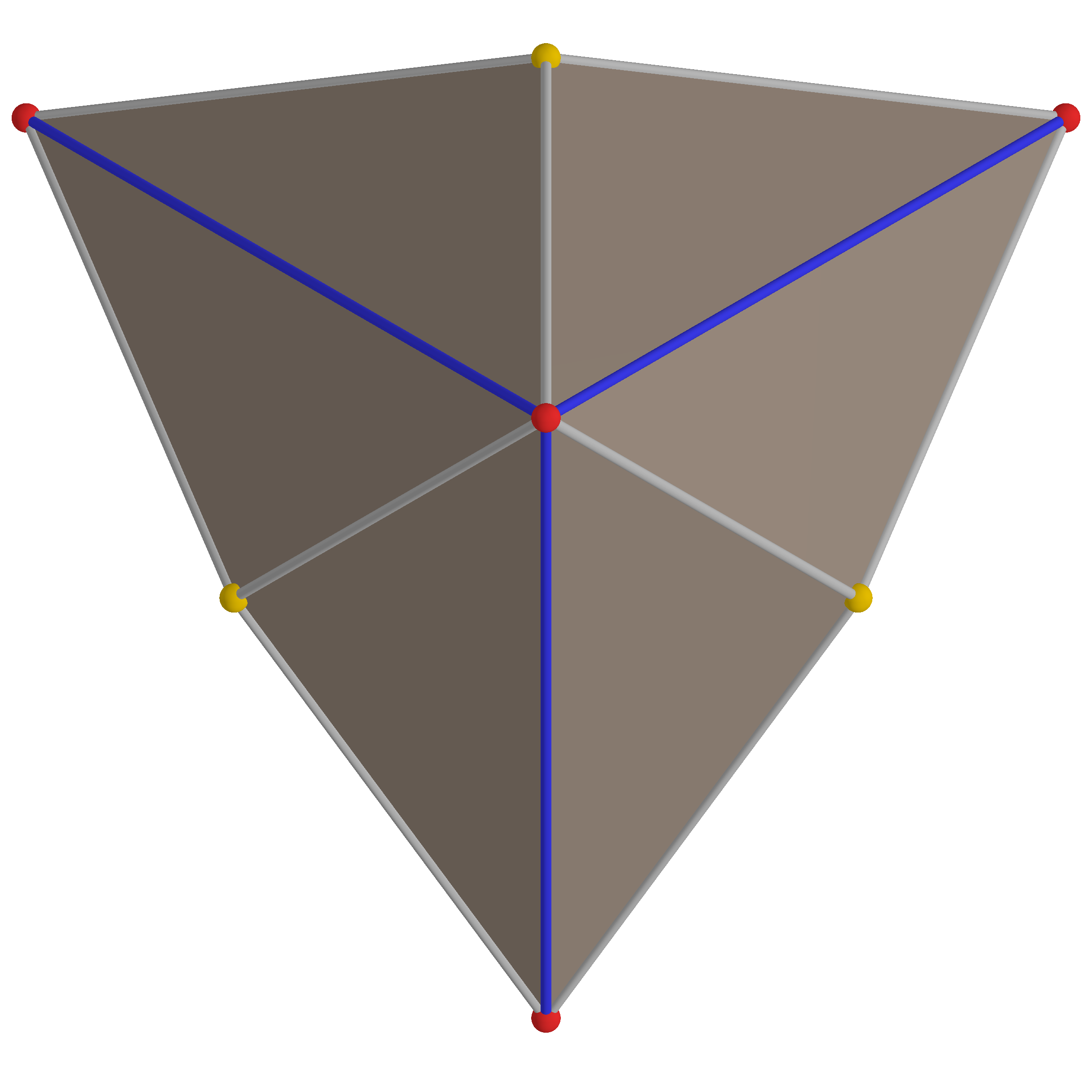 | 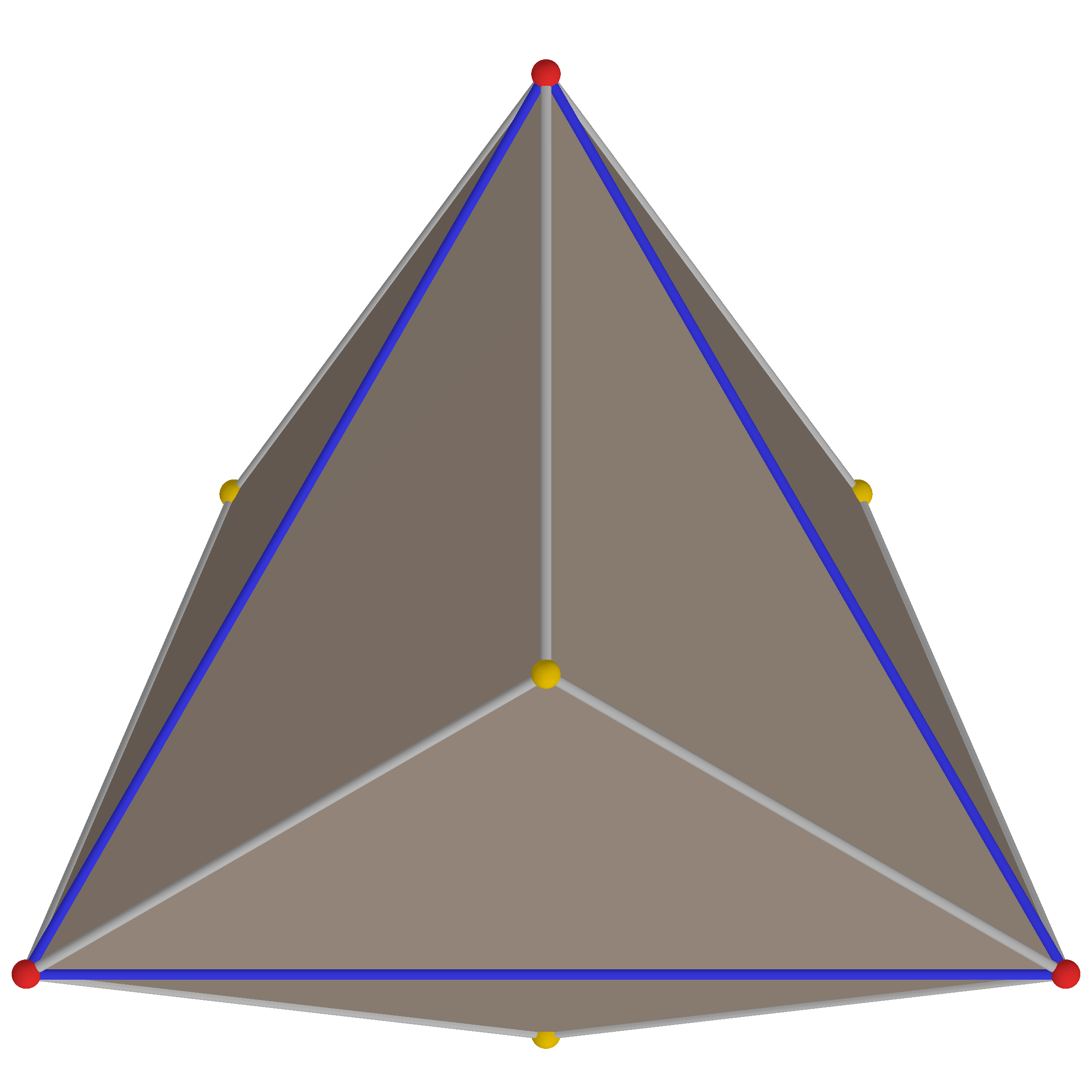 |
|---|---|---|---|---|
| (쌍대 화합물) |  |  |  | 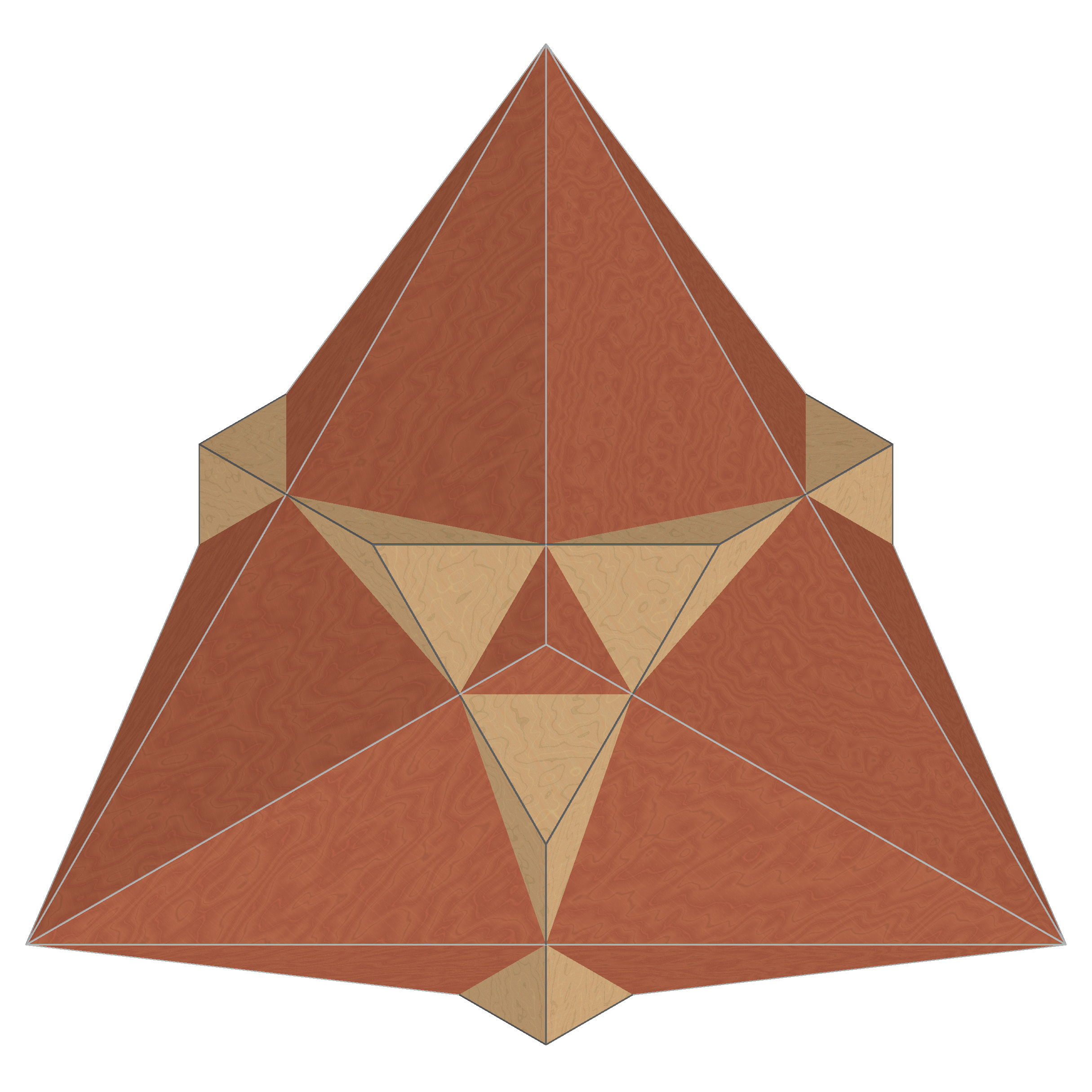 |
| (쌍대) 깎은 사면체 |  | 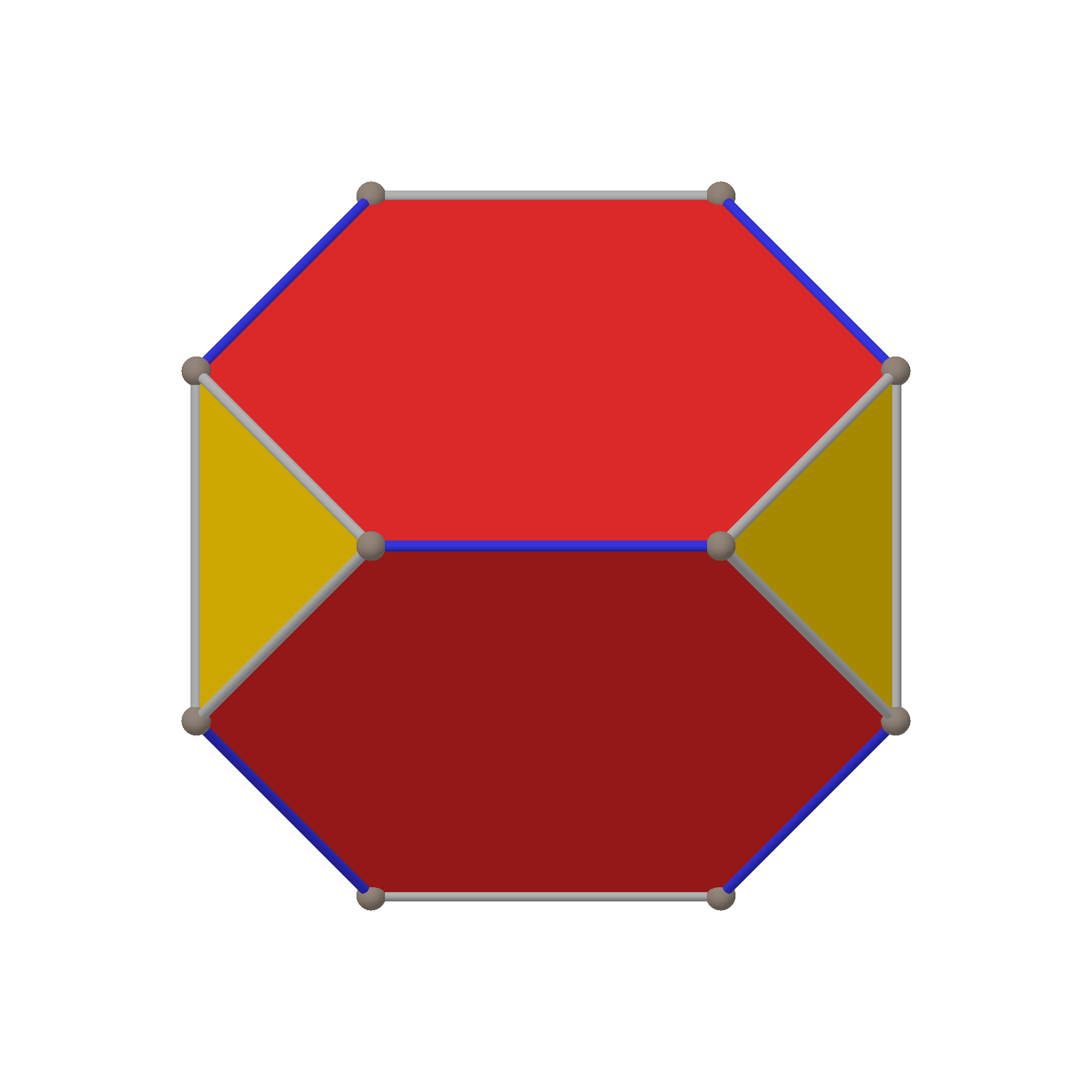 |  |  |
| 투영 대칭 | [1] | [2] | [3] | |
5. 변형
삼각 뿔꼴 정사면체는 정다포체인 5-세포체의 전개도를 나타낸다.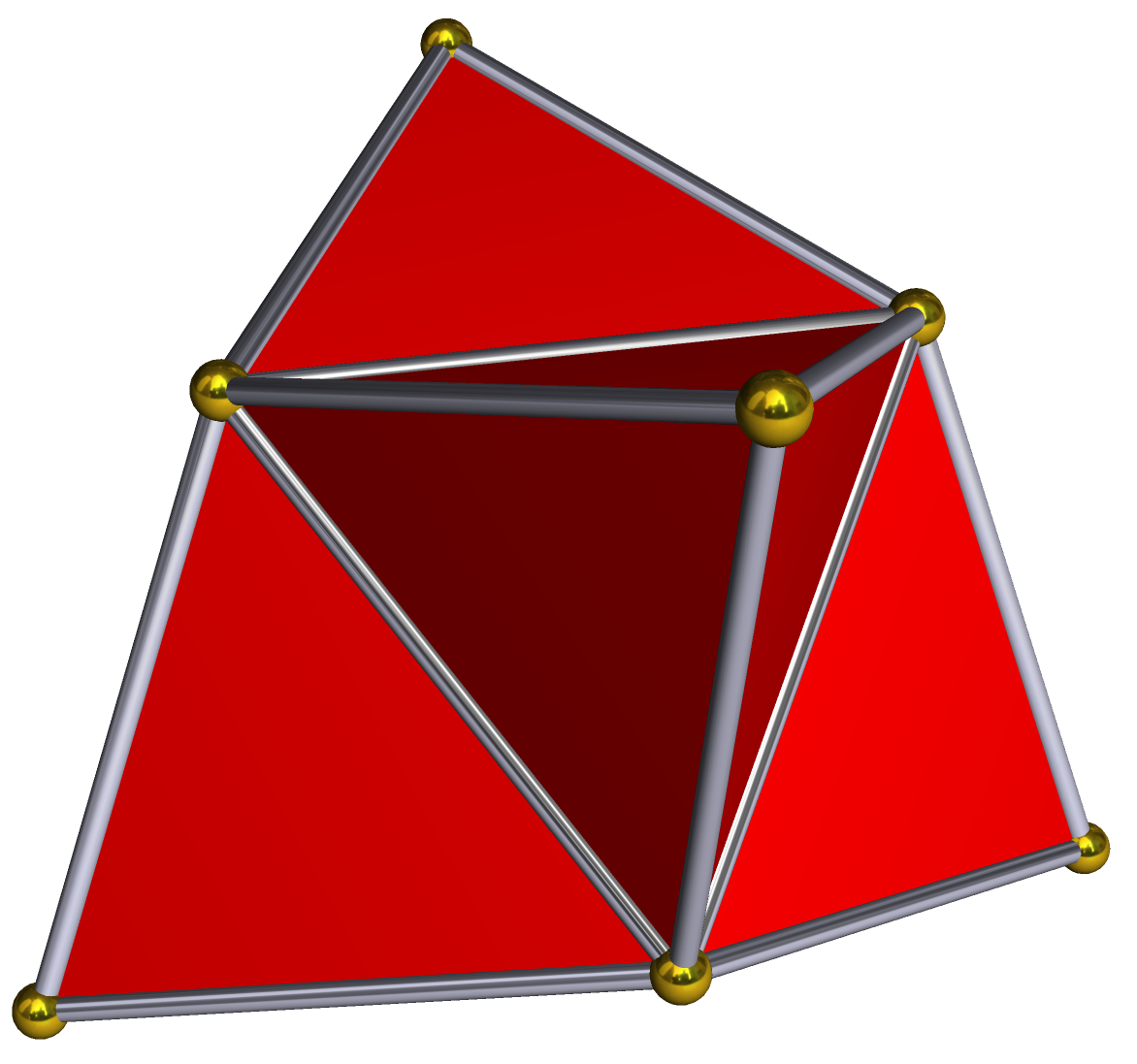
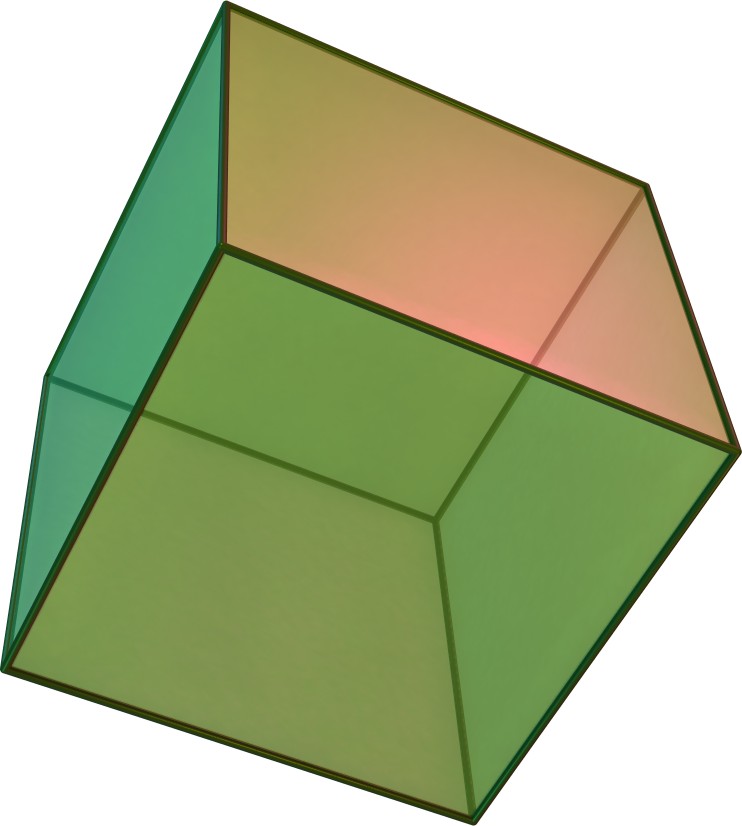
만약 삼각형이 직각 이등변 삼각형이라면, 면은 공면적이 되어 정육면체를 형성한다. 이것은 사면체의 6개 모서리를 정육면체 내부에 추가하여 볼 수 있다.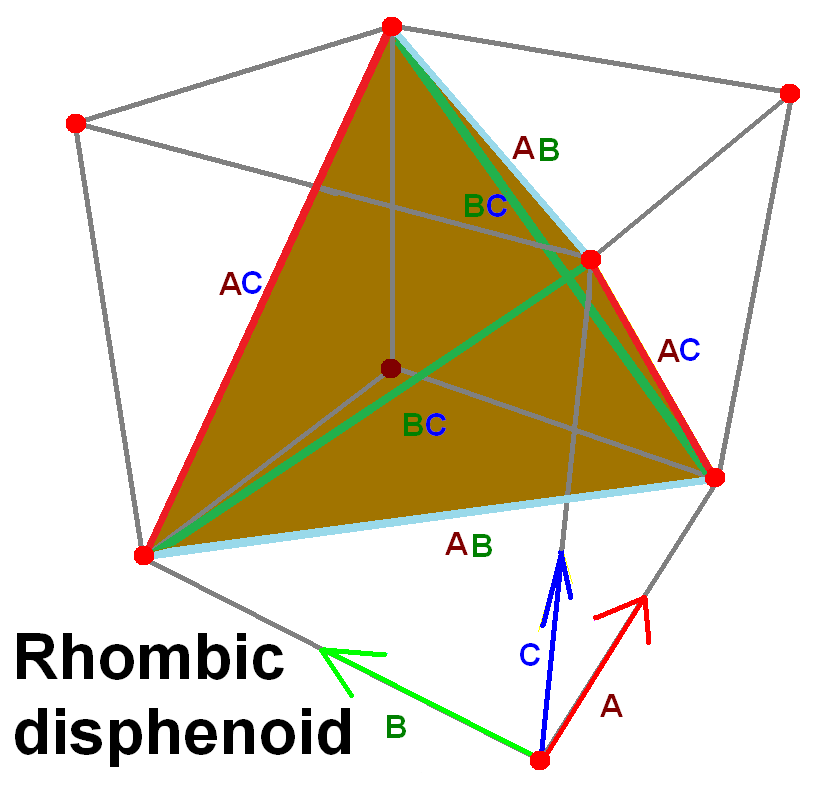
모듈러 종이접기에서 이것은 6개의 소노베 모듈을 연결하여 삼각 뿔꼴 사면체를 만드는 결과이다.
6. 별모양화

이 손대칭 도형은 밀러의 규칙에 의해 허용되는 13개의 별모양화 중 하나이다.
7. 관련 다면체
삼각사면체는 정사면체를 기본 형태로 하여 각 면에 각뿔을 추가하여 만들 수 있다. 정육면체의 각 면에 각뿔을 추가하여 조금 더 높이 들어 올린 형태로도 만들 수 있다. 절단된 사면체와 삼각사면체로 복합 다면체를 만들 수도 있다.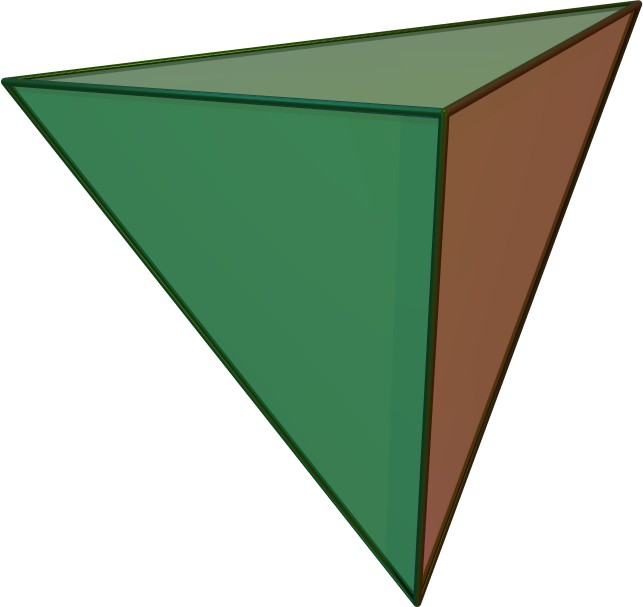
7. 1. 관련 타일링
삼각사면체는 면-추이 도형으로 (*n32) 반사 대칭을 가지며, 쌍곡 평면으로 확장되는 다면체와 타일링 시퀀스의 일부이다.| 잘린 타일링의 *n*32 대칭 변형 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 대칭 *n32 [n,3] | 구면 | 유클리드 | 조밀한 쌍곡선 | 파라코. | 비조밀 쌍곡선 | |||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | [12i,3] | [9i,3] | |
| 삼각육면체 도형 |  |  |  |  |  |  |  |  | ||
| 구성 | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | ||
8. 성질
삼각사면체를 구성하는 이등변삼각형의 꼭지각은 약 112.89°, 밑각은 약 33.56°이다. 짧은 변과 긴 변의 비율은 3:5이다.
구체적으로, 둔각은 arccos(-7/18) ≈ 112.88538047616°, 예각은 arccos(5/6) ≈ 33.55730976192°이다.
참조
[1]
서적
Symmetries of things
[2]
웹사이트
Triakis Tetrahedron - Geometry Calculator
https://rechneronlin[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com