마름모십이면체
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
마름모십이면체는 12개의 마름모로 이루어진 다면체로, 각 마름모의 긴 대각선은 짧은 대각선의 √2배이며 예각은 약 70.53°이다. 이는 카탈란 다면체이자 입방팔면체의 쌍대 다면체이며, 면 전이적 성질을 갖는다. 모서리 길이 a일 때, 내접구, 중간구, 꼭짓점을 지나는 구의 반지름과 표면적, 부피를 계산할 수 있으며, 정육면체와 정팔면체의 꼭짓점의 합집합의 볼록 껍질로도 볼 수 있다. 마름모십이면체는 공간 채우기 다면체이며, 석류석 결정, 벌집, 다이아몬드 등의 자연 현상과 응용 분야에서 나타난다. 빌린스키 십이면체, 델토이드십이면체와 같은 위상 동등 형태가 존재하며, 별모양화가 가능하다. 또한, 초입방체와 24-포체와 관련이 있다.
마름모십이면체는 12개의 합동인 마름모로 이루어진 다면체이다. 각 마름모의 긴 대각선과 짧은 대각선의 길이 비는 이다. 마름모의 예각은 약 70.53°, 둔각은 약 109.47°이다. 두 면이 이루는 이면각은 120°이다.
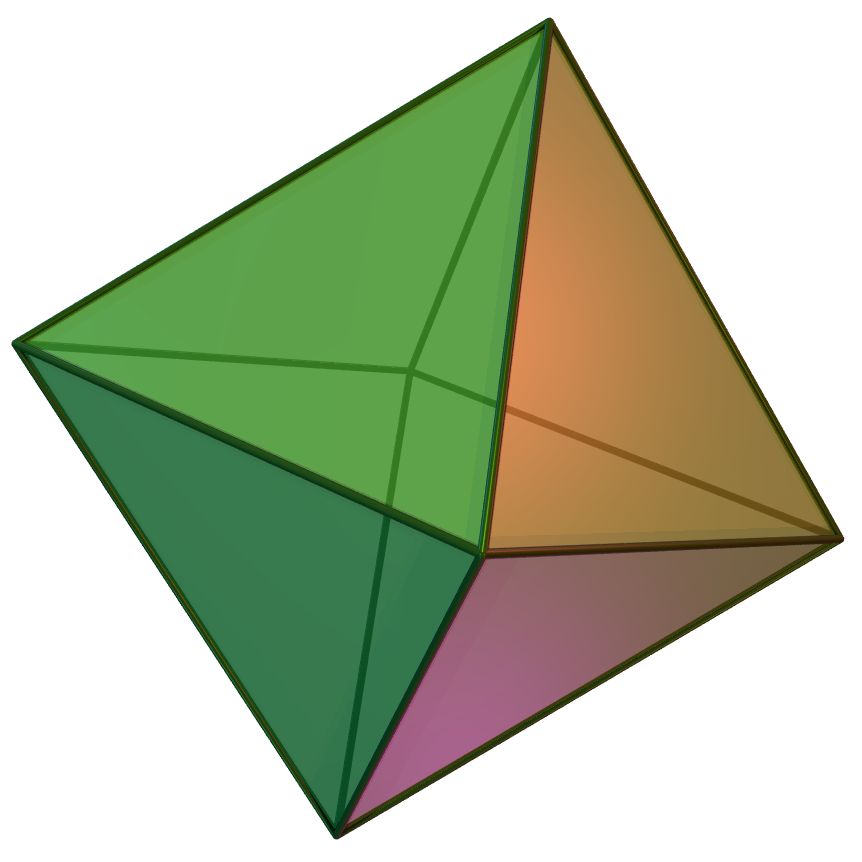
쌍대다면체는 육팔면체이다. 마름모의 둔각 3개가 모인 꼭짓점 8개를 이으면 정육면체가 되고, 예각 4개가 모인 꼭짓점 6개를 이으면 정팔면체가 된다. 이 방법으로 만든 정육면체와 정팔면체를 겹치면 서로의 모서리 중앙 부분이 완전히 겹치는 복합체가 된다.
마름모십이면체는 단독으로 3차원 유클리드 공간을 채울 수 있는 공간채우기 다면체이다. 마치 육각형이 평면을 채우는 것처럼, 마름모십이면체는 공간을 채우도록 쌓을 수 있다. 모든 복사본이 면과 면이 맞닿도록 벌집을 공간 채우기할 수 있기 때문에 평행다면체의 일종이다.[1] 마름모십이면체벌집은 모든 마름모십이면체로 채워진 벌집의 예시이다. 반입방벌집과 쌍대이며, 면심입방격자의 보로노이 테셀레이션으로 볼 수 있다. 석류석과 같은 일부 광물은 마름모십이면체 결정 습성을 형성한다.[1]
석류석 결정은 마름모십이면체 형태를 띤다.[1] 꿀벌은 벌집을 만들 때 마름모십이면체의 기하학을 사용한다.[1] 마름모십이면체는 다이아몬드와 다이아몬도이드의 단위 셀에도 나타난다.[1]
마름모십이면체는 다른 대칭 구조를 가지며, 평행다면체로서 공간 채우기 잘린팔면체의 변형과 유사하다.[3] 예를 들어, 4개의 정사각형 면과 60도 마름모꼴 면을 가지고, D4h 이면체 대칭(16차)을 가지는 경우가 있다. 이는 위아래에 정사각뿔이 붙어있는 입방팔면체로 볼 수 있다.
마름모십이면체는 면이나 모서리를 확장하여 새로운 다면체를 형성할 때까지 이어 붙여 별모양으로 만들 수 있다. 도르먼 루크(Dorman Luke)는 이러한 몇 가지 별모양 마름모십이면체를 설명했다.[1] 첫 번째 별모양 다면체는 종종 별모양 십이면체라고 불리며, 각 면에 마름모꼴 밑면의 피라미드를 붙여 마름모꼴 십이면체로 볼 수 있다. 피라미드의 높이는 인접한 면의 면 평면에 측면이 놓이도록 한다. 루크는 두 번째와 세 번째 별모양 다면체(바깥쪽으로 확장), 두 번째를 세 번째에서 제거하여 형성된 것, 그리고 이전 것에 원래의 마름모꼴 십이면체를 다시 추가하여 형성된 것 등 네 가지 별모양 다면체를 더 설명한다.
마름모십이면체와 관련된 다면체는 다음과 같다.
2. 성질
마름모십이면체는 카탈란 다면체이며, 쌍대다면체는 아르키메데스 다면체인 입방팔면체이다. 이들은 팔면체 대칭을 공유한다. 마름모십이면체는 면 전이적이며, 마름모삼십면체를 제외하고 모서리 전이적인 성질을 갖는 두 개의 카탈란 다면체 중 하나이다(다른 하나는 볼록 다면체가 아니다).
마름모십이면체는 정육면체와 정팔면체의 꼭짓점들의 합집합의 볼록 껍질로 볼 수 있다. 네 개의 마름모가 만나는 여섯 개의 꼭짓점은 정팔면체의 꼭짓점에 해당하고, 세 개의 마름모가 만나는 여덟 개의 꼭짓점은 정육면체의 꼭짓점에 해당한다.
마름모십이면체의 그래프는 해밀턴 경로가 아니다.
2. 1. 공식
한 모서리의 길이가 인 마름모십이면체의 겉넓이 와 부피 는 다음과 같다.
:
:
내접구(마름모십이면체의 각 면에 접하는)의 반지름은 다음과 같다.
:
중간구의 반지름은 다음과 같다.
:
6개의 4차 회전 대칭을 갖는 꼭짓점을 지나는 구(8개의 3차 회전 대칭을 갖는 꼭짓점은 지나지 않음)의 반지름은 다음과 같다.
:
8개의 3차 회전 대칭을 갖는 꼭짓점을 지나는 구의 반지름은 모서리 길이와 정확히 같다.
:
구성면인 마름모의 형태는 다음과 같다.[20]3. 다른 도형과의 관계
정팔포체의 한 꼭짓점을 중심으로 한 3차원 투영 모습의 겉 부분이다.
정이십사포체의 3차원 단면 중 하나이며, 정이십사포체와 가장 가까운 3차원 도형이다.
4. 공간 채우기
5. 자연 및 응용
우주선 반작용 휠 배치에서 4개의 휠을 사면체 형태로 배치할 때, 3차원 공간에 투영하여 얻을 수 있는 3차원 다면체는 마름모십이면체이다.[2] 이 다면체는 HEALPix 그리드의 기반이 되어 우주 마이크로파 배경 지도를 저장하고 조작하는 데 사용된다.
프톨레마이오스 시대 이집트에서 마름모십이면체 모양의 주사위가 발견되었다. 면에는 1부터 12까지의 숫자를 나타내는 그리스 문자가 새겨져 있다.
6. 위상 동등 형태
1960년, 스탄코 빌린스키는 12개의 합동인 마름모꼴 면을 가진 두 번째 마름모십이면체인 빌린스키 십이면체를 발견했다. 이는 위상적으로는 동일하지만 기하학적으로는 다르다. 이 형태의 마름모꼴 면은 황금비를 갖는다.
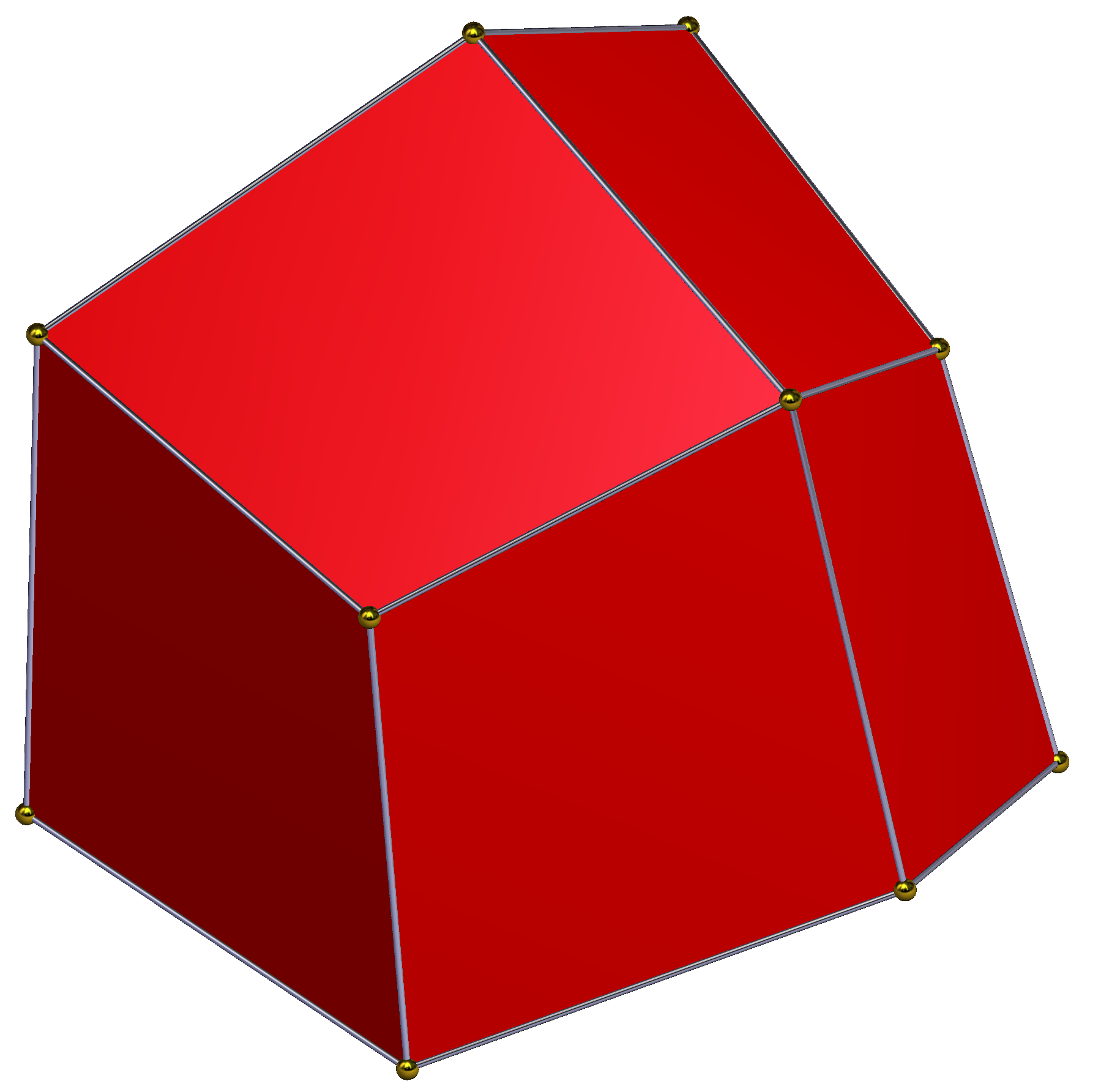
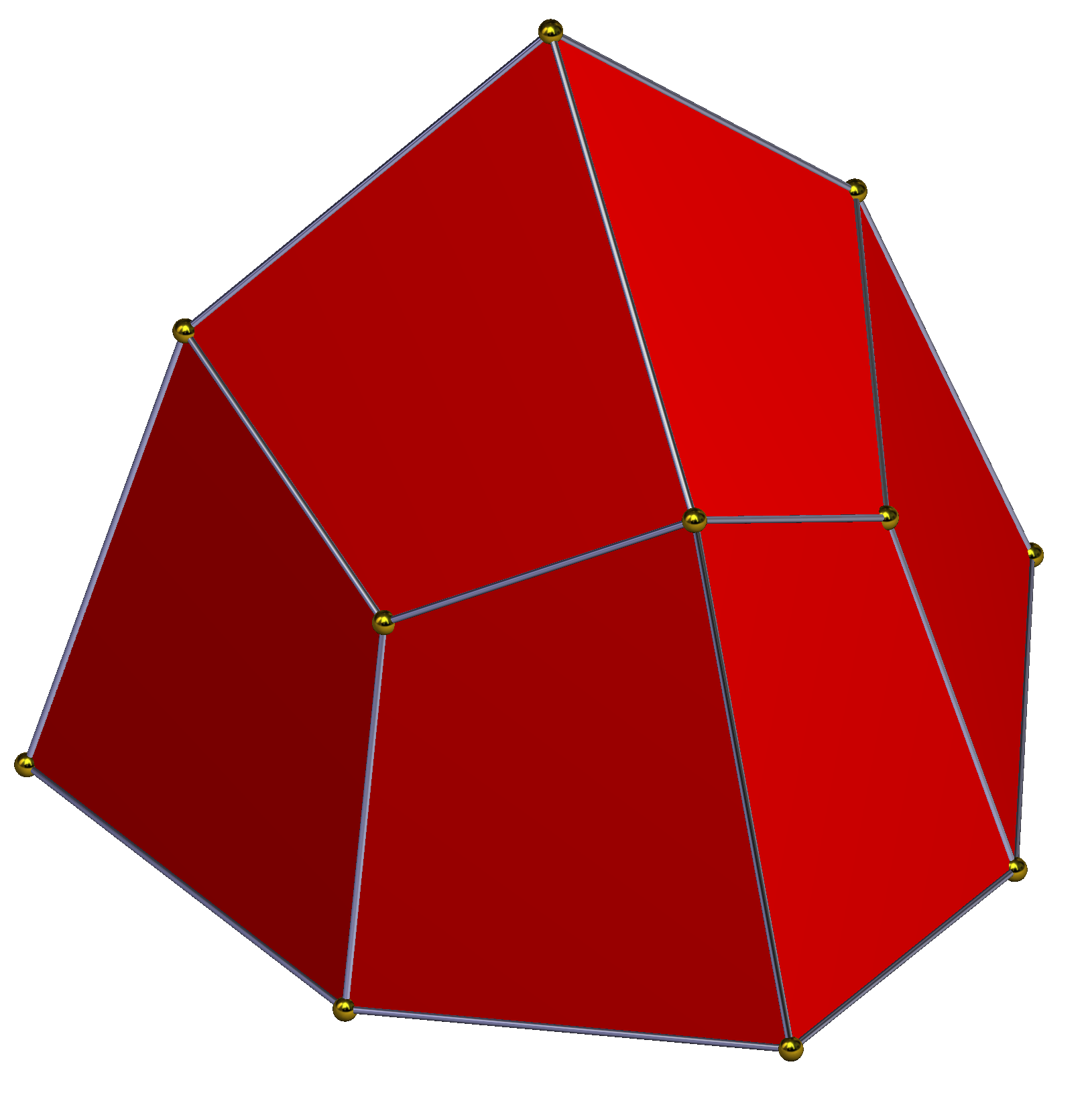
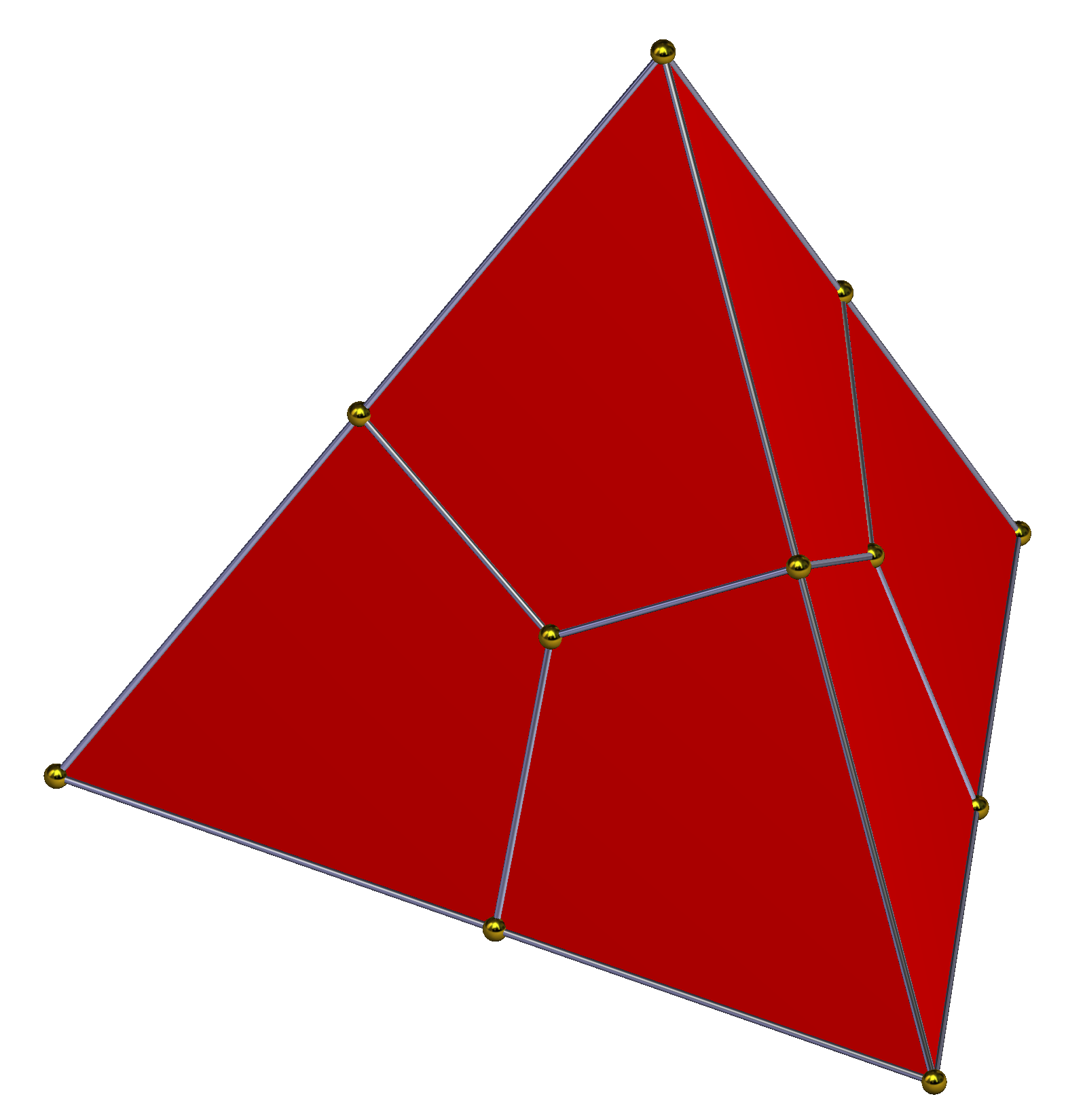
''델토이드십이면체''는 마름모십이면체의 또 다른 위상 동등 형태이다.[4] 이것은 등면체이며 사면체 대칭(24차)을 가지고, 마름모꼴 면을 연(델토이드)으로 왜곡한다. 이것은 4개씩 번갈아가며 안쪽 또는 바깥쪽으로 조정된 8개의 꼭짓점을 가지며, 극한의 경우 사면체 외곽선이 된다. 변형은 (''a'',''b'')로 매개변수화할 수 있으며, 여기서 ''b''와 ''a''는 면의 네 꼭짓점으로 정의된 사면체의 부피가 0, 즉 평면 면이 되도록 서로 의존한다. (1,1)은 마름모꼴 해이다. ''a''가 1/2에 접근함에 따라 ''b''는 무한대로 접근한다. 항상 1/''a'' + 1/''b'' = 2가 성립하며, ''a'', ''b'' > 1/2이다.
:(±2, 0, 0), (0, ±2, 0), (0, 0, ±2)
:(''a'', ''a'', ''a''), (−''a'', −''a'', ''a''), (−''a'', ''a'', −''a''), (''a'', −''a'', −''a'')
:(−''b'', −''b'', −''b''), (−''b'', ''b'', ''b''), (''b'', −''b'', ''b''), (''b'', ''b'', −''b'')(1,1) (7/8, 7/6) (3/4, 3/2) (2/3, 2) (5/8, 5/2) (9/16, 9/2) 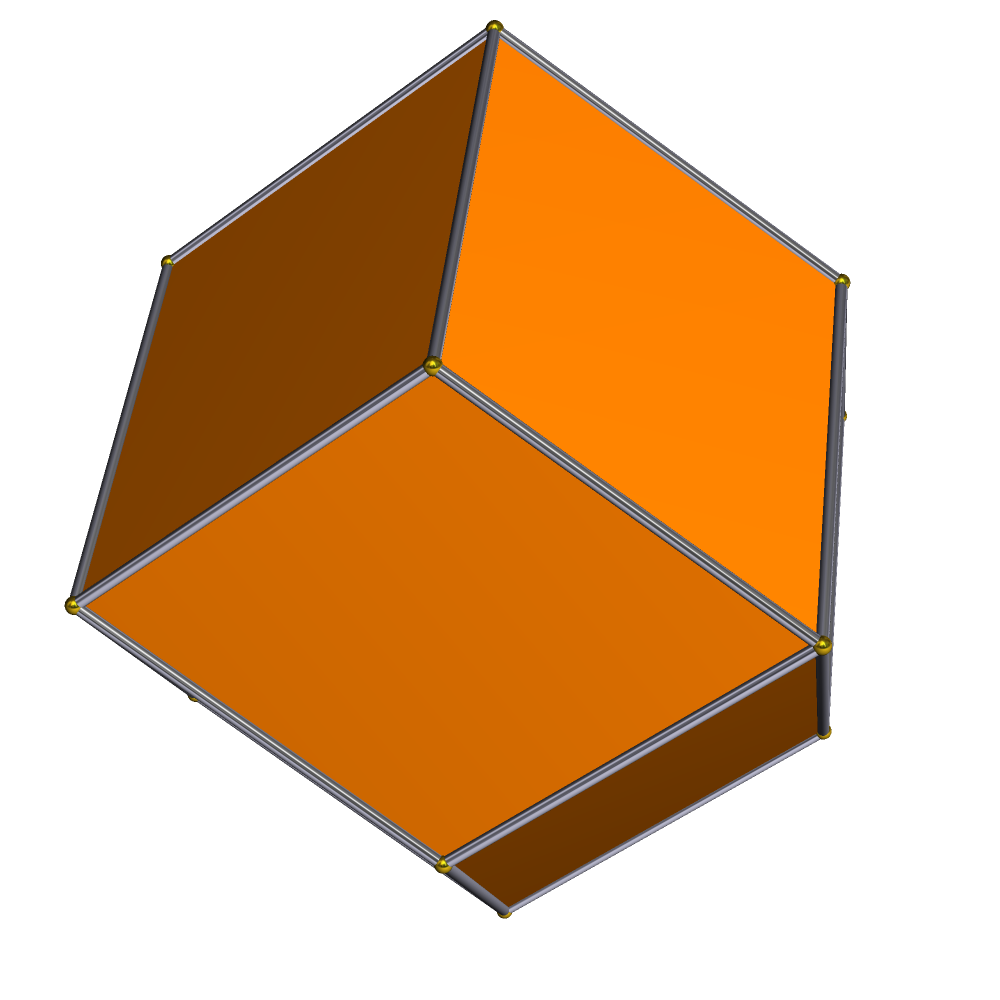
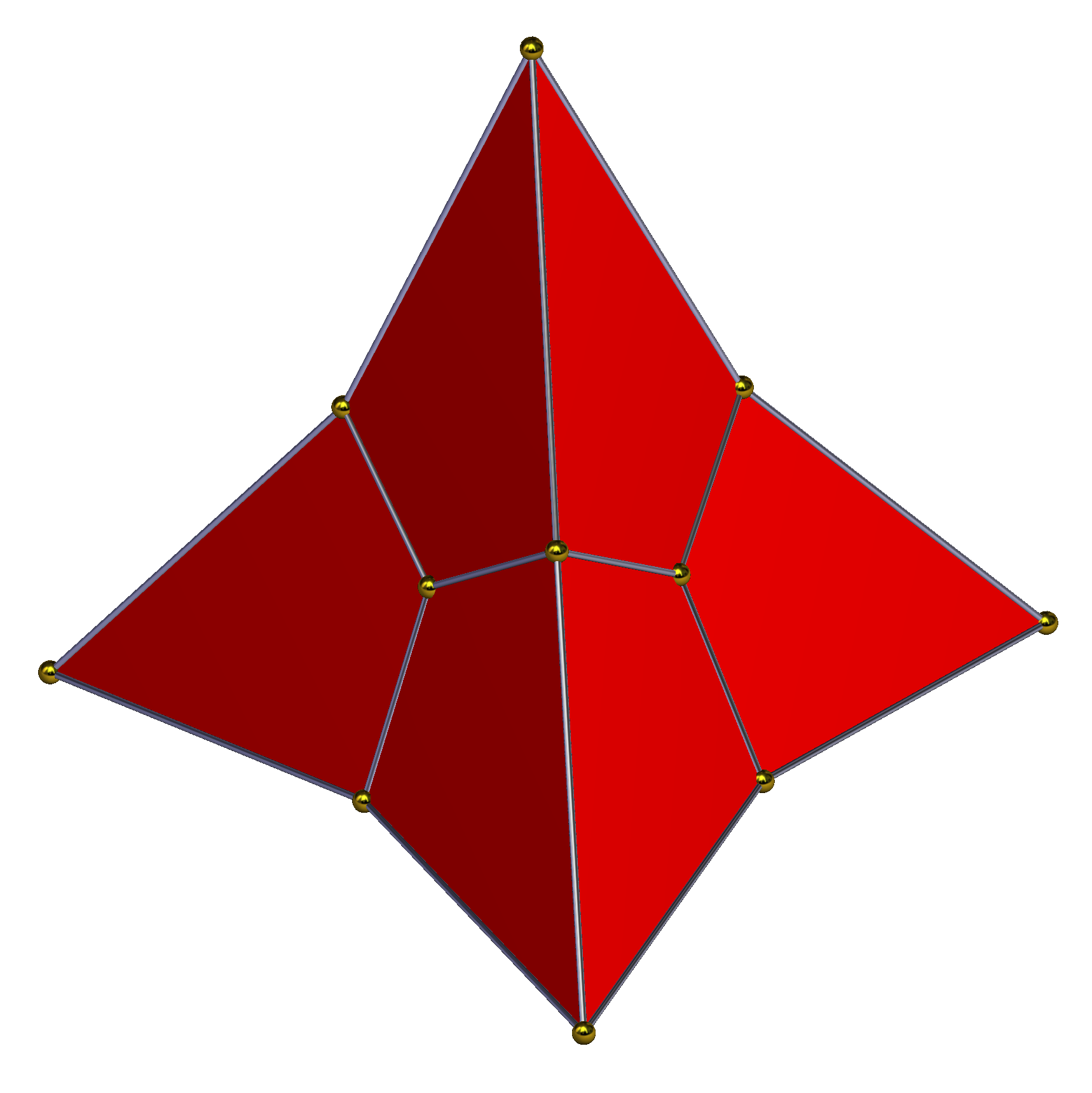
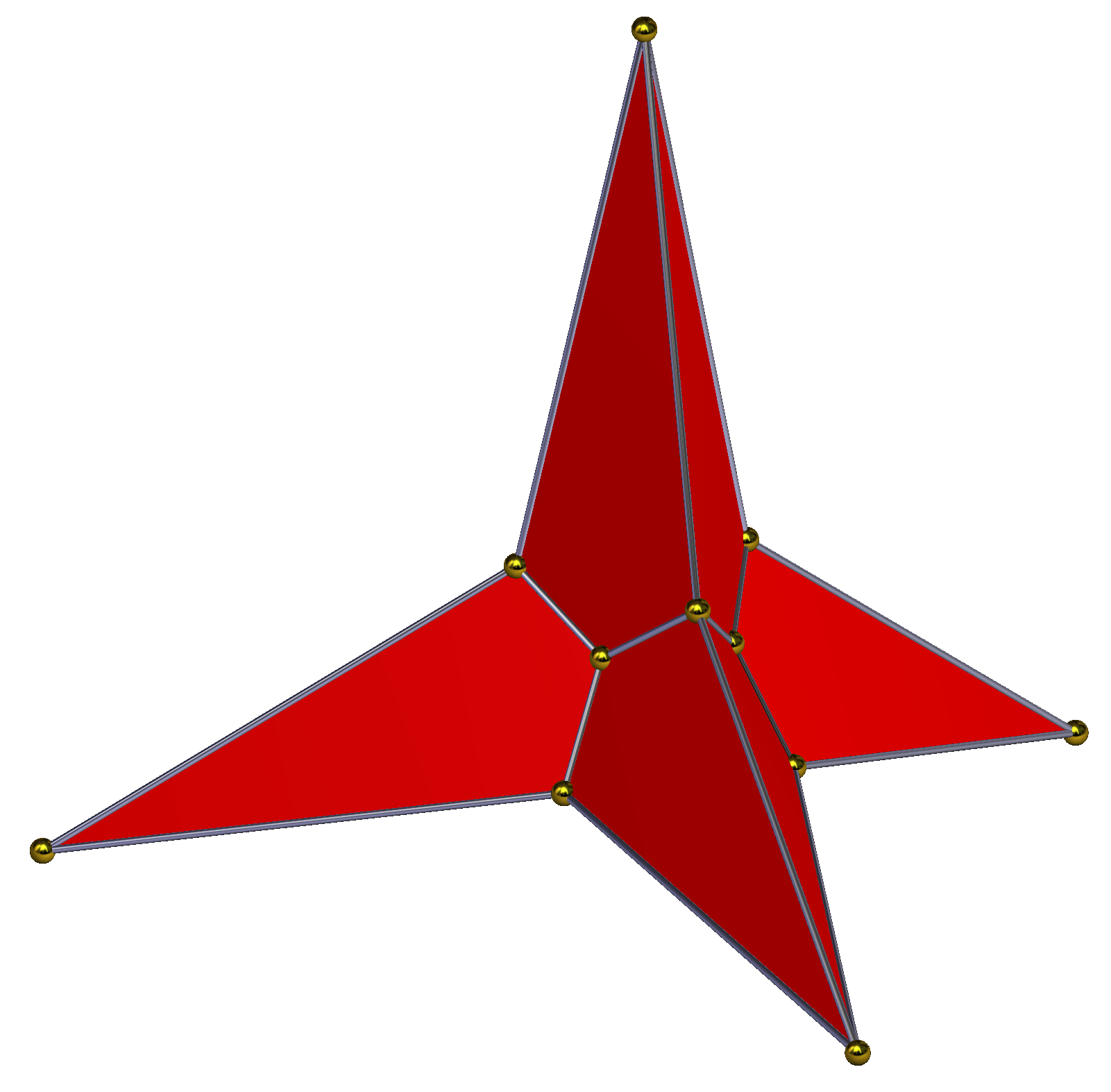
7. 별모양화
8. 관련 다면체
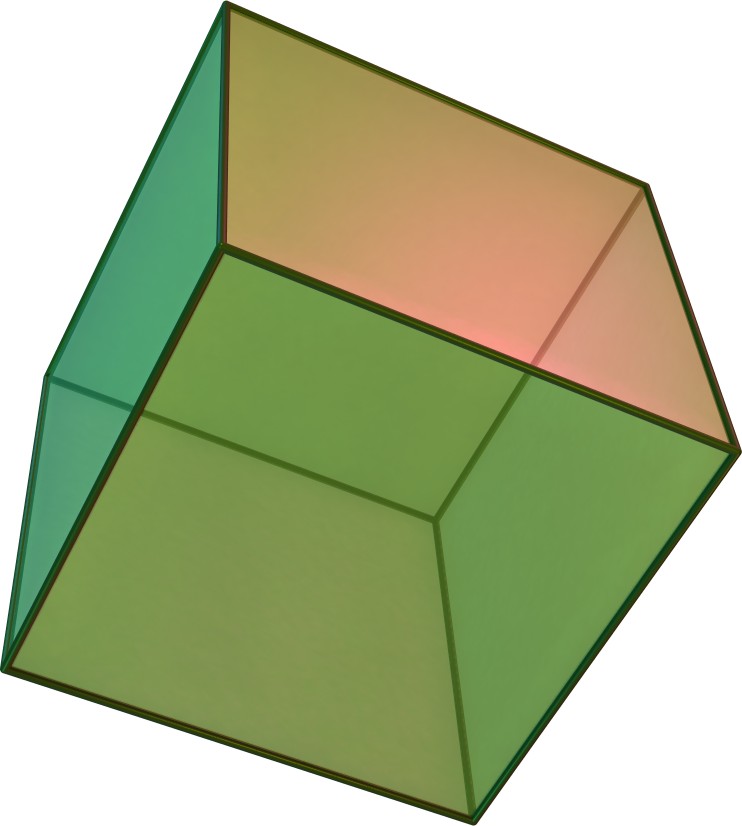
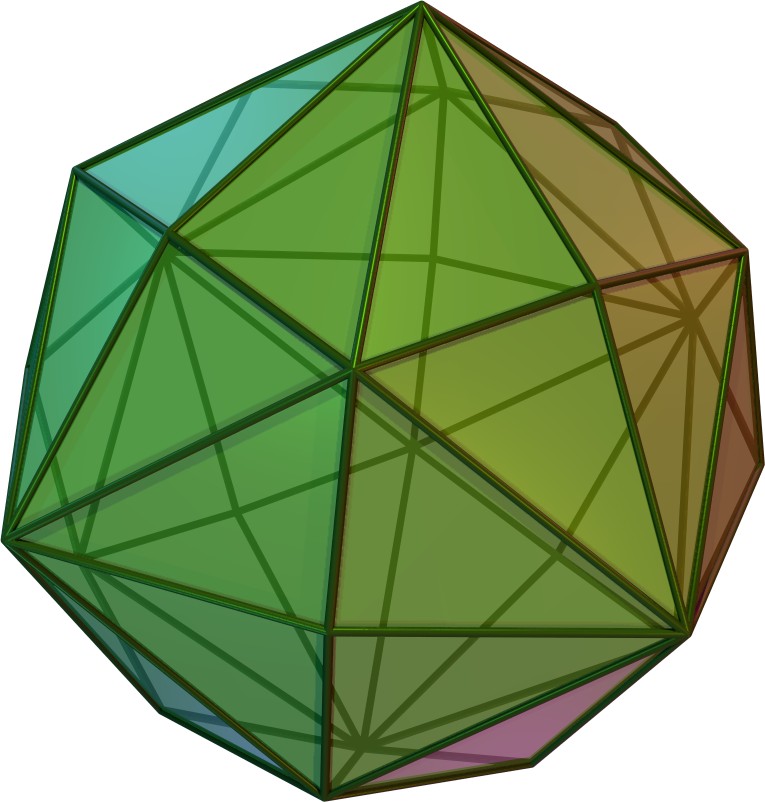
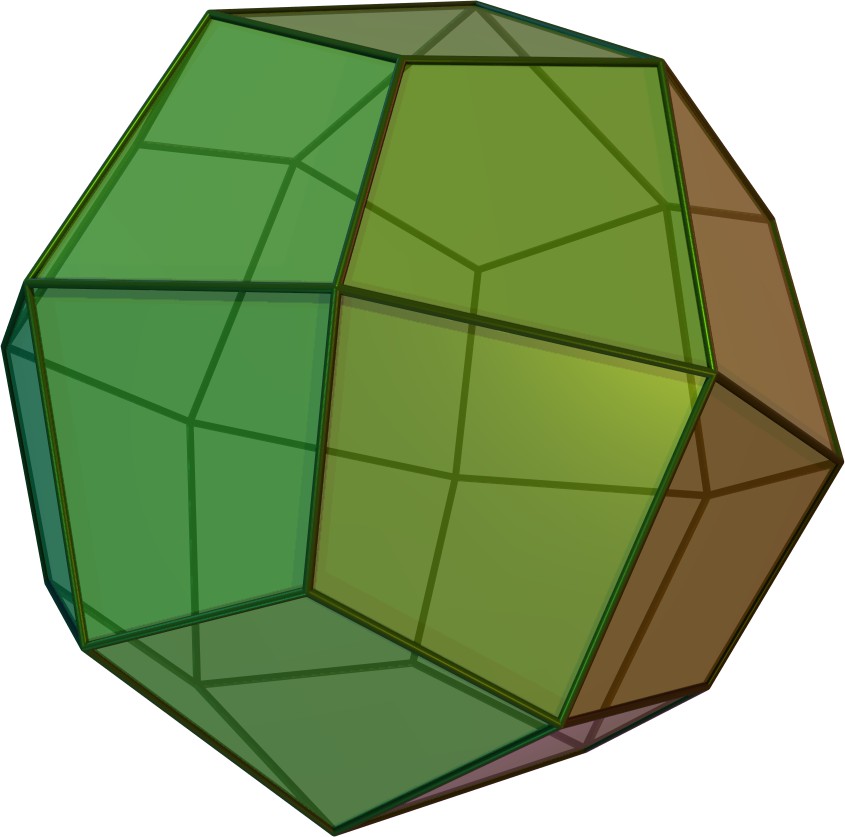
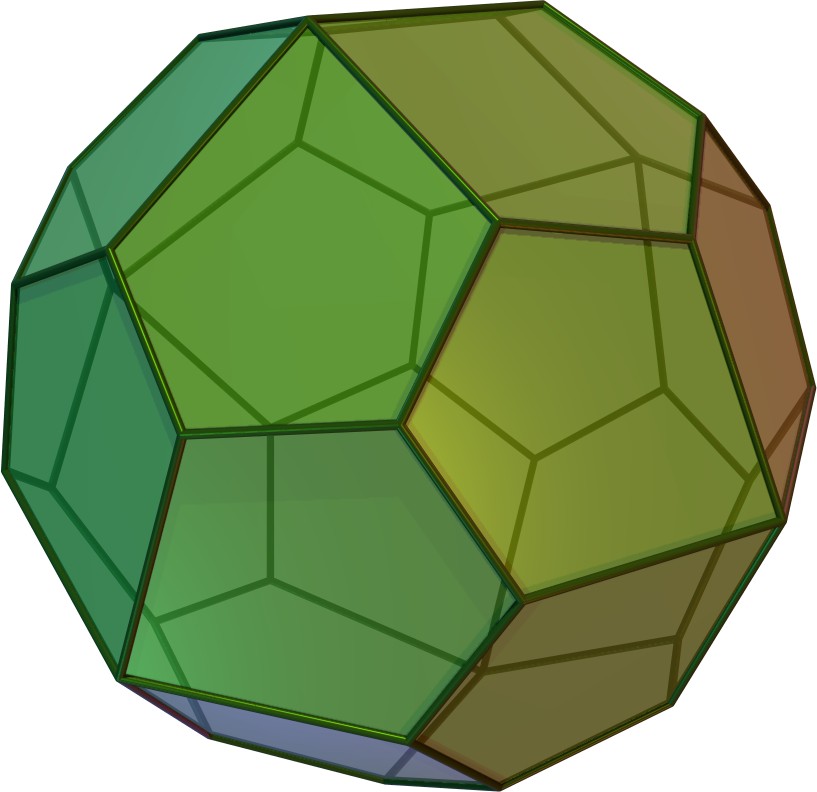
1960년, 스탄코 빌린스키는 12개의 합동인 마름모꼴 면을 가진 두 번째 마름모십이면체인 빌린스키 십이면체를 발견했다.[3] 이 형태의 마름모꼴 면은 황금비를 갖는다.
마름모십이면체는 초입방체를 3차원으로 정점 우선 투영한 결과의 껍질을 형성한다.[5] 또한 정이십사포체의 최대 단면을 형성하며, 3차원으로 정점 우선 평행 투영한 결과의 껍질도 형성한다.
참조
[1]
웹사이트
Dodecahedral Crystal Habit
http://www.khulsey.c[...]
2009-04-12
[2]
웹사이트
Maximum Torque and Momentum Envelopes for Reaction-Wheel Arrays
https://ntrs.nasa.go[...]
2020-08-20
[3]
서적
Order in Space: A design source book
[4]
서적
Economic Mineralogy: A Practical Guide to the Study of Useful Minerals
https://archive.org/[...]
[5]
Youtube
There are SIX Platonic Solids
https://www.youtube.[...]
2015-11-30
[6]
서적
Convex Polyhedra
Springer
[7]
논문
Regular-faced convex polyhedra
[8]
서적
Polyhedra
https://archive.org/[...]
Cambridge University Press
[9]
웹사이트
The Rhombic Dodecahedron as a Cube with Pyramids - Some Basic Measurement
https://old.maa.org/[...]
[10]
논문
2642. Unitary Construction of Certain Polyhedra
[11]
서적
Regular polytopes
Dover Publications
[12]
서적
Multi-shell Polyhedral Clusters
https://books.google[...]
Springer
[13]
논문
Zonohedra and zonotopes
http://www.ics.uci.e[...]
[14]
논문
The Bilinski dodecahedron and assorted parallelohedra, zonohedra, monohedra, isozonohedra, and otherhedra
[15]
논문
Stellations of the rhombic dodecahedron
[16]
논문
Le jeu alexandrin de l'icosaèdre
[17]
서적
The Geometrical Foundation of Natural Structure: A Source Book of Design
https://archive.org/[...]
Dover Publications, Inc.
[18]
논문
Zonohedrification
http://www.georgehar[...]
[19]
웹사이트
Rhombic Dodecahedron
https://archive.lib.[...]
2018-08-29
[20]
서적
CRC Concise Encyclopedia of Mathematics, Second Edition
https://books.google[...]
CRC Press
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

