십육원수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 산술
3. 응용
참조

1. 개요

십육원수는 16개의 기저 원소를 갖는 초복소수 체계로, 실수 선형 결합으로 표현된다. 덧셈과 뺄셈은 계수별로 이루어지며, 곱셈은 분배 법칙을 따르지만 교환 및 결합 법칙은 성립하지 않는다. 십육원수는 멱결합성과 유연 등식을 만족하며 영인자를 포함하므로 나눗셈 대수가 아니다. 십육원수의 곱셈표는 35개의 삼중항으로 표현되며, 이는 오쿼터니언의 케일리-딕슨 구성을 통해 생성된다. 십육원수의 노름이 1인 쌍의 곱이 0인 공간은 예외적 리 군 G₂와 위상 동형이며, 렙톤과 쿼크를 표현하고 머신 러닝 응용 분야에 활용될 수 있다.

더 읽어볼만한 페이지

다원수 - 팔원수
팔원수는 실수체 위의 8차원 노름 나눗셈 대수로서, 사원수 대수에 케일리-딕슨 구성을 적용하여 얻어지며, 교환 및 결합 법칙은 만족하지 않으나 교대 대수의 성질을 갖고, 수학 및 물리학 분야에서 활용된다.
다원수 - 사원수
사원수는 윌리엄 로언 해밀턴이 도입한 수 체계로, 덧셈과 곱셈 연산이 정의되며 3차원 공간 회전을 표현하는 데 유용한 실수, 복소수의 일반화된 4차원 벡터 공간이다.
비결합대수 - 비결합 대수
비결합 대수는 환과 유사한 대수 구조로서 곱셈의 결합 법칙이 성립하지 않으며, 결합성, 교환성, 반교환성, 야코비 항등식, 조르당 항등식, 멱결합성, 교대 결합성, 유연성 등의 항등식을 만족하는 대수들을 연구하며, 벡터곱, 리 대수, 요르단 대수, 교대 대수 등이 그 예시이다.
비결합대수 - 요르단 대수
요르단 대수는 2가 가역원인 가환환 K 위의 가군 A와 교환 법칙을 만족시키는 쌍선형 이항 연산, 그리고 이 연산의 항등원 1_A로 정의되는 대수 구조이며, 요르단 항등식을 만족하고 양자역학의 관측 가능량과 관련되며, 직합, 몫, 동위 연산, 피어스 분해 등의 연산을 가진다.

십육원수
개요
이름	세데니온
종류	초복소수 대수
단위	e₀, ..., e₁₅
항등원	e₀
성질	멱결합성 분배법칙
수학적 특성
기호	⟨math⟩S⟨/math⟩
차원	16
구성	세데니온은 실수의 16차원 초복소수 대수이다. 세데니온은 팔원수의 케일리-딕슨 대수이다. 즉, ⟨math⟩S⟨/math⟩ = 팔원수⊗팔원수이다.
성질 (추가)	비결합적 비교환적 분할 대수가 아님 (영인자를 가짐)
참고
관련 개념	복소수 사원수 팔원수 초복소수

2. 산술

모든 십육원수는 실수 스칼라 계수를 가지는 16개의 단위 십육원수 $e_0, e_1, e_2, \dots, e_{15}$ 의 선형 결합으로 표현될 수 있다. 여기서 $e_0 = 1$ 은 곱셈에 대한 항등원이다. 이 단위 십육원수들은 십육원수 전체가 이루는 실수체 위의 16차원 벡터 공간의 기저를 형성한다. 따라서 임의의 십육원수 $x$ 는 다음과 같은 형태로 유일하게 나타낼 수 있다.

: $x = x_0 e_0 + x_1 e_1 + x_2 e_2 + \cdots + x_{14} e_{14} + x_{15} e_{15}$

여기서 $x_0, x_1, \dots, x_{15}$ 는 실수 계수이다.

십육원수의 덧셈과 뺄셈은 각 기저 원소에 해당하는 계수별로 수행된다. 즉, 두 십육원수 $x = \sum_{i=0}^{15} x_i e_i$ 와 $y = \sum_{i=0}^{15} y_i e_i$ 에 대해 합과 차는 다음과 같이 정의된다.

: $x + y = \sum_{i=0}^{15} (x_i + y_i) e_i$

: $x - y = \sum_{i=0}^{15} (x_i - y_i) e_i$

십육원수의 곱셈은 덧셈에 대해 분배 법칙을 만족한다. 두 십육원수의 곱은 각 기저 원소 사이의 곱셈 결과를 이용하여 계산된다. 기저 원소 간의 구체적인 곱셈 규칙과 십육원수 곱셈의 상세한 성질(예: 결합 법칙 불성립, 영인자 존재 등)은 하위 섹션에서 자세히 다룬다.

케일리-딕슨 구성에 따라 십육원수는 그 구성 과정에서 사용된 하위 차원의 대수들을 포함한다. 구체적으로 십육원수는 팔원수( $e_0$ 부터 $e_7$ 까지로 생성됨)를 포함하며, 따라서 사원수( $e_0$ 부터 $e_3$ 까지), 복소수( $e_0, e_1$ ), 그리고 실수( $e_0$ )도 자연스럽게 포함하게 된다.

2. 1. 곱셈

십육원수의 곱셈은 덧셈에 대해 분배 법칙을 만족한다. 두 십육원수의 곱은 각 십육원수를 구성하는 기저 원소

e_i

(

i=0, \dots, 15

) 사이의 곱셈 결과를 선형 결합으로 확장하여 계산된다. 여기서

e_0 = 1

은 곱셈에 대한 항등원이다.

십육원수의 곱셈은 팔원수의 곱셈과 마찬가지로 교환 법칙과 결합 법칙을 만족하지 않는다. 또한, 팔원수와는 달리 교대성도 만족하지 않는다. 그러나 십육원수는 멱결합성과 유연성이라는 성질을 가진다. 멱결합성은 임의의 십육원수

x

에 대해 거듭제곱

x^n

이 모순 없이 잘 정의됨을 의미한다.

십육원수는 곱셈에 대한 항등원

e_0 = 1

을 가지며, 많은 원소가 곱셈에 대한 역원을 가지지만, 체를 이루지는 못한다. 이는 십육원수가 영인자를 포함하기 때문인데, 영인자란 0이 아닌 두 원소를 곱했을 때 결과가 0이 되는 경우를 말한다. 예를 들어,

(e_3 + e_{10})(e_6 - e_{15}) = 0

이다. 케일리-딕슨 구성을 통해 십육원수로부터 만들어지는 더 높은 차원의 초복소수 체계들은 모두 영인자를 가진다.

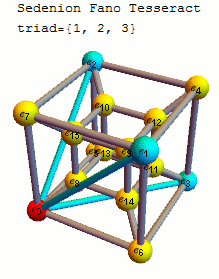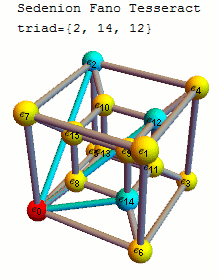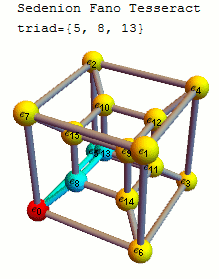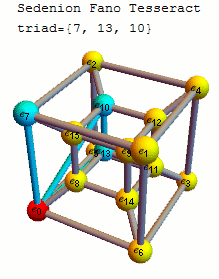
십육원수의 기저 원소

e_0, e_1, \dots, e_{15}

사이의 곱셈 규칙은 다음 표와 같다.

'''기저 원소 곱셈표'''
×	$e_0$	$e_1$	$e_2$	$e_3$	$e_4$	$e_5$	$e_6$	$e_7$	$e_8$	$e_9$	$e_{10}$	$e_{11}$	$e_{12}$	$e_{13}$	$e_{14}$	$e_{15}$
$e_0$	$e_0$	$e_1$	$e_2$	$e_3$	$e_4$	$e_5$	$e_6$	$e_7$	$e_8$	$e_9$	$e_{10}$	$e_{11}$	$e_{12}$	$e_{13}$	$e_{14}$	$e_{15}$
$e_1$	$e_1$	$-e_0$	$e_3$	$-e_2$	$e_5$	$-e_4$	$-e_7$	$e_6$	$e_9$	$-e_8$	$-e_{11}$	$e_{10}$	$-e_{13}$	$e_{12}$	$e_{15}$	$-e_{14}$
$e_2$	$e_2$	$-e_3$	$-e_0$	$e_1$	$e_6$	$e_7$	$-e_4$	$-e_5$	$e_{10}$	$e_{11}$	$-e_8$	$-e_9$	$-e_{14}$	$-e_{15}$	$e_{12}$	$e_{13}$
$e_3$	$e_3$	$e_2$	$-e_1$	$-e_0$	$e_7$	$-e_6$	$e_5$	$-e_4$	$e_{11}$	$-e_{10}$	$e_9$	$-e_8$	$-e_{15}$	$e_{14}$	$-e_{13}$	$e_{12}$
$e_4$	$e_4$	$-e_5$	$-e_6$	$-e_7$	$-e_0$	$e_1$	$e_2$	$e_3$	$e_{12}$	$e_{13}$	$e_{14}$	$e_{15}$	$-e_8$	$-e_9$	$-e_{10}$	$-e_{11}$
$e_5$	$e_5$	$e_4$	$-e_7$	$e_6$	$-e_1$	$-e_0$	$-e_3$	$e_2$	$e_{13}$	$-e_{12}$	$e_{15}$	$-e_{14}$	$e_9$	$-e_8$	$e_{11}$	$-e_{10}$
$e_6$	$e_6$	$e_7$	$e_4$	$-e_5$	$-e_2$	$e_3$	$-e_0$	$-e_1$	$e_{14}$	$-e_{15}$	$-e_{12}$	$e_{13}$	$e_{10}$	$-e_{11}$	$-e_8$	$e_9$
$e_7$	$e_7$	$-e_6$	$e_5$	$e_4$	$-e_3$	$-e_2$	$e_1$	$-e_0$	$e_{15}$	$e_{14}$	$-e_{13}$	$-e_{12}$	$e_{11}$	$e_{10}$	$-e_9$	$-e_8$
$e_8$	$e_8$	$-e_9$	$-e_{10}$	$-e_{11}$	$-e_{12}$	$-e_{13}$	$-e_{14}$	$-e_{15}$	$-e_0$	$e_1$	$e_2$	$e_3$	$e_4$	$e_5$	$e_6$	$e_7$
$e_9$	$e_9$	$e_8$	$-e_{11}$	$e_{10}$	$-e_{13}$	$e_{12}$	$e_{15}$	$-e_{14}$	$-e_1$	$-e_0$	$-e_3$	$e_2$	$-e_5$	$e_4$	$e_7$	$-e_6$
$e_{10}$	$e_{10}$	$e_{11}$	$e_8$	$-e_9$	$-e_{14}$	$-e_{15}$	$e_{12}$	$e_{13}$	$-e_2$	$e_3$	$-e_0$	$-e_1$	$-e_6$	$-e_7$	$e_4$	$e_5$
$e_{11}$	$e_{11}$	$-e_{10}$	$e_9$	$e_8$	$-e_{15}$	$e_{14}$	$-e_{13}$	$e_{12}$	$-e_3$	$-e_2$	$e_1$	$-e_0$	$-e_7$	$e_6$	$-e_5$	$e_4$
$e_{12}$	$e_{12}$	$e_{13}$	$e_{14}$	$e_{15}$	$e_8$	$-e_9$	$-e_{10}$	$-e_{11}$	$-e_4$	$e_5$	$e_6$	$e_7$	$-e_0$	$-e_1$	$-e_2$	$-e_3$
$e_{13}$	$e_{13}$	$-e_{12}$	$e_{15}$	$-e_{14}$	$e_9$	$e_8$	$e_{11}$	$-e_{10}$	$-e_5$	$-e_4$	$e_7$	$-e_6$	$e_1$	$-e_0$	$e_3$	$-e_2$
$e_{14}$	$e_{14}$	$-e_{15}$	$-e_{12}$	$e_{13}$	$e_{10}$	$-e_{11}$	$e_8$	$e_9$	$-e_6$	$-e_7$	$-e_4$	$e_5$	$e_2$	$-e_3$	$-e_0$	$e_1$
$e_{15}$	$e_{15}$	$e_{14}$	$-e_{13}$	$-e_{12}$	$e_{11}$	$e_{10}$	$-e_9$	$e_8$	$-e_7$	$e_6$	$-e_5$	$-e_4$	$e_3$	$e_2$	$-e_1$	$-e_0$

2. 2. 십육원수의 성질

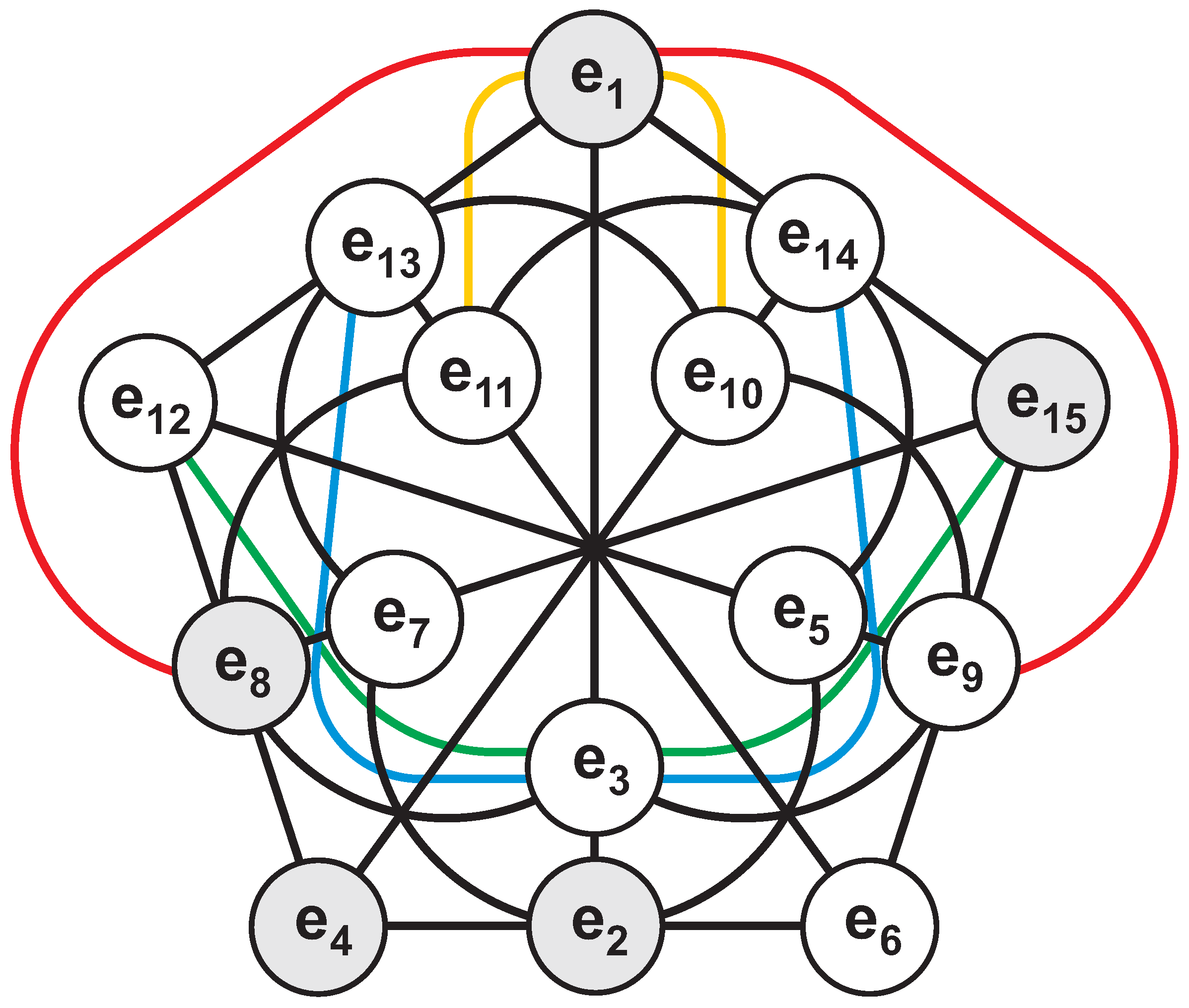
PG(3,2) 구조 그림. 세데니언의 곱셈 규칙을 나타낸다. 동일한 선 위의 세 점(세 개의 세데니언 허수 단위) 중 두 개의 곱은 부호를 무시하면 세 번째 점이 된다.

십육원수의 기저 원소들 사이의 곱셈은 다음과 같은 규칙을 따른다.

모든 $i$ 에 대해 $e_0 e_i = e_i e_0 = e_i$ 이다. (즉, $e_0$ 는 곱셈 항등원 1이다.)
$i \neq 0$ 일 때, $e_i e_i = -e_0 = -1$ 이다.
$i, j \neq 0$ 이고 $i \neq j$ 일 때, $e_i e_j = -e_j e_i$ 이다. (즉, 0이 아닌 서로 다른 기저 원소는 반교환한다.)

팔원수와 마찬가지로 십육원수의 곱셈은 교환 법칙과 결합 법칙을 만족하지 않는다. 팔원수와 달리 십육원수는 교대대수도 되지 않는다. 그러나 십육원수는 멱결합성을 가지므로, 임의의 십육원수

x

에 대해 거듭제곱

x^n

은 잘 정의된다. 또한 유연 등식(

(xy)x = x(yx)

)을 만족한다.

임의의 십육원수는 실수를 계수로 하는 16개의 단위 십육원수

e_0 = 1, e_1, e_2, \dots, e_{15}

의 선형 결합으로 표현될 수 있다. 즉, 십육원수 전체 '''S'''는 실수체 '''R''' 위의 16차원 벡터 공간을 이룬다.

십육원수는 곱셈에 대한 항등원(

e_0

)을 가지고 많은 원소가 곱셈 역원을 가지지만, 체를 이루지는 못한다. 이는 0이 아니면서 곱하면 0이 되는 영인자가 존재하기 때문이다. 예를 들어,

(e_3 + e_{10})(e_6 - e_{15}) = 0

이다. 케일리-딕슨 구성을 통해 십육원수로부터 만들어지는 모든 초복소수계는 영인자를 포함한다.

단위 십육원수의 곱셈표는 다음과 같다.

style="font-weight:bold; font-size:larger;" | 기저 원소의 곱셈표
×	1	e₁	e₂	e₃	e₄	e₅	e₆	e₇	e₈	e₉	e₁₀	e₁₁	e₁₂	e₁₃	e₁₄	e₁₅
1	1	e₁	e₂	e₃	e₄	e₅	e₆	e₇	e₈	e₉	e₁₀	e₁₁	e₁₂	e₁₃	e₁₄	e₁₅
e₁	e₁	−1	e₃	−e₂	e₅	−e₄	−e₇	e₆	e₉	−e₈	−e₁₁	e₁₀	−e₁₃	e₁₂	e₁₅	−e₁₄
e₂	e₂	−e₃	−1	e₁	e₆	e₇	−e₄	−e₅	e₁₀	e₁₁	−e₈	−e₉	−e₁₄	−e₁₅	e₁₂	e₁₃
e₃	e₃	e₂	−e₁	−1	e₇	−e₆	e₅	−e₄	e₁₁	−e₁₀	e₉	−e₈	−e₁₅	e₁₄	−e₁₃	e₁₂
e₄	e₄	−e₅	−e₆	−e₇	−1	e₁	e₂	e₃	e₁₂	e₁₃	e₁₄	e₁₅	−e₈	−e₉	−e₁₀	−e₁₁
e₅	e₅	e₄	−e₇	e₆	−e₁	−1	−e₃	e₂	e₁₃	−e₁₂	e₁₅	−e₁₄	e₉	−e₈	e₁₁	−e₁₀
e₆	e₆	e₇	e₄	−e₅	−e₂	e₃	−1	−e₁	e₁₄	−e₁₅	−e₁₂	e₁₃	e₁₀	−e₁₁	−e₈	e₉
e₇	e₇	−e₆	e₅	e₄	−e₃	−e₂	e₁	−1	e₁₅	e₁₄	−e₁₃	−e₁₂	e₁₁	e₁₀	−e₉	−e₈
e₈	e₈	−e₉	−e₁₀	−e₁₁	−e₁₂	−e₁₃	−e₁₄	−e₁₅	−1	e₁	e₂	e₃	e₄	e₅	e₆	e₇
e₉	e₉	e₈	−e₁₁	e₁₀	−e₁₃	e₁₂	e₁₅	−e₁₄	−e₁	−1	−e₃	e₂	−e₅	e₄	e₇	−e₆
e₁₀	e₁₀	e₁₁	e₈	−e₉	−e₁₄	−e₁₅	e₁₂	e₁₃	−e₂	e₃	−1	−e₁	−e₆	−e₇	e₄	e₅
e₁₁	e₁₁	−e₁₀	e₉	e₈	−e₁₅	e₁₄	−e₁₃	e₁₂	−e₃	−e₂	e₁	−1	−e₇	e₆	−e₅	e₄
e₁₂	e₁₂	e₁₃	e₁₄	e₁₅	e₈	−e₉	−e₁₀	−e₁₁	−e₄	e₅	e₆	e₇	−1	−e₁	−e₂	−e₃
e₁₃	e₁₃	−e₁₂	e₁₅	−e₁₄	e₉	e₈	e₁₁	−e₁₀	−e₅	−e₄	e₇	−e₆	e₁	−1	e₃	−e₂
e₁₄	e₁₄	−e₁₅	−e₁₂	e₁₃	e₁₀	−e₁₁	e₈	e₉	−e₆	−e₇	−e₄	e₅	e₂	−e₃	−1	e₁
e₁₅	e₁₅	e₁₄	−e₁₃	−e₁₂	e₁₁	e₁₀	−e₉	e₈	−e₇	e₆	−e₅	−e₄	e₃	e₂	−e₁	−1

십육원수 대수 '''S'''는 켤레 연산( $*$ )을 갖는 대수이다. 십육원수 $x = \sum_{i=0}^{15} x_i e_i$ 에 대해 켤레원 $x^*$ 는 $x^* := x_0 e_0 - \sum_{i=1}^{15} x_i e_i$ 로 정의된다. 이를 이용하여 노름 $N(x)$ 를 $N(x) := x x^* = \sum_{i=0}^{15} x_i^2$ 로 정의할 수 있다. (또는 $\|x\| := \sqrt{x x^*}$ ). 십육원수 대수 ('''S''', ''N'')는 이차 대수이지만, 노름이 곱셈적이지 않아 합성 대수는 아니다.

2. 3. 사원수 부분대수

십육원수 곱셈표는 35개의 삼중항(triplet)으로 표현될 수 있다. 이 삼중항들은 팔원수로부터 케일리-딕슨 구성을 사용하여 만들어진다. 팔원수 자체는 굵게 표시된 7개의 삼중항 집합으로 표현되는데, 이는 복소수에서 사원수를 구성하고, 다시 사원수로부터 케일리-딕슨 구성을 통해 팔원수를 만드는 과정에 기반한다. 팔원수를 구성하는 7개의 삼중항 집합은 480가지 경우가 가능하다.

각 삼중항을 구성하는 세 인덱스의 이진수 표현은 비트 XOR 연산을 하면 0이 되는 특징이 있다. 35개의 삼중항은 다음과 같다.

{ '''{1, 2, 3}''', '''{1, 4, 5}''', '''{1, 7, 6}''', {1, 8, 9}, {1, 11, 10}, {1, 13, 12}, {1, 14, 15},

'''{2, 4, 6}''', '''{2, 5, 7}''', {2, 8, 10}, {2, 9, 11}, {2, 14, 12}, {2, 15, 13}, '''{3, 4, 7}''',

'''{3, 6, 5}''', {3, 8, 11}, {3, 10, 9}, {3, 13, 14}, {3, 15, 12}, {4, 8, 12}, {4, 9, 13},

{4, 10, 14}, {4, 11, 15}, {5, 8, 13}, {5, 10, 15}, {5, 12, 9}, {5, 14, 11}, {6, 8, 14},

{6, 11, 13}, {6, 12, 10}, {6, 15, 9}, {7, 8, 15}, {7, 9, 14}, {7, 12, 11}, {7, 13, 10} }

2. 4. 영인자

십육원수는 곱셈에 대한 항등원

e_0

과 곱셈의 역원을 가지지만, 영인자(zero divisor)가 존재하기 때문에 나눗셈 대수는 아니다. 즉, 0이 아닌 두 십육원수를 곱하여 0이 되는 경우가 존재한다. 예를 들어,

(e_3 + e_{10})(e_6 - e_{15}) = 0

이다.

케일리-딕슨 구성을 통해 십육원수로부터 만들어지는 모든 초복소수 시스템 역시 영인자를 포함한다.

십육원수에는

(e_a + e_b) \circ (e_c + e_d) = 0

을 만족하는 84개의 영인자 집합

\{e_a, e_b, e_c, e_d\}

이 존재한다. 그 목록은 다음과 같다.

\begin{array}{c}\text{십육원수 영인자 } \{ e_a, e_b, e_c, e_d \} \\\text{여기서 } (e_a + e_b) \circ (e_c + e_d) = 0 \\\begin{array}{ccc}1 \leq a \leq 6, & c > a, & 9 \leq b \leq 15 \\\end{array} \\\\\begin{array}{lccr}\{ 9 \leq d \leq 15 \} & \{ -9 \geq d \geq -15 \} &\{ 9 \leq d \leq 15 \} & \{ -9 \geq d \geq -15 \}\\\end{array} \\\\\begin{array}{lccr}\{e_1, e_{10}, e_5, e_{14}\} & \{e_1, e_{10}, e_4, -e_{15}\} &\{e_1, e_{10}, e_7, e_{12}\} & \{e_1, e_{10}, e_6, -e_{13}\} \\\{e_1, e_{11}, e_4, e_{14}\} & \{e_1, e_{11}, e_6, -e_{12}\} &\{e_1, e_{11}, e_5, e_{15}\} & \{e_1, e_{11}, e_7, -e_{13}\} \\\{e_1, e_{12}, e_2, e_{15}\} & \{e_1, e_{12}, e_3, -e_{14}\} &\{e_1, e_{12}, e_6, e_{11}\} & \{e_1, e_{12}, e_7, -e_{10}\} \\\{e_1, e_{13}, e_6, e_{10}\} & \{e_1, e_{13}, e_2, -e_{14}\} &\{e_1, e_{13}, e_7, e_{11}\} & \{e_1, e_{13}, e_3, -e_{15}\} \\\{e_1, e_{14}, e_2, e_{13}\} & \{e_1, e_{14}, e_4, -e_{11}\} &\{e_1, e_{14}, e_3, e_{12}\} & \{e_1, e_{14}, e_5, -e_{10}\} \\\{e_1, e_{15}, e_3, e_{13}\} & \{e_1, e_{15}, e_2, -e_{12}\} &\{e_1, e_{15}, e_4, e_{10}\} & \{e_1, e_{15}, e_5, -e_{11}\} \\\\\{e_2, e_9,    e_4, e_{15}\} & \{e_2, e_9,    e_5, -e_{14}\} &\{e_2, e_9,    e_6, e_{13}\} & \{e_2, e_9,    e_7, -e_{12}\} \\\{e_2, e_{11}, e_5, e_{12}\} & \{e_2, e_{11}, e_4, -e_{13}\} &\{e_2, e_{11}, e_6, e_{15}\} & \{e_2, e_{11}, e_7, -e_{14}\} \\\{e_2, e_{12}, e_3, e_{13}\} & \{e_2, e_{12}, e_5, -e_{11}\} &\{e_2, e_{12}, e_7, e_9   \} & \{e_2, e_{13}, e_3, -e_{12}\} \\\{e_2, e_{13}, e_4, e_{11}\} & \{e_2, e_{13}, e_6, -e_9   \} &\{e_2, e_{14}, e_5, e_9   \} & \{e_2, e_{14}, e_3, -e_{15}\} \\\{e_2, e_{14}, e_7, e_{11}\} & \{e_2, e_{15}, e_4, -e_9   \} &\{e_2, e_{15}, e_3, e_{14}\} & \{e_2, e_{15}, e_6, -e_{11}\} \\\\\{e_3, e_9,    e_6, e_{12}\} & \{e_3, e_9,    e_4, -e_{14}\} &\{e_3, e_9,    e_7, e_{13}\} & \{e_3, e_9,    e_5, -e_{15}\} \\\{e_3, e_{10}, e_4, e_{13}\} & \{e_3, e_{10}, e_5, -e_{12}\} &\{e_3, e_{10}, e_7, e_{14}\} & \{e_3, e_{10}, e_6, -e_{15}\} \\\{e_3, e_{12}, e_5, e_{10}\} & \{e_3, e_{12}, e_6, -e_9   \} &\{e_3, e_{14}, e_4, e_9   \} & \{e_3, e_{13}, e_4, -e_{10}\} \\\{e_3, e_{15}, e_5, e_9   \} & \{e_3, e_{13}, e_7, -e_9   \} &\{e_3, e_{15}, e_6, e_{10}\} & \{e_3, e_{14}, e_7, -e_{10}\} \\\\\{e_4, e_9,    e_7, e_{10}\} & \{e_4, e_9,    e_6, -e_{11}\} &\{e_4, e_{10}, e_5, e_{11}\} & \{e_4, e_{10}, e_7, -e_9   \} \\\{e_4, e_{11}, e_6, e_9   \} & \{e_4, e_{11}, e_5, -e_{10}\} &\{e_4, e_{13}, e_6, e_{15}\} & \{e_4, e_{13}, e_7, -e_{14}\} \\\{e_4, e_{14}, e_7, e_{13}\} & \{e_4, e_{14}, e_5, -e_{15}\} &\{e_4, e_{15}, e_5, e_{14}\} & \{e_4, e_{15}, e_6, -e_{13}\} \\\\\{e_5, e_{10}, e_6, e_9   \} & \{e_5, e_9,    e_6, -e_{10}\} &\{e_5, e_{11}, e_7, e_9   \} & \{e_5, e_9,    e_7, -e_{11}\} \\\{e_5, e_{12}, e_7, e_{14}\} & \{e_5, e_{12}, e_6, -e_{15}\} &\{e_5, e_{15}, e_6, e_{12}\} & \{e_5, e_{14}, e_7, -e_{12}\} \\\\\{e_6, e_{11}, e_7, e_{10}\} & \{e_6, e_{10}, e_7, -e_{11}\} &\{e_6, e_{13}, e_7, e_{12}\} & \{e_6, e_{12}, e_7, -e_{13}\}\end{array}\end{array}

3. 응용

노름이 1인 십육원수 중에서 곱해서 0이 되는 쌍들의 공간이 예외적 리 군 G₂의 콤팩트 형태와 위상동형이라는 연구가 있다. 여기서 '영 인자'는 곱이 0이 되는 원소의 쌍을 의미한다.

또한, 불변 게이지 대칭 SU(3)_c × U(1)_em과 관련된 3세대 렙톤과 쿼크를 복소화된 십육원수의 대수 ℂ ⊗ S를 사용하여 나타낼 수 있다는 연구가 있다. 이 연구에 따르면, 특정 원시 멱등원 사영자 ρ₊ = 1/2(1 + ie₁₅) (여기서 e₁₅는 파노 평면에서 팔원수 𝕆의 e₇과 유사한 허수 단위)를 사용하여 십육원수의 표준 기저에 작용시키면, 대수가 복소화된 팔원수 ℂ ⊗ 𝕆에 대한 세 개의 분할 기저 원소 집합으로 나뉘고, 이들의 왼쪽 작용은 세 개의 클리포드 대수 Cl(6) 복사본을 생성한다. 이 클리포드 대수는 불변 SU(3)_c × U(1)_em 게이지 대칭을 가진 단일 세대의 페르미온을 설명하는 최소 왼쪽 아이디얼을 포함한다. 연구자들은 이 세 개의 복소화된 팔원수 부분 대수가 쿼크 혼합을 설명하는 CKM 행렬과 중성미자 진동을 설명하는 PMNS 행렬의 이론적 기반을 형성할 수 있다고 언급했다.

십육원수를 이용한 신경망은 머신러닝 응용 분야에서 효율적이고 간결한 표현을 제공하며, 여러 시계열 및 교통 예측 문제를 해결하는 데 사용된 사례가 있다.^[4]^[5]

참조

_[1] 웹사이트 Ensembles de nombre https://mathsci.kais[...] Forum Futura-Science 2011-09-06
_[2] 논문 THE BASIC SUBALGEBRA STRUCTURE OF THE CAYLEY-DICKSON ALGEBRA OF DIMENSION 32 (TRIGINTADUONIONS) https://arxiv.org/ab[...] 2009
_[3] 서적 2002
_[4] 논문 Metacognitive Sedenion-Valued Neural Network and its Learning Algorithm 2020
_[5] 간행물 Traffic4cast at NeurIPS 2020 – yet more on the unreasonable effectiveness of gridded geo-spatial processes https://proceedings.[...] PMLR 2021-08-07

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com