정사각수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
정사각수는 음이 아닌 정수 n에 대해 n² 꼴로 나타낼 수 있는 수이다. 정사각수는 m개의 점을 정사각형으로 배열할 수 있을 때 m이 된다. n번째 정사각수는 n²으로 표현되며, 처음 n개의 홀수의 합과 같다. 모든 정사각수는 홀수 개의 약수를 가지며, 라그랑주의 네 제곱수 정리에 따르면 모든 양의 정수는 4개 이하의 정사각수의 합으로 나타낼 수 있다. 또한 정사각수는 사각뿔수의 개념으로 확장될 수 있으며, 유리수의 제곱으로 표시되는 수를 제곱수라고도 한다.
더 읽어볼만한 페이지
- 도형수 - 세제곱수
세제곱수는 정수를 세 번 곱한 수로, 단위 길이 변을 가진 정육면체를 쌓아 더 큰 정육면체를 만들 수 있는 수이며, 모든 정수는 9개 이하의 세제곱수의 합으로 표현 가능하다는 특징이 있다. - 도형수 - 삼각수
삼각수는 1부터 n까지의 자연수 합으로, n(n+1)/2로 계산되며, 삼각형 모양으로 표현되고 조합론적 문제 해결에 활용되는 수이다. - 정수열 - 실베스터 수열
실베스터 수열은 각 항이 이전 항들의 곱에 1을 더한 값으로 정의되는 정수 수열로서, 재귀적으로 정의되며 이중 지수 함수적으로 증가하고, 이집트 분수 및 탐욕 알고리즘과 관련이 있으며, 역수 합은 1로 수렴한다. - 정수열 - 소수 (수론)
소수는 1과 자기 자신만을 약수로 가지는 1보다 큰 자연수이며, 무한히 많고 정수론의 기본 정리에서 중요한 역할을 하며 다양한 분야에 응용된다.
| 정사각수 | |
|---|---|
| 정의 | |
| 정의 | 어떤 정수를 제곱한 수 (자기 자신을 곱한 수) |
| 다른 이름 | 사각수 정사각수 |
| 성질 | |
| 0의 제곱 | 02 = 0 |
| 음수의 제곱 | 음수를 제곱하면 양수가 됨 |
| 제곱근 | 제곱근은 항상 존재함 |
| n번째 제곱수 | n번째 제곱수는 1부터 시작하여 n개의 홀수를 더한 값과 같음 |
| 제곱수 판별법 | 마지막 자리 숫자가 2, 3, 7, 8인 수는 제곱수가 아님 |
| 연속하는 제곱수의 합 | 연속하는 두 제곱수의 합은 항상 홀수임 |
| 제곱수의 개수 | 1부터 n까지의 제곱수의 개수는 floor(sqrt(n))임 |
| 예시 | |
| 예시 | 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, ... |
2. 정의
음이 아닌 정수 에 대하여 의 꼴로 나타낼 수 있는 수를 '''정사각수'''라고 한다. 정사각수 ''m''은 ''m''개의 점을 정사각형으로 배열할 수 있을 때, 그리고 그 때만 정사각수이다.
| -- |
| -- |
| -- |
| -- |
| -- |
모든 정사각수는 홀수개의 약수를 가지는 반면, 다른 자연수는 짝수개의 약수를 가진다. 정사각수는 완전수가 아니다.
번째 정사각수는 로 표현된다. 위의 그림에서 볼 수 있듯이, 이는 처음 개의 홀수의 합과 같다. 공식은 다음과 같다.
:
예를 들어, 이다.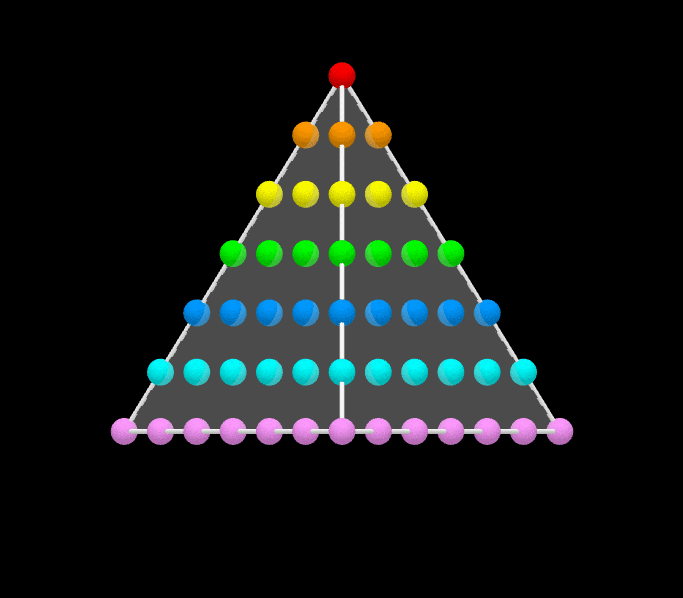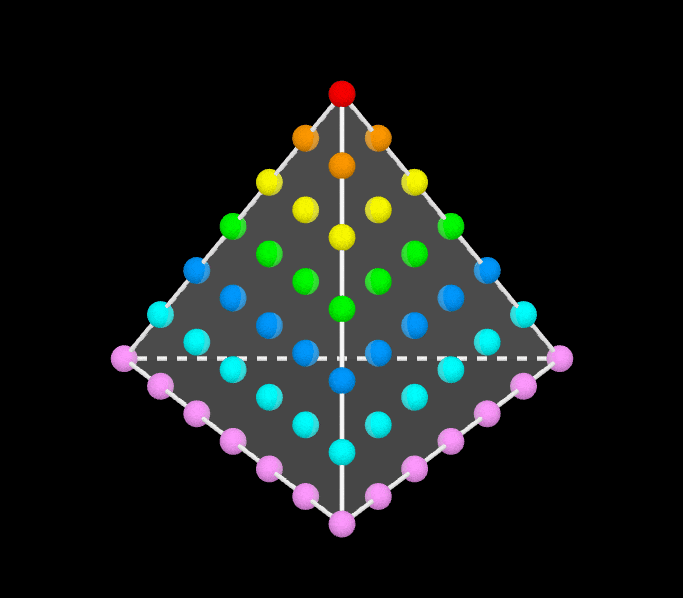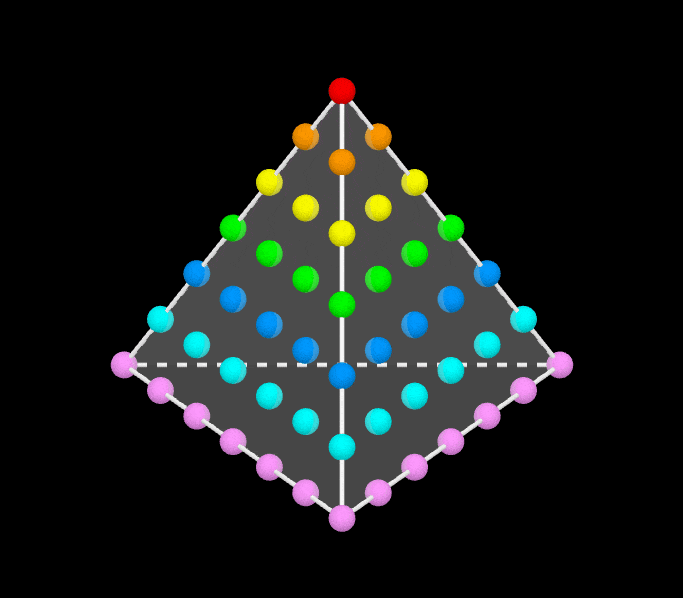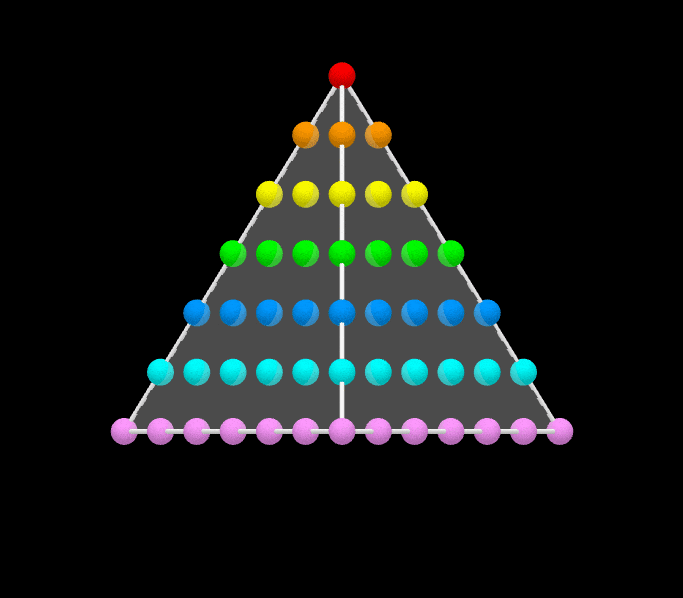
처음 20개의 정사각수는 다음과 같다.
: 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, …
3. 성질
정사각수는 1부터 시작하는 연속된 홀수의 합과 같다. 즉, 음이 아닌 정수 에 대하여 다음이 성립한다.
:
이는 다음과 같이 그림으로 나타낼 수 있다.
라그랑주 네 제곱수 정리에 따르면, 모든 자연수는 최대 4개의 정사각수의 합으로 표현할 수 있다. 또한, 31개의 수를 제외한 모든 자연수는 서로 다른 제곱수의 합으로 나타낼 수 있다.
두 개의 연속하는 삼각수의 합은 정사각수이며, 모든 홀수 제곱수는 중심 팔각수이다.
어떤 소수 p가 정사각수 m을 나누면, p²도 m을 나눈다.
정사각수 ''m''은 ''m''개의 점을 정사각형으로 배열할 수 있을 때 정사각수가 된다.-- -- -- -- --
3. 1. 홀수와 짝수 정사각수
짝수의 제곱은 짝수이며, 4로 나누어 떨어진다. 홀수의 제곱은 홀수이며, 모듈러 산술에서 8을 modulo로 1과 합동이다. 즉, 모든 홀수 제곱수는 8로 나눴을 때 나머지가 1이다.
3. 2. 특정 경우
3. 3. 진법 관련 성질
3. 4. 다른 수와의 관계
4. 사각뿔수
'''정사각수'''의 개념을 공간으로 확장하여, 물체를 사각뿔을 이루도록 공간에 배치했을 때의 물체의 총 수를 '''사각뿔수'''라고 한다.
제 사각뿔수는 제1 정사각수에서부터 제 정사각수까지의 합이고, 그 값 은 으로 쓸 수 있다.
사각뿔수를 1항부터 써보면 다음과 같다.
1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, ...
사각뿔수와 사면체수는 서로 밀접한 연관이 있다. 예를 들어, 이웃한 두 사면체수를 더하면 사각뿔수가 된다. 사면체수는 1, 4, 10, 20, 35, 56, .. 등이 있는데, 1+4=5, 4+10=14처럼 이웃한 두 사면체수의 합은 정확히 사각뿔수가 된다. n번째 사면체수를 , n번째 사각뿔수를 라고 하고 이 공식을 일반화하면 가 된다. 이 공식은 사각뿔수와 사면체수의 공식을 가지고 계산하면 쉽게 알 수 있다.
5. 일반화
유리수의 제곱으로 표시되는 유리수를 제곱수라고도 한다. 더 나아가 일반적으로는, 가환체 의 곱셈군 의 부분 집합 } ( 등으로 표기)의 원소를 제곱수 또는 제곱원이라고 부르는 경우가 있다. 주로 일 때 의미를 가진다.
6. 관련 정리
- '''니코마코스의 정리'''
처음 ''n''개의 세제곱의 합은 처음 ''n''개의 양의 정수의 합의 제곱이다.
- '''두 제곱수의 합 정리'''
형태의 소수는 두 개의 제곱수의 합으로 나타낼 수 있다.
- '''다각수 정리'''
다각수 정리에 의해 모든 자연수는 많아야 4개의 제곱수의 합으로 나타낼 수 있다(사제곱수 정리).
- '''와링의 문제'''
와링의 문제는 라그랑주의 네 제곱수 정리를 일반화한 것이다.
참조
[1]
문서
Some authors also call squares of rational numbers perfect squares.
[2]
서적
The Mechanical Universe: Introduction to Mechanics and Heat
https://books.google[...]
Cambridge University Press
2008-01-14
[3]
간행물
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com




