칸토어 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

칸토어 함수는 0과 1 사이의 값을 갖는 함수로, 삼진법 전개를 이진법 전개로 변환하여 정의된다. 이 함수는 연속이지만 절대 연속은 아니며, 칸토어 집합의 비가산 집합에서는 미분 불가능하다. 칸토어 함수는 특이 함수의 대표적인 예시이며, 누적 분포 함수로도 볼 수 있다. 칸토어 함수는 자기 유사성을 가지며, 일반화된 형태와 응용 분야를 가진다.

더 읽어볼만한 페이지

게오르크 칸토어 - 칸토어 역설
칸토어 역설은 가장 큰 기수가 존재한다는 가정의 모순을 통해 기수들의 모임이 집합이 아닌 고유 모임임을 보이는 역설이다.
게오르크 칸토어 - 칸토어의 정리
칸토어의 정리는 집합 X의 멱집합의 크기가 X의 크기보다 항상 크다는 것을 나타내며, 임의의 기수 κ에 대해 2^κ > κ가 성립한다는 내용으로, 칸토어의 대각선 논법으로 증명되고 집합론의 역설과 관련되어 전체 집합의 존재를 가정할 때 칸토어의 역설을 유발한다.
프랙탈 - 브라운 운동
브라운 운동은 액체나 기체 속 미세 입자가 매질 분자와 충돌하여 불규칙하게 움직이는 현상으로, 아인슈타인과 스몰루호프스키의 이론적 설명과 페랭의 실험적 검증을 통해 원자 존재 입증에 기여했으며, 확산/랑주뱅 방정식으로 모델링되어 다양한 분야에 응용된다.
프랙탈 - 프랙탈 우주론
프랙탈 우주론은 우주의 구조가 프랙탈 기하학적 특성을 갖는다는 이론이며, 관측 결과는 우주가 균질하다는 것을 보여주지만, 이론적 연구에서는 큰 규모나 미시적 규모에서 프랙탈 구조를 제안하기도 한다.
측도론 - 디랙 델타 함수
디랙 델타 함수는 원점에서 무한대 값을 갖고 그 외 지점에서 0의 값을 갖는 수학적 개념으로, 분포 또는 측도로 정의되며, 순간적인 충격이나 점 형태 현상 모델링에 활용되고 푸리에 변환, 스케일링, 평행 이동 등의 성질을 가진다.
측도론 - 바이어슈트라스 함수
바이어슈트라스 함수는 특정 조건의 상수 $a$ 와 $b$ 를 사용하여 $f(x)= \sum_{n=0}^\infin a^n\cos (b^n\pi x)$ 와 같은 무한 급수 형태로 정의되며 모든 점에서 연속이지만 어느 곳에서도 미분 불가능한 자기 유사성을 지닌 최초로 연구된 프랙탈 중 하나이다.

칸토어 함수
개요
칸토어 함수
정의	[0, 1] 구간에서 정의된 함수
값의 범위	[0, 1]
특징	연속 함수 거의 모든 곳에서 도함수가 0 절대 연속 함수가 아님
별칭	악마의 계단 (Devil's staircase) 칸토어 삼항 함수 (Cantor ternary function) 르베그 함수 (Lebesgue function) 르베그의 특이 함수 (Lebesgue's singular function) 칸토어-비탈리 함수 (Cantor-Vitali function) 칸토어 계단 함수 (Cantor staircase function) 칸토어-르베그 함수 (Cantor-Lebesgue function)
역사
발견	게오르크 칸토어(1884)
연구	Scheeffer(1884) 르베그(1904) 비탈리(1905)
성질
연속성	칸토어 함수는 구간 [0, 1]에서 연속 함수이다.
도함수	칸토어 함수는 칸토어 집합의 여집합에서 도함수가 0이다.
절대 연속성	칸토어 함수는 절대 연속 함수가 아니다.

2. 정의

칸토어 함수는 여러 가지 방법으로 정의될 수 있다.

칸토어 함수 ''c'' : [0,1] → [0,1]는 다음과 같이 정의된다.

# ''x''를 삼진법으로 나타낸다.

# ''x''의 삼진법 표현에 1이 있으면, 첫 번째 1 이후의 모든 자릿수를 0으로 바꾼다.

# 모든 2를 1로 바꾼다.

# 결과를 이진법으로 해석하면 ''c''(''x'')가 된다.

몇 가지 예는 다음과 같다.

1/4는 삼진법으로 0.02020202...이다. 1이 없으므로 2를 1로 바꾸면 0.01010101...이다. 이진법으로 읽으면 1/3이다. 따라서 ''c''(1/4) = 1/3이다.
1/5는 삼진법으로 0.01210121...이다. 첫 번째 1 이후를 0으로 바꾸면 0.01000000...이다. 이진법으로 읽으면 1/4이다. 따라서 ''c''(1/5) = 1/4이다.
200/243는 삼진법으로 0.21102이다. 첫 번째 1 이후 0으로 바꾸면 0.21이고, 2를 1로 바꾸면 0.11이다. 이진법으로 읽으면 3/4이다. 따라서 ''c''(200/243) = 3/4이다.

칸토어 함수는 칸토어 집합과 밀접하게 관련되어 있으며, 프랙탈의 일종이다. 칸토어 집합 ''C''는 구간 [0, 1]에서 삼진법 전개에 1을 포함하지 않는 수들의 집합이다. (단, 1 뒤에 0만 오는 경우는 제외) 칸토어 집합은 무한히 많은 점을 가지지만, 길이는 0이다. 칸토어 함수의 하우스도르프 측도는

D = \log(2)/\log(3)

이며, 칸토어 함수는 다음과 같이 정의할 수 있다.

:

f(x)=H_D(C \cap (0,x)).

2. 1. 삼진법을 이용한 정의

칸토어 함수는 다음과 같이 3진법을 이용하여 정의할 수 있다.

:[0, 1] 구간의 실수 ''x''에 대하여,

# ''x''를 삼진 소수로 전개한다.

# 삼진수 전개에서 1이 나타나면, 첫 번째 1 이후의 모든 자릿수를 0으로 바꾼다.

# 남아있는 2를 모두 1로 바꾼다.

# 결과를 이진 소수로 해석하여 함숫값 ''c''(''x'')를 얻는다.

몇 가지 예시는 다음과 같다.

1/4는 삼진법으로 0.02020202...이다. 1이 없으므로 0.02020202... 그대로 2를 1로 바꾸면 0.01010101...이다. 이를 이진법으로 해석하면 1/3이므로, ''c''(1/4) = 1/3이다.
1/5는 삼진법으로 0.01210121...이다. 첫 번째 1 이후를 0으로 바꾸면 0.01000000...이다. 2가 없으므로 그대로 이진법으로 읽으면 1/4이다. 따라서 ''c''(1/5) = 1/4이다.
200/243은 삼진법으로 0.21102이다. 첫 번째 1 이후를 0으로 바꾸면 0.21이다. 2를 1로 바꾸면 0.11이다. 이진법으로 읽으면 3/4이므로, ''c''(200/243) = 3/4이다.
0은 삼진법으로 0.0000...이므로, 이진법으로도 0이다. 따라서 ''c''(0) = 0이다.
1은 삼진법으로 0.2222...이다. 2를 1로 바꾸면 0.1111...이며, 이진법으로 1이다. 따라서 ''c''(1) = 1이다.

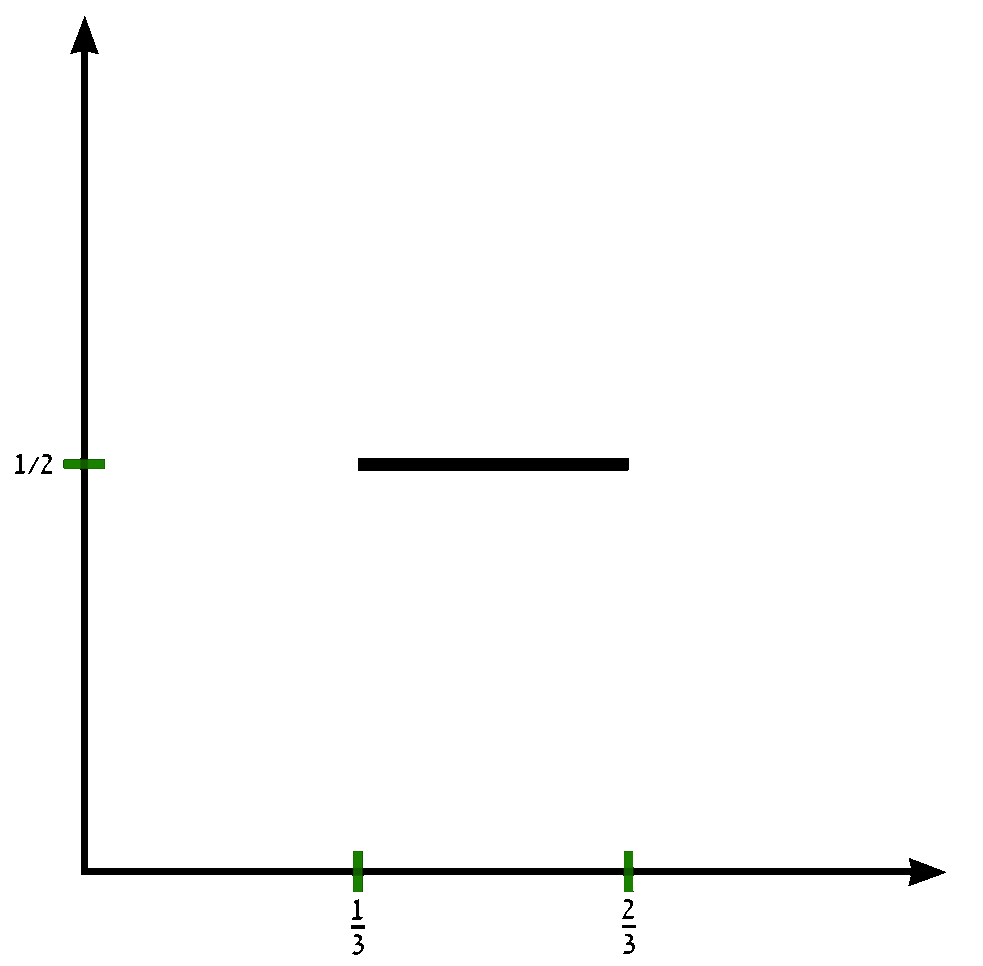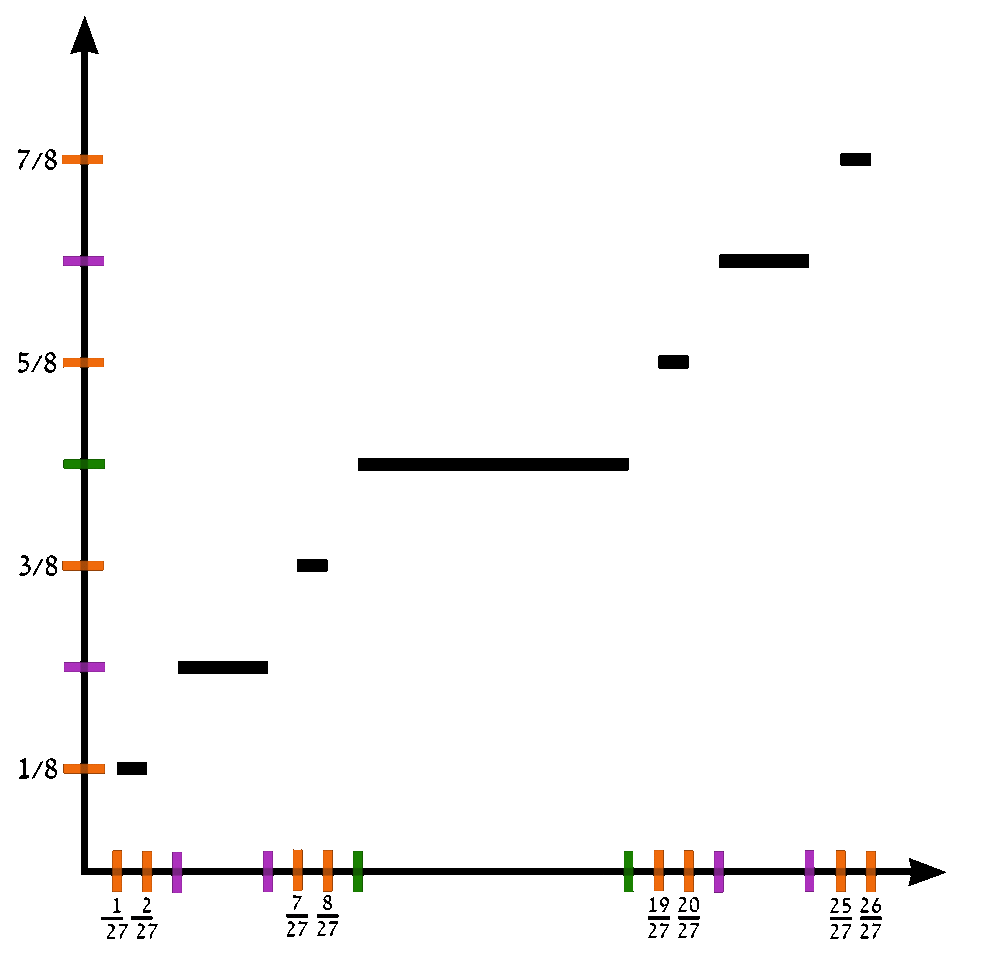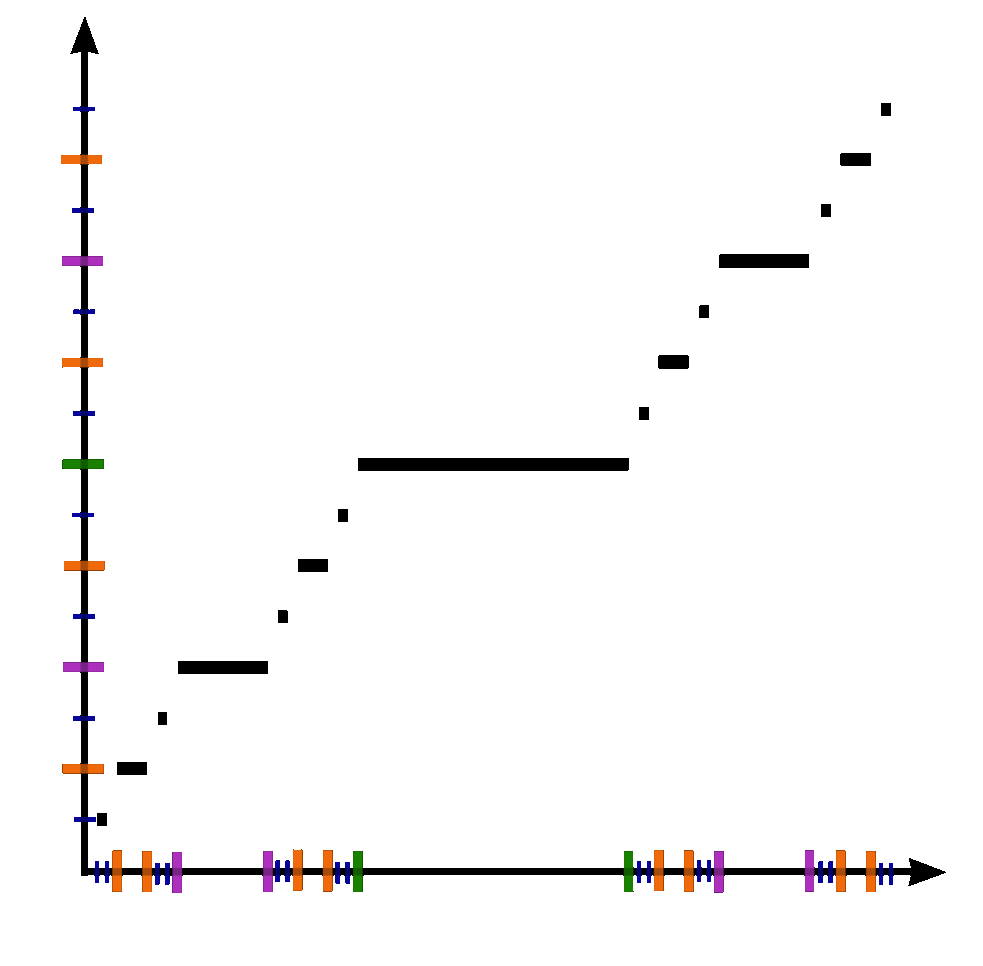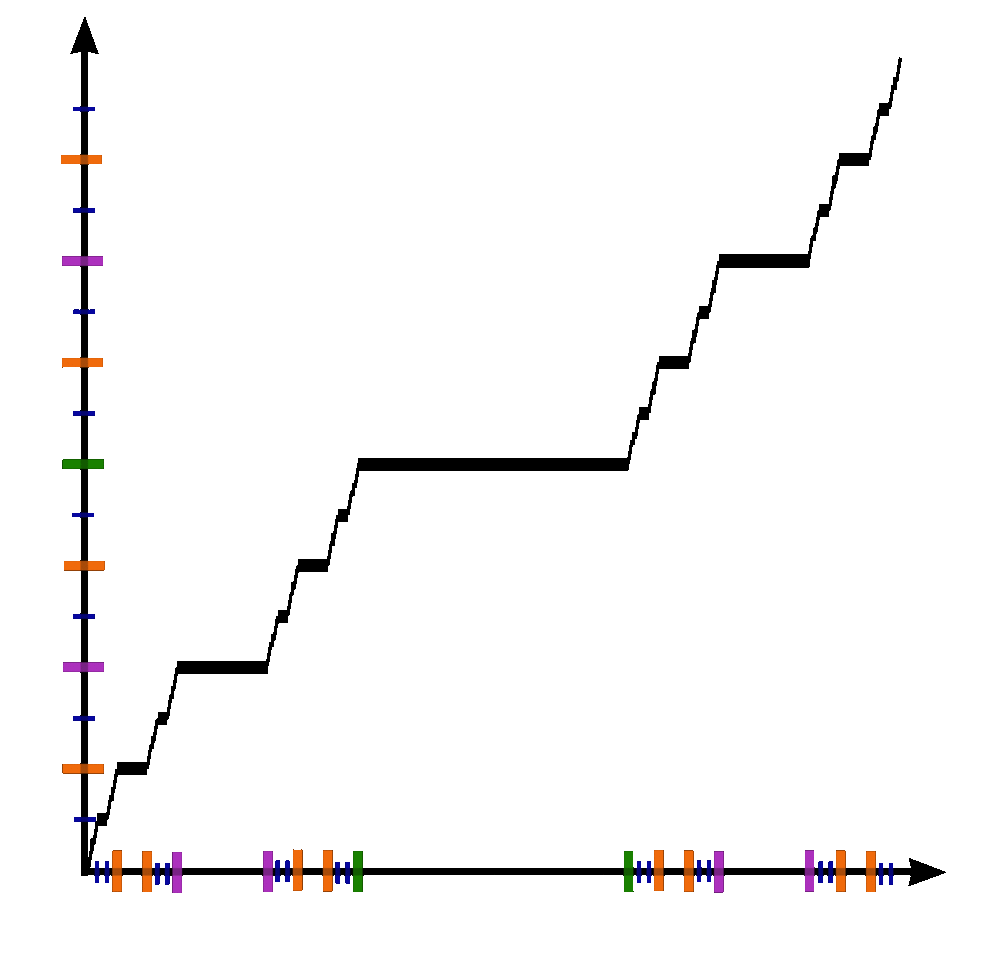
2. 2. 재귀적 정의

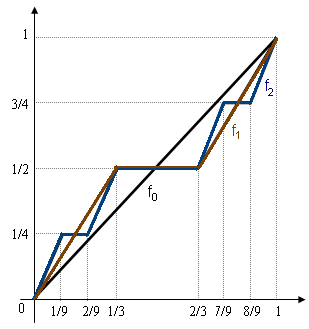
칸토어 함수는 다음과 같은 과정을 통해 재귀적으로 정의할 수 있다. 먼저 단위 구간 [0, 1]에서 시작하여, 함수 ''f''₀(''x'') = ''x'' 로 정의한다. 그 후, 각 구간을 3등분하여 가운데 구간의 함수값을 1/2로 고정하고, 양쪽 구간에서는 이전 단계 함수의 값을 조정하는 과정을 반복한다.

좀 더 자세히 설명하면, 임의의 정수 ''n'' ≥ 0 에 대해, 함수 ''f''_''n''+1(''x'')는 ''f''_''n''(''x'')를 이용하여 다음과 같이 정의된다.

:

f_{n+1}(x) =\begin{cases}\frac{1}{2} \times f_n(3x) &\mbox{if } 0 \le x < \frac{1}{3} \\\frac{1}{2} &\mbox{if } \frac{1}{3} \le x < \frac{2}{3} \\\frac{1}{2} + \frac{1}{2} \times f_n(3x - 2) &\mbox{if } \frac{2}{3} \le x \le 1\end{cases}

이러한 정의는 각 단계에서 양 끝점(1/3과 2/3)에서 서로 일치한다. 모든 ''n''에 대하여 ''f''_''n''(0) = 0 이고 ''f''_''n''(1) = 1이기 때문이다.

이 과정을 반복하면 함수열 {''f''_''n''}은 칸토어 함수 ''f''로 수렴하며, 이 수렴은 균등 수렴(uniform convergence)이다. 즉, 다음이 성립한다.

:

\max_{x \in [0, 1]} |f(x) - f_n(x)| \le 2^{-n+1} \, \max_{x \in [0, 1]} |f_1(x) - f_0(x)|.

초기 함수 ''f''₀(''x'')는 ''f''₀(0) = 0, ''f''₀(1) = 1 을 만족하는 유계 함수라면 어떤 함수를 사용해도 상관없다.

2. 3. 프랙탈 부피를 이용한 정의

칸토어 함수는 칸토어 집합의 부분집합의 ''D''-차원 부피 ''H''_''D''를 사용하여 정의할 수 있다. 여기서 D는 하우스도르프 측도이며, 칸토어 집합의 프랙탈 차원은

D = \log(2)/\log(3)

이다. 식으로 표현하면 다음과 같다.

:

f(x)=H_D(C \cap (0,x)).

3. 성질

칸토어 함수는 연속 함수와 측도에 관한 직관에 반하는 성질을 지닌다. 거의 어디서나 미분계수가 0이지만, x가 0에서 1로 변함에 따라 c(x) 역시 0에서 1로 증가하며 그 사이의 모든 값을 취한다. 칸토어 함수는 절대 연속이 아니면서 유계 변동을 가지는 함수의 예시이다.

칸토어 함수는 칸토어 분포의 누적 분포 함수로 볼 수 있다. 칸토어 분포는 이산적인 부분이 없어 대응하는 측도는 원자가 없다. 따라서 칸토어 함수는 도약 불연속점을 가지지 않는다.

칸토어 함수는 단조 비감소 함수이며, 그 그래프는 호의 길이가 2인 가측 곡선을 정의한다.^[8]

3. 1. 연속성

칸토어 함수는 모든 점에서 연속이다. 거의 어디서나 기울기가 0이지만(함수가 증가할 확률이 0%), x가 0에서 1로 감에 따라서 c(x)도 0에서 1로 가며, 그 사이의 모든 값들을 지난다. 칸토어 함수는 균등 연속 (정확히는 멱지수가 ''α'' = log 2/log 3인 횔더 연속)이지만 절대 연속은 아닌 함수의 예시로 가장 많이 인용되는 함수이다. 이 함수는 (0.''x''₁''x''₂''x''₃...''x''_n022222..., 0.''x''₁''x''₂''x''₃...''x''_n200000...)의 형태의 구간에서 상수함수이고, 칸토어 집합에 속하지 않는 모든 점은 이 구간에 속해있어서 칸토어 집합 외부에서는 기울기가 0이다. 반면에, 위에서 설명한 끝점을 포함하는 비가산 칸토어 집합의 부분집합은 미분계수가 존재하지 않는다.

칸토어 함수는 칸토어 분포라 불리는 이산적인 부분이 없는 분포의 누적 확률 분포 함수로 볼 수 있다. 즉, 대응하는 측도는 원자가 없다. 이것은 함수에서 비약 불연속점이 없는 이유이다(어떤 비약 불연속점은 측도의 원자로 대응한다).

3. 2. 미분 불가능성

칸토어 함수는 연속 함수이지만 절대 연속 함수가 아니며, 거의 어디서나 기울기가 0이다. 그러나 칸토어 집합의 비가산 부분집합에서는 미분계수가 존재하지 않는다.^[8] 칸토어 집합에 속하지 않는 모든 점은 (0.''x''₁''x''₂''x''₃...''x''_n022222..., 0.''x''₁''x''₂''x''₃...''x''_n200000...) 형태의 구간에 속해 있어서 이 구간에서는 상수함수이고 기울기가 0이다.

3. 3. 특이 함수

칸토어 함수는 특이 함수의 대표적인 예시이다.^[8] 칸토어 함수는 연속성과 측도에 관한 직관에 반하는 성질을 갖는다. 모든 곳에서 연속이고 거의 모든 곳에서 도함수가 0이지만,

x

가 0에서 1로 갈 때 0에서 1로 증가하며 그 사이의 모든 값을 갖는다. 칸토어 함수는 균등 연속이지만 절대 연속은 아닌 함수의 예시로 가장 많이 인용된다. 더 정확하게는 지수 ''α'' = log 2/log 3인 홀더 연속이다.

칸토어 함수는 (0.''x''₁''x''₂''x''₃...''x''_n022222..., 0.''x''₁''x''₂''x''₃...''x''_n200000...) 형태의 구간에서 상수함수이고, 칸토어 집합에 속하지 않는 모든 점은 이러한 구간에 속해있어서 칸토어 집합 외부에서는 기울기가 0이다. 반면에, 위에서 설명한 끝점을 포함하는 비가산 칸토어 집합의 부분집합은 미분계수가 존재하지 않는다.

칸토어 함수는 칸토어 분포라 불리는 확률 분포의 누적 분포 함수로 볼 수 있다. 이 분포는 이산적인 부분이 없어 대응하는 측도는 원자가 없다. 따라서 함수에서 비약 불연속점이 없다.

하지만, 칸토어 함수의 상수부분이 아닌 부분은 확률 밀도 함수의 적분으로 나타낼 수 없다. 어떤 구간에서 거의 어디서나 영이 아닌 어떤 추정 확률 밀도 함수를 적분하면 이 분포에서 확률이 0인 구간에 양의 확률을 주기 때문이다.

3. 4. 절대 연속성

칸토어 함수는 절대 연속이 아니다. 칸토어 함수는 균등 연속(정확히는 멱지수가 ''α'' = log 2/log 3인 횔더 연속이다)이지만 절대 연속은 아닌 함수의 예시로 가장 많이 인용되는 함수이다.^[8] 모든 절대 연속 함수는 유계 변동을 갖는 연속 함수이지만, 칸토어 함수는 유계 변동을 갖지만, 절대 연속은 아니다.

임의의 양수 ''ε'' < 1 및 ''δ''에 대해 칸토어 함수가 누적적으로 ''ε'' 이상 증가하는 총 길이 < ''δ''인 유한 개의 상호소 부분 구간이 존재한다. 사실, 모든 ''δ'' > 0에 대해

\sum\limits_{k=1}^M (y_k-x_k)<\delta

및

\sum\limits_{k=1}^M (c(y_k)-c(x_k))=1

을 만족하는 유한 개의 상호소 구간 (''x_k'',''y_k'') (1 ≤ ''k'' ≤ ''M'')이 존재한다.

3. 5. 증가함수

칸토어 함수는 단조증가 함수이며, 특히 그 그래프는 가측 곡선을 정의한다. 그래프의 호의 길이는 2이다.^[8]

f(0)=0

및

f(1)=1

인 모든 단조증가 함수의 그래프는 길이가 2보다 크지 않다는 점에 유의해야 한다. 이러한 의미에서, 칸토어 함수는 극단적인 예이다.

3. 6. 누적 분포 함수

칸토어 함수는 칸토어 분포의 누적 분포 함수이다. 칸토어 함수는 칸토어 집합을 지지집합으로 가지는 1/2-1/2 베르누이 측도 μ의 누적 확률 분포 함수로 볼 수 있다. 식으로 표현하면 다음과 같다.^[8]

:

c(x)=\mu([0,x])

.

칸토어 분포라 불리는 이 분포는 이산적인 부분이 없다. 즉, 대응하는 측도는 원자가 없다. 이것은 함수에서 비약 불연속점이 없는 이유이다(어떤 비약 불연속점은 측도의 원자로 대응한다).^[8]

하지만, 칸토어 함수의 상수부분이 아닌 부분은 확률 밀도 함수의 적분으로 나타낼 수 없다. 어떤 구간에서 거의 어디서나 영이 아닌 어떤 추정 확률 밀도 함수를 적분하면, 이 분포에서 확률이 0인 구간에 양의 확률을 주기 때문이다.^[8]

4. 자기 유사성

칸토어 함수는 여러 대칭성을 갖는다. 0과 1 사이의 값( $0\le x\le 1$ )에 대해 반사 대칭이 성립한다.

: $c(x)=1-c(1-x)$

또한, 왼쪽과 오른쪽에 각각 확대 및 축소 변환이 존재한다.

: $c\left(\frac{x}{3}\right) = \frac{c(x)}{2}$

: $c\left(\frac{x+2}{3}\right) = \frac{1+c(x)}{2}$

이러한 확대는 연속적으로 적용될 수 있으며, 이는 이진 모노이드를 생성한다. 이를 표현하기 위해 몇 가지 보조 함수를 정의한다. 먼저 반사를 다음과 같이 정의한다.

: $r(x)=1-x$

그러면 첫 번째 자기 대칭성은 다음과 같이 표현할 수 있다.

: $r\circ c = c\circ r$

여기서 $\circ$ 기호는 함수 합성을 나타낸다. 즉, $(r\circ c)(x)=r(c(x))=1-c(x)$ 이며, 다른 경우에도 마찬가지이다. 왼쪽 및 오른쪽 확대를 위해 왼쪽 매핑을 다음과 같이 정의한다.

: $L_D(x)= \frac{x}{2}$ 및 $L_C(x)= \frac{x}{3}$

그러면 칸토어 함수는 다음을 만족한다.

: $L_D \circ c = c \circ L_C$

마찬가지로, 오른쪽 매핑을 다음과 같이 정의한다.

: $R_D(x)= \frac{1+x}{2}$ 및 $R_C(x)= \frac{2+x}{3}$

그러면 다음이 성립한다.

: $R_D \circ c = c \circ R_C$

두 변환은 서로 미러링될 수 있는데, 그 관계는 다음과 같다.

: $L_D \circ r = r\circ R_D$

: $L_C \circ r = r\circ R_C$

이러한 연산은 임의로 쌓을 수 있다. 예를 들어 왼쪽-오른쪽 이동의 시퀀스 $LRLLR$ 을 생각해보자. 첨자 C와 D를 추가하고, 명확성을 위해 몇 부분을 제외하고 합성 연산자 $\circ$ 를 생략하면 다음과 같다.

: $L_D R_D L_D L_D R_D \circ c = c \circ L_C R_C L_C L_C R_C$

L과 R 문자의 임의의 유한 길이 문자열은 이진 유리수에 해당한다. 모든 이진 유리수는 정수 ''n''과 ''m''에 대해 $y=n/2^m$ 로 표현 가능하고, $b_k\in \{0,1\}.$ 인 비트의 유한 길이 $y=0.b_1b_2b_3\cdots b_m$ 로 나타낼 수 있다. 따라서 모든 이진 유리수는 칸토어 함수의 일부 자기 대칭에 일대일로 대응한다.

$g_0$ 및 $g_1$ 을 L 및 R로 표기하고 함수 합성을 통해 모노이드로 확장하면, $g_{010}=g_0g_1g_0$ 와 같이 쓸 수 있다. 일반적으로 ''A'', ''B''가 이진수 문자열일 때 $g_Ag_B=g_{AB}$ 로 쓸 수 있다. 이진 모노이드 ''M''은 모든 유한 길이의 왼쪽-오른쪽 이동으로 구성된 모노이드이다. $\gamma\in M$ 을 모노이드의 일반적인 요소로 쓰면, 칸토어 함수에 해당하는 자기 대칭은 다음과 같다.

: $\gamma_D\circ c= c\circ \gamma_C$

이진 모노이드 자체는 무한 이진 트리에서 왼쪽-오른쪽 이동의 유한한 수로 볼 수 있으며, 트리의 무한히 먼 "잎"은 칸토어 집합의 점에 해당한다. 따라서 모노이드는 칸토어 집합의 자기 대칭성을 나타낸다. 실제로 많은 프랙탈이 이진 모노이드로 설명 가능하다. 드 람 곡선에서 더 많은 예시를 찾을 수 있다. 자기 유사성을 갖는 다른 프랙탈은 다른 종류의 모노이드로 설명된다. 이진 모노이드 자체는 모듈러 군 $SL(2,\mathbb{Z}).$ 의 하위 모노이드이다.

칸토어 함수는 민코프스키 물음표 함수와 매우 유사하며, 수정된 형태이지만 정확히 동일한 대칭 관계를 갖는다.

5. 일반화

칸토어 함수는 다양한 방식으로 일반화될 수 있다.

0과 1 사이의 실수 ''y''의 이진 표현을

: $y=\sum_{k=1}^\infty b_k 2^{-k}$

라고 할 때, 다음 함수 ''C''_''z''(''y'')를 생각할 수 있다.

: $C_z(y)=\sum_{k=1}^\infty b_k z^{k}.$

헤르만 민코프스키의 민코프스키의 물음표 함수는 시각적으로 칸토어 함수와 유사하며, 칸토어 함수를 "매끄럽게 만든" 형태와 비슷하다. 칸토어 함수가 3진법 전개를 2진법 전개로 변환하여 구성되는 것처럼, 물음표 함수는 연분수 전개를 2진법 전개로 변환하여 구성된다. 물음표 함수는 모든 유리수에서 미분 계수가 0이라는 특징을 갖는다.

5. 1. 다른 밑을 사용한 일반화

실수 ''y'' (0 ≤ ''y'' ≤ 1)의 이진 표현은 다음과 같다.

:

y=\sum_{k=1}^\infty b_k 2^{-k}

여기서 ''b''_''k''는 0 또는 1의 값을 갖는 이진 자릿수이다. 이 때, 다음 함수 ''C''_''z''(''y'')를 생각할 수 있다.

:

C_z(y)=\sum_{k=1}^\infty b_k z^{k}.

''z'' = 1/3인 경우, 이 함수는 칸토어 함수의 역함수 ''x'' = 2''C''_1/3(''y'')를 정의한다. 즉, ''y'' = ''y''(''x'')는 칸토어 함수이다. 일반적으로 0 < ''z'' < 1/2 인 모든 ''z''에 대해, ''C''_''z''(''y'')의 그래프는 칸토어 함수를 옆으로 눕힌 형태와 유사하며, ''z'' 값이 0에 가까워질수록 그래프의 평탄한 부분(가운데 단계)이 넓어지는 특징을 보인다.

5. 2. 확률 측도를 이용한 일반화

칸토어 함수는 칸토어 집합에 대한 측도의 누적 분포 함수이다. 다른 칸토어 함수 또는 악마의 계단은 칸토어 집합이나 다른 프랙탈을 지지집합으로 가지는 다른 원자가 없는 확률 측도를 고려하여 얻을 수 있다.^[13] 칸토어 함수는 미분계수가 거의 어디서나 0이지만, 현재 연구는 우상극한과 좌하극한이 달라서 미분계수가 존재하지 않는 점들의 집합의 크기에 관한 문제에 집중하고 있다. 미분가능성의 해석은 보통 프랙탈 차원의 관점에서 주어지며, 보통 하우스도르프 차원을 가장 많이 선택한다. 이 연구는 1990년대에 칸토어 함수의 비미분가능성 집합의 하우스도르프 차원은 자신의 지지집합의 제곱

(\log2/\log3)^2

이라는 것을 밝힌 Darst에 의해서 시작되었다.^[13] 더 최근에는 케네스 팔코너는 이 제곱 관계는 모든 Ahlfor의 정규, 특이 측도에 적용된다는 것을 밝혔다:^[14]

:

\dim_{H}\left\{x : f'(x)=\lim_{h\to0^+}\frac{\mu([x,x+h])}{h}\text{ does not exist}\right\}=\left(\dim_{H}\mathrm{supp}(\mu)\right)^2

나중에, Troscheit은 자기 등각(self-conformal)이고 자기유사 집합에 의해 지지되는 더 일반적인 정상화 깁스 측도에 대해서 미분 계수가 존재하지 않는 집합의 더 포괄적인 그림을 얻었다.^[15]

6. 응용

칸토어 함수는 칸토어 집합과 밀접하게 관련되어 있다. 칸토어 집합 ''C''는 구간 [0, 1]에서 삼진법으로 표기했을 때, 1 뒤에 0만 나타나는 경우(1.000…은 0.222…로 바꿀 수 있다)를 제외하고 1이 나타나지 않는 숫자의 집합이다. 칸토어 집합은 비가산 무한 개의 점(0차원 크기)을 가지지만, 길이(1차원 크기)는 0인 프랙탈이다. D차원 크기 $H_D$ (하우스도르프 측도 관점에서)는 유일하게 유한한 값을 가지며, 이 $D = \log(2)/\log(3)$ 는 ''C''의 분수 차원이다. 칸토어 함수는 칸토어 집합 부분의 D차원 크기로 정의할 수 있다.

6. 1. 해석학

칸토어 함수는 연속성과 측도에 관한 직관에 반하는 함수이다. 이 함수는 어디서나 연속이고 거의 어디서나 기울기가 0이지만(즉 함수가 증가할 확률이 0%) x가 0에서 1로 감에 따라서 c(x)도 0에서 1로 가며, 그 사이의 모든 값들을 지난다. 칸토어 함수는 균등 연속(정확히는 멱지수가 ''α'' = log 2/log 3인 횔더 연속이다)이지만 절대 연속은 아닌 함수의 예시로 가장 많이 인용되는 함수이다. 이 함수는 (0.''x''₁''x''₂''x''₃...''x''_n022222..., 0.''x''₁''x''₂''x''₃...''x''_n200000...)의 형태의 구간에서 상수함수이고, 칸토어 집합에 속하지 않는 모든 점은 이 구간에 속해있어서 칸토어 집합의 외부에서는 기울기가 0이다. 반면에, 위에서 설명한 끝점을 포함하는 칸토어 집합의 비가산 부분집합은 미분계수가 존재하지 않는다.

칸토어 함수는 칸토어 집합을 지지집합으로 가지는 1/2-1/2 베르누이 측도 μ의 누적 확률 분포 함수로 볼 수 있다: c(x)=μ([0,x]). 칸토어 분포라 불리는 이 분포는 이산적인 부분이 없다. 즉, 대응하는 측도는 원자가 없다. 이것은 함수에서 비약 불연속점이 없는 이유이다(어떤 비약 불연속점은 측도의 원자로 대응한다).

6. 2. 동역학계

칸토어 집합 ''C''는 구간 [0, 1]에서 삼진법 표기 시 1 뒤에 0만 나타나는 경우(1.000…으로, 1을 제거하기 위해 0.222…로 바꿀 수 있다)를 제외하고 1이 나타나지 않는 숫자의 집합으로 정의할 수 있다. 칸토어 집합은 (비가산) 무한히 많은 점(0차원 크기)을 가지지만 길이(1차원 크기)는 0인 프랙탈이다. D차원 크기

H_D

(하우스도르프 측도 관점에서)만이 유일하게 유한한 값을 가지며, 이

D = \log(2)/\log(3)

는 ''C''의 분수 차원이다.

참조

_[1] 서적 Vestrup
_[2] 서적 Thomson Bruckner Bruckner
_[3] 웹사이트 Cantor Staircase Function http://mathworld.wol[...]
_[4] 서적 Bass
_[5] 간행물 The Hausdorff Dimension of the Nondifferentiability Set of the Cantor Function is [ ln(2)/ln(3) ]2 1993-09-01
_[6] 간행물 One-sided multifractal analysis and points of non-differentiability of devil's staircases 2004-01-01
_[7] 간행물 Hölder differentiability of self-conformal devil's staircases 2014-03-01
_[8] 웹사이트 real analysis - Arc length of the Cantor function - Mathematics Stack Exchange https://math.stackex[...]
_[9] 서적 Vestrup
_[10] 서적 Thomson Bruckner Bruckner
_[11] URL http://mathworld.wol[...]
_[12] 서적 Bass
_[13] 저널 The Hausdorff Dimension of the Nondifferentiability Set of the Cantor Function is [ ln(2)/ln(3) ]2 1993-09-01
_[14] 저널 One-sided multifractal analysis and points of non-differentiability of devil's staircases http://journals.camb[...] 2004-01-01
_[15] 저널 Hölder differentiability of self-conformal devil's staircases http://journals.camb[...] 2014-03-01

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com