전개형 게임
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
전개형 게임은 게임 이론의 한 분야로, 여러 플레이어가 순차적으로 행동하며 각 행동의 결과를 알 수 있는 게임을 의미한다. 게임 트리를 사용하여 게임의 진행 과정을 시각적으로 표현하며, 각 플레이어의 선택, 정보 집합, 보수 등을 포함한다. 전개형 게임은 완전 정보, 불완전 정보, 완전 기억, 불완전 기억 등 다양한 정보 유형과 기억 유형을 가질 수 있으며, 표준형 게임으로 변환하여 분석할 수도 있다.
더 읽어볼만한 페이지
- 게임 이론 - 대연정
대연정은 의원내각제 또는 이원집정부제 국가에서 대립하는 거대 정당들이 국가적 위기 극복, 정치적 봉쇄, 또는 비례대표제 하의 연립 내각 구성의 필요에 따라 연합하는 정부 형태로, 정치적 안정과 국민 통합에 기여할 수 있지만 유권자 선택권 제한 및 소수 정당 약진의 우려도 있다. - 게임 이론 - 완전 정보
완전 정보 게임은 게임 이론에서 모든 플레이어가 게임의 모든 정보를 공유하는 게임을 의미하며, 체스, 틱택토, 오목 등이 이에 해당한다. - 수학 - 회귀 분석
회귀 분석은 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하고 분석하는 통계적 기법으로, 최소 제곱법 개발 이후 골턴의 연구로 '회귀' 용어가 도입되어 다양한 분야에서 예측 및 인과 관계 분석에 활용된다. - 수학 - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다. - 경제학에 관한 - 노예제
노예제는 한 사람이 타인에게 소유되어 재산처럼 취급받으며 의지에 반해 노동을 강요당하고 보수 없이 사회적 이동이 제한되는 제도로, 고대부터 널리 존재했으나 18세기 이후 폐지 운동으로 대부분 국가에서 금지되었지만 현대에도 다양한 형태로 남아있다. - 경제학에 관한 - 민간 부문
민간 부문은 이윤 추구를 목표로 하는 경제 주체들로 이루어진 영역으로, 국가 경제 체제에 따라 비중과 역할이 다르며, 고용 창출의 원천이 되지만 여러 문제점을 야기하여 국가의 규제를 받는다.
2. 게임의 구성 요소
전개형 게임은 다음과 같은 요소들로 구성된다.[1][2]
- 게임 트리: 게임의 진행 상황을 나타내는 구조이다.
- 플레이어: 게임에 참가하는 주체이다. 합리적인 플레이어와 가상 플레이어(우연 또는 자연)가 있다.
- 차례(Move): 게임 트리에서 플레이어의 의지 또는 우연에 의해 선택이 이루어지는 지점이다.
- 정보 집합: 플레이어가 자신의 차례에 어떤 노드에 있는지 정확히 알 수 없는 경우, 그 노드들의 집합을 의미한다.
- 보수(Payoff): 게임의 결과에 따라 각 플레이어가 얻는 이득 또는 손실이다.
이러한 구성 요소들은 게임의 규칙과 진행 방식을 정의하며, 플레이어의 전략과 게임의 결과를 분석하는 데 사용된다.
2. 1. 게임 트리
게임 트리는 게임의 진행 과정을 시각적으로 표현하는 도구로, 뿌리 트리 구조를 갖는다. 게임 트리는 노드(node)와 가지(branch)로 구성된다.[1][2]- 노드(node): 게임의 각 단계를 나타내며, 다음과 같이 구분된다.
- 결정 노드(decision node): 플레이어가 선택을 하는 지점.
- 최종 노드(terminal node): 게임이 종료되는 지점으로, 각 플레이어의 보상(payoff)이 결정된다.
- 가지(branch): 플레이어의 선택 또는 우연에 의한 결과를 나타낸다.
게임 트리의 각 비터미널 노드는 ''n''+1개의 하위 집합으로 나뉘는데, 이는 ''n''명의 플레이어와 기회(또는 자연)라고 하는 가상의 플레이어를 위한 것이다. 각 플레이어의 노드 하위 집합을 "플레이어의 노드"라고 하며, 완전한 정보 게임은 기회 노드의 빈 집합을 갖는다. 기회 플레이어의 각 노드는 나가는 간선에 대한 확률 분포를 갖는다.[1][2]
합리적인 플레이어의 각 노드 집합은 정보 집합으로 분할되는데, 이는 플레이어가 이동할 때 특정 선택을 구별할 수 없도록 만든다. 동일한 정보 집합의 두 노드의 나가는 간선 간에는 일대일 대응이 있으며, 정보 집합의 모든 나가는 간선의 집합은 동치류로 분할된다. 각 클래스는 플레이어의 움직임에 대한 가능한 선택을 나타낸다.[1][2]
플레이는 루트에서 터미널 노드까지 트리를 통과하는 경로이다. 기회 노드에서는 확률 분포에 따라 가지가 선택되고, 합리적인 플레이어의 노드에서는 플레이어가 간선에 대한 동치류 중 하나를 선택한다. 플레이어는 어떤 간선이 따라가고 있는지 알지 못하지만, 외부 관찰자는 간선을 정확하게 결정할 수 있다.[1][2]
조합 게임 이론 및 인공 지능에서 정의된 게임 트리에서 완전 정보 두 플레이어 게임은 결과(예: 승리, 패배 또는 무승부)가 있는 전개형 게임으로 표현될 수 있다. 틱택토, 체스, 무한 체스 등이 그 예시이다.[1][2] 백개먼과 같은 게임은 불완전한 정보가 없지만 기회의 움직임이 있다. 포커는 기회의 움직임과 불완전한 정보를 모두 가지고 있다.

위 그림에서 초기 노드는 참가자 1에 속하며, 이는 참가자 1이 먼저 움직인다는 것을 나타낸다. 참가자 1은 ''U''와 ''D'' 중에서 선택하고, 참가자 2는 참가자 1의 선택을 관찰한 다음 ''U''와 ''D'' 중에서 선택한다. 보수는 (0,0), (2,1), (1,2), (3,1)과 같다. 만약 참가자 1이 ''D''를 플레이하면, 참가자 2는 ''U''를 플레이하여 참가자 1은 1을 받게 된다. 만약 참가자 1이 ''U''를 플레이하면, 참가자 2는 ''D''를 플레이하고 참가자 1은 2를 받게 된다. 참가자 1은 1보다 2를 선호하므로 ''U''를 플레이하고 참가자 2는 ''D''를 플레이하며, 이것이 부분 게임 완전 균형이다.

위 그림의 게임은 플레이어 2가 플레이어 1이 무엇을 하는지 알지 못한다는 점을 제외하면 이전 게임과 동일하다. 즉, 불완전 정보 게임이다.
2. 2. 플레이어
전개형 게임에서 플레이어는 게임에 참여하여 의사 결정을 내리는 주체를 의미한다. 플레이어는 합리적이거나 가상의 존재(우연 또는 자연)일 수 있다.[1]합리적인 플레이어는 자신의 이익을 최대화하기 위해 전략적으로 행동하는 플레이어를 말한다. 예를 들어, 한국 정치 상황에서 더불어민주당과 국민의힘은 각각 자신들의 정치적 목표를 달성하기 위해 노력하는 합리적인 플레이어로 볼 수 있다. 이들은 선거에서 승리하고, 정책을 추진하며, 지지층을 확대하기 위해 다양한 전략을 사용한다.[2]
가상의 플레이어는 실제 의사 결정 주체가 아니라 게임의 불확실성을 나타내기 위해 도입되는 플레이어이다. '우연' 또는 '자연'이라고도 불리는 이 플레이어는 특정 확률 분포에 따라 행동한다. 예를 들어, 남북 관계에서 '북한'이라는 플레이어의 행동은 예측하기 어려울 수 있다. 이때 '자연'이라는 가상의 플레이어를 도입하여 북한의 행동을 확률적으로 모델링할 수 있다.
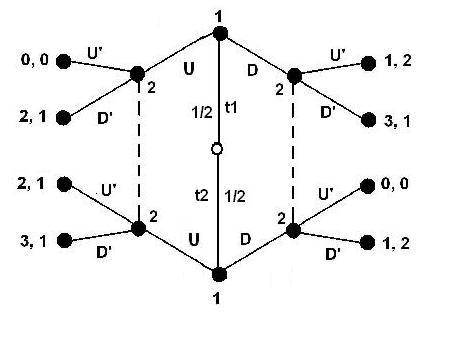
위 그림은 완전 정보(모든 플레이어와 보수가 모든 사람에게 알려짐)이지만 불완전 정보(고용주는 자연의 움직임이 무엇인지 모름)의 게임을 나타낸다. 초기 노드는 중앙에 있으며 채워져 있지 않으므로 자연이 먼저 움직인다. 자연은 동일한 확률로 플레이어 1의 유형(t1 또는 t2)을 선택하며, 이는 플레이되는 서브게임의 보수를 선택하는 것과 같다. 플레이어 1은 자신의 유형을 알고 있지만, 플레이어 2는 자연의 선택을 관찰하지 못하므로 플레이어 1의 유형을 모른다. 그러나 플레이어 2는 플레이어 1의 행동을 관찰할 수 있으므로 완전한 정보를 가지고 있다. 즉, 게임의 모든 단계에서 모든 플레이어는 다른 플레이어에 의해 무엇이 플레이되었는지 알고 있으며, 개인 정보의 경우 모든 플레이어는 자연에 의해 무엇이 플레이되었는지 알고 있다. 정보 집합은 파선으로 표시된다.[2]
2. 3. 차례 (Move)
게임 트리의 분기점은 정점 이외의 노드이며, '''차례'''(move)라고도 불린다. 각 차례에서는 한 명의 플레이어의 의지 또는 우연에 의해, 그 차례에서 나오는 선택지 중 하나가 선택되어 그 다음 차례로 전이된다. 우연에 의해 선택이 이루어지는 차례는 '''우연 차례'''(chance move)라고 한다.[2] 플레이어 갑의 의지로 선택이 이루어지는 차례를 갑의 차례라고 부른다.[2]2. 4. 정보 집합 (Information Set)
플레이어는 자신의 차례에 어떤 노드에 있는지 정확히 알 수 없다. 이때 이 노드들의 집합을 정보 집합이라고 한다. 정보 집합은 점선이나 루프로 표시되며, 불완전 정보 게임을 나타내는 핵심 요소이다.[1][2]정보 집합은 다음과 같은 결정 노드의 집합이다.
- 집합의 모든 노드는 하나의 플레이어에 속한다.
- 게임이 정보 집합에 도달하면, 움직이려는 플레이어는 정보 집합 내의 노드를 구별할 수 없다. 즉, 정보 집합에 두 개 이상의 노드가 포함된 경우, 해당 집합에 속한 플레이어는 집합 내의 어떤 노드에 도달했는지 알 수 없다.
확장형에서는 정보 집합이 해당 집합의 모든 노드를 연결하는 점선 또는 때로는 해당 집합의 모든 노드 주위에 그려진 루프로 표시된다.
게임이 둘 이상의 멤버를 가진 정보 집합을 갖는 경우, 해당 게임은 불완전 정보를 갖는다고 한다. 완전 정보를 가진 게임은 게임의 어떤 단계에서든, 모든 플레이어가 게임 초기에 무슨 일이 일어났는지 정확히 알고 있는 게임이다. 즉, 모든 정보 집합은 싱글톤 집합이다.[1][2] 완전 정보가 없는 모든 게임은 불완전 정보를 갖는다.
정보 분할이란 턴의 집합을 정보 집합으로 분할하는 것이다. 플레이어 A의 정보 집합이란 A의 턴으로 이루어진 집합이며, 하나의 정보 집합 안에 있는 턴에 있을 때, A는 그 정보 집합 안의 어떤 턴에 있는지 알 수 없다.
예를 들어, 많은 카드 게임에서는 각 플레이어는 자신의 패와 펼쳐진 패만 알 수 있으며, 다른 플레이어의 패와 남은 패는 알 수 없다. 즉, 자신이 플레이하려고 할 때, 현재 국면은 여러 국면 중 어느 하나일 뿐이다. 이때, 자신의 패와 펼쳐진 패는 알 수 있지만 다른 패의 상태는 알 수 없으므로, 현재 국면에는 알 수 없는 패의 조합 수만큼 가능성이 있다. 이러한 가능한 국면, 즉 턴의 모든 집합이 정보 집합이 된다. 체스 등 많은 보드 게임처럼 자신의 턴의 상태를 모두 알 수 있는 게임은 모든 정보 집합이 단 하나의 턴을 가지는 게임으로 정의할 수 있으며, 이러한 게임을 완전 정보 게임이라고 부른다. 마작, 7 포커, 대부호, 우노 등은 상대의 패가 보이지 않으므로 불완전 정보 게임이다.
2. 5. 보수 (Payoff)
Payoff영어는 게임의 결과에 따라 각 플레이어가 얻는 이득 또는 손실을 의미한다. ''n''-튜플의 형태로 표현되는데, 예를 들어 (2, 1)은 플레이어 1에게는 2, 플레이어 2에게는 1의 보상이 주어짐을 뜻한다.[1]정당의 경우 의석수, 지지율, 정책 실현 등이 보수가 될 수 있으며, 남북 관계에서는 경제 협력, 안보 강화 등이 보수가 될 수 있다.
오른쪽 그림의 게임에는 두 명의 참가자 1과 2가 있다. 비단말 노드의 숫자는 해당 결정 노드가 어떤 참가자에 속하는지 나타낸다. 단말 노드의 숫자는 참가자에게 주어지는 보수를 나타낸다. (예: 2,1은 참가자 1에게 보수 2, 참가자 2에게 보수 1을 나타낸다). 그래프 각 변의 레이블은 해당 변이 나타내는 행동의 이름이다.
게임의 진행은 다음과 같다. 참가자 1은 ''U''와 ''D'' 중에서 선택하고, 참가자 2는 참가자 1의 선택을 관찰한 다음 ''U''와 ''D'' 중에서 선택한다. 보수는 (U,U')는 (0,0), (U,D')는 (2,1), (D,U')는 (1,2), (D,D')는 (3,1)이다.
만약 참가자 1이 ''D''를 플레이하면, 참가자 2는 자신의 보수를 극대화하기 위해 ''U''를 플레이하고, 참가자 1은 1만 받게 된다. 하지만, 만약 참가자 1이 ''U''를 플레이한다면, 참가자 2는 ''D''를 플레이하여 자신의 보수를 극대화하고, 참가자 1은 2를 받게 된다. 참가자 1은 1보다 2를 선호하므로 ''U''를 플레이하고 참가자 2는 ''D''를 플레이한다. 이것이 부분 게임 완전 균형이다.
조합 게임 이론 및 인공 지능에서 정의된 게임 트리에서 완전 정보 두 플레이어 게임은 결과(예: 승리, 패배 또는 무승부)가 있는 전개형 게임으로 표현될 수 있다. 이러한 게임의 예로는 틱택토, 체스, 무한 체스가 있다.[2]
3. 정보의 종류
전개형 게임은 정보의 완전성 여부에 따라 다음과 같이 분류할 수 있다.
- '''완전 정보 게임 (Game with Perfect Information)''' : 모든 플레이어가 게임의 모든 단계에서 게임 초기에 무슨 일이 일어났는지 정확히 알고 있는 게임이다. 모든 정보 집합은 홑원소 집합으로 구성된다.
- '''불완전 정보 게임 (Game with Imperfect Information)''' : 플레이어가 게임의 일부 정보를 모르는 경우이다. 정보 집합이 둘 이상의 노드를 포함할 수 있다.
- '''완비 정보 게임 (Game with Complete Information)''' : 모든 플레이어가 게임의 규칙(게임 트리)을 알고 있는 게임이다.
- '''불완비 정보 게임 (Game with Incomplete Information)''' : 플레이어가 게임의 규칙, 보수, 또는 상대방의 유형(type)을 정확히 모르는 경우이다.
3. 1. 완전 정보 게임 (Game with Perfect Information)
Perfect information영어 게임은 게임의 어떤 단계에서든 모든 플레이어가 게임 초기에 무슨 일이 일어났는지 정확히 알고 있는 게임이다.[1][2] 즉, 모든 정보 집합은 홑원소 집합이다. 완전 정보가 없는 모든 게임은 불완전 정보를 갖는다.조합 게임 이론 및 인공 지능에서 정의된 게임 트리에서 완전 정보 두 플레이어 게임은 결과(예: 승리, 패배 또는 무승부)가 있는 전개형 게임으로 표현될 수 있다. 이러한 게임의 예로는 틱택토, 체스, 무한 체스가 있다.[1][2]
체스 등 많은 보드 게임처럼 자신의 차례의 상태를 모두 알 수 있는 게임은 모든 정보 집합이 단 하나의 차례를 가지는 게임으로 정의할 수 있으며, 이러한 게임을 '''완전 정보 게임'''이라고 부른다.
3. 2. 불완전 정보 게임 (Game with Imperfect Information)
불완전 정보 게임은 플레이어가 게임의 일부 정보를 모르는 경우를 의미한다. 즉, 정보 집합이 둘 이상의 노드를 포함할 수 있다. 포커와 같은 카드 게임이 불완전 정보 게임의 예시이다.
예를 들어, 남북 협상 과정에서 상대방의 의도를 정확히 파악하기 어려운 경우가 불완전 정보 게임에 해당한다.
마작, 7 포커, 대부호, 우노 등 상대의 패가 보이지 않는 게임들은 불완전 정보 게임에 해당한다. 가위바위보와 같이 각 플레이어가 동시에 행동을 결정하는 동시 턴 게임은, 각 플레이어가 순서대로 행동을 결정하지만 모든 플레이어가 행동을 결정하기 전까지는 다른 플레이어의 행동이 공개되지 않는 불완전 정보 게임과 동일하다.
3. 3. 완비 정보 게임 (Game with Complete Information)
완비 정보 게임(Game with complete information)은 모든 플레이어가 게임의 규칙(게임 트리)을 알고 있는 게임을 의미한다. 현실의 전쟁이나 경제 행위는 대부분 완비 정보 게임이 아니며, 불완비 정보 게임(Game with incomplete information)이다.[1][2] 하지만 불완비 정보 게임은 정보가 불명확한 부분을 우연 차례로 대체하여 완비 정보 게임으로 표현할 수 있다.
예를 들어, 포커는 카드가 배포되는 기회의 움직임과 다른 플레이어가 비밀리에 보유한 카드라는 불완전 정보를 모두 가지고 있어 불완비 정보 게임이다.
3. 4. 불완비 정보 게임 (Game with Incomplete Information)
하사니에 따르면, 플레이어가 게임의 규칙, 보수, 또는 상대방의 유형(type)을 정확히 모르는 경우를 불완전 정보 게임이라고 한다. 이러한 불완전 정보 게임은 하사니 변환을 통해 완전하지만 불완비한 정보를 가진 게임으로 변환될 수 있다.[1]예를 들어, 고용주가 구직자를 고용할지 여부를 고려하는 게임을 생각해 볼 수 있다. 구직자의 능력은 높거나 낮을 수 있으며, 이는 무작위로 결정된다. 이 경우, 자연을 일종의 플레이어로 모델링하여 지원자의 능력을 선택하게 할 수 있다. 자연은 보수를 가지지 않으며, 게임 트리에서 채워지지 않은 노드로 표현된다. 자연 선택 노드에서 나오는 간선은 발생할 사건의 확률로 표시된다.[2]
위 그림에서 자연은 플레이어 1의 유형을 선택하고, 플레이어 1은 자신의 유형을 알지만, 플레이어 2는 자연의 선택을 관찰하지 못한다. 그러나 플레이어 2는 플레이어 1의 행동을 관찰할 수 있으므로, 완전 정보 게임이다. 이처럼 개인 정보의 경우, 모든 플레이어는 자연에 의해 무엇이 플레이되었는지 알 수 있다. 정보 집합은 파선으로 표시된다.[2]
이 게임에서 유일한 완전 베이즈 균형은 유형 1이 'D'를 플레이하고, 유형 2가 'U'를 플레이하며, 플레이어 2가 'D'를 관찰하면 'U'를 플레이하고, 'U'를 관찰하면 무작위로 플레이하는 것이다. 이를 통해 플레이어 1은 자신의 행동을 통해 자신의 유형을 플레이어 2에게 신호하게 된다.[2]
4. 완전성과 기억
게임의 완전성은 정보와 관련된 중요한 개념이다. 일부 교과서에서는 전개형 게임을 보상만 있는 게임 트리로 정의하고, 다른 요소들은 나중에 추가하기도 한다. 그러나 이 문서는 1953년 해럴드 W. 쿤이 소개한 일반적인 정의를 따르며, 이는 1928년 존 폰 노이만의 초기 정의를 확장한 것이다.
''n''명의 플레이어를 가진 전개형 게임은 다음과 같이 구성된다.
- 유한한 ''n''개의 플레이어 집합
- 게임 트리
- 게임 트리의 각 터미널(잎) 노드는 ''보상''의 ''n''-튜플을 가짐
- 게임 트리의 비터미널 노드는 ''n''+1개의 하위 집합으로 분할됨 (각 플레이어에 하나씩, 그리고 기회(또는 자연) 플레이어를 위한 특별한 하위 집합)
- 기회 플레이어의 각 노드는 나가는 간선에 대한 확률 분포를 가짐
- 합리적인 플레이어의 각 노드 집합은 정보 집합으로 분할됨
- 동일한 정보 집합의 두 노드의 나가는 간선 간에는 일대일 대응이 있음
- 트리에서 루트에서 터미널 노드까지의 모든 경로는 각 정보 집합을 최대 한 번만 통과
- 게임의 완전한 설명은 플레이어 간의 공통 지식
플레이어의 순수 전략은 모든 정보 집합(그의)에 대해 정확히 하나의 나가는 간선 클래스를 선택하는 선택으로 구성된다. 완전한 정보 게임에서 정보 집합은 단일 집합이다. 기회 노드가 있는 게임에서 보상은 각 플레이어가 모든 게임 결과에 대해 정의된 폰 노이만-모겐슈테른 효용 함수를 갖는다고 가정하고, 모든 합리적인 플레이어가 사전 무작위 결과를 기대 효용으로 평가한다.
조합 게임 이론 및 인공 지능에서 정의된 게임 트리에서 완전 정보 두 플레이어 게임은 결과(예: 승리, 패배 또는 무승부)가 있는 전개형 게임으로 표현될 수 있다. 이러한 게임의 예로는 틱택토, 체스, 무한 체스가 있다.[1][2] 백개먼과 같은 미니맥스 트리를 이용한 게임은 불완전한 정보가 없지만(모든 정보 집합은 단일 집합), 기회의 움직임이 있다. 예를 들어, 포커는 기회의 움직임(카드가 배포됨)과 불완전한 정보(다른 플레이어가 비밀리에 보유한 카드)를 모두 가지고 있다.
완전한 확장형 표현은 다음을 명시한다.
- 게임의 참가자
- 모든 참가자에 대해 그들이 움직일 수 있는 모든 기회
- 각 참가자가 각 움직임에서 할 수 있는 것
- 각 참가자가 모든 움직임에 대해 아는 것
- 모든 가능한 움직임 조합에 대해 각 참가자가 받는 보수
위 그림의 게임에는 두 명의 참가자, 1과 2가 있다. 비단말 노드의 숫자는 해당 결정 노드가 어떤 참가자에 속하는지 나타내고, 단말 노드의 숫자는 참가자에게 주어지는 보수를 나타낸다. 그래프의 각 변의 레이블은 해당 변이 나타내는 행동의 이름이다.
만약 참가자 1이 ''D''를 플레이한다면, 참가자 2는 자신의 보수를 극대화하기 위해 ''U''를 플레이할 것이고, 따라서 참가자 1은 1만 받게 된다. 하지만, 만약 참가자 1이 ''U''를 플레이한다면, 참가자 2는 ''D''를 플레이하여 자신의 보수를 극대화하고 참가자 1은 2를 받게 된다. 참가자 1은 1보다 2를 선호하므로 ''U''를 플레이하고 참가자 2는 ''D''를 플레이할 것이다. 이것이 부분 게임 완전 균형이다.
'''정보 집합'''은 다음과 같은 결정 노드의 집합이다.
- 집합의 모든 노드는 하나의 플레이어에 속한다.
- 게임이 정보 집합에 도달하면, 움직이려는 플레이어는 정보 집합 내의 노드를 구별할 수 없다.
확장형에서는 정보 집합이 해당 집합의 모든 노드를 연결하는 점선 또는 때로는 해당 집합의 모든 노드 주위에 그려진 루프로 표시된다.
게임이 둘 이상의 멤버를 가진 정보 집합을 갖는 경우, 해당 게임은 '''불완전 정보'''를 갖는다고 한다. '''완전 정보'''를 가진 게임은 게임의 어떤 단계에서든, 모든 플레이어가 게임 초기에 무슨 일이 일어났는지 정확히 알고 있는 게임이다. 즉, 모든 정보 집합은 싱글톤 집합이다.[1][2] 완전 정보가 없는 모든 게임은 불완전 정보를 갖는다.
위 그림의 게임은 첫번째 게임과 동일하지만, 플레이어 2는 플레이어 1이 무엇을 하는지 알지 못한다.
두 번째 게임에서는 플레이어 1이 ''D''를 플레이하고 플레이어 2가 ''U''를 플레이하며, 플레이어 2는 플레이어 1이 반드시 ''D''를 플레이할 것이라는 믿음을 갖는 완전 베이즈 균형이 존재한다.
이 게임을 '''내시 균형'''[3]을 더 쉽게 풀기 위해, '''정규형'''으로 변환할 수 있다.[4] 이는 '''동시/순차''' 게임이므로, 플레이어 1과 플레이어 2는 각각 두 개의 '''전략'''을 갖는다.[5]
각 움직임 조합에 대한 고유한 보상이 있는 2x2 행렬을 갖게 된다. 정규형 게임을 사용하여 게임을 풀고 두 플레이어 모두에게 지배 전략을 식별할 수 있다.
- 플레이어 1이 Up (U)을 플레이하면, 플레이어 2는 Down (D')을 플레이하는 것을 선호한다 (보상 1>0).
- 플레이어 1이 Down (D)을 플레이하면, 플레이어 2는 Up (U')을 플레이하는 것을 선호한다 (보상 2>1).
- 플레이어 2가 Up (U')을 플레이하면, 플레이어 1은 Down (D)을 플레이하는 것을 선호합니다 (보상 1>0).
- 플레이어 2가 Down (D')을 플레이하면, 플레이어 1은 Down (D)을 플레이하는 것을 선호합니다 (3>2).
이러한 선호도는 행렬 내에 표시될 수 있으며, 두 플레이어 모두 선호도가 있는 상자는 내시 균형을 제공한다. 이 특정 게임은 (D,U')의 단일 해를 가지며 (1,2)의 보상을 갖는다.
플레이어가 게임의 정확한 보수가 무엇인지 또는 상대방의 '''유형'''이 무엇인지 정확히 모를 수도 있다. 이러한 종류의 게임은 '''불완전 정보'''를 가지고 있다. 확장형에서는 소위 '''하사니 변환'''을 사용하여 완전하지만 불완전한 정보를 가진 게임으로 표현된다. 이 변환은 게임에 ''자연의 선택'' 또는 ''신의 선택''이라는 개념을 도입한다.
왼쪽 그림의 게임은 완전 정보(모든 플레이어와 보수가 모든 사람에게 알려짐)이지만 불완전 정보(고용주는 자연의 움직임이 무엇인지 모름)의 게임이다.
4. 1. 완전 기억 게임 (Game with Perfect Recall)
Game with perfect recall영어은 한국어로 완전 기억 게임이라고 번역되며, 모든 플레이어가 자신의 과거 선택지를 모두 기억하는 게임을 의미한다.[1] [2] 완전 정보 게임은 항상 완전 기억 게임이다.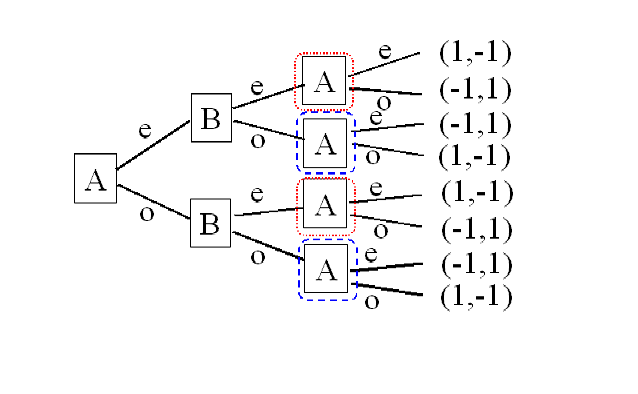
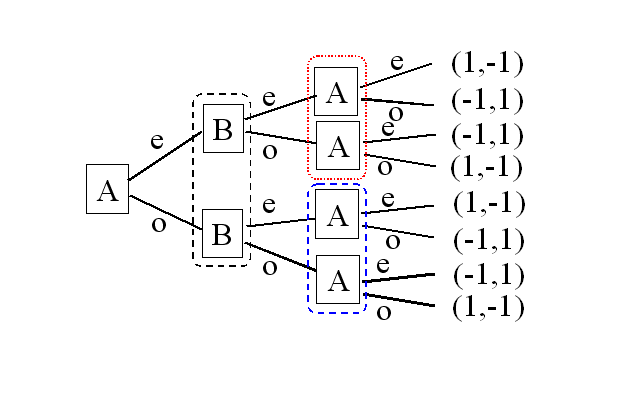
4. 2. 불완전 기억 게임 (Game with Imperfect Recall)
모든 플레이어가 자신의 과거 선택지를 모두 기억하는 게임을 완전 기억 게임이라고 부른다. 완전 정보 게임은 완전 기억 게임이다. 완전 기억이며 불완전 정보인 게임 트리의 예는 그림 3과 같다. 불완전 기억 게임 트리의 예는 그림 4와 같다. 그림 4의 플레이어 A처럼 한 수 전의 기억을 상실하는 플레이어는 상상하기 어렵지만, 예를 들어 플레이어 A를 2명의 팀으로 생각하고, 턴과 턴 사이에는 다른 팀원이 지시하며 팀원끼리는 정보 교환이 불가능하다고 하면, 현실적인 한 예가 된다.5. 한국 정치에서의 응용
전개형 게임은 한국 정치의 다양한 상황을 분석하는 데 유용하게 활용될 수 있다.
6. 전개형 게임과 표준형 게임
일부 입문 교과서에서는 전개형 게임을 게임 트리에 보상만 있는 것으로 정의하고(불완전하거나 불완전한 정보 없음), 다른 요소들을 세분화하여 다음 장에서 추가하기도 한다. 그러나 이 문서는 1953년 해럴드 W. 쿤이 소개하고 1928년 폰 노이만의 초기 정의를 확장한 일반적인 정의를 따른다. ''n''명의 플레이어를 가진 전개형 게임은 다음과 같이 구성된다.
- 유한한 ''n''개의 (합리적인) 플레이어 집합
- 게임 트리
- 게임 트리의 각 터미널(잎) 노드는 모든 가능한 플레이의 끝에서 각 플레이어에 대한 보상을 나타내는 ''보상''의 ''n''-튜플을 갖는다.
- 게임 트리의 비터미널 노드는 ''n''+1개의 하위 집합으로 분할된다. 각 (합리적인) 플레이어에 대해 하나씩, 그리고 기회(또는 자연)라고 하는 가상의 플레이어를 위한 특별한 하위 집합이 있다. 각 플레이어의 노드 하위 집합을 "플레이어의 노드"라고 한다. (완전한 정보 게임은 기회 노드의 빈 집합을 갖는다.)
- 기회 플레이어의 각 노드는 나가는 간선에 대한 확률 분포를 갖는다.
- 합리적인 플레이어의 각 노드 집합은 정보 집합으로 더 분할되는데, 이는 플레이어가 이동할 때 특정 선택을 구별할 수 없도록 만든다.
- * 동일한 정보 집합의 두 노드의 나가는 간선 간에는 일대일 대응이 있으며, 따라서 정보 집합의 모든 나가는 간선의 집합은 동치류로 분할되며, 각 클래스는 플레이어의 움직임에 대한 가능한 선택을 나타낸다.
- * 트리에서 루트에서 터미널 노드까지의 모든 (유향) 경로는 각 정보 집합을 최대 한 번만 통과할 수 있다.
- 위 매개변수로 지정된 게임의 완전한 설명은 플레이어 간의 공통 지식이다.
플레이는 루트에서 터미널 노드까지 트리를 통과하는 경로이다. 기회에 속하는 임의의 주어진 비터미널 노드에서, 나가는 분기는 확률 분포에 따라 선택된다. 합리적인 플레이어의 노드에서, 플레이어는 간선에 대한 동치류 중 하나를 선택해야 하며, 이는 정확히 하나의 나가는 간선을 결정하지만, (일반적으로) 플레이어는 어떤 간선이 따라가고 있는지 알지 못한다. 따라서 플레이어의 순수 전략은 모든 정보 집합(그의)에 대해 정확히 하나의 나가는 간선 클래스를 선택하는 선택으로 구성된다. 완전한 정보 게임에서 정보 집합은 단일 집합이다. 기회 노드가 있는 게임에서 보상이 어떻게 해석되어야 하는지는 덜 분명하다. 각 플레이어가 모든 게임 결과에 대해 정의된 폰 노이만-모겐슈테른 효용 함수를 갖는다고 가정한다. 이 가정은 모든 합리적인 플레이어가 사전 무작위 결과를 기대 효용으로 평가할 것임을 의미한다.
조합 게임 이론 및 인공 지능에서 정의된 게임 트리에서 완전 정보 두 플레이어 게임은 결과(예: 승리, 패배 또는 무승부)가 있는 전개형 게임으로 표현될 수 있다. 이러한 게임의 예로는 틱택토, 체스, 무한 체스가 있다.[1][2] 백개먼과 같은 미니맥스 트리를 이용한 게임은 불완전한 정보가 없지만(모든 정보 집합은 단일 집합), 기회의 움직임이 있다. 예를 들어, 포커는 기회의 움직임(카드가 배포됨)과 불완전한 정보(다른 플레이어가 비밀리에 보유한 카드)를 모두 가지고 있다.
게임의 나무는 점으로 표시되는 노드와 두 점을 잇는 유향 선분인 가지로 이루어진다. 노드는 상태라고도 불리며 게임의 한 국면을 나타낸다. 가지는 한 명의 플레이어의 의지 또는 우연에 의한 선택으로, 어떤 노드에서 다른 노드로 전이될 수 있음을 나타내는 것으로 선택지라고도 불린다. 노드는 분기점과 정점으로 나뉜다. 정점은 거기에서 가지가 나오지 않는 노드, 즉 게임이 종료된 국면을 나타내는 점이며, 각 플레이어의 '''이득'''이 주어진다. 이득은 '''이득 함수'''라고도 불리며, 플레이어의 수만큼의 성분 수를 갖는 벡터량으로 나타낼 수 있다. 분기점은 정점 이외의 노드이며, '''차례'''라고도 불린다. 각 차례에서는 한 명의 플레이어의 의지 또는 우연에 의해, 그 차례에서 나오는 선택지 중 하나가 선택되어 그 다음 차례로 전이된다. 우연에 의해 선택이 이루어지는 차례를 '''우연 차례'''라고 부른다. 또한 플레이어 갑의 의지로 선택이 이루어지는 차례를 갑의 차례라고 부른다. '''플레이어 분할'''이란 차례의 집합을 각 플레이어의 차례로 분할한 것이다. '''우연 차례의 확률 분포족'''이란 우연 차례에서의 확률 분포를 정한 것이다. 거기에 전이하는 선택지가 하나도 없는 분기점을 밑점이라고 부르며, 이는 게임의 초기 상태, 즉 출발 국면이다.
표준형 게임은 전략형 게임이라고도 불리며, 각 플레이어의 선택 조합에 해당하는 이득으로 표현된다.
6. 1. 표준형 게임 (Normal-form game)
표준형 게임은 전략형 게임(strategic-form game)이라고도 불리며, 각 플레이어의 선택 조합에 따른 보수를 나타낸다. 예를 들어 "짝수-홀수 게임"에서 각 플레이어의 선택은 짝수 또는 홀수 두 가지이며, 4가지 조합의 보수를 표준형으로 표현할 수 있다. 이때, 한쪽 플레이어가 먼저 선택을 하고 다른 플레이어는 무엇을 선택했는지 알지 못한 채 자신의 선택을 한다고 가정하면 전개형 표현이 된다. 후발 주자의 턴에서 정보 집합은 두 개의 분기점을 포함하며, 이 게임은 불완전 정보 게임임을 알 수 있다.[1]표준형 게임에서 각 플레이어의 선택을 순수 전략이라고 부른다. 단순히 전략이라고 하면, 각 순수 전략에 그것을 선택하는 확률을 부여한 것을 의미한다. "짝수-홀수 게임"의 예시에서는 짝수를 60% 확률로, 홀수를 40% 확률로 내는 것이 하나의 전략이다. 게임 이론의 초기 주요 과제는 표준형 게임에서의 전략과 평균적 보수의 관계를 분석하는 것이었고, 보수표가 알려져 있다는 것을 전제로 하였다.[1]
가위바위보와 같이 각 플레이어가 동시에 행동을 결정하는 게임을 동시 턴 게임이라고 부르는데, 이는 각 플레이어가 순서대로 행동을 결정하지만 모든 플레이어가 행동을 결정하기 전까지는 다른 플레이어의 행동이 공개되지 않는 불완전 정보 게임과 동일하다. "홀짝 게임" 또한 동시 턴 게임의 예시이다.[1]
6. 2. 전개형 게임과 표준형 게임의 관계
전개형 게임은 게임 트리를 통해 게임의 순서를 명확하게 나타내는 반면, 표준형 게임(전략형 게임)은 각 플레이어의 선택 조합에 따른 이득으로 표현된다. 예를 들어, 홀짝 게임에서 각 플레이어는 짝수 또는 홀수를 선택하며, 그 결과에 따른 이득은 다음과 같이 표준형으로 나타낼 수 있다.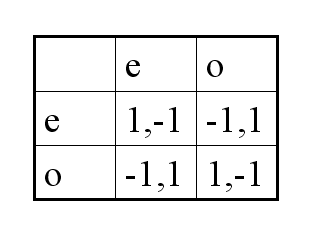
만약 한 플레이어가 먼저 선택하고, 다른 플레이어는 그 선택을 모른 채 선택한다면, 이는 전개형 게임으로 표현될 수 있다. 이때, 후수 플레이어의 정보 집합은 두 개의 분기점을 포함하므로, 이 게임은 불완전 정보 게임이 된다.
표준형 게임에서 각 플레이어의 선택은 순수 전략이라고 불린다. 각 순수 전략에 선택 확률을 부여한 것을 단순히 전략이라고 한다. 예를 들어, 홀짝 게임에서 짝수를 60%, 홀수를 40% 확률로 내는 것이 전략의 한 예시이다. 게임 이론의 초기 주요 과제는 표준형 게임에서 전략과 평균 이득 간의 관계를 분석하는 것이었으며, 이득표가 이미 알려져 있다는 전제하에 진행되었다.
참조
[1]
기타
Infinite Games, Yurii Khomskii (2010)
https://www.math.uni[...]
[2]
Youtube
Infinite Chess, PBS Infinite Series
https://www.youtube.[...]
[3]
서적
Strategy : an introduction to game theory
2013-05-09
[4]
서적
Strategy : an introduction to game theory
2013-05-09
[5]
서적
Strategy : an introduction to game theory
2013-05-09
[6]
서적
岩波数学辞典-第3版
岩波書店
1985-12
[7]
서적
ゲーム理論
有斐閣
1997-01
[8]
서적
入門ゲーム理論―戦略的思考の科学
日本評論社
2003-03
[9]
서적
ゲーム理論入門
日本経済新聞社
2001-01
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
