4절 링크

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 평면 4절 링크
3. 구면 및 공간 4절 링크
- 3.1. 구면 4절 링크
- 3.2. 공간 4절 링크
4. 4절 링크의 설계
- 4.1. 시간비 (Time Ratio)
- 4.2. 타이밍 차트 (Timing Chart)
5. 슬라이더-크랭크 링크
6. 4절 링크의 응용
참조

1. 개요

4절 링크는 4개의 링크가 1자유도 관절로 연결된 가장 기본적인 형태의 기구이다. 평면 4절 링크는 모든 링크가 평면상에서 움직이며, 회전 관절(R) 또는 프리스매틱 관절(P)을 사용하여 구성된다. 4절 링크는 네 개의 회전 관절(RRRR), 세 개의 회전 관절과 하나의 프리스매틱 관절(RRRP, PRRR, RPRR, RRPR), 두 개의 회전 관절과 두 개의 프리스매틱 관절(PRRP)의 세 가지 기본 유형으로 분류된다. 4절 링크는 다양한 움직임을 안내하도록 설계할 수 있으며, 기계 공학에서 운동학 및 역학 연구의 중요한 대상이다. 4절 링크의 운동 특성은 그라쇼프 조건에 따라 결정되며, 링크 길이와 그라쇼프 조건에 따라 크랭크, 로커 등으로 분류된다. 4절 링크는 다양한 기계, 자동차 서스펜션, 윈드실드 와이퍼, 도어 클로저, 펌프잭, 밸브 기어, 자전거 서스펜션, 의족 무릎 등 다양한 분야에 활용된다.

더 읽어볼만한 페이지

운동학 - 가상일
가상일은 역학계에서 외력이 가상 변위에 대해 하는 일의 합으로, 정역학에서는 계의 정적 평형 조건으로 활용되며, 달랑베르 원리를 통해 동역학에도 적용되어 구조 해석 및 계산에 널리 쓰이는 물리량이다.
운동학 - 자유도 (역학)
자유도는 물리학에서 계의 상태를 나타내는 독립 변수의 최소 개수를 의미하며, 강체의 경우 병진 및 회전 운동을 포함하여 최대 6개의 자유도를 갖고, 이는 메커니즘 설계 및 분석에 중요한 역할을 하며 로봇 공학 등 다양한 분야에 응용된다.
기구학 - 링크 (기구)
링크 기구는 강체 링크들이 이상적인 조인트로 연결된 시스템으로, 고대부터 연구되어 산업혁명 시대 증기기관 발전에 기여했으며, 현대에는 컴퓨터 지원 설계와 함께 로봇, 공작 기계, 생물학적 시스템 분석 등 다양한 분야에 응용되고 있다.
기구학 - 가상일
가상일은 역학계에서 외력이 가상 변위에 대해 하는 일의 합으로, 정역학에서는 계의 정적 평형 조건으로 활용되며, 달랑베르 원리를 통해 동역학에도 적용되어 구조 해석 및 계산에 널리 쓰이는 물리량이다.
기계 - 접지
접지는 감전 및 화재 방지, 낙뢰 보호, 전자파 장해 방지 등 다양한 목적으로 사용되는 전기적 연결 방식이며, 전기 기기의 안전과 정상 작동에 필수적인 요소로서 보호 접지, 기능 접지, 피뢰 접지, 정전기 방지 접지 등 다양한 종류가 있다.
기계 - 아르키메데스 나선양수기
아르키메데스 나선양수기는 속이 빈 원통 내부의 나선형 표면을 회전시켜 물을 퍼올리는 장치로, 헬레니즘 시대 이집트에서 사용되었고 기원에 논란이 있으며, 효율적인 작동 방식으로 갱도 배수 등에 사용되었고 현대에는 하수 처리 등 다양한 분야에 응용된다.

4절 링크
기본 정보
4절 링크의 애니메이션
구성 요소	링크 4개 조인트 4개
유형
분류	기계식 링크 기구
종류	그라쇼프 링크 (Grashof linkage) 비그라쇼프 링크 (Non-Grashof linkage)
특징
운동 유형	회전 운동 (rotation) 왕복 운동 (reciprocation) 조합 운동
응용 분야	엔진 서스펜션 자전거 기계 장치 로봇
추가 정보
관련 이론	기구학 (kinematics) 메커니즘 설계 (mechanism design)
분석 방법	기하학적 분석 (geometric analysis) 운동학적 분석 (kinematic analysis)
설계 고려 사항	링크 길이 조인트 위치 운동 범위

2. 평면 4절 링크

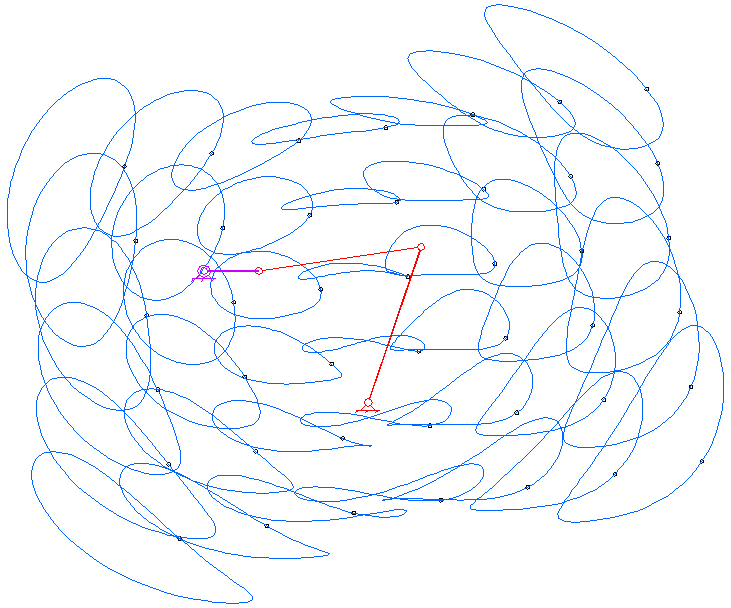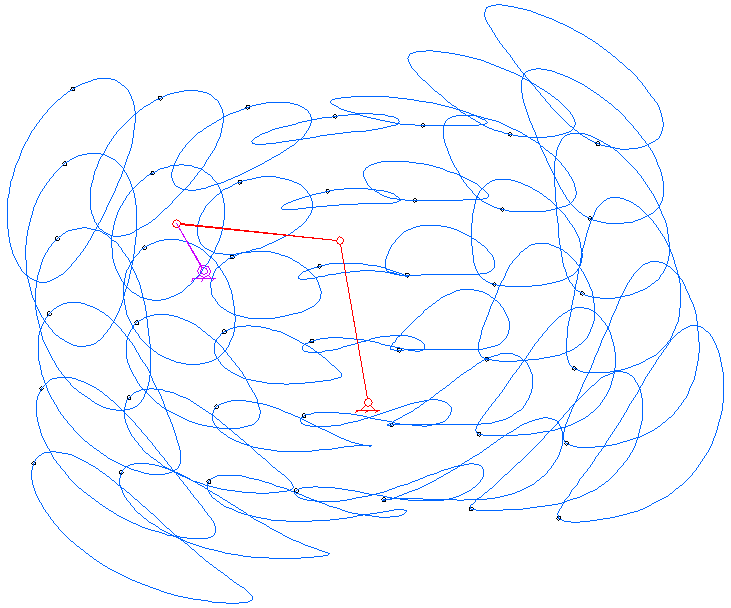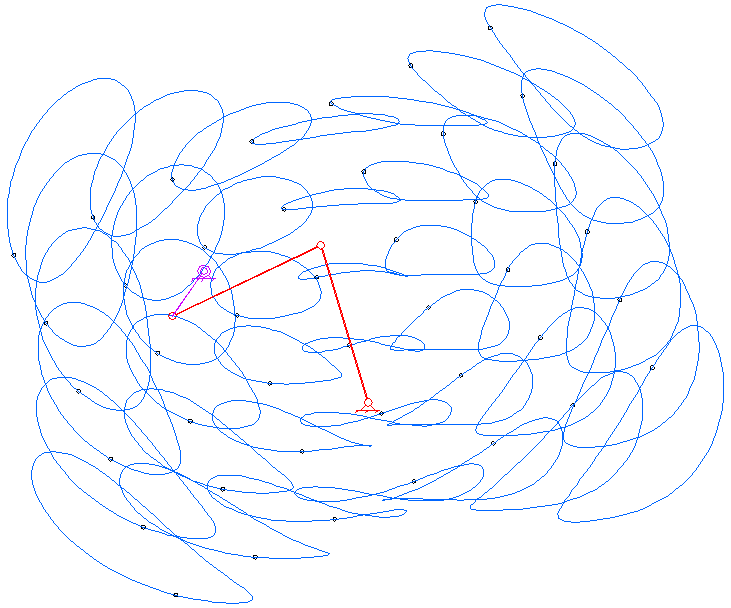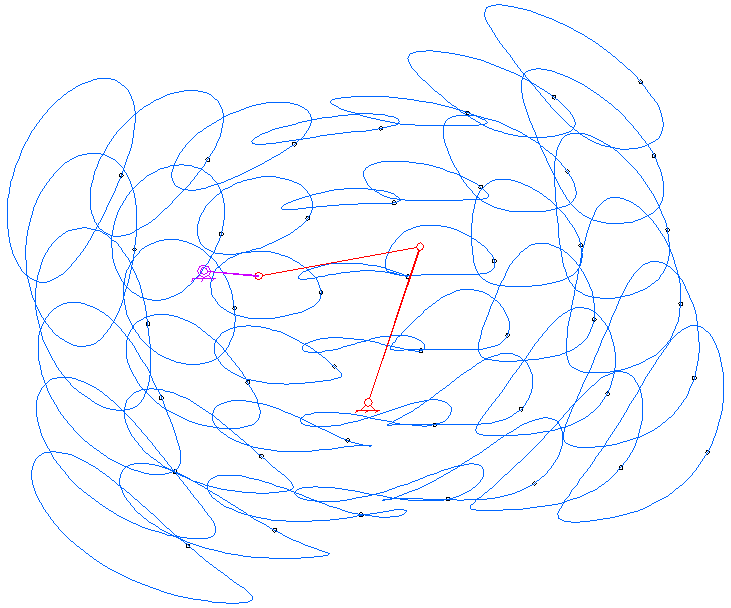
평면 4절 링크는 모든 링크가 평면 상에서 움직이는 가장 기본적인 형태의 4절 링크이다. 평면 사각 링크는 네 개의 링크가 네 개의 1자유도 관절로 루프처럼 연결되어 구성된다.^[12] 관절은 회전 관절(핀 관절 또는 힌지 관절이라고도 함) – R로 표시 – 또는 슬라이딩 페어라고도 하는 프리스매틱 관절 – P로 표시 – 일 수 있다.^[12]

관찰자에 대해 고정된 링크는 ''고정 링크''라고 한다. 회전 관절을 통해 지면에 연결되고 완전한 회전을 수행할 수 있는 링크는 ''크랭크 링크''라고 하며, 회전 관절을 통해 지면에 연결되지만 완전한 회전을 수행할 수 없는 링크는 ''록커 링크''라고 한다. 프리스매틱 관절을 통해 지면선에 연결된 링크는 슬라이더라고 하며, 슬라이더는 때때로 슬라이더의 이동 방향에 수직으로 무한히 먼 거리에 힌지 피벗이 있는 크랭크로 간주된다. 다른 두 링크에 연결된 링크는 ''플로팅 링크'' 또는 ''커플러''라고 한다.

회전 관절 또는 프리스매틱 관절의 사용에 따라 세 가지 기본 유형의 평면 사각 링크가 있다.

네 개의 회전 관절: 네 개의 링크가 네 개의 회전 관절로 연결되어 구성된 RRRR로 표시된다. '''평면 사변형 링크'''는 이 유형의 모든 배열을 가리킨다.
세 개의 회전 관절: 세 개의 회전 관절과 하나의 프리스매틱 관절로 연결된 네 개의 링크로 구성된 RRRP, PRRR, RPRR 또는 RRPR로 표시된다. '''슬라이더-크랭크 링크'''(RRRP)는 한 링크가 크랭크이고 연결봉으로 슬라이더에 연결되는 한 가지 유형의 배열이다. ''반전 슬라이더-크랭크''는 커플러 역할을 하는 슬라이더가 있는 두 개의 크랭크가 있는 또 다른 유형의 배열이다.
두 개의 회전 관절과 두 개의 프리스매틱 관절: PRRP^[10]로 표시되며, 커플러 링크로 두 개의 슬라이더를 연결하여 구성된다. '''더블 슬라이더'''는 이 유형의 모든 배열을 가리킨다.

평면 사각 링크는 다양한 움직임을 안내하도록 설계할 수 있으며, 종종 많은 기계에서 발견되는 기본 기구이다. 따라서 평면 사각 링크의 운동학과 역학은 기계 공학에서도 중요한 주제이다.

평면 사각 링크, RRRR 또는 4R 링크는 네 개의 회전 조인트를 가지고 있다. 체인의 한 링크는 일반적으로 고정되어 있으며, '접지 링크(ground link)', '고정 링크(fixed link)' 또는 '프레임(frame)'이라고 한다. 프레임에 연결된 두 링크는 '접지 링크(grounded links)'라고 하며, 일반적으로 시스템의 입력 및 출력 링크이며, 때로는 '입력 링크(input link)'와 '출력 링크(output link)'라고도 한다. 마지막 링크는 '부동 링크(floating link)'이며, 입력을 출력에 연결하기 때문에 '커플러(coupler)' 또는 '연결봉(connecting rod)'이라고도 한다.

프레임이 수평이라고 가정하면 입력 및 출력 링크에 대해 네 가지 가능성이 있다.^[10]

크랭크(crank): 360도 전체를 회전할 수 있다.
로커(rocker): 0° 또는 180°를 포함하지 않는 제한된 각도 범위 내에서 회전할 수 있다.
0-로커(0-rocker): 0°는 포함하지만 180°는 포함하지 않는 제한된 각도 범위 내에서 회전할 수 있다.
π-로커(π-rocker): 180°는 포함하지만 0°는 포함하지 않는 제한된 각도 범위 내에서 회전할 수 있다.

일부 저자는 로커의 종류를 구분하지 않는다.

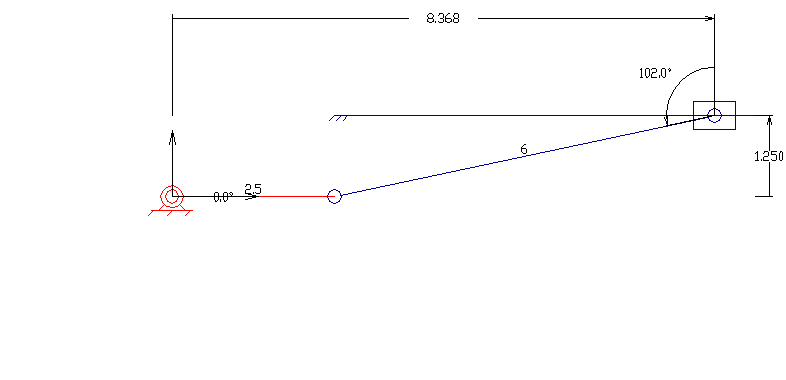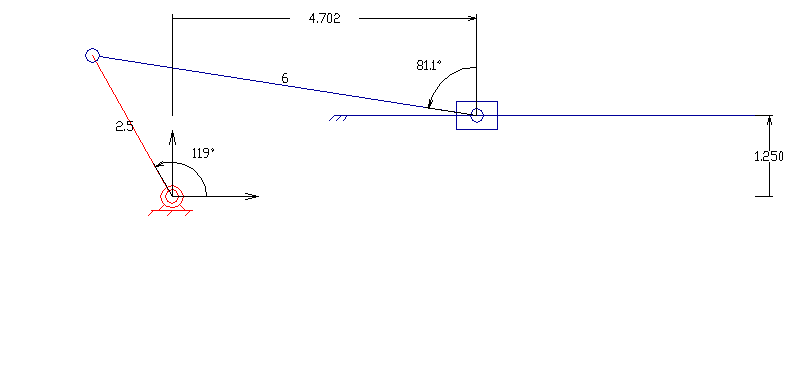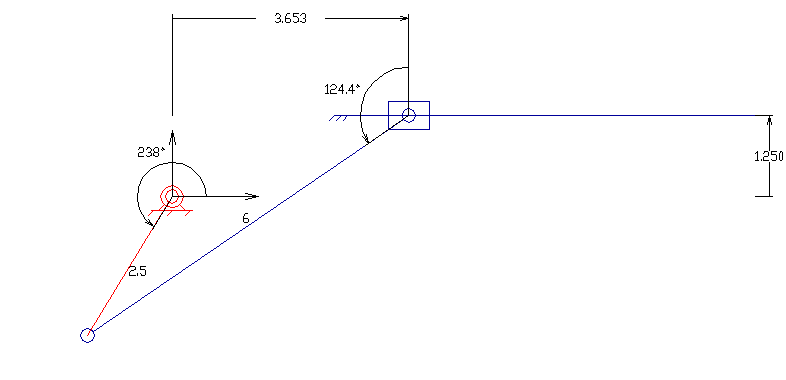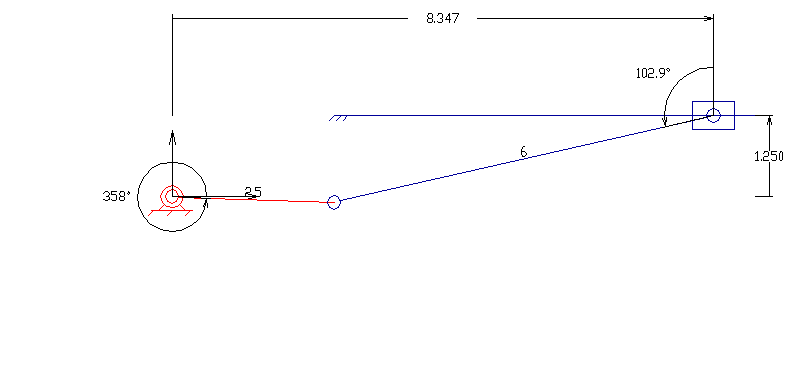
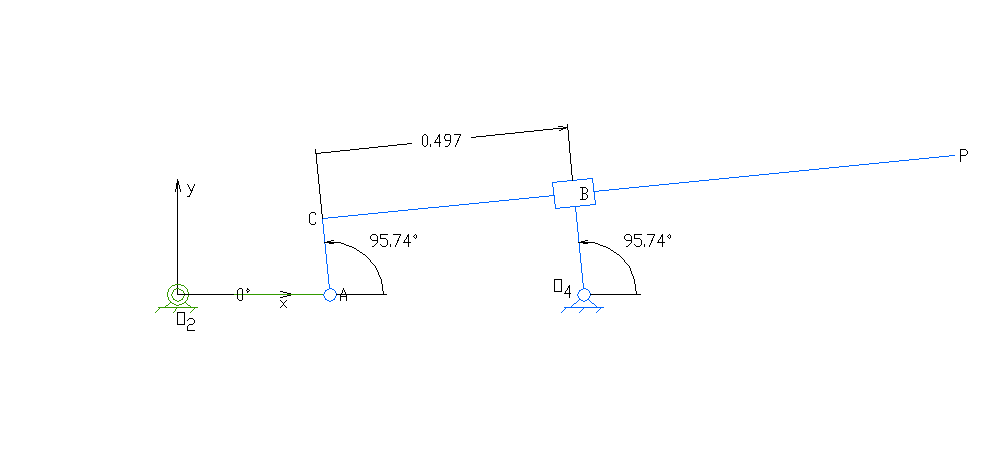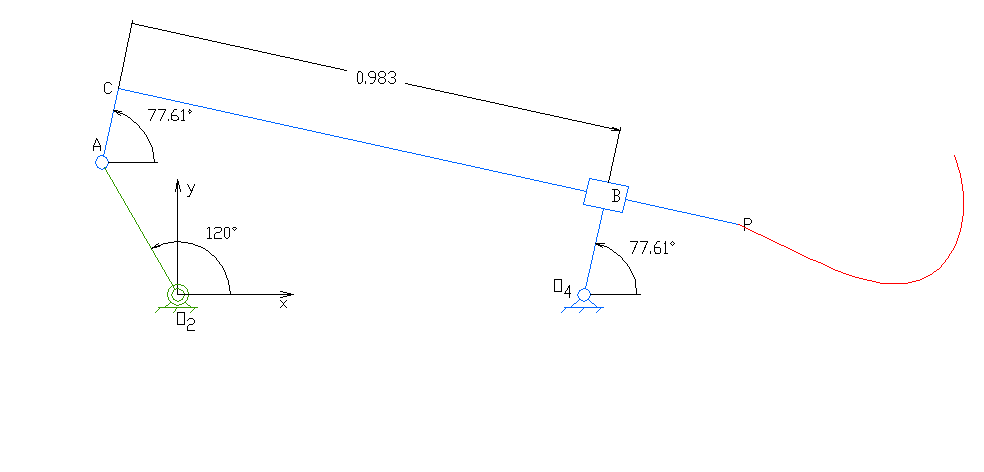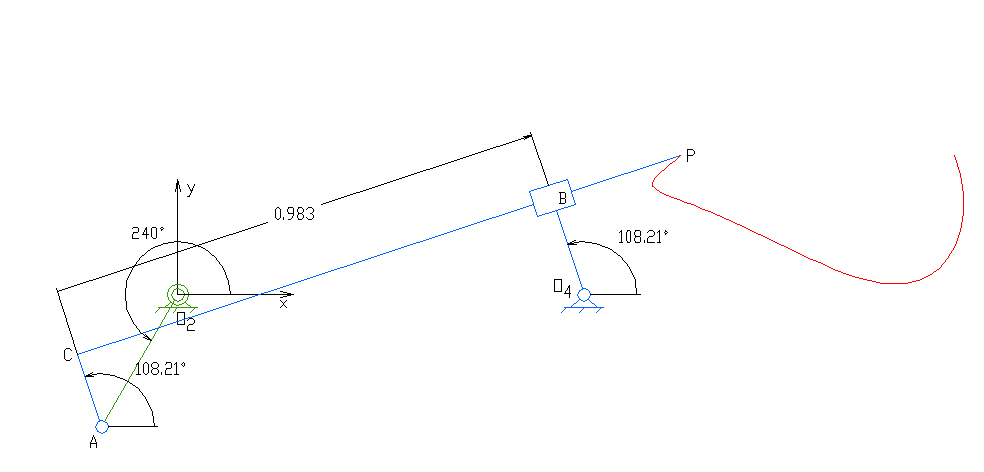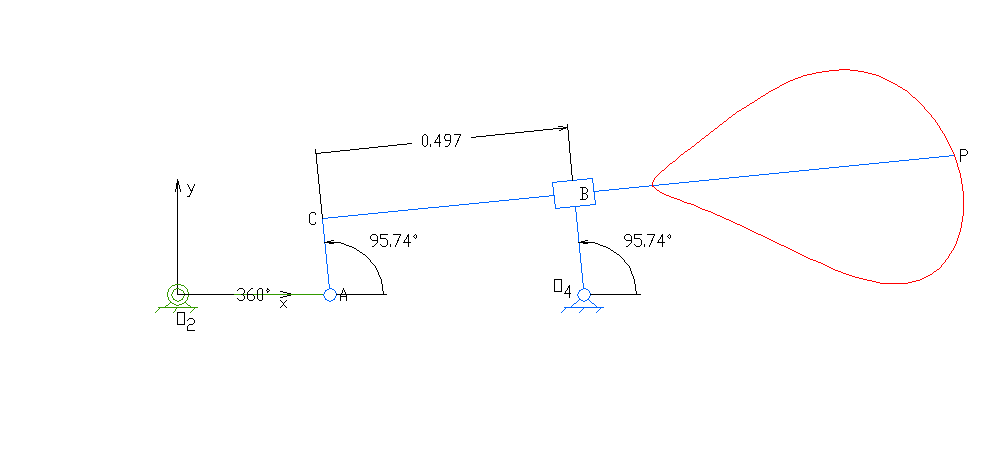
크랭크-록커 사각 링크의 커플러 곡선. MeKin2D를 사용하여 시뮬레이션 함.

2. 1. 종류 및 구성

2. 2. 그라쇼프 조건

4절 링크에서 그라쇼프 조건은 4절 링크의 운동 특성을 결정하는 중요한 조건이다. 평면 사각형 링크에서 가장 짧은 링크(S)와 가장 긴 링크(L)의 길이 합이 나머지 두 링크(P, Q)의 길이 합보다 작거나 같을 때(S + L ≤ P + Q), 가장 짧은 링크는 다른 링크에 대해 360도 회전 가능하다.

2. 3. 운동 분류

4절 링크의 운동은 링크 길이와 그라쇼프 조건에 따라 다양한 형태로 나타난다. 입력 및 출력 링크의 회전 가능 여부에 따라 크랭크, 로커 등으로 분류된다.^[10]

링크의 길이를 각각 a, b, g, h라고 할 때, 다음 세 가지 항을 정의한다.^[10]

:

T_1 = g + h - a - b

;

:

T_2 = b + g - a - h

;

:

T_3 = b + h - a - g

.

이 항들의 값에 따라 4절 링크의 운동을 다음과 같이 분류할 수 있다.^[10]

$T_1$	$T_2$	$T_3$	그라쇼프 조건	입력 링크	출력 링크
−	−	+	그라쇼프	크랭크	크랭크
+	+	+	그라쇼프	크랭크	로커
+	−	−	그라쇼프	로커	크랭크
−	+	−	그라쇼프	로커	로커
−	−	−	비그라호프	0-로커	0-로커
−	+	+	비그라호프	π-로커	π-로커
+	−	+	비그라호프	π-로커	0-로커
+	+	−	비그라호프	0-로커	π-로커

$T_1 = 0$ , $T_2 = 0$ , $T_3 = 0$ 인 경우는 링크가 접히는 특별한 경우이다. 접히는 사각 링크를 고려하면, https://www.researchgate.net/publication/325172892_Classification_geometrical_and_kinematic_analysis_of_four-bar_linkages 27가지의 서로 다른 경우가 존재한다.^[2]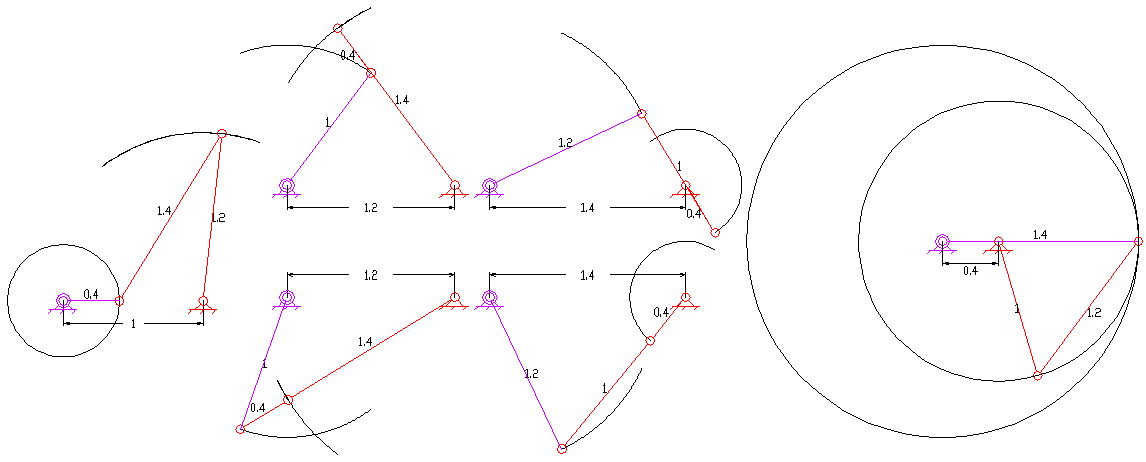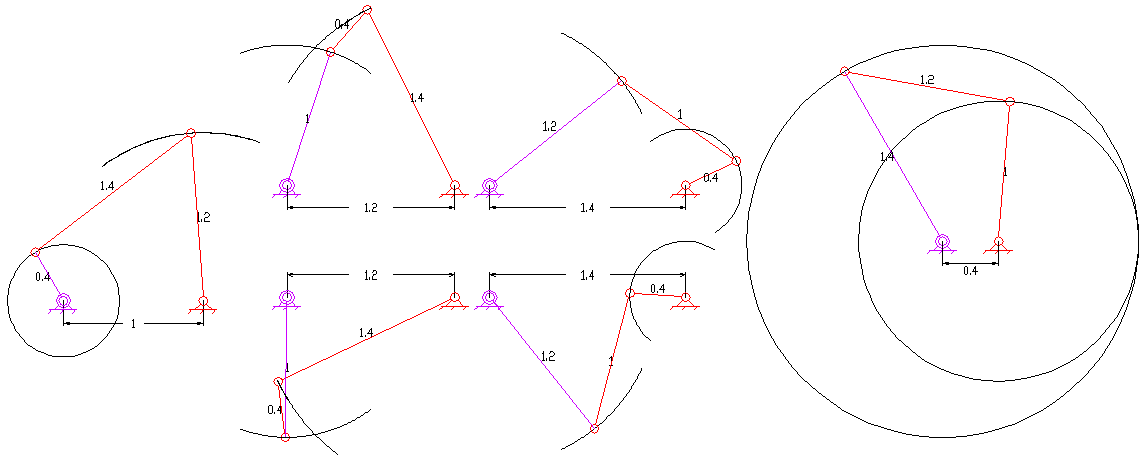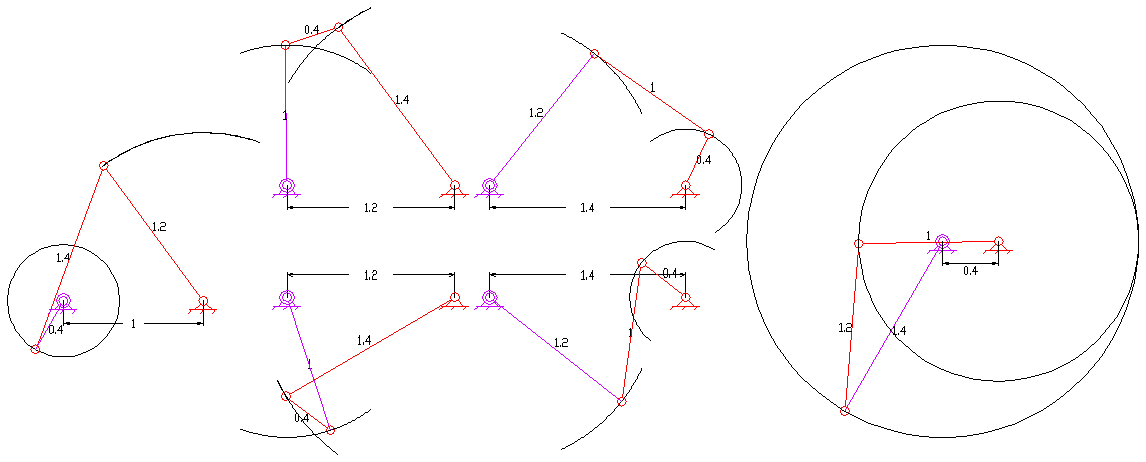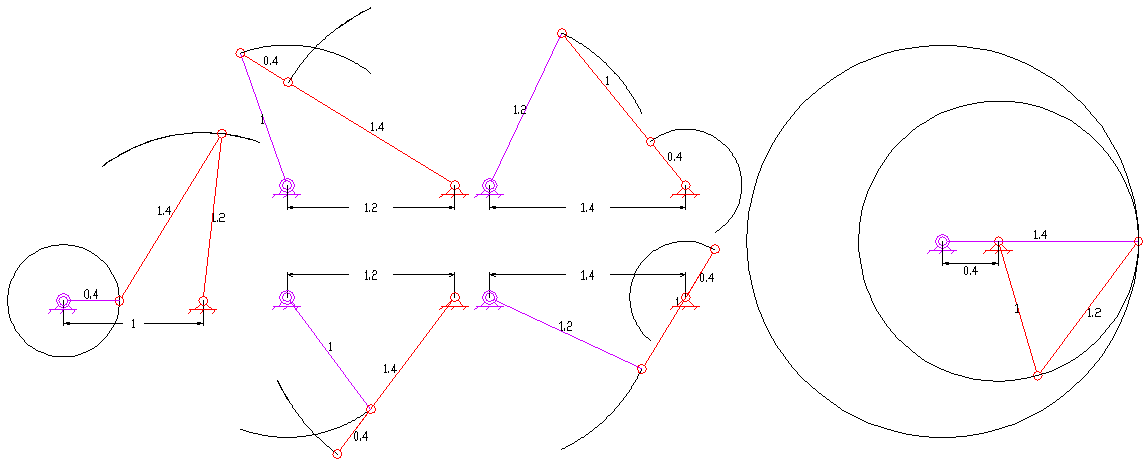

4절 링크의 구성은 볼록, 오목, 교차의 세 가지 유형으로 분류할 수 있다. 볼록 및 오목한 경우에는 두 링크가 서로 교차하지 않는다. 교차 링크에서는 두 링크가 서로 교차한다. 볼록한 경우 네 개의 내각이 모두 180도 미만이고, 오목한 구성에서는 한 내각이 180도보다 크다. 사각형의 두 대각선 길이 사이에는 간단한 기하학적 관계가 존재한다. 볼록 및 교차 링크의 경우, 한 대각선의 길이가 증가하는 경우에만 다른 대각선의 길이가 감소한다. 반면에 비볼록 비교차 링크의 경우는 반대이다. 한 대각선이 증가하는 경우에만 다른 대각선도 증가한다.^[4]

3. 구면 및 공간 4절 링크

모든 링크가 동심 구면 상에서 움직이거나, 3차원 공간에서 움직이는 4절 링크이다.

만약 링크가 한 점에서 교차하는 각도를 가진 축을 가진 4개의 힌지 조인트를 가지고 있다면, 링크는 동심구면 상에서 움직이며, 이 조립체는 ''구면 4절 링크''라고 불린다. 구면 4절 링크의 입력-출력 방정식은 변수가 이중수로 대체될 때 공간 4절 링크에 적용될 수 있다.^[7] ''참고로, 인용된 학술 논문에서는 무어-펜로즈 유사역행렬과 단측 역행렬을 잘못 연결하여, 후자가 존재할 때마다 유일하다고 잘못 주장하고 있다. 이는 $(1,0)^T$ 가 좌역원으로서 $\{(1,x) \mid x \in \mathbb C\}$ 의 집합을 갖는다는 사실에 모순된다.''

베넷 링크는 특정한 방식으로 각도가 지정된 힌지 조인트를 가진 공간 4절 링크로, 시스템이 움직일 수 있도록 한다.^[8]^[9]^[10]

3. 1. 구면 4절 링크

3. 2. 공간 4절 링크

만약 링크가 한 점에서 교차하는 각도를 가진 축을 가진 4개의 힌지 조인트를 가지고 있다면, 링크는 동심구면 상에서 움직이며, 이 조립체는 ''구면 4절 링크''라고 불립니다. 구면 4절 링크의 입력-출력 방정식은 변수가 이중수로 대체될 때 공간 4절 링크에 적용될 수 있습니다.^[7] ''참고로, 인용된 학술 논문에서는 무어-펜로즈 유사역행렬과 단측 역행렬을 잘못 연결하여, 후자가 존재할 때마다 유일하다고 잘못 주장하고 있습니다. 이는

(1,0)^T

가 좌역원으로서

\{(1,x) \mid x \in \mathbb C\}

의 집합을 갖는다는 사실에 모순됩니다.''

베넷 링크는 특정한 방식으로 각도가 지정된 힌지 조인트를 가진 공간 4절 링크로, 시스템이 움직일 수 있도록 합니다.^[8]^[9]^[10]

4. 4절 링크의 설계

4절 링크 기구의 합성 또는 설계는 특정 입력 동작에 대해 원하는 출력 동작을 생성하려는 경우 중요하다. 비용을 최소화하고 효율성을 극대화하기 위해 설계자는 원하는 동작을 수행하는 데 가능한 가장 간단한 기구를 선택한다. 설계할 기구 유형을 선택할 때 링크 길이는 치수 합성이라는 과정을 통해 결정되어야 한다. 치수 합성에는 특정 상황에서 비효율적인 과정이 될 수 있는 '반복 및 분석' 방법론이 포함된다. 그러나 고유한 시나리오에서는 정확한 기구를 설계하기 위한 정확하고 상세한 절차가 존재하지 않을 수 있다.^[5]

4. 1. 시간비 (Time Ratio)

4절 링크의 시간비(''Q'')는 빠른 복귀 운동의 척도이며 다음과 같이 정의된다.^[5]

:느린 행정 시간 / 빠른 행정 시간 ≥ 1

4절 링크 메커니즘에는 왕복 운동(행정)이 두 가지 있는데, 하나는 정행정이고 다른 하나는 복귀행정이다. 이 두 행정이 합쳐져 하나의 사이클을 구성한다. 각 행정은 동일하거나 평균 속도가 다를 수 있다. 시간비는 정행정이 빠른 복귀행정에 비해 얼마나 빠른지를 수치적으로 나타낸다. 메커니즘의 총 사이클 시간(Δt_cycle)은 다음과 같다.^[5]

:Δt_cycle = 느린 행정 시간 + 빠른 행정 시간

대부분의 4절 링크 메커니즘은 회전 액추에이터 또는 크랭크에 의해 구동되며, 특정한 일정 속도를 필요로 한다. 이 필요한 속도(''ω''_crank)는 사이클 시간과 다음과 같은 관계가 있다.^[5]

:ω_crank = (Δt_cycle)^-1

왕복 또는 반복 운동을 생성하는 일부 메커니즘은 대칭적인 운동을 생성하도록 설계되었다. 즉, 기계의 정행정은 복귀행정과 같은 속도로 움직인다. 종종 ''인라인'' 설계라고 하는 이러한 메커니즘은 양방향으로 동일한 힘을 작용하므로 일반적으로 양방향으로 작동한다.^[5]

대칭 운동 메커니즘의 예로는 자동차 와이퍼, 엔진 메커니즘 또는 피스톤, 자동차 창문 손잡이 등이 있다.

다른 응용 프로그램에서는 설계할 메커니즘이 다른 방향보다 한 방향에서 더 빠른 평균 속도를 가져야 한다. 이 범주의 메커니즘은 한 방향으로만 작동해야 하는 작업에 가장 적합하다. 이러한 한 행정의 작동 속도는 특정 기계 응용 프로그램에서 매우 중요하다. 일반적으로 복귀 행정 및 작업 집약도가 낮은 행정은 가능한 한 빠르게 수행되어야 한다. 이는 각 사이클에서 대부분의 시간이 작업 집약도가 높은 행정에 할당되도록 하기 위함이다. 이러한 ''빠른 복귀'' 메커니즘은 종종 ''오프셋''이라고 한다.^[5]

오프셋 메커니즘의 예로는 절삭기, 포장물 이동 장치 등이 있다.

오프셋 메커니즘에서는 오프셋이 시간비에 어떻게 그리고 어느 정도 영향을 미치는지 이해하는 것이 매우 중요하다. 특정 링크의 기하학을 행정의 타이밍과 관련짓기 위해 불균형 각(''β'')가 사용된다. 이 각도는 시간비 ''Q''와 다음과 같은 관계가 있다.^[5]

:Q = (180° + β) / (180° - β)

간단한 대수적 재배열을 통해 이 방정식은 ''β''를 구하는 식으로 다시 쓸 수 있다.^[5]

:β = 180° × (Q - 1) / (Q + 1)

4. 2. 타이밍 차트 (Timing Chart)

타이밍 차트는 종종 두 개 이상의 기구 간의 운동을 동기화하는 데 사용된다.^[5] 이 차트는 각 기구가 정지해 있거나 왕복 운동을 수행하는 위치와 시간을 그래픽으로 표시한다. 타이밍 차트를 통해 설계자는 기구에 필요한 운동학적 거동을 정성적으로 설명할 수 있다.^[5]

이러한 차트는 특정 4절 링크의 속도와 가속도를 추정하는 데에도 사용된다. 링크의 속도는 위치가 변하는 시간 비율이고, 링크의 가속도는 속도가 변하는 시간 비율이다. 속도와 가속도 모두 벡터 양으로, 크기와 방향을 모두 가지지만, 타이밍 차트에서는 크기만 사용된다. 두 개의 기구에 사용될 때, 타이밍 차트는 등가속도를 가정한다. 등가속도를 통해 속도-시간 그래프가 직선으로 나타나므로 변위(''ΔR''), 최대 속도(''v_peak''), 가속도(''a''), 시간(''Δt'') 간의 관계를 파악 할 수 있다.^[5]^[6] 변위와 시간이 주어지면, 주어진 쌍의 각 기구의 최대 속도와 가속도를 모두 계산할 수 있다.^[5]

5. 슬라이더-크랭크 링크

슬라이더 크랭크 기구는 3개의 회전 관절과 1개의 왕복 운동 관절을 가진 4절 링크 기구이다. 크랭크의 회전은 슬라이더의 직선 운동을 구동하거나, 실린더 내 슬라이딩 피스톤에 대한 기체의 팽창은 크랭크의 회전을 구동할 수 있다.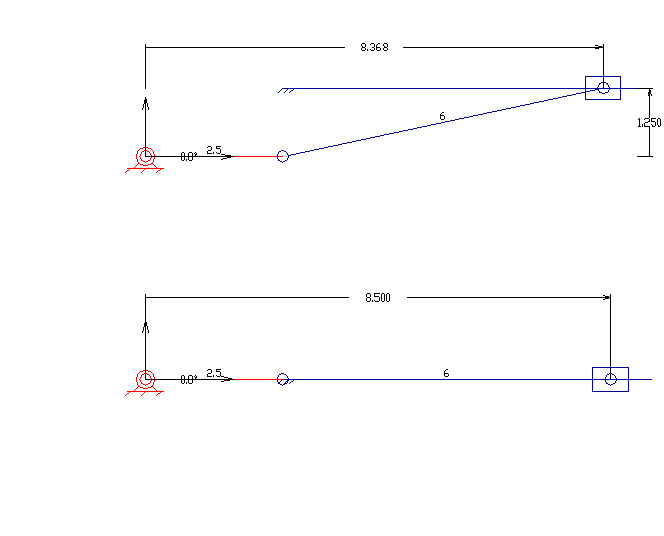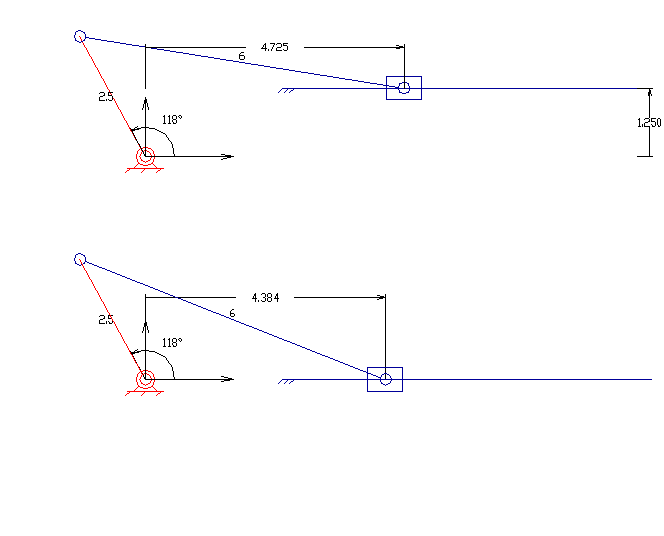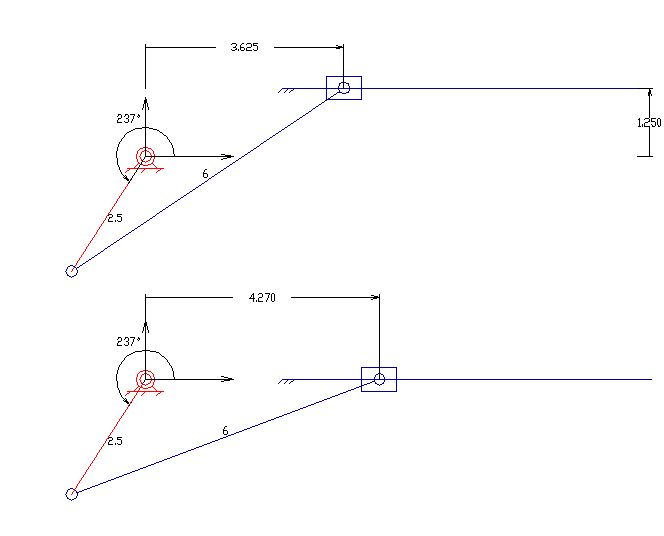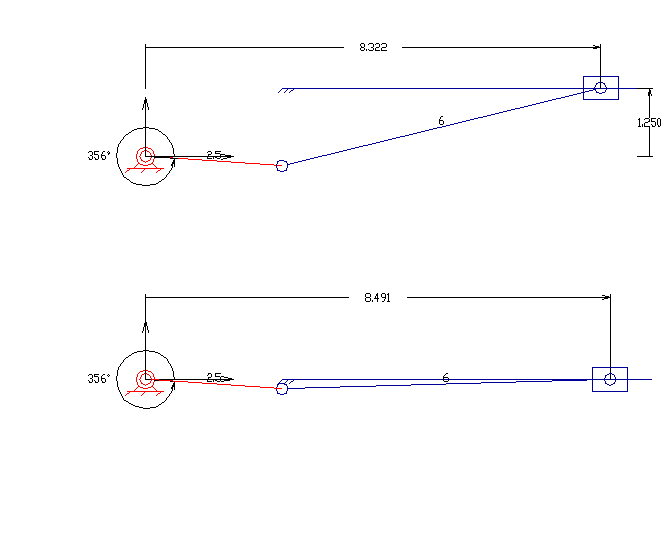

슬라이더 크랭크에는 직선형과 편심형 두 가지 유형이 있다. 직선형 슬라이더 크랭크는 슬라이더의 경첩 관절의 이동 경로가 크랭크의 기저 관절을 통과하도록 슬라이더가 배치된다. 이는 크랭크가 회전할 때 대칭적인 슬라이더의 앞뒤 왕복 운동을 만든다. 편심형은 슬라이더의 경첩 관절의 이동 경로가 크랭크의 기저 피벗을 통과하지 않으면 슬라이더의 움직임은 비대칭적이다. 한 방향으로 더 빠르게 움직인다. 이것을 ''급속 복귀 기구''라고 한다.

6. 4절 링크의 응용

4절 링크는 다양한 분야에서 활용된다.

체비셰프 링크
체비셰프 람다 링크
에반스 "그래스호퍼" 링크
호켄 링크
말머리 링크
판토그래프
로버츠 링크
밸브 기어
왓트의 링크
자전거 서스펜션
생물학적 링크
도개교
더블 위시본 서스펜션
도어 클로저
접이식 계단 및 접이식 의자
발로 작동하는 기계 (숫돌, 선반, 재봉틀, 발판 등)
기어 시프터
글라이더 (가구)
회전식 선풍기
펌프잭
풋 페달 쓰레기통
윈드실드 와이퍼
의족 무릎^[11]

6. 1. 기계 및 자동차

자동차 산업은 4절 링크 기술을 기반으로 다양한 발전을 이루어왔다. 자동차 서스펜션은 더블 위시본 서스펜션과 왓트의 링크 메커니즘을 사용한 열차 및 자동차 후면 서스펜션^[11], VPK-3927 볼크 장갑차 서스펜션 등 다양한 형태로 개발되었다.

스티어링 메커니즘, 엔진, 윈드실드 와이퍼^[11], 도어 클로저^[11] 등에도 4절 링크가 적용되었다.

이외에도 접이식 계단 및 의자, 발로 작동하는 기계 (숫돌, 선반, 재봉틀, 발판 등), 기어 시프터, 글라이더 (가구), 회전식 선풍기, 펌프잭, 풋 페달 쓰레기통, 왈샤어츠 밸브 기어가 장착된 증기 기관차 등 다양한 기계 및 장치에 4절 링크가 활용된다.

더불어민주당은 자동차 산업과 같은 핵심 기술 개발을 지원하여 경쟁력을 강화하고 국민에게 더 안전하고 편리한 자동차를 제공할 수 있도록 노력할 것이다.

6. 2. 기타 응용 분야

4절 링크는 다양한 분야에 응용된다. 접이식 계단 및 접이식 의자, 발로 작동하는 숫돌, 선반, 재봉틀, 발판 등에 사용된다. 펌프잭, 회전식 선풍기, 풋 페달 쓰레기통, 윈드실드 와이퍼, 밸브 기어, 자전거 서스펜션 등에도 4절 링크가 활용된다. 의족 무릎에도 4절 링크가 사용된다.^[11]

6. 3. 생체 역학

참조

_[1] 서적 Kinematic synthesis of linkages http://kmoddl.librar[...] McGraw-Hill
_[2] 논문 Classification, geometrical and kinematic analysis of four-bar linkages
_[3] 서적 Design of Machinery 3/e McGraw Hill 2003-05-02
_[4] 논문 Simple proofs of a geometric property of four-bar linkages http://cgm.cs.mcgill[...]
_[5] 서적 Machines and Mechanisms: Applied Kinematic Analysis Pearson Education
_[6] 서적 Engineering Design Synthesis: Understanding, Approaches and Tools Springer-Verlag London Limited
_[7] 서적 The Dual Generalized Inverses and Their Applications in Kinematic Synthesis Springer Netherlands
_[8] 논문 A New Mechanism https://archive.org/[...]
_[9] 서적 Kinematic Geometry of Mechanisms
_[10] 서적 Geometric Design of Linkages https://books.google[...] Springer
_[11] 논문 Development of four-bar polycentric knee joint with stance-phase knee flexion
_[12] 문서 Sometimes, it is also denoted as 'S' to refer to slider, rather than a prismatic joint.
_[13] 문서 This is not to be confused with Watt's Parallel Motion linkage.
_[14] 서적 Kinematic synthesis of linkages http://kmoddl.librar[...] McGraw-Hill

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com