K-최근접 이웃 알고리즘
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
K-최근접 이웃 알고리즘(k-NN)은 훈련 데이터를 기반으로 새로운 데이터를 분류하는 기계 학습 알고리즘이다. 이 알고리즘은 각 데이터 항목을 다차원 공간의 벡터로 표현하고, 새로운 데이터와 가장 가까운 k개의 훈련 데이터(이웃)를 찾아, 이웃들의 분류 정보를 바탕으로 새로운 데이터의 분류를 결정한다. k-NN은 구현이 쉽고, 데이터의 양이 충분하면 높은 정확도를 보이지만, 데이터가 많아질수록 계산량이 증가하는 단점이 있다. 가중 k-NN, 차원 축소, 데이터 축소 등의 기법을 통해 성능을 향상시킬 수 있으며, 패턴 인식, 추천 시스템, 의료, 금융, 이상 탐지 등 다양한 분야에서 활용된다.
더 읽어볼만한 페이지
- 통계적 분류 - 서포트 벡터 머신
서포트 벡터 머신(SVM)은 지도 학습 모델로서 분류와 회귀 분석에 사용되며, 데이터 집합을 기반으로 새로운 데이터의 범주를 판단하는 비확률적 이진 선형 분류 모델을 생성하고, 커널 트릭을 통해 비선형 분류에도 활용될 수 있다. - 통계적 분류 - 민감도와 특이도
민감도와 특이도는 의학적 진단에서 검사의 정확성을 평가하는 지표로, 민감도는 실제 양성인 대상 중 양성으로 나타나는 비율, 특이도는 실제 음성인 대상 중 음성으로 나타나는 비율을 의미하며, 선별 검사에서 두 지표를 모두 높여 질병을 정확하게 진단하는 것을 목표로 한다. - 기계 학습 알고리즘 - 강화 학습
강화 학습은 에이전트가 환경과의 상호작용을 통해 누적 보상을 최대화하는 최적의 정책을 학습하는 기계 학습 분야이며, 몬테카를로 방법, 시간차 학습, Q-러닝 등의 핵심 알고리즘과 탐험과 활용의 균형, 정책 경사법 등의 다양한 연구 주제를 포함한다. - 기계 학습 알고리즘 - 기댓값 최대화 알고리즘
- 분류 알고리즘 - 인공 신경망
- 분류 알고리즘 - 퍼셉트론
퍼셉트론은 프랭크 로젠블랫이 고안한 인공신경망 모델로, 입력 벡터에 가중치를 곱하고 편향을 더한 값을 활성화 함수에 통과시켜 이진 분류를 수행하는 선형 분류기 학습 알고리즘이며, 초기 신경망 연구의 중요한 모델로서 역사적 의미를 가진다.
2. 알고리즘
k-최근접 이웃(k-NN) 알고리즘은 "유유상종", 즉 비슷한 특성을 가진 데이터는 서로 가까이 위치한다는 가정에 기반한다. k-NN 알고리즘은 다음 절차로 구성된다.[26]
1. 입력 데이터와 모든 학습 데이터 간의 유사도(거리)를 측정한다.
2. 유사도가 높은 상위 k개의 데이터를 선출한다.
3. 선출된 데이터의 다수결 또는 평균으로 결과를 낸다.
예를 들어, 과거 100일 동안의 날씨(비, 흐림, 맑음)와 환경(기온, 습도, 풍속) 데이터가 있다고 가정하자. k=5인 k-NN 분류를 사용하면, 오늘의 환경과 가장 비슷한 5일의 데이터를 찾는다. 만약 그 5일의 날씨가 비, 비, 맑음, 비, 비였다면, 다수결에 따라 오늘 날씨를 비로 예측한다.
이항 분류에서는 동률을 피하기 위해 k를 홀수로 설정한다. 회귀 분석에서는 k개 이웃의 속성값 평균을 사용하며, 가까운 이웃에 더 큰 가중치를 부여할 수도 있다.
k-NN 알고리즘은 훈련 데이터를 다차원 특징 공간에 벡터로 표현한다. 훈련 단계에서는 이 벡터와 클래스 레이블을 저장한다. 분류 단계에서는 분류되지 않은 벡터(질의점)에 대해 k개의 훈련 데이터 중 가장 빈번한 분류명을 할당한다. 일반적으로 유클리드 거리를 사용하지만, 맨해튼 거리 등 다른 거리를 사용할 수도 있다.
2. 1. 작동 원리

훈련 데이터는 각각 항목 분류명을 갖는 다차원 특징 공간에서의 벡터이다. 알고리즘의 훈련 단계는 오직 훈련 표본의 특징 벡터와 항목 분류명을 저장하는 것이다.
분류 단계에서 k는 사용자 정의 상수이고, 분류명이 붙지 않은 벡터(질의 또는 검증점)는 k개의 훈련 표본 사이에서 가장 빈번한 분류명을 할당함으로써 분류된다.
연속 변수에서 가장 흔하게 사용되는 거리 척도는 유클리드 거리이다. 문자 분류와 같은 이산 변수의 경우 '''중첩 거리'''(또는 해밍 거리)와 같은 다른 척도가 사용될 수 있다. 예를 들어 유전자 표현 미세 배열 데이터의 경우, k-NN은 피어슨과 스피어만 같은 상관 계수를 사용해 왔다.[29] 종종 거리 척도가 큰 여백 최근접 이웃이나 이웃 성분 분석과 같은 특별한 알고리즘으로 학습된다면 k-NN의 분류 정확성을 상당히 향상시킬 수 있다.
“과반수 의결”에 따른 분류의 단점은 항목 분포가 편향될 때 나타난다. 다시 말해서, 더 빈번한 항목의 데이터가 새로운 데이터의 예측을 지배하는 경향이 있다. 왜냐하면, 더 빈번한 항목의 데이터가 다수를 이루어서 k개의 최근접 이웃의 대부분이 되는 경향이 있기 때문이다.[30] 이 문제를 해결하는 한 가지 방법은 검증점과 k개의 최근접 이웃 각각의 거리를 고려하여 분류에 가중치를 주는 것이다. 각각 k개의 최근접 점의 항목(회귀 문제의 경우 값)에 그 점에서 검증점까지의 거리에 반비례하는 가중치를 곱한다. 편향을 해결하는 또 다른 방법은 데이터 표현을 추상화하는 것이다. 예를 들어 자기조직화지도(SOM)에서 각 노드는 원래의 훈련 데이터 밀도와 상관없이 유사점의 군집 대표(중심)이다. k-NN은 SOM에도 적용될 수 있다.
2. 2. 가중 k-NN
기본 k-NN 알고리즘은 k개의 모든 이웃에게 동일한 영향력을 부여하지만, 가중 k-NN은 각 이웃의 거리에 따라 다른 가중치를 부여한다. 즉, 더 가까운 이웃에게 더 큰 영향력을 주어 예측의 정확도를 높인다.[5]예를 들어, 검증점과 k개의 최근접 이웃 각각의 거리를 고려하여 분류에 가중치를 줄 수 있다. 각각 k개의 최근접 점의 항목(회귀 문제의 경우 값)에 그 점에서 검증점까지의 거리에 반비례하는 가중치를 곱한다.[30]
k-최근접 이웃 분류기는 k개의 가장 가까운 이웃에 의 가중치를 할당하고 나머지 모든 이웃에는 0의 가중치를 할당하는 것으로 볼 수 있다. 이것은 가중치가 부여된 최근접 이웃 분류기로 일반화될 수 있다. 즉, i번째 가장 가까운 이웃에 의 가중치가 할당되며, 이다.[9]
2. 3. 매개변수 선택
- k* 값은 데이터에 따라 결정된다. 일반적으로 *k* 값이 크면 분류에서 잡음의 영향을 줄일 수 있지만,[31] 클래스 간의 경계가 불분명해진다. *k* 값의 선택에는 다양한 휴리스틱이 사용된다. (예: 초월매개변수 최적화) *k*=1일 때의 k-최근접 이웃법을 최근접 이웃법이라고 하며, 가장 가까운 훈련 예제의 클래스를 채택한다.[26]
k-최근접 이웃 알고리즘의 정확도는 잡음이 많은 특징이나 부적절한 특징에 의해 크게 손상될 수 있다. 특징 척도가 그 중요성과 일치하지 않는 경우에도 마찬가지이다. 이 부분을 개선하기 위해 특징 선택 연구가 진행되고 있다. 특징 척도를 최적화하기 위해 진화형 알고리즘을 이용하거나,[32] 훈련 데이터와 훈련 클래스 간의 상호 정보량에 따라 특징의 척도를 결정하는 방법도 자주 사용된다.
이항 분류의 경우, *k*를 홀수로 하면 동표가 되는 문제를 피할 수 있다.[33]
3. 특징
k-NN은 구현이 쉽고 이해하기 쉬운 간단하고 직관적인 알고리즘이다. 알고리즘의 훈련 단계는 훈련 샘플의 특징 벡터와 클래스 레이블을 저장하는 것으로만 구성되어 별도의 훈련 과정이 필요하지 않으므로 새로운 데이터에 대한 적응이 빠르다.[26] 하지만, 다량의 훈련 집합에 대해 많은 계산량을 요구하므로, 데이터가 많아질수록 계산량이 급격히 증가하는 단점이 있다. 적절한 최근접 이웃 탐색 알고리즘을 사용하면 다량의 데이터 집합에 대해서도 k-NN 계산이 가능하도록 할 수 있다.[35]
"과반수 의결"에 따른 분류의 단점은 항목 분포가 편향될 때 나타난다. 더 빈번한 항목의 데이터가 새로운 데이터의 예측을 지배하는 경향이 있는데, 이 문제를 해결하는 한 가지 방법은 검증점과 k개의 최근접 이웃 각각의 거리를 고려하여 분류에 가중치를 주는 것이다.[30]
k-NN은 매우 일관성 있는 결과를 도출한다. 이 알고리즘은 데이터의 수가 무한대로 증가할수록 오차율이 베이즈 오차율(주어진 데이터의 분포에서 달성할 수 있는 최소 오차율)의 두 배보다 항상 나쁘지 않음을 보장한다.[36]
4. 차원 축소
k-NN 알고리즘은 고차원 데이터에서 차원의 저주로 인해 성능이 저하될 수 있다.[38] 이는 고차원에서 유클리드 거리가 유용하지 않기 때문이다. 모든 벡터가 탐색 질의 벡터와 대부분 같은 거리를 갖게 되어, 탐색 공간에서 질의 점과 모든 데이터 점 사이의 거리가 거의 같아지기 때문이다.[17]
이러한 문제를 해결하기 위해 k-NN 알고리즘을 사용하기 전에 차원 축소를 수행하는 것이 일반적이다. 특징 추출과 차원 축소는 주성분 분석(PCA), 선형 판별 분석(LDA), 또는 정준 상관 분석(CCA) 기법을 전처리 과정으로 사용하여 한 단계로 결합할 수 있다. 그 후 축소된 차원 공간에서 k-NN을 사용하여 군집화를 수행할 수 있다. 기계 학습에서 이 과정을 저차원 매장이라 부른다.[39] k-NN 맥락에서 차원의 저주는 기본적으로 고차원에서는 모든 벡터가 검색 쿼리 벡터와 거의 등거리에 있기 때문에 유클리드 거리가 유용하지 않다는 것을 의미한다.
5. 데이터 축소

대규모 데이터셋에서 k-NN 알고리즘의 계산 비용을 줄이기 위해, 프로토타입 선택, 데이터 압축 등의 방법을 사용할 수 있다.
'''압축된 근접 이웃'''(CNN, Hart 알고리즘)은 k-NN 분류를 위해 데이터 집합을 축소하려는 목적으로 설계된 알고리즘이다.[43] 이 알고리즘은 훈련 데이터로부터 프로토타입의 집합 ''U''를 선택하고, 이를 통해 1NN이 모든 데이터 집합을 분류하는 것만큼 정확하게 ''U''와 1NN이 데이터들을 분류할 수 있다.
주어진 훈련 집합 ''X''에 CNN을 반복적으로 수행한다.
# ''X''의 모든 요소를 탐색하여, ''U''로부터 가장 가까운 프로토타입을 가지는 ''x''를 찾는다(''U''는 ''x''와 다른 분류명을 가진다).
# ''X''로부터 ''x''를 삭제하고 그것을 ''U''에 더한다.
# ''U''에 더 이상 프로토타입을 더할 수 없을 때까지 탐색을 반복한다.
분류하기 위해 ''X'' 대신에 ''U''를 사용한다. 프로토타입이 아닌 데이터들은 "흡수된" 점이라고 한다.
경계율을 줄이기 위해서는 학습 데이터들을 탐색하는 것이 효율적이다.[44] 학습 데이터 ''x''의 경계 비율은 아래와 같다.
: ''a''(''x'') = '' x' '' - ''y'' / ''x'' - ''y''
'' x' '' - ''y'' 는 ''x''와 색이 다른 가장 가까운 데이터인 ''y''까지의 거리를 나타내고, ''x'' - ''y'' 는 ''y''와 가장 가까운 데이터인 ''x' ''까지의 거리를 나타낸다(''x' ''는 ''x''와 같은 분류명을 가진다).
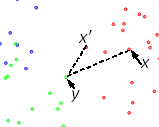
경계율은 [0,1] 구간 내의 값인데, 왜냐하면 '' x' '' - ''y'' 는 ''x'' - ''y'' 를 절대 초과하지 않기 때문이다. 이 순서는 프로토타입의 집합인 ''U''로의 포함을 위한 우선권을 항목들의 경계에 준다. ''x''와 다른 분류명을 가지는 점은 ''x'' 외부에 있다고 한다. 경계율의 계산은 오른쪽에 도식으로 나타나 있다. 점 데이터들은 색으로 분류명이 붙여졌는데, 초기의 점은 ''x''이고 분류명은 빨간색이다. 외부의 점들은 파란색과 초록색이다. ''x''의 외부 점들 중 가장 가까운 점은 ''y''이다. ''y''에 가장 가까운 빨간 점은 ''x' ''이다. 경계율 ''a''(''x'') = '' x' '' - ''y'' / ''x'' - ''y'' 은 초기의 점 ''x''의 속성이다.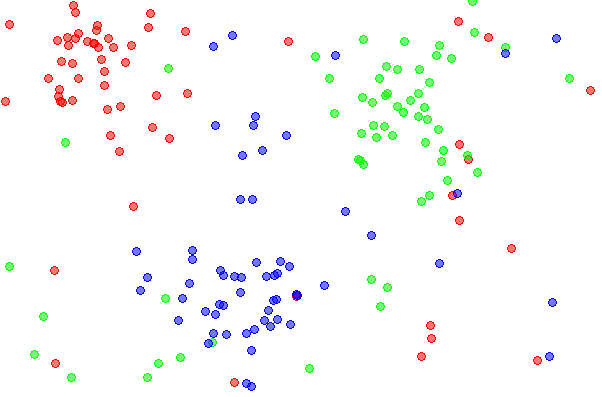
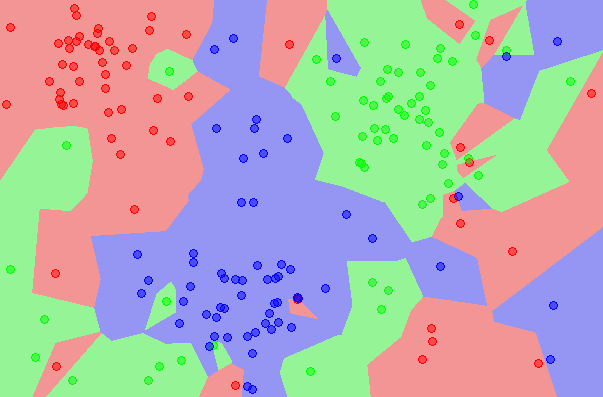
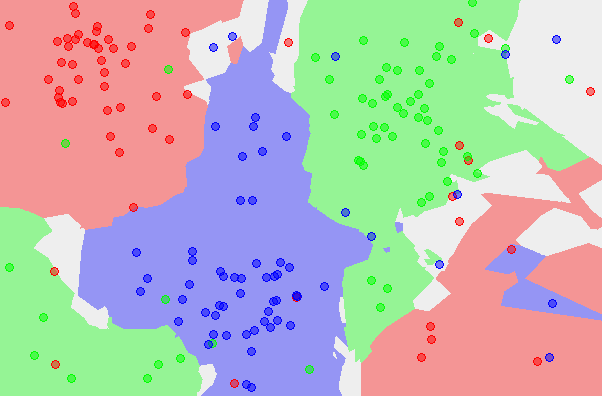
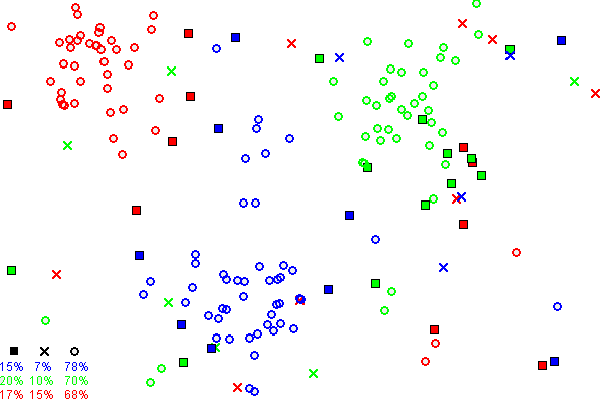
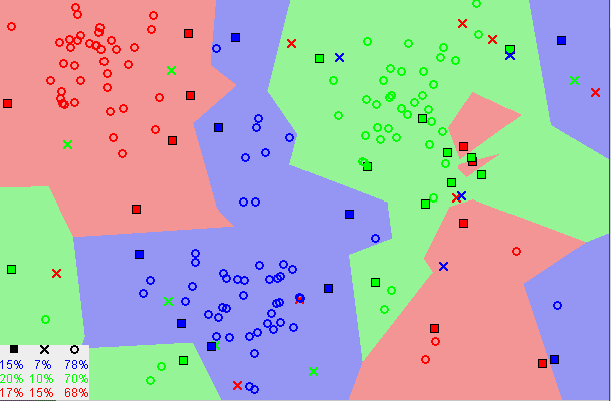
아래 도식은 CNN의 과정을 보여준다. 3개의 항목(빨강, 초록, 파랑)이 있다. 그림 1: 초기에, 각 항목별로 60개의 점이 존재한다. 그림 2: 1NN 분류 지도를 보여주는데, 각각의 픽셀은 모든 데이터를 사용하여 1NN에 의해 분류된다. 그림 3: 5NN 분류 지도를 보여준다. 하얀 구역은 5NN 투표에서 결과가 동률이 나와 분류되지 않은 지역에 대응된다(예를 들어, 5개의 최근접 이웃들 중 2개의 초록, 2개의 빨강과 1개의 파란 점이 있는 경우). 그림 4: 축소된 데이터 집합을 보여준다. X 표시는 (3,2)NN 규칙에 의해 선택된 항목 이상치들을 나타낸다(이 인스턴스들의 모든 세 최근접 이웃들이 다른 항목에 속한다). 사각형은 프로토타입을 나타내며, 빈 원은 흡수된 점을 나타낸다. 좌하측 모서리는 항목 이상치, 프로토타입, 흡수된 점들의 개수를 나타낸다. 이 예시에서는 프로토타입의 수가 항목에 따라 15%에서 20%까지로 다양하다. 그림 5: 프로토타입에 기초한 1NN 분류 지도를 나타낸 것인데, 초기 데이터 집합에 기반한 1NN 분류 지도와 매우 비슷함을 알 수 있다. 이 그림들은 Mirkes 애플릿을 사용하여 만들었다.[27]
6. 통계적 설정
훈련 데이터 집합의 크기가 무한대로 접근함에 따라, 1-최근접 이웃 분류기(k=1)는 베이즈 오류율(데이터의 분포가 주어졌을 때 달성 가능한 최소 오류율)의 두 배보다 나쁘지 않은 오류율을 보장한다.[29]
7. 가중 최근접 이웃 분류기
k-최근접 이웃 분류기는 k개의 가장 가까운 이웃에게 1/k의 가중치를 주고, 나머지 모든 이웃에게는 0의 가중치를 주는 방식으로 볼 수 있다.[9] 이는 가중 최근접 이웃 분류기로 일반화할 수 있는데, 이 경우 i번째로 가까운 이웃에게 ${\displaystyle w_{ni}}$의 가중치를 할당하며, ${\displaystyle \sum _{i=1}^{n}w_{ni}=1}$이다. 가중 최근접 이웃 분류기의 강한 일관성에 대한 유사한 결과도 성립한다.[9]
${\displaystyle C_{n}^{wnn}}$을 가중치 ${\displaystyle \{w_{ni}\}_{i=1}^{n}}$를 갖는 가중 최근접 이웃 분류기라고 하자. 클래스 분포에 대한 규칙성 조건 하에서, 과잉 위험은 다음과 같은 점근적 전개를 가진다.
:${\displaystyle {\mathcal {R}}_{\mathcal {R}}(C_{n}^{wnn})-{\mathcal {R}}_{\mathcal {R}}(C^{\text{Bayes}})=\left(B_{1}s_{n}^{2}+B_{2}t_{n}^{2}\right)\{1+o(1)\},}$
여기서 상수 ${\displaystyle B_{1}}$과 ${\displaystyle B_{2}}$에 대해 ${\displaystyle s_{n}^{2}=\sum _{i=1}^{n}w_{ni}^{2}}$이고 ${\displaystyle t_{n}=n^{-2/d}\sum _{i=1}^{n}w_{ni}\left\{i^{1+2/d}-(i-1)^{1+2/d}\right\}}$이다.
최적 가중치 체계 ${\displaystyle \{w_{ni}^{*}\}_{i=1}^{n}}$는 위 식의 두 항을 균형있게 조정하여 다음과 같이 주어진다. ${\displaystyle k^{*}=\lfloor Bn^{\frac {4}{d+4}}\rfloor }$로 설정하고,
:${\displaystyle w_{ni}^{*}={\frac {1}{k^{*}}}\left[1+{\frac {d}{2}}-{\frac {d}{2{k^{*}}^{2/d}}}\{i^{1+2/d}-(i-1)^{1+2/d}\}\right]}$ (${\displaystyle i=1,2,\dots ,k^{*}}$에 대해) 그리고
:${\displaystyle w_{ni}^{*}=0}$ (${\displaystyle i=k^{*}+1,\dots ,n}$에 대해).
최적 가중치를 사용하면 과잉 위험의 점근적 전개에서 주요 항은 ${\displaystyle {\mathcal {O}}(n^{-{\frac {4}{d+4}}})}$가 된다. 배깅된 최근접 이웃 분류기를 사용할 때도 유사한 결과가 나타난다.
8. 오류율
k-최근접 이웃 분류기의 오류율에 대한 많은 연구 결과가 있다.[15] k-최근접 이웃 분류기는 이 발산하고 이 일 때 0으로 수렴하는 조건에서 강하게(즉, 에 대한 모든 결합 분포에 대해) 일치한다.
크기가 인 훈련 집합을 기반으로 하는 k-최근접 이웃 분류기를 이라고 하자. 특정 규칙성 조건 하에서 초과 위험은 다음과 같은 점근적 전개를 제공한다.[16]
:
여기서 과 는 상수이다.
를 선택하면 위 식의 두 항 사이에서 절충이 가능하며, 이 경우 -최근접 이웃 오류는 최적의 (미니맥스) 비율 로 베이즈 오류로 수렴한다.
9. 응용 분야
K-최근접 이웃 알고리즘(k-NN)은 패턴 인식, 추천 시스템, 의료, 금융, 이상 탐지 등 다양한 분야에 응용된다.
- 패턴 인식: 이미지 인식, 문자 인식, 얼굴 인식 등에 사용된다. 예를 들어, 손글씨 숫자를 인식하는 문제에서 k-NN 알고리즘은 새로운 손글씨 숫자의 특징 벡터를 기존에 학습된 숫자들의 특징 벡터와 비교하여 가장 가까운 k개의 숫자를 찾고, 그중 가장 많은 숫자로 분류한다.
- 추천 시스템: 사용자에게 상품, 영화, 음악 등을 추천하는 데 활용된다. 사용자의 과거 구매 기록이나 선호도를 바탕으로 유사한 사용자를 찾고, 그 사용자들이 선호하는 상품을 추천하는 방식이다.
- 의료: 질병 진단, 유전자 분석 등에 사용된다. 환자의 증상이나 유전자 정보를 바탕으로 유사한 환자들을 찾고, 그 환자들의 질병 정보를 참고하여 진단을 내릴 수 있다.
- 금융: 신용 평가, 주가 예측 등에 활용된다. 개인의 신용 정보나 과거 주가 데이터를 바탕으로 유사한 패턴을 찾고, 이를 통해 신용 등급을 평가하거나 미래 주가를 예측할 수 있다.
- 이상 탐지: 불량품 검출, 네트워크 침입 탐지 등에 사용된다. 정상적인 데이터와 다른 패턴을 보이는 데이터를 이상치로 간주하고, 이를 탐지하는 데 k-NN 알고리즘을 활용할 수 있다. 예를 들어, 제조 공정에서 불량품을 검출하기 위해 제품의 특징 벡터를 정상 제품의 특징 벡터와 비교하여 이상 여부를 판단할 수 있다.[24][25]
참조
[1]
보고서
Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties
https://apps.dtic.mi[...]
USAF School of Aviation Medicine, Randolph Field, Texas
[2]
텍스트
[3]
서적
The elements of statistical learning : data mining, inference, and prediction : with 200 full-color illustrations
Springer
2001
[4]
학술지
Comparing Correlation Coefficients as Dissimilarity Measures for Cancer Classification in Gene Expression Data
[5]
학술지
Alternative k-nearest neighbour rules in supervised pattern recognition : Part 1. k-Nearest neighbour classification by using alternative voting rules
[6]
서적
Miscellaneous Clustering Methods
John Wiley & Sons, Ltd.
[7]
학술지
Melting point prediction employing k-nearest neighbor algorithms and genetic parameter optimization
[8]
학술지
Choice of neighbor order in nearest-neighbor classification
[9]
학술지
Consistent nonparametric regression
[10]
학술지
Variable kernel density estimation
[11]
학술지
Efficient statistical classification of satellite measurements
https://archive.org/[...]
2012-08-09
[12]
학술지
Nearest neighbor pattern classification
http://ssg.mit.edu/c[...]
[13]
학술지
Geometric proximity graphs for improving nearest neighbor methods in instance-based learning and data mining
2005-04
[14]
서적
A Probabilistic Theory of Pattern Recognition
[15]
서적
A probabilistic theory of pattern recognition
Springer
[16]
학술지
Optimal weighted nearest neighbour classifiers
[17]
학술지
When is "nearest neighbor" meaningful?
https://minds.wiscon[...]
[18]
학회
Structure preserving embedding
http://www.cs.columb[...]
[19]
학회
Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining - KDD '01
[20]
서적
High Performance Discovery in Time Series
Springer
[21]
학술지
Output-sensitive algorithms for computing nearest-neighbor decision boundaries
[22]
학술지
The Condensed Nearest Neighbor Rule
[23]
웹사이트
KNN and Potential Energy: applet
http://www.math.le.a[...]
University of Leicester
[24]
학회
Proceedings of the 2000 ACM SIGMOD international conference on Management of data - SIGMOD '00
[25]
학술지
On the evaluation of unsupervised outlier detection: measures, datasets, and an empirical study
[26]
웹사이트
第3章 機械学習(教師あり学習)
https://www.stat.go.[...]
총務省統計研究研修所
[27]
학술지
An introduction to kernel and nearest-neighbor nonparametric regression
[28]
텍스트
[29]
웹사이트
Comparing Correlation Coefficients as Dissimilarity Measures for Cancer Classification in Gene Expression Data
http://citeseerx.ist[...]
Brazilian Symposium on Bioinformatics (BSB 2011)
[30]
학술지
Alternative k-nearest neighbour rules in supervised pattern recognition : Part 1. k-Nearest neighbour classification by using alternative voting rules
[31]
서적
Miscellaneous Clustering Methods
John Wiley & Sons, Ltd
[32]
학술지
Melting point prediction employing k-nearest neighbor algorithms and genetic parameter optimization
[33]
학술지
Choice of neighbor order in nearest-neighbor classification
[34]
학술지
Variable kernel density estimation
[35]
학술지
Efficient statistical classification of satellite measurements
https://archive.org/[...]
2012-08-09
[36]
저널
Nearest neighbor pattern classification
[37]
저널
Geometric proximity graphs for improving nearest neighbor methods in instance-based learning and data mining
2005-04-00
[38]
논문
When is “nearest neighbor” meaningful?
[39]
논문
Structure preserving embedding
ACM
[40]
논문
Random projection in dimensionality reduction: applications to image and text data
ACM
[41]
서적
High Performance Discovery in Time Series
Springer
[42]
저널
Output-sensitive algorithms for computing nearest-neighbor decision boundaries
[43]
저널
The Condensed Nearest Neighbor Rule
[44]
웹사이트
KNN and Potential Energy: applet.
http://www.math.le.a[...]
2012-01-19
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com