대사조절분석

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

대사 조절 분석은 생화학적 경로의 제어 및 조절을 연구하는 데 사용되는 수학적 접근 방식이다. 제어 계수, 합산 정리, 탄력성 계수, 연결성 정리, 반응 계수, 제어 방정식 등을 활용하여 대사 시스템의 특성을 분석한다. 대사 조절 분석은 외부 환경 변화에 대한 시스템의 반응을 이해하고, 약물 개발 등 생명 공학 분야에 기여한다. 다양한 소프트웨어 도구가 개발되어 있으며, 고전 제어 이론과 유사한 개념을 공유한다.

더 읽어볼만한 페이지

시스템 생물학 - 바이오펑크
바이오펑크는 사이버펑크의 하위 장르로, 유전자 재조합 기술 발전 이후의 근미래 사회에서 생명공학 혁명의 결과와 사회 변화를 다루며, 전체주의 정부나 거대 기업이 생명공학을 악용하는 디스토피아적 배경 속에서 인체 실험 결과물의 투쟁을 묘사하고 생명윤리, 사회 정의, 인간성에 대한 철학적 질문을 제기한다.
시스템 생물학 - 세포 신호전달
세포 신호전달은 세포가 환경 변화에 적응하고 다른 세포와 소통하기 위해 사용하는 복잡한 과정이며, 수용체를 통해 신호를 감지하고 다양한 신호전달 경로를 통해 세포의 생리학적 활동을 조절한다.
수리생물학 - 계산신경과학
계산신경과학은 컴퓨터 과학과 신경과학의 융합 분야로, 뇌의 정보 처리 과정을 계산 모델로 연구하며, 뇌 기능 설명, 뉴런 및 신경망 모델링, 인공지능 활용 비교 연구, 계산 임상 신경과학 발전 등을 포함한다.
수리생물학 - Folding@home
Folding@home은 단백질 폴딩 연구를 위해 전 세계 컴퓨터 자원을 활용하여 알츠하이머병, 헌팅턴병 등 질병 연구에 기여하는 분산 컴퓨팅 프로젝트이다.
생화학 기법 - 크산토프로테인 반응
크산토프로테인 반응은 단백질 내 방향족 아미노산이 진한 질산에 의해 니트로화되어 황색으로 변하고, 알칼리성 조건에서 등황색으로 변하는 단백질 검출 및 정성 분석에 사용되는 반응이다.
생화학 기법 - 단백질-단백질 상호작용
단백질-단백질 상호작용은 단백질 간의 결합을 의미하며, 결합의 지속성, 결합력, 구성 단백질 종류에 따라 다양한 유형으로 분류되고, 물 분자에 의해 조절되며, 연구 방법과 데이터베이스를 통해 질병 연구 및 신약 개발에 응용된다.

대사조절분석
대사 조절 분석
Metabolic Control Analysis
분야	생화학, 시스템 생물학
목적	대사 경로 내 효소 및 기타 요인들의 상대적인 영향력 정량화
주요 개념	조절 계수 탄성 계수 플럭스 조절 계수 농도 조절 계수
응용 분야	약물 표적 식별 대사 공학 질병 모델링
관련 용어	대사 경로 효소 기질 플럭스 항상성
역사	1960년대 후반, 헨리히 카셀과 데이비드 번즈에 의해 독립적으로 개발

2. 제어 계수 (Control Coefficients)

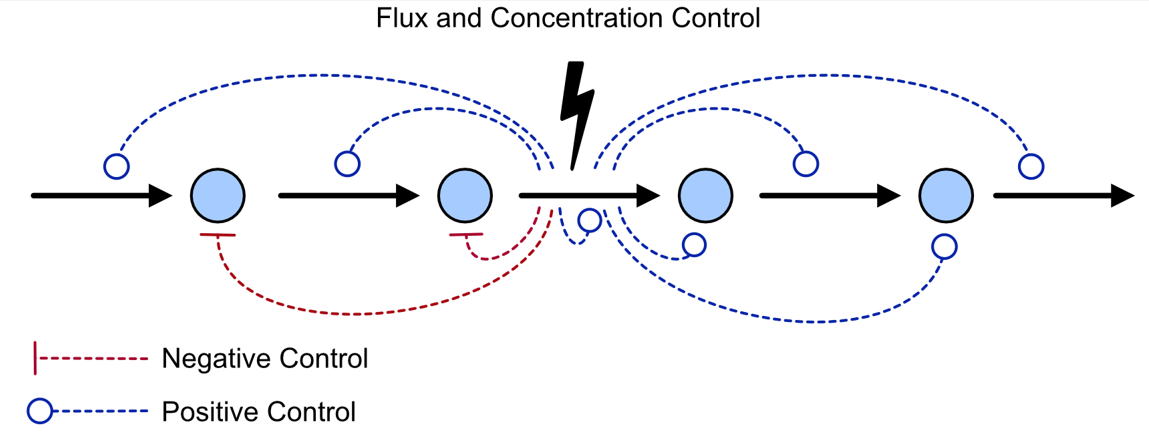
제어 계수^[10]^[11]^[12]는 경로 흐름(J) 또는 대사 산물 농도(S)와 같은 시스템 변수의 상대적인 정상 상태 변화를 매개 변수의 상대적인 변화, 예를 들어 효소 활성 또는 특정 단계 $i$ 의 정상 상태 속도( $v_i$ ) 변화에 대해 측정하는 지표이다. 이는 시스템의 특정 부분(예: 한 효소의 활성)에 변화가 생겼을 때, 전체 시스템의 상태(예: 최종 생성물의 생산 속도 또는 특정 중간 대사 산물의 농도)가 얼마나 민감하게 변하는지를 정량적으로 나타낸다.

주요 제어 계수로는 흐름 제어 계수와 농도 제어 계수가 있다. 흐름 제어 계수는 특정 단계의 변화가 전체 경로의 흐름(flux)에 미치는 영향을 나타내고, 농도 제어 계수는 특정 단계의 변화가 특정 대사 산물의 농도에 미치는 영향을 나타낸다. 각 계수에 대한 자세한 내용은 하위 섹션에서 다룬다.

2. 1. 흐름 제어 계수 (Flux Control Coefficient)

제어 계수^[10]^[11]^[12]는 경로 흐름(J) 또는 대사 산물 농도(S)와 같은 시스템 변수의 상대적인 정상 상태 변화를 매개 변수의 상대적인 변화, 예를 들어 효소 활성 또는 단계

i

의 정상 상태 속도(

v_i

)에 대한 변화를 측정한다.

흐름 제어 계수는 경로 흐름(J)의 변화를 특정 단계

i

의 속도(

v_i

) 변화에 대해 나타내며, 다음과 같이 정의된다.

:

C^J_{v_i} = \left( \frac{dJ}{dp} \frac{p}{J} \right) \bigg/ \left( \frac{\partial v_i}{\partial p}\frac{p}{v_i} \right) = \frac{d\ln J}{d\ln v_i}

2. 2. 농도 제어 계수 (Concentration Control Coefficient)

제어 계수^[10]^[11]^[12]는 경로 흐름(J)이나 대사 산물 농도(S)와 같은 시스템 변수가 매개 변수(예: 효소 활성 또는 단계

i

의 정상 상태 속도

v_i

) 변화에 얼마나 민감하게 반응하는지를 측정하는 지표이다. 즉, 특정 효소의 활성이 변했을 때 전체 시스템의 정상 상태가 얼마나 변하는지를 나타낸다.

여러 제어 계수 중 농도 제어 계수는 특정 대사 산물의 농도(S) 변화가 특정 단계(

i

)의 효소 활성(

v_i

) 변화에 얼마나 영향을 받는지 나타낸다. 이는 다음과 같이 정의된다.

:

C^S_{v_i}  = \left( \frac{dS}{dp} \frac{p}{S} \right)  \bigg/ \left( \frac{\partial v_i}{\partial p} \frac{p}{v_i} \right) = \frac{d\ln S}{d\ln v_i}

이 식은 매개 변수

p

(예: 효소 농도)의 변화에 따른 대사 산물 농도 S의 상대적 변화율을, 동일한 매개 변수 변화에 따른 효소 활성

v_i

의 상대적 변화율로 나눈 값이다. 간단히 말해, 특정 효소의 활성이 약간 변했을 때 특정 대사 산물의 농도가 상대적으로 얼마나 변하는지를 나타내는 값이다.

3. 합산 정리 (Summation Theorems)

대사조절분석에서 합산 정리는 시스템 내 효소들의 조절 기여도를 나타내는 중요한 개념이다. 주요 합산 정리로는 플럭스 조절 합산 정리와 농도 조절 합산 정리가 있으며, 이는 각각 1970년대 초와 1960년대 후반에 카서/번스 그룹^[10]과 하인리히/라포포트 그룹^[11]에 의해 독립적으로 발견되었다.

이러한 정리들은 대사 플럭스나 대사 산물 농도와 같은 시스템 속성이 개별 화학 반응 단계가 아닌, 시스템 내 모든 단계에 의해 공유되고 조절된다는 것을 수학적으로 보여준다. 즉, 특정 단계의 조절 기여도 변화는 시스템 내 다른 단계들의 조절 기여도 변화로 보상되어 전체 시스템의 안정성을 유지하는 원리를 설명한다. 각 합산 정리에 대한 자세한 내용은 해당 하위 섹션에서 다룬다.

3. 1. 플럭스 조절 합산 정리

플럭스 조절 합산 정리는 1970년대 초와 1960년대 후반에 카서/번스 그룹^[10]과 하인리히/라포포트 그룹^[11]에 의해 독립적으로 발견되었다. 플럭스 조절 합산 정리는 대사 플럭스가 시스템적 속성이며 플럭스 조절은 시스템 내의 모든 화학 반응에 의해 공유됨을 함의한다. 단일 반응이 플럭스에 대한 조절을 변경하면, 다른 모든 반응에 의한 동일한 플럭스에 대한 조절 변경으로 보상된다.

:

\sum_i C^J_{v_i} = 1

:

\sum_i C^s_{v_i} = 0

3. 2. 농도 조절 합산 정리

플럭스 조절 합산 정리는 1970년대 초와 1960년대 후반에 카서/번스 그룹^[10]과 하인리히/라포포트 그룹^[11]에 의해 독립적으로 발견되었다. 플럭스 조절 합산 정리는 대사 플럭스가 시스템적 속성이며 플럭스 조절은 시스템 내의 모든 화학 반응에 의해 공유됨을 함의한다. 단일 반응이 플럭스에 대한 조절을 변경하면, 다른 모든 반응에 의한 동일한 플럭스에 대한 조절 변경으로 보상된다.

:

\sum_i C^J_{v_i} = 1

:

\sum_i C^s_{v_i} = 0

4. 탄력성 계수 (Elasticity Coefficients)

탄력성 계수는 효소 또는 기타 화학 반응이 환경 변화에 국소적으로 반응하는 정도를 측정한다. 이러한 변화에는 기질, 생성물, 조절제 농도와 같은 요인이 포함된다. 자세한 내용은 탄력성 계수 문서를 참고하라.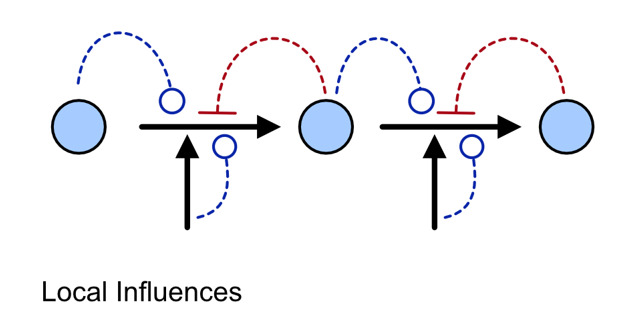

5. 연결성 정리 (Connectivity Theorems)

연결성 정리는^[10]^[11] 탄력성 계수와 조절 계수 사이의 구체적인 관계를 나타낸다. 이 정리는 개별 반응의 동역학적 특성과 경로의 시스템 특성 간의 밀접한 관계를 강조하기 때문에 중요하다. 연결성 정리에는 플럭스에 대한 것과 농도에 대한 것, 두 가지 기본적인 정리 집합이 존재한다.

5. 1. 플럭스 연결성 정리

연결성 정리는^[10]^[11] 탄력성과 조절 계수 사이의 구체적인 관계를 나타낸다. 이 정리는 개별 반응의 동역학적 특성과 경로의 시스템 특성 간의 밀접한 관계를 강조하기 때문에 유용하다. 연결성 정리에는 플럭스에 대한 것과 농도에 대한 것, 두 가지 기본적인 정리 집합이 존재한다.

플럭스 연결성 정리는 다음과 같이 표현된다.

:

\sum_i C^J_i \varepsilon^i_s = 0

5. 2. 농도 연결성 정리

연결성 정리는^[10]^[11] 탄력성과 조절 계수 사이의 구체적인 관계를 나타낸다. 이 정리는 개별 반응의 동역학적 특성과 경로의 시스템 특성 간의 밀접한 관계를 강조하기 때문에 유용하다. 두 가지 기본적인 정리 집합이 존재하며, 하나는 플럭스에 대한 것이고 다른 하나는 농도에 대한 것이다.

농도 연결성 정리는 시스템 종

S_n

과 국소 종

S_m

이 다른 경우(

n \neq m

)와 같은 경우(

n = m

)로 나뉘며, 각각의 관계는 다음과 같다.

:

\sum_i C^{s_n}_i \varepsilon^i_{s_m} = 0 \quad (n \neq m)

:

\sum_i C^{s_n}_i \varepsilon^i_{s_m} = -1 \quad (n = m)

6. 반응 계수 (Response Coefficient)

반응 계수는 Kacser와 Burns에 의해 도입된 개념으로,^[10] 생화학적 경로가 영양소나 약물과 같은 외부 환경 요인에 어떻게 반응하는지를 정량적으로 설명하는 지표이다. 이 계수는 외부 요인이 경로에 미치는 영향을 평가하는 데 사용될 수 있으며, 특히 제약 산업에서 약물의 효과를 예측하고 평가하는 데 중요한 역할을 한다.^[15] 반응 계수의 상세한 정의와 수학적 표현은 아래 섹션에서 다룬다.

6. 1. 반응 계수 정리

Kacser와 Burns는 생화학적 경로가 외부 환경에 어떻게 반응하는지를 설명하기 위해 반응 계수라는 개념을 도입했다.^[10] 이 계수는 기호 R로 표시된다. 반응 계수는 영양소나 약물 등이 경로에 미치는 영향을 평가하는 데 사용될 수 있어 중요한 지표이며, 특히 제약 산업과 밀접한 관련이 있다.^[15]

반응 계수는 다음과 같은 반응 계수 정리를 통해 대사 조절 분석의 핵심 개념과 연결된다.

R^X_m = C^X_{i} \varepsilon^{i}_m

여기서 각 기호는 다음을 의미한다.

$X$ : 플럭스 또는 대사 산물 농도와 같이 선택된 관찰 가능한 값
$i$ : 외부 요인이 목표로 하는 단계
$C^X_{i}$ : 목표 단계의 조절 계수
$\varepsilon^{i}_m$ : 외부 요인 $m$ 에 대한 목표 단계의 탄성도

이 정리의 핵심은 치료 약물과 같은 외부 요인이 두 가지 경로를 통해 유기체의 표현형에 영향을 미친다는 점이다. 첫째는 약물이 표적 단백질에 얼마나 효과적으로 결합하고 단백질 활성에 영향을 미치는가이며, 이는 탄성도

\varepsilon^{i}_m

로 설명된다. 둘째는 표적의 변화가 네트워크의 다른 부분으로 전달되어 최종적으로 표현형에 얼마나 영향을 미치는가이며, 이는 조절 계수

C^X_{i}

로 나타낸다.

따라서 약물 작용이나 다른 외부 요인의 효과는 이 두 가지 요소, 즉 표적에 대한 직접적인 영향(탄성도)과 그 영향이 시스템 전체로 퍼지는 정도(조절 계수)가 모두 클 때 가장 크다. 예를 들어, 약물이 특정 단백질의 활성을 바꾸는 데 매우 효과적이더라도, 그 변화가 최종 표현형에 제대로 전달되지 않으면 약물의 효과는 크게 줄어든다.

만약 약물이나 외부 요인

m

이 여러 작용 부위(예:

n

개의 부위)를 표적으로 삼는다면, 표현형 요인

X

에 대한 전체 반응은 각 부위에서의 개별 반응을 모두 더한 값이다.

R_m^X=\sum_{i=1}^n C_{i}^X \varepsilon_m^{i}

7. 제어 방정식 (Control Equations)

합산 정리와 연결 정리를 결합하면, 특정 경로 내 효소들의 제어 계수(Control Coefficients)를 해당 효소들의 탄성 계수(Elasticity Coefficients)와 관련된 폐쇄형 표현식으로 나타낼 수 있다.^[1] 예를 들어, 간단한 선형 경로에서 각 단계의 효소가 전체 경로의 속도(플럭스, Flux)나 중간 대사물 농도에 미치는 영향을 정량적으로 분석하는 것이 가능하다.

구체적인 예시로, 2단계 또는 3단계로 이루어진 가상의 대사 경로에 대해 합산 정리와 연결 정리를 적용하여 각 효소의 플럭스 제어 계수( $C^J$ )와 농도 제어 계수( $C^S$ )를 유도할 수 있다. 이러한 방정식을 통해 특정 조건에서 어떤 효소가 경로 전체의 속도를 주로 조절하는지(속도 결정 단계) 등을 파악할 수 있다. 하지만 실제 생화학 경로에서는 여러 효소가 복합적으로 제어에 관여하는 경우가 일반적이다.^[1]

7. 1. 2단계 경로 예시

합산 정리와 연결 정리를 결합하면 제어 계수를 탄성 계수와 관련된 폐쇄형 표현식으로 나타낼 수 있다. 가장 간단하면서도 자명하지 않은 경로인 다음 경우를 예로 들어보자.

:

X_o \rightarrow S \rightarrow X_1

여기서

X_o

와

X_1

은 농도가 변하지 않는 고정 경계 종이라고 가정한다. 그래야 경로가 정상 상태에 도달할 수 있다. 첫 번째 단계(

X_o \rightarrow S

)의 속도를

v_1

, 두 번째 단계(

S \rightarrow X_1

)의 속도를

v_2

라고 하자. 이 경로의 플럭스 제어 계수(

C^J

)에 대해 합산 정리와 연결 정리를 적용하면 다음과 같은 두 식을 얻을 수 있다.

:

C^J_{v_1} + C^J_{v_2} = 1

(합산 정리)

:

C^J_{v_1} \varepsilon^{1}_s + C^J_{v_2} \varepsilon^{2}_s = 0

(연결 정리)

여기서

\varepsilon^{1}_s

는 첫 번째 단계의 속도(

v_1

)가 물질 S의 농도 변화에 얼마나 민감한지를 나타내는 탄성 계수이고,

\varepsilon^{2}_s

는 두 번째 단계의 속도(

v_2

)가 물질 S의 농도 변화에 얼마나 민감한지를 나타내는 탄성 계수이다.

이 두 연립 방정식을 풀면 각 단계의 플럭스 제어 계수를 탄성 계수로 표현할 수 있다.

:

C^J_{v_1} = \frac{\varepsilon^{2}_s}{\varepsilon^{2}_s - \varepsilon^{1}_s}

:

C^J_{v_2} = \frac{-\varepsilon^{1}_s}{\varepsilon^{2}_s - \varepsilon^{1}_s}

이 식들을 이용해 특정 상황에서의 경로 제어를 분석할 수 있다. 예를 들어, 첫 번째 단계가 생성물 S의 농도 변화에 전혀 영향을 받지 않는다고 가정해 보자. 즉,

\varepsilon^{1}_s = 0

인 경우이다. 이 경우 플럭스 제어 계수는 다음과 같이 간단해진다.

:

C^J_{v_1} = \frac{\varepsilon^{2}_s}{\varepsilon^{2}_s - 0} = 1

:

C^J_{v_2} = \frac{-0}{\varepsilon^{2}_s - 0} = 0

이 결과는 전체 경로의 플럭스가 전적으로 첫 번째 단계에 의해서만 제어된다는 것을 의미한다. 이런 상황은 흔히 교과서에서 설명하는 속도 결정 단계에 해당한다. 즉, 첫 번째 단계가 전체 반응 속도를 결정하는 병목 지점이 되는 것이다. 하지만 실제 생화학 경로에서 특정 단계가 생성물 농도에 전혀 영향을 받지 않는 경우(

\varepsilon^{1}_s = 0

)는 드물기 때문에, 전형적인 속도 결정 단계가 명확하게 관찰되는 경우는 많지 않다. 대신 여러 단계가 다양한 정도로 플럭스 제어에 기여하는 경우가 일반적이다.

같은 방식으로 중간 대사물 S의 농도 제어 계수(

C^s

)도 유도할 수 있다.

:

C^s_{v_1} = \frac{1}{\varepsilon^{2}_s - \varepsilon^1_s}

:

C^s_{v_2} = \frac{-1}{\varepsilon^{2}_s - \varepsilon^1_s}

7. 2. 3단계 경로 예시

다음과 같은 간단한 3단계 경로를 고려해 볼 수 있다.

:

X_o \rightarrow S_1 \rightarrow S_2 \rightarrow X_1

여기서

X_o

와

X_1

는 고정된 경계 종(boundary species)이다. 이 경로에 대한 제어 방정식은 간단한 2단계 경로와 유사한 방식으로 유도할 수 있지만, 조금 더 복잡하다.

유속 제어 계수는 다음과 같다.

:

C^J_{e_1} = \frac{\varepsilon^{2}_1 \varepsilon^{3}_2}{D}

:

C^J_{e_2} = -\frac{\varepsilon^{1}_1 \varepsilon^{3}_2}{D}

:

C^J_{e_3} = \frac{\varepsilon^{1}_1 \varepsilon^{2}_2}{D}

여기서 분모 D는 다음과 같이 정의된다.

:

D = \varepsilon^{2}_1 \varepsilon^{3}_2 -\varepsilon^{1}_1 \varepsilon^{3}_2 + \varepsilon^{1}_1 \varepsilon^{2}_2

분자의 모든 항이 분모에도 나타나는데, 이는 유속 제어 계수 합산 정리가 충족되도록 한다.

마찬가지로, 농도 제어 계수도 유도할 수 있다. 중간 대사물

S_1

의 경우, 제어 계수는 다음과 같다.

:

C^{S_1}_{e_1} = \frac{\varepsilon^{3}_2 - \varepsilon^{2}_2}{D}

:

C^{S_1}_{e_2} = - \frac{\varepsilon^{3}_2}{D}

:

C^{S_1}_{e_3} = \frac{\varepsilon^{2}_2}{D}

그리고 중간 대사물

S_2

의 경우, 제어 계수는 다음과 같다.

:

C^{S_2}_{e_1} = \frac{\varepsilon^{2}_1}{D}

:

C^{S_2}_{e_2} = -\frac{\varepsilon^{1}_1}{D}

:

C^{S_2}_{e_3} = \frac{\varepsilon^{1}_1 - \varepsilon^{2}_1}{D}

모든 농도 제어 계수에서 분모 D는 유속 제어 계수에서와 동일하며, 정규화 상수로서 작용한다.

8. 교란을 이용한 유도

대사 조절 분석에서는 시스템에 가해진 교란(perturbation)의 영향을 분석하여 제어 방정식을 유도할 수 있다. 예를 들어, 두 효소 $e_1$ 과 $e_2$ 가 각각 반응 속도 $v_1$ 과 $v_2$ 를 결정하는 시스템을 생각해 보자. 이 시스템에서 어느 효소의 양이 변하면 중간 물질 $x$ 의 정상 상태(steady state) 농도와 정상 상태 반응 속도 $v$ 가 변하게 된다.

만약 효소 $e_1$ 의 양에 $\delta e_1$ 만큼의 작은 변화(교란)를 준다고 가정해 보자. 이 변화는 여러 영향을 미치는데, 우선 $v_1$ 을 증가시키고, 이는 다시 $x$ 의 농도를 증가시키며, 결과적으로 $v_2$ 도 증가시킨다. 시간이 지나면 시스템은 새로운 정상 상태에 도달하게 된다. 이 과정을 $v_1$ 과 $v_2$ 의 변화에 초점을 맞춰 설명할 수 있다.

$v_2$ 의 변화량 $\delta v_2$ 는 중간 물질 $x$ 의 변화량 $\delta x$ 때문에 발생한다. 변화량이 작다고 가정하면, 이 관계는 다음과 같이 표현할 수 있다.

: $\delta v_2 = \frac{\partial v_2}{\partial x} \delta x$

여기서 편미분 계수 $\partial v_2/\partial x$ 는 $x$ 의 변화에 대해 $v_2$ 가 얼마나 민감하게 반응하는지를 나타낸다. 만약 $v_2$ 에 대한 속도 법칙을 안다면 (예: $v_2 = k_2 x$ ), 이 계수( $k_2$ )를 계산할 수 있다.

마찬가지로, $e_1$ 의 변화( $\delta e_1$ )로 인한 $v_1$ 의 변화( $\delta v_1$ )도 계산할 수 있다. 이때 $v_1$ 의 변화는 $e_1$ 자체의 변화와 그로 인한 $x$ 의 변화 두 가지 요인에 의해 발생한다. 이를 식으로 나타내면 다음과 같다.

: $\delta v_1 = \frac{\partial v_1}{\partial e_1} \delta e_1 + \frac{\partial v_1}{\partial x} \delta x$

시스템이 새로운 정상 상태에 도달하면, 들어오고 나가는 속도의 변화는 같아야 한다. 즉, $\delta v_1 = \delta v_2$ 가 성립한다. 이 조건을 이용하여 위 두 식을 같다고 놓으면 다음과 같다.

: $\frac{\partial v_2}{\partial x} \delta x = \frac{\partial v_1}{\partial e_1} \delta e_1 + \frac{\partial v_1}{\partial x} \delta x$

이 식을 $\delta x / \delta e_1$ 에 대해 정리하면, $e_1$ 의 변화에 따른 $x$ 의 변화율을 알 수 있다.

: $\frac{\delta x}{\delta e_1} = \dfrac{\dfrac{\partial v_1}{\partial e_1}}{\dfrac{\partial v_1}{\partial x} - \dfrac{\partial v_2}{\partial x}}$

교란 $\delta e_1$ 을 극한으로 작게 만들면( $\delta e_1 \rightarrow 0$ ), 좌변은 미분 계수 $dx/de_1$ 로 수렴한다.

: $\lim_{\delta e_1 \rightarrow 0} \frac{\delta x}{\delta e_1} = \frac{dx}{de_1} = \dfrac{\dfrac{\partial v_1}{\partial e_1}}{\dfrac{\partial v_1}{\partial x} - \dfrac{\partial v_2}{\partial x}}$

이 식의 단위를 없애고 상대적인 변화율로 표현하기 위해 양변에 $e_1/x$ 를 곱하여 스케일링(scaling)할 수 있다. 스케일링된 미분 계수들은 탄성도(elasticity, $\varepsilon$ )와 농도 제어 계수(concentration control coefficient, $C^x_{e}$ )로 정의된다.

: $\frac{dx}{de_1} \frac{e_1}{x}= \frac{\dfrac{\partial v_1}{\partial e_1}\dfrac{e_1}{v_1}}{\left( \dfrac{\partial v_1}{\partial x} - \dfrac{\partial v_2}{\partial x} \right) \dfrac{x}{v}}$

정상 상태에서는 $v_1 = v_2 = v$ 이므로, 식은 다음과 같이 정리된다.

: $C^x_{e_1} = \frac{\varepsilon^1_{e_1}}{\varepsilon^1_x - \varepsilon^2_x}$

여기서 $\varepsilon^1_{e_1}$ 은 $e_1$ 에 대한 $v_1$ 의 탄성도, $\varepsilon^1_x$ 는 $x$ 에 대한 $v_1$ 의 탄성도, $\varepsilon^2_x$ 는 $x$ 에 대한 $v_2$ 의 탄성도를 의미한다.

일반적으로 반응 속도 $v_1$ 은 효소 농도 $e_1$ 에 직접 비례한다 (예: 미카엘리스-멘텐 동역학에서 $v= e_1 k_{cat} x/(K_m + x)$ ). 이 경우, $v_1$ 을 $e_1$ 에 대해 미분하고 스케일링하면 탄성도 $\varepsilon^{v_{1}}_{e_1}$ 는 1이 된다. 이 결과를 적용하면 농도 제어 계수 식은 다음과 같이 단순화된다.

: $C^x_{e_1} = \frac{1}{\varepsilon^1_x - \varepsilon^2_x}$

마찬가지로 효소 $e_2$ 에 교란을 가하여 분석하면, $e_2$ 에 대한 $x$ 의 농도 제어 계수를 얻을 수 있다. (단, $v_2$ 가 $e_2$ 에 직접 비례한다고 가정하면 $\varepsilon^2_{e_2} = 1$ 이다.)

: $C^x_{e_2} = \frac{-\varepsilon^2_{e_2}}{\varepsilon^1_x - \varepsilon^2_x} = \frac{-1}{\varepsilon^1_x - \varepsilon^2_x}$

이 농도 제어 계수들은 각 효소( $e_1$ , $e_2$ )가 중간 물질 $x$ 의 정상 상태 농도를 얼마나 제어하는지를 정량적으로 나타낸다.

같은 방식으로, 효소 농도의 교란이 정상 상태 플럭스(flux, $J$ )에 미치는 영향도 분석할 수 있다. 플럭스는 단위 시간당 대사 경로를 통해 흐르는 물질의 양을 의미하며, 대사 공학(metabolic engineering) 분야에서 생산 속도를 조절하는 데 중요한 지표가 된다. 선형 경로에서는 정상 상태에서 모든 반응 속도가 같으므로 플럭스는 $J$ 로 표현된다 ( $J = v_1 = v_2$ ). 플럭스 제어 계수(flux control coefficient, $C^J_{e}$ )는 다음과 같이 유도된다.

: $C^J_{e_1} = \frac{\varepsilon^2_x}{\varepsilon^2_x - \varepsilon^1_x}, \quad C^J_{e_2} = \frac{-\varepsilon^1_x}{\varepsilon^2_x - \varepsilon^1_x}$

이 식들은 각 효소가 전체 경로의 플럭스를 얼마나 제어하는지를 보여준다. 여기서 핵심은 효소 농도의 변화, 즉 효소 활성은 외부 작용(예: 유전자 발현 조절)에 의해 발생해야 한다는 점이다.

9. 시스템 방정식을 이용한 유도

제어 방정식은 생화학 시스템 방정식을 사용하여 더욱 엄밀하게 유도할 수 있다.

$\dfrac{dt} = {\bf N} {\bf v} ({\bf x} (p), p)$

여기서 ${\bf N}$ 는 화학량론 행렬이고, ${\bf x}$ 는 화학 종의 벡터이며, ${\bf p}$ 는 시스템에 영향을 미칠 수 있는 매개변수(또는 입력)의 벡터이다. 대사 조절 분석에서 핵심 매개변수는 효소 농도이다. 이 접근 방식은 Heinrich, Rapoport 및 Rapoport^[16]와 Reder 및 Mazat에 의해 대중화되었다.^[17] 이 접근 방식에 대한 자세한 내용은 Heinrich & Schuster^[18] 및 Hofmeyr에서 찾을 수 있다.^[19]

10. 선형 경로의 속성 (Properties of a Linear Pathway)

선형 생화학 경로는 일련의 효소 촉매 반응 단계이다. 아래 그림은 중간체 S₁과 S₂를 포함하는 3단계 경로를 보여준다. 정상 상태를 유지하기 위해 경계 종 X_o와 X₁은 고정되어 있다.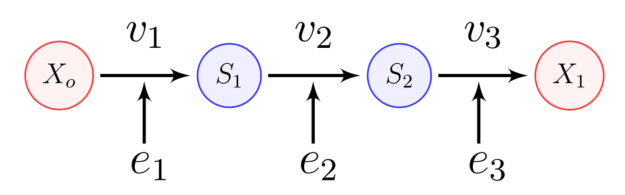

정상 상태에서는 각 단계의 반응 속도가 동일하다. 이는 X_o에서 X₁으로의 전체 플럭스가 존재함을 의미한다.

선형 경로는 다음과 같은 몇 가지 잘 알려진 속성을 가지고 있다:^[20]^[21]^[22]

# 플럭스 조절은 경로의 처음 몇 단계에 편향되는 경향이 있다. 평형 상수가 커질수록 플럭스 조절은 첫 번째 단계로 더 많이 이동한다.

# 플럭스 조절은 평형에 가까운 반응에서는 작다.

# 가역성을 가정하면, 특정 단계의 플럭스 조절은 그 단계 이후의 평형 상수들의 곱에 비례한다. 예를 들어, 3단계 경로에서 두 번째 단계의 플럭스 조절은 두 번째 및 세 번째 평형 상수의 곱에 비례한다.

모든 경우에, 이러한 행동 양식에 대한 근거는 탄력성이 경로를 통해 변화를 전달하는 방식 측면에서 설명될 수 있다.

11. 대사 조절 분석 소프트웨어

대사 조절 분석에서 탄성도 및 조절 계수를 직접 계산할 수 있는 여러 소프트웨어 도구가 있다.

COPASI (GUI)
PySCeS^[23] (파이썬)
SBW^[24] (GUI)
libroadrunner^[25] (파이썬)
VCell

12. 고전 제어 이론과의 관계

고전적인 제어 이론은 공학적 프로세스 및 기계의 동적 시스템 제어를 다루는 수학 분야이다. 2004년 브라이언 잉걸스(Brian Ingalls)는 고전 제어 이론과 대사 조절 분석이 본질적으로 동일하다는 연구를 발표했다.^[26] 잉걸스는 두 이론 간의 유일한 차이점으로 주파수 영역에서의 분석 범위를 지적했다. 대사 조절 분석은 0 주파수 응답에 국한되는 반면, 고전 제어 이론은 이러한 제한이 없다.

또 다른 중요한 차이점은 고전 제어 이론^[27]에는 화학 양론과 질량 보존 개념이 없다는 점이다. 이러한 개념의 부재는 고전 제어 이론의 활용을 더 어렵게 만들 뿐만 아니라, 화학 양론적 네트워크가 가지는 구조적 특성과 그로부터 얻을 수 있는 유용한 생물학적 통찰력을 간과하게 만든다.

참조

_[1] 서적 Understanding the Control of Metabolism Portland Press 1997
_[2] 서적 The Regulation of Cellular Systems Chapman and Hall 1996
_[3] 논문 Metabolic control
_[4] 논문 A Frequency Domain Approach to Sensitivity Analysis of Biochemical Systems 2004
_[5] 서적 Biochemical systems analysis: a study of function and design in molecular biology Addison–Wesley 1976
_[6] 논문 Analysis of sequential reactions
_[7] 논문 Chemical reaction network structure and the stability of complex isothermal reactors—I. The deficiency zero and deficiency one theorems https://linkinghub.e[...] 1987
_[8] 간행물 Stability of Complex Reaction Networks https://onlinelibrar[...] Wiley 2023-12-06
_[9] 논문 Sensitivity and Robustness in Chemical Reaction Networks https://www.jstor.or[...] 2009
_[10] 논문 The control of flux
_[11] 논문 A linear steady-state treatment of enzymatic chains. General properties, control and effector strength
_[12] 논문 Control analysis of metabolic systems
_[13] 논문 Structural Thermokinetic Modelling 2022-05-11
_[14] 논문 Optimal enzyme rhythms in cells 2016
_[15] 논문 Metabolic Control Analysis: A Tool for Designing Strategies to Manipulate Metabolic Pathways 2008
_[16] 논문 Metabolic regulation and mathematical models 1978-01-01
_[17] 논문 Metabolic control theory: A structural approach 1988-11
_[18] 논문 The Regulation of Cellular Systems https://link.springe[...] 1996
_[19] 논문 Metabolic control analysis in a nutshell https://www.academia[...]
_[20] 논문 A Linear Steady-State Treatment of Enzymatic Chains. General Properties, Control and Effector Strength 1974-02
_[21] 서적 Biochemical systems analysis. A study of function and design in molecular biology. Addison-Wesley 1976
_[22] 논문 A brief note on the properties of linear pathways 2020-08-28
_[23] 논문 Modelling cellular systems with PySCeS 2005-02-15
_[24] 서적 Proceedings of the 2006 Winter Simulation Conference 2006-12
_[25] 논문 Tellurium: An extensible python-based modeling environment for systems and synthetic biology 2018-09
_[26] 논문 On the Relationship between Sensitivity Coefficients and Transfer Functions of Reaction Kinetic Networks 2011-05-19
_[27] 서적 Control systems engineering 2019
_[28] 서적 Understanding the Control of Metabolism Portland Press 1997
_[29] 서적 The Regulation of Cellular Systems Chapman and Hall 1996
_[30] 논문 Metabolic control

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com