열저항

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

열저항은 단위 시간당 단위 열 에너지가 구조물을 통과할 때 구조물 양단 간의 온도 차이를 나타내는 척도이다. 열전도율의 역수이며, 전자 부품의 열 관리, 건축 단열, 자동차 설계, 조리 도구 설계 등 다양한 분야에서 활용된다. 열저항은 벌크 열저항과 계면 열저항으로 구분되며, JEDEC 표준에 따라 측정된다. 열 흐름과 전기 흐름 사이의 유사성을 통해 전기 저항에 비유되기도 하지만, 물리적 특성 차이로 인해 차이가 있다. 복합 벽의 열 저항은 직렬 및 병렬 연결을 통해 계산할 수 있으며, 방사형 시스템에서도 열 저항 개념이 적용된다.

더 읽어볼만한 페이지

열전도 - 뉴턴의 냉각 법칙
뉴턴의 냉각 법칙은 물체의 열 손실률이 물체와 주변 환경 간의 온도 차이에 비례하며, 과도 냉각 분석에 활용된다.
열전도 - 히트파이프
히트파이프는 작동 유체의 증발과 응축을 통해 열을 효율적으로 전달하는 폐쇄형 열전달 장치로, NASA의 우주 프로그램에서 위성 트랜스폰더의 열 평형을 위해 개발된 후 컴퓨터 CPU 냉각, 태양열 집열 등 다양한 분야에 적용되고 있다.
전자공학 - 전자전
전자전은 적의 전투 능력을 저하시키기 위해 전자기 에너지를 사용하는 군사 작전이며, 전자 공격, 전자 보호, 전자 지원의 세 가지 영역으로 나뉘어 통신 방해, 레이더 교란, 스텔스 기술 등을 포함한다.
전자공학 - 옴의 법칙
옴의 법칙은 1827년 게오르크 옴이 발표한, 전압(V)은 전류(I)와 저항(R)의 곱(V=IR)으로 표현되는, 전압, 전류, 저항 간의 관계를 나타내는 기본 법칙이다.

열저항
열전도율 및 열저항
일반 정보
기호	G (열전도율), R (열저항), θ
단위	와트/켈빈 (W/K) (열전도율), 켈빈/와트 (K/W) (열저항)
기본 단위	kg⋅m²⋅s⁻³⋅K⁻¹ (열전도율), kg⁻¹⋅m⁻²⋅s³⋅K (열저항)
차원	L²MT⁻³Θ⁻¹ (열전도율)
상세 정보
열전도율	열을 전달하는 능력
열저항	열 흐름에 대한 저항
설명
열전도율 정의	온도가 1켈빈(K) 차이 날 때, 물체가 단위 시간당 전달하는 열에너지의 양.
열저항 정의	주어진 온도차에 의해 단위 시간당 전달되는 열에너지에 대한 온도차의 비.
관련 항목
관련 개념	열전도 열관류율 열용량 열확산율 단열

2. 열저항의 정의 및 종류

열저항은 크게 두 가지로 나눌 수 있다.

벌크 열저항: 일반적으로 열저항이라고 불리는, 균질한 물체 내부의 열저항이다.
계면 열저항 (접촉 열저항^[10]): 균질한 두 물체가 접촉하는 계면에서의 열저항이다.

2. 1. 벌크 열저항

일반적으로 열저항이라고 불리는, 균질한 물체 내부의 열저항을 벌크 열저항이라고 한다. 복합 재료로 이루어진 복합체의 열저항은 진정한 의미의 벌크 열저항은 아니지만, 균질하다고 간주할 수 있는 계에서는 벌크 열저항으로 생각하는 경우가 많다.

2. 2. 계면 열저항 (접촉 열저항)

서로 다른 두 물체가 접촉하는 계면에서의 열저항을 계면 열저항 또는 접촉 열저항이라고 부른다.^[10] 이 열저항은 접촉면의 요철, 표면 거칠기, 압착 압력, 접촉하고 있는 물체의 경도, 열전도율, 접촉면에 개재되어 있는 물질의 열전도율, 접촉면의 산화 상태에 따라 증감한다. 미시적인 시점에서 본 경우, 단량체 레벨에서의 화학 결합에 의존하지 않는 복합체에서도 그 복합체에는 계면 열저항이 존재한다.

일반적으로 측정에는 각 물체의 벌크 열저항과 복합시켰을 경우의 열저항의 차이로부터 산출하지만, 한쪽 물체의 막 두께가 매우 작은 경우에는 '''열 반사율법''' 등을 이용하여 직접 측정하는 것도 가능하다.

3. 열저항의 측정 및 표준

접합부-공기 간 열 저항은 주변 조건에 따라 크게 달라질 수 있으며, 이는 접합부-주변 열 저항이 경계 조건 독립적(BCI)이 아니라는 것을 의미한다.^[3]^[4] JEDEC는 전자 패키지의 열 저항 측정을 위한 표준을 제공한다.

표면 실장 기술 관련 접합부-보드 간 열 저항 측정을 위한 JEDEC 표준은 JESD51-8이다.^[5]

접합부-케이스 간 열 저항 측정을 위한 JEDEC 표준(JESD51-14)은 비교적 최근에 발표된 표준이다.^[6]^[7]^[8]

3. 1. 전자 부품 열저항 측정

접합부-공기 간 열 저항은 주변 조건에 따라 크게 달라질 수 있다.^[3] 이는 접합부-주변 열 저항이 경계 조건 독립적(BCI)이 아니라는 의미이다.^[4] JEDEC는 자연 대류 조건에서 전자 패키지의 접합부-공기 간 열 저항을 측정하기 위한 표준(JESD51-2)과 강제 대류 조건에서 측정하기 위한 또 다른 표준(JESD51-6)을 가지고 있다.

표면 실장 기술과 관련된 접합부-보드 간 열 저항 측정을 위한 JEDEC 표준은 JESD51-8이다.^[5]

접합부-케이스 간 열 저항 측정을 위한 JEDEC 표준(JESD51-14)은 2010년 말에 출판된 비교적 새로운 표준으로, 단일 열 흐름과 노출된 냉각 표면을 가진 패키지만을 다룬다.^[6]^[7]^[8]

4. 열저항의 응용

열전도율과 열저항은 건축 단열, 전자 냉각, 자동차 설계, 조리 도구 설계, 열교환기, 항공우주, 극저온 공학, 에너지 효율, 의료 기기, 식품 가공, 재료 과학, 환경 과학, 난방, 환기 및 공조(HVAC), 열 포장, 태양 에너지 시스템, 제조 공정, 지열 에너지, 열화상 등 다양한 분야에서 응용된다.

건축 단열: 에너지 효율적인 건물 설계를 위해 단열재를 사용하여 열 전달을 줄인다.
전자 냉각: 전자 부품의 과열을 방지하기 위해 방열판 및 열 관리 시스템을 설계한다.
자동차 설계: 자동차 엔진 부품 및 냉각 시스템 설계에 열저항이 고려된다.
조리 도구 설계: 균일한 열 분배와 효율적인 조리를 위해 열전도율이 중요하다.
열교환기: 유체 간 효율적인 열 전달을 위해 열전도율이 사용된다.
항공우주: 극한 환경에서 온도 변화 관리를 위해 열저항 및 열전도율이 중요하다.
극저온 공학: 극저온 시스템 설계에 열 특성 이해가 필수적이다.
에너지 효율: 효율적인 열교환기 설계에 열저항 및 열전도율이 활용된다.
의료 기기: 정확한 작동 온도 유지에 열 관리가 중요하다.
식품 가공: 공정 최적화와 장비 설계에 열전도율 지식이 사용된다.
재료 과학: 신소재 개발에 열전도율 데이터가 사용된다.
환경 과학: 열 전달 이해 및 토양 온도 프로파일 연구에 열저항이 고려된다.
난방, 환기 및 공조(HVAC): HVAC 시스템 최적화에 열저항 이해가 활용된다.
열 포장: 민감한 제품 보호를 위해 열전도율 및 열저항 보장이 중요하다.
태양 에너지 시스템: 태양열 집열기 및 열 에너지 저장 시스템 설계에 열저항 이해가 중요하다.
제조 공정: 열전도율 제어가 필수적이다.
지열 에너지: 지열 열교환기 및 에너지 생산에 열전도율이 활용된다.
열화상: 온도 변화 감지를 위해 열전도율 원리가 사용된다.

4. 1. 전자 냉각

전자 부품의 과열을 방지하기 위해 방열판 및 열 관리 시스템 설계에 열저항 개념이 활용된다.^[1]

4. 2. 건축 단열

에너지 효율적인 건물 설계를 위해 단열재를 사용하여 열 전달을 줄이는 데 열저항에 대한 이해가 도움이 된다.^[1]

4. 3. 자동차 설계

자동차 엔지니어는 열저항을 사용하여 냉각 시스템을 최적화하고 엔진 및 기타 차량 부품의 과열을 방지한다.^[1] 엔진 부품 및 자동차 냉각 시스템을 설계할 때 열저항을 평가한다.^[1] 대한민국의 자동차 산업은 현대자동차와 기아를 중심으로 친환경차 개발에 주력하고 있으며, 이에 따라 배터리 및 모터의 열 관리 기술이 중요해지고 있다.

4. 4. 조리 도구 설계

열전도율은 균일한 열 분배와 조리 효율을 보장하기 위해 조리 도구 설계를 할 때 중요하다. 열전도율을 평가하면 균일하게 열이 분배되도록 조리 도구를 설계할 수 있다.

4. 5. 열교환기

난방, 환기 및 공조(HVAC) 및 화학 처리와 같은 산업에서 열교환기는 유체 간에 열을 효율적으로 전달하기 위해 열전도율을 사용한다.

4. 6. 항공우주

우주선 및 항공기에서 열저항 및 열전도율은 극한 환경에서 온도 변화를 관리하는 데 중요하다. 우주선 및 항공 시스템을 설계하려면 온도 극단을 관리하기 위해 열전도율과 열저항을 고려해야 한다.

4. 7. 극저온 공학

초전도체 및 의료 응용 분야에 사용되는 극저온 시스템 설계를 위해서는 열 특성에 대한 이해가 필수적이다.^[1]

4. 8. 에너지 효율

에너지 부문에서 발전소 및 에너지 효율적인 기기의 효율적인 열교환기 설계에 열저항 및 열전도율이 활용된다.

4. 9. 의료 기기

자기 공명 영상(MRI) 장치 및 레이저 시스템과 같은 의료 기기에서 정확한 작동 온도를 유지하는 데 열 관리가 중요하다. 적절한 열 관리를 보장하는 것은 의료 기기 및 레이저 시스템의 안전과 성능에 매우 중요하다.^[1]

4. 10. 식품 가공

식품 산업은 살균 및 요리와 같은 공정을 최적화하고 오븐 및 냉장 장치와 같은 식품 가공 장비를 설계하기 위해 열전도율에 대한 지식을 사용한다.

4. 11. 재료 과학

연구자들은 에너지 저장 및 고급 코팅을 포함한 다양한 응용 분야를 위해 열전도율 데이터를 사용한다.^[1]

4. 12. 환경 과학

기후 연구에서 지구의 대기 및 해양에서의 열 전달을 이해하기 위해 열저항을 고려한다.^[1] 환경 및 농업 연구를 위해 토양 온도 프로파일을 연구하는 데에도 열저항 평가가 유용하다.^[1]

4. 13. 난방, 환기 및 공조(HVAC)

열저항에 대한 이해는 더 나은 에너지 효율성을 위해 난방, 환기 및 공조(HVAC) 시스템을 최적화하는 데 도움이 된다.^[1]

4. 14. 열 포장

운송 중 민감한 제품을 보호하려면 적절한 열전도율과 열저항을 보장하는 것이 중요하다.^[1]

4. 15. 태양 에너지 시스템

태양 에너지 시스템에서 열저항을 이해하는 것은 태양열 집열기 및 열 에너지 저장 시스템 설계를 위해 중요하다.

4. 16. 제조 공정

용접, 열처리, 금속 주조 등의 공정에서는 열전도율 제어가 필수적이다.^[1]

4. 17. 지열 에너지

지열 열교환기 및 에너지 생산에 열전도율을 활용한다.

4. 18. 열화상

적외선 카메라 및 열화상 장치는 온도 변화를 감지하기 위해 열전도율의 원리를 사용한다.

5. 절대 열 저항

절대 열 저항은 단위 시간 동안 단위 열 에너지가 구조물을 통과할 때 구조물 양단 간의 온도 차이를 나타낸다. 이는 열전도도의 역수이다. 절대 열 저항의 SI 단위는 켈빈/와트(K/W) 또는 이와 동일한 섭씨 온도/와트(°C/W)이다. (두 단위는 간격이 같으므로 동일하다: Δ''T'' = 1 K = 1 °C.)

재료의 열 저항은 대부분의 전기 부품이 열을 발생시키고 냉각이 필요하기 때문에 전자 공학자들에게 매우 중요하다. 전자 부품은 과열되면 오작동하거나 고장나며, 일부 부품은 이를 방지하기 위해 설계 단계에서 정기적으로 조치를 취해야 한다.

6. 전기 저항과의 유사성 및 문제점

열 흐름과 전류 흐름 사이에는 유사성이 있기 때문에 열저항을 전기 저항에 비유하여 설명하기도 한다. 옴의 법칙에 익숙한 전기 기술자들은 열저항 관련 계산을 할 때 옴의 법칙을 비유로 자주 사용한다.^[2]

유형	열적	전기적 비유
물리량	열 $Q$ [J]	전하 $q$ [C]
전위	온도 $T$ [K]	전위 $V$ [V = J/C]
플럭스	열전달률 $\dot{Q}$ [W = J/s]	전류 $I$ [A = C/s]
플럭스 밀도	열 플럭스 $\mathbf{q}$ [W/m²]	전류 밀도 $\mathbf{j}$ [C/(m²·s) = A/m²]
저항	열저항 $R$ [K/W]	전기 저항 $R$ [Ω]
컨덕턴스	열 컨덕턴스 $G$ [W/K]	전기 컨덕턴스 $G$ [S]
비저항	열 비저항 [(m·K)/W]	전기 비저항 $\rho$ [Ω·m]
전도율	열전도율 $k$ [W/(m·K)]	전기 전도율 $\sigma$ [S/m]
집중 요소 선형 모델	뉴턴 냉각 법칙 $\Delta T = \dot{Q} R$	옴의 법칙 $\Delta V = IR$
분산 선형 모델	푸리에 법칙 $\mathbf{q} = - k \boldsymbol{\nabla} T$	옴의 법칙 $\mathbf{J} = \sigma \mathbf{E} = -\sigma \boldsymbol{\nabla} V$

푸리에 법칙(열전도)과 옴의 법칙(전류)은 유사한 형태를 가지지만, 열전도율과 전기 전도율의 물리적 특성 차이 때문에 정상적인 상황에서 열 흐름과 전기 흐름은 다르게 작동한다. 필립스 연구원 클레멘스 J. M. 라산스는 2008년에 발표한 논문에서, 전기적 관점에서 절연체는 도체보다 약 20 자릿수나 덜 전도성이 있는 반면, 열적 관점에서 "절연체"와 "도체"의 차이는 약 3 자릿수에 불과하다고 언급했다. 따라서 전기 저항과 열 저항 사이에 실질적인 유사성이 있다고 결론짓는 것은 적절하지 않다.^[4]

7. 복합 벽에서의 열 저항

복합 벽에서 열은 직렬 및 병렬 경로를 통해 전달될 수 있다. 여러 층으로 구성된 벽을 통과하는 열전달을 고려할 때, 열 저항의 개념을 활용하는 것이 유용하다.

직렬로 연결된 열 저항의 경우, 전체 열 저항은 각 저항의 합과 같다. 병렬로 연결된 열 저항의 경우, 전체 열 저항은 각 저항의 역수의 합의 역수로 계산된다.

열 흐름이 다차원적일 때, 등온 표면 또는 단열 표면을 가정하여 열 저항을 계산할 수 있다. 실제 열전달 값은 이러한 가정에 따라 달라질 수 있으며, 전도율 차이가 클수록 그 차이는 더 커진다.^[9]

7. 1. 직렬 열 저항

저항이 직렬로 연결된 경우, 전체 저항은 각 저항의 합과 같다.

:

R_ { \rm tot } = R_A + R_B + R_C + ...

7. 2. 병렬 열 저항

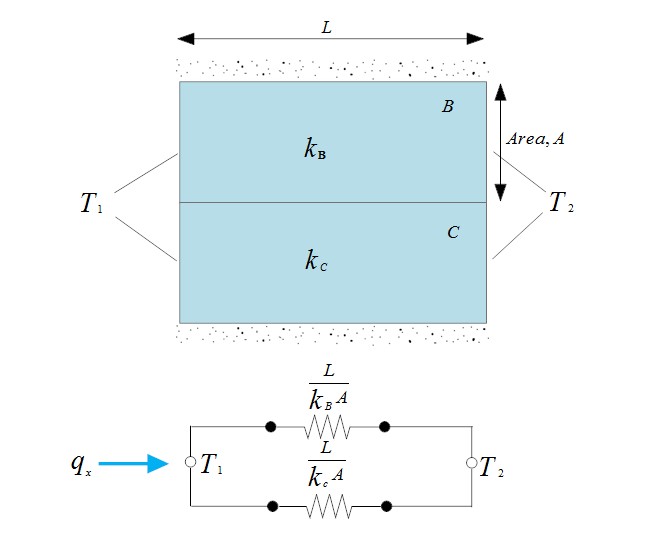
전기 회로와 유사하게 정상 상태 조건에서 총 열 저항은 다음과 같이 계산할 수 있다.

:

{ {1 \over R_{\rm tot}} = {1 \over R_B} + {1 \over R_C} }

위 식을 단순화하면 다음과 같다.

:

{R_{\rm tot} = {R_B R_C \over R_B + R_C} }

전도에 대한 열 저항 항을 사용하면 다음을 얻는다.

:

{R_{t,\rm cond} = {L \over (k_b + k_c)A}}

7. 3. 직렬 및 병렬 조합 열 저항

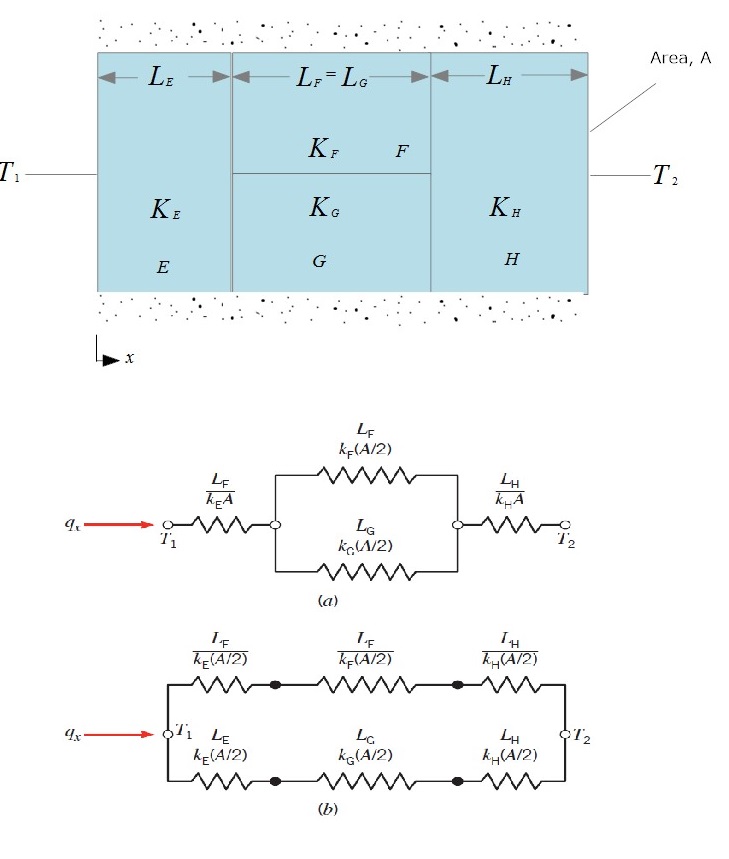
열 흐름이 다차원적임에도 불구하고, 일차원 조건을 가정하는 것이 적합한 경우가 종종 있다. 이러한 경우, 두 가지 다른 회로를 사용할 수 있다. 그림 (a)의 경우, x 방향에 수직인 표면에 대해 등온 표면을 가정하고, (b)의 경우 x 방향에 평행한 단열 표면을 가정한다. 총 저항

R_{tot}

과 열 전달의 실제 해당 값에 대해 서로 다른 결과를 얻을 수 있으며,

q

로 묶인다. 다차원 효과가 더 중요해지면 이러한 차이는

k_f - k_g

가 증가함에 따라 커진다.^[9]

8. 방사형 시스템에서의 열 저항

구형 및 원통형 시스템은 반경 방향의 온도 구배로 인해 1차원 시스템으로 취급될 수 있다. 정상 상태 조건에서 방사형 시스템을 분석하는 데에는 표준 방법을 사용할 수 있으며, 이는 열 방정식의 적절한 형태 또는 푸리에의 법칙의 적절한 형태로 시작하는 대체 방법으로 시작한다.^[9] 열 발생이 없는 정상 상태 조건의 속이 빈 원통의 경우, 열 방정식의 적절한 형태는 다음과 같다.

: ${ {1 \over r}{d\over dr} \left(kr{dT \over dr} \right) = 0 }$

여기서 ${k}$ 는 변수로 취급된다. 푸리에의 법칙의 적절한 형태를 고려할 때, ${k}$ 를 변수로 취급하는 것의 물리적 의미는 원통형 표면을 가로질러 에너지가 전도되는 속도를 고려할 때 분명해지며, 이는 다음과 같이 나타낸다.

: ${ q_r = -kA {dT \over dr} = -k(2\pi rL){dT \over dr}}$

여기서 ${A = 2\pi rL}$ 는 열 전달이 발생하는 방향에 수직인 면적이다. 식 1은 양 ${kr(dT/dr)}$ 이 반경 ${r}$ 에 의존하지 않음을 의미하며, 식 5에서 열 전달 속도 ${q_r}$ 은 반경 방향에서 상수임을 알 수 있다.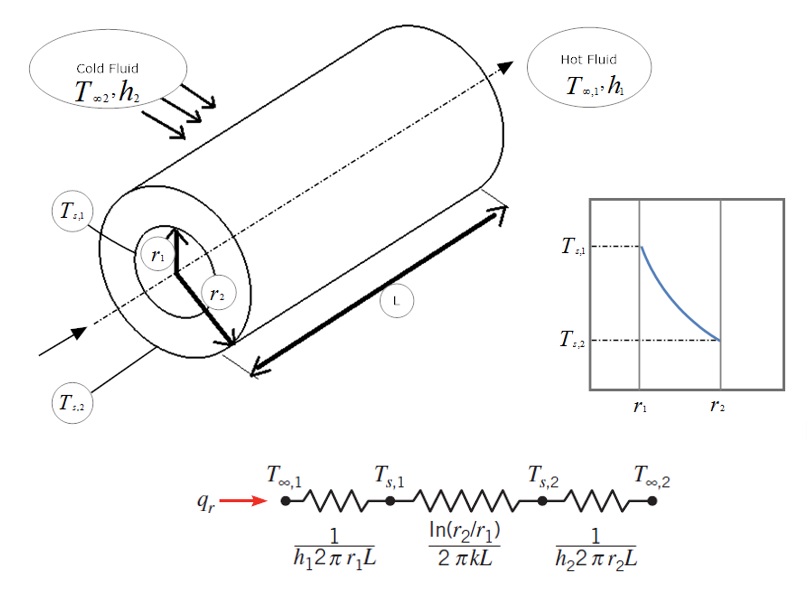

원통 내의 온도 분포를 결정하기 위해, 식 4는 적절한 경계 조건을 적용하여 풀 수 있다.

{k }

가 상수라고 가정하면

:

{ T(r) = C_1\ln r + C_2 }

다음 경계 조건을 사용하여 상수

{C_1}

과

{C_2}

를 계산할 수 있다.

:

{ T(r_1) = T_{s,1} }

그리고

{ T(r_2) = T_{s,2} }

일반 해는 다음과 같다.

:

{ T_{s,1} = C_1 \ln r_1 + C_2 }

그리고

{ T_{s,2} = C_1 \ln r_2 + C_2 }

{C_1}

과

{C_2}

를 풀고 일반 해에 대입하면 다음을 얻는다.

:

{ T(r) = {T_{s,1} - T_{s,2} \over {\ln(r_1/r_2) } } \ln \left( {r \over r_2} \right) + T_{s,2} }

온도의 로그 분포는 썸네일 그림에 스케치되어 있다.

식 7의 온도 분포를 식 5의 푸리에의 법칙과 함께 사용하면, 열 전달 속도는 다음과 같은 형태로 표현될 수 있다.

:

{\dot{Q}_r = {2\pi Lk (T_{s,1} - T_{s,2}) \over \ln(r_2/r_1)} }

마지막으로, 원통형 벽의 방사형 전도에서 열 저항은 다음과 같다.

:

{ R_{t,\mathrm{cond}}  = {\ln(r_2/r_1) \over 2\pi Lk}               }

여기서

{r_2 > r_1}

참조

_[1] 간행물 Using FEA for Thermal Analysis Desktop Engineering magazine 2014-06
_[2] 웹사이트 The Design of Heatsinks http://sound.whsites[...] 2016-09-05
_[3] 서적 Advanced Flip Chip Packaging https://archive.org/[...] Springer Science & Business Media
_[4] 논문 Ten Years of Boundary-Condition- Independent Compact Thermal Modeling of Electronic Parts: A Review
_[5] 서적 Heat Transfer: Thermal Management of Electronics CRC Press
_[6] 서적 Thermal Management for LED Applications Springer Science & Business Media
_[7] 웹사이트 Experiment vs. Simulation, Part 3: JESD51-14 http://www.electroni[...] 2013-02-22
_[8] 컨퍼런스 2011 27th Annual IEEE Semiconductor Thermal Measurement and Management Symposium
_[9] 서적 Principles of Heat and Mass Transfer John Wiley & Sons; 7th Edition, Interna edition 2013
_[10] 서적 伝熱工学資料丸善

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com