처짐각법

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 처짐각 방정식
- 2.1. 처짐각 방정식의 유도
3. 평형 조건
- 3.1. 절점 평형
- 3.2. 전단 평형
4. 해석 절차
5. 예제
참조

1. 개요

처짐각법은 구조물의 변위와 처짐각을 이용하여 부재 단부에 발생하는 모멘트를 계산하는 구조 해석 방법이다. 처짐각 방정식은 부재의 강성도, 처짐, 처짐각을 통해 모멘트를 나타내며, 절점 평형과 전단 평형 조건을 만족해야 한다. 이 방법은 절점의 회전각을 미지수로 하여 연립 방정식을 풀고, 이를 통해 재단 모멘트를 계산하는 방식으로 구조물을 해석한다.

더 읽어볼만한 페이지

구조역학 - 가상일
가상일은 역학계에서 외력이 가상 변위에 대해 하는 일의 합으로, 정역학에서는 계의 정적 평형 조건으로 활용되며, 달랑베르 원리를 통해 동역학에도 적용되어 구조 해석 및 계산에 널리 쓰이는 물리량이다.
구조역학 - 거더
교량 건설에 사용되는 구조 부재인 거더는 하중을 지지하며, 시공 방식과 형태에 따라 다양하게 제작된다.

처짐각법
개요
명칭	처짐각법
영문 명칭	Slope deflection method
일본어 명칭	たわみ角法 (たわみかくほう)
설명	구조물의 부재 양단에서 발생하는 모멘트를 처짐각과 부재의 상대 변위를 사용하여 계산하는 구조 해석 방법이다.
역사
개발자	조지 A. 마니
개발 연도	1915년
참고 문헌	Studies in Engineering
특징
적용 가능 구조물	연속보 라멘 구조
고려 사항	휨 변형 전단 변형 무시 (일반적인 가정)
장점	부정정 구조물의 해석에 효과적이다. 컴퓨터를 이용한 해석에 적합하다.
단점	계산 과정이 복잡할 수 있다. 고차 부정정 구조물에 적용 시 계산량이 많아진다.
관련 개념
관련 이론	구조역학 재료역학
관련 방법	모멘트 분배법 직접 강성법

2. 처짐각 방정식

처짐각 방정식은 구조물의 각 절점에서 발생할 수 있는 변위(자유도)로 인해 부재의 끝단(부재단)에 생기는 모멘트를 부재의 강성도와 부재 양단의 변위, 즉 처짐과 처짐각으로 나타내는 식이다. 부재 AB의 A단과 B단에서 발생하는 모멘트 $M_{ab}$ , $M_{ba}$ 는 각각 다음과 같이 표현된다.

: $M_{ab} = \frac{EI_{ab}}{L_{ab}} \left( 4 \theta_a + 2 \theta_b - 6 \frac{\Delta}{L_{ab}} \right)$

: $M_{ba} = \frac{EI_{ab}}{L_{ab}} \left( 2 \theta_a + 4 \theta_b - 6 \frac{\Delta}{L_{ab}} \right)$

여기서 $\theta_a$ , $\theta_b$ 는 각각 A단과 B단의 처짐각이며, $\Delta$ 는 A와 B 지점 사이의 상대적인 처짐(상대변위)이다. $L_{ab}$ 는 부재의 길이, $E$ 는 탄성 계수, $I_{ab}$ 는 부재의 단면 이차 모멘트이며, $EI_{ab}$ 는 부재의 휨 강성을 나타낸다.

처짐각 방정식은 종종 강도계수 $K=\frac{I_{ab}}{L_{ab}}$ 와 부재 양단을 연결하는 직선의 회전각인 현회전각 $\psi =\frac{ \Delta}{L_{ab}}$ 를 도입하여 다음과 같이 더 간단한 형태로 나타내기도 한다.

: $M_{ab} = 2EK \left( 2 \theta_a + \theta_b - 3 \psi \right)$

: $M_{ba} = 2EK \left( \theta_a + 2 \theta_b - 3 \psi \right)$

2. 1. 처짐각 방정식의 유도

처짐각 방정식은 구조물의 각 점이 움직일 수 있는 방향(자유도)에 해당하는 변위가 발생했을 때, 기둥이나 보와 같은 구조 부재의 끝부분(부재단)에 생기는 모멘트를 부재의 강성도와 부재 양단의 변위(처짐과 처짐각)로 나타내는 식이다. 부재 AB의 A단과 B단에 발생하는 모멘트

M_{ab}

,

M_{ba}

는 각각 다음과 같이 표현된다.

:

M_{ab} = \frac{EI_{ab}}{L_{ab}} \left( 4 \theta_a + 2 \theta_b - 6 \frac{\Delta}{L_{ab}} \right)

:

M_{ba} = \frac{EI_{ab}}{L_{ab}} \left( 2 \theta_a + 4 \theta_b - 6 \frac{\Delta}{L_{ab}} \right)

여기서

\theta_a

,

\theta_b

는 각각 A단과 B단의 처짐각이며,

\Delta

는 A와 B 지점 사이의 상대적인 처짐(상대변위)이다.

L_{ab}

는 부재의 길이,

E

는 탄성 계수,

I_{ab}

는 부재의 단면 이차 모멘트이며,

EI_{ab}

는 부재의 휨 강성을 나타낸다.

처짐각 방정식은 때때로 강도계수(stiffness factor)

K=\frac{I_{ab}}{L_{ab}}

와 부재 양단을 연결하는 직선의 회전각인 현회전각

\psi =\frac{ \Delta}{L_{ab}}

를 도입하여 다음과 같이 더 간단한 형태로 나타내기도 한다.

:

M_{ab} = 2EK \left( 2 \theta_a + \theta_b - 3 \psi \right)

:

M_{ba} = 2EK \left( \theta_a + 2 \theta_b - 3 \psi \right)

이 처짐각 방정식을 유도하기 위해, 경간 길이

L_{ab}

와 휨 강성

EI_{ab}

를 가진 단순 보 AB를 생각해보자. 이 보의 양단에 각각 시계방향으로 모멘트 하중

M_{ab}

,

M_{ba}

가 작용하면, 하중의 작용 방향과 같은 방향으로 처짐각

\theta_a

,

\theta_b

가 발생한다. 또한, 지점 A와 B 사이의 상대적인 처짐

\Delta

로 인해 시계방향의 현회전각

\psi = \Delta/L_{ab}

가 발생한다고 가정한다.

이때, 단위하중법이나 모멘트면적법과 같은 구조 역학의 원리를 이용하면 부재 양단의 모멘트와 처짐각, 현회전각 사이의 관계를 다음과 같이 유도할 수 있다.

:

\theta_a - \frac{\Delta}{L_{ab}}= \frac{L_{ab}}{3EI_{ab}} M_{ab} - \frac{L_{ab}}{6EI_{ab}} M_{ba}

:

\theta_b - \frac{\Delta}{L_{ab}}= - \frac{L_{ab}}{6EI_{ab}} M_{ab} + \frac{L_{ab}}{3EI_{ab}} M_{ba}

위의 두 식은 각각 A단과 B단에서의 처짐각(

\theta_a

,

\theta_b

)과 현회전각(

\Delta/L_{ab}

)의 관계를 양단의 모멘트(

M_{ab}

,

M_{ba}

)로 나타낸 것이다. 이 두 식을 연립하여

M_{ab}

와

M_{ba}

에 대해 풀면, 처짐각

\theta_a

,

\theta_b

와 현회전각

\Delta/L_{ab}

로 양단 모멘트를 표현하는 처짐각 방정식을 얻을 수 있다.

3. 평형 조건

처짐각법에서 구조물의 평형을 해석하기 위해서는 두 가지 주요 평형 조건을 고려해야 한다. 첫째는 각 절점에서의 모멘트 평형이고, 둘째는 특정 상황에서 필요한 전단 평형이다.

절점 평형은 각 절점에 연결된 부재들의 끝단 모멘트(고정단 모멘트 포함)와 해당 절점에 직접 작용하는 외부 모멘트의 합이 0이 되어야 한다는 조건이다. 이는 구조물의 모든 절점에서 만족되어야 한다.

횡방향 변위나 지점 침하 등으로 인해 부재가 회전(현회전각 발생)하는 경우에는 절점 평형 조건만으로는 부족하며, 추가적으로 전단력 평형 조건을 고려해야 한다.

3. 1. 절점 평형

절점 평형 방정식은 각 부재의 재단 모멘트(member end moment)로 인해 각 절점에서 발생하는 모멘트의 평형을 나타내는 식이다. 즉, 특정 절점에 작용하는 고정단 모멘트와 그 절점에 연결된 모든 부재의 재단 모멘트의 합이 절점에 직접 가해지는 외부 모멘트와 같아야 한다는 조건이다. 자유도를 가진 각 절점은 다음의 평형 조건을 만족해야 한다.

:

\Sigma \left( M^{f} + M_{member} \right) = \Sigma M_{joint}

여기서 각 기호는 다음을 의미한다.

$M_{member}$ : 부재의 재단 모멘트
$M^{f}$ : 고정단 모멘트
$M_{joint}$ : 절점에 직접 재하된 외부 모멘트

이때 모든 모멘트는 동일한 부호 규약(예: 시계방향을 양(+)으로 가정)을 따라야 한다.

예를 들어, 어떤 구조물의 절점 A, B, C에서 각각 모멘트 평형을 만족해야 한다면, 다음과 같은 방정식을 세울 수 있다. (수식은 특정 예시에 대한 값이며, 일반적인 형태는 아님)

:

\Sigma M_A = M_{AB} + M_{AB}^f = 0.4EI \theta_A + 0.2EI \theta_B - 14.7 = 0

:

\Sigma M_B = M_{BA} + M_{BA}^f + M_{BC} + M_{BC}^f = 0.2EI \theta_A + 1.2EI \theta_B + 0.4EI \theta_C - 2.033 = 0

:

\Sigma M_C = M_{CB} + M_{CB}^f + M_{CD} + M_{CD}^f = 0.4EI \theta_B + 1.2EI \theta_C - 4.167 = 0

여기서

M_{AB}

는 A절점에서 부재 AB가 받는 재단 모멘트,

M_{AB}^f

는 부재 AB의 A단에서의 고정단 모멘트,

\theta_A

는 A절점의 처짐각,

EI

는 부재의 휨 강성을 나타낸다. 다른 항들도 유사하게 정의된다. 이 연립 방정식을 풀어 각 절점의 미지 변수(처짐각 등)를 구할 수 있다.

3. 2. 전단 평형

횡방향 변위나 지점의 침하 등으로 인해 부재의 회전(현회전각)이 발생하는 구조물을 처짐각법으로 해석하는 경우, 절점 평형 방정식에 더하여 전단력의 평형 조건이 필요하다. 프레임 구조물에 현 회전이 발생하면, 추가적인 평형 조건인 전단 평형 조건을 고려해야 한다.

4. 해석 절차

처짐각법은 절점의 처짐각과 부재의 현회전각을 미지수로 하여 변위의 적합조건에 맞도록 하중을 나타낸 뒤, 힘의 평형조건을 만족시키는 해를 구하는 방법이다. 해석 결과로 직접 얻는 해는 변위이다.

예를 들어, 절점 A, B, C의 회전각 $\theta_A$ , $\theta_B$ , $\theta_C$ 을 미지수로 설정한다. 이 예제에서는 지점 침하 등으로 인한 현회전각은 없다고 가정한다.

먼저 각 부재의 고정단 모멘트를 계산한다.

: $M _{AB} ^f = - \frac{P a b^2 }{L ^2} = - \frac{10 \times 3 \times 7^2}{10^2} = -14.7 \ kN\cdot m$

: $M _{BA} ^f = \frac{P a^2 b}{L^2} = \frac{10 \times 3^2 \times 7}{10^2} = 6.3 \ kN\cdot m$

: $M _{BC} ^f = - \frac{qL^2}{12} = - \frac{1 \times 10^2}{12} = - 8.333 \ kN\cdot m$

: $M _{CB} ^f = \frac{qL^2}{12} = \frac{1 \times 10^2}{12} = 8.333 \ kN\cdot m$

: $M _{CD} ^f = - \frac{PL}{8} = - \frac{10 \times 10}{8} = -12.5 \ kN\cdot m$

: $M _{DC} ^f = \frac{PL}{8} = \frac{10 \times 10}{8} = 12.5 \ kN\cdot m$

평형 방정식을 세우고 연립하여 풀면 다음과 같은 절점 변위(회전각)를 얻는다.

: $\theta_A = \frac{40.219}{EI}$

: $\theta_B = \frac{-6.937}{EI}$

: $\theta_C = \frac{5.785}{EI}$

계산된 절점 변위를 이용하여 최종적인 재단 모멘트를 구한다.

: $M_{AB} = 0.4 \times 40.219 + 0.2 \times \left( -6.937 \right) - 14.7 = 0$

: $M_{BA} = 0.2 \times 40.219 + 0.4 \times \left( -6.937 \right) + 6.3 = 11.57$

: $M_{BC} = 0.8 \times \left( -6.937 \right) + 0.4 \times 5.785 - 8.333 = -11.57$

: $M_{CB} = 0.4 \times \left( -6.937 \right) + 0.8 \times 5.785 + 8.333 = 10.19$

: $M_{CD} = 0.4 \times 5.785 - 12.5 = -10.19$

: $M_{DC} = 0.2 \times 5.785 + 12.5 = 13.66$

5. 예제

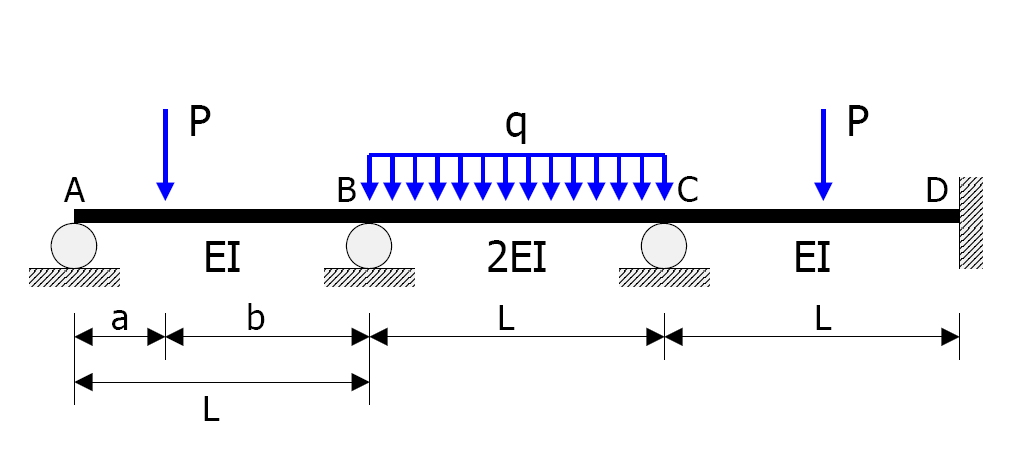
오른쪽 그림과 같은 연속보 구조물을 처짐각법으로 해석하는 예제이다.

부재 AB, BC, CD의 길이는 모두 $L = 10m$ 로 같다.
휨 강성은 각각 EI, 2EI, EI이다.
부재 AB는 지점 A로부터 $a = 3m$ 의 위치에 크기 $P = 10 \ kN$ 인 집중 하중이 작용한다.
부재 BC는 부재 전체에 걸쳐 $q = 1 \ kN/m$ 의 등분포 하중이 작용한다.
부재 CD는 중앙에 크기 $P = 10 \ kN$ 인 집중 하중이 작용한다.

계산 과정에서 시계 방향의 회전각과 모멘트를 양(+)으로 가정한다. 절점 A, B, C에서의 회전각

\theta_A

,

\theta_B

,

\theta_C

를 미지수로 간주한다. 지점 침하로 인한 부재의 상대 변위는 없다고 가정한다.

각 부재의 고정단 모멘트는 다음과 같이 계산된다.

:

M _{AB} ^f = - \frac{P a b^2 }{L ^2} = - \frac{10 \times 3 \times 7^2}{10^2} = -14.7 \mathrm{\,kN \,m}

:

M _{BA} ^f = \frac{P a^2 b}{L^2} = \frac{10 \times 3^2 \times 7}{10^2} = 6.3 \mathrm{\,kN \,m}

:

M _{BC} ^f = - \frac{qL^2}{12} = - \frac{1 \times 10^2}{12} = - 8.333 \mathrm{\,kN \,m}

:

M _{CB} ^f = \frac{qL^2}{12} = \frac{1 \times 10^2}{12} = 8.333 \mathrm{\,kN \,m}

:

M _{CD} ^f = - \frac{PL}{8} = - \frac{10 \times 10}{8} = -12.5 \mathrm{\,kN \,m}

:

M _{DC} ^f = \frac{PL}{8} = \frac{10 \times 10}{8} = 12.5 \mathrm{\,kN \,m}

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com