맨위로가기

페르미 황금률

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

페르미 황금률은 엔리코 페르미의 이름을 따서 명명되었지만, 폴 디랙이 이 공식을 유도하는 데 크게 기여했다. 이 공식은 섭동을 받는 해밀토니안의 고유 상태를 갖는 계를 기술하며, 단위 시간당 전이 확률을 계산하는 데 사용된다. 페르미 황금률은 섭동 이론을 사용하여 유도되며, 불연속 또는 연속 스펙트럼의 최종 상태를 고려한다. 이 원리는 주사 터널링 현미경, 양자 광학, 드렉스하거 실험 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

  • 섭동 이론 - 섭동 이론 (양자역학)
    섭동 이론은 양자역학에서 해밀토니안에 작은 변화가 가해졌을 때 에너지 준위와 파동 함수의 변화를 근사적으로 계산하는 방법으로, 시간 무관 및 시간 의존 섭동 이론으로 나뉘며 다양한 양자계에 적용된다.
  • 섭동 이론 - 근삿값의 순서
    근삿값의 순서는 과학 및 공학에서 현실의 값을 추정하고 설명하는 데 사용되는 개념으로, 0차, 1차, 2차 및 고차 근사를 포함하며, 테일러 급수를 활용하여 계산될 수 있고, 데이터 양과 상황에 맞는 차수 선택이 중요하다.
  • 물리학 방정식 - 슈뢰딩거 방정식
    슈뢰딩거 방정식은 양자역학에서 시스템의 시간적 변화를 기술하는 기본 방정식으로, 파동 함수에 대한 편미분 방정식이며, 시스템의 총 에너지를 나타내는 해밀토니안 연산자를 포함하고, 양자 상태를 기술하며, 다양한 양자역학적 현상을 설명하는 데 사용된다.
  • 물리학 방정식 - 맥스웰 방정식
    맥스웰 방정식은 전기장과 자기장의 상호 작용을 기술하는 네 개의 연립 편미분 방정식으로, 전자기파의 존재와 속도를 예측하여 빛이 전자기파임을 밝히고 고전 전자기학의 기본이 된다.
  • 수리물리학 - 라플라스 변환
    라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다.
  • 수리물리학 - 불확정성 원리
    불확정성 원리는 1927년 베르너 하이젠베르크가 발표한 양자역학의 기본 원리로, 입자의 위치와 운동량 등 짝을 이루는 물리량들을 동시에 정확하게 측정하는 것이 불가능하며, 두 물리량의 불확정성은 플랑크 상수에 의해 제한된다.
페르미 황금률
페르미 황금률
다른 이름페르미의 황금 규칙
분야양자역학
설명전이율을 계산하는 데 사용되는 공식
발견자엔리코 페르미
발표 년도1950년
관련 개념전이 진폭
시간 의존 섭동 이론
밀도 함수 이론
양자화학
적용 분야원자 물리학
분자 물리학
응집물질물리학
양자 광학

2. 역사적 배경

페르미 황금률은 엔리코 페르미의 이름이 붙었지만, 이 공식을 유도하는 데 대부분의 연구는 폴 디랙이 수행했다.[1] 폴 디랙은 20년 전에 상수, 섭동의 행렬 요소, 에너지 차이의 세 가지 요소로 구성된 거의 동일한 방정식을 발표했다.[2] 페르미는 이 공식의 중요성을 인정하여 "황금률 2번"이라고 불렀다.[3] 이는 어떤 과학적 발견이 실제 발견자가 아닌 다른 사람의 이름으로 불리는 스티글러의 법칙의 한 예시이다.[18]

3. 전이율과 그 유도

페르미 황금률은 초기 상태가 섭동을 받지 않은 해밀토니안의 고유 상태인 계에서, 섭동 해밀토니안의 효과를 고려하여 전이율을 계산하는 방법이다. 섭동이 시간에 무관하면 계는 초기 상태와 같은 에너지를 가진 상태로만 전이한다. 반면 섭동이 시간에 따라 각진동수(ω)로 조화 진동하면, 초기 상태와 특정 에너지 차이(ħω)를 가진 상태로 전이한다.

단위 시간당 전이 확률(Γ)은 1차 근사에서 다음과 같이 주어진다.[5][6]

:\Gamma_{i \to f} = \frac{2 \pi}{\hbar} \left| \langle f|H'|i \rangle \right|^2 \rho(E_f),

여기서 \langle f|H'|i \rangle는 섭동의 행렬 요소(브라-켓 표기법)이고, \rho(E_f)는 최종 상태의 상태 밀도이다.

이 공식은 시간에 따른 섭동 이론을 사용하여 유도되며, 측정 시간이 전이에 필요한 시간보다 훨씬 크다는 가정을 포함한다. 이 전이 확률은 "붕괴 확률"이라고도 하며, 평균 수명의 역수와 관련이 있다. 따라서 계가 초기 상태에 있을 확률은 시간에 따라 지수적으로 감소한다.

페르미 황금률은 디랙에 의해 정립되었으며,[17] 상수, 섭동의 행렬 요소, 에너지 차이 세 가지로 이루어진 동등한 공식화를 제시했다. 페르미가 이 관계식을 "두 번째 황금률"이라고 부르면서 현재의 이름이 붙여졌다.[18]

페르미 황금률은 행렬 요소의 크기만을 고려하지만, 행렬 요소의 위상에도 전이 과정에 대한 추가 정보가 포함되어 있다. 이는 전자 수송에서 반고전적인 볼츠만 방정식에서 황금률을 보완한다.[19]

섭동 해밀토니안이 시간에 주기적으로 의존하는 경우(\hat{H} = \hat{H}_0 + \hat{H}'(t), \hat{H}'(t) = \hat{H}' e^{-i \omega t}), 슈뢰딩거 방정식을 상호작용 표상으로 변환하여 1차항까지 섭동 전개하면 전이 확률을 유도할 수 있다.

시간 t에서 초기 상태 \psi(0) = \psi_\mathrm{i}에서 최종 상태 \psi_\mathrm{f}로의 전이 진폭은 다음과 같다.

:\begin{align}

\langle \psi_\mathrm{f} | \psi(t) \rangle

= -2 i e^{ i (E_\mathrm{f} - E_\mathrm{i} - \hbar \omega) t / 2 \hbar}

\frac{\langle \psi_\mathrm{f} | \hat{H'} | \psi_\mathrm{i} \rangle}{E_\mathrm{f} - E_\mathrm{i} - \hbar \omega}

\sin \frac{(E_\mathrm{f} - E_\mathrm{i} - \hbar \omega) t}{2 \hbar}

\end{align}



충분한 시간이 경과한 후의 전이 확률은 다음과 같으며,

:p_{\mathrm{f} \gets \mathrm{i}}(t)

\to \frac{2 \pi t}{\hbar} \left| \langle \psi_\mathrm{f} | \hat{H'} | \psi_\mathrm{i} \rangle \right|^2 \delta (E_\mathrm{f} - E_\mathrm{i} - \hbar \omega)

\quad (t \to \infty)

단위 시간당 전이 확률은 페르미 황금률로 주어진다.

: T_{\mathrm{f} \gets \mathrm{i}}

= \frac{2 \pi}{\hbar} \left| \langle \psi_\mathrm{f} | \hat{H'} | \psi_\mathrm{i} \rangle \right|^2

\delta(E_\mathrm{f} - E_\mathrm{i} - \hbar \omega)

3. 1. 불연속 스펙트럼의 최종 상태

최종 상태가 불연속적인 경우, 시간에 따른 슈뢰딩거 방정식을 사용하여 전이 확률 진폭을 계산할 수 있다. 우선, 섭동을 받는 계의 상태를 다음과 같이 전개한다.[7]

:|\psi(t)\rang = \sum_n a_n(t) e^{- i E_n t / \hbar} |n\rang

여기서 a_n(t)는 시간에 따라 변하는 계수이며, 디랙 그림에서 확률 진폭을 나타낸다. 이 상태는 시간에 따른 슈뢰딩거 방정식을 따르며, 해밀토니안과 상태를 전개하여 1차 근사에서 다음의 미분 방정식계를 얻는다.

:

\mathrm{i}\hbar \frac{da_k(t)}{dt} = \sum_n \langle k| H'|n\rangle a_n(t) e^{\mathrm{i}t(E_k - E_n)/\hbar}.

이 방정식은 정확하지만, 일반적으로 풀기 어렵다. 따라서 약한 일정한 섭동 H'에 대해 섭동 이론을 적용한다. t=0에서 섭동이 시작되면, H' = 0일 때 a_n(t) = \delta_{n,i}이므로, 계는 초기 상태 i에 머무른다.

k \ne i인 상태에 대해 a_k(t)는 H' \ne 0 때문에 0이 아닌 값을 가지며, 이 값들은 약한 섭동으로 인해 작다고 가정한다. 1차 보정을 위해 위 방정식에 0차 형태 a_n(t) = \delta_{n,i}를 대입하면,

:

\mathrm{i}\hbar \frac{da_k(t)}{dt} = \langle k|H'|i\rangle e^{\mathrm{i}t(E_k - E_i)/\hbar},

이 식을 적분하여 다음을 얻는다.

:

\mathrm{i}\hbar a_k(t) = \int_0^t\langle k|H'(t')|i\rangle e^{\mathrm{i}\omega_{ki} t'} dt'



여기서 \omega_{ki} \equiv (E_k - E_i)/\hbar이다. 초기 상태(i번째)에서 최종 상태(f번째)로의 전이 확률은 다음과 같이 주어진다.

:w_{fi} = |a_f(t)|^2=\frac{1}{\hbar^2} \left|\int_0^t \langle f|H'(t')|i\rangle e^{\mathrm{i}\omega_{fi} t'} dt'\right|^2

주기적인 섭동 H'(t) = Fe^{-\mathrm{i}\omega t} + F^\dagger e^{\mathrm{i}\omega t} (여기서 F는 시간에 무관한 연산자)에 대한 해는 다음과 같다.[7]

:a_f(t) = - \langle f|F|i\rangle \frac{e^{\mathrm{i}(\omega_{fi}-\omega) t}}{\hbar (\omega_{fi}-\omega)} - \langle f|F^\dagger|i\rangle \frac{e^{\mathrm{i}(\omega_{fi}+\omega) t}}{\hbar (\omega_{fi}+\omega)}.

이 식은 에너지 E_i를 갖는 초기 상태에 대해 최종 상태 에너지가 E_f-E_i \neq \pm \hbar \omega여야 유효하다. 즉, 공명 조건 근처에서 전이 확률이 크게 증가한다.

섭동 주파수가 E_k-E_n=\hbar(\omega+\varepsilon) (\varepsilon는 작은 양)인 경우, 다음과 같이 나타낼 수 있다.

:i\hbar\frac{da_k}{dt}= \langle k|F|n\rangle e^{i\varepsilon t}a_n, \quad i\hbar\frac{da_n}{dt}= \langle n|F^\dagger|k\rangle e^{-i\varepsilon t}a_k.

이 경우, 두 개의 독립적인 해는 다음과 같다.

:a_n = Ae^{ i\alpha_1 t},\, a_k=-A\hbar \alpha_1 e^{ i\alpha_1 t}/\langle n|F^\dagger|k\rangle

:a_n = Be^{-i\alpha_2 t},\, a_k= B\hbar \alpha_2 e^{-i\alpha_2 t}/\langle n|F^\dagger|k\rangle

여기서

:\alpha_1=-\frac{1}{2}\varepsilon+\Omega, \quad \alpha_2 = \frac{1}{2}\varepsilon + \Omega, \quad \Omega = \sqrt{\frac{1}{4}\varepsilon^2 + |\eta|^2}, \quad \eta = \frac{1}{\hbar}\langle k|F|n\rangle

이고 상수 A와 B는 정규화 조건에 의해 결정된다.

t=0에서 계가 |\psi_k\rang 상태에 있다면, |\psi_n\rang 상태에서 계를 발견할 확률은 다음과 같이 주어진다.

:w_{kn}=\frac

3. 2. 연속 스펙트럼의 최종 상태

연속 스펙트럼이 불연속 스펙트럼 위에 있으므로, E_f-E_i>0이며, 공명 에너지 E_i+\hbar\omega 근처에 있는 에너지 E_f가 중요한 역할을 한다. 즉, \omega_{fi} \approx \omega인 경우이다. 이 경우, a_f(t)에 대한 첫 번째 항만 고려하면 충분하다. 시간 t=0부터 섭동이 시작되었다고 가정하면, 전이 진폭은 다음과 같다.

:a_f(t) = -\frac{\mathrm{i}}{\hbar}\int_0^t\langle f|H'(t')|i\rangle e^{\mathrm{i}\omega_{fi} t'} dt' = - \langle f|F|i\rangle \frac{e^{\mathrm{i}(\omega_{fi}-\omega) t}-1}{\hbar (\omega_{fi}-\omega)}

a_f의 제곱 절댓값은 다음과 같다.

:|a_f|^2= 4 | \langle f|F|i\rangle|^2 \frac{\sin^2((\omega_{fi}-\omega)t/2)}{\hbar^2(\omega_{fi}-\omega)^2}

따라서, 큰 t에 대한 단위 시간당 전이 확률은 다음과 같다.

:\frac{dw_{fi}}{dt} = \frac{d}{dt}|a_f|^2 = \frac{2\pi}{\hbar}| \langle f|F|i\rangle|^2 \delta(E_f - E_i - \hbar\omega)

위 식의 델타 함수는 \Delta = \omega_{fi} - \omega라고 정의하면, \sin^2(\Delta t/2) / \Delta^2의 시간 미분은 \sin(\Delta t) / (2\Delta)이며, 큰 t에서 델타 함수처럼 동작한다는 사실로부터 유도된다. (싱크 함수#디랙 델타 함수와의 관계 참조)

페르미 황금률의 '일정한 붕괴율'은 방사능의 지수적 입자 붕괴 법칙의 기초가 된다.[8] 그러나 지나치게 긴 시간 동안에는 a_k(t) 항의 장기적인 증가로 인해 최저차 섭동 이론이 무효화된다.

페르미 황금률에는 행렬 요소 \langle f|H'|i \rangle의 크기만 포함되지만, 이 행렬 요소의 위상은 전이 과정에 대한 추가적인 정보를 포함한다. 이는 전자 수송에 대한 반고전적 볼츠만 방정식 접근법에서 황금률을 보완하는 식에 나타난다.[9]

일반적으로 황금률은 위와 같이 진술되고 유도되지만, 최종 상태(연속체) 파동 함수는 종종 모호하게 설명되고 올바르게 정규화되지 않는다. 연속체를 생성하기 위해서는 공간적 구속이 없어야 하며, 이는 스펙트럼을 이산화한다. 따라서 연속체 파동 함수는 무한한 범위를 가지며, 정규화 \langle f|f \rangle = \int d^3\mathbf{r} \left|f(\mathbf{r})\right|^2는 1이 아니라 무한하다. 상호 작용이 연속 상태의 에너지에 의존하지만 다른 양자수에는 의존하지 않는 경우, 에너지 \varepsilon 를 갖는 연속체 파동 함수 | \varepsilon\rangle를 \langle \varepsilon|\varepsilon ' \rangle=\delta(\varepsilon-\varepsilon ')로 써서 정규화하는 것이 일반적이다. 여기서 \delta는 디랙 델타 함수이며, 상태 밀도의 제곱근에 해당하는 인자가 |\varepsilon_i\rangle에 포함된다.[10] 이 경우, 연속체 파동 함수의 차원은 1/\sqrt{\text{[energy]}}이며, 황금률은 다음과 같다.

: \Gamma_{i \to \varepsilon_i} = \frac{2\pi}{\hbar} |\langle \varepsilon_i|H'|i\rangle|^2 .

여기서 \varepsilon_i는 불연속 상태 i와 같은 에너지를 갖는 연속 상태를 나타낸다.

4. 응용

페르미 황금률은 다양한 물리 현상에 응용된다.

주사 터널링 현미경(STM)에서 페르미 황금률은 터널링 전류를 유도하는 데 사용된다. 양자 광학에서는 두 개의 불연속적인 상태 사이의 에너지 준위 전이를 설명하는 데 사용된다.[14] 또한, 들뜬 상태의 붕괴 확률이 상태 밀도에 의존한다고 예측하는데, 이는 거울 근처의 쌍극자 붕괴율을 측정하는 드렉스하거 실험으로 확인할 수 있다.[15][16]

4. 1. 주사 터널링 현미경 (STM)

주사 터널링 현미경(Scanning tunneling microscope)에서 페르미 황금률은 터널링 전류를 유도하는 데 사용된다. 그 형태는 다음과 같다.

: w = \frac{2 \pi}{\hbar} |M|^2 \delta (E_{\psi} - E_{\chi} ),

여기서 M은 터널링 행렬 요소(tunneling matrix element)이다.

4. 2. 양자 광학

양자 광학에서 페르미 황금률은 두 개의 불연속적인 상태 사이의 에너지 준위 전이를 설명할 때 사용된다.[14] 이때 페르미 황금률은 다음과 같이 표현된다.[14]

:\Gamma_{i \to f} = \frac{2 \pi}{\hbar} \left|\langle f| H' |i \rangle\right|^2 g(\hbar\omega),

여기서 g(\hbar\omega)는 주어진 에너지에서 광자 상태의 밀도이고, \hbar\omega는 광자 에너지이며, \omega는 각진동수이다. 이러한 표현은 최종 (광자) 상태의 연속체가 존재한다는 것, 즉 허용된 광자 에너지의 범위가 연속적이라는 사실에 기반한다.[14]

4. 3. 드렉스하거 실험 (Drexhage Experiment)

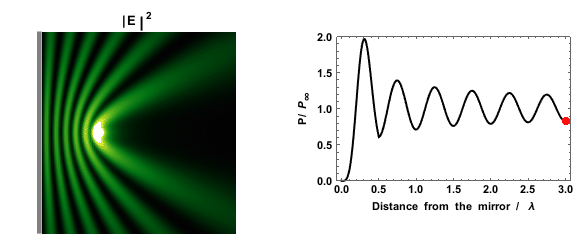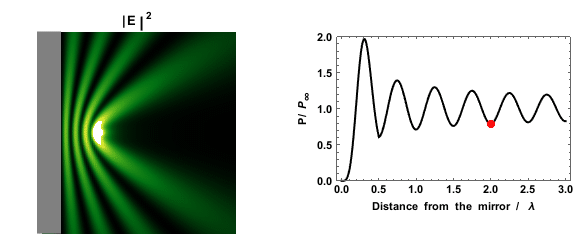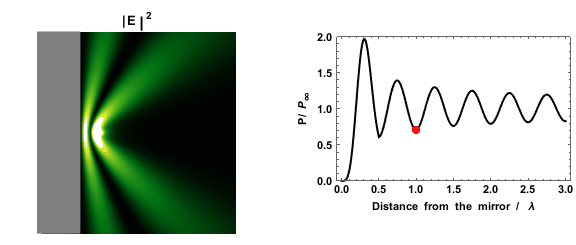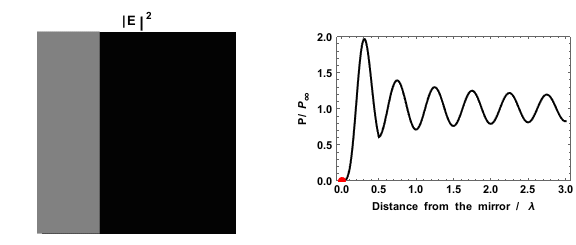
거울로부터의 거리에 따라 쌍극자의 복사 패턴과 전체 방출 전력(붕괴율에 비례)이 달라짐


페르미 황금률은 들뜬 상태가 붕괴될 확률이 상태 밀도에 의존한다고 예측한다. 이는 거울 근처의 쌍극자의 붕괴율을 측정하여 실험적으로 확인할 수 있다. 거울이 있으면 상태 밀도가 더 높거나 낮은 영역이 만들어지기 때문에 측정된 붕괴율은 거울과 쌍극자 사이의 거리에 따라 달라진다.[15][16]

참조

[1] 서적 Quantum Mechanics Prentice Hall
[2] 학술지 The Quantum Theory of Emission and Absorption of Radiation 1927-03-01
[3] 서적 Nuclear Physics University of Chicago Press
[4] 서적 Nuclear Physics University of Chicago Press
[5] 웹사이트 R Schwitters' UT Notes on Derivation http://www.ph.utexas[...]
[6] 서적 Wave Mechanics: Volume 5 of Pauli Lectures on Physics Dover Books on Physics
[7] 서적 Quantum mechanics: non-relativistic theory (Vol. 3) Elsevier
[8] 서적 Quantum Mechanics Wiley, John & Sons, Inc.
[9] 학술지 Coordinate Shift in Semiclassical Boltzmann Equation and Anomalous Hall Effect
[10] 서적 Quantum Mechanics Vol II Chapter XIII Complement D_{XIII} Wiley
[11] 서적 Quantum Mechanics of One- and Two-Electron Atoms Springer, Boston, MA
[12] 서적 Fundamentals of Semiconductors - Physics and Materials Properties Springer
[13] 학술지 Optical quantum confinement and photocatalytic properties in two-, one- and zero-dimensional nanostructures
[14] 서적 Quantum Optics: An Introduction Oxford University Press
[15] 학술지 Variation of the Fluorescence Decay Time of a Molecule in Front of a Mirror
[16] 학술지 Influence of a dielectric interface on fluorescence decay time
[17] 학술지 The Quantum Theory of Emission and Absorption of Radiation 1927-03-01
[18] 서적 Nuclear Physics University of Chicago Press
[19] 학술지 Coordinate Shift in Semiclassical Boltzmann Equation and Anomalous Hall Effect


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com